Abstract
Many calcium channels can distinguish between ions of the same charge but different size. For example, when cations are in direct competition with each other, the ryanodine receptor (RyR) calcium channel preferentially conducts smaller cations such as Li+ and Na+ over larger ones such as K+ and Cs+. Here, we analyze the physical basis for this preference using a previously established model of RyR permeation and selectivity. Like other calcium channels, RyR has four aspartate residues in its GGGIGDE selectivity filter. These aspartates have their terminal carboxyl group in the pore lumen, which take up much of the available space for permeating ions. We find that small ions are preferred by RyR because they can fit into this crowded environment more easily.
Introduction
Calcium-selective ion channels have a wide range of selectivity, permeation, and gating properties. From the selectivity and permeation point of view, there are roughly two general classes of calcium channels: 1), the surface-membrane calcium channels (e.g., L-, T-, P/Q-, and N-type channels), which tend to have a micromolar Ca2+ affinity (1,2) and relatively smaller conductance (3); and 2), the intracellular calcium channels (e.g., the ryanodine receptor (RyR) and the inositol triphosphate receptor (IP3R)), which have a much weaker millimolar Ca2+ affinity (4–7). These two calcium channel types share very little homology, but both have a mixture of four glutamates and aspartates in their selectivity filters (8–13).
While selectivity and permeation of Ca2+ is the main physiological function of these channels, monovalent cations also play an important role. For example, RyR and IP3R’s poor Ca2+ selectivity allows them to simultaneously conduct K+ countercurrent to prevent large changes in membrane potential during Ca2+ release (14,15). Nonphysiological monovalent cations are also important because by studying them, we can improve our understanding of ion channel selectivity and permeation.
Selectivity among different monovalents has become an important topic in the years since the structure of the potassium channel was published (16). The potassium channel’s physiological selectivity hinges on distinguishing between ions of different size, with one of the primary determinants being the dehydration energy difference between Na+ and K+ (17–20). Interestingly, RyR shares a relatively large homology with the potassium channel in the selectivity filter (21–24). However, there are significant differences between the two pores, namely, the eight negative charges of RyR (11–13) and the 2–3 times larger diameter of RyR (25,26). This leads to a RyR selectivity in favor of the smaller Na+ over the larger K+ (27,28) (this study), the opposite of what happens in the potassium channel. Therefore, understanding size selectivity in RyR gives us a broader picture of selectivity in all channels.
In the last few years, selectivity in calcium channels has been studied with various methods, and two distinctly different models of the selectivity filter have emerged. The model proposed by Nonner et al. (29) describes the glutamates and aspartates, as well as their negatively charged, terminal carboxyl (COO–) groups, as protruding into the lumen of the selectivity filter, whereas the model of Corry et al. (30) describes the carboxyl groups as being in the protein, outside of the permeation pathway. In the first model, the pore is a liquid-like environment because the glutamates and aspartates are flexible and so the carboxyl groups can rearrange around the permeating cations. The role of the fluctuations of the carboxyl groups is to coordinate the ions; the better the coordination, the better the selectivity. In the second model, the lumen of the selectivity filter contains only the permeating cations and the carboxyl groups cannot rearrange to screen them. Selectivity in this model is almost exclusively the result of electrostatics (30) and therefore it cannot distinguish between two ion species of the same valence (31,32). The model pore of Nonner et al. (29), however, predicts large differences in affinity between monovalent cations (28,29,33–37).
The difference in selectivity between these models of the L-type calcium channel is due to the direct (i.e., very close-range) interactions of the carboxyl groups with the permeating cations; only with the carboxyl groups in the permeation pathway does the pore have micromolar Ca2+ affinity (38). The carboxyls in the pore make a highly charged environment that attracts cations, while at the same time making a very crowded, liquid-like environment where ions must compete for space with each other and the carboxyls. In this charge/space competition (CSC) mechanism, selectivity is a balance of electrostatic and excluded-volume forces (i.e., two ions cannot overlap) (28,29,33–42).
The importance of this balance of forces has recently been studied in RyR using a Poisson-Nernst-Planck/density functional theory (PNP/DFT) model. That analysis showed the bulk of the energetics that favors Ca2+ over monovalent cations is provided by the screening of the permeant ions by the carboxyls (28). It was also found that, with all else being equal, when monovalents compete with Ca2+ for the pore, the smaller ones compete much more effectively because it is energetically easier to insert a small ion than a bigger one (28). In this work, we continue the study of selectivity in RyR by considering monovalent versus monovalent selectivity using the same RyR model.
The advantage of using this model is that it reproduces all the known experimental permeation and selectivity data of RyR from two major labs in more than 180 ionic mixtures and several mutants, including the new experiments described here (28,37,43,44). Other calcium channel models, at best, reproduce a very small amount of experimental data (30,38) and in many cases only consider ion binding in the selectivity filter, not current (29,33–36,38,40–42). The RyR model also predicted (before experiments confirmed them) all of the known anomalous mole fraction effects of RyR (28,37) and how they change with voltage and concentrations (43). In addition, the model predicted and experiments confirmed that Ca2+ selectivity of RyR actually decreases with increasing luminal Ca2+ concentration (44). Collectively, these results strongly suggest that the model captures the physics of both permeation and selectivity when one, two, or (as we show here) three cation species compete for the pore. The PNP/DFT approach has an additional advantage over the particle simulations used in the other calcium channel model: it naturally decomposes the energetics of selectivity into distinct energy terms that allow one to understand selectivity.
Using this approach, we find that there are large differences only for the nonelectrostatic energy terms; the electrostatic energies, from both the mean electrostatic potential and the ions’ ability to screen other ions, were very similar across the ion species we studied. The only large energetic difference between monovalent cations is in the term that quantifies how easily the ions fit between the carboxyl groups that are inside the selectivity filter lumen. Small ions are preferred by RyR because they fit much more easily than larger ions. While small ions can get closer to other ions to screen their charge better, this advantage is secondary.
Theory and Methods
Experiments
Single channel measurements were performed as previously described using Mueller-Rudin-type planar lipid bilayers containing a 5:3:2 mixture of bovine brain phosphatidylethanolamine, phosphatidylserine, and phosphatidylcholine (25 mg of total phospholipid/ml n-decane) (12). Proteoliposomes containing the purified RyRs were added to the cis (cytosolic) chamber of the bilayer apparatus and fused with the lipid bilayer. Single-channel currents were measured with the indicated buffer solutions on both sides of the lipid bilayer, and 2–20 μM Ca2+ and 1 mM or no ATP in the cis chamber of the bilayer apparatus. The trans (luminal) side of the bilayer was defined as ground. Electrical signals were filtered at 2 kHz, digitized at 10 kHz, and analyzed as described previously (12). All data are from the RyR2 (cardiac muscle) isoform.
Models
In this work, we used our previously published model (28) without any changes. The geometry of the pore and the locations of the amino acids used in the model are shown in Fig. 1. Further details may be found in Gillespie (28).
Figure 1.
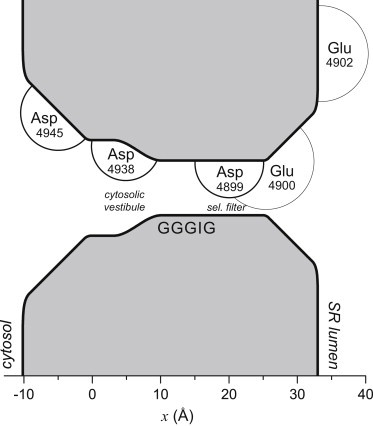
Geometry of the model RyR pore. In the experiments and calculations, the lumen of the sarcoplasmic reticulum (SR) is electrically grounded. The circle around each labeled amino acid is meant to illustrate the range of the motion of the terminal carboxyl group. Aspartates (thick circles) and glutamates (thin circles) are given a radius of 5 Å and 7 Å, respectively. Only the amino acids of one of the four identical RyR subunits is shown. Asp-4945, Asp-4938, Asp-4899, Glu-4900, and Glu-4902 are the only amino acids explicitly modeled in the theory. The GGGIG sequence (4894–4898 in the numbering) at the cytosolic end of the selectivity filter is only a reference point for readers familiar with the RyR sequence. Throughout, we use the RyR1 numbering scheme of the amino acids (34).
The ions are modeled as charged, hard spheres and their flux through the pore is described by a combination of 1D Poisson-Nernst-Planck theory and density functional theory (PNP/DFT) of fluids (45):
| (1) |
| (2) |
where ρi and μi are the concentration and electrochemical potential, respectively, of ion species i throughout the pore and baths; Ji is the flux of species i; and A(x) is the area of the equi-chemical potential surfaces that is estimated as previously described (46,47). In the pore, this corresponds to the cross-sectional area whose radius is shown in Fig. 1. The dielectric constant ε of the system is 78.4. ε0 is the permittivity of free space, k is the Boltzmann constant, and T = 298.15 K is the temperature. The functions and are the mean electrostatic potential and the diffusion coefficient of species i, respectively.
The 1D description of Eqs. 1 and 2 assumes that there are no significant radial effects on the concentrations, for example those caused by a hard-wall model of the lumen/protein interface. Such a simple ion size/rigid pore model is not used here. Instead, we assume that the walls are relatively flexible. This is supported by experiment; large cations with diameters of ∼7 Å flow through RyR with low conductance (25), but the pore can stretch to conduct the ∼10-Å-diameter neomycin with sufficiently high voltage (26).
DFT of ions
The electrochemical potentials μi are described by DFT of electrolytes (39,48), which decomposes them into four terms:
| (3) |
where is the thermal de Broglie wavelength, a constant that will drop out later since potentials are only defined up to a constant. These terms represent the different contributions to the energy required to insert an ion of species i at location x.
If ions were point charges, the ideal gas and mean electrostatic potential terms would make the familiar Poisson-Nernst-Planck theory of drift-diffusion (49,50). The size of the ions is described by the screening and excluded-volume terms. The excluded-volume term describes the energetic penalty to find space for an ion among all the other ions. It is a penalty (i.e., a positive energy) because other ions (and waters) will overlap with the new ion, which is not allowed, and therefore must move out of the way. The screening term, on the other hand, is a favorable term (i.e., a negative energy) because it measures how well ions rearrange to screen each other to minimize the instantaneous electrical potential. Roughly speaking, the more perfectly screened the ions are, the easier it is to insert another ion, and small ions do a better job of screening because they approach closer to the charge. It found that the screening term is important for RyR Ca2+ versus monovalent cation selectivity (28). It is also what gives ions an activity coefficient that is generally <1 (51).
One important aspect of all of the terms in Eq. 3 is that they are not instantaneous measures of these energies. Rather, they are long-time averages at each location, just like the concentrations on which they depend. Therefore, the mean electrostatic potential, given by the Poisson equation (Eq. 2), is the average electrostatic potential, not an instantaneous electrostatic potential. Because of this, affects all of the monovalent ion concentrations equally strongly (Eq. 3).
Some important aspects of the instantaneous electrostatic potential are lost in a mean-field theory where only the mean electrostatic potential is considered. For example, small ions will bind closer than large ions to the side chains of the aspartate and glutamate residues, and therefore they will experience a stronger electrostatic interaction and at the same time screen the charge more effectively. While mean-field theories such as PNP miss this effect, this is exactly the interaction that is captured in the screening term: averages the Coulombic interactions using the radial distribution function (which includes ion sizes) (51), whereas PNP does not.
RyR and ion dehydration
Something not included in the model is ion dehydration/resolvation. In many channels, ions must shed their hydration shells of nearest waters to enter the channel; this is an energetic penalty. They are then resolvated by the channel protein when the side chains or backbone carbonyl oxygens interact directly with the ions as the waters would have; this is generally energetically favorable because the protein side chains or carbonyl oxygens tend to be at least partially charged. Since it takes a lot of energy to dehydrate an ion, this can be a very important part of the energetics of selectivity (e.g., in the potassium channel (17–20)).
In RyR, however, empirical evidence shows that ion dehydration is not a significant component of selectivity or permeation. For example, Mg2+ permeates the RyR equally as well as Ca2+ (5). This is significant because the Gibbs energy of solvation of Mg2+ is 130 kT larger than that for Ca2+ (52). This very large difference is enough to prevent Mg2+ permeation through the L-type calcium channel (3). The fact that the large dehydration energy of Mg2+ is not a hindrance to its conduction is one indication that ion dehydration is not a major factor in RyR.
This may seem somewhat surprising given the well-established homology between the RyR selectivity filter and that of the potassium channel (21–24). RyR is, however, significantly wider; large-ion conduction experiments indicate a minimum RyR pore radius of ∼7 Å (25,27) that can stretch to 10 Å (26). This makes the need to strip waters off ions significantly less than in the much narrower potassium channel (53).
The model also lends credence to this idea. Because the model is based on physics and not data fitting of individual data points, if ion dehydration/resolvation played a major role, then the model should fail to reproduce the experimental data. Only nine data points were used to establish the model parameters, so all of the other hundreds of data points are purely the result of the physics that is in the model (28,37). By ignoring ion dehydration, we are hypothesizing that ion dehydration is much smaller than the other terms in Eq. 3, for example, that the electrostatic energy of being surrounded by carboxyl groups in the selectivity filter is much more favorable than ion dehydration is a penalty.
As described in the Introduction, this PNP/DFT model reproduces and predicts the current/voltage relations of native RyR in more than 120 previously published ionic solutions (28,37,43,44) and another 60 ionic solutions presented here, as well as the current/voltage relations of various charge-neutralizing mutations (28,37). If ion dehydration/resolvation were a significant contributor to either permeation or selectivity, one would surmise that a model that did not include this would not be able to reproduce or predict data over the wide range of conditions as this model has (e.g., micromolar to molar concentrations, ±150 mV voltage ranges, and hundreds of various mixtures of Li+, Na+, K+, Rb+, Cs+, Mg2+, and Ca2+), even if under some conditions there may have been a cancellation of errors. This indicates that the model correctly describes, at least to first order, the physics of RyR permeation and selectivity.
Energetics of selectivity
To study binding selectivity (i.e., the amount of an ion species that accumulates at one location in the pore), we consider identical baths and zero applied voltage so that the ions are in equilibrium. Then, all of the electrochemical potentials are constant everywhere and there are no ion fluxes from any species. In Eq. 3, the left-hand side is then a constant, namely, the electrochemical potential of the baths. The right-hand side contains the components of the electrochemical potential as they change with location in the baths and into the channel and selectivity filter. Because the left-hand side is constant at equilibrium, any change with location in one term on the right-hand side must be countered with a change in the opposite direction by the other terms.
We will examine how the components of the electrochemical potential compare among monovalent cations of different size. To do that, Eq. 3 for ion species i is rewritten as
| (4) |
where indicates the screening chemical potential at x minus the bath value, and similarly for the HS term. To compare two different ion species (e.g., K+ and Cs+), Eq. 4 for the two species can be subtracted:
| (5) |
Eq. 5 defines the binding selectivity (the left-hand side) in terms of the ratio of concentrations at the same location x. (In this example, a positive term favors the binding of Cs+ whereas a negative term favors K+.) To have one ion species at a higher concentration, at least one of the four components on the right-hand side must favor that ion species. In line with previous work (28,54), we call these terms advantages because they reflect which ion species has an energetic advantage for ion binding in each term. The number advantage describes which ion species has a higher bath concentration and is therefore more likely to enter the channel. The mean (i.e., long-time averaged) electrostatic advantage favors the ion species with the higher valence. Here, all of the ions are monovalents, so this term is always zero. The screening advantage favors small, high-valence ions because they neutralize the charge of other ions (screen) better than large, low-valence ions. This is one way in which ion size comes into selectivity; the other way is through the excluded-volume advantage.
This same type of analysis has been used previously to understand Ca2+ versus monovalent selectivity in RyR (28). That work showed that RyR is a Ca2+ channel because of its electrostatic advantages, both in the mean electrostatic advantage and in the screening advantage. Moreover, the model predicted that RyR calcium selectivity diminishes as [Ca2+] increases because the pore becomes more charge-neutral. This decreases the mean electrostatic advantage, whereas the screening advantage was predicted to remain unchanged. This was recently verified experimentally (44), showing that breaking the energetics into these contributions correctly captures the reasons for selectivity.
Lastly, we describe an aspect of the electrochemical potential that we will use later. Each component in Eq. 3 (except the ideal gas term) for species i depends on the concentrations of all ion species, not just species i. This means that even if an ion species is present at only trace concentrations, its electrochemical potential at any point in space is not zero; it takes energy to insert even one ion into the mix of ions already present at that point. Later, we will use this idea to compare the electrochemical potentials of three different ions (Na+, K+, and Cs+) even if only two of them (e.g., Na+ and K+) are in the baths.
Assumptions and approximations
Like all models, this model includes assumptions and approximations. They generally fall into two categories: the description of the channel and the physics used to describe the ions and the ion current.
The structure of the channel was inferred from experimental mutation data as previously described in detail (28,37). This was necessary (and continues to be so) because although a low-resolution structure of RyR has been well established for some time (21–23), a high-resolution structure has not yet been determined (55) (Montserrat Samso, Virginia Commonwealth University, personal communication, 2014), especially not for the selectivity filter. So far, structures that include the pore have a resolution of ∼10 Å and only certain isolated domains (e.g., the N-terminal domain (56–58)) have yielded high-resolution x-ray crystallographic structures. Given these limitations, the overall structure of the selectivity filter and pore shown in Fig. 1 was chosen to reflect the well-established structural homology with the potassium channel (21–24) and the fact, as described above, that the RyR pore is significantly wider, in line with a previous molecular dynamics study by Shirvanyants et al. (59). That study showed large fluctuations in the selectivity filter diameter from 0 to 6 Å. One shortcoming of our model is that these fluctuations are not included in the 1D model used here, which necessarily requires a fixed diameter.
On the physics side, the use of mean-field equations, like the PNP equations, has been criticized as not being valid in narrow channels (60). However, in a recent study by one author of Ref. 60, the opposite was found when the size of the ions was taken into account (61). Specifically, when the density profiles were taken from Brownian dynamics simulations (whose description of ions is very similar to that used here), even a 1D Nernst-Planck theory reproduced the full current-voltage curve of the Brownian dynamics simulation. Therefore, the permeation physics of the Nernst-Planck equation is probably correct because we are not considering single-file channels where conservation of momentum is important. Comparisons with simulations show that DFT correctly computes the profiles of hard-sphere ions in many systems (62,63). Moreover, our 1D DFT RyR profiles are very similar to cross-sectional averages of full 3D simulations (Dezső Boda, University of Pannonia, personal communication, 2014), so it is probable that the 1D Nernst-Planck equation used here is applicable. However, more studies on crowded channels should be done, which is work we plan to continue (64–66).
One also cannot rule out the possibility that approximations that underlie the DFT (e.g., the mean spherical approximation) may scale similarly to physics that is not included (e.g., ion dehydration), resulting in a cancellation of errors. We have tested this previously (67) and are continuing to do so.
Results
In this work, we examine the competition of monovalent cations for the RyR pore. Specifically, we analyze the energetic differences between Na+, K+, and Cs+, which differ in both size and RyR conductance; their unhydrated crystal diameters are 2.04, 2.76, and 3.40 Å (68), respectively, and their experimentally measured conductances in 250 mM symmetric conditions are 481, 800, and 519 pS (37), respectively. We also conducted experiments using Li+, which has a crystal diameter of 1.33 Å and conductance of 210 pS.
Comparing the model with experiments
The first thing to know is whether the model can successfully compute the competition between multiple monovalent cations. Previous studies using the same RyR model compared model and experimental results when two cation species competed for the pore, but only under a limited set of conditions. Specifically, they considered bi-ionic conditions and two mole fraction experiments where the relative concentrations of two cation species was changed (28,37). In Fig. 2, we show more comparisons of the model with experiments. For all of the results shown in the figure (described below), none of the previously published parameters of the model (28) were changed in any way.
Figure 2.
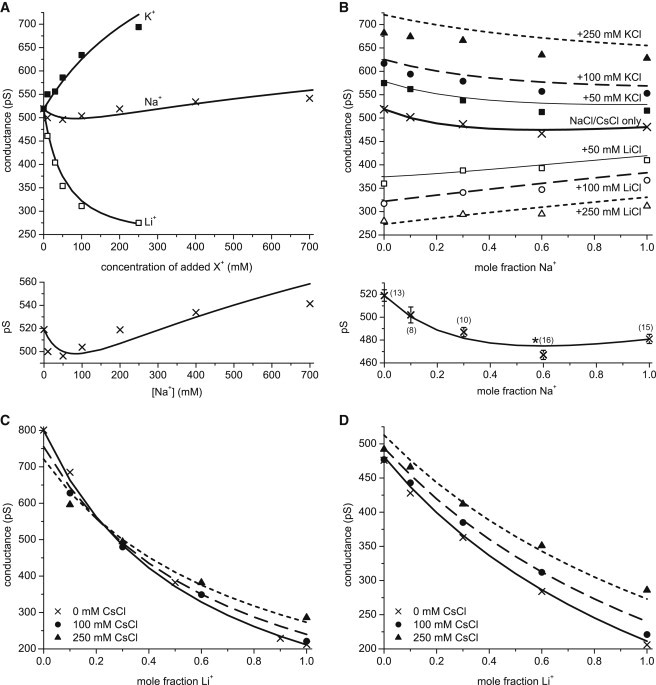
(A–D) Comparison of the model with experiments in which two (A) or three (B–D) monovalent cations compete for the pore. (A) Salting-out experiment in which XCl is added to 250 mM CsCl. Conductance is plotted as [X+] is changed for X+ = Li+ (□), Na+ (×), and K+ (▪). Below the main figure, the Na+ curve (×) is redrawn on a different scale to show its minimum. (B) Two sets of experiments in which Na+, Cs+, and Li+ compete for the pore or Na+, Cs+, and K+ compete for pore while all three ion species’ concentrations are changed. The mole fraction of Na+ is changed as [Na+] + [Cs+] is constant at 250 mM (× and thick solid line). For the other curves, 50 mM (box symbols), 100 mM (circles), or 250 mM (triangles) of either Li+ (open symbols) or K+ (solid symbols) is in the bath in addition to the Na+/Cs+ mixture. The error between theory and experiment is largest for the top dotted line, but the relative error for that line is always less than 6%. Below the main figure, the Na+ curve (×) is redrawn on a different scale to show its minimum. It also shows the number of recordings in parentheses and error bars. The point at mole fraction 0.6 was shown earlier to be statistically significantly smaller than its two neighbors (denoted with ∗), experimentally verifying the minimum. (C) Li+, K+, and Cs+ compete for the pore while all three ion species’ concentrations are changed. The mole fraction of Li+ is changed as [Li+] + [K+] is constant at 250 mM (× and solid line). For the other curves, 100 mM (●) or 250 mM (▲) of Cs+ is in the bath in addition to the Li+/K+ mixture. (D) Li+, Na+, and Cs+ compete for the pore while all three ion species’ concentrations are changed. The mole fraction of Li+ is changed as [Li+] + [Na+] is constant at 250 mM (× and solid line). For the other curves, 100 mM (●) or 250 mM (▲) of Cs+ is in the bath in addition to the Li+/Na+ mixture. In all panels, both the cytosolic and luminal baths are identical. All standard error bars are approximately the size of the symbol or smaller.
One kind of experiment we conducted was a salting-out experiment in which [CsCl] was kept at 250 mM while more and more LiCl, NaCl, or KCl was added to the baths. This is the experiment shown in Fig. 2 A. Not only does the model reproduce the large changes in conductance when Li+ or K+ are added, but the model also reproduces the minimum in the conductance when Na+ is added to the Cs+. This minimum is similar to the anomalous mole fraction effect (AMFE) that was predicted by the model for this mixture of these two ion species (37), shown as the thick solid line in Fig. 2 B. Both of these curves are redrawn below the main graphs in Fig. 2, A and B, to explicitly show their minima.
In Fig. 2, B–D, three monovalents are competing for the pore. The model predicts all of the features of the experimental results. For example, the Na+/Cs+ AMFE (Fig. 2 B, thick solid line) disappears when either Li+ or K+ is present in addition to the Na+/Cs+ mixture (Fig. 2 B, box symbols). Also, the model reproduces the crossing of the curves in Fig. 2 C and the crossover concentration. The relative error between the model and experiments is always less than 6% when three cations are competing for the pore.
All experiments were done after the calculations were performed. Therefore, the curves shown in the Fig. 2 are predictions of the model based on the physics of ion permeation and selectivity contained in the model. While one can never eliminate the possibility of canceling errors, one can infer that if the physics in the model is wrong (e.g., if ion dehydration plays a major role or if drift-diffusion does not correctly describe ion permeation), then the model should fail to reproduce experiments. Fig. 2 shows that the model seems to get the proportions of the three cations in the pore correct, which would not be possible if many of the energies were several kT off. Given how well the model predicted these challenging and nonlinear results, we will now use the model to analyze how RyR selects among monovalent cations of different sizes.
One cation species competing for the pore
To start the analysis of selectivity, let us first consider the concentration profiles of the individual ions when they are not competing with each other for the pore, that is, when there is only one cation species in the baths. This is shown in Fig. 3 A for 250 mM symmetric conditions.
Figure 3.
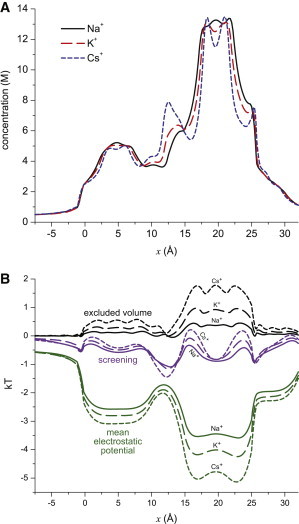
(A) Concentration profiles throughout the pore of Na+ (solid, black), K+ (long-dashed, red), and Cs+ (dotted, blue). For each curve, XCl (X = Na, K, or Cs) is at 250 mM in both baths and the other two cations are not represent. (B) Profiles of the terms in Eq. 4: excluded volume (black), screening (purple), and mean electrostatic potential (green). Each group has a curve for the three cations: Na+ (solid), K+ (long-dashed), and Cs+ (dotted). To see this figure in color, go online.
Overall, the profiles are very similar. They reach a maximum of ∼13 M in the selectivity filter where the protein charge is the highest. Other local bumps in concentration of ∼5 M occur near the other charged amino acids (shown in Fig. 1). All of the ions have the same concentration in the charged regions because the negative charges of the amino acids must be neutralized as much as possible. As previously shown, there are always approximately three monovalents in the filter (37).
A more nuanced examination of the profiles shows that the larger the ion, the more oscillations there are. Cs+, especially, has two distinct peaks in the selectivity filter (between x = 15 Å and 25 Å) and another on the cytosolic side of the filter (between x = 10 Å and 15 Å). This is a commonly found feature of large ions. In regions where ions must be present to neutralize a charge, their large size prevents other ions from being near them. This results in distinct layers of ions, seen in the profiles as peaks of high concentration and troughs of low concentration (69–71).
The idea that it is more difficult for large ions to find space in regions crowded with charged amino acid groups (the COO– terminal groups of the aspartates and glutamates) and other ions is reflected in the energetics. This is shown in Fig. 3 B, where the excluded volume, screening, and mean electrostatic potential terms from Eq. 4 are plotted.
For all of the ions, the excluded volume term is positive because the pore is more crowded than the bath. Therefore, it is more difficult for the ions to find space in the pore than in the bath, resulting in an energetic penalty (a positive energy in Fig. 3 B). Conversely, because the pore is charged, there is a negative electrostatic potential pulling the cations in. Similarly, screening is easier when more negative charges are around, and thus the screening term is negative (favoring ions accumulating in the pore).
The biggest difference among the three cations is in the excluded volume and mean electrostatic potential terms; the differences in the screening term are relatively small in comparison. In the excluded volume term, the largest ion (Cs+) has the largest energetic penalty, as expected, whereas the smallest ion (Na+) barely has any excluded volume penalty.
Since all of the ions have roughly the same concentrations throughout the pore as they try to neutralize the protein charge, it follows from Eq. 4 that any differences between the cations in one energetic term must be counteracted by another term. In this case, the difference in the excluded volume terms is made up by the mean electrostatic potential. Specifically, because the large Cs+ has more difficulty in finding space, a larger (more negative) electrostatic potential is necessary to pull in sufficient numbers of Cs+.
Two and three cation species competing for the pore
Now, let us examine what occurs when the ions compete with each other for the pore. Fig. 4 shows the concentration profiles for the three cations as the bath K+ concentration is increased from 0 mM (A) to 125 mM (B) and 250 mM (C) whereas the Na+ and Cs+ concentrations remain constant at 125 mM each.
Figure 4.
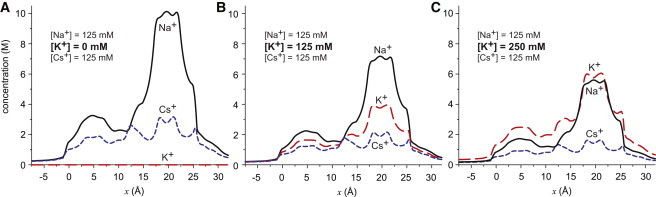
The concentration profiles throughout the pore of Na+ (solid, black), K+ (long-dashed, red), and Cs+ (dotted, blue) as [K+] in both baths is increased from 0 mM (left) to 125 mM (middle) to 250 mM (right). In all panels, [Na+] and [Cs+] are 125 mM. To see this figure in color, go online.
In the absence of K+, only Na+ and Cs+ are competing for the pore, and even though they are at the same concentration in the baths, there is a large discrepancy in their concentrations in the pore; there are far more Na+ than Cs+ (Fig. 4 A). This is also true when all three cations have the same bath concentration (Fig. 4 B); the ions’ concentrations are inversely related to their size. In fact, only when [K+] is twice [Na+] is the K+ concentration in the selectivity filter the same as the Na+ concentration (Fig. 4 C).
The energetic origin of this difference is shown in Fig. 5. There, the excluded-volume and screening terms of Eq. 4 are shown for all six mixtures of cations examined so far in Figs. 3 A and 4. In this case, only these two terms are shown because now we want to consider the differences in energetics between ion species, as in Eq. 5. Since all of the ions have the same charge, their mean electrostatic potential is the same in each experiment. Fig. 5 A shows the profiles along the pore of the two terms, whereas Fig. 5 B shows the values in the middle of the selectivity filter for individual experiments.
Figure 5.
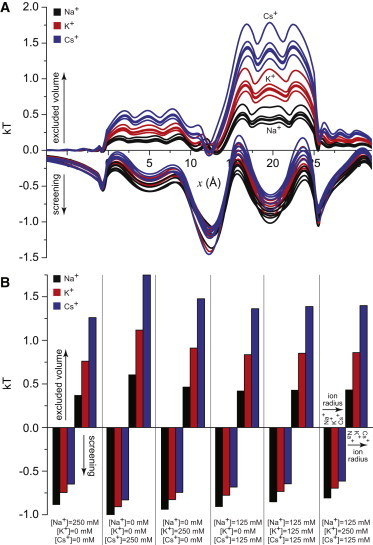
(A) Profiles of the excluded-volume and screening terms in Eq. 4 for Na+ (black), K+ (red), and Cs+ (blue) for the six conditions whose concentration profiles are shown in Figs. 3A and 4 (enumerated at the bottom of panel B). The group of lines for the excluded-volume term is positive, whereas the group for the screening term is negative. (B) Bar graph of the values of the lines in panel A in the middle of the selectivity filter (x = 20 Å). To see this figure in color, go online.
The aggregate results of Fig. 5 A show how the excluded-volume and screening terms behave in general. Specifically, it can be seen that the screening terms are approximately the same for all cations under all conditions. This is significant because smaller ions are better screeners, something that usually gives them an energetic advantage. However, here this advantage is relatively small compared to the excluded-volume term. Unlike the screening term, this term stratifies into three layers, one for each cation, indicating significant differences among the ions. Collectively, this shows that the only substantive difference between the cations is how their size makes it difficult for them to find space, rather than how their size makes it difficult to screen; this screening effect is secondary.
This is borne out in the results of the individual experiments shown in Fig. 5 B. In each case, the smaller ions are marginally better screeners, but more importantly, they have a significantly smaller energetic penalty for finding space in the selectivity filter. Specifically, the screening advantage of the small Na+ over the large Cs+ is always <0.25 kT. This is about five times larger than bulk, indicating that Na+ has a significant increase in screening ability because its charge can get closer to the negative carboxyl groups. However, its excluded volume advantage is consistently larger at ∼1 kT. These energetic differences may seem small, but the ratio of Na+ to Cs+ concentration is the exponential of this difference when these two ions compete head to head, creating an ∼3.5-fold difference in concentration in the selectivity filter (Fig. 4).
Discussion
Whether an ion channel spans intra- or extracellular membranes, it faces a sea of ions from which it must pick ions to conduct. The atomic cations tend to be monovalent (Na+ and K+) or divalent (Ca2+ and Mg2+) and so a channel must be able to select among ions of the same charge whose main difference is size. Many monovalent cation-selective channels, such as the neuronal sodium and potassium channels, exclude essentially all other physiological ions; their selectivity is for their namesake ion only (72). Similarly, many extracellular calcium channels have such high Ca2+ affinity that they exclude virtually all other ions under physiological conditions, even if they do conduct monovalent cations in the absence of Ca2+ (3,27).
Intracellular calcium channels like RyR and IP3R offer a more nuanced view of size selectivity. They conduct both monovalent and divalent cations, even in mixtures. Both RyR and IP3R have a Ca2+ to K+ permeability ratio of only ∼7, and both conduct Mg2+ (5,6). In fact, the conductance of K+ and Mg2+ at the same time as Ca2+ is important for their physiological roles in intracellular calcium release (14,15,44). Moreover, these channels can distinguish between monovalents of different size, preferring small ones to large ones (27).
This can be seen, for example, in experiments with RyR where Ca2+ was added to symmetric 100 mM NaCl and separately to 100 mM CsCl (28). Individually, Na+ and Cs+ have approximately the same conductance through RyR (480 and 520 pS, respectively, as shown in Fig. 2 B), so there is little difference in how fast the ions move through the channel. However, only 10 μM Ca2+ significantly affects Cs+ current, while ten times more is needed to affect Na+ current (28). Viewed in terms of ion competition for the pore, Cs+ is more easily displaced by Ca2+ than Na+. Consistent with this idea, the block of these monovalent cation currents by Ca2+ was significantly weaker with Na+ (28) and virtually nonexistent with the smaller Li+ (43).
In RyR experiments involving only combinations of monovalent cations under bi-ionic conditions, there is consistently a current from the small cation at zero applied potential (73). In other words, even though there are equal concentrations of, say, K+ on one side of the channel and Cs+ on the other, there is a net K+ current unless a voltage is applied that opposes K+ movement. With Li+ instead of Cs+, Li+ current flows. In both cases, it is the smaller cation that is favored. Also, as shown in Fig. 2 A, the addition of Li+ to Cs+ produces a much steeper change in conductance than the addition of K+, which is larger than Li+, suggesting that small ions more easily displace larger ones.
By what mechanism do smaller cations displace larger ones? To illustrate, consider the addition of Na+ to 250 mM Cs+. For reference, the energetics profiles of Cs+ in the absence of Na+ are shown in Fig. 3 B. Initially, at very low [Na+], very few Na+ are present in any part of the channel (e.g., the selectivity filter or the cytosolic vestibule). As [Na+] increases, more Na+ are drawn in by the electrostatic potential. This mean electrostatic potential, however, applies equally strongly to both the Na+ and Cs+ ions, and therefore this force will not favor one ion species over the other (it disappears in Eq. 5).
The one difference between these ion species is that Na+ has a crystal diameter that is 1.36 Å smaller than that of the Cs+ (68) and therefore has only 18.2% the volume of Cs+. The smaller radius allows the charge of the Na+ to get closer to another charge and therefore screen it better. This difference in the instantaneous electrostatic potential felt by Na+ (compared with Cs+) gives Na+ an advantage in the SC term of Eq. 5. Moreover, the smaller volume allows the Na+ to squeeze into a crowded space more easily. This gives it an even larger advantage in the HS term of Eq. 5. To understand how these terms change as the [Na+] increases continuously, we can also look at the ratio of the Na+ and Cs+ concentrations in different parts of the channel (Fig. 6). Specifically, we consider crowded and relatively uncrowded parts of the channel, namely, the selectivity filter and the cytosolic vestibule (Fig. 1).
Figure 6.
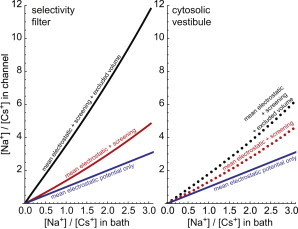
Ratio of Na+ to Cs+ concentrations in the selectivity filter (solid lines) and in the cytosolic vestibule (symbols) as a function of their bath concentration ratio. The effect of the screening advantage (SC) is shown in red and the effect of the excluded-volume term (HS) is shown in black. The blue line, shown for reference, is the bath concentration ratio. To see this figure in color, go online.
The blue line in Fig. 6 depicts what would happen if there were no differences between Na+ and Cs+, for example, if electrostatic forces dominated as in the model of Corry et al. (30). In that case, the concentration ratios in each part of the channel would be the same as in the baths; only the number advantage term in the Eq. 5 would matter. However, both the excluded volume and screening advantages of Na+ affect the final Na+ to Cs+ ratios. Specifically, in Fig. 6, the red line/symbols show the effect of having only the screening term and ignoring the excluded-volume term, while the black line/symbols include the effects of both the excluded-volume and screening terms.
In both the crowded selectivity filter (lines in Fig. 6) and the much less crowded vestibule (symbols), the screening term favors Na+; the red line and symbols in Fig. 6 are above the blue line. Moreover, the screening is almost identical in both parts of the channel; the red line and red symbols are virtually the same. This means that the screening is more or less independent of crowding. On the other hand, the excluded-volume term favors Na+ a lot more in the selectivity filter than in the vestibule; the black line and symbols in Fig. 6 are very different. This means that the ability to find space in the selectivity filter crowded with three permeating ions and eight oxygens leads to large discrimination between Na+ and Cs+. Put another way, in the densely packed selectivity filter, Na+ having a much smaller volume is a substantial advantage over Cs+, whereas in the less crowded vestibule this is less so.
Overall, the same conclusions hold for all combinations of different monovalent cations (data not shown). The larger the size difference between these ions, the more the smaller one is favored in the selectivity filter because it can find space in the selectivity filter more easily, and not because it screens the carboxyl groups of the channel protein better. This preferential accumulation of small ions in the selectivity filter is then reflected in the current because the selectivity filter is the bottleneck for permeation. This makes reproducing the experimental results in Fig. 2 significant, because it requires the model to compute the correct proportions of three species, something that has not been done by other models (30).
The fact that RyR by and large selects monovalent cations by size (27) is due to both this mechanism and RyR’s apparent small dehydration/resolvation penalty for ions, unlike the much narrower potassium channel. This probably makes RyR relatively unique among selective ion channels, since sodium, potassium, and other calcium channels tend to be narrow compared to nonselective channels like α-hemolysin. RyR is wide enough to conduct a large current, but still narrow enough to have substantial Ca2+ selectivity (albeit much weaker compared to the L-type calcium channel).
In channels where ion dehydration/resolvation is important, the selectivity sequence will not be smallest to largest. Because it is significantly easier to strip waters off a large ion than a small one, channels in which this is important can have a selectivity sequence of largest to smallest. Therefore, crowded channels are quite likely to have a range of very different selectivity sequences because each will balance small ion selectivity based on finding space with the penalty for ion dehydration in a different way. This was recently explored in a study that showed that almost all Eisenman selectivity sequences were possible, with the addition of several new ones (74). RyR is then very useful because it allows one to strip away the competing factor of ion dehydration and understand the physics of a relatively simpler system.
Conclusions
Experiments show that RyR can distinguish among many kinds of monovalent cations by size. Here, we used a model of RyR permeation and selectivity to understand why this happens, and found that it occurs because the selectivity filter has much of the lumen taken up by amino acid groups from the protein and the smaller ions fit better. Other kinds of calcium channels, as well as many other channel types, can also distinguish between ions of the same charge but different size. Therefore, this study may also help to illuminate the physics of selectivity and permeation in those channels.
Acknowledgments
D.G. was supported by NIH grant R01-AR054098 (Michael Fill, principal investigator). G.M. was supported by NIH grants AR 018687 and HL 073051.
References
- 1.Almers W., McCleskey E.W., Palade P.T. A non-selective cation conductance in frog muscle membrane blocked by micromolar external calcium ions. J. Physiol. 1984;353:565–583. doi: 10.1113/jphysiol.1984.sp015351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Almers W., McCleskey E.W. Non-selective conductance in calcium channels of frog muscle: calcium selectivity in a single-file pore. J. Physiol. 1984;353:585–608. doi: 10.1113/jphysiol.1984.sp015352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hess P., Lansman J.B., Tsien R.W. Calcium channel selectivity for divalent and monovalent cations. Voltage and concentration dependence of single channel current in ventricular heart cells. J. Gen. Physiol. 1986;88:293–319. doi: 10.1085/jgp.88.3.293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Smith J.S., Coronado R., Meissner G. Sarcoplasmic reticulum contains adenine nucleotide-activated calcium channels. Nature. 1985;316:446–449. doi: 10.1038/316446a0. [DOI] [PubMed] [Google Scholar]
- 5.Tinker A., Williams A.J. Divalent cation conduction in the ryanodine receptor channel of sheep cardiac muscle sarcoplasmic reticulum. J. Gen. Physiol. 1992;100:479–493. doi: 10.1085/jgp.100.3.479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bezprozvanny I., Ehrlich B.E. InsP3 receptor: functional properties and regulation. In: Peracchia C., editor. Handbook of Membrane Channels. Academic Press; New York: 1994. pp. 511–526. [Google Scholar]
- 7.Ramos-Franco J., Galvan D., Fill M. Location of the permeation pathway in the recombinant type 1 inositol 1,4,5-trisphosphate receptor. J. Gen. Physiol. 1999;114:243–250. doi: 10.1085/jgp.114.2.243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang J., Ellinor P.T., Tsien R.W. Molecular determinants of Ca2+ selectivity and ion permeation in L-type Ca2+ channels. Nature. 1993;366:158–161. doi: 10.1038/366158a0. [DOI] [PubMed] [Google Scholar]
- 9.Ellinor P.T., Yang J., Tsien R.W. Ca2+ channel selectivity at a single locus for high-affinity Ca2+ interactions. Neuron. 1995;15:1121–1132. doi: 10.1016/0896-6273(95)90100-0. [DOI] [PubMed] [Google Scholar]
- 10.Talavera K., Staes M., Nilius B. Aspartate residues of the Glu-Glu-Asp-Asp (EEDD) pore locus control selectivity and permeation of the T-type Ca(2+) channel α(1G) J. Biol. Chem. 2001;276:45628–45635. doi: 10.1074/jbc.M103047200. [DOI] [PubMed] [Google Scholar]
- 11.Gao L., Balshaw D., Meissner G. Evidence for a role of the lumenal M3-M4 loop in skeletal muscle Ca(2+) release channel (ryanodine receptor) activity and conductance. Biophys. J. 2000;79:828–840. doi: 10.1016/S0006-3495(00)76339-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang Y., Xu L., Meissner G. Probing the role of negatively charged amino acid residues in ion permeation of skeletal muscle ryanodine receptor. Biophys. J. 2005;89:256–265. doi: 10.1529/biophysj.104.056002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xu L., Wang Y., Meissner G. Two rings of negative charges in the cytosolic vestibule of type-1 ryanodine receptor modulate ion fluxes. Biophys. J. 2006;90:443–453. doi: 10.1529/biophysj.105.072538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gillespie D., Fill M. Intracellular calcium release channels mediate their own countercurrent: the ryanodine receptor case study. Biophys. J. 2008;95:3706–3714. doi: 10.1529/biophysj.108.131987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guo T., Nani A., Fill M. Sarcoplasmic reticulum K(+) (TRIC) channel does not carry essential countercurrent during Ca(2+) release. Biophys. J. 2013;105:1151–1160. doi: 10.1016/j.bpj.2013.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Doyle D.A., Morais Cabral J., MacKinnon R. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- 17.Varma S., Rempe S.B. Tuning ion coordination architectures to enable selective partitioning. Biophys. J. 2007;93:1093–1099. doi: 10.1529/biophysj.107.107482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Varma S., Sabo D., Rempe S.B. K+/Na+ selectivity in K channels and valinomycin: over-coordination versus cavity-size constraints. J. Mol. Biol. 2008;376:13–22. doi: 10.1016/j.jmb.2007.11.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Varma S., Rogers D.M., Rempe S.B. Perspectives on: ion selectivity: design principles for K+ selectivity in membrane transport. J. Gen. Physiol. 2011;137:479–488. doi: 10.1085/jgp.201010579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Noskov S.Y., Roux B. Importance of hydration and dynamics on the selectivity of the KcsA and NaK channels. J. Gen. Physiol. 2007;129:135–143. doi: 10.1085/jgp.200609633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ludtke S.J., Serysheva I.I., Chiu W. The pore structure of the closed RyR1 channel. Structure. 2005;13:1203–1211. doi: 10.1016/j.str.2005.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Samsó M., Wagenknecht T., Allen P.D. Internal structure and visualization of transmembrane domains of the RyR1 calcium release channel by cryo-EM. Nat. Struct. Mol. Biol. 2005;12:539–544. doi: 10.1038/nsmb938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Samsó M., Feng W., Allen P.D. Coordinated movement of cytoplasmic and transmembrane domains of RyR1 upon gating. PLoS Biol. 2009;7:e85. doi: 10.1371/journal.pbio.1000085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ramachandran S., Chakraborty A., Meissner G. Structural determinants of skeletal muscle ryanodine receptor gating. J. Biol. Chem. 2013;288:6154–6165. doi: 10.1074/jbc.M112.433789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tinker A., Williams A.J. Probing the structure of the conduction pathway of the sheep cardiac sarcoplasmic reticulum calcium-release channel with permeant and impermeant organic cations. J. Gen. Physiol. 1993;102:1107–1129. doi: 10.1085/jgp.102.6.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mead F., Williams A.J. Block of the ryanodine receptor channel by neomycin is relieved at high holding potentials. Biophys. J. 2002;82:1953–1963. doi: 10.1016/S0006-3495(02)75544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lindsay A.R., Manning S.D., Williams A.J. Monovalent cation conductance in the ryanodine receptor-channel of sheep cardiac muscle sarcoplasmic reticulum. J. Physiol. 1991;439:463–480. doi: 10.1113/jphysiol.1991.sp018676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gillespie D. Energetics of divalent selectivity in a calcium channel: the ryanodine receptor case study. Biophys. J. 2008;94:1169–1184. doi: 10.1529/biophysj.107.116798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nonner W., Catacuzzeno L., Eisenberg B. Binding and selectivity in L-type calcium channels: a mean spherical approximation. Biophys. J. 2000;79:1976–1992. doi: 10.1016/S0006-3495(00)76446-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Corry B., Allen T.W., Chung S.-H. Mechanisms of permeation and selectivity in calcium channels. Biophys. J. 2001;80:195–214. doi: 10.1016/S0006-3495(01)76007-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Corry B., Vora T., Chung S.-H. Electrostatic basis of valence selectivity in cationic channels. Biochim. Biophys. Acta. 2005;1711:72–86. doi: 10.1016/j.bbamem.2005.03.002. [DOI] [PubMed] [Google Scholar]
- 32.Chung S.-H., Corry B. Three computational methods for studying permeation, selectivity and dynamics in biological ion channels. Soft Matter. 2005;1:417–427. doi: 10.1039/b512455g. [DOI] [PubMed] [Google Scholar]
- 33.Nonner W., Gillespie D., Eisenberg B. Ion accumulation in a biological calcium channel: effects of solvent and confining pressure. J. Phys. Chem. B. 2001;105:6427–6436. [Google Scholar]
- 34.Boda D., Busath D.D., Sokołowski S. Monte Carlo simulations of the mechanism of channel selectivity: the competition between volume exclusion and charge neutrality. J. Phys. Chem. B. 2000;104:8903–8910. [Google Scholar]
- 35.Boda D., Henderson D., Busath D.D. Monte Carlo study of the effect of ion and channel size on the selectivity of a model calcium channel. J. Phys. Chem. B. 2001;105:11574–11577. [Google Scholar]
- 36.Boda D., Henderson D., Busath D.D. Monte Carlo study of the selectivity of calcium channels: improved geometry. Mol. Phys. 2002;100:2361–2368. [Google Scholar]
- 37.Gillespie D., Xu L., Meissner G. (De)constructing the ryanodine receptor: modeling ion permeation and selectivity of the calcium release channel. J. Phys. Chem. B. 2005;109:15598–15610. doi: 10.1021/jp052471j. [DOI] [PubMed] [Google Scholar]
- 38.Boda D., Nonner W., Gillespie D. Volume exclusion in calcium selective channels. Biophys. J. 2008;94:3486–3496. doi: 10.1529/biophysj.107.122796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gillespie D., Nonner W., Eisenberg R.S. Coupling Poisson-Nernst-Planck and density functional theory to calculate ion flux. J. Phys. Condens. Matter. 2002;14:12129–12145. [Google Scholar]
- 40.Boda D., Valiskó M., Gillespie D. The effect of protein dielectric coefficient on the ionic selectivity of a calcium channel. J. Chem. Phys. 2006;125:34901. doi: 10.1063/1.2212423. [DOI] [PubMed] [Google Scholar]
- 41.Boda D., Valiskó M., Gillespie D. Combined effect of pore radius and protein dielectric coefficient on the selectivity of a calcium channel. Phys. Rev. Lett. 2007;98:168102. doi: 10.1103/PhysRevLett.98.168102. [DOI] [PubMed] [Google Scholar]
- 42.Boda D., Nonner W., Gillespie D. Steric selectivity in Na channels arising from protein polarization and mobile side chains. Biophys. J. 2007;93:1960–1980. doi: 10.1529/biophysj.107.105478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gillespie D., Giri J., Fill M. Reinterpreting the anomalous mole fraction effect: the ryanodine receptor case study. Biophys. J. 2009;97:2212–2221. doi: 10.1016/j.bpj.2009.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gillespie D., Chen H., Fill M. Is ryanodine receptor a calcium or magnesium channel? Roles of K+ and Mg2+ during Ca2+ release. Cell Calcium. 2012;51:427–433. doi: 10.1016/j.ceca.2012.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Evans R. Density functionals in the theory of nonuniform fluids. In: Henderson D., editor. Fundamentals of Inhomogeneous Fluids. Marcel Dekker; New York: 1992. pp. 85–176. [Google Scholar]
- 46.Nonner W., Eisenberg B. Ion permeation and glutamate residues linked by Poisson-Nernst-Planck theory in L-type calcium channels. Biophys. J. 1998;75:1287–1305. doi: 10.1016/S0006-3495(98)74048-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gillespie D. Rush University; Chicago, IL: 1999. A Singular Perturbation Analysis of the Poisson-Nernst-Planck System: Applications to Ionic Channels. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gillespie D., Nonner W., Eisenberg R.S. Density functional theory of charged, hard-sphere fluids. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;68:031503. doi: 10.1103/PhysRevE.68.031503. [DOI] [PubMed] [Google Scholar]
- 49.Chen D., Lear J., Eisenberg B. Permeation through an open channel: Poisson-Nernst-Planck theory of a synthetic ionic channel. Biophys. J. 1997;72:97–116. doi: 10.1016/S0006-3495(97)78650-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kurnikova M.G., Coalson R.D., Nitzan A. A lattice relaxation algorithm for three-dimensional Poisson-Nernst-Planck theory with application to ion transport through the gramicidin A channel. Biophys. J. 1999;76:642–656. doi: 10.1016/S0006-3495(99)77232-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Barthel J.M.G., Krienke H., Kunz W. Springer; New York: 1998. Physical Chemistry of Electrolyte Solutions: Modern Aspects. [Google Scholar]
- 52.Fawcett W.R. Thermodynamic parameters for the solvation of monatomic ions in water. J. Phys. Chem. B. 1999;103:11181–11185. [Google Scholar]
- 53.Lipkind G.M., Fozzard H.A. KcsA crystal structure as framework for a molecular model of the Na(+) channel pore. Biochemistry. 2000;39:8161–8170. doi: 10.1021/bi000486w. [DOI] [PubMed] [Google Scholar]
- 54.Boda D., Giri J., Gillespie D. Analyzing the components of the free-energy landscape in a calcium selective ion channel by Widom’s particle insertion method. J. Chem. Phys. 2011;134:055102. doi: 10.1063/1.3532937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ludtke S.J., Serysheva I.I. Single-particle cryo-EM of calcium release channels: structural validation. Curr. Opin. Struct. Biol. 2013;23:755–762. doi: 10.1016/j.sbi.2013.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lobo P.A., Van Petegem F. Crystal structures of the N-terminal domains of cardiac and skeletal muscle ryanodine receptors: insights into disease mutations. Structure. 2009;17:1505–1514. doi: 10.1016/j.str.2009.08.016. [DOI] [PubMed] [Google Scholar]
- 57.Tung C.-C., Lobo P.A., Van Petegem F. The amino-terminal disease hotspot of ryanodine receptors forms a cytoplasmic vestibule. Nature. 2010;468:585–588. doi: 10.1038/nature09471. [DOI] [PubMed] [Google Scholar]
- 58.Kimlicka L., Lau K., Van Petegem F. Disease mutations in the ryanodine receptor N-terminal region couple to a mobile intersubunit interface. Nat. Commun. 2013;4:1506. doi: 10.1038/ncomms2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Shirvanyants D., Ramachandran S., Dokholyan N.V. Pore dynamics and conductance of RyR1 transmembrane domain. Biophys. J. 2014;106:2375–2384. doi: 10.1016/j.bpj.2014.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Corry B., Kuyucak S., Chung S.-H. Tests of continuum theories as models of ion channels. II. Poisson-Nernst-Planck theory versus Brownian dynamics. Biophys. J. 2000;78:2364–2381. doi: 10.1016/S0006-3495(00)76781-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Song C., Corry B. Testing the applicability of Nernst-Planck theory in ion channels: comparisons with Brownian dynamics simulations. PLoS ONE. 2011;6:e21204. doi: 10.1371/journal.pone.0021204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gillespie D., Valiskó M., Boda D. Density functional theory of the electrical double layer: the RFD functional. J. Phys. Condens. Matter. 2005;17:6609–6626. [Google Scholar]
- 63.Valiskó M., Boda D., Gillespie D. Selective adsorption of ions with different diameter and valence at highly-charged interfaces. J. Phys. Chem. C. 2007;111:15575–15585. [Google Scholar]
- 64.Boda D., Kovács R., Kristóf T. Selective transport through a model calcium channel studied by local equilibrium Monte Carlo simulations coupled to the Nernst-Planck equation. J. Mol. Liq. 2014;189:100–112. [Google Scholar]
- 65.Boda D., Csányi É., Kristóf T. Dynamic Monte Carlo simulation of coupled transport through a narrow multiply-occupied pore. J. Chem. Phys. 2014;118:700–707. [Google Scholar]
- 66.Berti C., Furini S., Fiegna C. Three-dimensional Brownian dynamics simulator for the study of ion permeation through membrane pores. J. Chem. Theory Comput. 2014;10:2911–2926. doi: 10.1021/ct4011008. [DOI] [PubMed] [Google Scholar]
- 67.Boda D., Henderson D., Gillespie D. The role of solvation in the binding selectivity of the L-type calcium channel. J. Chem. Phys. 2013;139:055103. doi: 10.1063/1.4817205. [DOI] [PubMed] [Google Scholar]
- 68.Shannon R.D., Prewitt C.T. Effective ionic radii in oxides and fluorides. Acta Crystallogr. B. 1969;25:925–946. [Google Scholar]
- 69.Nielaba P., Forstmann F. Packing of ions near an electrolyteelectrode interface in the HNC/LMSA approximation to the RPM model. Chem. Phys. Lett. 1985;117:46–48. [Google Scholar]
- 70.Lamperski S., Outhwaite C.W. Exclusion volume term in the inhomogeneous Poisson-Boltzmann theory for high surface charge. Langmuir. 2002;18:3423–3424. [Google Scholar]
- 71.Lamperski S., Bhuiyan L.B. Counterion layering at high surface charge in an electric double layer. Effect of local concentration approximation. J. Electroanal. Chem. 2003;540:79–87. [Google Scholar]
- 72.Hille B. Sinauer Associates; Sunderland, MA: 2001. Ion Channels of Excitable Membranes. [Google Scholar]
- 73.Chen D.P., Xu L., Eisenberg B. Selectivity and permeation in calcium release channel of cardiac muscle: alkali metal ions. Biophys. J. 1999;76:1346–1366. doi: 10.1016/S0006-3495(99)77297-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Krauss D., Eisenberg B., Gillespie D. Selectivity sequences in a model calcium channel: role of electrostatic field strength. Eur. Biophys. J. 2011;40:775–782. doi: 10.1007/s00249-011-0691-6. [DOI] [PMC free article] [PubMed] [Google Scholar]


