Designing Cell-Targeted Therapeutic Proteins Reveals the Interplay between Domain Connectivity and Cell Binding

Abstract

The therapeutic efficacy of cytokines is often hampered by severe side effects due to their undesired binding to healthy cells. One strategy for overcoming this obstacle is to tether cytokines to antibodies or antibody fragments for targeted cell delivery. However, how to modulate the geometric configuration and relative binding affinity of the two domains for optimal activity remains an outstanding question. As a result, many antibody-cytokine complexes do not achieve the desired level of cell-targeted binding and activity. Here, we address these design issues by developing a computational model to simulate the dynamics and binding kinetics of natural and engineered fusion proteins such as antibody-cytokine complexes. To verify the model, we developed a modular system in which an antibody fragment and a cytokine are conjugated via a DNA linker that allows for programmable linker geometry and protein spatial configuration. By assembling and testing several anti-CD20 antibody fragment-interferon α complexes, we showed that varying the linker length and cytokine binding affinity controlled the magnitude of cell-targeted signaling activation in a manner that agreed with the model predictions, which were expressed as dose-signaling response curves. The simulation results also revealed that there is a range of cytokine binding affinities that would achieve optimal therapeutic efficacy. This rapid prototyping platform will facilitate the rational design of antibody-cytokine complexes for improved therapeutic outcomes.

Introduction

Clinical applications of protein drugs are often limited due to the tendency of such drugs to act on healthy, nontarget cells. These undesired interactions lead to toxicities and reduce the therapeutic index, the ratio between the minimum dose that causes toxicity and the minimum dose that is therapeutically effective. This is particularly a problem for cytokine therapeutics. Cytokines are key signaling proteins that bind to cell-surface receptors and activate a set of well-defined cell signaling networks. Several cytokines, such as interferon (IFN) and interleukin-2, have already been clinically approved and many more are under development (1). However, systemic administration of cytokines often leads to severe side effects due to their pleiotropic actions (2–7), which limits their effectiveness.

Side effects are particularly noteworthy for INFα, which was one of the first biotechnology products and is currently used to treat hepatitis B, hepatitis C, and metastatic melanoma. Commercial forms include INFα-2a (Roferon) and INFα-2b (Intron A), which correspond to natural human IFNs, and PEG INFα-2a (Pegasys) and INFα-2b (PEG-Intron), which are PEGylated derivatives with a much longer serum half-life due to their increased Stokes radius and decreased filtration through the kidney into the urine (8). INFα is produced directly in response to viral infection and initiates a Th1 immune response, which is also effective for killing cancer cells. However, it also induces flu-like symptoms, which are extremely burdensome for hepatitis patients, who typically receive a 1-year course of treatment, and may lead to discontinuation (8). In addition, INFα might be useful at higher doses for many cancers, but the side effects have likely prevented the development of such therapies (9). PEGylation of INFα allows for less frequent dosing, but does not appear to lessen the side effects. Clinical studies have suggested that the side effects are dose dependent and result from effects on numerous organ systems (7), so increasing the target-cell specificity could bring substantial patient benefit.

Thus far, targeted delivery by genetic fusion of cytokines to antibodies or antibody fragments via polypeptide linkers has shown limited success in addressing this issue (recently reviewed in Kontermann (1)). One reason for this failure is that the fused cytokine can still act on nontarget cells. Another possibility is that the geometry of an antibody-cytokine fusion does not allow effective cytokine-receptor binding. If the bound configuration results in steric hindrance or a majority of time spent in nonproductive conformations, the effectiveness of targeting is limited. At this time, a reliable technique for designing antibody-fusion proteins to maximize specific, targeted binding does not exist.

It was previously demonstrated that cell-targeting specificity could be improved by modulating the relative binding affinity of the antibody and cytokine (10). Mutating the cytokine to weaken its binding affinity reduces its activity on all cell types, whereas fusing it to an antibody rescues its activity only on cell types that express the antibody’s target by increasing its effective local concentration. For targeting to be effective, the antibody’s affinity should be substantially higher than the cytokine’s. Based on this principle, a new class of antibody-cytokine fusions called chimeric activators, which exhibit a 10- to 20-fold increase in signal activation on the target cells, was developed. However, it is not clear how to rationally design the appropriate cytokine-binding affinity for a given antibody-cytokine pair. Also, estimates based on the relative binding affinity alone were not sufficient to quantitatively predict the actual targeting effect (10,11).

The activity of an antibody-cytokine chimera is also regulated by its geometric configuration. The domains must be arranged in a spatial configuration that allows the appropriate protein-protein interactions. The geometric configuration of an antibody-cytokine fusion can be modulated by modifying the linker between the two protein domains. The length and flexibility of the linker have a significant impact on the accessibility of the antibody and cytokine to their respective binding targets. For example, a sufficient separation between the two protein domains is necessary for optimal fusion protein activity (12–19). Moreover, rigid linkers often result in better protein domain separation and fusion protein activity compared with flexible linkers (12–19). However, it is not clear how the geometric configuration for optimal antibody-cytokine fusion activity can be quantitatively modulated in a given context.

The development of multicomponent targeted protein therapeutics has been hampered by a lack of understanding of the interplay between the spatial and kinetic rate elements within such proteins, even though these are engineerable. Our broader goal in this work was to develop a theory that characterizes the contributions of these spatial and kinetic rate elements well enough to define a function TI(L, m, e) that can reliably predict the behavior of a given construct in a given experimental or therapeutic context, where TI is the therapeutic index, L is the spatial properties of the system, m is the kinetic rate parameter information, and e is the experimental context. We define the term “targeting effect” to mean the ratio of EC₅₀ values (half-maximal effective concentrations) between nontarget and target cells. The linker effect is the ratio of EC₅₀ values between constructs with different linker lengths. The mutation effect is the ratio of targeting effects between constructs with different mutations applied to the cytokine that affect its binding kinetics. The linker effect and mutation effect correspond to the two types of variables that we can control, namely, spatial and kinetic variables.

We developed a unified computational and experimental approach to quantitatively evaluate how the combination of a given linker geometry and reduction in cytokine binding affinity affects the activity of an antibody-cytokine complex. To demonstrate the utility of our system, we investigated the effects of linker length and IFNα binding affinity on the activity of IFNα complexes that target a B cell antigen, CD20. This was motivated by recent work in which an anti-CD20 antibody-IFNα fusion protein eradicated B cell lymphoma tumors with reduced IFNα toxicity in mouse models (20), and previous chimeric-activator work that showed success in targeting IFNα to cells expressing epidermal growth factor receptor (10) and targeting erythropoietin to red blood cell precursors (11).

We apply a two-component computational modeling approach that is composed of a constrained Brownian dynamics (CBD) simulation method and an ordinary differential equation (ODE) model (Fig. 1 C). The CBD simulation uses a coarse-grained 3D model of an antibody-cytokine complex (Fig. 1, A and B) to determine how a given linker geometry will affect the cytokine binding dynamics. The CBD simulation results, along with other IFNα-receptor binding parameters, are used as inputs for the ODE model to generate the simulated pharmacodynamics of the antibody-cytokine complexes. The ODE model tracks the kinetic transitions among all possible protein binding states on the cell surface (Fig. 1 F) and generates quantitative predictions that can be compared directly with experimental in vitro Stat1 phosphorylation (an immediate downstream measure of binding) for target and nontarget cells (see Materials and Methods for details). Based on computational practicality and available data, we take a full-system modeling approach that is characteristic of recent directions in systems biology (21). The model is based on physical mechanisms rather than arbitrary functional fits, and as such contains only parameters with direct physical meaning that are either already determined or amenable to future experimental verification.

Figure 1.

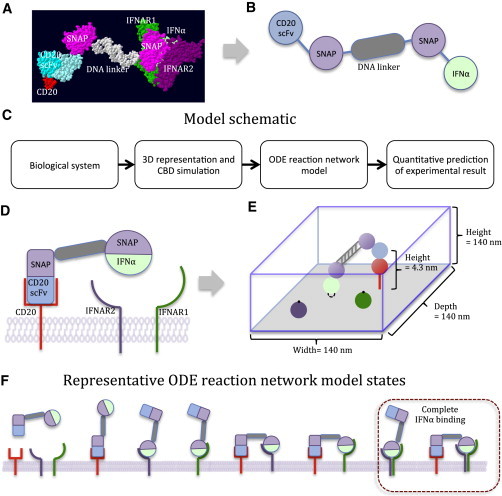
Two-component simulation model. (A) All-atom representation of the chimeric activator complex. The complex consists of an anti-CD20 scFv-SNAP fusion protein conjugated to an oligonucleotide that is hybridized to its complementary strand, which in turn is conjugated to an IFNα-SNAP fusion protein. (B) Coarse-grained representation of the chimeric activator complex. Each domain of the chimeric activator complex is represented as a simple geometric object for simulation. (C) Schematic of the CBD and ODE simulation model. (D) Simplified representation of complex with its binding partners, CD20, IFNAR1, and IFNAR2. (E) CBD simulation approach to computing the effect of the linker on targeted IFNα binding. We create a 3D representation of the complex with the anti-CD20 scFv bound to its antigen on the target (CD20+) cell surface. The model then tracks the constrained Brownian motions of the components of the complex and calculates the accessibility of IFNα to its receptors. (F) ODE model for tracking chimeric activator binding states. The ODE model simulates and tracks the kinetic transitions of all possible bound states of an anti-CD20 scFv-IFNα complex on the cell surface. When IFNα is bound to both IFNAR1 and IFNAR2, we refer to this state as complete IFNα binding, which leads to Stat1 phosphorylation. The separate entities in the diagram correspond to populations tracked in the ODE model. To see this figure in color, go online.

To test the computational model, we developed a modular, self-assembling platform on which an antibody fragment and a cytokine are conjugated via a DNA linker (Figs. 1 A and S1 in the Supporting Material). The predictable Watson-Crick basepairing and rigidity of double-stranded DNA (persistence length ∼50 nm (22,23)) allow for programmable linker geometry. Protein-DNA conjugation was accomplished by SNAP-tagging chemistry (24). The assembled DNA-protein complexes then function as a form of antibody-cytokine complex. The activity of these complexes on cells that express or do not express CD20 (the antibody target) can then be measured and compared with our model predictions. Our results provide mechanistic insights that will aid in the design of antibody-cytokine complexes for improved therapeutic outcomes.

Materials and Methods

CBD modeling

We extend the CBD simulation system described by Robinson-Mosher et al. (25) for our antibody-cytokine complexes. (An illustrative simulation corresponding to the complex with a 15 bp linker is provided in Movie S1.) To represent rigid DNA linkers and better represent the protein domains, we add the capacity to handle capsule-shaped rigid structures and electrostatic interactions between the charged DNA and cell membrane. We assume a uniform charge distribution along the length of the DNA and a uniform planar charge density on the cell membrane, and account for Debye-Hückel charge screening due to the ionic strength of the medium. To handle nonspherical rigid structures, one must address nonisotropic diffusion coefficients and nonsphere-sphere steric interactions. We use the Perrin friction factors for a prolate spheroid for the diffusion terms (26). We handle steric constraints by treating each rigid structure as a capsule, noting that the surface of a capsule is defined by the set of points equidistant from a line segment. The distance between two capsules or a capsule and sphere can therefore be determined in closed form from the formulae for segment-segment or point-segment distance, which allows a closed-form expression for the constraint.

CBD simulations for chimeric activators were initialized with the anti-CD20 antibody single-chain variable fragment (scFv) constrained to remain bound to CD20 in the cell membrane (Fig. 1 E) to compare the effects of different linker types on IFN binding in the target-bound configuration. The scFv is connected to a SNAP domain by a short flexible linker, thence to the DNA linker (15, 30, or 45 bp in length), thence to a second SNAP domain, and thence to the IFN domain. SNAP is a modified human O⁶-alkylguanine-DNA alkyltransferase that specifically and covalently binds to benzylguanine (BG)-labeled substrates (24).

The domains are connected by 9 Å flexible linkers fixed to precise points on the domain surface, except for the connection between SNAP and the anti-CD20 scFv, which is a 21 Å flexible linker. The CD20 molecule is centered in the x-z plane at the bottom of the simulation domain, with dimensions of 140 × 140 × 140 nm³ to avoid edge effects, which corresponds roughly to the density of CD20 on K562 cells (although the density does not affect the simulation model). The simulation parameters of the medium correspond approximately to human blood, with a temperature of 37°C, dynamic viscosity of 3.5 cP (27), dielectric constant of 74.5 (28), and ionic strength of 300 mol/m³ (29). The charge of the DNA linker is −2e per basepair and the charge density of the membrane is .2 e/Ų, a parameter that was estimated based on fitting the model to the data. Each simulation is run for 1 ms, the first 10 μs of which are discarded to allow the system to randomize. The measured quality of binding in arbitrary binding units (ABU) corresponds to the amount of time the IFN molecule spends near a productive binding configuration with respect to the distance from the cell membrane of the binding site on IFN receptors (25).

To turn the ABU into a usable quantity in the ODE model, we must be able to use it to calculate a rate parameter. The binding activity of a molecule of IFNα tethered near the cell membrane via linkage to bound anti-CD20 scFv is equivalent to the binding activity of a freely diffusing IFNα molecule that is constrained to stay within a certain height above the membrane. (Due to the geometry and electrostatics of the system, this height may not be simply interpretable as a linker length.) Therefore, we conducted simulations with freely diffusing IFN monomer confined to a range of heights between 10 and 240 nm above the membrane and measured the same ABU quantities, which allowed us to fit a power law relationship converting ABU to an equivalent height above the membrane h = (8941.7/ABU)^.822. We then used this value as a parameter in the ODE model to compute rates by assuming that the height can be used to compute an effective on-rate (see below).

ODE model to predict Stat1 phosphorylation

Our ODE model uses experimental conditions, affinity values from the literature and experiment, and CBD simulation results to predict Stat1 phosphorylation at a given dose for comparison with experiment. The model is implemented via in-house-written MATLAB scripts (described in Table S2) using standard built-in functions. The model tracks the concentration of free binder (which may be either antibody-cytokine complex or IFNα alone), unbound IFNAR1, IFNAR2, and CD20, and the population of binder bound to any subset of IFNAR1, IFNAR2, and CD20. The model is expressed in terms of transition rates between binding states based on the current concentrations in each state (Fig. 1 F), along with rates of endocytosis. Rate parameters are determined either from the literature or, in the case of the binding affinities between the IFN domains of our fusion constructs and their receptors, according to a fit to the experimental results observed on K562 wild-type (WT; nontarget) cells.

Similarly to the work of Doldán-Martelli et al. (30), we use the model previously described by Lauffenburger and Linderman (31) for the binding of two molecules associated with a cell membrane to model the dynamics of IFNα or anti-CD20 scFv binding to IFNAR1, IFNAR2, or CD20, given that the complex is already bound to one of the three. The two membrane constituents must be close enough to one another for simultaneous binding to be geometrically possible, given the linker properties; the rate at which this occurs is referred to as k₊ (see Lauffenburger and Linderman (31) for details). Once the membrane constituents are in close proximity to each other, binding occurs according to the familiar rate constants for association in solution, modified by the increased local concentration due to tethering. The 2D reaction-limited association rate is then

$$k_{on}^{\prime }=k_{on}/\left(h{N}_A\right)$$

where h is as described above and N_A is Avogadro’s number. The overall 2D on-rate for IFNα binding to IFNAR2 given the initial binding to CD20 is then

$$k_c={\left(\frac{1}{k_{+}}+\frac{1}{k_{on}^{\prime }}\right)}^{-1}$$

We express all of our binding states as 3D concentrations, so we must convert k_c to a 3D on-rate,

$$k_c^{3D}=k_c{N}_{A}V/A$$

where V is the total fluid volume and A is the total surface area of the cells that are present.

The experimental conditions are a volume of 100 μL, 1.5 × 10⁵ cells, 1062 molecules of IFNAR1 and 3021 molecules of IFNAR2 per K562 WT cell, 890 molecules of IFNAR1 and 2725 molecules of IFNAR2 per K562 CD20+ cell (measured experimentally using QuantiBrite beads; BD Biosciences, San Jose, CA), 250,000 molecules of CD20 per K562 CD20+ cell (also measured experimentally using QuantiBrite beads), a surface area of 584 μm² per cell (32), and an assay time of 30 min. The output of the ODE system is the integral over time of the amount of colocalized IFNAR1 and IFNAR2, which is the sum of the binder-IFNAR1-IFNAR2 and binder-IFNAR1-IFNAR2-CD20 species concentrations. The Stat1 phosphorylation curve is generated by running the model for a range of binder concentrations, typically between 10⁻¹⁴ and 10⁻⁶ M with samples every 10^.3 M.

Our observable, Stat1 phosphorylation, has a direct functional relation to the stability of the IFNα-IFNAR1-IFNAR2 ternary complex. However, Stat1 signaling need not be linearly proportional to ternary complex formation, so it is necessary to construct a standard curve. We ran the simulation model using the IFN-SNAP fusion as the binder, with values of the IFNAR1 and IFNAR2 binding kinetics taken from Jaks et al. (33), and used the resulting binding curve along with the experimentally measured Stat1 phosphorylation to construct a standard curve relating binding to the observed Stat1 phosphorylation (previous work related a similar value to cell proliferation (30)). We used this standard curve to convert the predicted binding results for our constructs to predicted Stat1 phosphorylation curves for direct comparison with experiment.

Computing predicted targeting effect

We calculate the targeting effect for a DNA-protein complex as the ratio of the EC₅₀ values computed for K562 and K562 CD20+ cells. We compute the EC₅₀ values by generating predicted Stat1 phosphorylation curves as above, finding the minimum and maximum values, and using MATLAB to locate the concentration at which the curve reaches the mean value.

BG-DNA conjugation

Complementary oligonucleotide pairs of 15, 20, 30, 35, 40, and 45 nucleotides that do not form secondary structures and have stable hybridization at 37°C were designed using NUPACK (34) (see Table S1 for the oligonucleotide sequences). The 5′ end of the oligonucleotides was first modified with a primary amine via a C₆ linker (purchased from Integrated DNA Technologies, Coralville, IA). To couple BG to the amine-modified oligonucleotides, 10 mM of BG-GLA-NHS (item S9151S; New England Biolabs, Ipswich, MA) in DMSO was incubated with 1 mM of the amine-modified oligonucleotides in PBS at 30°C overnight. Excess BG-GLA-NHS was then removed using Illustra Microspin G-25 columns (item 27-5325-01; GE Healthcare, Boston, MA). The concentration of the purified BG-modified oligonucleotide was measured using NanoDrop (Thermo Scientific, Tewksbury, MA). The conjugation of BG and DNA was verified by high-performance liquid chromatography (Fig. S2).

Expression and characterization of SNAP-tagged proteins

Human type I IFNα 2a (IFNα; GenBank ID: AET86951.1) WT and the R144A mutant were genetically fused via a Gly₄Ser linker to the N-terminus of SNAP-tag (N9181S; NEB, New England Biolabs, Ipswich, MA), which was then followed by a C-terminal 6×His tag (Fig. S1 A, GenBank accession numbers KM043782 and KM043781). Anti-CD20 scFv (designed based on Wu et al. (35)) was genetically fused via a Gly₄Ser linker to the N-terminus of SNAP-tag, again followed by a C-terminal 6xHis tag (Figs. 1 A and S1 A; GenBank accession number KM043780). The SNAP-tagged proteins were expressed in E. coli and purified using HisPur Cobalt spin columns (item 90092; Thermo Scientific, Tewksbury, MA). The activity of the SNAP-tagged proteins was characterized by biochemical, biophysical, and cell-based assays.

DNA-protein complex assembly

To assemble the anti-CD20 scFv-DNA-IFNα complexes, 1.33 μM of anti-CD20 scFv-SNAP and 1.33 μM SNAP-IFNα(R144A) were incubated with 2 μM forward and reverse strands of BG-oligonucleotides, respectively, for 1 h at room temperature (Fig. S1 B). The excess BG-oligonucleotides were then removed using 30 kDa MWCO spin columns (item UFC503024; Millipore, Billerica, MA). The oligonucleotide-labeled anti-CD20 scFv-SNAP and SNAP-IFNα(R144A) were then mixed at an equimolar ratio and incubated at room temperature for another hour. To confirm the assembly, the DNA-protein complexes were resolved by electrophoresis using 2% agarose gels in Tris-acetate-EDTA buffer supplemented with 25 mM of MgCl₂ for 25 min on ice. The migration of the DNA or DNA-protein complexes was visualized by ethidium bromide staining (Figs. 2 D and S2).

Figure 2.

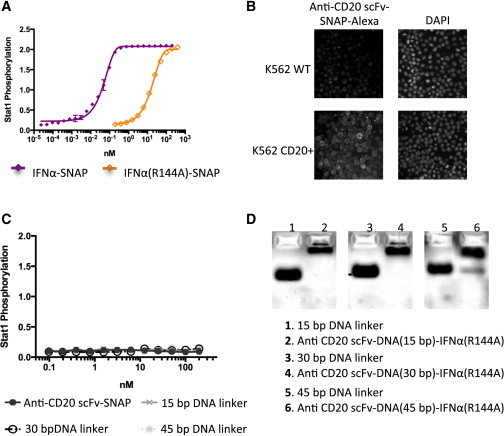
The SNAP-tagged proteins are biologically active. (A) Stat1 phosphorylation in K562 CD20+ cells induced by SNAP-IFN fusion proteins after 30 min. Both IFNα(WT)-SNAP and IFNα(R144A mutant)-SNAP induced robust Stat1 phosphorylation in K562 CD20+ cells (the EC₅₀ values were 0.04 nM and 17.13 nM, respectively). The decrease in IFNα activity due to the R144A mutation was consistent with previous reports (4,8). (B) Fluorescent staining of K562 WT and CD20+ cells with DAPI and anti-CD20 scFv-SNAP conjugated to Alexa Fluor 546. (C) Stat1 phosphorylation assay control performed in K562 CD20+ cells with the non-IFN components of the chimeric activator complex. (D) Gel-shift assay to demonstrate oligonucleotide conjugation to protein complexes via changes in electrophoretic mobility. To see this figure in color, go online.

K562 cell culture

K562 WT (item CCL-243; ATCC, Manassas, VA) and the transformed K562 CD20+ cells were a generous gift from Dr. Yvonne Chen. The CD20 expression was confirmed by immunostaining (Fig. S3). K562 WT and CD20+ cells were cultured in RPMI medium (item 22400-105; Life Technologies, Bedford, MA) supplemented with 10% fetal bovine serum at 37°C with 5% CO₂ and maintained by renewing the medium every 3 days. For experiments involving the DNA-protein complexes, the cell culture medium was also supplemented with 12.5 mM of MgCl₂ during the course of the experiments.

ELISA

K562 WT and CD20+ cells were seeded in V-bottom 96-well plates at 1.5 × 10⁵/well. After incubation with the stimulating proteins or complexes for 30 min, the cells were spun down in the plates and lysed with 105 μL of lysis buffer (item 9803; Cell Signaling Technology, Danvers, MA) per well by incubation on ice for 20 min. The lysates were then spun down at 4°C to remove the insoluble fraction. To quantify the level of phosphorylated Stat1 in each lysate sample, the PathScan phospho-stat1 (Tyr701) sandwich ELISA kit (item 7234S; Cell Signaling Technology) was used according to the manufacturer’s protocol. Briefly, 100 μL of the soluble lysate from each sample was added to one anti-phospho-Stat1 antibody-coated well. After an overnight incubation at 4°C, the wells were washed with the ELISA wash buffer included in the kit. The phosphorylated Stat1 detection antibody was then added to each well followed by 1 h incubation at 37°C. Horseradish peroxidase-linked streptavidin and TMB (3,3’, 5,5’-tetramethylbenzidine) were then used to detect the bound antibody. The level of Stat1 phosphorylation was then determined by measuring the absorbance at 450 nm on a plate reader. The effective half-maximum concentrations (EC₅₀) of Stat1 phosphorylation were determined from the dose-signaling curves using a four-parameter sigmoidal fit in GraphPad Prism (La Jolla, CA).

Results

Two-component computational model for antibody-cytokine complex activity

The CBD simulation model first creates a 3D representation of the antibody-cytokine complex on the target cell surface and then tracks the constrained Brownian motions of the components of the complex (Fig. 1 E). The simulations are initialized with the antibody fragment constrained to remain bound to the target antigen on the cell membrane. The simulation predicts the increase in effective IFNα concentration near the cell membrane as a result of CD20 binding (see Materials and Methods for details), which can then be used to compute the rate parameters. We developed the CBD simulation method by extending the molecular-dynamics simulation framework previously developed in our group (25). We added the capacity to handle nonspherical rigid structures for modeling rigid linkers and protein domain geometry. We also considered the electrostatic interactions between the negatively charged DNA and cell membrane (see Materials and Methods for details).

Our ODE model generates predicted Stat1 phosphorylation curves that depend on experimental conditions, binding affinity values, and CBD simulation results that are used to compute rate parameters. The model tracks the concentration of molecules in each possible binding state over time. In the case of the anti-CD20 scFv-IFNα complexes, the possible binding states are the free anti-CD20 scFv-IFNα complex; unbound IFNAR1, IFNAR2, and CD20; and the population of every binding permutation (Fig. 1 F). The output of the ODE system is the integral over time of the amount of IFNα-IFNAR1-IFNAR2 ternary complex (i.e., complete IFNα binding), which is then converted to the Stat1 phosphorylation level (see Materials and Methods for details). This generates predicted Stat1 phosphorylation curves for direct comparison with experiment.

Modular antibody-cytokine complexes with DNA linkers

We assembled IFNα complexes that target B cells by synthesizing SNAP-IFNα, SNAP-IFNα(R144A), anti-CD20 scFv-SNAP, and BG-modified oligonucleotides (Fig. S1). SNAP-tagged IFNα and anti-CD20 scFv are conjugated to BG-labeled oligonucleotides and form a DNA-protein complex through DNA hybridization (36,37). The R144A mutation, which weakens IFNα-IFNAR2 binding, was introduced to achieve increased specificity for target cells via the chimeric activator effect (i.e., when a fusion protein is constructed consisting of one domain that binds to a target epitope and one domain that stimulates cell signaling, the increase in signaling on cells that express the target epitope over those that do not is greater if the affinity of the stimulating domain for its receptor is weakened compared with the WT) (10).

The SNAP-tagged proteins were biologically active. IFNα-SNAP induced 398.4-fold greater Stat1 phosphorylation than IFNα(R144A)-SNAP in K562 CD20+ cells (Fig. 2 A; the EC₅₀ values were 0.04 nM and 17.13 nM, respectively). The decrease in IFNα activity due to the mutation was roughly consistent with previous reports (4,10). The anti-CD20 scFv-SNAP was also functional, as demonstrated by the specific binding of fluorescently labeled scFv to the K562 CD20+ cell surface (Fig. 2 B). As an experimental control, we showed that the anti-CD20 scFv-SNAP and the BG-modified DNA linkers did not induce Stat1 phosphorylation (Fig. 2 C). To verify the formation of the anti-CD20-DNA-IFNα complexes, we performed a gel-shift assay. Assembled DNA-protein complexes showed retarded gel migration compared with the DNA linkers alone (Fig. 2 D). The sequences of the DNA linkers are shown in Table S1.

Predicted and observed effects of linker geometry and IFNα binding affinity

By performing CBD simulations of the DNA-protein complexes with 15, 30, and 45 bp DNA linkers, we predicted a monotonic decrease in the IFNα binding enhancement due to anti-CD20 binding with increasing linker length (Fig. 3 D). We expected that longer linkers would exhibit reduced binding enhancement as a result of the greater proportion of time spent far away from the membrane (Fig. 3, A and B) and the greater repulsion due to the increased negative charge. Although it is also possible for a linker to exhibit reduced binding enhancement because it is too short to span the two receptors (25,38), this was not expected in our system due to the inclusion of the SNAP domains (Fig. 1 B). The predicted binding enhancement in ABU (Fig. 3 C) for the 15 bp linker complex was ∼30 times greater than that of the 45 bp linker, which led to an ∼17-fold difference in predicted k′_on (see Materials and Methods).

Figure 3.

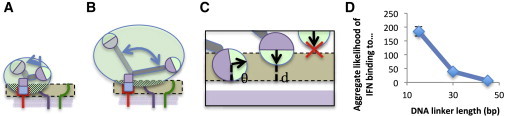
CBD simulation results. The CBD simulation results allow us to compute the effects of linker length on the ability of IFN to bind to its receptors. (A) Exploration of space near the membrane by IFNα when the anti-CD20 scFv is bound to CD20. The green ellipse is the full space sampled by IFNα, the tan region is where it is possible for IFNα to bind to its receptors, and the purple region is the cell membrane. The shaded region is the intersection between the sampled space and the possible binding region. (B) Longer linkers increase the proportion of conformations where IFNα cannot bind. (C) Expanded diagram of the possible binding region, showing the conditions that affect the calculated likelihood of binding. The measure of the likelihood of binding in a given configuration takes into account both the distance of the IFNα binding site from the optimal height off the membrane, d, and the angular distance of binding site from its optimal orientation, θ. The CBD simulation computes the likelihood of binding at every step in time and aggregates the results to compute an overall binding likelihood measure for a given construct (in ABU). (D) The likelihood of binding in ABU as a function of linker length was calculated via CBD simulation. We ran 40 simulations, each 1 ms long, for each linker length. To see this figure in color, go online.

Modeling of signal transduction also led to a prediction that increasing linker length would decrease the cell-targeted signaling activation by anti-CD20 scFv-DNA-IFNα(R144A) complexes (see Fig. 3 D and Materials and Methods). We first simulated the activity of the anti-CD20 scFv-DNA-IFNα(R144A) complexes on target cells and generated the predicted Stat1 phosphorylation level as a function of the complex concentration (Fig. 4 A, bottom). The simulations predicted a 22.5-fold targeting effect for Stat1 phosphorylation on target versus nontarget cells and a 11.2-fold linker effect between the 15 bp and 45 bp linker complexes (Fig. 4 A, bottom).

Figure 4.

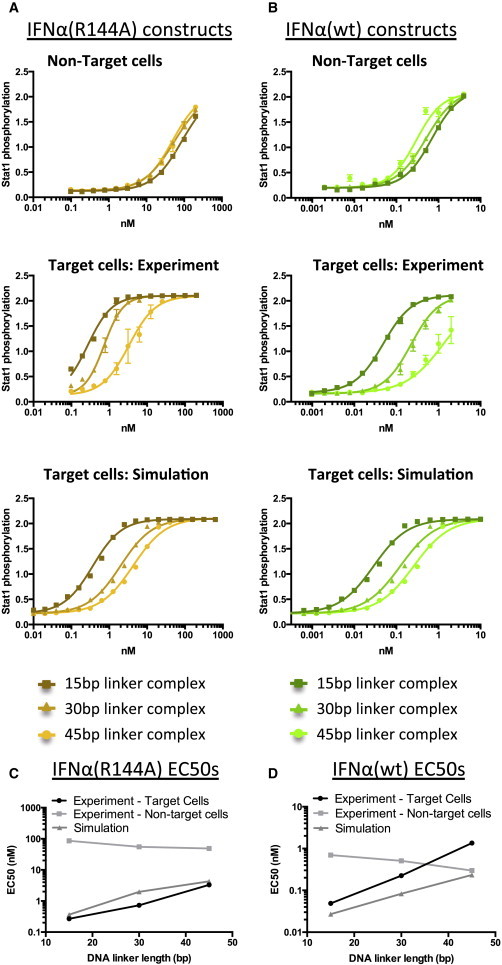
The linker length and IFNα binding affinity modulate the targeted cell signaling activation by antibody-cytokine complexes. K562 (nontarget) and K562 CD20+ (target) cells were incubated with DNA-protein complexes (as shown in Fig. 1A, with three different DNA linker lengths) for 30 min, lysed, and assayed for Stat1 phosphorylation by ELISA. Simulations were performed using the two-component approach described in Fig. 1 to model the experimental results. (A and B) Stat1 phosphorylation curves are shown for DNA-protein complexes incorporating (A) IFNα(R144A)-SNAP and (B) IFNα(WT)-SNAP. (C and D) EC₅₀ values were calculated and compared for the experimental and simulated data by fitting a four-parameter logistic function to the curves for the (C) IFNα(R144A)-SNAP and (D) IFNα(WT)-SNAP complexes. To see this figure in color, go online.

To test the validity of our model predictions, we measured the activation of Stat1 phosphorylation, a measure of IFNα signaling, in cells with and without CD20 expression. The assembled DNA-protein complexes induced enhanced IFNα signaling in the target (CD20+) cells in a manner that qualitatively agreed with the simulation results (Fig. 4, A and C). We stimulated K562 WT and K562 CD20+ cells with assembled anti-CD20 scFv-DNA-IFNα(R144A) complexes. We evaluated the potency of the DNA-protein complexes by determining the EC₅₀ from the Stat1 phosphorylation curves. The complex with the short (15 bp) linker showed a 42.2-fold targeting effect for Stat1 phosphorylation. The signaling enhancement decreased as the linker length increased (12.3-fold decrease in EC₅₀ when the linker length increased from 15 to 45 bp). There was no substantial linker effect in the nontarget cells (Fig. 4 A, top).

The enhanced signaling due to CD20 targeting was diminished when WT IFNα was used instead of IFN(R144A). The simulation results predicted a 17.2-fold targeting effect for Stat1 phosphorylation and an 8.7-fold difference in EC₅₀ between the 15 and 45 bp linker complexes (Fig. 4 B, bottom). There was qualitative agreement with the experimental results (Fig. 4, B and D). The complex with the 15 bp linker showed a 14.9-fold targeting effect for Stat1 phosphorylation, and there was a 27.8-fold difference between the 15 and 45 bp linker complex (Fig. 4B middle). There was no substantial linker effect in the nontarget cells (Fig. 4 B, top).

Relationship of the targeting effect with IFN binding affinity

It has been shown that the activity of IFNα is proportional to the product of the subunit binding affinities (39). We therefore consider adjustments to these affinities to be good candidates for modifying the activity of our DNA-protein complexes. It was previously shown that fusions constructed using weakened mutant versions of IFNα achieve a greater targeting effect than those obtained using the WT (the chimeric activator effect (10)), but no model exists at present to indicate how strong a mutation will be optimal. We investigated the effect of mutations in the binding affinity of IFNα for each of its receptors on the targeting effect.

Our simulations predicted that there is an optimal range of IFNα receptor subunit binding affinities, rather than a single optimum, to achieve a maximal targeting effect. As observed above (Fig. 4), the binding affinity of IFNα plays a critical role in modulating the cell-targeted signaling activation. We show a targeting effect landscape corresponding to a range of k_on^IFNAR1 from 10⁴ to 10¹⁰ and k_on^IFNAR2 from 10² to 10¹⁰, with other parameters corresponding to WT IFNα and the 15 bp linker (Fig. 5). The targeting effect declines substantially for k_on^IFNAR2 values above ∼10⁵ and somewhat for k_on^IFNAR1 values above ∼10⁸. The ability to generate this landscape for a given antibody/cytokine system will allow one to select the appropriate mutation strength for optimal targeting.

Figure 5.

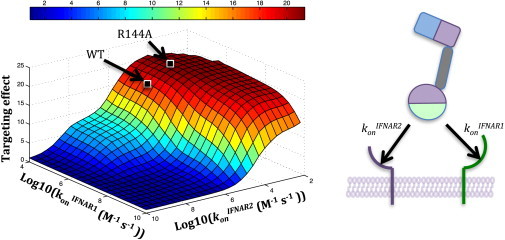
Simulation across a range of receptor binding affinities predicts a region of maximal targeting effect. We performed ODE simulations for a wide range of physiologically plausible k_on^IFNAR1 and k_on^IFNAR2 values to predict Stat1 phosphorylation curves for both K562 WT and K562 CD20+ cells. We used k_off^IFNAR1 and k_off^IFNAR2 values corresponding to those of WT IFNα and linker parameters corresponding to the 15 bp linker (holding k_on constant and instead plotting against k_off results in an essentially identical landscape). The targeting effect was computed as the ratio of the Stat1 phosphorylation EC₅₀ values on the K562 WT cells to those on the K562 CD20+ cells. The results indicate that the targeting effect is relatively low for high on-rate values and quickly increases to a steady maximum. The approximate locations of IFNα WT and R144A are indicated on the landscape. Optimal chimeric activator designs will require binding affinities to be chosen within the maximal targeting effect region. To see this figure in color, go online.

Discussion

The broad goal of this work was to develop a system for predicting the therapeutic behavior of artificial therapeutic fusion proteins as a function of genetically engineerable features. Such features include the binding geometry, length, flexibility, and charge of linkers between domains, and the affinities, on-rates, and off-rates of individual domains for their targets. A priori, it seems likely that the system behavior would be a complicated, nondecomposable function of these variables, and that the resulting design space for engineered proteins could be quite large. In particular, human intuition and static modeling may not be sufficient to guide the design, and current methods for producing antibody-cytokine fusions are too laborious to allow a thorough exploration of the design space.

Protein engineers have attempted to create chimeric multidomain protein complexes for many years. The design approach remains largely focused on the qualitative functional combination and use of nonmutant natural protein domains (40). Ideally, targeted antibody-cytokine fusions designed for simultaneous binding of both antibody and cytokine to the same target cell should be driven by the antibody element, but the on-rates and affinities of antibodies and nonmutant cytokines are often similar. This complex 3D dynamic process requires coordination of the spatial configuration and binding affinity of the protein domains.

We developed a two-component computational model to quantitatively evaluate the effects of geometric configuration and relative binding affinity on antibody-cytokine fusion activity. We also implemented an experimental system that allows users to rapidly build and test antibody-cytokine fusions with varying linker and binding properties. We applied this combined approach to quantitatively evaluate the effects of linker length on anti-CD20 scFv-IFNα chimeric complexes, which potentially can be used to treat B cell lymphoma (20).

We found that increasing the length of a stiff DNA linker decreased the magnitude of the cell-targeted signal activation, as predicted by both modeling and experiment (Fig. 4). We also found that the targeting effect of our scFv-DNA-cytokine construct can be expected to reach a maximal plateau for low values of IFNα binding affinity for its receptors, which is consistent with observations in previous chimeric activator studies and offers an approach for designing chimeric activator constructs in the future (Fig. 5).

Here, we took a fine-grained approach to mechanistic numerical modeling of the IFNα signaling system. Previous studies modeled chimeric cytokine complexes by treating IFN binding as though it were a single event (30). However, the dynamics of signaling via colocalization of two IFNα receptors is substantially different from that of signaling via a single receptor (31,33,41). By accurately capturing the details of the cytokine-receptor binding dynamics, we can better determine the important factors that modulate the system behavior.

The presence of free parameters in a modeling system limits the model’s predictive power, especially if they can be adjusted to fit any possible set of observable data. The application of our model is limited by imperfect knowledge of some of the system parameters, which are thus necessarily free parameters; however, the necessity to account for multiple linker lengths and both the IFNα WT and R144A mutant complexes reduces the possibility of overfitting. We also constrained the parameter values that had to be estimated by information from the literature on what is plausible. The binding affinity for the anti-CD20 scFv is not known a priori and was estimated as the value that best fit both the WT and R144A mutant data.

The initial version of the model did not account for electrostatic forces between the cell membrane and the charged DNA linker. We had to take these forces into account to explain the dramatic difference in effect between the different linker lengths. To fit with the data, the corresponding membrane charge density was ∼10 times higher than the previously reported range (31,42). We hypothesize that the negatively charged sialic acids on protein-linked oligosaccharides, which are farther away from the membrane, would suffer less Debye-Hückel shielding than the phosphates on phospholipids. Given these assumptions, the model results showed good agreement with the experimentally determined values and provided an adequate mechanistic explanation for the experimental results. It is also noteworthy that with the addition of about eight sialic acids in the engineering of erythropoietin into darbepoetin, receptor binding and activity on cells decreased significantly even though the protein-protein interaction surface of erythropoietin was unaffected (43). Taken together, these results indicate that modulation of the overall charge may be a practical protein-engineering strategy to modify the activity of ligands acting on mammalian cells without introducing mutations that might disrupt protein-protein interactions in unpredictable ways.

Although we primarily focused on evaluating the effects of linker length on antibody-cytokine complex activity, in theory our two-component computational model can be applied to simulate the binding events of other multidomain proteins with a complex geometric configuration. With the increasing popularity of antibody fusions, bispecific antibodies, and various forms of multimeric antibodies for development as therapeutics (1,44), our computational approach will provide valuable quantitative insights into the design principles of these protein complexes.

Our results provide not only further support for the effectiveness of the chimeric activator approach to targeted therapeutics but also mechanistic insights into how to modulate the relative binding affinity for optimal therapeutic efficacy. This quantitative analysis will help investigators determine the appropriate mutations for the cytokine to achieve the desired targeted therapeutic effect. Here, we focused on optimizing the specificity of IFNα signaling for target cells. To extend the approach to a more direct prediction of therapeutic efficacy, it will be necessary to model the binding dynamics over a longer period of time and take additional factors, such as receptor downregulation and trafficking, into account. In addition, although the same modeling approach is applicable to receptor antagonists as well as the agonist we discuss here, the experimental readout would be quite different.

The biological response to a cytokine is a complicated function of receptor binding strength and the trafficking properties of the ligand-receptor complex. This includes the propensity of the activated receptor to be endocytosed, to be either recycled or degraded, and for the ligand to remain with or dissociate from its receptor in the low-pH environment of the endosome (45). It is thought that if the ligand remains receptor bound, it will be degraded or recycled along with the receptor, but if it dissociates in the endosome, a fixed fraction will be recycled. For example, Sarkar et al. (46) engineered G-CSF to show enhanced recycling out of cells by introducing histidines that would become protonated in the endosome, induce G-CSF/G-CSFR dissociation, and help the mutant G-CSF avoid being degraded along with the receptor after endocytosis. Binding at pH 7.4 was essentially unaffected by these mutations. In our case, trafficking of the engineered ligand may be influenced by the behavior of both of the receptors to which it is bound. Modifying the ligand to remain endosomally associated with either the targeting or activity receptor may be an additional engineering strategy to enhance cell-specific signaling. Our model provides a good measure of the effect of our engineering on initial binding and signaling. Additional modeling including endocytic trafficking processes (47) could help predict the behavior of engineered fusion proteins in vivo.

To our knowledge, our work is the first to challenge this type of modeling with experiments on the effects of linker geometry in target-active element protein complexes. We believe our unified computational modeling and experimental approach provides a strong basis for elucidating the general design principles of antibody-cytokine fusions and, in theory, other multidomain proteins or protein complexes. This will help us to move toward rational design of engineered proteins with optimal biophysical properties.

Supporting Citations

References (48,49) appear in the Supporting Material.