Transmembrane Protein Diffusion in Gel-Supported Dual-Leaflet Membranes

Abstract

Tools to measure transmembrane-protein diffusion in lipid bilayer membranes have advanced in recent decades, providing a need for predictive theoretical models that account for interleaflet leaflet friction on tracer mobility. Here we address the fully three-dimensional flows driven by a (nonprotruding) transmembrane protein embedded in a dual-leaflet membrane that is supported above and below by soft porous supports (e.g., hydrogel or extracellular matrix), each of which has a prescribed permeability and solvent viscosity. For asymmetric configurations, i.e., supports with contrasting permeability, as realized for cells in contact with hydrogel scaffolds or culture media, the diffusion coefficient can reflect interleaflet friction. Reasonable approximations, for sufficiently large tracers on low-permeability supports, are furnished by a recent phenomenological theory from the literature. Interpreting literature data, albeit for hard-supported membranes, provides a theoretical basis for the phenomenological Stokes drag law as well as strengthening assertions that nonhydrodynamic interactions are important in supported bilayer systems, possibly leading to overestimates of the membrane/leaflet viscosity. Our theory provides a theoretical foundation for future experimental studies of tracer diffusion in gel-supported membranes.

Introduction

Supported lipid bilayers have been studied for many decades, with applications in biosensing (1) and drug delivery (2). Many studies have focused on lateral diffusion, because it facilitates membrane signaling (3). Among the tracers that have been studied in supported membranes are proteins (4,5), lipids (6), lipopolymers (7), and lipid rafts (8). Several lateral diffusion models are available (9–14). However, these demand that the two leaflets are so tightly coupled that they behave as a single infinitesimally thin fluid layer (with a finite viscosity). More recently, dual-leaflet models have emerged to help to distill experimental evidence that interleaflet slip can sometimes—but not always—influence tracer mobilities (14–16). Whereas some studies have demonstrated that leaflets appear to be so tightly coupled that they behave as a single membrane (17,18), others have suggested that interleaflet slip can be important and even quantified (19–22).

Interpreting experiments is challenging, and has been controversial, because there are many factors that influence measured tracer mobilities (5,17,18,23–25). At the highest level, these factors include the measurement method (fluorescence recovery after photobleaching, nuclear magnetic resonance, and/or fluorescence correlation spectroscopy); the tracer and its fluorescent tag; the membrane and its composition; the support and its membrane synthesis; and the buffer. These all present significant challenges for theoretical models, which have customarily reduced the problem to one of identifying an effective cylindrical tracer size and membrane viscosity (9,10,12), also accounting for hydrodynamic interaction with a solid support (11,12).

Single-leaflet models have brought important physical insights and intricate methods of mathematical and numerical analysis (as summarized by Wang and Hill (14)), but have not been without controversy when adopted to interpret experiments. Noteworthy is the study of Gambin et al. (23), which examines the role of peptide size on lateral diffusion, and shows that, in contrast to the well-known theory of Saffman and Delbrück (9) (SD), diffusion can be considerably more sensitive to tracer size, scaling with the reciprocal radius rather than the much-weaker logarithmic scaling of the SD theory.

The experiments of Ramadurai et al. (5) corroborated the SD scaling for proteins in the membranes of giant unilamellar vesicles, whereas those of Harb et al. (25) revealed reciprocal square scaling for larger (complexes) in glass-supported DMPC (dimyristoylphosphatidylcholine) bilayers. Such a scaling is predicted by dissipative particle dynamics (coarse-grained) computations (26), but only at short to intermediate timescales, and for inclusions, such as lipid rafts, in solvent-supported membranes. Note that the scaling hinges on the inclusions having internal lateral degrees of freedom, so is unlikely to apply to the experiments of Harb et al. (25), which were undertaken with mono-, di-, and trimeric assemblies of heptomeric pores using fluorescence recovery after photobleaching, thus probing diffusion on long timescales.

Several experimental studies have sought to quantify the interleaflet friction coefficient. The pioneering experiments of Merkel et al. (19) furnished interleaflet friction coefficients in the range ≈5 × 10⁵ – 2 × 10⁷ Pa s cm⁻¹ for DOPC bilayers, and ≈3 × 10⁵ – 3 × 10⁷ Pa s cm⁻¹ for DMPC bilayers. The authors den Otter and Shkulipa (21) reported an interleaflet friction coefficient ≈2 × 10⁴ – 7 × 10⁶ Pa s cm⁻¹ for DPPC bilayers, and Jönsson et al. (22) established ≈2 × 10⁵ Pa s cm⁻¹ for egg PC bilayers. These clearly span a very wide range, highlighting the need for a tractable theoretical model to connect measured tracer diffusion coefficients to membrane and tracer properties.

Recently, biomedical and advanced-materials applications have identified needs to understand the interaction of bilayer membranes with soft, porous scaffolds, including extracellular matrices and hydrogels (27–29). Theory is required to quantify how the porosity of such networks—controlled by the polymer and cross-linking density—may influence tracer diffusion and, indeed, impact leaflet coupling. Wang and Hill (14) developed a single-leaflet model to quantify how varying the hydrogel porosity bridges the pure-fluid and solid-supported regimes. This has been advanced to elucidate the roles of interfacial slip for monotopic and transmembrane tracers in bilayers with finite interleaflet slip (30). However, the model adopted a phenomenological lubrication interaction between the leaflets and an impenetrable support (neglecting the three-dimensional hydrodynamic disturbances in the porous supports), thereby leaving open the question as to how porous such a support must be for the lubrication approximation to break down.

In this article, we theoretically address the lateral migration of a (nonprotruding) transmembrane protein embedded in a dual-leaflet membrane that is supported above and below by unbounded porous half-spaces. The model quantifies how the three-dimensional hydrodynamic disturbances on each side of a dual-leaflet membrane impact transmembrane-protein dynamics and interleaflet coupling. In the biological context, such configurations occur when cells are embedded in three-dimensional hydrogel scaffolds or cultured on planar supports; the internal leaflet is coupled to the intracellular cytoskeleton whereas the external leaflet is coupled to a soft support, such as a gel or extracellular matrix.

Gel-Supported Dual-Leaflet Model presents the governing equations, and derives coupled dual integral equations, which are subsequently solved numerically. Results and Discussion presents the results as tracer mobilities, which are typically measured as lateral self-diffusion coefficients, and 1), quantifies how the dimensionless mobility depends on the interleaflet friction; 2), furnishes theoretical predictions of transmembrane-protein diffusion coefficients; and 3), identifies the reduced parameter space for the analytical theory of Hill and Wang (30). In the absence of suitable data for gel-supported membranes, we apply the model to interpret the transmembrane protein diffusion coefficients of Peters and Cherry (17) and Gambin et al. (23), concluding with a brief Summary section.

Gel-Supported Dual-Leaflet Model

As depicted schematically in Fig. 1, the model advanced here approximates an integral-membrane protein as a disk with radius a and thickness 2h translating with velocity U in a gel-supported lipid bilayer with membrane viscosity η_m and thickness 2h. The two leaflets slip relative to each other with a friction coefficient b₁₂. Note that it is convenient to adopt another dependent parameter γ₁₂ (which is a reciprocal squared slip length), defined such that b₁₂ = γ₁₂η_mh. Moreover, η_mh is customarily termed a two-dimensional membrane viscosity, furnishing a stress per unit of membrane contour length in a leaflet with thickness h. Finally, the hydrogels are approximated as Brinkman porous media with Brinkman screening lengths $\ell$₁ and $\ell$₂, and respective solvent viscosities η₁ and η₂ that we will set to the bulk shear viscosity of water, η.

Figure 1.

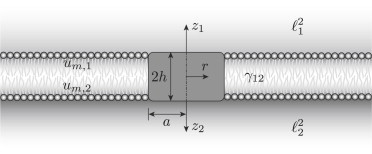
A planar phospholipid bilayer with membrane viscosity η_m and membrane thickness 2h bears a cylindrical inclusion (disk) with radius a. The membrane is supported above and below by hydrogels with permeabilities $\ell$²₁ and $\ell$²₂, both saturated by a solvent with shear viscosity η. The top and bottom leaflets slip relative to each other with a friction coefficient γ₁₂.

The membrane velocity and pressure satisfy modified Stokes equations

$$-\nabla p_{m,1}+{\eta }_{m,1}{\nabla }^2{\mathbf{u}}_{m,1}+{\mathbf{f}}_1+{\mathbf{f}}_i=0,$$ (1)

$$-\nabla p_{m,2}+{\eta }_{m,2}{\nabla }^2{\mathbf{u}}_{m,2}+{\mathbf{f}}_2-{\mathbf{f}}_i=0,$$ (2)

where

$${\mathit{f}}_1=\frac{1}{h}{\mathit{e}}_z\cdot {\mathit{\sigma }}_1,$$

$${\mathit{f}}_2=-\frac{1}{h}{\mathit{e}}_z\cdot {\mathit{\sigma }}_2,\text{and}$$

$${\mathit{f}}_i={\eta }_m{\gamma }_{12}\left({\mathit{u}}_{m,2}-{\mathit{u}}_{m,1}\right).$$

Here, f₁ and f₂ are body forces from the shear stress exerted by the solvent at the top and bottom surfaces: e_z is an upward unit vector,

$${\mathit{\sigma }}_j=-p_j\mathit{I}+{\eta }_j\left[\nabla {\mathit{u}}_j+{\left(\nabla {\mathit{u}}_j\right)}^T\right]$$

is the solvent stress tensor, and f_i is the body force from interleaflet friction. In the hydrogels, the solvent velocity and pressure satisfy the conservation equations of Brinkman (31),

$$-\nabla p_j+\eta {\nabla }^2{\mathbf{u}}_j-{\eta }_j{\ell }_j^{-2}{\mathbf{u}}_j=0\text{and}\nabla \cdot {\mathbf{u}}_j=0,$$ (3)

where subscripts j = 1,2 identify the top and bottom half-spaces.

Extensive algebraic details of the following mathematical solution are available elsewhere (14). Therefore, in the remainder of this section, we summarize the principal steps leading to the lateral force F on the tracer when it translates at velocity U. The reader may turn immediately to Results and Discussion, noting that the dimensionless mobility 4πηa|U/F| depends on $\ell$₁/a, $\ell$₂/a, and the three dimensionless parameters Λ₁, Λ₂, and ϵ₁₂ defined below in Eq. 6.

Taking the curl of the momentum equations with vanishing slip between the tracer and leaflets at r = a furnishes four integral equations to be solved for functions a_m,1(k) and a_m,2(k), which construct the membrane velocity disturbances via Hankel transformations (14). Vanishing slip between each leaflet and its respective solvent furnishes a_m,1(k) = a₁(k) and a_m,2(k) = a₂(k), where a₁(k) and a₂(k) construct the solvent velocity disturbances (32). Below, the functions a₁(k) and a₂(k), and the variables k (reciprocal length) and r, are scaled appropriately with the disk radius a, giving

$$\begin{array}{c}1=\underset{0}{\overset{\infty }{\int }}{a}_1\left(k\right)\frac{2}{k}{J}_1\left(kr\right)\text{d}k\\ 1=\underset{0}{\overset{\infty }{\int }}{a}_2\left(k\right)\frac{2}{k}{J}_1\left(kr\right)\text{d}k\end{array}\}r\le 1,$$ (4)

and

$$\begin{array}{c}0=\underset{0}{\overset{\infty }{\int }}k\left[a_1\left(k\right)\left(k^2+{\text{Λ}}_1\sqrt{k^2+{\left(a/{\ell }_1\right)}^2}+{ϵ}_{12}^2\right)-a_2\left(k\right){ϵ}_{12}^2\right]J_1\left(kr\right)\text{d}k\\ 0=\underset{0}{\overset{\infty }{\int }}k\left[a_2\left(k\right)\left(k^2+{\text{Λ}}_2\sqrt{k^2+{\left(a/{\ell }_2\right)}^2}+{ϵ}_{12}^2\right)-a_1\left(k\right){ϵ}_{12}^2\right]J_1\left(kr\right)\text{d}k\end{array}\}r>1,$$ (5)

where

$$\begin{array}{l}{\text{Λ}}_1=\frac{{\eta }_{1}a}{{\eta }_{m,1}h},\hfill \\ {\text{Λ}}_2=\frac{{\eta }_{2}a}{{\eta }_{m,2}h},\hfill \\ \text{and}{ϵ}_{12}^2={\gamma }_{12}{a}^2.\hfill \end{array}$$ (6)

After constructing the pressure and deviatoric stresses in the membrane and solvents, the force on the disk is

$$\begin{array}{c}\mathbf{F}=-\frac{2\pi {\eta }_{1}a\mathbf{U}}{{\text{Λ}}_1}{\int }_0^{\infty }\left[a_1\left(k\right)\left(k^2{a}^2+{\text{Λ}}_{1}a\sqrt{k^2+{\ell }_1^{-2}}+{ϵ}_{12}^2\right)-a_2\left(k\right){ϵ}_{12}^2\right]J_2\left(ka\right)\text{d}k\\ -\frac{2\pi {\eta }_{2}a\mathit{U}}{{\text{Λ}}_2}{\int }_0^{\infty }\left[a_2\left(k\right)\left(k^2{a}^2+{\text{Λ}}_{2}a\sqrt{k^2+{\ell }_2^{-2}}+{ϵ}_{12}^2\right)-a_1\left(k\right){ϵ}_{12}^2\right]J_2\left(ka\right)\text{d}k.\end{array}$$ (7)

To ascertain a₁(k) and a₂(k), the coupled integral equations above are solved by writing Eq. 5 as

$$\begin{array}{c}{Ϝ}_1\left(k\right)a_1\left(k\right)-k{ϵ}_{12}^2{a}_2\left(k\right)={\text{Ψ}}_1\left(k\right)\\ {Ϝ}_2\left(k\right)a_2\left(k\right)-k{ϵ}_{12}^2{a}_1\left(k\right)={\text{Ψ}}_2\left(k\right)\end{array}\}r>1,$$ (8)

where

$${Ϝ}_1\left(k\right)=k\left(k^2+{\text{Λ}}_1\sqrt{k^2+{\left(a/{\ell }_1\right)}^2}+{ϵ}_{12}^2\right),$$

$${Ϝ}_2\left(k\right)=k\left(k^2+{\text{Λ}}_2\sqrt{k^2+{\left(a/{\ell }_2\right)}^2}+{ϵ}_{12}^2\right).$$

Then, substituting a₁(k) and a₂(k) from Eq. 8 into Eqs. 4 and 5 gives

$$\begin{array}{c}1={\int }_0^{\infty }\left\{\frac{2{Ϝ}_2\left(k\right){\text{Ψ}}_1\left(k\right)}{k\left[{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4\right]}+\frac{2{ϵ}_{12}^2{\text{Ψ}}_2\left(k\right)}{{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4}\right\}{J}_1\left(kr\right)\text{d}k\\ 1={\int }_0^{\infty }\left\{\frac{2{ϵ}_{12}^2{\text{Ψ}}_1\left(k\right)}{{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4}+\frac{2{Ϝ}_1\left(k\right){\text{Ψ}}_2\left(k\right)}{k\left[{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4\right]}\right\}{J}_1\left(kr\right)\text{d}k\end{array}\}r\le 1$$ (9)

and

$$\begin{array}{c}0={\int }_0^{\infty }{\text{Ψ}}_1\left(k\right)J_1\left(kr\right)\text{d}k\\ 0={\int }_0^{\infty }{\text{Ψ}}_2\left(k\right)J_1\left(kr\right)\text{d}k\end{array}\}r>1.$$ (10)

Tranter (33) and Sneddon (34) have shown how to reduce dual integral equations to a system of algebraic equations by representing the unknown functions as an infinite series of Bessel functions, and then imposing an orthogonality condition. Accordingly, we let

$${\text{Ψ}}_1\left(k\right)=k^{1-\beta }\sum _{n=0}^{\infty }{a}_{1,n}\left(k\right)J_{2n+1+\beta }\left(k\right),$$ (11)

$${\text{Ψ}}_2\left(k\right)=k^{1-\beta }\sum _{n=0}^{\infty }{a}_{2,n}\left(k\right)J_{2n+1+\beta }\left(k\right),$$ (12)

where β > 0 is an arbitrary constant that only affects the series convergence, and a_1,n and a_2,n are constants that vary with the independent model parameters (Λ₁, Λ₂, ϵ₁₂, $\ell$₁/a, and $\ell$₂/a. Then, substituting Eqs. 11 and 12, and following Sneddon (34), we eventually find

$$\begin{array}{l}\underset{0}{\overset{\infty }{\int }}\sum _{n=0}^{\infty }\left\{\frac{2{Ϝ}_2\left(k\right)a_{1,n}\left(k\right)}{k\left[{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4\right]}+\frac{2{ϵ}_{12}^2}{{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4{a}_{2,n}\left(k\right)}\right\}\\ k^{1-2\beta }{J}_{2n+1+\beta }\left(k\right)J_{2\nu +1+\beta }\left(k\right)\text{d}k\\ =\frac{{\delta }_{0\nu }}{2^{\beta }\text{Γ}\left(\beta +2\right)},\end{array}$$ (13)

$$\begin{array}{l}\underset{0}{\overset{\infty }{\int }}\sum _{n=0}^{\infty }\left\{\frac{2{ϵ}_{12}^2{a}_{1,n}\left(k\right)}{{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4}+\frac{2{Ϝ}_1\left(k\right)a_{2,n}\left(k\right)}{k\left[{Ϝ}_1\left(k\right){Ϝ}_2\left(k\right)-k^2{ϵ}_{12}^4\right]}\right\}\\ k^{1-2\beta }{J}_{2n+1+\beta }\left(k\right)J_{2\nu +1+\beta }\left(k\right)\text{d}k\\ =\frac{{\delta }_{0\nu }}{2^{\beta }\text{Γ}\left(\beta +2\right)},\end{array}$$ (14)

where ν = 0,1,2,…,N. Constructing the membrane pressures and viscous stresses, the force on the disk can be written (32)

$$\mathit{F}=-\frac{\pi {\eta }_{1}a\mathbf{U}{a}_{\mathrm{1,0}}}{{\text{Λ}}_1{2}^{\beta -1}\text{Γ}\left(2+\beta \right)}-\frac{\pi {\eta }_{2}a\mathbf{U}{a}_{\mathrm{2,0}}}{{\text{Λ}}_2{2}^{\beta -1}\text{Γ}\left(2+\beta \right)},$$ (15)

where a_1,0 and a_2,0 are from the solution of Eqs. 13 and 14.

Results and Discussion

All calculations below were undertaken with β = 0.5 and N = 12, which provided suitable accuracy and computational economy for this problem (35,36). As a demonstration of the accuracy, Fig. 2 shows the dimensionless mobility 4πηa|U/F| versus Λ₁ for symmetric bilayers (Λ₁ = Λ₂) supported on a single hydrogel. Here, the dimensionless interleaflet friction coefficient ϵ₁₂ = γ₁₂a² = 0.01 reflects weak leaflet coupling. Nevertheless, for the highly permeable gel supports (top line with $\ell$₁/a → ∞), the mobility correctly approaches the mobility for single-leaflet, fluid-supported membranes (with thickness 2h). Accordingly, 4πηa|U/F|→ π/4 (red dashed line) when Λ₁ → ∞ (10), and

$$4\pi \eta a\left|\frac{U}{F}\right|\to \frac{\text{Λ}}{2}\left[\ln \left(\frac{2}{\text{Λ}}\right)-0.577\right],$$ (16)

when Λ₁ = Λ₂ = Λ = ηa/(η_mh) → 0 (9). The other lines demonstrate how the stronger hydrodynamic coupling of the proximal leaflet to the gel support hinders tracer diffusion, similarly to the single-leaflet, gel-supported model of Wang and Hill (14).

Figure 2.

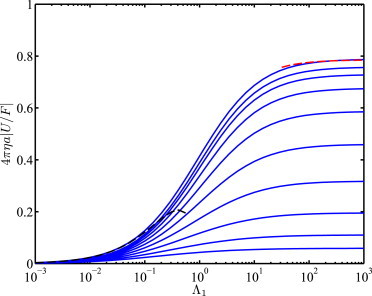
Scaled mobility (diffusion coefficient) 4πηa|U/F| versus Λ₁ for symmetric (Λ₂/Λ₁ = 1), weakly coupled (ϵ₁₂ = 0.01) bilayers that are asymmetrically supported ($\ell$₂/$\ell$₁ = 1000) on gels with dimensionless permeabilities $\ell$₁/a = ∞, 8, 4, 2, 1, 0.5, 0.25, 0.125, 0.125/2, and 0.125/4 (top to bottom) (calculations with N = 12). (Dashed lines) Theories of Saffman and Delbrück (9) (Λ << 1) and Hughes et al. (10) (Λ >> 1) for $\ell$₁/a = $\ell$₂/a → ∞. To see this figure in color, go online.

To scrutinize the role of interleaflet friction, Fig. 3 shows the dimensionless mobility 4πη_mh|U/F| versus the interleaflet friction coefficient, again for symmetric bilayers supported on single hydrogel. The left and right panels compare gels with low and high permeability. As expected from Fig. 2, increasing the permeability increases the mobility. More importantly, these calculations demonstrate a relatively weak influence of interleaflet friction. As the solid-supported dual-leaflet model of Hill and Wang (30) has shown, the effects of interleaflet slip are accentuated when there is strong coupling (of one leaflet) to a single support.

Figure 3.

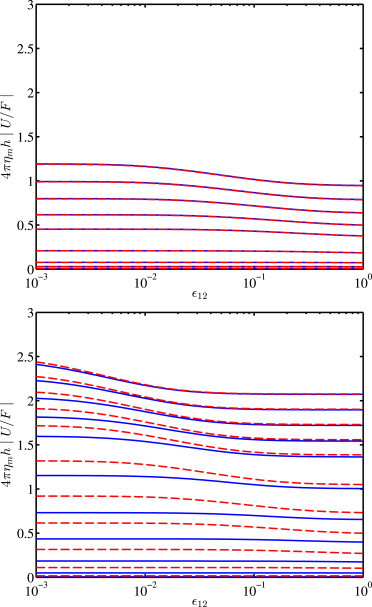
Scaled mobility (diffusion coefficient) 4πη_mh|U/F| versus the interleaflet friction coefficient ϵ₁₂ for symmetric bilayers (Λ₂/Λ₁ = 1) that are asymmetrically supported ($\ell$₂/$\ell$₁ = 1000) on hydrogels with low $\ell$₁/a = 0.01 (top) and higher $\ell$₁/a = 1 (bottom) gel permeability: Λ = 100, 10, 2, 0.5, 0.16, 0.04, 0.01, 0.005, 0.0025, 0.0025/2, and 0.0025/4 (bottom to top) (calculations with N = 12). (Solid lines) Gel-supported dual-leaflet model. (Dashed lines) Solid-supported dual-leaflet model of Hill and Wang (30) evaluated with a lubrication film thickness δ = $\ell$₁. To see this figure in color, go online.

Accordingly, Fig. 4 shows the dimensionless mobility versus the dimensionless reciprocal gel permeability. The left panel is for bilayers sandwiched between gels having equal permeabilities ($\ell$₂/$\ell$₁ = 1), whereas the right panel is for bilayers supported on a single gel ($\ell$₂/$\ell$₁ = 1000). As expected, the solid-supported model of Hill and Wang (30) breaks down when a/$\ell$₁ is sufficiently small and Λ₁ is sufficiently large. For example, if we take the radius of a protein to be a ∼ 2.5 nm, and estimate the Brinkman screening length from the mesh size of a weakly cross-linked gel with storage modulus G′ ∼ 100 Pa, then $\ell$ ∼ (k_BT/G′)^1/3 ≈ 3.5 nm ((37), where k_BT ∼ 10⁻²¹ J is the thermal energy), therefore, a/$\ell$ ∼ 1.

Figure 4.

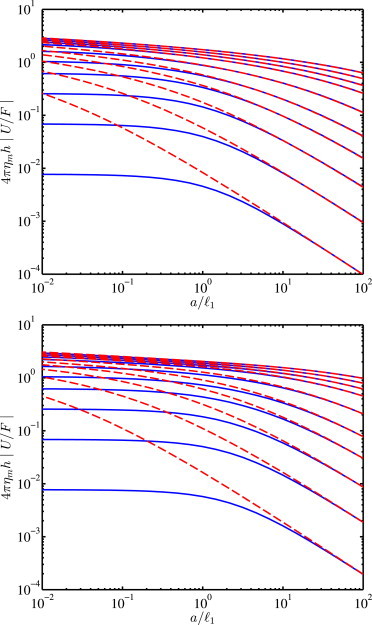
Scaled mobility (diffusion coefficient) 4πη_mh|U/F| versus dimensionless reciprocal hydrogel permeability a/$\ell$₁ for symmetric bilayers (Λ₂/Λ₁ = 1) with weak interleaflet friction (ϵ₁₂ = 0.01): $\ell$₂/$\ell$₁ = 1 (top) and 1000 (bottom) with Λ₁ = 100, 10, 2, 0.5, 0.16, 0.04, 0.01, 0.005, 0.0025, and 0.0025/2 (bottom to top) (calculations with N = 12). (Solid lines) Gel-supported dual-leaflet model; (dashed lines) solid-supported dual-leaflet model of Hill and Wang (30) evaluated with a lubrication film thickness δ = $\ell$₁. To see this figure in color, go online.

The influence of a hydrogel on tracer diffusion should therefore be sensitive to the gel concentration and cross-linking density. For bilayers next to glass, we will see below that the effective values of a/$\ell$₁ must be ≳ 1 with Λ₁ ≲ 1 to fit experiments, in which case a phenomenological solid-supported model furnishes a satisfactory approximation. Of course, nonhydrodynamic influences may also hinder tracer diffusion, but it is unknown how this friction is distributed among the tracer and leaflets. On the one hand, tracers present a small area, but can protrude to various extents from the membrane (e.g., Gambin et al. (23)), whereas leaflets present a much larger surface area due to the slowly decaying velocity disturbance around a tracer.

Diffusion coefficients are shown in Fig. 5 versus the interleaflet coefficient b₁₂ (top panel) and the Brinkman screening length $\ell$₂ (bottom panel). Increasing the strength of the interleaflet coupling decreases the diffusion coefficient, spanning the range D_s ≈ 2.48–2.75 μm² s⁻¹ (blue line). According to the solid-supported dual-leaflet model, the diffusion coefficient spans the range D_s ≈ 2.54–2.86 μm² s⁻¹ (red line). Thus, the solid-supported dual-leaflet model also captures the modest variation with respect to the interleaflet friction, but with a minor constant offset (top panel).

Figure 5.

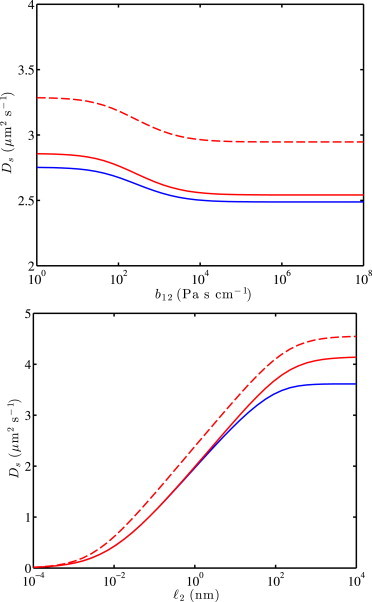
Theoretical predictions of transmembrane protein self-diffusion coefficients. (Top) Transmembrane protein diffusion coefficient versus the interleaflet friction coefficient b₁₂ = γ₁₂η_mh. Other parameters are chosen to mimic lipid diffusion based on literature estimates (5,15): η = 0.001 Pa s, η_m = 0.08 Pa s, h = 2.5 nm, a = 2 nm, $\ell$₁ = δ₁ = η_mh/η, and $\ell$₂ = δ₂ = 2a. (Bottom) Transmembrane protein diffusion coefficient versus the Brinkman screening length $\ell$₂ with b₁₂ = 2 × 10⁶ Pa s cm⁻¹. (Solid lines) Gel-supported dual-leaflet model (blue) and the solid-supported dual-leaflet model of Hill and Wang (30) (red), both with no slip (δ_N → 0) between the tracer and leaflets. (Dashed lines) Solid-supported dual-leaflet model with perfect slip (δ_N → ∞) between the tracer and leaflets. To see this figure in color, go online.

Literature highlighted in the Introduction identified interleaflet friction coefficients b₁₂ ≳ 10⁴ Pa s cm⁻¹. From the left panel in Fig. 5, this is a regime where interleaflet slip plays a negligible role, due, in part, to the low permeability of the gel support ($\ell$ = 2a = 5 nm). The right panel shows how the diffusivity increases with the gel permeability when the interleaflet friction coefficient b₁₂ = 2 × 10⁶ Pa s cm⁻¹ (15) and other parameters are the same as in the left panel. The diffusion coefficient reaches a plateau D_s ≈ 3.6 μm² s⁻¹ according to the present gel-supported model, and D_s ≈ 4.2 μm² s⁻¹ according to the solid-supported dual-leaflet model. This difference is comparable to the many other factors that can influence experimentally measured integral membrane mobilities (17).

We now turn to the experiments in which Peters and Cherry (17) measured the self-diffusion coefficient of bacteriorhodopsin in DMPC bilayer membranes, reporting D_s ≈ 3.4 μm² s⁻¹ at 32°C with a (lowest) phospholipid/protein ratio 2:10. From the Saffman-Delbrück theory, Peters and Cherry (17) estimated a membrane viscosity η_m = 0.11 Pa s (Λ ≈ 0.004) with solvent viscosity η = 0.00076 Pa s, tracer radius a = 2 nm, and bilayer thickness 2h = 4.5 nm. Note that these membranes formed the walls of large multilamellar vesicles having an average wall thickness of 10–20 bilayers; moreover, the diffusion coefficient was also found to vary significantly with the tracer concentration. Such considerations prohibit a quantitative analysis, inasmuch as protein mobility in the interior bilayers could be hindered by the close proximity of neighboring bilayers. Nevertheless, the calculations presented in Fig. 5 indicate that frictional coupling of the leaflets to their neighboring supports likely has a greater influence on the mobility than interleaflet friction. Moreover, a diffusion coefficient D_s ≈ 3.4 μm² s⁻¹ seems to reflect weak friction between the leaflets and supporting medium. As indicated in the right panel of Fig. 5, D_s ≈ 3.4 μm² s⁻¹ reflects a sizeable lubrication film thickness $\gtrsim 100$ nm, corresponding to $\ell$₁ = $\ell$₂ = η_mh/η ≈ 326 nm (11). On the other hand, extrapolating the experimental data to infinite protein dilution would increase the diffusion coefficient, thereby requiring commensurate adjustments to the model parameters, perhaps motivating a weaker interleaflet friction coefficient, lower membrane viscosity, or smaller protein size.

Some of the foregoing inferences are confirmed when considering the data of Gambin et al. (23), who demonstrated a breakdown of the Saffman-Delbrück theory for transmembrane proteins. This was revealed by examining the scaling of the lateral diffusion coefficient with respect to the radius of the hydrophobic domain contained within the membrane. Fig. 6 compares data (symbols) from their Figs. 2 and 3 with the soft- and solid-supported dual-leaflet models. Note that the circles are taken directly from their Fig. 3, whereas the squares are obtained from the normalized data in their Fig. 2 by scaling with an arbitrary constant D₀ = 5 μm² s⁻¹. Gambin et al. (23) correlated this data with a phenomenological power-law whereby the lateral diffusion coefficient D_s scales with the reciprocal protein size.

Figure 6.

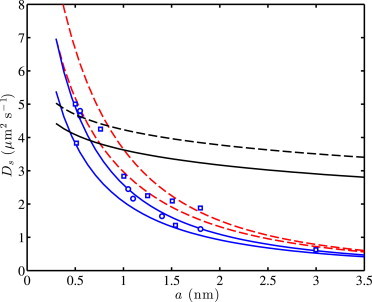
Theoretical predictions of transmembrane protein self-diffusion coefficients D_s according to the gel-supported dual-leaflet model (blue solid lines) compared with experimental data from Gambin et al. (23) for transmembrane peptides (with prescribed radius a) in vesicle bilayers pressed against glass: η = 0.00076 Pa, η_m,1 = η_m,2 = 0.02 Pa s, $\ell$₁ = 0.01 nm, $\ell$₂ = η_mh/η ≈ 59 nm (pure aqueous half-space), γ₁₂a² → 0 (upper), γ₁₂a² → ∞ (lower), and 2h = 4.5 nm. (Dashed red lines) Solid-supported dual-leaflet model of Hill and Wang (30) with perfect slip between the tracer and leaflets (δ_N → ∞). (Black lines) According to the gel- (with δ_N → 0, solid) and solid-supported (with δ_N → ∞, dashed) models with γ₁₂a² → ∞ (tightly coupled leaflets), η_m,1 = η_m,2 = 0.11 Pa s, and $\ell$₁ = $\ell$₂ = η_mh/η ≈ 336 nm (pure aqueous half-spaces) (η = 0.00076 Pa and 2h = 4.5 nm). (Symbols) From Fig. 2 (squares) and Fig. 3 (circles) of Gambin et al. (23); note that we have transformed the normalized data in their Fig. 2 (squares) by scaling with a value for NBD-PE (D₀ = 5 μm² s⁻¹). To see this figure in color, go online.

Note that the ∼a⁻¹ theoretical scaling demonstrated in Fig. 6 (blue and red lines) could be achieved only by adopting a strong frictional coupling between the proximal leaflet and its support. In the experiments of Gambin et al. (23) (circles in Fig. 6), the membranes were the leaflets of (deflated) giant unilamellar vesicles pressed against the wall of a microchannel for fluorescence recovery after photobleaching. Otherwise, the scaling is as demonstrated by Gambin et al. (23) according to the Saffman-Delbrück theory, as indicated by the black lines in Fig. 6, which are calculated here with a leaflet viscosity η_m = 0.11 Pa s (17).

The solid blue lines in Fig. 6 are the present gel-supported model with negligible (upper) and perfect (lower) frictional coupling between the leaflets. Note that the solid-supported dual-leaflet model agrees almost exactly with the gel-supported model under these conditions, so we have plotted the solid-supported theory with perfect slip between the tracer and leaflets, i.e., a Navier-slip length δ_N → ∞ (30). Although this increases the diffusivity, as expected, it does not significantly change the ∼a⁻¹ scaling with respect to particle size.

Thus, taking the tracer-leaflet and interleaflet friction coefficients to be of secondary importance, the principal parameters responsible for the $\sim a^{-1}$ scaling are the membrane viscosity and the leaflet-support friction coefficient. In Fig. 6, we have adjusted these two parameters accordingly, finding η_m = 0.02 Pa s (with 2h = 4.5 nm) and $\ell$₁ ≈ 0.01 nm with $\ell$₂ = η_mh/η ≈ 59 nm. Note that the resulting leaflet viscosity is approximately five times lower than established by Peters and Cherry (17), and more than 10 times lower than the value adopted by Gambin et al. (23). Moreover, the low membrane viscosity is accompanied by a very strong coupling of the leaflet to the support, with a lubrication thickness ($\ell$₁) that is sufficiently thin (i.e., less than the size of a water molecule) to suggest that leaflet-support frictional forces are of nonhydrodynamic origin.

Unfortunately, this interpretation does not resolve uncertainty in the literature over the membrane viscosity and interleaflet friction. Instead, it turns attention toward the membrane-support interaction, which upon closer examination can vary considerably in the literature from one study to another. For example, the membranes in the study of Peters and Cherry (17) formed the walls of large multilamellar vesicles pressed between microscope coverslips, whereas those in the experiments of Gambin et al. (23) were of (deflated) giant unilamellar vesicles pressed against the wall of a microchannel. In other literature, lateral diffusion coefficients are measured in membranes synthesized from the fusion of small unilamellar vesicles on a variety of soft and solid-supported substrates. The gel-supported model under discussion here also points to the potentially significant role of tracer protrusion, which has often been overlooked based on the low solvent viscosity.

Finally, we caution that this theory is based on a continuum approximation that may break down, especially for tracers that are comparable to the size of the lipids that make up the membrane. It is unknown the extent to which tracer-leaflet slip, as modeled by adopting a nonzero Navier-slip length δ_N (compare solid and dashed lines in Fig. 6), mimics noncontinuum effects, as captured (albeit on much shorter timescales) by direct molecular and mesoscale simulation methods, such as those discussed briefly in the Introduction.

Summary

The gel-supported dual-leaflet model developed in this article generalizes the single-leaflet model of Wang and Hill (14) by coupling two leaflets with a phenomenological interleaflet friction parameter. Similarly to the single-leaflet model, the mobility decreases with increasing hydrogel concentration. The gel-supported dual-leaflet model also identifies the parameter space in which the much simpler solid-supported dual-leaflet model of Hill and Wang (30) furnishes accurate results through a judicious choice of the film-friction thicknesses δ = $\ell$ when δ ≲ 0.1a. Theoretical predictions of diffusion coefficients for transmembrane proteins with radius 2 nm are in the range D_s ≈ 2.5–2.8 μm² s⁻¹ when setting $\ell$₁ = η_mh/η to mimic an aqueous solvent on one side and $\ell$₂ = 4 nm on the other. This was done to mimic a rigid or porous support. We also adopted literature estimates of interleaflet friction coefficients and leaflet viscosities.

Another interpretation furnishes an unusually low leaflet viscosity η_m = 0.02 Pa s with a strong, possibly nonhydrodynamic, coupling of the proximal leaflet to its support. We showed that this yields the reciprocal-size scaling of the lateral diffusivity identified by Gambin et al. (23). Finally, our calculations show that interleaflet slip is of secondary importance (relative to leaflet-support slip) for fluid-supported transmembrane tracers, as has been widely adopted in the literature. This is not the case for the monotopic tracers addressed by Hill and Wang (30), and is not necessarily the case for supported membranes either. Thus, we hope that this model will assist future studies to probe the frictional coupling between the leaflets and the soft supports used for scaffolds and biophysical studies of membrane diffusion.