Right ventricular strain analysis from three-dimensional echocardiography by using temporally diffeomorphic motion estimation

Abstract

Purpose:

Quantitative analysis of right ventricle (RV) motion is important for study of the mechanism of congenital and acquired diseases. Unlike left ventricle (LV), motion estimation of RV is more difficult because of its complex shape and thin myocardium. Although attempts of finite element models on MR images and speckle tracking on echocardiography have shown promising results on RV strain analysis, these methods can be improved since the temporal smoothness of the motion is not considered.

Methods:

The authors have proposed a temporally diffeomorphic motion estimation method in which a spatiotemporal transformation is estimated by optimization of a registration energy functional of the velocity field in their earlier work. The proposed motion estimation method is a fully automatic process for general image sequences. The authors apply the method by combining with a semiautomatic myocardium segmentation method to the RV strain analysis of three-dimensional (3D) echocardiographic sequences of five open-chest pigs under different steady states.

Results:

The authors compare the peak two-point strains derived by their method with those estimated from the sonomicrometry, the results show that they have high correlation. The motion of the right ventricular free wall is studied by using segmental strains. The baseline sequence results show that the segmental strains in their methods are consistent with results obtained by other image modalities such as MRI. The image sequences of pacing steady states show that segments with the largest strain variation coincide with the pacing sites.

Conclusions:

The high correlation of the peak two-point strains of their method and sonomicrometry under different steady states demonstrates that their RV motion estimation has high accuracy. The closeness of the segmental strain of their method to those from MRI shows the feasibility of their method in the study of RV function by using 3D echocardiography. The strain analysis of the pacing steady states shows the potential utility of their method in study on RV diseases.

1. INTRODUCTION

Study of the right ventricle (RV) function is important for understanding the mechanism of congenital heart disease,^1,2 pulmonary hypertension,³ cardiomyopathy,⁴ and biventricular relation.^5,6 Motion analysis is critical for study of RV function since its motion abnormality is an important indicator of these conditions.⁷ Although large amount of quantitative motion analysis methods on the left ventricle (LV) has been reported,^8–10 studies of RV motion mostly focus on qualitative analysis.^11–16 Quantitative analysis of RV motion is more difficult because of its irregular shape, trabeculated endocardium, and thin myocardium wall in the image.

Early attempts for RV strain analysis were made by using MRI. Tagged-MRI provides intrinsic tagged-lines which can be used to estimate RV strains. 1D tagged-lines have been used to estimate the RV regional shortening in 2D planes.^17–19 3D modeling has been used for RV motion estimation in later works. Young et al.²⁰ used a finite element based method to track the mid myocardium surface motion from tagged-MR image sequences. Haber et al.²¹ used a volumetric finite element model to analyze the 3D motion of the myocardium from tagged-MR images. Tustison and Amini²² proposed a nonuniform rational B-spline based biventricular model and its parameters were estimated by fitting them to the corresponding points extracted from the tagged-lines and the contours.

Recently, with the development of transducer and computing technology, echocardiography has become one of the fastest-growing image modalities to study the RV motion.²³ It has advantages over other modalities in terms of its availability, portability, low cost, and minimal adverse secondary effects. Tissue Doppler imaging (TDI) has been a popular method to estimate the RV strain^24–28 because it can effectively provide quantitative evaluation of myocardial dynamics. However, this technique is angle-dependent so that only strains along directions which are parallel to the ultrasound wave propagation can be estimated. It is difficult to evaluate the strains along different directions within one image sequence. Alignment of the strain estimations of different view directions is difficult and tedious. Speckle tracking image (STI) has been an alternative technique to analysis the RV strains.^6,29–34 It depends on the assumption that the speckle pattern in the consecutive frames is preserved.^35,36 Most of the above studies use 2D echocardiography because of its high temporal resolution. It has limitations that the through-plane motion cannot be estimated and low efficiency in analyzing the whole RV volume. 3D echocardiography can provide a unified framework to estimate in-plane and through-plane strains and one-time strain analysis of the whole RV. However, 3D speckle tracking is challenging because the increased image size reduces the spatial and temporal resolutions so that the speckle patterns are not stable in consecutive frames.^36–38 3D speckle tracking of the RV is even more challenging in several points. First, RV has a very complex shape. Shape modeling methods in LV such as truncated ellipse or superquadrics⁸ do not work for RV analysis. Second, the endocardium rich of highly variable trabeculae muscles and the thin myocardial wall lead to fuzzy boundary and further degrade the STI quality, which means that higher tracking ability is required in RV analysis.

In our earlier work, we have proposed a temporally diffeomorphic motion estimation method for RV strain analysis and presented preliminary results in the conference of Functional Imaging and Modeling of the Heart (FIMH’13).³⁹ To our best knowledge, it is the first time that the full volume 3D echocardiography sequences are used to estimate the right ventricular free wall (RVFW) strains. In this study, we extend the RVFW modeling and present more detailed segmental strain results. We first validate the accuracy of our motion estimation method using sonomicrometry. Then we apply the method to image sequences of five open-chest pigs under different steady states. The steady states include baseline under normal condition and those induced by stimulating the RV myocardial wall from the different pacing sites. The RVFW is divided into 12 segments and the average segmental strains along the radial (RS), circumferential (CS), and longitudinal (LS) directions and the principal strains are analyzed. We present the difference of the average segmental strains in each steady states and possible explanation in biomechanics are made.

2. METHOD

2.A. Diffeomorphic motion estimation

We provide a review of the diffeomorphic registration based motion estimation method proposed in our earlier work. Assume that we have an image sequence I_n, n = 0, 1, …, N_s. We embed it into a time range of [0, T], T = N_s − 1, with each frame sequentially located at the integer time points. The diffeomorphism is defined by a velocity field with a differential equation of dϕ/dt = v(ϕ(x, t), t), ϕ(x, 0) = x, with t ∈ [0, T] and x ∈ Ω ⊂ R³. The deformation between any two time points is a diffeomorphism if the velocity field v is smooth. The motion estimation problem is stated as an optimization of a variational energy of the velocity field v(x, t)

$${\displaystyle \hat{\mathbf{v}}=arg\underset{\mathbf{v}\in V}{inf}\lambda {\int }_0^T\Vert \mathbf{v}(\mathbf{x},t){\Vert }_V^{2}dt+\sum _{n=1}^{n=T}{E}_{\mathrm{SSD}}(I_{n-1},I_n({\mathbf{\varphi }}_{n-1,n}\left)\right),}$$ (1)

with the first term being a regularizer to evaluate the spatiotemporal smoothness and the second term being a similarity measurement which evaluates the summed squared difference (SSD) of the voxel intensity between I_n−1 and the unwarped frame I_n(ϕ_n−1,n), with ϕ_n−1,n being the deformation from I_n−1 to I_n. The regularization term is defined as weighted sum of a spatial and a temporal regularization term

$${\displaystyle \Vert \mathbf{v}{\Vert }_V^2={\int }_{\Omega }\left(\sum _{i,j=1,2,3}{\left(\frac{{\partial }^2{v}_j}{\partial {x_i}^2}\right)}^2+w_t{\left|\frac{{\partial }^2\mathbf{v}}{\partial t^2}\right|}^2\right)d\mathbf{x}=E_{\mathrm{sr}}+E_{\mathrm{tr}},}$$ (2)

with the first term being the magnitude of second order spatial derivative of the velocity field, which is denoted as E_sr, and the second term being the second order time derivative of the velocity field, which is denoted as E_tr. Optimization of Eq. (1) searches a spatiotemporally smooth function which minimizes the SSD similarity between all consecutive frames.

The optimization is solved by using numerical method. We use a parameterized function for velocity field.^40,41 It is discretized temporally into a series of 3D cubic B-spline functions at time t_k, k = 0, 1, …, N_t, t_k = kΔt, Δt = 1/N_f, with N_f being the number of time steps between two consecutive frames and N_t = N_f∗(N_s − 1) being the total number of B-spline functions. The B-spline function at time point t_k is defined as v(x, t_k) = ∑c_m;kβ(x − x_m), with c_m;k being the control vectors located on a uniform grid of x_m at t_k and β(x − x_m) being the 3D B-spline kernel function at x_m which is the tensor product of the 1D B-spline functions. Then ϕ(x, t) can be expressed as the forward Euler integral of velocity field v(x, t) by assuming that the velocity of each point is piecewise constant within a time step. The transformation ϕ_{0, tk} is related with ϕ_{0, tk−1} by

$${\displaystyle {\mathbf{\varphi }}_{0,t_k}={\mathbf{\varphi }}_{0,t_{k-1}}+\mathbf{v}({\mathbf{\varphi }}_{0,t_{k-1}},t_{k-1})\Delta t=(\mathbf{Id}+{\mathbf{v}}_{k-1}\Delta t)\circ {\mathbf{\varphi }}_{0,t_{k-1}},}$$ (3)

with Id being the identity transformation and v_k = v(x, t_k) the velocity field at t_k. The transformation ϕ_n−1,n is denoted by composition of all small deformation under the velocity field between time t_(n−1)∗Nf and t_n∗Nf

$${\displaystyle {\mathbf{\varphi }}_{n-1,n}=\prod _{(n-1)N_f}^{n{N}_f-1}(\mathbf{Id}+{\mathbf{v}}_k).}$$ (4)

By using Eq. (4), each SSD summand term in Eq. (1) is related only to the velocity field parameters within the time of consecutive frames, so the derivative of the each SSD summand with respect to the velocity field can be evaluated independently. The temporal regularization term at a time point [Eq. (2)] makes the velocity field temporally second-order smooth and its derivative with respect to velocity field parameters at the time point depends on the velocity field parameters before and after it. The integral of the temporal regularization at all time points makes the velocity field to be globally smooth.

2.B. Optimization

We use the steepest descent method to optimize Eq. (1).

The derivatives of the total energy with respect to the B-spline parameters are calculated analytically. The derivative of E_SSD(I_n−1(x), I_n(ϕ_n−1,n)) with respect to the B-spline parameters c_m;k is

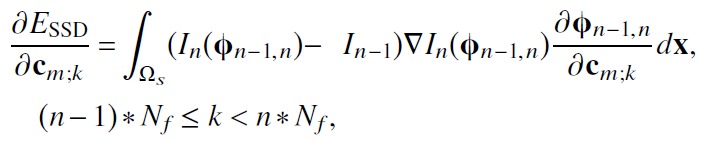(5)

with Ω_s being the domain which is controlled by c_m;k and for other value of k the derivative is zero. For the derivative of the spatial regularization with respect to the pth component of c_m;k, we have

$${\displaystyle \frac{\partial {\mathit{E}}_{\mathrm{sr}}}{\partial {\mathbf{c}}_{m,p;k}}={\int }_{{\Omega }_s}\sum _{i=1,2,3}\frac{{\partial }^2{v}_p}{\partial {\mathit{x}}_i^2}\frac{{\partial }^2\mathbf{\beta }(\mathbf{x}-{\mathbf{x}}_m)}{\partial {\mathit{x}}_i^2}d\mathbf{x}.}$$ (6)

For the derivative of the temporal regularization term, we approximate the result by assuming the small displacement between two time steps

$${\displaystyle \frac{\partial {\mathit{E}}_{\mathrm{tr}}}{\partial {\mathit{c}}_{m,p;k}}={\int }_{{\Omega }_s}(2\ast v_{m,p;k}-v_{m,p;k-1}-v_{m,p;k+1})\frac{{\partial }^2\mathbf{\beta }(\mathbf{x}-{\mathbf{x}}_m)}{\partial {\mathit{x}}_p^2}d\mathbf{x}.}$$ (7)

2.C. Strain analysis

We use Green–Lagrange strain⁴² in our study and the strain tensor is defined by

$${\displaystyle \mathbf{ϵ}=\frac{1}{2}(\mathbf{F}{\mathbf{F}}^{\mathbf{T}}-\mathbf{I}),}$$ (8)

with F being the transformation gradient matrix (Jacobian matrix) and I being the 3 × 3 identity matrix. The strainalong direction d is estimated by projecting the strain tensor to it using equation

$${\displaystyle E_{\mathbf{d}}={\mathbf{d}}^T\mathbf{ϵ}\mathbf{d}.}$$ (9)

It reflects the elongation of an elastic body along the direction d. In cardiac function analysis, we usually evaluate strains in local cardiac coordinate system along RS, CS, and LS directions.

In addition to the strains estimated along directions of local cardiac coordinate axes, the principal strains are also frequently used. Principal strains are estimated by projecting the strain tensor along the directions of its eigenvectors. The eigenvectors describe a coordinate system in which there are only normal strain components and no shear strain components. In our study, we denote the three principal strains as E₁ (maximum principal strain), E₂ (secondary principal strain), and E₃ (minimum principal strain) in descending order of the eigenvalues. The E₁ and E₃ define the largest and smallest stretch of the elastic body.

2.D. Implementation

In our implementation, we used a series of B-spline transformations with grid spacing of six voxels in each dimension to represent the velocity field. The values of λ and w_t were experimentally chosen to be 0.01 and 0.001. The algorithm was implemented in matlab (Ref. 43) with a Windows XP 64-bit system on an eight-core 2.13 GHz Xeon CPU machine with 30GB RAM. The most frequently called subroutines such as the 3D B-spline interpolation of the displacement field and the trilinear interpolation of the image were implemented by using OpenMP⁴⁴ to effectively support multiprocessors. The typical execution time for a 3D sequence of 24 frames with frame size of 131 × 123 × 104 was about 2 h.

3. DATASETS AND EXPERIMENT

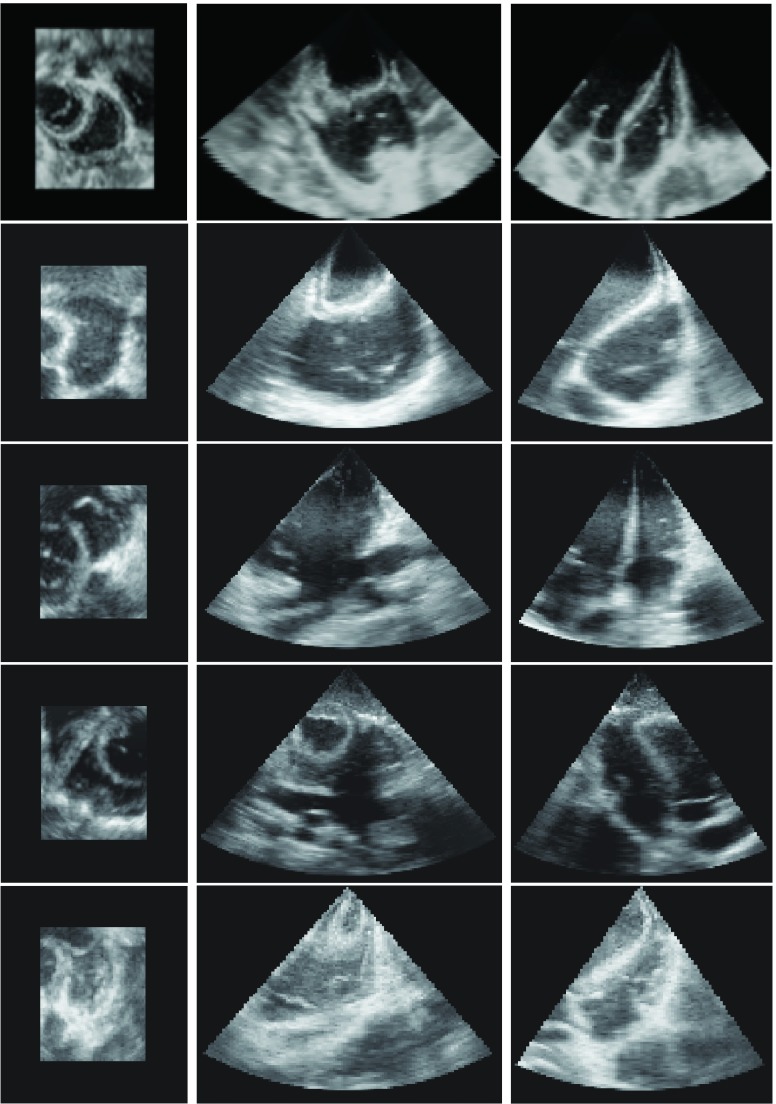
We validated the motion estimation method by using 3D echocardiography sequences of five open-chest young adult pigs (about 15 Kg) under different steady states. Each pig was placed in supine position during the experiment under anesthesia. A median sternotomy was performed under hemodynamic monitoring and the pericardium was split from apex to base to expose the heart. All experiments were approved by the institutional animal care and use committee. We acquired image sequences of steady states of baseline under normal condition and three others with a pacemaker connected to the myocardium. In this study, we used pacing sites at RV, RV apex, and RV outflow duct (RVOT), respectively. We used the Medtronic⁴⁵ 5348 single chamber temporary pacemaker for our experiment. There was at least 15 min to recover to normal after each pacing steady state. The images were acquired by using a Philips IE33 system with an X7-2 matrix array transducer transmitting at a frequency of 3.5 MHz. ECG-gating is used to combine a series of wedge-shaped subvolumes to create reconstructed full volume image. The average frame rate of the ECG-gating is 33 (FPS). A typical echocardiography sequence has 24 frames with frame size 131 × 123 × 104 and voxel size of 0.96 mm³. The 3D orthogonal views of the end-diastolic (ED) frames of the five pigs are shown in Fig. 1.

FIG. 1.

The axial, sagittal, and coronal views of the ED frame of the five open-chest pigs.

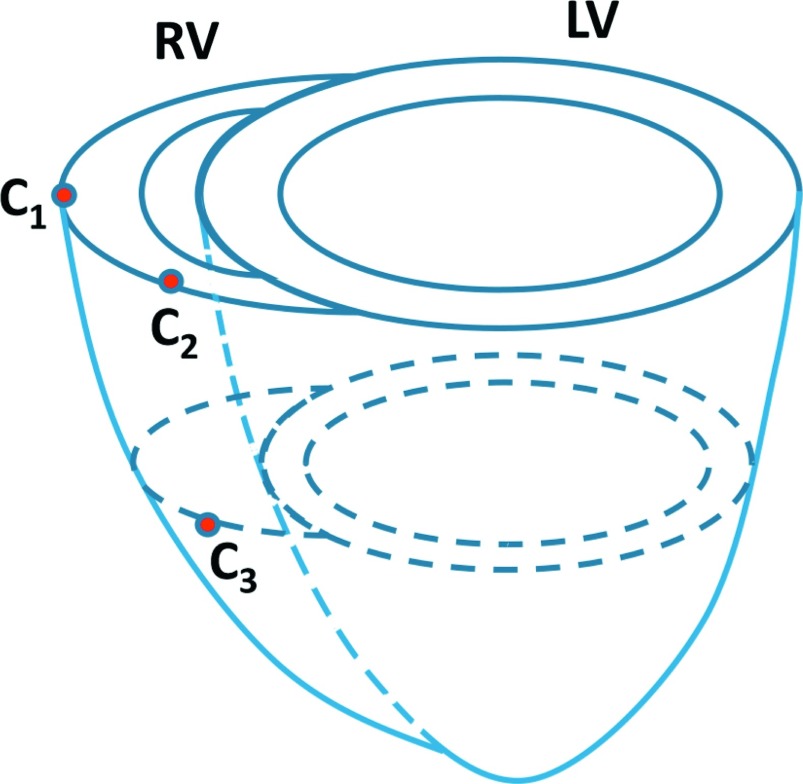
We first validated the RV motion estimation method by using sonomicrometry.⁴⁶ Sonomicrometry utilizes piezoelectric transducers (crystals) to measure distances within the myocardium. We implanted three sonomicrometers in the myocardium of each pig. The position of the sonomicrometers is illustrated in Fig. 2. For each steady state, two pairs of points distance (C₁ − C₂, C₂ − C₃) varying with time were recorded with a 70 Hz sample rate in the sonomicrometry by using SonoSOFT software (Sonometrics⁴⁶). At least three cardiac cycles were recorded. Digital data were inspected for correct identification of end-diastolic and end-systolic points using SonoView software (Sonometrics) and then the data of three cardiac cycles were averaged. The echocardiography image sequence was acquired immediately after the record of the sonomicrometry. The sonomicrometry distances data were interpolated to have same number of samples as the number of echocardiography frame. We compared the image-derived peak two-point strains, which were defined as the ratio of the maximum relative shortening to the initial distance, with those derived from sonomicrometry.

FIG. 2.

Illustration of the sonomicrometer positions on the myocardium.

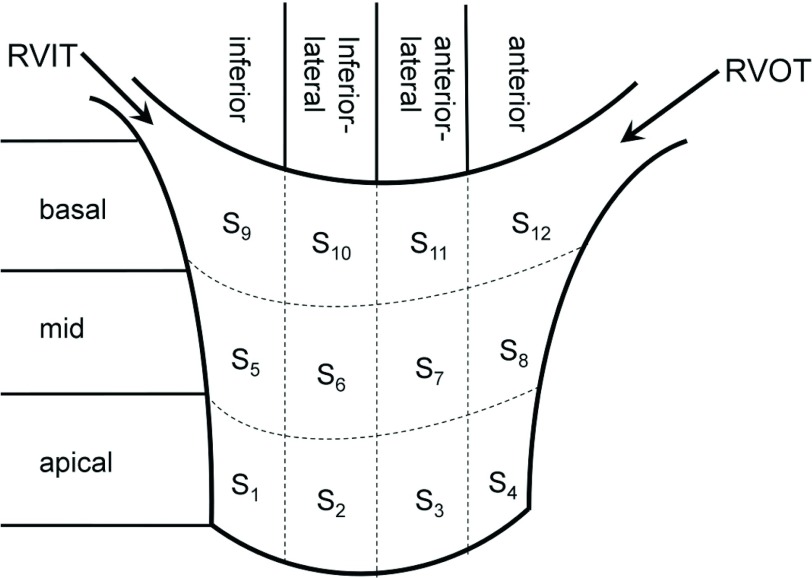
Subsequently, we evaluated the strain on RV myocardium under different steady states. The variation of the strain patterns in different steady states was analyzed. For each steady state, we used an affine registration to normalize the RV pose of the five pigs. The image sequence of one pig was chosen as the reference, and the image sequences of other four pigs were aligned with the reference sequence so that the RV short-axis and long-axis planes were parallel with the xy-plane and the z-axis, respectively, in all sequences. The RV endocardium and epicardium in the ED frame were segmented using a semiautomatic method. The short-axis segmentation begins from the most apical plane to the plane where tricuspid valve appears. We first labeled the contours of the RV endocardium and epicardium in each short-axis planes by using smooth and closed B-spline curves. We manually picked some points along the RV endocardium and epicardium and then a constant number of points were uniformly sampled on each contours (see Fig. 4 as an example of endocardium segmentation). Triangle meshes were then generated by connecting points in each two neighboring contours anticlockwisely. Transmurally intermediate meshes were interpolated linearly from the endocardium to the epicardium. In order to analyze the RVFW strain in detail, the RVFW was divided horizontally as inferior, inferiorlateral, anteriorlateral, and anterior (1, 2, 3, 4) and vertically as apical, mid, and basal (1, 2, 3) segments. The specific names and positions of the 12 RV segments used in our study are shown in Fig. 3.

FIG. 4.

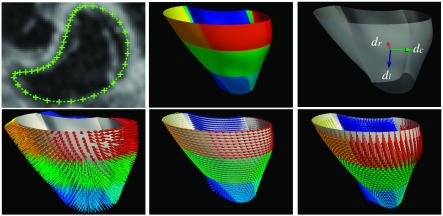
The cardiac coordinate system in our experiments. The left top figure shows the endocardium contour. The mid top figure shows the 12 endocardium segments in colors. The top right figure shows the radial (d_r), circumferential (d_c), and longitudinal (d_l) directions in a vertex of the endocardium. The bottom row shows the d_r, d_c, and d_l directions in all mesh vertices.

FIG. 3.

The names and positions of 12 RV segments used in our study.

In order to evaluate the strains by using Eq. (9), we need to define radial, circumferential, and longitudinal directions at each vertex of the triangle mesh. The radial direction d_r of a vertex was defined as the averaged normal direction of the triangles which joined at the vertex. We defined the normal direction of short-axis planes as n_sa, the circumferential direction d_c was defined as the cross-product of n_sa with d_r, and the longitudinal direction was defined as the cross-product of d_r with d_c. We illustrate the cardiac coordinate system in Fig. 4 and the bottom row of it shows the three orthogonal directions in an example RV mesh.

4. RESULTS

4.A. Validation with sonomicrometry

We first show the result of the sonomicrometry validation in Fig. 5. The left figure shows the scatter plot of the 40 peak two-point strains estimated from our method and those from the sonomicrometry. The 40 peak strains in each measurement come from the two point pairs in each of the five pigs under the four steady states. The correlation between the peak strains is 0.82. The middle and right plots show two example two-point strain curves in sonomicrometry and in our methods. We can see the curves are similar. The correlations of the sono strain curve with the echocardiography strain curve are 0.91 and 0.92, indicate that our method has good temporal consistency with the ground truth.

FIG. 5.

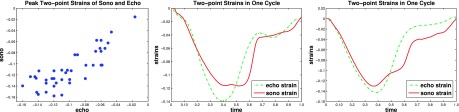
The result from the sonomicrometry validation. Left figure shows the peak two-point strains estimated from the sonomicrometry and echocardiography. The middle and right figures show the correlation between the sonomicrometry-derived and echocardiography-derived two-point strains of two pairs of sonomicrometers.

4.B. Global motion

The global motion was measured by the displacement field. A typical RV myocardium point trajectories in 2D orthogonal planes in a cardiac cycle and the 3D myocardium points displacement at end-systole (ES) are shown in Fig. 6. We can see that the estimated point trajectories are spatiotemporally smooth. The motion of myocardium points is mainly along the radial and longitudinal directions. The average segmental displacements in five pigs are listed in Table I. The numbers show that the average displacement is dominant in the radial and longitudinal directions while the circumferential displacement is smaller. Among the radial and longitudinal directions, the displacement increases in order of apical, mid, and basal segments. The magnitude of the displacement also increases from apical to the basal segments.

FIG. 6.

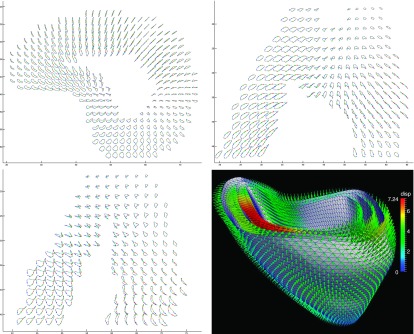
The myocardium point trajectories in the 2D orthogonal views and the 3D displacement field in the ES (arrow points from the ED coordinates to the ES coordinates).

TABLE I.

The average radial, circumferential, longitudinal, and total displacement (mm) of five pigs in 12 segments at ES. The displacement is represented in form of mean(SD). S₁ to S₁₂ stand for the RVFW segments. ${\overline{M}}_{\mathrm{apx}}$, ${\overline{M}}_{\mathrm{mid}}$, and ${\overline{M}}_{\mathrm{bas}}$ are the mean displacements of the apical, mid, and basal segments.

	Apex					Mid					Base
Displacement	S1	S2	S3	S4	${\overline{M}}_{\mathrm{apx}}$	S5	S6	S7	S8	${\overline{M}}_{\mathrm{mid}}$	S9	S10	S11	S12	${\overline{M}}_{\mathrm{bas}}$
Radial	1.82	1.55	1.00	0.81	1.29	1.89	2.88	2.61	1.51	2.22	1.75	3.12	2.95	1.26	2.27
	(1.25)	(0.63)	(1.06)	(0.51)	(0.92)	(1.06)	(0.97)	(0.53)	(0.88)	(0.97)	(1.22)	(1.32)	(0.56)	(0.39)	(1.18)
Circumferential	−0.46	0.49	0.71	1.01	0.44	−1.41	0.07	1.03	0.92	0.15	−1.27	−0.37	0.70	−0.09	−0.26
	(1.07)	(1.15)	(0.44)	(0.77)	(0.99)	(1.11)	(1.63)	(1.08)	(0.90)	(1.48)	(0.90)	(2.16)	(1.10)	(1.01)	(1.44)
Longitudinal	0.57	0.64	0.62	0.43	0.56	1.72	1.48	1.52	1.13	1.47	2.07	2.29	1.95	1.32	1.91
	(0.83)	(0.53)	(0.60)	(0.61)	(0.59)	(1.77)	(1.31)	(1.51)	(0.83)	(1.27)	(0.58)	(1.12)	(2.10)	(1.63)	(1.37)
Magnitude	2.50	2.08	1.68	1.63	1.97	3.42	3.79	3.74	2.56	3.38	3.48	4.62	4.21	2.72	3.76
	(1.54)	(0.91)	(0.94)	(0.78)	(1.03)	(1.75)	(1.38)	(0.66)	(0.73)	(1.21)	(0.79)	(1.44)	(1.03)	(0.76)	(1.20)

4.C. Local motion

The local motion of RVFW was described by its segmental strains. We obtained similar ES segmental strain patterns for the five pigs. The average segment RS, CS, and LS are shown in Table II. We can see that RS and CS decrease in order of mid, basal, and apical segments. The LS decreases in order of mid, apical, and basal segments in the endocardium, while in the midwall and epicardium it decreases in order of apical, mid, and basal segments. The RS increases from the endocardium through the midwall to the epicardium in apical segments, while in the mid and basal segments, midwall have the largest RS, followed by the epicardium and endocardium. The six lateral segments (S₂, S₃, S₆, S₇, S₁₀, S₁₁) have much larger RS than the other side segments. This indicates that RS is stimulated from the mid segments of the midwall. The CS and LS decrease from endocardium through the midwall to the epicardium. This indicates that the LS and CS are stimulated from the endocardium segments.

TABLE II.

The average RS, CS, and LS (%) in the 12 segments of five pigs at ES. The strains are in form of mean(SD). S₁ to S₁₂ stand for the RVFW segments. ${\overline{M}}_{\mathrm{apx}}$, ${\overline{M}}_{\mathrm{mid}}$, and ${\overline{M}}_{\mathrm{bas}}$ are the mean of the four apical, mid, and basal segments.

	Apex					Mid					Base
Strains		S1	S2	S3	S4	${\overline{M}}_{\mathrm{apx}}$	S5	S6	S7	S8	${\overline{M}}_{\mathrm{mid}}$	S9	S10	S11	S12	${\overline{M}}_{\mathrm{bas}}$
	Endo	9.0	18.1	10.3	11.6	12.3	8.6	35.5	23.5	13.5	20.3	4.8	32.6	24.2	3.8	16.4
(13.0)		(17.7)	(5.8)	(9.9)	(11.7)	(9.6)	(21.5)	(19.0)	(19.5)	(19.3)	(9.5)	(6.8)	(11.3)	(21.5)	(17.6)
RS	Midwall	13.2	25.4	15.4	15.3	17.3	15.6	48.3	43.6	22.6	32.5	13.8	47.1	29.9	4.5	23.8
		(14.1)	(18.7)	(8.1)	(14.1)	(13.7)	(10.1)	(18.1)	(20.4)	(27.9)	(22.9)	(9.4)	(7.5)	(10.5)	(19.9)	(20.3)
Epi	17.1	26.4	18.9	14.8	19.3	19.8	40.9	39.8	19.3	30.0	18.9	36.7	22.4	0.5	19.4
	(15.7)	(14.1)	(12.5)	(12.4)	(13.1)	(10.4)	(11.8)	(13.4)	(27.4)	(18.8)	(12.1)	(3.4)	(5.2)	(13.7)	(16.2)
	Endo	−7.0	−12.3	−10.2	−6.4	−9.0	−12.3	−14.7	−18.9	−13.2	−14.8	−15.1	−11.3	−15.6	−7.5	−12.3
(4.5)		(3.7)	(2.1)	(2.4)	(3.9)	(3.7)	(3.4)	(2.3)	(2.9)	(3.8)	(4.9)	(8.0)	(3.3)	(7.9)	(6.6)
CS	Midwall	−3.9	−10.2	−7.6	−5.7	−6.9	−8.9	−10.2	−13.4	−8.6	−10.3	−11.2	−6.3	−11.8	−7.1	−9.1
		(5.9)	(3.7)	(2.0)	(2.8)	(4.3)	(4.4)	(4.0)	(1.8)	(3.5)	(3.7)	(5.3)	(8.2)	(4.5)	(4.3)	(5.8)
Epi	−2.6	−7.9	−5.2	−5.0	−5.2	−6.3	−5.7	−7.8	−4.7	−6.1	−7.5	−2.6	−8.1	−5.1	−5.8
	(5.7)	(4.0)	(1.8)	(3.5)	(4.1)	(4.6)	(4.0)	(3.5)	(4.3)	(3.9)	(4.9)	(7.3)	(5.7)	(3.3)	(5.4)
	Endo	−7.9	−11.0	−11.5	−10.9	−10.3	−8.7	−15.2	−14.0	−9.9	−12.0	−5.1	−11.2	−9.4	−9.8	−8.9
(4.5)		(3.7)	(2.1)	(2.4)	(3.9)	(3.7)	(2.4)	(2.3)	(2.9)	(3.8)	(4.9)	(8.0)	(3.3)	(7.9)	(6.6)
LS	Midwall	−7.0	−11.1	−11.9	−10.1	−10.0	−5.2	−10.4	−10.7	−5.9	−8.0	−7.2	−5.8	−8.7	−9.4	−7.7
		(3.4)	(2.4)	(5.6)	(3.8)	(4.0)	(4.5)	(5.0)	(6.5)	(0.3)	(5.7)	(5.0)	(6.5)	(2.7)	(4.0)	(4.5)
Epi	−5.9	−9.5	−10.4	−8.6	−8.6	−5.3	−8.1	−8.3	−7.9	−7.4	−6.1	−6.1	−7.0	−7.2	−6.6
	(4.9)	(3.3)	(4.8)	(3.0)	(4.1)	(3.7)	(1.4)	(5.2)	(3.2)	(3.5)	(5.6)	(2.7)	(1.4)	(3.9)	(3.4)

The average principal strains in the 12 segments at ES are shown in Table III. We can see that E₁ has the maximum positive strain value and E₃ has the minimum strain value in each segment. From our experiment, the eigenvector directions associated with the largest eigenvalue have good agreement with the radial directions of the RV myocardium. E₁ has maximum at the epicardium in apical segments, while it has maximum at the midwall in both the mid and basal segments. E₂ and E₃ decrease from the endocardium through the midwall to the epicardium.

TABLE III.

The average principal segment strains (%) of five pigs at ES. The strain are in form of mean(SD). S₁ to S₁₂ stand for the RVFW segments. ${\overline{M}}_{\mathrm{apx}}$,${\overline{M}}_{\mathrm{mid}}$, and ${\overline{M}}_{\mathrm{bas}}$ are the mean of the four apical, mid, and basal segments.

	Apex					Mid					Base
Strains		S1	S2	S3	S4	${\overline{M}}_{\mathrm{apx}}$	S5	S6	S7	S8	${\overline{M}}_{\mathrm{mid}}$	S9	S10	S11	S12	${\overline{M}}_{\mathrm{bas}}$
	Endo	16.8	21.4	14.6	16.0	17.2	16.1	39.1	27.5	19.1	25.4	13.0	40.8	35.9	37.0	31.7
(18.1)		(15.7)	(5.0)	(10.3)	(12.2)	(9.7)	(22.9)	(18.8)	(20.8)	(19.1)	(8.1)	(8.8)	(13.1)	(13.8)	(10.5)
E1	Midwall	20.2	27.7	18.8	19.5	21.5	23.5	53.8	49.5	30.0	39.2	21.7	57.2	42.5	38.3	39.9
		(19.1)	(17.7)	(6.9)	(14.2)	(14.1)	(12.4)	(18.9)	(22.0)	(32.8)	(24.2)	(10.3)	(8.9)	(14.5)	(30.6)	(20.9)
Epi	22.2	28.7	22.7	19.2	23.2	25.7	47.6	48.6	28.5	37.6	25.8	45.4	34.7	29.6	33.9
	(18.7)	(13.8)	(12.6)	(13.1)	(13.7)	(12.4)	(11.6)	(19.8)	(34.3)	(22.1)	(13.8)	(2.9)	(14.7)	(20.1)	(14.9)
	Endo	−7.6	−9.0	−8.9	−6.9	−8.1	−9.2	−12.9	−14.0	−9.0	−11.3	−7.1	−9.4	−9.8	−10.2	−9.1
(1.5)		(1.8)	(0.5)	(1.7)	(1.6)	(3.2)	(4.2)	(3.1)	(5.3)	(4.3)	(5.1)	(3.8)	(6.4)	(3.9)	(4.6)
E2	Midwall	−5.0	−7.6	−7.2	−6.4	−6.5	−5.9	−8.6	−10.2	−5.5	−7.6	−1.7	−4.2	−7.1	−6.3	−4.8
		(2.1)	(3.2)	(1.3)	(3.1)	(2.5)	(2.6)	(3.9)	(3.4)	(5.1)	(4.0)	(7.1)	(3.9)	(6.7)	(3.9)	(5.5)
Epi	−2.5	−5.8	−5.1	−5.4	−4.7	−2.2	−4.3	−6.0	−2.1	−3.7	−0.7	−0.6	−4.2	−3.2	−1.9
	(3.0)	(4.2)	(2.1)	(4.2)	(3.4)	(3.4)	(3.7)	(5.1)	(4.9)	(4.2)	(8.1)	(4.1)	(6.7)	(6.1)	(6.1)
	Endo	−15.1	−17.6	−17.1	−14.8	−16.1	−19.3	−20.6	−22.9	−19.6	−20.6	−21.4	−21.2	−21.7	−16.2	−20.1
(2.7)		(2.1)	(4.0)	(5.0)	(3.5)	(3.0)	(4.4)	(3.0)	(1.6)	(3.2)	(6.8)	(4.9)	(1.3)	(6.5)	(5.0)
E3	Midwall	−13.0	−16.0	−15.7	−13.7	−14.6	−16.1	−17.3	−19.9	−16.1	−17.4	−17.4	−17.6	−19.7	−16.4	−17.8
		(2.3)	(2.6)	(5.1)	(4.9)	(3.8)	(4.1)	(4.9)	(4.7)	(2.8)	(4.1)	(7.2)	(4.0)	(0.5)	(7.8)	(5.2)
Epi	−11.1	−13.8	−14.4	−12.5	−13.0	−13.0	−13.4	−16.6	−12.7	−13.9	−13.2	−13.5	−17.0	−15.9	−14.9
	(1.9)	(3.4)	(5.5)	(4.7)	(3.9)	(4.5)	(4.9)	(5.7)	(4.4)	(4.7)	(6.8)	(2.8)	(2.0)	(7.8)	(5.2)

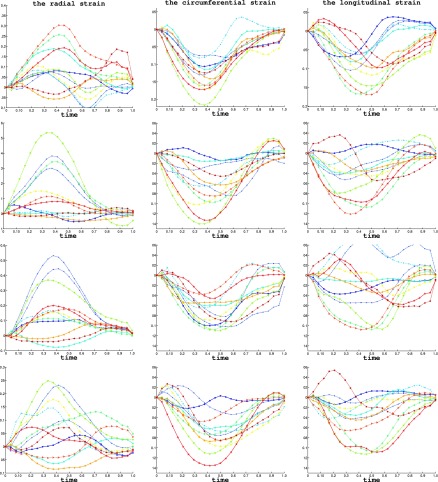
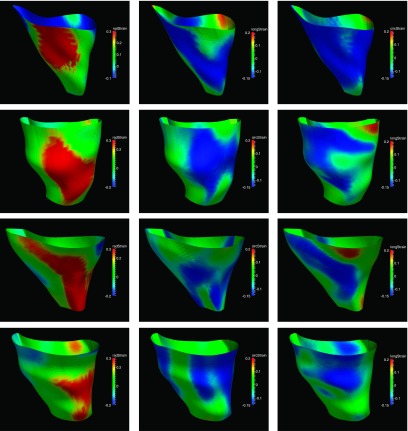
The segmental strain curves with respect to time for a typical pig are shown in Fig. 7. The RS, CS, and LS with colormap on the myocardium in a cardiac cycle generated by using Paraview software⁵⁶ are shown in Figs. 8, 9, and 10, respectively. Due to limit of space, we display one mesh for every two frames in each cardiac cycle. The RS, CS, and LS generally reach to maximum simultaneously at ES. The RS is more dominant in the six lateral segments. The basal and mid segments have larger RS than the apical segments. The CS and LS are more uniformly distributed in all segments.

FIG. 7.

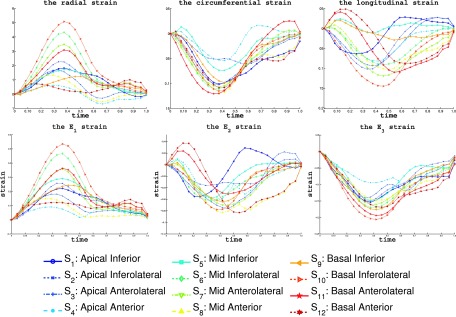
The RVFW segmental strains of a typical echocardiography sequence in a baseline cardiac cycle. The top row shows the average value of RS, CS, and LS of the 12 segments. The bottom rows shows the principal strains E₁, E₂, and E₃. The cardiac time is normalized to 1. The bottom shows the markers for each segments in the strain plots.

FIG. 8.

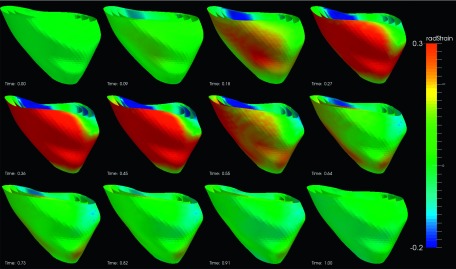
Radial strain of an example echocardiography sequence varying with time in a cardiac cycle. (The cardiac time is normalized between 0 and 1.)

FIG. 9.

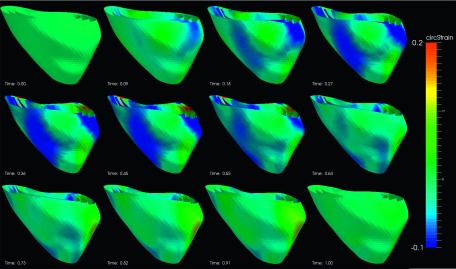
Circumferential strain of an example echocardiography sequence varying with time in a cardiac cycle. (The cardiac time is normalized between 0 and 1.)

FIG. 10.

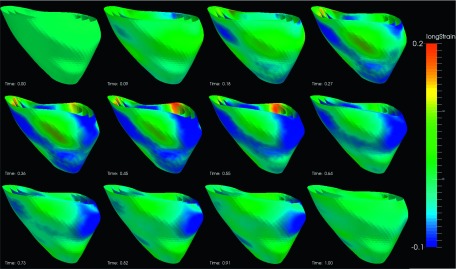
Longitudinal strain of an example echocardiography sequence varying with time in a cardiac cycle. (The cardiac time is normalized between 0 and 1.)

4.D. Transmural myocardial strain

We analyzed the transmural strains variation by using a multiple layer cardiac mesh. The mesh consisted of five layers, of which the three intermediate layers were interpolated from the endocardium to the epicardium along the transmural direction. We denote the five layers from the endocardium to epicardium as L₁, L₂, L₃, L₄, and L₅. The average RS, CS, and LS in each segments at ES were estimated and listed in the Table IV. We can see that the segmental strains in different transmural layers have similar strain patterns at ES. For RS, in the apical segments, they increase from the endocardium to the epicardium. In the mid segment, they increase first then reach maximum at subepicardium and then decrease at epicardium. In the basal segments, they increase first and reach maximum at midwall then decrease. The CS and LS decrease linearly from endocardium to the epicardium.

TABLE IV.

The RS, CS, and LS (%) in the transmural layers of a typical pig at ES. S₁ to S₁₂ are the RVFW segments. ${\overline{M}}_{\mathrm{apx}}$, ${\overline{M}}_{\mathrm{mid}}$, and ${\overline{M}}_{\mathrm{bas}}$ are the mean strain of the apical, mid, and basal segments.

		Apex					Mid					Base
Layers		S1	S2	S3	S4	${\overline{M}}_{\mathrm{apx}}$	S5	S6	S7	S8	${\overline{M}}_{\mathrm{mid}}$	S9	S10	S11	S12	${\overline{M}}_{\mathrm{bas}}$
RS	L1	8.0	7.3	5.1	5.0	6.4	18.9	24.9	8.7	6.5	14.7	5.8	28.9	17.9	3.4	9.4
	L2	12.6	12.9	9.2	6.4	10.2	21.7	42.7	26.1	15.1	26.4	3.4	49.6	33.5	1.1	21.9
	L3	17.3	18.7	12.6	6.9	13.9	23.5	53.9	40.4	18.6	34.1	13.3	58.1	41.3	2.7	28.8
	L4	21.7	22.8	14.2	7.6	16.6	27.3	56.0	46.7	15.5	36.4	20.4	53.1	38.2	0.2	27.9
	L5	25.5	25.1	14.2	7.8	18.1	29.9	49.9	41.3	9.0	32.5	22.5	41.4	27.6	3.6	22.0
CS	L1	−10.6	−7.6	−13.0	−8.0	−9.8	−11.5	−16.1	−21.7	−17.0	−16.5	−13.5	−16.0	−17.2	−12.4	−14.8
	L2	−9.3	−6.3	−11.3	−6.3	−8.3	−7.6	−14.3	−17.3	−14.6	−13.4	−12.3	−13.3	−14.2	−10.8	−12.7
	L3	−7.8	−5.0	−9.5	−4.7	−6.8	−4.2	−12.1	−12.6	−11.9	−10.2	−10.6	−10.4	−10.8	−9.4	−10.3
	L4	−6.8	−3.7	−7.8	−4.2	−5.6	−2.5	−9.5	−7.7	−9.7	−7.4	−8.4	−7.9	−7.3	−8.4	−8.0
	L5	−6.1	−2.2	−6.0	−3.8	−4.5	−0.8	−7.2	−3.2	−7.8	−4.7	−5.9	−5.9	−4.6	−7.7	−6.0
LS	L1	−5.9	−10.2	−6.2	−5.6	−7.0	−8.2	−16.7	−13.3	−10.1	−12.1	−8.0	−15.5	−4.2	−0.7	−7.1
	L2	−4.3	−10.5	−7.1	−5.9	−6.9	−3.5	−14.5	−12.7	−10.3	−10.3	−4.8	−11.8	−5.3	−2.5	−6.1
	L3	−2.5	−10.0	−7.5	−6.0	−6.5	−0.2	−11.6	−10.5	−9.4	−7.8	−1.8	−8.0	−6.0	−3.6	−4.9
	L4	−0.5	−8.7	−6.9	−5.8	−5.5	−1.9	−9.0	−8.3	−7.9	−5.8	−0.4	−5.5	−6.1	−3.5	−3.7
	L5	−1.1	−7.0	−6.2	−5.6	−4.4	−2.7	−6.4	−6.2	−6.5	−4.1	−2.1	−3.5	−5.2	−2.3	−2.2

4.E. Principal strains direction

The average principal strains in all RVFW segments are shown in the bottom row of the Fig. 7. From Fig. 7, we can see that E₁ is most similar to the RS during a cardiac cycle. This means that the largest elongation direction during cardiac cycle is along the radial direction of the myocardium. In Fig. 11, the directions of the E₃ are shown as line segments at each vertices. We can see that the directions of E₃ become almost uniformly distributed at the time of ES. The E₃ directions at the ES are orthogonal to the myofiber orientation¹⁴ which indicates that the cross fiber shortening is dominant at the time of ES. Similarly, the E₂ directions are also more uniformly distributed in the ES. The directions of the E₂ at time ES are mostly consistent with the RV myofiber orientation.

FIG. 11.

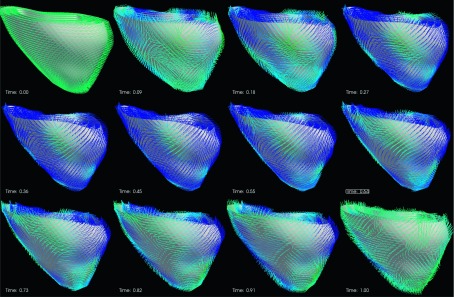
The direction of the E3 strain in a cardiac cycle. (The cardiac time is normalized between 0 and 1.) The strain direction is represented by a line segment at each vertex of the myocardium.

4.F. Pacing steady states

We have observed similar variations of segmental strains under varying steady states for different pigs. We use a typical pig to show its strain pattern variation in different steady states. For simplicity, we use endocardium strains for an example. The strain curves of one cardiac cycle of four steady states are shown in Fig. 12.

FIG. 12.

From top to bottom, it shows the RS, CS, and LS of a same pig under baseline, RV pacing, RV Apex pacing and RVOT pacing steady states. (The color and marker style of the curves are same as in 7.)

The first row shows the average RS, CS, and LS in each segment of the baseline.

The second row in Fig. 12 shows the average segmental strains in the case of RV pacing. The average RS in mid segments was significantly larger than the baseline. The RS was also more dominant in the lateral segments than baseline. The average CS and LS in all segments were smaller than those in the baseline.

The third row in Fig. 12 shows the average segmental strains in the case of RV apex pacing. We can see after RV apex pacing the average RS in apical segments increased significantly over the baseline. However, it was smaller in the basal segments. The radial elongation is more dominant in the lateral segments (S₂, S₃) than baseline. The average CS in all segments were smaller than the baseline. Similarly, nearly all segments had smaller LS than the baseline.

The fourth row in Fig. 12 shows the strains in the case of RVOT pacing. The average RS in apical is slightly larger than that of baseline. The average CS and LS are smaller than baseline. The region near side segments opposite to right ventricular inflow tract (RVIT) (S₅, S₉, S₁₀) has negative RS and the segments near RVOT (S₃, S₄, S₇, S₈, S₁₁, S₁₂) have larger RS. That means RS is dominant in the segments near RVOT. The average CS of all segments is smaller than that in baseline. The average of LS in all segments is smaller than that of baseline.

The corresponding strains on RVFW at ES are shown in Fig. 13 with colormap and the values of the ES strain and their average in apical, mid, and basal segments are listed in Table V. From Fig. 13, we can see that the maximum variation of the RS occurs at regions near the pacing sites. In Table V, we can see that in RV pacing steady state, the lateral mid segments (S₆, S₇) have significant increase in RS than baseline. Similarly, in RV apex pacing, the two lateral apical segments (S₂, S₃) have significant increase in RS than baseline. In RVOT pacing, the apical and mid segments near RVOT (S₃, S₄, S₇, S₈) have significant increase in RS than baseline. This might indicate that the electric stimulation makes the RV myofiber stretching most near the pacing sites. However, due to the potential being propagated more slowly though the myofiber rather than through the Purkinje system, the CS and LS are smaller than those of the baseline.

FIG. 13.

The endocardium RVFW of a typical pig colormapped with RS, CS and LS at ES in baseline, RV pacing, RV apex pacing and RVOT pacing.

TABLE V.

The average endocardium segment strains (%) at ES in the four steady states. S₁ to S₁₂ are the RVFW segments. ${\overline{M}}_{\mathrm{apx}}$, ${\overline{M}}_{\mathrm{mid}}$, and ${\overline{M}}_{\mathrm{bas}}$ are the mean strain of all apical, mid, and basal segments. BSL, RV, RVA, and RVOT stand for baseline, RV pacing, RV apex pacing, and RVOT pacing, respectively.

		Apex					Mid					Base
States		S1	S2	S3	S4	${\overline{M}}_{\mathrm{apx}}$	S5	S6	S7	S8	${\overline{M}}_{\mathrm{mid}}$	S9	S10	S11	S12	${\overline{M}}_{\mathrm{bas}}$
BSL	RS	8.0	7.3	5.1	5.0	6.4	18.9	24.9	8.7	6.5	14.7	−5.8	28.9	17.9	3.4	9.4
	CS	−10.6	−7.6	−13.0	−8.0	−9.8	−11.5	−16.1	−21.7	−17.0	−16.5	−13.5	−16.0	−17.2	−12.4	−14.8
	LS	−5.9	−10.2	−6.2	−5.6	−7.0	−8.2	−16.7	−13.3	−10.1	−12.1	−8.0	−15.5	−4.2	−0.7	−7.1
RVP	RS	−1.0	38.2	30.0	0.6	16.9	0.6	34.3	53.4	13.5	25.4	−2.4	11.4	8.0	0.5	4.2
	CS	−0.4	−6.3	−2.8	−6.5	−4.0	−1.6	−9.4	−14.0	−9.9	−8.7	−5.7	−8.3	−13.3	−3.6	−7.7
	LS	−1.2	−4.7	−2.9	−0.1	−1.6	−3.7	−10.3	−7.0	−4.2	−6.3	−3.4	−11.9	−9.6	−0.2	−6.3
RVA	RS	9.4	41.4	50.9	16.7	29.6	−7.2	11.4	36.9	14.9	14.0	−1.7	15.4	19.5	−4.0	7.3
	CS	−9.5	−5.6	−8.5	−6.5	−7.5	−5.8	−10.0	−9.3	−8.5	−8.4	−5.5	−3.7	−3.4	−6.2	−4.7
	LS	−3.5	−5.5	5.7	6.9	−0.9	−1.2	−6.4	−9.4	−0.5	−4.1	−1.7	−10.3	−2.1	−0.9	−2.2
RVOT	RS	2.9	10.7	20.8	12.7	11.8	−4.9	8.5	28.0	18.7	12.6	−7.7	−4.0	4.7	6.3	−0.02
	CS	−2.6	−0.9	−5.7	−4.0	−2.8	−6.5	−6.2	−10.1	−7.1	−7.5	−6.7	−6.5	−11.8	−6.2	−7.8
	LS	−0.2	−0.0	−2.2	−2.0	−1.0	−3.5	−7.1	−7.2	−1.9	−4.9	−4.5	−7.9	−10.3	−0.3	−5.8

5. DISCUSSION

We have proposed a temporally diffeomorphic motion estimation method and applied it to strain analysis of 3D echocardiography sequences of different steady states.

Our proposed method used an intensity-based approach which was not limited to specific image modality. It was a general method and it has four advantages over the existing methods on RV motion estimation from MRI and LV motion estimation from echocardiography. First, our method automatically searched for a transformation which can maintain spatiotemporal smoothness even under low spatial and temporal image resolutions. Such temporal smoothness was not considered in most of the existing RV motion estimation methods based on MRI.^20,21 Although a spatiotemporally smooth 4D transformation was also used in the work of Tustison and Amini,²² it requires intensive human interaction. Methods proposed for LV tracking from 3D echocardiography did not consider the temporal smoothness^47,48 either. Second, our method optimized the image similarity by using a frame-to-frame approach. In the LV tracking methods,^40,49 they used an approach which optimized the similarity between the reference frame and all of the following frames. The speckle patterns in the distant frames of the RV images were usually unstable which degraded the tracking accuracy. Third, there was no need of feature extraction or surface modeling in our motion estimation method. The results of surface model based methods usually depended on the accuracy of the surface extraction,^8,20 while the motion estimation in our method used all of the voxel information and had subvoxel accuracy. For RV images, our method was also more efficient because there is no need to modeling the complex shape of its endocardial and epicardial surfaces. Finally, our method optimized the velocity field in a spatiotemporally smooth functional space, which made the transformation of myocardial wall to be diffeomorphic, which was physically plausible for the heart motion. Our method has a limitation that the physical constraints on myocardium are not included. It has been demonstrated that physical constraints such as myocardium incompressibility^40,50 can improve the performance of LV motion estimation. However, a segmentation of the myocardium is necessary, which is not a trivial task.

We used sonomicrometry as ground truth to evaluate the accuracy of motion estimation. It has been used as reference measurement in the LV function studies.^51–53 In this study, the high correlation value between the image derived peak two-point strains and those derived by sonomicrometry demonstrated that our estimated motion had good agreement with real motion.

In our study, we estimated both the global and local motions. Longitudinal and total displacement were largest at the base segments. This was similar to reports by other researchers.^20,21 Our estimated principal strains of E₂ and E₃ in apical, mid, and basal segments on endocardium were −8.1%, −11.3%, −9.1% and −16.1%, −20.6%, −20.1%, respectively, and they were close to those estimated by Haber et al.²¹ by using tagged-MRI, which were −10%, −13%, −9% and −23%, −24%, −19%, respectively. Our estimated maximum principal strain E₁ in apical, mid, and basal segments on endocardium were 17.2%, 25.4%, 31.7%, while they were 30%, 33%, 26% in Ref. 21. One of the possible reasons for the large difference in E₁ from other research results was that it has larger standard deviation due to the difficulty to labeling the endocardium and epicardium. Another reason may be that the apical strains were underestimated in this study due to two limitations of the image acquisition. First, due to requirement of the frame rate, the cross section of the image was in an acute angle shape, which frequently led to incomplete RV apical images. Second, images at apex where the ultrasound probe contacted with heart wall usually had echoes which were difficult to track due to lack of meaningful information. These phenomenon of underestimation or failure of speckle tracking in the RV apex have also been reported in previous studies.^24,51

In our method, the motion estimation and the cardiac model editing were separated. That means the motion estimation complexity did not depend on the cardiac mesh complexity. It was flexible to use different cardiac meshes for different strain analysis requirements with the same estimated displacement field. In our study, we used a 12-segments model by dividing each of the apical, mid, and basal segments into four segments. We have found that the six lateral segments have larger RS than side segments. Our method also provided a general way to evaluate the strains along transmural layers. Our result showed decrease of the CS along transmural direction which was consistent with result of other researcher.⁵²

We used both the geometrical directions (radial, circumferential, longitudinal) and the mathematical directions (eigenvectors of strain tensor) to evaluate the strains. These directions were all defined at each vertex of the cardiac mesh. The maximum principal strain direction has good agreement with that of the radial direction. The directions of E₂ and E₃ were oblique in the RV myocardium and were closely related to the RV myofiber direction and the cross-fiber direction. The radial, circumferential, and longitudinal directions were estimated when the cardiac mesh was generated. It did not depend on the cardiac deformation. The principal strain directions were acquired after the deformation was estimated.

Most of the studies on RV pacing focused on its effect on the LV function and dyssynchrony.^54,55 There were no RV strains study of image sequences under different steady states generated by varying the pacing sites. In our study, we have found that the segments closest to the pacing sites exhibited largest increase of RS. The CS and LS in all segments became smaller than baseline. Our method can be applied to search for the optimal RV pacing site with which myocardium segmental strain patterns are most similar to those of baseline.

6. CONCLUSION

In this paper, we proposed a temporally diffeomorphic motion estimation method and validated with 3D echocardiographic sequences of open-chest pig hearts. The results from the sonomicrometry show that our method has good consistency with sonomicrometry in strain estimation, which means our method has high accuracy under different cardiac conditions. We applied the method to the RVFW strain analysis of the different steady states. Segmental strain of different steady states were studied and possible reasons were analyzed. The consistency of the strain measurements in our method with those from MRI shows our method is feasible to study RV functions from 3D echocardiography.