Small molecule solvation changes due to the presence of salt are governed by the cost of solvent cavity formation and dispersion

Abstract

We are interested in the free energies of transferring nonpolar solutes into aqueous NaCl solutions with salt concentrations upwards of 2 M, the Hofmeister regime. We use the semi-explicit assembly (SEA) computational model to represent these electrolyte solutions. We find good agreement with experiments (Setschenow coefficients) on 43 nonpolar and polar solutes and with TIP3P explicit-solvent simulations. Besides being much faster than explicit solvent calculations, SEA is more accurate than the PB models we tested, successfully capturing even subtle salt effects in both the polar and nonpolar components of solvation. We find that the salt effects are mainly due to changes in the cost of forming nonpolar cavities in aqueous NaCl solutions, and not mainly due to solute-ion electrostatic interactions.

I. INTRODUCTION

Beginning with Hofmeister more than 120 years ago, it has been known that adding salts at high concentrations can precipitate proteins differentially and alter the free energies of dissolving nonpolar solutes in water. Salt ions affect the structures, functions, and dynamics of biomolecules.^1–5 The types and concentrations of ions in water can affect the interactions between nonpolar solutes, promoting or hindering their aggregation states.^6–11

When modeling molecular systems, ions are often included explicitly^12–17 in order to best incorporate their detailed effects. This involves adding individual particles of specific size, charge, and van der Waals interactions in an environment of explicit water molecules, and there have been many types of explicit ion models developed for this purpose.^18–24 In some cases, implicit-solvent modeling has been useful because of the computational efficiency of continuum modeling. Ions are typically treated with general salt-effect terms in implicit solvents, such as the Boltzmann term in the Poisson-Boltzmann (PB) solvent model for calculation of solvation free energies.²⁵ Such modeling supposes that: (1) an ion interacts with other ions through the average density and (2) ion size is infinitesimal.^25,26 Such assumptions can be problematic where molecular structural effects are important.

In this work, we model the effects of salt ions on solvation using the recently developed field-variation approach to the semi-explicit assembly (SEA) model of water.^27–29 It involves mapping of polar and nonpolar hydration free energies (ΔG_hyd) for a series of simple spherical particles onto more complex molecular geometries. Instead of using pure water simulations in building our mapping contours, we instead use electrolyte solutions of increasing concentration. As opposed to the ΔG_hyd­ that we would get from a pure water solvent contour, this will give us solvation free energies (ΔG_solv) specific to the given electrolytic environment, and the ΔG_solv trends for the specific environments (see Figure 1) should be preserved, this while maintaining the same performance characteristics as the only change is the shape of the spherical particle free energy contours from the new solvent environment. Because the ion concentration is systematically increasing, we should also be able to project to intermediate concentrations and obtain intermediate ion-effect trends. We evaluate here this approach in comparisons between explicit solvent free energy calculations and experimentally derived solvation trends and we investigate the primary sources of ion specific effects in solvation.

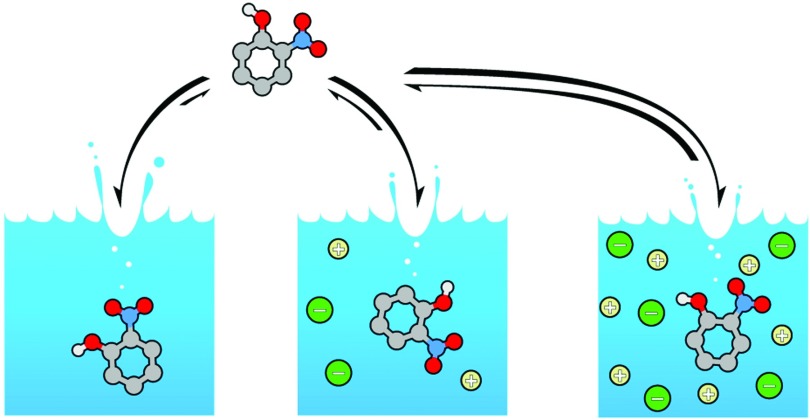
FIG. 1.

Illustration of the solvation series of 2-nitrophenol as a function of increasing NaCl concentration. As the number of ions increases, the air-to-solution equilibrium shifts away from solution solvation.

II. THEORY AND METHODS

A. Molecular dynamics protocol in pure water or NaCl solutions

We performed alchemical free energy calculations to compute solvation free energies in explicit solvent of both model Lennard-Jones (LJ) spheres and 43 neutral form polar and nonpolar small molecules with experimental hydration and Setschenow coefficients for NaCl solutions, this with a simulation protocol similar to our previous pure TIP3P water studies.³⁰ The model LJ sphere calculations were for construction of environment contours for the nonpolar and field-variant polar terms of SEA, while the small molecule calculations were for explicit solvent calculation comparison values. Solvation free energies were calculated with thermodynamic integration (TI).^31,32 A brief summary of the protocols follows, with emphasis on differences with previous studies.³³

Neutral solutes were solvated in either a dodecahedral TIP3P³⁴ water box or NaCl solution box, with at least 1.5 nm from the solute to the nearest box edge. Separate simulations were performed at different alchemical intermediate λ values with a window spacing and equilibration protocol as described in previous work.³³ NPT ensemble production simulations of either 5 ns or 10 ns in length were performed at each λ value to calculate free energies with TI for the neutral molecule and model spheres, respectively. As in previous studies, simulations were run with periodic boundary conditions with smooth particle mesh Ewald for electrostatics and switched LJ interactions with long-range energy and pressure corrections. The real-space electrostatic cutoffs are 14 Å for model sphere simulations and 10 Å for neutral molecule simulations. We tested using a 14 Å cutoff for some of the neutral molecules, but the results were identical with the shorter cutoff. Other simulation parameters were the same as those in previous studies,³³ and all explicit solvent simulations were performed with GROMACS 4.5.5.^35–37

The polar part solvation free energy (ΔG_pol) for model spheres with LJ σ values of 1.4, 2.2, 3.0, and 3.8 Å, LJ ɛ values of 0.03125, 0.0625, 0.125, and 0.25 kcal/mol, and charges of −1.0, −0.5, −0.4, −0.2, −0.1, +0.5, and +1.0 were calculated for both 1.05 M and 2.18 M NaCl solutions, containing 14 and 28 NaCl pairs, respectively. We found the specific salt effects on the cation ΔG_pol values to be minimal, so the use of only two positive charges in this series was sufficient to capture the contour changes. The TIP3P matched Joung and Cheatham Na⁺ and Cl⁻ LJ parameters were used to represent NaCl.²⁰ The nonpolar model sphere contour, which contains both the cost of solvent cavity formation and dispersion related effects, was constructed using LJ σ values of 0.6, 1.4, 2.2, 3.0, 3.8, 4.6, and 5.4 Å and LJ ɛ values of 0.015625, 0.0625, 0.125, 0.25, 0.5, 1.0, and 4.0 kcal/mol in these same 1.05 M and 2.18 M NaCl solutions.

The 43 small molecule solutes, tabulated in the supplementary material,³⁸ were modeled using the GAFF force field parameters³⁹ and AM1-BCC⁴⁰ partial charges. Their calculated solvation energies in TIP3P water, 1.05 M, and 2.18 M NaCl solutions were obtained from the above alchemical free energy simulation protocol, and we refer to these results as “TIP3P values.” Experimental ΔG_hyd in water were obtained directly from other studies,³⁰ while experimental ΔΔG_solv (and ΔG_solv) in NaCl were calculated from corresponding Setschenow coefficients reported in other studies; see the supplementary material for calculation details.^38,41 Finally, ΔG_solv values for a subset of these 43 solutes were performed in 0.51 M NaCl solutions (7 NaCl pairs) for concentration interpolation comparisons.

B. SEA ΔG_solv calculation in NaCl solutions

We have recently developed a field variant of the SEA model for water in our lab and we have observed it to reproduce the solvation energy in water for a wide range of solutes: atomic ions, nonpolar solutes, neutral polar solutes, and molecular ions, with accuracy comparable to explicit solvent models.²⁸ Here we use this model to calculate solvation energy, ΔG_solv, in 1.05 M or 2.18 M NaCl solutions by using free energy contour constructions in such electrolyte solutions. The protocol is briefly described as follows, with emphasis on differences from pure water calculations.²⁸

The SEA ΔG_solv results are a combination of separate nonpolar (ΔG_np) and polar (ΔG_pol) solvation free energy calculations in NaCl solution. When calculating ΔG_np in NaCl solutions, we follow all protocols as in the standard SEA^27,42 ΔG_np calculations except that the ΔG_np-σ-ε table was re-constructed with data from above model sphere simulations in NaCl solutions. The r_w-σ-ɛ table is the same as that in pure water,⁴² this because we observed no significant change in the location of the 1st peak of the water oxygen g(r) around neutral model spheres in the salt solutions. We did not observe significant penetration of Na⁺ and Cl⁻ into these spheres’ 1st solvation shell (Figure S2 in the supplementary material).³⁸

To calculate the ΔG_pol term, we first construct a solvent accessible surface for a given solute molecule, then we sum up the associated ΔG_pol values for each exposed surface patch to yield the solute's total ΔG_pol.²⁸ In more detail:

• 1.Calculate the average sphere-solvent distance (r_sol) in the 1st solvation shell for the model sphere (with various σ, ɛ, q values) simulations and build an r_sol-σ-ɛ-q table. We found that both positively charged and neutral sphere r_sol values were identical to their r_w values in pure TIP3P water as the above discussion indicates. However, Na⁺ ions sometimes penetrated into negatively charged sphere 1^st solvation shells. In such cases, we calculate r_O and r_Na from water oxygen and Na⁺'s RDF separately and take their weighted average as r_sol (r_sol = n_O · r_O + n_Na · r_Na)/n_total), where n_oxygen is the number of water oxygens in the 1st solvation shell, r_O is the 1st peak in the RDF, and n_Na and r_Na are corresponding numbers for Na⁺.
• 2.Calculate model sphere ΔG_pol values in NaCl solutions, and build ΔG_pol contours as a function of the curvature and electric field at the sphere solvent accessible surfaces: ΔG_pol-C-E (C = 1/r_sol, E = q/r_sol²).
• 3.To calculate ΔG_pol for any given solute, first calculate the average distances between solute atoms and solvent (r_sol) using their LJ parameters and partial charges (q) from interpolation with the above r_sol-σ-ɛ-q surface, and build a Lee-Richards solvent accessible surface with these r_sol values. This initial surface was followed by an adaptive surface refinement procedure that accounts for strongly charged atoms attracting neighboring atom water molecules, squeezing these more distant solute-solvent boundaries.²⁸ In this procedure, we first calculate a new effective charge at each surface patch with its local electric field and curvature. We then rebuild this patch with new r_sol values interpolated from the above r_sol-σ-ɛ-q surface using the new effective charge.
• 4.
  Calculate the associated energy for each exposed surface patch by inputting its curvature and electric field in the above ΔG_pol-C-E contour. The sum of all these patch ΔG_pol values yields the solute's total ΔG_pol,

  $$\Delta G_{pol}=\sum _{i=1}^M{a}_i\Delta G_{pol}(E_i,C_i),$$ (1)

  where a_i is the surface patch's area, calculated as a unit-less ratio of the patch's area over the corresponding solute atom's total area (exposed + buried), M is the number of exposed surface patches, C_i is the curvature, approximated as 1/r_is, where r_is is the distance from surface patch i to its corresponding atom s. Finally, E_i is the electric field at surface patch i, with contributions from all solute atoms: $E_i=\frac{1}{4\pi {\varepsilon }_0}{\sum }_{s=1}^N\frac{q_s}{r_{si}^2}{\widehat{\mathbf{r}}}_{si}$, where N is the number of solute atoms, r_si is the distance between atom s and surface patch i, and ${\widehat{\mathbf{r}}}_{si}$ is the unit vector between them. Refer to our recent publications^28,29 for more details.

C. Poisson-Boltzmann ΔG_pol calculations in pure water or NaCl solutions

We used the adaptive Poisson-Boltzmann solver (APBS) v 1.4,⁴³ pbsa^44–46 in AMBER tools 1.4,⁴⁷ and Delphi v6.5^48,49 to calculate PB ΔG_pol values in this work. To be consistent with the SEA and TIP3P calculations, atom LJ parameters were assigned using GAFF³⁹ with AM1-BCC⁴⁰ partial charges. The van der Waals surface was used as the dielectric boundary, continuum dielectric constants of 2 and 78 were used for solute and solvent, respectively, the water probe radius was set to 1.4 Å, and a PB grid resolution of 0.25 Å was chosen. In NaCl solution calculations, both the nonlinear Poisson-Boltzmann equation (NPBE) and linear Poisson-Boltzmann equation (LPBE) with various ion exclusion radii were tested (see the supplementary material for the results),³⁸ though we should expect the NPBE to perform better in the higher electrolyte concentrations of interest in this study.

III. RESULTS AND DISCUSSION

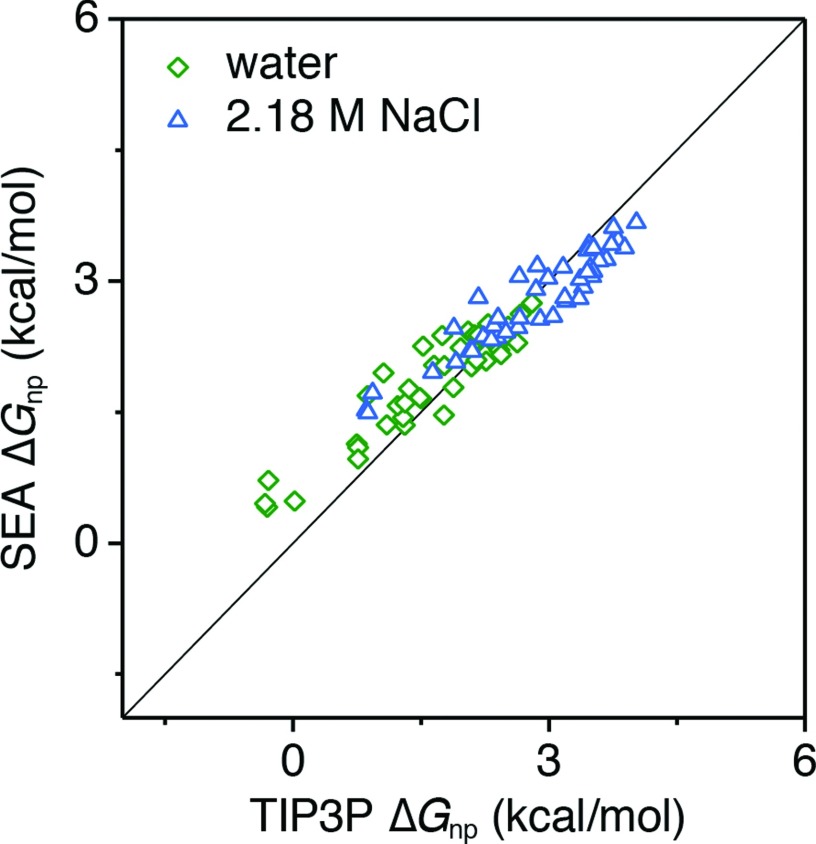
Figure 2 compares the nonpolar part of the solvation free energy (both in water and in a 2.18 M NaCl solution) calculated with our SEA model relative to explicit TIP3P water. SEA reproduces these 43 solutes’ TIP3P ΔG_np both in water and in NaCl solution, with coefficients of determination (R²) of 0.87 (water) and 0.88 (NaCl). The root mean squared errors (RMSE) are also well below kT at 0.39 kcal/mol and 0.36 kcal/mol for water and NaCl solutions, respectively. In comparison, the linear surface area approach, γA + b, employed by most prevailing implicit solvent models (e.g., PBSA or GBSA), yields an R² of 0.15 and RMSE of 1.2 kcal/mol relative to pure TIP3P results for these solutes.⁴² Most current implicit approaches do not adjust ΔG_np in response to the salt concentration of the solution. This is due to the lack of experimental data for fitting γ and b, though this would in principle be possible with salt concentration dependent data for the linear alkanes. Optimizing γ and b would potentially fix systematic offsets and linear trend issues for the alkanes; however, we suspect the accuracy for comparisons on a large set of solutes would be no better than that in water.

FIG. 2.

ΔG_np for neutral solutes in both water and 2.18 M NaCl compared to TIP3P simulations. The ∼1.5 kcal/mol hydrophobic shift in solvation seen in the concentrated NaCl solution is reproduced by the SEA nonpolar term.

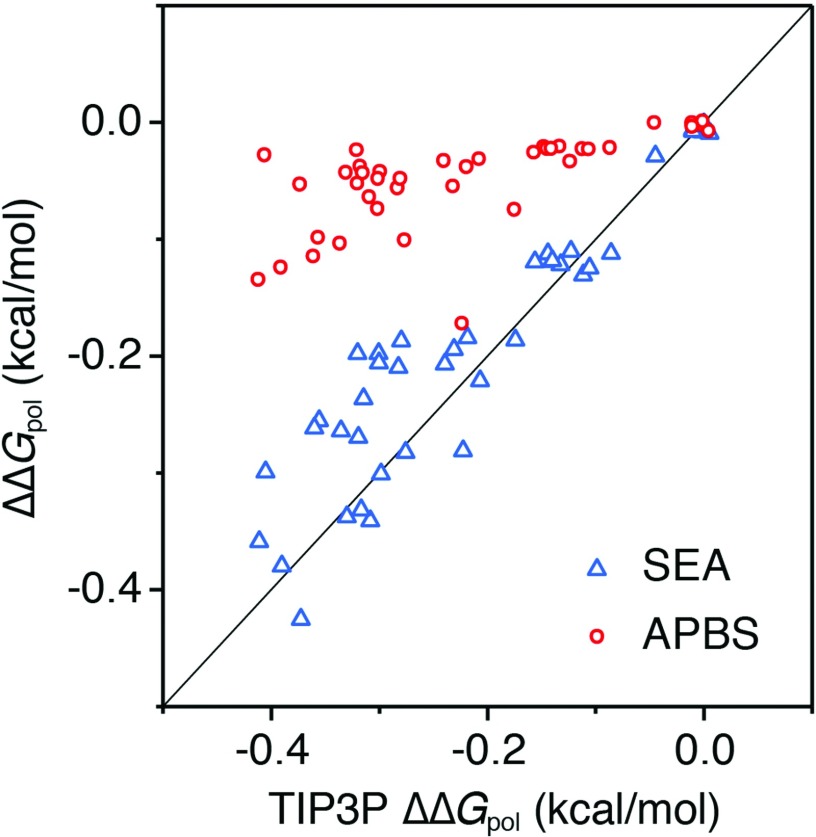
Besides ΔG_np, we also show independent analysis of ΔG_pol, which is the major component of ΔG_solv for most polar and charged solutes. We compare SEA ΔG_pol results in both water and in a 2.18 M NaCl solution with corresponding TIP3P and PB (both nonlinear NPBE and linear LPBE) results. SEA reproduces the TIP3P results in both water (r² = 0.92, RMSE = 0.81 kcal/mol) and the NaCl solution (r² = 0.92, RMSE = 0.82 kcal/mol) (see Figure S3 in the supplementary material).³⁸ The agreement we see with TIP3P is not unexpected given our previous findings.²⁸ The field version of SEA works by better representing how explicit solvent surface occupancy deviates from a simple union of spheres surface, and this effect appears to translate well to heterogeneous solvent environments. Since we observe a change in ΔG_pol from water to a concentrated salt solution, the ΔΔG_pol from water to salt solution is a useful metric for the magnitude of the ion-effects in solvation. SEA reproduces this TIP3P ΔΔG_pol with an R² of 0.88 and RMSE of 0.05 kcal/mol (Figure 3). The thing to notice about these results is that, while in good agreement, the magnitude of ΔΔG_pol is quite small, indicating that changes in ΔΔG_np tend to dominate how the solvation of these small molecule solutes changes as a function of ion concentration. To put these results in context with other implicit approaches, we also find that PB reproduces TIP3P ΔG_pol well both in water (R² = 0.91, RMSE = 1.0 kcal/mol) and in the concentrated NaCl solution (NPBE, R² = 0.91, RMSE = 1.1 kcal/mol) (see Figure S3 in the supplementary material).³⁸ However, the sensitive ΔΔG_pol test shows that the NPBE results are usually less than one-third the magnitude of TIP3P ΔΔG_pol. The pbsa and Delphi NPBE ΔΔG_pol results are no better, though their ΔG_pol in water are close to TIP3P results (see Figure S4–S7 in the supplementary material),³⁸ and LPBE ΔΔG_pol results are expectedly even smaller (see Figure S8 in the supplementary material).³⁸ Much of this difference in the small and sensitive ΔΔG_pol values likely comes from the Boltzmann term lacking consideration of ion sizes, and ion-water and ion-ion correlations.^25,26 While the Boltzmann term is designed to model ion-screening effects at low and moderate salt concentrations,⁵⁰ it is not necessarily expected to capture ion-effects at high salt concentrations.

FIG. 3.

Field variant of SEA and APBS nonlinear PB ΔΔG_pol for neutral solutes in 2.18 M NaCl compared to TIP3P simulations. While small in overall magnitude, SEA correctly reproduces the explicit solvent ion-effect trends.

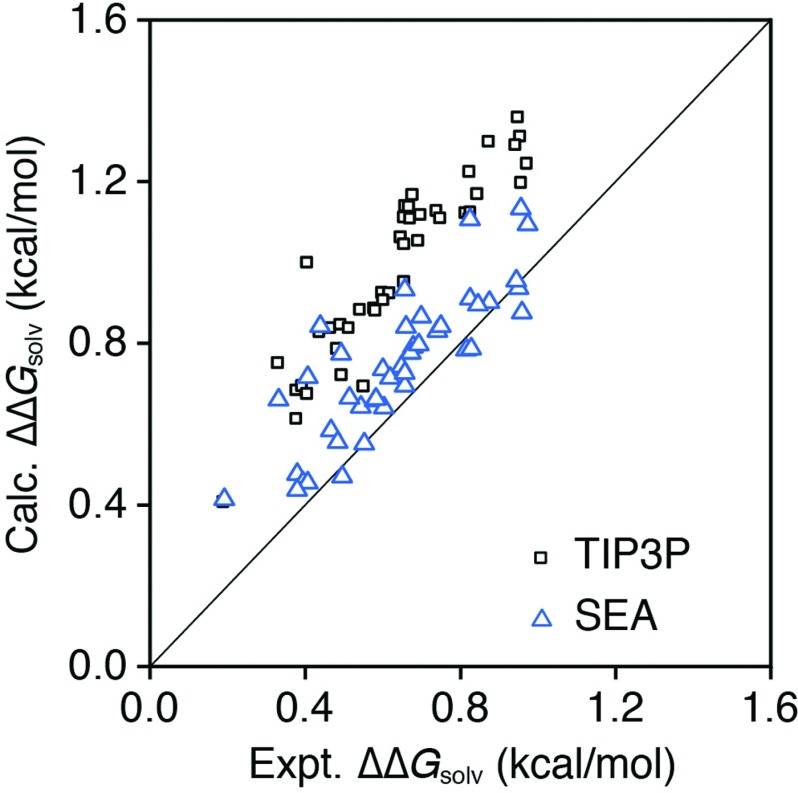
While SEA reproduces explicit solvent behavior for both nonpolar and polar solvation in electrolyte solutions well, is similar agreement seen with experiments? To investigate, we compared ΔG_solv for both SEA and TIP3P with experimental results (Figure S9 in the supplementary material),³⁸ and measure RMSE values of 1.55 and 1.00 kcal/mol, respectively, in the concentrated salt solution and 1.53 and 0.87 kcal/mol in water. More interestingly, the mean errors for SEA and TIP3P relative to experiment are 0.55 and 0.74 kcal/mol, respectively, in 2.18 M NaCl and 0.45 and 0.44 kcal/mol in water. These results indicate that the force field depiction of these small molecules is systematically hydrophobic in this explicit solvent, and comparison of these errors with the previous RMSEs indicate that solvation predictions with SEA tend to be more noisy than explicit solvent calculations. This relative noise can be seen in Figure 4, which shows a comparison of the resulting SEA and TIP3P ΔΔG_solv values. The ΔΔG_solv values for explicit solvent calculations correlate well with experimental numbers calculated from Setschenow coefficients (slope = 1.05, R² = 0.85), but with a positive shift of roughly 0.3 kcal/mol. This positive error comes mainly from the nonpolar part of the solvation free energy as TIP3P ΔΔG_solv results for the alkanes also suffer from similar positive error (Figure S10 in the supplementary material).³⁸ This systematic error, seen across all 43 solutes regardless of the specific functional groups, may indicate limitations in the current force field LJ parameters for solute atoms or ions used in the calculations. We note that this systematic error is predicted to drop to ∼0.08 kcal/mol in a 0.5 M NaCl solution from a derived linear scaling relationship of ΔΔG_solv as a function of ion concentration (see discussion below). The SEA ΔΔG_solv is close to both explicit solvent and experimental results, with RMSEs of 0.25 and 0.15 kcal/mol, respectively. Figure 4 shows 0.3 and 0.1 kcal/mol systematic offsets in explicit and SEA results relative to experimental values. These results indicate that the ion-effects on solvation are systematically enhanced over that seen in experiments by these respective offset magnitudes. The reason for this systematic shift again appears to trace back to the specifics of the ion LJ parameters in the surrounding solutions.

FIG. 4.

SEA and TIP3P ΔΔG_solv for neutral solutes in 2.18 M NaCl compared to experimental numbers calculated from Setschenow coefficients. Both approaches capture the experimental trend, though they slightly offset. This indicates an over enhancement of ion-effects from the simulation parameters.

Separating the change in total solvation due to salt into nonpolar and polar terms reveals some clues behind the driving forces in the solvation behavior of solute molecules. In all of the 43 solutes considered, the ΔΔG_np is positive with an absolute magnitude greater than the corresponding ΔΔG_pol. This positive nonpolar difference is consistent with both a cavity model^7,51,52 and a structure model.^6,8,53 In a cavity model, NaCl increases the surface tension, making it more energetically costly to open a cavity in the solution to accommodate a nonpolar solute.^7,51,54 In a water structure model, it is difficult for nonpolar molecules to enter the highly electrostricted first solvation shells of small ions, leading to a salting-out effect.⁸ In general, more solvated salt ions in the surrounding environment results in fewer regions of water not being pinned by ions. Each salt ion that is close enough to the cavity first shell will cause electrostatic restrictions on the first-shell water molecules. The more salt there is, the more electrostatic restriction there is of first-shell waters, reducing the configurational partition function for waters that form the first shell. Because this is not primarily due to salt ions interacting with any solute charge, it appears in the nonpolar term. It is hard to separate the cavity and water structure concepts for changes in the nonpolar solvation term because surface tension changes are largely correlated with ion-induced water structure changes.⁵⁵ Countering this, we observe negative polar solvation differences for all but the purely nonpolar solutes investigated. These negative ΔΔG_pol may result from stronger electrostatic interactions of polar solutes with the charges present in an electrolyte solution than that seen in a pure water environment.

Overall, we observe that for solvation in NaCl solutions, the unfavorable nonpolar effect is stronger than the favorable polar effect over this set of solutes. This is consistent with a recent MD study showing that NaCl salted out 15 small neutral solutes,⁵¹ but this runs contrary to the standard expectation that polar-term effects are the dominant contributors to solvation, aside from purely nonpolar solutes which have extremely small ΔG_pol values.³⁰ Two factors contribute to the overall trend in ΔΔG_solv. (1) ΔΔG_pol are small numbers, much smaller than ΔG_pol, because the salt's concentration (2.18 M) is much lower than water's (∼55 M). The smaller number of potential neutral solute-ion versus solute-water interactions, coupled with ions being generally further away from the solute than water (Figure S11 in the supplementary material),^38,55 result in the overall small ΔΔG_pol. (2) As ΔG_np in water results from a delicate balance repulsive cavity and attractive dispersion nonpolar terms,³⁰ shifts in this balance can lead to quite large ΔΔG_np, even similar in magnitude to the original ΔG_np. We observe the resulting ΔΔG_np values correlate well with the van der Waals surface area (Figure S12 in the supplementary material),³⁸ i.e., the ion-effect is larger for larger solutes, supporting the cavity formation model penalty explanation for solvation trends with increasing ion concentration. These trends may extend to other salts with ions of moderate charge density and when the H-bonding hydrogen donor/acceptor equilibrium in the solution is close to that in pure water.^9,10

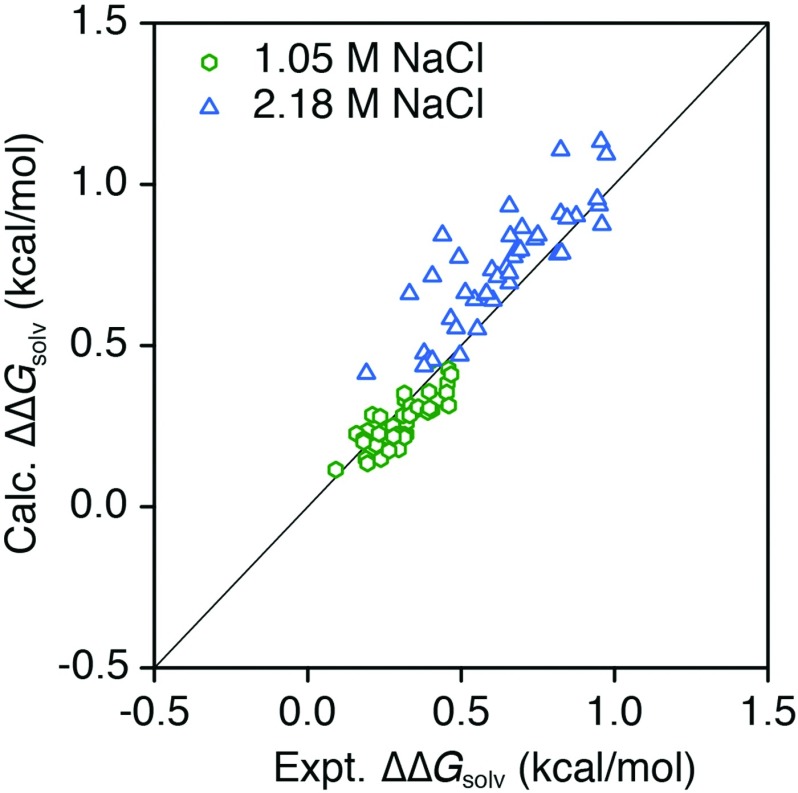
Finally, we show in Figure 5 how the ΔΔG_solv calculated by SEA scales with NaCl concentration. We see that as the ion concentration increases, the spread of the calculated distribution relative to experimental Setschenow coefficients increases. This indicates that each solute in the set is affected by ions uniquely, an increasing solvation penalty with increasing solute size and increasing solvation benefit with increasing solute polarity. We observe a slight over emphasis of the ion-effect on solvation and this is likely tied to the specifics of the ion force field parameters. Intermediate ion-concentration systems can easily be treated via interpolation between the contour grids that make up the concentration series.

FIG. 5.

Calculated ΔΔG_solv for neutral solutes in 1.05 M and 2.18 M NaCl from SEA compared to experimental values calculated from Setschenow coefficients.

IV. CONCLUSIONS

We have adapted a new field variant of the SEA model of solvation to predict solvation free energies of small molecule solutes into salt solutions. This process does not required changes to the method, only new contour tables used in surface construction and free energy interpolation. We find that SEA reproduces both the ion-specific effects observed in explicit solvent simulations and experimental Setschenow coefficients. This agreement is considerably better than is obtained from the nonlinear PB methods we tested. The principal salt effects that we see on small molecule solvation free energies are attributable to changes in the nonpolar solvation term. Because of these findings and the general computational efficiency of the solvation method, we believe this work may be useful for more complex solvation environment modeling in biology and chemistry.⁵⁶