Stochastic precision analysis of two-dimensional cardiac strain estimation in vivo

Abstract

Ultrasonic strain imaging has been applied to echocardiography and carries great potential to be used as a tool in the clinical setting. Two-dimensional (2-D) strain estimation may be useful when studying the heart due to the complex, three-dimensional deformation of the cardiac tissue. Increasing the framerate used for motion estimation, i.e. motion estimation rate (MER), has been shown to improve the precision of the strain estimation, although maintaining the spatial resolution necessary to view the entire heart structure in a single heartbeat remains challenging at high MERs. Two previously developed methods, the temporally unequispaced acquisition sequence (TUAS) and the diverging beam sequence (DBS), have been used in the past to successfully estimate in vivo axial strain at high MERs without compromising spatial resolution. In this study, a stochastic assessment of 2-D strain estimation precision is performed in vivo for both sequences at varying MERs (65, 272, 544, 815 Hz for TUAS; 250, 500, 1000, 2000 Hz for DBS). 2-D incremental strains were estimated in five healthy volunteers using a normalized cross-correlation function and a least-squares strain estimator. Both sequences were shown capable of estimating 2-D incremental strains in vivo. The conditional expected value of the elastographic signal-to-noise ratio (E(SNRe|ε)) was used to compare strain estimation precision of both sequences at multiple MERs over a wide range of clinical strain values. The results here indicate that axial strain estimation precision is much more dependent on MER than lateral strain estimation, while lateral estimation is more affected by strain magnitude. MER should be increased at least above 544 Hz to avoid suboptimal axial strain estimation. Radial and circumferential strain estimations were influenced by the axial and lateral strain in different ways. Furthermore, the TUAS and DBS were found to be of comparable precision at similar MERs.

1. Introduction

Strain estimation using ultrasound has exhibited great promise for clinical integration due to its non-invasiveness, low cost, and ease of use (Pellikka et al., 2013; Thomas and Popović, 2006). The echocardiographic exam is a routine procedure in clinical cardiology used to assess cardiac tissue health and blood flow, although strain measurements are currently less utilized. However, cardiac strain imaging has been performed by several research groups in the past and has been shown to possess significant clinical utility (Suffoletto et al., 2006; Sutherland et al., 2004; Tanaka et al., 2010). A popular approach for strain estimation is to track the reflected radiofrequency (RF) signals in the time domain, using algorithms such as cross-correlation or sum-absolute difference to estimate cardiac tissue displacement (Langeland et al., 2003). Strain can then be estimated by the spatial gradient of the displacement field.

Doppler-based techniques for computing strain have also been reported, but are cumbersome for cardiac tissue applications due to the inherent angle dependence of the measurements, as well as the difficulty of measuring in more than one dimension (Castro et al., 2000; D’hooge et al., 2000). Although initial work was primarily concerned with imaging the axial (along the ultrasound beam) strain field, several techniques have been developed to compute two- and three-dimensional strains (Baraldi et al., 1996; Crosby et al., 2009; Duan et al., 2005; Kaluzynski et al., 2001; Konofagou and Ophir, 1998; Papademetris et al., 2001; Suffoletto et al., 2006). Increasing the dimensionality of the strain measurement is of particular importance in cardiac imaging since heart motion is a complex, three-dimensional phenomenon.

The quality of ultrasonic strain estimation using cross-correlation has been shown previously to be influenced by several parameters. In the axial direction, Varghese and Ophir developed a theoretical framework, namely the Strain Filter, which describes the influence of several estimation parameters and system properties on the signal-to-noise ratio of the computed strains (SNRe) (Varghese and Ophir, 1997). These parameters include strain magnitude, correlation coefficient, transducer center frequency, signal bandwidth, and sonographic signal-to-noise ratio (SNRs). Konofagou et. al extended this analysis to strain in the lateral direction with similar results, and also found that element pitch, beam overlap, beam width, and interpolation method further influenced SNRe in the lateral direction (Konofagou et al., 2000). Other studies, using a variety of motion estimation techniques, have reported the influence of cross-correlation window size, window shape, recorrelation techniques, and beam density (Konofagou and Ophir, 1998; Korukonda and Doyley, 2011; Lopata et al., 2009; Luo and Konofagou, 2009).

The magnitude of the strains being measured in both directions also influences the quality of the estimation, which is an inherent claim of the Strain Filter concept itself. Very high strains cause large amounts of decorrelation which decrease the precision of the strain estimator. Conversely, the estimation of very low strains may be affected by electronic noise. Of the two, it is often the decorrelation induced by very large strains that is more detrimental to strain estimation in cardiac applications. One particular focus of researchers for many years has been framerate, since the smaller inter-frame (incremental) strains imaged at higher framerates exhibit less RF signal decorrelation, and hence better motion estimation (Alam and Ophir, 1997; Chen et al., 2009; D’hooge et al., 2000; Hasegawa and Kanai, 2011; Wang et al., 2008).

However, a fundamental tradeoff exists in ultrasound physics between depth, beam density, and framerate. This tradeoff is described by the classic ultrasound range equation, which states that framerate is proportional to the speed of sound and inversely proportional to imaging depth and the number of lines. For cardiac applications in humans, the imaging depth is typically at least 12–20 cm in order to visualize all four chambers in apical views. Increasing framerate in a conventional sequence comes at the cost of decreasing the number of lines for a given depth; i.e., increasing the temporal resolution decreases the spatial resolution. Indeed, early attempts to increase framerate used smaller fields of view (D’hooge et al., 2002; Konofagou et al., 2002) or sparse sector scans (Kanai and Koiwa, 2001). Thus, achieving high framerates while maintaining a high beam density and field of view is a challenging task for many cardiac strain estimation techniques. To simultaneously maintain a full view and high framerate, ECG gating (Wang et al., 2008) and/or motion matching techniques (Provost et al., 2010) have been used to align several smaller, separately acquired sectors of the heart. However, these techniques require imaging over multiple heart cycles and operate under the assumption of periodic motion, which precludes the study of aperiodic arrhythmias (Provost et al., 2011).

The work presented here utilizes two custom imaging sequences (Provost et al., 2012, 2011) which allow for imaging at both a high temporal and high spatial resolution during a single heartbeat. These two techniques use different methods of beam formation and transmission, although we will show that they are both capable of measuring 2-D strains in vivo. For each sequence, depth, beam density, and field of view were chosen to mimic a typical clinical configuration while the effective framerate was varied. A stochastic method for precision evaluation based on the Strain Filter is presented and used to compare the two sequences at multiple framerates and over a wide range of strain magnitudes. The relationship between the in vivo precision assessment and the theoretical Strain Filter is also explored.

2. Methods

2.1 Imaging Sequences

Two custom imaging sequences described previously were used in the study in order to achieve high framerate imaging in a single heartbeat without compromising field of view, depth, or number of lines. The first sequence is referred to as the temporally unequispaced acquisition sequence (TUAS), and relies on modifying the transmission order of conventionally-focused beams to achieve high framerate acquisition and motion estimation (Provost et al., 2012). The second imaging sequence, referred to as the diverging beam sequence, uses a single, diverging beam to interrogate the tissue instead of multiple focused beams (Papadacci et al., 2014; Ponnle et al., 2011; Provost et al., 2011). The differences between these two custom sequences and the conventional sequence can be seen in Figure 1 and will be elaborated upon in the following paragraphs.

Figure 1.

a) Beam profile for focused (left) and unfocused (right) transmits, temporal profiles for b) conventional, c) TUAS, and d) unfocused sequences.

Conventional echocardiography is performed by emitting and receiving focused acoustic beams in a sequential fashion. The raw data received by the transducer, i.e. the element data, is then beamformed to produce a collection of RF lines. A single image frame in time consists of N consecutive lines that form a circular sector field of view; typically, at least 64 lines that cover a 90° field of view are used. 2-D displacement estimation may be performed by matching a small segment of a single RF line to RF data found in a 2-D window taken from the subsequent frame in time. Figure 1b illustrates the temporal profile of displacement estimation using a traditional sequence. Each of the displacement estimations (u_n and u_n+1) is performed using the same spatial line, which is highlighted in blue. The time elapsed between two consecutive acquisitions of the same line used for displacement estimation is denoted by t_ME. Alternatively, the time elapsed between two motion estimation measurements is denoted as t_MS. The inverses of these two time intervals are referred to as the motion estimation rate (MER) and motion sampling rate (MSR), respectively. In practical terms, the MER influences the quality of the motion estimation, while the MSR influences the temporal sampling frequency of that motion estimation. In conventional ultrasound imaging, the MER is equal to the MSR (Figure 1b). In this study, the effect of various MERs will be studied since motion estimation quality is much more influenced by MER than by MSR.

The utility of TUAS is derived from the fact that by decreasing the MSR, a higher MER can be achieved. The increase of MER in TUAS is achieved by the repeated acquisition of smaller sectors of the heart (Figure 1c). These repeated acquisitions allow for a few lines to be imaged twice over a very short period of time, increasing the MER, although those same lines are not imaged again for an extended period of time, decreasing the MSR. Since motion estimation relies on the repeated acquisition of the same line, the MER for each sequence will depend on the number of lines per repeated sector. Table 1 lists the sector sizes used in this report and the corresponding MERs. The 1-sector sequence at 272 Hz can be considered a conventional sequence with a standard beam order; however, to achieve an even lower MER of 65 Hz, motion estimation was also performed over the large, MSR interval (i.e. t_ms in Figure 1) instead of the smaller MER interval.

Table 1.

MERs for TUAS

# sectors	transmits per sector	MER (Hz)
1a	12	65
1	12	272
2	6	544
3	4	897

^aMotion estimation performed over MSR interval

The DBS differs more drastically from the conventional sequence than does TUAS. Instead of multiple, focused beams being transmitted per frame, the DBS uses a diverging wave that interrogates the entire view only once per frame (Figure 1a,d). The reconstruction of the entire field of view is made possible by the acquisition of RF data for each individual transducer element, permitting synthetic focusing in postprocessing to generate multiple image lines. This synthetic focusing procedure is performed for both the TUAS and DBS, and is described in further detail in the next section. Because each frame is formed using only a single transmit, motion estimation can be performed on a given frame using both the previous and next frame in the sequence. Therefore, similar to a conventional sequence, the MER and MSR for the DBS are equivalent, although greatly increased relative to the conventional sequence due to the fact that only a single transmit per frame is required. Individual frames were acquired at a MER of 2000 Hz, and were also down-sampled in time to 250, 500, and 1000 Hz.

The ultrasound system used in this study allowed for control over the pressure intensity emitted by the transducer. Since it is possible to increase the native SNRs of the reflected echo signals by increasing pressure, each sequence was designed to emit the maximum amount of pressure while staying comfortably within the safety guidelines as outlined by the United States Food and Drug Administration for adult cardiac imaging (I_SPTA ≤ 430 mW/cm²). A previously described set-up consisting of a water bath and hydrophone (Harris, 1988) was used to test and optimize both sequences and a maximum I_SPTA of approximately 390 mW/cm² was obtained for each sequence.

2.2 Experimental Set-up

Using a protocol approved by the Institutional Review Board of Columbia University, five, healthy male volunteers aged 23–30 were scanned in the lateral decubitus position by a trained cardiac sonographer. All patients were scanned with a 2.5 MHz phased-array probe connected to a Verasonics V-1 system (Redmond, WA) using both TUAS and DBS. For each sequence, acquisition lasted for 2 seconds to ensure the capture of an entire cardiac cycle. The same echocardiographic view was taken in all patients; namely, the parasternal short-axis view at the papillary muscle level. Because the study objective was to analyze and compare both axial and lateral strain estimations, the short-axis view was chosen so that the strain magnitudes would be similar in each direction.

Three TUAS acquisitions of different sector sizes were acquired per patient, which allowed for the construction of RF data at four effective MERs (Table 1). A single DBS acquisition at 2000 Hz was also obtained in each patient. Lower MERs of 250, 500, and 1000 Hz were achieved by skipping frames during motion estimation. All DBS strain estimations were performed at a MSR of 65 Hz to match the temporal sampling frequency of the TUAS estimations.

2.3 Data Acquisition

For each sequence, element data received by the transducer was sampled at 10 MHz and recorded for each of the 64 individual traducer elements. The data were fairly large, approximately 1GB for two seconds, and were transferred to an on-board CPU and stored. For beamforming, a standard delay-and-sum algorithm was used to perform synthetic focusing and reconstruct 120 lines of post-beamformed RF data per frame at an axial sampling rate of 20 MHz. For the TUAS, this corresponds to the construction of 10 RF lines per transmit beam; while in the DBS, all 120 lines were constructed from a single transmit. A 90° field of view at a depth of 20 cm was used to mimic standard clinical settings. ECG measurements were triggered by the ultrasound system and acquired in parallel with the ultrasound measurements. A slight delay (< 20 ms) existed between the ECG and ultrasound data, which was corrected for.

2.4 Strain Estimation

A fast, normalized cross-correlation function was used on RF lines from adjacent frames to compute two-dimensional motion (Konofagou and Ophir, 1998; Luo and Konofagou, 2010). The cross-correlation function used a 1-D kernel (length = 5.85 mm, overlap = 90%) in a 2-D search to estimate both axial and lateral displacements. The correlation kernel size was selected to be approximately 10 wavelengths, which was proposed in a previous study using cross-correlation (Chen et al., 2007). When searching in the lateral direction, RF data was linearly interpolated by a factor of 10 in order to improve lateral displacement resolution. A least-squares kernel (10.3 × 10.5 mm) was then used to compute the 2-D axial and lateral strains. The calculated displacements used a reference point of the first frame in each estimation pair, yielding incremental (inter-frame) displacements and strains as opposed to performing accumulation over the entire cardiac cycle. Therefore, the strain values at each point in time reflect the behavior of the tissue at that specific time point, without being influenced by any previous behavior. A relatively large strain kernel was used due to the high noise inherent to incremental strains. Radial and circumferential strains were also derived using a coordinate transformation and taking the center of the left ventricular (LV) cavity as the centroid. A standard B-mode image was reconstructed from the RF data, allowing for segmentation of the myocardial border. These contours were automatically tracked throughout the cardiac cycle using a previously described technique (Luo and Konofagou, 2008). 2-D spatial filtering of the displacements and strains was performed only for the strain images presented in the first section of the results.

2.5 Performance Evaluation

A stochastic metric of precision, E(SNRe|ε), has been used here in order to compare the strain estimation of the various sequences used in this study (Provost et al., 2012). First, the elastographic signal-to-noise-ratio (SNR_e) was calculated for each sequence over the entirety of the heart cycle. SNR_e is computed for every point in an image using

$${\mathit{SNR}}_e=\frac{\mathrm{\mu }(\epsilon )}{\sigma (\epsilon )},$$ (1)

where μ(ε) and σ(ε) refer to the mean and standard deviation of the strain magnitude within a small two-dimensional window (3.0 × 3.2mm). Since both strain and SNR_e were computed for each point in the myocardium throughout systole, a large number (>600,000) of strain-SNR_e pairs were generated for each sequence. This paired data can be used to generate a two-dimensional histogram (f(SNR_e,ε)) that displays the probability density function (pdf) of SNR_e for a set of discrete strain values. However, since the strain distribution measured in the heart is non-uniform, the 2-D pdf will be biased towards strain values that occur more frequently. To remove this bias, the conditional pdf was calculated according to

$$f({\mathit{SNR}}_e\mid \epsilon )=\frac{f({\mathit{SNR}}_e,\epsilon )}{f(\epsilon )},$$ (2)

where f(SNR_e,ε) is the 2-D pdf and f(ε) is the 1-D strain distribution. It is important to keep in mind that f(SNR_e|ε), f(SNR_e,ε), and f(ε) will be affected by the quality of strain estimation and thus be dependent on the MER. Figure 2 shows an example plot of the conditional pdf of axial strains taken with TUAS and DBS at 544 Hz and 500 Hz respectively. To simplify the information obtained from the 2-D conditional pdf, which manifests as the 3-D plot in Figure 2, the conditional expected value of SNR_e for each strain was calculated as

Figure 2.

Conditional pdfs of axial strains taken with the TUAS at 544 Hz (left) and DBS at 500 Hz (right) in a single patient. Horizontal lines denoting the transition zones which separate the CRLB from the BB have been drawn at the local minima of the pdfs.

$$E({\mathit{SNR}}_e\mid \epsilon )={\int }_0^{+\infty }{\mathit{SNR}}_{e}f({\mathit{SNR}}_e\mid \epsilon ){\mathit{dSNR}}_e.$$ (3)

E(SNRe|ε) curves are generated for each sequence, which allows for a relatively easy comparison to be performed between different sequences for a wide range of strain values. An example E(SNRe|ε) curve can also be seen in Figure 2.

However, since incremental strains are being used, it is important to keep in mind that the same deformation will be measured differently by sequences at different MERs. For instance, a 1% strain measured at 1000 Hz would be measured as a 2% strain at 500 Hz. Therefore, in order to compare strain magnitudes between sequences, strains have been multiplied by MER for normalization. Final magnitudes of normalized strain are presented in decibels, with the reference of 0 dB being a 1% strain measured at 100 Hz:

$$\mathit{normalized}\epsilon =20log\left(\frac{\mathit{MER}\ast \epsilon }{100Hz\ast 1\%}\right).$$ (4)

3. Results

3.1 Two-Dimensional Strains within a Single Heartbeat

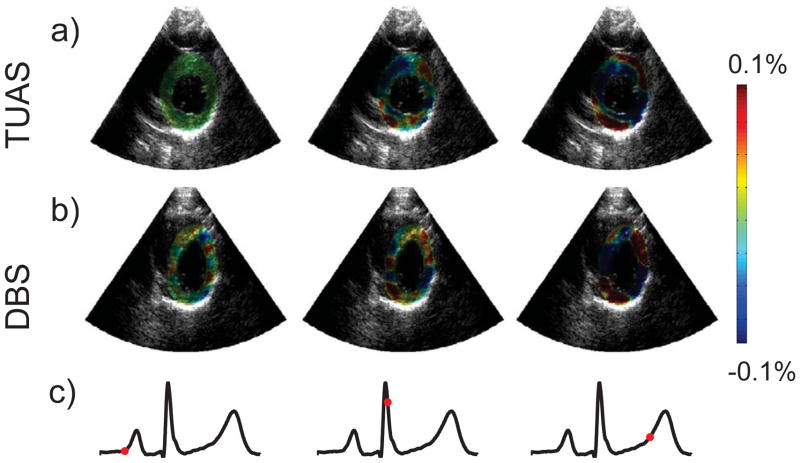
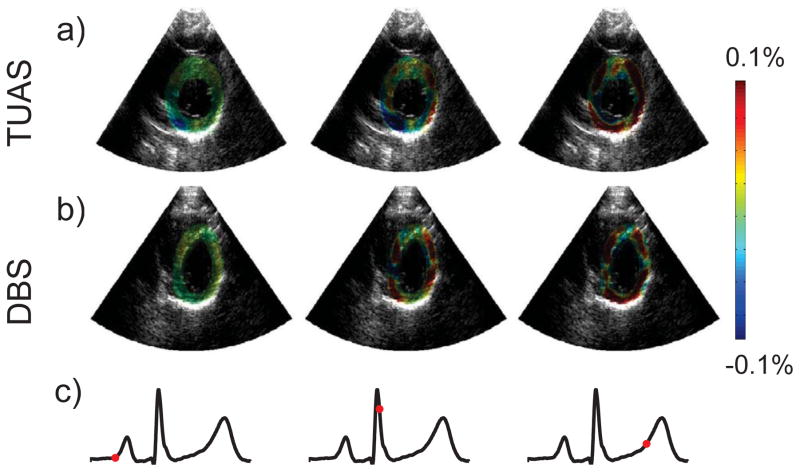
Figures 3–6 display incremental strain images of the left ventricle (LV) during contraction taken with the TUAS and DBS at 544 Hz and 500 Hz respectively. Images were synchronized in time using ECG recordings, which are displayed below the strain images. The exact point in the cardiac cycle from which each image was taken is denoted by the red dot on the ECG tracing. The first image in each series was taken towards the end of diastole, directly before the P-wave. Both sequences show relatively low strains all directions at this time. The following two images in each series were taken during systole following the initiation of ventricular contraction. Positive axial strains can be seen in the anterior and posterior walls of the LV, with negative axial strain occupying the septal and lateral walls. In the lateral direction, the distributions of positive and negative strains are reversed, with negative lateral strains occurring in the anterior and posterior walls and positive lateral strains occurring in the septal and lateral walls. Radial and circumferential strains appeared more uniform, especially in the late systolic frame. Positive radial strain and negative circumferential strain are clearly occurring in much of the LV wall during late systole. In the early systolic frame, the radial and circumferential strain distributions are less uniform, especially in the septum. In all cases, the magnitudes of the strains increase from early systole to late systole, which are the second and third images in each series respectively.

Figure 3.

Comparison of incremental axial strains during LV contraction for a) TUAS at 544 Hz and b) DBS at 500 Hz with the c) corresponding time point on the ECG. The three images in each series were taken near the end of diastole (left), during early systole (middle), and during late systole (right).

Figure 6.

Comparison of incremental circumferential strains during LV contraction for a) TUAS at 544 Hz and b) DBS at 500 Hz with the c) corresponding time point on the ECG. The three images in each series were taken near the end of diastole (left), during early systole (middle), and during late systole (right).

3.2 Expected SNRe - Axial Strain

E(SNRe|ε) curves are shown in Figures 7–10 for both sequences at various MERs. In the axial case, the curves exhibit a two-peaked, bimodal distribution. The locations of both peaks shift towards larger values of strains for higher MERs. This shift becomes less apparent at MERs >544 Hz, in which case the locations of the first peak are clustered at approximately 10 dB. This phenomenon was observed for both the TUAS and DBS, although the shifting behavior is more apparent using TUAS since the MERs tested are lower. The amplitudes of the first peaks also increase with MER while the amplitudes of the second peaks decrease, causing the curve to approach a single-peaked distribution at higher MERs. The maximum value of E(SNRe|ε) for any sequence is 5.71, occurring for the DBS at an MER of 2000 Hz and a strain of 8.91 dB. This magnitude corresponds to an incremental strain magnitude of 0.14% measured at 2000 Hz. Figure 11 plots curves for both sequences at similar MERs—272 and 544 Hz for TUAS, along with 250 and 500 Hz for DBS. Both sequences produce E(SNRe|ε) curves with approximately the same shape and magnitude at similar MERs.

Figure 7.

Expected SNRe curves for axial strain estimation using the TUAS and DBS at various MERs.

Figure 10.

Expected SNRe curves for circumferential strain estimation using the TUAS and DBS at various MERs.

Figure 11.

Expected SNRe curves for axial (left) and radial (right) strain estimation using the TUAS and DBS at similar MERs.

C. Expected SNRe - Lateral Strain

In contrast to the bimodal distributions observed for the axial direction at low MERs, all E(SNRe|ε) curves appear unimodal for the lateral direction regardless of MER. Also, the rightward shift with increasing MER observed in the axial case is not as clear in the lateral direction. At higher MERs, the locations of the peaks do not change significantly and are clustered around 40 dB. Unlike in the axial direction, the magnitudes of the peaks of the curves do not seem to significantly change with MER; the maximum magnitude of each curve is approximately 4.5. However, the 65 Hz TUAS curve is shifted by approximately 15 dBs to the left of the other curves. Again, at similar MERs, the TUAS and DBS curves appear similar in magnitude and shape.

D. Expected SNRe – Radial and Circumferential Strain

E(SNRe|ε) curves for radial and circumferential strains are similar to each other and share characteristics of both the axial and lateral E(SNRe|ε) curves. The distributions of both the radial and circumferential curves are unimodal, similar to the lateral curves. There also is an increase in magnitude of the peaks of these curves with MER, similar to the axial curves. However, the peak magnitudes of these curves are not as high as either the axial or lateral curves. Radial E(SNRe|ε) seems to increase in amplitude with MER more than the circumferential E(SNRe|ε), especially at the higher MERs of the DBS. The maximum value of E(SNRe|ε) for radial and circumferential strains are 4.72 and 3.69, occurring for the DBS sequences at 2000 Hz and 1000 Hz respectively.

4. Discussion

The precision of cardiac strain estimation using RF cross-correlation is often reduced due to RF signal decorrelation caused by the large incremental strains that occur during contraction. Increasing the MER is a well-accepted method of reducing this decorrelation, thus increasing precision. However, it is difficult to achieve high MER sequences while maintaining a high spatial resolution. It is even more difficult to achieve both of these goals by imaging single cardiac cycle. The two sequences presented here can be used within a single heart cycle at higher MERs without compromising spatial resolution, and have been applied to 2-D strain imaging.

The series of strain images in Figures 3–6 suggest that both sequences can reliably be used to estimate two-dimensional cardiac strains in vivo. The strain distributions imaged by each sequence agree with the expectations derived from knowledge of cardiac mechanics (Artis et al., 2008; Lee and Konofagou, 2008). At the onset of the P-wave, the atria are just beginning to contract while the ventricles are at rest. The strains imaged at this time were very low as expected. During contraction, the myocardium of the left ventricle begins to thicken in the radial direction and shorten in the circumferential direction. Radial thickening would manifest as positive axial strain in the anterior and posterior walls, along with negative axial strain in the septal and lateral walls. The lateral strain distribution would be reversed since the axial and lateral directions are relatively orthogonal at each point. The expected behavior is observed in all directions using either sequence. Furthermore, the strains imaged by the TUAS and DBS at the same point in time seem to be fairly consistent in terms of both magnitude and distribution. The least agreement between sequences occurs during early systole when the myocardium is just beginning to contract, creating incremental strains that are changing very rapidly in both space and time. Here it is very difficult to observe the exact same strain image in both sequences, especially considering the limited MSR. Towards the end of systole when the contractile behavior is more uniform, the strain distributions imaged by both sequences become more similar. There is less agreement for radial and circumferential strains, which is expected. Since radial and circumferential strains are created by combining both axial and lateral strains, errors from each estimation direction are combined and propagated. Furthermore, unlike axial and lateral strains, radial and circumferential strains are largely influenced by the myocardial segmentation, since the centroid for the coordinate transformation is defined by the manually drawn mask.

A previous study on TUAS has noted the two-peaked nature of the axial SNRe distribution, noting the switch to a single-peaked distribution above an MER of 452 Hz (Provost et al., 2012). This particular shape is explained to be a result of the transition zone that occurs in the Strain Filter presented by Varghese and Ophir (Varghese and Ophir, 1997). The transition zone occurs at high strains when decorrelation becomes too significant and motion is estimated on the basis of RF signal amplitude only, i.e. the signal envelope, instead of using both the amplitude and the phase information. Smaller strains below the transition zone are estimated using both amplitude and phase information, with estimation quality being governed by a modified version of the Cramer-Rao lower bound (CRLB) for time-delay estimators (Walker and Trahey, 1995). For larger strains above the transition zone, phase information is lost due to significant signal decorrelation, and the estimation quality is instead governed by the Barankin bound (BB). For strains near the transition zone, the method of motion estimation is ambiguous and inconsistent, causing a local minimum of SNRe (Provost et al., 2012). In this work using E(SNRe|ε), similar, two-peaked results are reported, with the disappearance of the second peak above an MER of 544. The disappearance of the second peak is due to the fact that smaller incremental strains will be measured at high MERs. If MER is sufficiently high, the measured strain values will be small enough to fall below the transition zone, leading to a disappearance of the second peak. Figure 2 shows the approximate location of the transition zone, along with the locations of the CRLB and BB within the strain magnitude spectrum.

Motion estimation using RF signal envelope has consistently been shown to be less accurate than using both phase and amplitude (Ma and Varghese, 2013; Walker and Trahey, 1994); thus, any axial motion estimation technique should aim to minimize the amount of strains estimated using only the envelope. The work presented here indicates that sequences with a single-peaked axial distribution of E(SNRe|ε) should be preferred over a sequence with a two-peaked distribution.

The E(SNRe|ε) distribution of the lateral strain estimation is single-peaked for all MERs. A single-peaked distribution is expected for the lateral direction due to the difference method of motion estimation compared to the axial direction. Although axial phase information is used to increase the accuracy of the lateral motion estimation, there is no lateral phase information inherent in a collection of 1D RF lines. Therefore, the lateral cross-correlation function is only sensitive to variations in the lateral envelope. It is somewhat surprising that the amplitude and shape of the lateral curves do not change significantly with MER, although the width of the curve at 65 Hz appears significantly smaller than the other curves. However, Lee et al. has previously reported that lateral estimation quality is much less influenced by MER than axial estimation (Lee, 2010). Luo and Konofagou have reported that the quality of lateral estimation is largely dependent on number of beams, element size, and element spacing (Luo and Konofagou, 2009). The locations of the peaks of the lateral curves occur at higher strain values compared to the axial curves. An explanation for this phenomenon is provided later in this section.

Radial and circumferential strains are each derived from axial and lateral strains, so it is reasonable that the radial and circumferential E(SNRe|ε) curves will reflect characteristics of both the axial and lateral curves. Lateral strain seems to dictate the location of the E(SNRe|ε) curves along the x-axis, as the peaks of the radial and circumferential curves are closer to 40 dB than 10 dB. On the other hand, axial strain seems to determine the amplitude of radial and circumferential E(SNRe|ε), as increasing amplitude with MER is observed similar to the axial direction. However, the amplitude increase for the radial and circumferential E(SNRe|ε) is not as significant as the axial E(SNRe|ε), which is likely due to contributions from the lateral direction which show no change in E(SNRe|ε) amplitude. Interestingly, the amplitude increase with MER for the DBS is more significant for radial strain compared to circumferential strain. In general, the amplitude of the radial and circumferential curves are decreased compared to both the axial and lateral curves. As discussed above, this is likely due to the accumulation of errors that occurs when combining the axial and lateral components of strain.

There is also a discernible rightward shift of E(SNRe|ε) curve peaks in the axial direction as MER increases. This trend is much more noticeable at the lower MERs of TUAS (MER ≤ 544 Hz) and is fairly insignificant at the higher MERs (MER > 544 Hz) of both sequences. To explain this shift, recall that strain magnitudes are normalized by the multiplication of MER. For the 815 Hz sequence, a maximum occurs at an axial normalized strain of 10 dB, which corresponds to a strain of 0.4% estimated at 815 Hz. This strain magnitude reflects the optimal deformation amount for a motion estimation performed at 815 Hz. However, for the same value of normalized strain, estimation with a 65 Hz MER will experience significantly more decorrelation compared to an MER of 815 Hz, since the estimation interval is longer. Therefore, the peaks corresponding to optimal motion estimation for the 65 Hz sequence must exist at a lower normalized strain value, where there will be less decorrelation. The same explanation can be applied to the lateral, radial, and circumferential E(SNRe|ε) curves as well, although this shift is much less apparent. It is clear that the 65 Hz TUAS curve is shifted left by approximately 25 dB for axial/lateral E(SNRe|ε) and 17 dB for radial/circumferential E(SNRe|ε) compared to all other curves due to the reasons provided above. It is unclear why this shift does not persist at the higher MERs in the lateral, radial, and circumferential directions. As discussed previously, the locations of the radial and circumferential E(SNRe|ε) curves seem to be influenced more by the lateral direction than the axial direction.

Considering the explanation of the axial curve shift above, the absence of a significant shift in the lateral direction provides an important insight into the reliability of the 2D strain estimator used. The similarity of the lateral E(SNRe|ε) curves indicates that the lateral motion estimator used in this study is only tailored to estimate precisely over a small range of normalized strain. This range of normalized strain occurs at much higher values compared to axial strain due to the difficulty of estimating small strains using the lateral estimator. Even though the lateral RF data is interpolated by a factor of 10 to increase resolution, the lateral direction still lacks the phase information that allows for the precise axial estimation of small strains around 10 dB. Also, since decorrelation seems to affect lateral E(SNRe|ε) equally at 250 Hz and 2000 Hz, it is clear that increasing MER is not the best solution to increase the precision of the lateral strain estimation.

The high MERs used in this study were achieved by the use of two different sequences, the TUAS and DBS. The differing nature of the beam used by each sequence was thought to potentially have an impact on the quality of strain estimation, especially in the lateral direction. Indeed, previous studies using simulations and ex vivo phantoms have explicitly shown the effect of the beamwidth, among other parameters, on the quality of lateral motion estimation (Konofagou et al., 2000; Korukonda and Doyley, 2011; Luo and Konofagou, 2009). A comparison between the two sequences can be performed at similar MERs, since the parameters of depth, field of view, and beam density are held constant in the data processing phase (Figure 11). In comparing the TUAS at 272 and 544 Hz with the DBS at 250 and 500 Hz, it was clear that each sequence produced fairly similar curves for all strain directions. The similarities in the curves extend to both magnitude and shape. This observation indicates that, in terms of our evaluation metric, the 2-D strains estimated by each sequence are equivalently precise, assuming that imaging and strain estimation parameters are held constant.

To better qualify this result, it is important to remember that the maximum pressure transmitted by each sequence is similar. Because DBS uses a diverging beam, the voltage supplied to the transducer was able to be increased above that of the TUAS in order to reach the desired I_SPTA value. Previous investigations into the effect of beam width on strain estimation did not normalize the pressure intensity between sequences of different beam widths. Furthermore, these previous studies compared the effect of widening the transmit beams in a conventional sequence; there are few studies which compare a conventionally-focused sequence consisting of multiple transmits per frame to a diverging sequence containing a single transmit per frame (Park et al., 2007). The TUAS and DBS are characterized both by different beam widths and different transmit densities—the TUAS used 12, narrow transmits per frame while the DBS used a single, wide transmit per frame (Figure 1). Previous work has shown that lateral SNRe seems to be influenced both by beam width and beam density; optimizing the combination of these parameters using the advanced hardware available in newer systems is thus an interesting area for future study. It is also noteworthy that synthetic focusing was used for beamforming and allowed the creation of the same number of RF lines per frame for both TUAS and DBS, which may have contributed to their apparent similarity.

It is difficult to assess the quality of an in vivo data set because there is typically no ground truth measurement available. E(SNRe|ε) was shown to be able to differentiate sequences based on MER and may be a useful tool to stochastically evaluate the precision of an in vivo data set. However, the use of SNRe does have some limitations, especially for axial and lateral strains which have alternating positive and negative values in the short axis view of the heart. A small kernel size (3.0 × 3.2 mm) was used for the SNRe computation to limit the issues caused by this inhomogeneity. Although some SNRe samples may still have been affected by the alternating axial and lateral strain distributions, a large number of SNRe samples (>600,000) were obtained for each sequence so that the overall behavior of E(SNRe|ε) would not be overly influenced by the border zones between the positive and negative strains. Also, it is important to emphasize that although SNRe is a good measure of precision, it does not reflect the accuracy of these strains. Feasibility of 2-D strain estimation TUAS and DBS was observed qualitatively by inspecting the strain images (Figures 3–6), which provided reasonable results. The accuracy of the 2D strain estimation performed here has been previously validated in simulations (Lee et al., 2007) and using MR tagging (Lee et al., 2008).

5. Conclusions

This paper presents the implementation of two different imaging sequences used to obtain precise, high framerate, 2-D cardiac strain estimation in vivo over a single heart cycle. Qualitative results in a standard clinical imaging setting indicate that each method can be used to obtain physiologic strains. A metric of precision based on the conditional expected value of the SNRe was explained and used to study the influence of framerate, or more specifically MER, on axial, lateral, radial, and circumferential strains. The results indicate a strong relationship with the concept of the Strain Filter. Strain estimation quality was found to increase with MER, at least in the axial and radial directions, and MER should be at least >544 Hz to avoid the suboptimal motion estimation governed by the Barankin bound. Results in the lateral direction indicate that lateral strain estimation is less tied to MER and depends more on the magnitude of the strains being measured. This study also finds little difference in 2-D strain estimation quality using 12, conventionally-focused beams compared to a single diverging beam.

Figure 4.

Comparison of incremental lateral strains during LV contraction for a) TUAS at 544 Hz and b) DBS at 500 Hz with the c) corresponding time point on the ECG. The three images in each series were taken near the end of diastole (left), during early systole (middle), and during late systole (right).

Figure 5.

Comparison of incremental radial strains during LV contraction for a) TUAS at 544 Hz and b) DBS at 500 Hz with the c) corresponding time point on the ECG. The three images in each series were taken near the end of diastole (left), during early systole (middle), and during late systole (right).

Figure 8.

Expected SNRe curves for lateral strain estimation using the TUAS and DBS at various MERs.

Figure 9.

Expected SNRe curves for radial strain estimation using the TUAS and DBS at various MERs.