Determining the optimal window length for pattern recognition-based myoelectric control: balancing the competing effects of classification error and controller delay

Abstract

Pattern recognition–based control of myoelectric prostheses has shown great promise in research environments, but has not been optimized for use in a clinical setting. To explore the relationship between classification error, controller delay, and real-time controllability, 13 able-bodied subjects were trained to operate a virtual upper-limb prosthesis using pattern recognition of electromyogram (EMG) signals. Classification error and controller delay were varied by training different classifiers with a variety of analysis window lengths ranging from 50 to 550 ms and either two or four EMG input channels. Offline analysis showed that classification error decreased with longer window lengths (p < 0.01). Real-time controllability was evaluated with the Target Achievement Control (TAC) Test, which prompted users to maneuver the virtual prosthesis into various target postures. The results indicated that user performance improved with lower classification error (p<0.01) and was reduced with longer controller delay (p<0.01), as determined by the window length. Therefore, both of these effects should be considered when choosing a window length; it may be beneficial to increase the window length if this results in a reduced classification error, despite the corresponding increase in controller delay. For the system employed in this study, the optimal window length was found to be between 150 and 250 ms, which is within acceptable controller delays for conventional multi-state amplitude controllers.

I. Introduction

Arm amputation is a significant disability that is estimated to affect over 41,000 people in the United States [1]. Passive or traditional body-powered prostheses are used by most individuals with upper-limb amputation but they are neither intuitive to operate nor do they adequately restore limb function. Myoelectric prostheses provide a more natural avenue for control and have been clinically implemented using multi-state amplitude-based controllers [2]. Such control systems can only be used for directing a small set of functions and are limited by the number of independent control sites and the amount of information extracted from the user’s electromyograph (EMG) signals. Pattern recognition–based control is a promising alternative that employs classification theory to extract the user’s intent from multiple EMG signals and has the potential to more accurately control a greater set of motions. However, pattern recognition–based control has had limited clinical implementation, and the optimal parameters for maximizing user performance have yet to be fully elucidated.

Effective real-time operation of a myoelectric prosthesis requires a quick and accurate response to the user’s EMG signals, regardless of the control method used. The relationship between controller error rates, controller delay, and real-time controllability has been investigated for conventional multi-state amplitude controllers [3-6]. These studies have demonstrated both the benefits of increased temporal information in decision making and the problems associated with a long controller delay. Parker et al. [4] derived theoretical error rates for up to 10 states of muscle activation and related the error rates to the time constant of a simple low-pass filter. Their work showed that longer time constants resulted in a smoother response and reduced the controller error. However, Hogan [6] noted that excessive controller delay caused amputees to overshoot their desired target when attempting to position an elbow, requiring them to correct the error. Paciga et al. [3] implemented three- and five-state amplitude controllers and objectively attempted to quantify the effect of controller delay. The error rate was found to increase by a factor of six (from 1.1% to 6%) when an artificially induced 200 ms controller delay was added to the inherent delay of the low-pass filter used to smooth the control channel. More recently, Farrell and Weir [5] investigated a range of artificially induced controller delays for a myopulse-based control system [7] and determined a noticeable reduction in controllability at delays greater than approximately 100 ms.

The previously mentioned studies used conventional amplitude-based controllers, and the results are generally thought to be applicable to pattern recognition systems. However, very few studies have attempted to relate the system classification error to real-time prosthesis controllability [8-11]. Furthermore, to our knowledge, there have been no studies of pattern recognition–based myoelectric control of powered prostheses that investigate the relationship between classification error, controller delay, and real-time controllability. A longer analysis window (see Section II) provides more EMG data to the control system and is expected to have greater accuracy in deducing the user’s intent. However, at some point the delay caused by the longer window is also expected to interfere with user performance. The objective of this work was to investigate the above relationships, determine the optimal window length with respect to real-time prosthesis performance, and determine if the controller delay estimates found for conventional myoelectric control methods are consistent with pattern recognition systems.

II. Background

It is generally accepted that the instantaneous value of a myoelectric signal is not a useful input for pattern recognition techniques, due to its random nature [2]. Instead, a window of data is required from which descriptive features are extracted and discriminated according to a pre-configured threshold or other pattern recognition algorithm. Englehart and Hudgins [12] described an overlapping analysis window technique that results in a dense decision stream (Fig. 1).

Fig. 1.

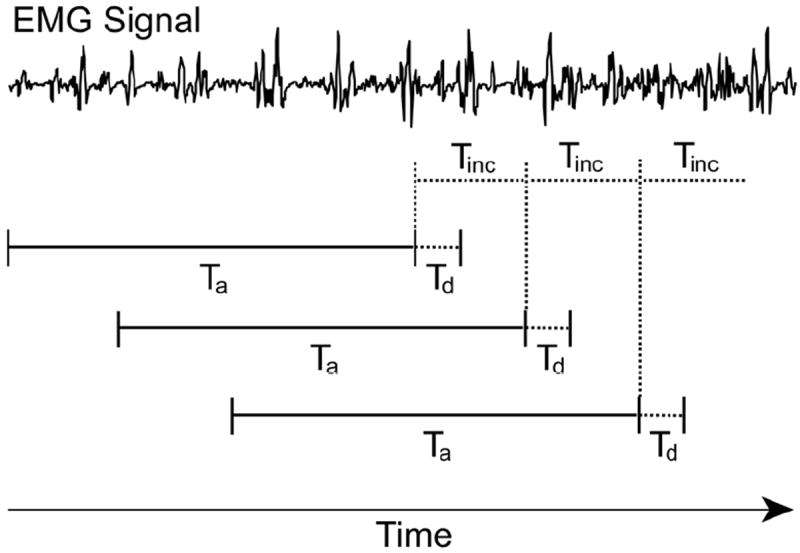
EMG data are analyzed using analysis windows of length T_a and window increments of length T_inc. The processing delay of the algorithm is represented as T_d.

The length of the analysis window, T_a, multiplied by the sampling rate, gives the number of samples of data for each channel used to formulate a classification decision; the window increment, T_inc, multiplied by the sampling rate, gives the number of new samples for each channel used in each successive analysis window; and the signal processing time, T_d, is the computation time associated with the pattern recognition algorithm. T_inc is usually much shorter than T_a, and would ideally be equivalent to T_d to produce the densest possible processing stream. Farrell and Weir [13] suggested that the average controller delay for such a construct was not only a function of T_d, but also included T_a and T_inc according to (1):

$$D=\frac{1}{2}{T}_a+\frac{1}{2}{T}_{\mathit{inc}}+T_d.$$ (1)

Equation (1) was experimentally verified by varying the analysis window length in a simple two-class pattern recognition system. With this overlapping analysis window technique, Englehart and Hudgins [12] found that the average classification error increases significantly with shorter window lengths. Their proposed algorithm, however, was not tested in the presence of real-time feedback to determine at what window lengths the system becomes uncontrollable due to high classification error rates (T_a too short) or excessive controller delay (T_a too long).

A number of different pattern recognition systems have been investigated for multifunction control of myoelectric prostheses [9, 11, 12, 14-22]. All of these pattern recognition systems rely on a set of features to represent the myoelectric signals and a pattern classifier algorithm that partitions the feature space into discrete movement classes. Although each of these classifier algorithms provide accurate recognition, a linear classifier has been shown to be sufficient for pattern classification if a proper feature set is chosen to represent the signals [23]. In a virtual, real-time usability study comparing several different feature sets and classifier combinations, Lock found no significant difference between the controllability of the resulting pattern recognition systems [8].

III. Methods

This study was performed on 13 able-bodied subjects who trained and operated a virtual prosthesis using pattern recognition. The study was approved by the Northwestern University Institutional Review Board and conducted at the Rehabilitation Institute of Chicago. For each subject, a broad range of analysis window lengths (T_a) were used to create a set of pattern recognition control systems with a spectrum of classification errors and controller delays. The control systems were trained with either two or four EMG channels in order to broaden the range of classification accuracies for each subject. Furthermore, two and four channel pattern recognition systems are a clinically feasible number of channels to implement.

For each subject, data were collected over two identical experimental sessions. At each session, four self-adhesive bipolar EMG electrodes were placed on the proximal forearm of the user’s dominant hand: the first electrode (#1) was placed over the main extensor bundle, determined by palpation; the second (#2) was placed over the main flexor bundle, determined by palpation; the third (#3) was placed on the radial aspect of the forearm, approximately equidistant between electrodes #1 and #2; and the fourth (#4) was placed on the ulnar aspect of the forearm, approximately equidistant between electrodes #1 and #2. The signals were amplified by a factor of approximately 2000, band-pass filtered between 20 and 500 Hz using a third-order Butterworth filter, and sampled at 1 kHz using an isolated 16-bit Measurement Computing USB-1616FS data acquisition card.

A. Practice Trials

After electrode placement, subjects were visually guided to complete four EMG data collection sequences by a custom-built computer software package. Each sequence was comprised of muscle contractions for seven motions: wrist flexion, wrist extension, wrist pronation, wrist supination, hand open, hand close, and a relaxed position. The order of the presented motions was randomized by the software, and the user was instructed to elicit contractions at a comfortable (self-selected) force level comparable to that of a firm handshake. Each contraction was held for 3 s, with a 3 s break between contractions, so that a total of 12 s of EMG data was collected for each posture. The arm was not constrained during these contractions and was free to move.

After data collection, four real-time pattern recognition systems were trained (classification decision boundaries computed from the recorded EMG data): two with analysis window lengths (T_a) of 200 ms, and two with window lengths of 400 ms. These window lengths were chosen for the practice trials, as described below, so that subjects could gain familiarity with the user interface, and the window lengths values were different than the ones tested in subsequent experimental trials to prevent biasing the experiment. One classifier for each window length was trained with all four EMG input channels, and the other classifier was trained with only two EMG input channels. The two-channel classifiers used signals from the extensor bundle electrode (#1) and the flexor bundle electrode (#2). For each of the four classifiers, four time-domain (TD) features (mean absolute value, number of zero crossings, waveform length, and number of slope sign changes [15]) were extracted from the corresponding channels of EMG data in each analysis window. A linear discriminant analysis (LDA) algorithm was used to partition the feature space into seven subspaces for pattern classification, as described by Duda [24]. The classification errors [23] and controllability [8] of this type of pattern recognition system has been compared to more complex control systems, where it was found to perform similarly. This pattern recognition system was therefore used in this study for ease of implementation and to keep signal processing delays, T_d, to a minimum. The value of T_d in this study was computed on a 2.5 GHz Intel® Core 2 Duo processor and was found to be approximately 500 μs. The time taken to render updates in the virtual environment varied depending on the motion class, but was consistently less than 20 ms. Consequently, a 25 ms window increment (T_inc) was selected to ensure that there was no data loss.

After the classifier was trained, it was used in real time to predict user commands and control a virtual prosthetic arm by directing the relative joint velocities to manifest the intended movement. The desired overall prosthesis velocity for the selected movement class, which was a percentage of the maximum velocity, was extracted from the same analysis window as the data used for the class decision. Velocities were calculated by averaging the mean absolute values of EMG signals for all channels, k, and multiplied by a gain factor, G:

$$\mathit{Desired\; Velocity}=G\left(\frac{1}{N}{\sum }_{k=1}^N\mathit{MA}{V}_k\right).$$ (2)

Subjects performed the Target Achievement Control (TAC) Test within the virtual reality environment to quantify controllability with the various window lengths. During the test, subjects were required to move the virtual prosthesis in real time into one of six prompted target postures within the virtual environment. These postures were oriented such that subjects were required to perform only one motion (e.g. wrist flexion) to successfully achieve the target posture. However, all trained motions (wrist flexion/extension, wrist pronation/supination, hand open/close) were active during the test, such that the subject would have to correct for any additional motions that were performed in error. To provide visual feedback, the virtual hand changed color when it reached the target posture within an acceptable tolerance (± 5 degrees for each degree of freedom). Trials ended successfully when subjects were able to keep the virtual hand in the target posture for 2 s. Trials ended unsuccessfully after 12 s if the subject did not complete a 2 s hold of the target posture. The maximum movement velocity of each degree of freedom was 100 degrees per second. The maximum movement velocity, acceptable tolerance, timeout value, and target postures were determined in pilot tests. Each TAC Test set included two trials for each of the six target postures, for a total of twelve trials per set. During these practice tests, the subjects were coached by the experimenter on how to reach the postures, so that they could learn how to use the pattern recognition system and become familiar with the virtual environment. All data (EMG data and TAC Test results) from the practice session were discarded.

B. Experimental Trials

All subjects were given a rest period of 5–10 min between the practice trials and the experimental trials. For the experimental trials, eight EMG data collection sequences were obtained from subjects in the same manner listed above (seven muscle contraction classes, 3 s contractions, randomized order, and self-selected contraction level). Four of the eight sequences (1–4) were used to train pattern classifiers with analysis window lengths of 50, 150, 250, 350, 450, and 550 ms, respectively. Similar to the practice trials, two-channel and four-channel classifiers were trained for each window length. Thus, a total of 12 different classifiers were trained. The performance of each classifier was assessed offline using the average classification error of the system when tested on data from sequences 5–8. The average classification error was calculated by dividing the number of erroneous class decisions by the total number of class decisions.

Each subject completed two TAC Tests with each of the 12 classifiers, which were presented blind to the subjects in random order. Real-time performance with the TAC Test was evaluated by monitoring the subjects’ completion rates for each set of conditions. The completion rate was the percentage of testing trials in a set in which the subject completed a 2 s hold of the target posture within 12 s.

C. Statistical Analysis

A linear mixed-effects model was created using SPSS Statistical Modeling Software (SPSS 15.0 SPSS Inc., Chicago IL, USA) to determine the relationship between window length and classification error. A linear mixed-effects model has the form

$$y=\mathrm{X}\beta +\mathrm{Z}\gamma +\epsilon ,$$ (3)

where y is a vector of responses, X is the known fixed-effects design matrix, β is a vector of fixed-effects parameters, Z is the random-effects design matrix, γ is the vector of random-effects parameters, and ε is a vector of residual error [25]. Classification error was the dependent variable; the number of channels, window length, and session, with all possible interactions, were set as fixed variables; and the subject was set as a random variable. The linear mixed-effects model uses the expectation maximization algorithm to find the best fit for the data within the model design parameters. The null hypotheses were that β and γ were equal to zero. The p-values for all pair-wise comparisons between model parameters were adjusted using a Bonferonni correction for multiple comparisons.

The completion rate data were also fit to a linear mixed-effects model which used subject as a random effect; window length, session, and channel as fixed effects; and classification error as a covariate. The order in which each control system was tested was also added to the model as a repeated effect.

IV. Results

A. Classification Error

Classification error was found to decrease with increasing window length (Fig. 2a). This was true for both two- and four-channel classifiers and at both experimental sessions. The linear mixed-effects model for classification error indicated that window length, number of channels, and session each had a significant effect on classification error (p<0.001 for each). There was no significant interaction between window length and experimental session (p=0.99). Two significant interactions were identified: (1) window length and number of channels (p<0.01), and (2) number of channels and session (p<0.01).

Fig. 2.

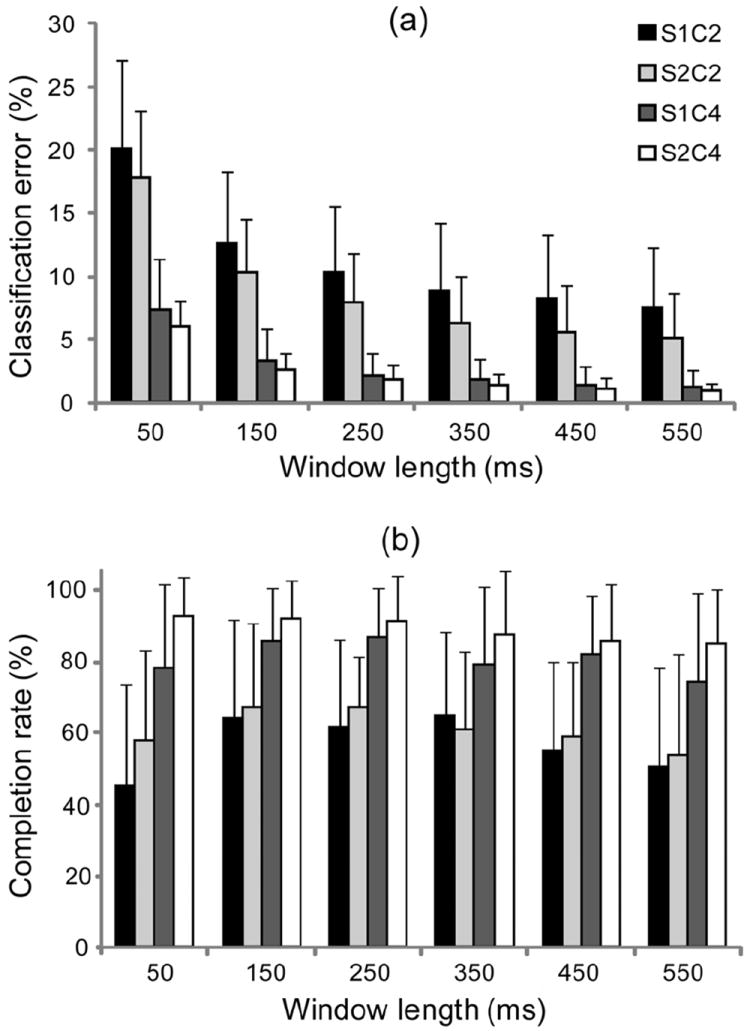
(a) Classification error averaged across all subjects and trials (grouped by experimental session and number of channels). (b) Completion rate averaged across all subjects and trials (grouped by experimental session and number of channels). Error bars denote 1 standard deviation. S1 = Session 1, S2 = Session 2, C2 = two-channel classifier, C4 = four-channel classifier.

The p-values shown in Table I indicate that when using four channels, 50 ms windows produce a significant difference in classification error when compared to window lengths greater than or equal to 150 ms. However, there is no significant difference in classification error between the 150, 250, 350, 450, or 550 ms conditions. When using two channels, there are additional significant differences: use of a 150 ms window length was shown to be statistically different from window lengths greater than or equal to 250 ms. There was also some evidence (p=0.05) to suggest that use of a 250 ms window was different from window lengths greater than or equal to 450 ms.

TABLE I.

p-Values Resulting From a Pair-Wise Comparison of Classification Errors Determined at Different Window Length Values

Two-Channel Condition						Four-Channel Condition
	150	250	350	450	550	150	250	350	450	550
50	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
150		0.033	0.000	0.000	0.000		1.000	1.000	0.452	0.234
250			0.735	0.050	0.05			1.000	1.000	1.000
350				1.000	1.000				1.000	1.000
450					1.000					1.000

Analysis for the two- and four-channel conditions are shown separately. Significant p values are highlighted in gray.

B. Completion Rate

The completion rate was highly variable between subjects, as shown in Fig. 2b. In general, completion rates increased at window lengths between 50 and 150 ms, plateaued between 150 – 250 ms, and then decreased at longer window lengths. For many subjects, we observed that the decrease in completion rate at longer window lengths was frequently accompanied by an overshoot of target postures. Mean completion rates were significantly higher when using four channels in comparison to two.

The results of the linear mixed-effects model for the completion rate indicated that window length, classification error, and number of channels each had significant effects on the motion completion rate (p < 0.01). Subjects tended to have higher completion rates during the second sessions, but this relationship was not found to be significant (p=0.06). All interactions between variables were found to be insignificant (p>0.10).

The completion rate model parameters (Fig. 3) represent the relative increase in completion rates associated with the six window length values, independent of the effects of the classification error covariate. Model parameters decreased with increasing window length, demonstrating that shorter window lengths were associated with higher completion rates. The p-values resulting from a pair-wise comparison of the model coefficients indicated a significant drop in completion rate at window lengths greater than 450 ms (Fig. 3). Although non-significant, there was also some evidence (p=0.069) that window lengths greater than or equal to 150 and less than or equal to 350 ms performed best.

Fig. 3.

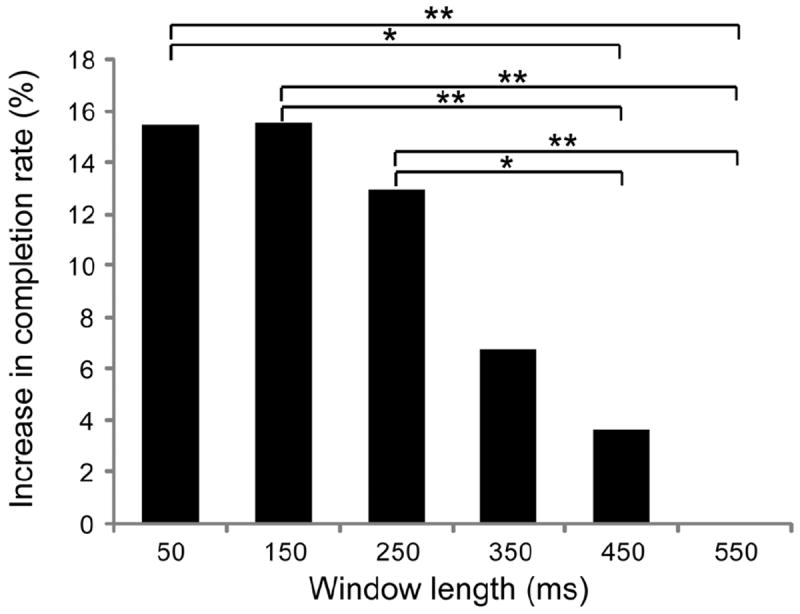
Linear mixed-effects model parameters representing the increase in completion rate percentage observed when using the associated window length. All parameters are normalized to the completion rate achieved with 550 ms windows. Asterisks represent p-values resulting from a pair-wise comparison of window length values as predictors of completion rates. Single asterisk (*) represents p<0.05; double asterisk (**) represents p<0.01.

The coefficient of the classification error term in the model was found to be significant (p<0.01) with a mean value of -1.4, meaning that every 1 percent increase in classification error resulted in a 1.4 percent reduction in completion rate. Therefore, lower classification errors (obtained at longer window lengths) yielded a positive contribution to completion rate, whereas longer analysis windows (when considered independently of classification error) yielded a negative contribution to completion rate (Fig. 4). The combination of these two effects provides the greatest increase to completion rate at window lengths of 150 and 250 ms. This was true for both two- and four-channel classifiers.

Fig. 4.

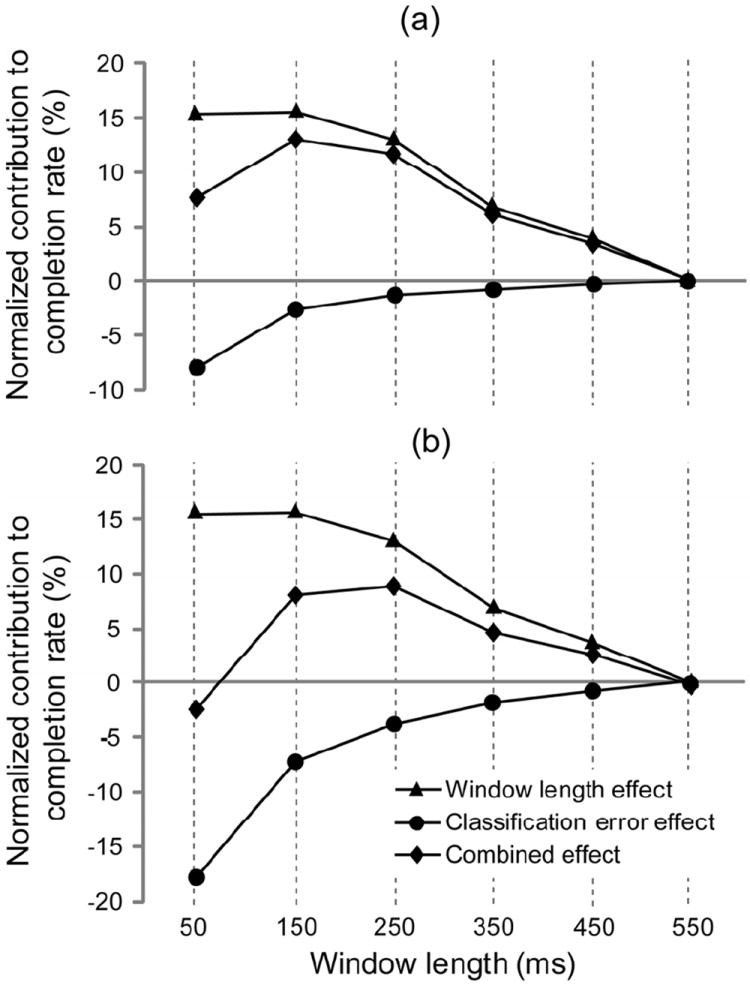
The mean classification error for the two-channel (a) and four-channel (b) conditions was used with the linear mixed-effects model parameters for window length effect and classification error effect to determine the combined effect of the two variables on the completion rate. The data was normalized to the 550 ms window length condition.

V. Discussion

Numerous previous studies have independently demonstrated both the benefit of increased temporal information [4] and the detriment of increased controller delay [3,5,6] on user performance with multi-state amplitude-based control of myoelectric prostheses. However, no prior study has concurrently investigated these effects in the setting of pattern recognition-based control, where the analysis window length influences both factors directly. This is significant because the hypothesized tradeoff between increased temporal information and increased controller delay would be critical in choosing an appropriate window length for pattern recognition: a window too short would increase classification error, while a window too long would produce excessive user-perceived delays. The results of this study confirm that manipulating the window length changes the degree of classification error and controller delay experienced by the user, and that a tradeoff between these two competing factors affects user performance.

In this study, increasing the analysis window length, and therefore the controller delay, caused users to overshoot their target in a manner previously described [6]. Increasing the window length also decreased the classification error (Fig. 2a). This result was expected, due to the increased amount of temporal information used to make the class decision, and agree with the results of Englehart et al. [12]. Classification error also decreased when four channels were used instead of two. This agrees with the results of a previous study on able-bodied control subjects by Hargrove et al. [10], which showed a significant reduction in classification error when the number of channels was increased from two to four, but no significant reduction when the number of channels was further increased. In a study on transradial amputee subjects, Li et al. [26] also showed a decrease in classification error when the number of channels was increased from two to four, and a small additional decrease when more than four electrodes were used. The improvements in classification error due to the increased number of channels can be attributed to a denser spatial sampling of the muscles of the forearm. In addition, the effects of window length on classification error were more significant when using two channels as opposed to four channels (Table I). The interplay between number of channels, window length, and classification accuracy is likely explained by a greater feature space overlap when using two channels compared to four channels. Longer window lengths, which provide greater temporal information, may result in a decrease in feature variability that allows for greater differentiation between the two-channel clusters, but provides less benefit to the four-channel clusters already more tightly distributed in feature-space. Classification error also decreased from the first to second session. This effect was suggested by the results of a previous study by Li. et al. [26], which noted that classification error decreased between two experimental sessions for transradial amputees, implying that the subjects learned to use pattern recognition systems better; however, this change was not significant.

The results of the linear mixed-effects model generated for completion rate were significant because they demonstrated that both classification error and controller delay were each independent predictors of user performance. The statistically significant coefficient for the classification error covariate was -1.4, indicating that completion rate improved with smaller levels of error. This finding is noteworthy, as it has not been previously described in the literature. Although it is intuitive to hypothesize that classification error is correlated with controllability, previous controllability studies conducted using pattern recognition systems have shown at most a weak, non-significant correlation between classification error and device controllability. Additionally, the results of the model demonstrate that completion rate is significantly influenced by window length as well. This window length parameter, which is independent from the classification error covariate, can be considered representative of the controller delay experienced by the user. The connection between window length and user performance (Fig. 3) therefore corroborates previous studies demonstrating the detrimental effects of increased controller delay observed in amplitude-based control systems [3,5,6].

Because window length dictates both the classification error and the controller delay, optimizing the effects of one parameter inevitably comes at the expense of the other. There is therefore a tradeoff between decreased classification error and increased controller delay that is an important consideration when choosing a window length for use with pattern recognition-based control. This tradeoff was demonstrated by the combined effect of classification error and window length on the linear mixed-effects model for completion rate (Fig. 4), which plateaued at window lengths of 150 and 250 ms. The subjects’ completion rates similarly plateaued at this range (Fig. 2b). According to (1), this plateau translates to a total controller delay of 88 and 138 ms, respectively, when using a 25 ms increment and 0.5 ms signal processing delay. This agrees well with the optimal delay of 100–125 ms suggested by Farrell and Weir [5]. The minimum acceptable delay found in this study was limited by the classification error of the system. The slightly larger maximum acceptable delay may be due to the maximum virtual environment movement velocity of 100 degrees per second, which was slower than the 221 degree per second and 123 degree per second prehensor velocities tested previously. Farrell and Weir found that slower movement velocities yielded higher estimates of optimal delay.

Finally, this study was limited in that it used able-bodied control subjects and a virtual environment. Subjects did not report difficulty operating within the virtual environment and demonstrated good control during practice sessions. The TAC Test is not a real-world functional test, but it does require subjects to control the prosthesis in all trained degrees of freedom in real time. We expect that the experimental findings will be applicable to amputees controlling physical prostheses.

VI. Conclusion

This work confirmed previous findings of decreased pattern recognition classification error when more spatial (i.e. more channels) and/or temporal (i.e. longer analysis windows) information is used. It also confirmed previous findings that long controller delays yield less controllable pattern recognition–based myoelectric control systems. The novel contribution of the work was developing the relationship between classification error and analysis window length on the real-time controllability of a virtual prosthesis. This relationship was previously speculated to exist, but this work provided quantifiable evidence that user performance depends on both the accuracy of pattern recognition classification and the length of controller delay. Therefore, subjects for whom classification error decreases substantially with longer window lengths may benefit from increasing the window length, despite the corresponding increase in controller delay. We found the optimal window length that enables best performance ranges from 150-250 ms. Additionally, this work showed a statistically significant relationship between classification error and prosthesis controllability, whereas previous studies have shown at most a weak correlation between these metrics.

Biographies

Lauren H. Smith received the B.S. degree in biomedical engineering in 2008 from Northwestern University, Evanston, IL, USA. She is currently pursuing the M.D. degree at the Feinberg School of Medicine at Northwestern University, Chicago, IL, USA. Her research interests include bioelectric signal analysis and clinical neurophysiology.

Levi J. Hargrove (S’05-M’08) received his B.Sc. and M.Sc. and PhD degrees in electrical engineering from the University of New Brunswick (UNB), Fredericton, NB, Canada, in 2003 2005, and 2007 respectively. He joined the Center for Bionic Medicine at the Rehabilitation Institute of Chicago in 2008. His research interests include pattern recognition, biological signal processing, and myoelectric control of powered prostheses. Dr. Hargrove is a member of the Association of Professional Engineers and Geoscientists of New Brunswick. He is also a Research Assistant Professor in the Department of Physical Medicine and Rehabilitation (PM&R) and Biomedical Engineering, Northwestern University. Evanston, IL, USA.

Blair A. Lock received the B.S. and M.S. degrees in electrical engineering, in 2003 and 2005, respectively, from the University of New Brunswick, Fredericton, NB, Canada, where he also received a diploma in technology management and entrepreneurship, in 2003. He works as a Research Engineer and is the Director of Operations at the Center for Bionic Medicine at the Rehabilitation Institute of Chicago, Chicago, IL. His research interests include pattern recognition for improved control of powered prostheses and virtual reality in rehabilitation.

Todd A. Kuiken (M’99–SM’07) received a bachelor’s degree in biomedical engineering in 1983 from Duke University, Durham, NC, USA; a doctorate in biomedical engineering in 1989 from Northwestern University, Evanston, IL, USA; and a medical doctor degree in 1990 from the Feinberg School of Medicine, Northwestern University Medical School, Chicago, IL, USA.

He completed his residency in physical medicine and rehabilitation at the Rehabilitation Institute of Chicago and Northwestern University Medical School, Chicago, IL, USA in 1995. In 1995 he was with the Rehabilitation Institute of Chicago and the Northwestern University Medical School as a Residency Trainee in physical medicine and rehabilitation. He is currently the Director of the Center for Bionic Medicine and of Amputee Services at the Rehabilitation Institute of Chicago, Chicago, IL, USA. He is also an Associate Professor in the Department of Physical Medicine and Rehabilitation (PM&R) and Biomedical Engineering, Northwestern University. Evanston, IL, USA. He is also the Associate Dean for Academic Affairs at the Feinberg School of Medicine, Northwestern University Medical School, Chicago, IL, USA.