A novel microfluidic flow focusing method

Abstract

A new microfluidic method that allows hydrodynamic focusing in a microchannel with two sheath flows is demonstrated. The microchannel network consists of a T-shaped main channel and two T-shaped branch channels. The flows of the sample stream and the sheath streams in the microchannel are generated by electroosmotic flow-induced pressure gradients. In comparison with other flow focusing methods, this novel method does not expose the sample to electrical field, and does not need any external pumps, tubing, and valves.

I. INTRODUCTION

Microfluidic lab-on-a-chip techniques have been used for counting and sorting particles or cells. In conventional flow cytometers, in order to count the particles/cells one by one, the width of the sample stream must be narrowed so that the sample particles/cells will move one by one in a single line. This is referred to as the flow focusing and is generally achieved by using two sheath streams flowing from the two sides of the sample stream. For a given flow channel, the ratio of the sample stream's flow rate to the flow rate of the sheath streams determines the size of the focused sample stream. In conventional flow cytometers, mechanical pumps are employed to control the flows of the sample stream and the sheath streams. It also needs large amounts of sheath flow reagent. The microfluidic flow cytometry devices can reduce the size of the devices, the amount of the sample, and the sheath fluid consumption. However, to develop microfluidic lab-on-chip flow cytometers, it is essential to develop microfluidic flow focusing techniques.^1–6

In recent years, a number of methods have been proposed to achieve the flow focusing in microfluidic channel. Among these flow focusing methods, sheath flow focusing is still the most common one that has been developed in microfluidic flow cytometers. Compared to other focusing approaches, sheath flow focusing is mostly determined by the flow-rate ratio between the sheath fluid and the particle suspension and thus potentially able to focus very small particles. Recently, Ligler's research group^7,8 proposed a three-dimensional (3D) sheath flow focusing method by using the grooved microchannels based on the chevron design. This method created a vertical focusing. The height and width of the sample stream can be controlled by the chevrons and the sheath-to sample flow rate ratio. In another paper, Nawaz et al.⁹ also developed a three-dimensional hydrodynamic device, and achieved flow focusing along both lateral and vertical directions. Lee et al.¹⁰ reported a contraction–expansion array (CEA) microchannel that allowed three-dimensional hydrodynamic focusing with a single sheath flow in a single-layer device. Their hydrodynamic focusing method requires external pumps (e.g., syringe pumps) to generate the pressure-driven flow. However, bulky pumps, tubing, and valves are difficult to be integrated into microfluidic flow cytometers. Electrokinetic sheath flow focusing differs from hydrodynamic sheath flow focusing. Electroosmotic flow (EOF) can be generated easily by a DC (direct current) potential difference between the inlet and outlet of a microfluidic channel. It does not require any mechanical parts and can produce a constant flow rate without any pulsing effects. Several research groups^11–15 have previously presented a T-shaped microchannel capable of realizing electrokinetic sheath flow focusing. For example, Xuan and Li¹⁶ investigated the electrokinetic flow focusing of particles in microfluidic cross-channels. The effect of the sheath flow focusing is mostly determined by the flow-rate ratio between the sheath streams and the stream of particle suspension and thus the dimension of the focused stream is tunable by adjusting the flow rate of the sheath flows. However, a strong electric field may destroy the cell membrane.

Sheathless flow focusing methods are proposed to overcome the weakness of the sheath flow focusing. Sheathless flow focusing typically depends on a force to operate the particles laterally to their equilibrium positions in the microchannel. Recently, Acoustic flow focusing has been developed for cell detection. For instance, Shi et al.^17,18 used a standing surface acoustic waves (SSAWs) method to realize on-chip micro-particle focusing. Goddard et al.¹⁹ evaluated the performance of a flow cytometer that used acoustic energy to focus particles/cells to the center of a flow stream. Suthanthiraraj et al.²⁰ presented the one-dimensional acoustic standing waves for focusing of flowing cells and particles in a rectangular flow channel. Jakobsson et al.²¹ also introduced a method to focus and orient red blood cells by using the ultrasonic standing waves on a microfluidic chip. Although the acoustic focusing method is simple and efficient, it typically requires a number of transducers which must be placed on the sides of focusing channel as closely as possible. This complicates the microchip fabrication and as well affects its integration with other functional components in a flow cytometer. Another approach utilizes the inertia of the fluid acting on particles/cells in a microchannel and allows precise cell positioning in the stream. Carlo et al.²² investigated the inertial focusing of particles in a straight microchannel. However, the inertial focusing depends on very high flow rate to generate the decent inertia motion in the microchannel. This is generally difficult to be realized in microchannels. Moreover, the equilibrium positions of the focused particle streams are sensitive to the particle's Reynolds number. Dielectrophoresis (DEP) is another sheathless focusing approach based on the interaction of the applied non-uniform electrical field and the induced charge on the particles. Recently, Chu et al.²³ presented a 3D particle focusing channel using the positive dielectrophoresis (pDEP). Demierre et al.²⁴ developed a novel geometrical arrangement of lateral metal electrodes and a patterned insulator, and utilized the “electrodeless” dielectrophoresis to achieve focusing and continuous separation. For electrode-based AC dielectrophoretic particle focusing, fabrication process of the microelectrodes in the microfluidic chip is generally complicated and expensive. The focusing efficiency is very sensitive to the dielectrophoretic force, as the dielectrophoretic force on the particles decays rapidly with the distance between the particle and the electrode. Furthermore, the electrical field often causes the adhesion of particles on the electrodes.

In this paper, in order to overcome the above-mentioned shortcomings, a novel microfluidic hydrodynamic flow focusing method was developed by using electroosmotic flows to induce pressure-driven flows for flow focusing.

II. PRINCIPLE OF THE NOVEL FLOW FOCUSING APPROACH

A schematic diagram of the proposed method is shown in Fig. 1. The flow focusing system consists of a T-shaped main microchannel and two T-shaped branch microchannels. The channel A-O-B is used as an electroosmotic pump where electroosmotic flow is generated by applying DC voltages via electrodes inserted in wells A, B, and O. All the wells are open to air. The direction of the EOF is from point O to both point A and point B due to the polarity of the electrodes shown in Fig. 1. The function of this electroosmotic pump is to draw the liquid from the main vertical channel via point O. Similarly, the two branch channels C-O′-D and C′-O″-D′ also are used as two electroosmotic pumps. Electrodes are inserted in the wells at the points C, O′, D, and C′, O″, and D′. All the wells are open to air. However, the direction of the EOF in these two branch channels is from both point C (C′) and point D (D′) to point O′ (O″) due to the reversed polarity of the electrodes shown in Fig. 1. These two electroosmotic pumps impel liquid into the main vertical channel via points O′ and O″, respectively. Because the direction of the EOF is from point O to both point A and point B, the cross-junction area near point O has a negative pressure that induces a pressure-driven flow in the main vertical channel. Meanwhile, the direction of the EOF generated in these two branch channels is from both point C (C′) and point D (D′) to point O′ (O″), the cross-junction areas near point O′ and point O″ have a positive pressure that generates a pressure-driven flow into the main vertical channel from the sides. Therefore, there are three flow streams in the vertical channel: one sample stream in the middle and two sheath flows on the sides. Adjusting the flow rate of these two sheath streams allows tuning the flow rate or the width of the sample stream. Using this method, the flow focusing is easily realized without any moving parts, external tubing, valves, and syringe pumps.

FIG. 1.

Schematic of the proposed sheath flow focusing method by using electroosmotic flow to induce pressure-driven flows.

It is desirable to understand the correlation between the controlling parameters of the electroosmotic pumps and the flow rate of the sample stream. According to Helmholtz–Smoluchowski equation, the electroosmotic flow velocity is given by

$$\overrightarrow{v}=-\frac{{\epsilon }_0{\epsilon }_{\mathrm{r}}{\zeta }_w}{\mu }\overrightarrow{\mathrm{E}}=-\frac{{\epsilon }_0{\epsilon }_{\mathrm{r}}{\zeta }_{\mathrm{w}}}{\mu }\frac{\overrightarrow{V}}{d}=k\overrightarrow{V},$$ (1)

where V is the applied voltage between the electrodes and d is the distance between the electrodes, ζ_w is the zeta potential at the channel wall, ε₀ and ε_r are the dielectric constant in vacuum and the dielectric constant of the solution, respectively.

As shown in Fig. 1, the voltages applied at points O, O′, and O″ are the same, zero volt. The voltages applied at point A and point B are the same, V_A = V_B. The voltages applied at points C, D, C′, and D′ are the same, V_C = V_D = V_C′ = V_D′. The EOF velocities in channel OA and OB are the same and are given by

$$\overrightarrow{v_A}=\overrightarrow{v_B}=k\overrightarrow{V_A},$$ (2)

and the corresponding volume flow rates are given by

$${\mathrm{Q}}_A={\mathrm{Q}}_B=k{V}_{A}A,$$ (3)

where A is the microchannel cross-section area and is assumed to be the same for all channels.

The EOF velocities in channel CO′, DO′, C′O″, and D′O″ are the same and are given by

$$\overrightarrow{v_C}=\overrightarrow{v_D}=\overrightarrow{v_{C\prime }}=\overrightarrow{v_{D\prime }}=k\overrightarrow{V_C},$$ (4)

and the corresponding volume flow rates are given by

$${\mathrm{Q}}_C={\mathrm{Q}}_D={\mathrm{Q}}_{C\prime }={\mathrm{Q}}_{D\prime }=k{V}_{C}A.$$ (5)

As shown in Fig. 1, there are three streams in the vertical channel, the sample stream and two sheath flow streams. These three streams will flow to point O and then into branch OA and branch OB. Therefore, the mass conservation at the steady state is given by

$$Q_A+Q_{\mathrm{B}}=Q_C+Q_D+Q_{C\prime }+Q_{D\prime }+Q_S\hspace{0.17em}\hspace{0.17em},$$ (6)

where Q_A, Q_B, Q_C, Q_D, Q_C′, and Q_D′ are the flow rates of channels OA, OB, CO′, DO′, C′O″, and D′O″, respectively; Q_S is the flow rate of the sample stream. Considering Eqs. (3) and (5), the above equation is reduced to

$$2Q_A=4Q_C+Q_S\hspace{0.17em}.$$ (7)

Substituting Eqs. (3) and (5) into Eq. (7) yields

$$\left|V_A\right|=2\left|V_C\right|+\frac{Q_S}{2kA}.$$ (8)

Equation (8) is a correlation among the flow rate of the sample stream and the applied voltages for the EOF pumps. There are three possibilities

• If |V_A| = |2V_C|, Q_S = 0. No liquid flowing into or out of the sample well.

• If |V_A| < |2V_C|, Q_S < 0. Some liquid flowing into the sample well.

• If |V_A| > |2V_C|, Q_S > 0. Some liquid flowing out of the sample well.

III. CHIP DESIGN AND FABRICATION

Fig. 2(a) shows the design of the flow focusing microfluidic chip. It has ten wells, A, B, C, D, C′, D′, O, O′, O″, and the sample well. It should be noted that this design of the chip is modified slightly from the schematic shown in Fig. 1. Because it is difficult to insert an electrode into the microchannel at the positions of O, O′, and O″, a small well (1.5 mm in diameter) is used at these points so that an electrode can be placed in the well. The main vertical microchannel is 100 μm in width and 5 mm in length. The three EOF pumping channels A-O-B, C-O′-D, and C′-O″-D′ all have a width of 25 μm and a length of 1 cm. The two branch channels connected to the main vertical channel have a width of 200 μm and a length of 3 mm. The diameter of wells A, B, C, D, C′, D′, and the sample well is 3 mm. In this design, the depth of all microchannels is 25 μm.

FIG. 2.

(a) Schematic of the design of the flow focusing chip based on electrokinetically induced pressure-driven flow. (b) A photograph of the PDMS-glass microfluidic chip made by soft lithography.

A polydimethylsiloxane (PDMS) microfluidic chip is fabricated by using the soft lithography protocol. First, a master is prepared by spin coating a film of SU-8 negative photoresist onto a silicon wafer. After pre-baking, a photomask bearing the microchannel geometry is placed on the top of the SU8 film. The photoresist film covered with the mask is then exposed to UV light. After post-baking and developing, a master could be obtained. A 10:1 (w/w) mixture of PDMS polymer base and the curing agent is then poured over the master and cured at 75 °C for 3 h after being degassed under vacuum. Following this step, the PDMS slab is solidified on the master and then peeled off from the master. Wells are punched on the PDMS slab at the designed locations. Finally, the PDMS slab and a glass slide are bonded together after treating them in an oxygen plasma device for 30 s to form the desired microchannel chip.

IV. NUMERICAL STUDIES

The mathematical model to describe the electrical field, the flow field, and the particles' motion is described below.

Electric field: When electrical potentials, Φ_e, are applied at wells as shown in Fig. 1, the electrical potential field in the microchannels, A-O-B, C-O′-D, and C′-O″-D′, is governed by Laplace's equation.

$${\nabla }^2{\varnothing }_e=0.$$ (9)

The boundary conditions of the electrical field are given by

$$\{\begin{array}{c}{\varnothing }_e={\varnothing }_1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}re\text{se}rvoirs\hspace{0.17em}A\hspace{0.17em}and\hspace{0.17em}B\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hfill \\ {\varnothing }_e={\varnothing }_2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}re\text{se}rvoirs\hspace{0.17em}C,\hspace{0.17em}D,\hspace{0.17em}{C}^{\prime }\hspace{0.17em}and\hspace{0.17em}{D}^{\prime }\hfill \\ {\varnothing }_e=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}point\hspace{0.17em}O,\hspace{0.17em}{O}^{\prime }\hspace{0.17em}and\hspace{0.17em}{O}^{″}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hfill \\ \overrightarrow{n}·\overrightarrow{J}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}walls\hfill \end{array}.$$ (10)

Velocity field: As explained before, the liquid flow in the system is generated by electroosmotic flow in channels A-O-B, C-O′-D, and C′-O″-D′ by the applied electrical fields in these channels. In the numerical simulations, the electroosmotic velocity boundary condition (Eq. (1)) is applied at the walls of the channel A-O-B, C-O′-D, and C′-O″-D′. No-slip boundary condition is set up for other walls.

These electroosmotic flows in turn induce a negative pressure in the cross-junction area near point O, a positive pressure in the cross-junction areas near point O′ and point O″. The steady state flow field in the system is governed by the Navier-Stokes equation and the continuity equation.

$$\nabla ·\overrightarrow{u}=0,$$ (11)

$$\rho \overrightarrow{u}·\nabla \overrightarrow{u}=-\nabla P+\mu {\nabla }^2\overrightarrow{u},$$ (12)

where ρ and μ are the density and viscosity of the liquid, u is velocity, ∇P is the pressure gradient. The non-slip velocity boundary condition is applied at the channel walls where the flow is caused by the induced pressure gradient.

Motion of particles: The motion of the particles is described by Newton's second law

$$m\frac{d^{2}x}{d{t}^2}=F,$$ (13)

where x is the position of the particle, m the mass of the particle, and F is the sum of all forces acting on the particle. As the density of the particles used in the experiments is about 1.06 g/cm³, which is very close to the density of water (1.0 g/cm³), the gravity force can be ignored. Therefore, in this study, the particles are subjected to hydrodynamic force—the drag force of the flowing liquid. Under low Reynolds' number, the drag force on a spherical particle is given by²⁵

$$F_D=\left(\frac{1}{{\tau }_p}\right)m\left(u-v\right),$$ (14)

where m is the mass of the particle, τ_p is the particle velocity response time, v is the velocity of the particle, and u is the velocity of the liquid. The particle velocity response time for spherical particles in a laminar flow is defined as

$${\tau }_p=\frac{\rho d^2}{18\mu },$$ (15)

where μ is the fluid viscosity, ρ is the particle density, and d is the particle diameter.

Numerical simulations were conducted to examine the effects of different parameters on the proposed flow focusing method. In the numerical study, COMSOL Multiphysics 4.2 a is used to solve the above mathematical model. In order to avoid the grid dependence, we examined different numbers of grids. Finally, the number of grids is chosen so that the numerical results will not change with further increase of the number of grids. The dimensions of the microchannels used in the simulation are identical to the real microfluidic chip as described in the above section. In the simulation, the initial velocity of the particles at the exit of the sample well is set to zero. To simulate the particle's motion, the electrical field and the flow field are solved first, and then coupled to the particle motion model via the velocity term in Eqs. (13) and (14). The numerical studies aim to investigate the effectiveness of the proposed method and the motion of the particles in the flow focusing channel.

A. Effects of different voltages applied for the three electroosmotic flow pumps

Equation (8) shows the dependence of the flow rate of the sample stream on the applied voltages for the EOF pumps. Three cases are examined to verify the predictions of Eq. (8). As shown in Fig. 1, the potentials at points O, O′, and O″ are always kept as 0 V. In the first case, −100 V is applied at the wells A and B, and +50 V is applied at the wells C, D, C′, and D′. The applied voltages satisfy the condition: |V_A| = |2V_C|. In Fig. 3, the velocity vectors and streamlines indicate that only the two sheath flows coming from the two branch channels are driven into the vertical channel due to the induced pressure difference. This is because, in this case, the flow rate of the electroosmotic pump generated in the channel AOB is equal to the flow rates of the two sheath flow streams produced by the two electroosmotic pumps, C-O′-D and C′-O″-D′. The numerical simulation result as shown in Fig. 3 confirmed that, when |V_A| = |2V_C|, there is no liquid flowing into or out of the sample well, i.e., Q_S = 0.

FIG. 3.

The streamlines and the velocity vectors in the flow focusing microchannel, under the condition: |V_A| = |2V_C|.

In the second case, the applied voltages are changed to meet the condition |V_A| < |2V_C|. In this case, −75 V is applied at the wells A and B, and +50 V is applied at the wells C, D, C′, and D′. However, in this case, the EOF pumping force generated in the channel A-B is not enough to suck out all liquid of the two sheath flow streams from the two branch channels. Thus, as shown in Fig. 4, the liquid coming from the two branch channels flows not only into the vertical channel but also into the sample well.

FIG. 4.

The streamlines and the velocity vectors in the flow focusing microchannel, under the condition: |V_A| < |2V_C|.

In the third case, |V_A| > |2V_C|, −150 V is applied at the wells A and B, and +50 V is applied at the wells C, D, C′, and D′. In this case, the EOF pump of the channel A-B is strong enough to draw out not only the two sheath flow streams but also some sample solution. Fig. 5 clearly shows that in the vertical channel, there are three streams. Two streams come from the two branch channels and one stream comes from the sample well. More importantly, it is obvious that the liquid flowing from the sample well is squeezed in the vertical channel by the two sheath flow streams. The above numerical simulation results clearly demonstrated that the direction of the sample flow and the flow focusing effect can be controlled by the applied voltages for the three EOF pumps.

FIG. 5.

The streamlines and the velocity vectors in the flow focusing microchannel, under the condition: |V_A| > |2V_C|.

B. The dependence of the flow focusing effect on the applied electric potentials

In the vertical channel, there are three streams, the sample stream in the middle, and two sheath streams on the two sides. The width of the focused sample stream can be estimated by the ratio of the flow rates

$$\frac{w_{\mathit{f}\mathit{s}}}{w}=\frac{Q_s}{Q_s+2·Q_b},$$ (16)

where Q_b and Q_s are the flow rates of the branch channel and the sample stream, respectively. w_fs and w are the width of the focused sample stream and the width of vertical channel (100 μm), respectively. Because of the symmetry of the system in this study, the flow rates from the two side channels are equal, i.e., Q_b = Q_C + Q_D. According to Eqs. (5) and (7), Eq. (16) can be re-written as

$$\frac{w_{\mathit{f}\mathit{s}}}{w}=\frac{Q_s}{Q_s+4·Q_C}=1-2·\frac{Q_C}{Q_A}=1-2·\left|\frac{V_C}{V_A}\right|,$$ (17)

where V_A and V_C are the voltages applied at well A and well C, respectively. (Note V_A = V_B and V_C = V_D = V_C′ = V_D′ as indicated in Fig. 1.) Equation (17) can be used to predict the width of the focused sample stream.

• V_A = −100 V and V_C = +50 V, $\hspace{0.17em}\left|\frac{V_C}{V_A}\right|=\frac{1}{2}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{w_{\mathit{f}\mathit{s}}}{w}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}_{\mathit{f}\mathit{s}}=0\hspace{0.17em}\mu \mathrm{m}$

• V_A = −150 V and V_C = +50 V, $\left|\frac{V_C}{V_A}\right|=\frac{1}{3}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{w_{\mathit{f}\mathit{s}}}{w}=\frac{1}{3},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}_{\mathit{f}\mathit{s}}=33.3\hspace{0.17em}\mu \mathrm{m}$

• V_A = −200 V and V_C = +75 V, $\left|\frac{V_C}{V_A}\right|=\frac{3}{8}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{w_{\mathit{f}\mathit{s}}}{w}=\frac{1}{4},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}_{\mathit{f}\mathit{s}}=25\hspace{0.17em}\mu \mathrm{m}$

• V_A = −300 V and V_C = +125 V, $\left|\frac{V_C}{V_A}\right|=\frac{5}{12}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{w_{\mathit{f}\mathit{s}}}{w}=\frac{1}{6},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}_{\mathit{f}\mathit{s}}=16.67\hspace{0.17em}\mu \mathrm{m}$

From the above analysis, it is clear that the width of the sample stream can be controlled by the applied voltages.

In order to further evaluate the effect of the flow focusing on the particles' motion, numerical simulations were conducted to study the trajectory of particles carried by the sample stream into the vertical channel. In the simulations, it is assumed that the initial position of the particles is at the entrance of the sample channel and the initial velocity of the particles is zero. The diameter of particle is 10 μm. For a good visualization effect, 1000 particles are considered. When the electric potentials are applied, the particles begin to move. As shown in Fig. 6, it is obvious that a parabolic profile of the moving particles is formed in the sample stream channel before the intersection of the vertical channel and the two branch channels. This is because the flow is a pressure-driven flow induced by electroosmotic flows. When the particles enter the intersection, they are squeezed into the center of the channel by the two sheath flows immediately.

FIG. 6.

The flow focusing effect on the trajectories of the particles as predicted by the numerical simulations. (a) −150 V is applied at wells A and B and 0 V is applied at point O; and +50 V is applied at wells C, D, C′, D′ and 0 V is applied at points O′ and O″. (b) −200 V is applied at wells A and B and 0 V is applied at point O; and +75 V is applied at wells C, D, C′, D′ and 0 V is applied at points O′ and O″. (c) −300 V is applied at wells A and B and 0 V is applied at point O; +125 V is applied at wells C, D, C′, D′ and 0 V is applied at points O′ and O″.

According to Eqs. (8) and (17), the focused sample stream can be formed under the condition of |V_A| > |2V_C|. Therefore, in the simulations, −150 V, −200 V, and −300 V applied at wells A and B are considered; correspondingly, +50 V, +75 V, and +125 V applied at wells C, D, C′, and D′ are considered. Fig. 6 shows the trajectories of the particles' motion under the three different conditions. From Fig. 6(a), the focused particle stream occupies approximately 1/3 of 100 μm wide vertical channel. When increasing the applied voltages, the width of the focused particle stream is reduced. As seen in Fig. 6(c), the width of the focused particle stream is squeezed to approximately 1/6 of 100 μm wide vertical channel. The numerical simulation results are in excellent agreement with the above theoretical analysis.

V. EXPERIMENTAL STUDY OF THE FLOW FOCUSING

In the experimental study, Rhodamine B and 7.0 μm carboxyl polymers microspheres (Bangs Laboratories Inc.) were used for visualizing the flow focusing effect. The particles were supplied in a suspension form with a concentration of 10% microspheres. The experimental system consists of the following major components: the microfluidic chip, a fluorescence microscope (AZ100, Nikon) and image system, three DC power supplies, and a data acquisition system. The microfluidic chip was fixed on the observation platform of the microscope. Three DC power supplies (CSI12001X, Circuit Specialists Inc., USA) were used to control the voltages applied to the different electrodes. A fluorescent microscope with a high intensity illumination system and a CCD camera (Retiga 2000 R, Nikon) were used to visualize the motion of the particles inside the microchannel. The images are captured by the digital camera and digitized by the computer software (NIS-Elements BR 3.0).

Initially, the channels and the wells A, B, C, D, C′, D′ and O, O′, O″ were filled with de-ionized water. The sample well was filled with the sample solution, which is diluted 25 times from the original solution with DI water. The liquid levels in different wells were carefully balanced so that there was no pressure difference among these wells. Once the voltages were applied, electroosmotic flows were generated in the channels and consequently pressure gradients, sample stream flow, and two sheath flows were produced in the vertical channel. The images of particle motion were obtained by the CCD camera and processed by the image analysis software.

To demonstrate that the liquid can be focused at the vertical channel by the applied electric fields, Rhodamine B is used as a tracer to visualize flow field in the vertical channel. Fig. 7 shows the fluorescent image (experimental) (a) and numerical simulation image (b) of the vertical channel when the dye solution is traveling. As shown in Fig. 7, the dye solution stream flowed into the vertical channel due to the electrokinetic-induced pressure-driven flow and was focused by the two sheath flows. The excellent agreement is obtained between the experimentally observed fluorescent images and the numerically simulated concentration field.

FIG. 7.

(a) A fluorescent image of flow focusing effect in the vertical microchannel. (b) A simulation image of flow focusing effect in the vertical microchannel (−150 V is applied at A, B and 0 V is applied at point O; +50 V is applied at C, D, C′, D′ and 0 V is applied at point O′ and O″).

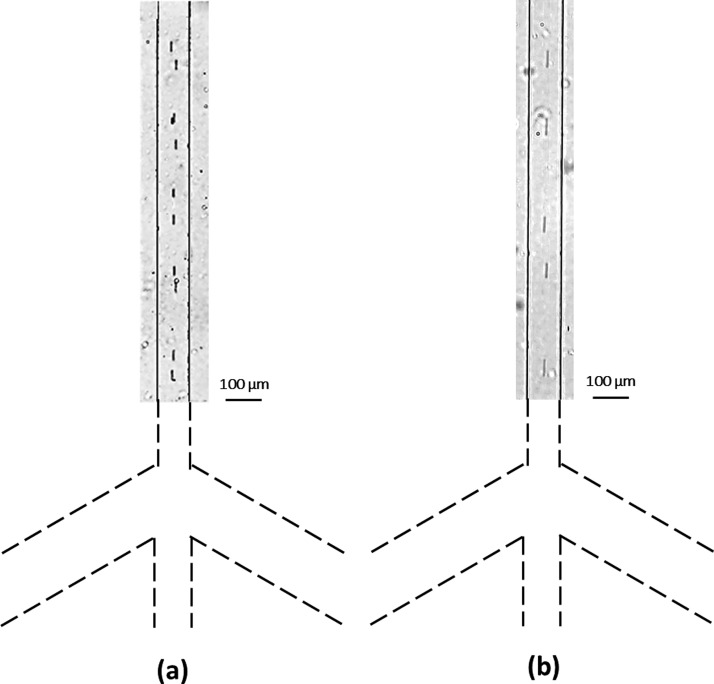
Fig. 8 shows the microscope images of 7 μm microspheres focused by two sheath flows in the vertical channel. These sequential images show how the particles are squeezed by the two sheath flows. As shown by the numerical simulation results in Fig. 6, the flow focusing effect can be improved by increasing the applied voltages at the wells. Fig. 9 shows the experimentally observed flow focusing effects of 7 μm microspheres passing through the vertical channel under different voltage conditions. In Fig. 9(a), the applied voltage at A, B was −150 V and the applied voltage at C, D, C′, D′ was +50 V. In Fig. 9(b), the applied voltage at A, B was increased to +200 V and the applied voltage at C, D, C′, D′ was increased to +75 V. It can be seen that the flow focusing effect of Fig. 9(b) is better. Judging by the separation distance between particles, the speed of the particles in the case of Fig. 9(b) is higher than that in the case of Fig. 9(a). It should be pointed out that when the applied voltage at A, B was increased to +300 V, the sample particle stream was focused even narrower; however, the speed of the particles was so high that it was very difficult for our camera system to capture the images of the single particle. For this reason, we could not show images of the focused particles under the condition of −300 V at A, B, and +125 V at C, D, C′, D′. Fig. 10 shows a comparison between the experimental result and the simulation result for the effect of flow focusing of 0.5 μm particles. In this case, the applied voltage at A, B is increased to 300 V and relevantly the applied voltage at C, D, C′, D′ is increased to 125 V. Clearly, in Fig. 10, the particle (0.5 μm) stream is squeezed greatly by these two sheath flows. In the numerical simulations, the width of the best focused stream is 1/6 of the width of the microchannel (100 μm), which is approximately 17 μm. However, in the experimental results, due to the poor quality of the images, the estimated width of the focused stream is approximately 18 μm to 20 μm.

FIG. 8.

A series of images showing the motion of 7 μm microspheres (the time interval is 1 s). In this experiment, −150 V was applied at wells A and B and 0 V was applied at point O; +50 V was applied at wells C, D, C′, D′ and 0 V was applied at point O′ and O″.

FIG. 9.

Experimentally observed flow focusing effect of 7 μm particles moving in the vertical channel. In the experiment (a), −150 V was applied at wells A and B and 0 V was applied at point O; +50 V was applied at wells C, D, C′, D′ and 0 V was applied at point O′ and O″. In the experiment (b), −200 V was applied at wells A and B and 0 V was applied at point O; +75 V was applied at wells C, D, C′, D′ and 0 V was applied at point O′ and O″.

FIG. 10.

The focusing effect of 0.5 μm diameter microsphere stream in the vertical channel. The comparison between the experimental result and the simulation result for the flow focusing effect (−300 V at is applied A, B and 0 V is applied at point O; +125 V is applied at C, D, C′, D′ and 0 V is applied at points O′ and O″). The width of the vertical channel is 100 μm.

Since the motion of the particles is caused by electroosmotic flow-induced pressure-driven flow, the velocity of the particles can be controlled by power of the EOF pumps, and hence by the applied electrical potentials. To verify this point, a series of experiments were conducted to measure the velocity of the 7 μm particles under different voltages applied to these EOF pumps. In these experiments, the electric potentials at the point O, O′ and O″ were kept at zero. −150 V, −200 V, and −250 V were applied at wells A and B, respectively. Correspondingly, +50 V, +75 V, and +100 V are applied at wells C, D, C′, and D′, respectively. Under a given condition, the velocities of at least 10 particles passing through the observed area under the microscope were measured by analyzing the sequential images. The average velocities of the particles are presented in Fig. 11. Each data point in Fig. 11 is the average value of the velocities of at least 10 particles under the same condition. The error bars show the standard deviation. From this figure, it is evident that the average velocity of the particles increases linearly with the applied voltages.

FIG. 11.

Average velocity of the 7 μm particles in the vertical channel under different applied voltages at wells A and B.

VI. CONCLUSIONS

In this study, a new microfluidic flow focusing method is demonstrated. The flows of the sample stream and two sheath streams are generated by the electroosmotic flow-induced pressure gradient. The flow focusing effect can be controlled by the voltages applied to the electroosmotic flow pumps. Theoretical analysis, numerical simulations, and experimental studies were conducted and verified this method. In comparison with other flow focusing methods, this novel approach eliminates the conventionally required components such as pumps, tubing, and valves, and has great potential of easy integration with other on-chip microfluidic functions.