Stability of Iowa mutant and wild type Aβ-peptide aggregates

Abstract

Recent experiments indicate a connection between the structure of amyloid aggregates and their cytotoxicity as related to neurodegenerative diseases. Of particular interest is the Iowa Mutant, which causes early-onset of Alzheimer's disease. While wild-type Amyloid β-peptides form only parallel beta-sheet aggregates, the mutant also forms meta-stable antiparallel beta sheets. Since these structural variations may cause the difference in the pathological effects of the two Aβ-peptides, we have studied in silico the relative stability of the wild type and Iowa mutant in both parallel and antiparallel forms. We compare regular molecular dynamics simulations with such where the viscosity of the samples is reduced, which, we show, leads to higher sampling efficiency. By analyzing and comparing these four sets of all-atom molecular dynamics simulations, we probe the role of the various factors that could lead to the structural differences. Our analysis indicates that the parallel forms of both wild type and Iowa mutant aggregates are stable, while the antiparallel aggregates are meta-stable for the Iowa mutant and not stable for the wild type. The differences result from the direct alignment of hydrophobic interactions in the in-register parallel oligomers, making them more stable than the antiparallel aggregates. The slightly higher thermodynamic stability of the Iowa mutant fibril-like oligomers in its parallel organization over that in antiparallel form is supported by previous experimental measurements showing slow inter-conversion of antiparallel aggregates into parallel ones. Knowledge of the mechanism that selects between parallel and antiparallel conformations and determines their relative stability may open new avenues for the development of therapies targeting familial forms of early-onset Alzheimer's disease.

INTRODUCTION

Deposits of amyloids are associated with a growing number of human illnesses. An example is Alzheimer's disease,¹ which is correlated with the appearance of fibrils in patient brains that are formed by β-amyloid (Aβ) peptides.² The amyloid deposits consist of elongated spines made of many β-sheets strands¹ held together by a dense hydrogen-bonded network and steric-zipper-like van der Waals and hydrophobic forces,³ which in turn depend on shape complementarity and the organization of β-sheets into either a parallel or antiparallel structure.⁴ Amyloid-forming peptides, such as Aβ, can simultaneously assemble into fibrils with different morphologies.⁵ Such fibril polymorphism arises from differences in packing of the peptides into parallel and antiparallel β-sheets, proto-filaments, filaments, and fibrils;⁶ and is important because the various fibril morphologies differ in growth rate and toxic potential.^7–9 Insight into this relationship is therefore crucial for understanding the disease mechanism, which in turn may open the way to new therapeutic strategies.

One possible avenue to probe this relationship is by comparing the wild type with the various pathogenic mutations that are known to modify the physicochemical properties of the peptide¹⁰ and to cause early onset of Alzheimer's disease. One example of these pathological Aβ mutants is the so-called Iowa mutant (D₂₃N Aβ), which has higher neurotoxicity than wild-type Aβ.¹¹ While the existing experimental structures of wild type Aβ are built out of in-register parallel β-sheets,¹² recent in vitro studies indicate Aβ (1–40) Iowa mutant (D₂₃N) fibrils can contain either parallel or antiparallel β-sheets.¹³ The antiparallel D₂₃N-Aβ_1–40 fibrils propagate less efficiently in seeded fibril growth and were found to be thermodynamically meta-stable, transient, intermediates that convert over time into fibrils with parallel structure. Evidence for this conversion results from measurements of intermolecular dipole-dipole couplings among ¹³C labels at A21 methyl carbons, however, there are no experimental structures of the parallel fibril Iowa mutant deposited in the Protein Data Bank.¹⁴ The larger stability of parallel configurations has been related to more ordered residues, longer β-strand segments, and interactions between cross-β units in parallel D₂₃NAβ_1–40 fibrils than found in antiparallel structures.¹⁴ Additional factors that lead to a predominance of parallel structures are the more efficient packing of hydrophobic side chains at the C-terminal interface in the twofold and/or polar zipper interactions involving Q15, N23, or N27 side chains.¹⁴

The solid state NMR data of the Iowa mutant fibrils suggest that antiparallel cross-β motifs could also exist in other cases.¹⁴ As antiparallel cross-β motifs also exist and are believed to be thermodynamically stable in polyglutamine,¹⁵ these NMR data cast further doubt on the widely accepted assumption that amyloid fibrils are built out of in-register parallel β-sheets.¹⁶ Instead, the data suggest coexistence of parallel and antiparallel conformations in Aβ. Even for wild type Aβ where the existing experimental structures are built only out of in-register parallel β-sheets, there is evidence that the wild type could exist to some extent in an antiparallel manner.¹⁷ Hence, while both forms are cytotoxic to neuronal cell cultures,¹⁴ it is reasonable to conjecture that the different pathologies are related to the different probabilities that both forms are observed in wild type and Iowa mutant.

Assuming such a scenario, it becomes important to understand the polymorphism and conformational stability of Aβ peptides. For this purpose, we have performed a series of molecular dynamic simulations of antiparallel and parallel twofolds (stacks) of Aβ₁₅₋₄₀ and D₂₃N Aβ_15–40 fibril-like oligomers. Such molecular dynamics stability studies suffer from the problem that the energy landscape of amyloid aggregation is rugged. The achievable scope of protein aggregation¹⁸ computer simulations is limited as aggregation and conversion between forms of aggregates happen on time scales not accessible by molecular dynamics. One way to circumvent this problem is through use of stability studies, which do not directly model amyloid assembly but provide indirect input on the various factors that modulate fibril formation. An evaluation of the stability of the pre-formed initial structures requires that the system evolve with its natural kinetics. This excludes the use of enhanced sampling techniques such as generalized ensemble sampling and replica exchange molecular dynamics. Since these techniques rely on artificial dynamics,^19–21 they make it difficult to interpret the changes in stability observed during the simulation. Instead, we test in the present work a different approach where the computational costs are lowered by using reduced solvent masses that lower friction and enhance conformational sampling.^22,23 Previous studies have also shown that reducing the masses of peptide side chain atoms in combination with solvent mass can enhance peptide conformation sampling^23,24 and, in the present paper, we evaluate the efficiency of this approach in the context of protein aggregation. The approach is similar to another method for increasing sampling efficiency, namely, raising the temperature of the system. However, unlike that method it avoids the problem that hydrophobicity is strongly temperature-dependent which, in the case of high temperature simulations, may lead to significantly altered dynamics.²⁵ Mass-scaling also will lead to artificial dynamics, but we conjecture that it leads to a smaller disturbance of the system and therefore smaller deviations from the natural dynamics. Using this improved sampling technique we then explore how the differences in stability between parallel and antiparallel forms are modulated by the sequence of amino acids in both wild type and Iowa mutants.

MATERIALS AND METHODS

In our simulations, we investigate the stability of aggregates of the wild type and the Iowa-mutant of Aβ, both in configurations with parallel β-sheets and such with anti-parallel β-sheets. The four start configurations are decamers built from two U-shaped penta-peptides with C terminal to C terminal interfaces whose structures were derived from the NMR amyloid fibrils (PDB codes, 2LNQ and 2LMO). The fibril-like oligomers used as starting configurations are made out of residues 15–40 for both Aβ₁₅₋₄₀ and D₂₃N Aβ_15–40 peptides, which are capped with acetyl and amide groups in order to have equal length in the simulated molecules. This helps to avoid systemic error when comparing differences in the stability of the preformed oligomers of Aβ and its Iowa mutant. We assume that the parallel D₂₃NAβ_1–40 oligomer structures closely resemble that of the parallel WT-Aβ_1–40 structures, and the anti-parallel D₂₃NAβ_1–40 oligomers closely resemble the anti-parallel WT-Aβ_1–40. We thus replace the residue N23 of the experimentally known D₂₃NAβ_15–40 fibril (PDB id of 2LNQ) with D to generate the anti-parallel wild type Aβ_15–40 fibril-like oligomer. The mutation is done by replacing the side chains of the targeted residues and keeping its original backbone conformations. The parallel D₂₃N Aβ_15–40 fibril model is generated in the same manner by replacing at position 23 an aspartic acid (D) with asparagine (N) in the experimentally determined wild-type Aβ_10–40 fibril (PDB id of 2LMO) structure and removing residues 10–14. The double-layered model of the D₂₃N-Aβ_15–40 antiparallel conformation is constructed from the experimentally derived single layer by setting the interlayer distance between two pentamers to values between 9 and 10.3 Å, which is in the range of values observed via x-ray.¹ The two β-strands belonging to each peptide are offset from one another along the oligomer axis by roughly 5 Å as in the experimental structure of the parallel wild-type Aβ_10–40 double-fold. This allows for a more meaningful comparison between the two different structural models. The interface in the antiparallel model was then staggered to create a steric zipper that minimized clashes between residues. This was done by maximizing the distance between the initial side chain distances and orienting the stagger such that the bulky phenylalanine was positioned between glycine and leucine.²⁶

We ran several long all-atom explicit water molecular dynamic simulations in order to explain the structural and energetic differences between the parallel and antiparallel arrangement of the wild type and Iowa mutant aggregates. Our molecular dynamics simulations use a combination of the CHARMM27 force field with CMAP corrections^27–29 with explicit water (TIP3P),^30,31 a common choice for exploring amyloid peptide aggregation,^32,33 as implemented in the GROMACS program version 4.6.2.³⁴ Hydrogen atoms are added with the pdb2gmx module of the GROMACS suite. The start configurations for all proteins are put in the center of a cubic box, with at least 12 Å between the solute and the edge of the box.¹⁵ We enforce periodic boundary conditions in all three directions to simulate a pseudo-infinite amyloid. In order to account for the periodicity, electrostatic interactions are calculated with the PME algorithm.^35,36 We use a time step of 2 fs. Hydrogen atoms are constrained with the LINCS³⁷ algorithm, while the Settle algorithm is used for water.³⁸ The temperature of 310 K is kept constant by the Parrinello-Donadio-Bussi algorithm³⁹ (τ = 0.1 fs) which is similar to Berendsen coupling but adds a stochastic term that ensures a proper canonical ensemble.^39,40 In a similar way, the pressure is kept constant at 1 bar by the Parrinello-Rahman algorithm⁴¹ (τ = 1 fs). After energy-minimizing the solvated start configuration using first the steepest descent method, followed by conjugate gradient, the system is equilibrated in two steps of 500 ps, first in a NVT ensemble and second in a NPT ensemble at 1 bar. After equilibration, 300 ns trajectories are analyzed for each system to monitor how the oligomer structures evolve with time; however, averages are only calculated over the last 100 ns to ensure equilibrium conditions. Data are saved at 4.0 ps intervals for further analysis. For each system, we run three distinct simulations with different initial velocity distributions. Since they start from the same initial structure, these three trajectories are correlated, and error estimates from standard deviations therefore have to be taken with a grain of salt. However, comparing the three trajectories gives some indication for reaching equilibrium and guarantees three maximal independent sets of measurements.

Two sets of simulations were run for each of the four cases: one with the physical mass of the atoms in the molecules, and one where these masses are scaled by a factor of 0.5. Since the viscosity is proportional to mass, the mass scaling leads to a reduced viscosity, which in turn allows faster sampling of configurations. Comparing the two sets of simulations allows us to quantify the improvement in sampling efficiency.

The molecular dynamics trajectories are analyzed with the tool set of the GROMACS package. Specifically, we monitor conformational changes and stability of the oligomer models through the time evolution of root means square deviations (RMSD) of the Cα atoms, root mean square fluctuation (RMSF), hydrophobic contacts distances, and hydrogen bonds, measured with the g_hbond and g_dist modules in GROMACS. Hydrogen bonds are defined by a distance cutoff between donor and acceptor of 0.36 nm and an angle cutoff of 30°. Configurations are visualized using PyMOL.⁴²

RESULT AND DISCUSSION

Sampling efficiency of protein aggregate simulations

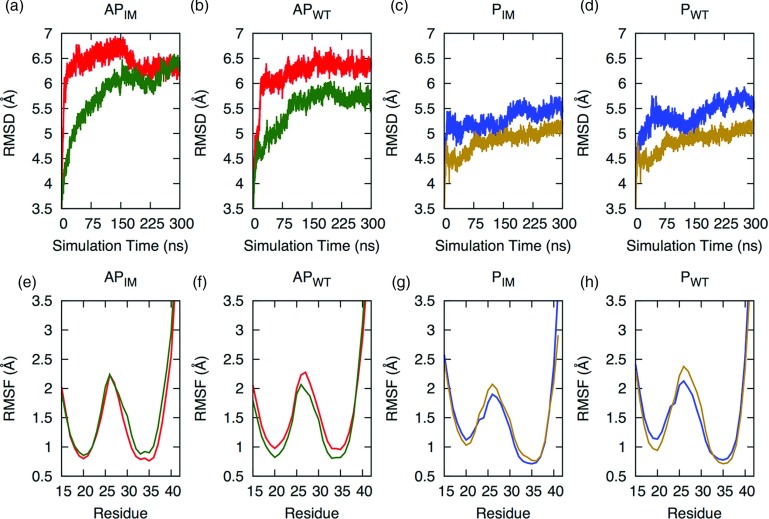
We begin our analysis by comparing molecular dynamics simulations of the four systems (wild type and Iowa mutant, with either parallel or anti-parallel β-sheet arrangement) that use physical masses with simulations. The physical masses are scaled by a factor of one half, corresponding to a reduced viscosity of the system. As a metric to evaluate the efficiency of the two methods, we have calculated the RMSD to the start configurations as reference. The expectation is that the RMSD increases faster in the systems with scaled mass than in the control system, with both eventually approaching a similar steady state. Such behavior is indeed observed for the antiparallel Iowa mutant protein system, where both the control system and the scaled mass simulations approach a final RMSD value of approximately 6 Å (Figure 1(a)). This value is reached in the scaled mass simulations after only 7 ns while the control, run with full physical mass, requires 104 ns to reach this value (i.e., in this example we find an approximately 15-fold increase in efficiency). The improvement is even more dramatic in the case of the wild type antiparallel model where the control system within 300 ns of simulation time never reaches the RMSD value of about 6.1 Å, whereas the scaled mass simulation approaches this value after only 30 ns (Figure 1(b)). Assuming again an increase in efficiency by a factor of 15, the control system would only approach this value after 450 ns, much longer than the simulation time of 300 ns for our systems. A qualitatively similar picture is also observed for the two systems with parallel sheet organization (Figures 1(c) and 1(d)). However, the gain in efficiency in both systems (wild type and mutant) is not large enough that the systems would approach a region of constant RMSD. This is not surprising, as the parallel configurations are expected to be much more stable.

FIG. 1.

Root-mean-square deviations (RMSD) and root-mean-square fluctuations (RMSF) values for Iowa mutant and wild type with physical mass (Green/Tan) and with scaled mass (Red/Blue). The increased sampling efficiency in scaled mass simulations is indicated by their growing variance. (a) and (e) show the RMSD and RMSF values for the antiparallel Iowa mutant (AP_IM), (b) and (f) show the same quantities for the antiparallel wild-type (AP_WT), (c) and (g) for the parallel Iowa mutant (P_IM), and (d) and (h) for the parallel wild-type (P_WT).

Note that in all cases similar root-mean-square-deviation values are approached. Comparison of the RMSF values for the last 100 ns of simulations (Figures 1(e)–1(h)) between the antiparallel and parallel full mass (green and tan, respectively) and the half mass (red and blue, respectively) shows little difference in the residue behavior of the equilibrated structure. From this, we conclude that the mass scaling does not alter the behavior of the overall structure to a large degree. We conclude that mass scaling can indeed enhance the sampling efficiency in simulations of protein aggregates, albeit more work needs to be done to optimize the mass tuning. This will be explored in future studies. In the present work, we use only our reduced mass simulations for further analysis, as the sampling efficiency in all four cases is higher than in the regular molecular dynamics runs.

Structural stability of wild type and Iowa mutant aggregates

Following the trajectories of the four systems, we find that the Aβ_15–40 and D₂₃N Aβ_15–40 decamers have very similar dynamic behavior. Both parallel β-sheet variants (Figures 1(c) and 1(d)) change less in their root-mean-square deviation values than the anti-parallel β-sheet variants (Figures 1(a) and 1(b)), but the RMSD values indicate that there are no significant differences in stability between the fibril-like oligomers of Aβ_15–40 and D₂₃N Aβ_15–40. A more sensitive quantity is the RMSF, which allows one to distinguish between flexible and stable residues. The average RMSF is calculated for 6 of the 10 peptide-chains for the last 100 ns in each system, with the 1st, 5th, 6th, and 10th chains removed due to aberrant flexibility caused by increased surface exposure. Both conformations of mutant and wild type are highly flexible at the ends and in the loop regions of the protein strands, and much less so in the β-strand regions. The C-terminal region has a high RMSF value that can be explained by its C–C terminal bilayer hydrophobic interactions resulting from an increased solvent exposure. While less pronounced, high RMSF values are observed also for the three N-terminal residues. Face-to-face interactions observed in β1 (residues 18–22) and C-terminal-to-C-terminal hydrophobic interactions between adjacent β2 layers (residues 30–38) appear to lead to similar relative stability in both antiparallel systems (Table I) as these residues have the same average RMSF value of 1 Å in both antiparallel systems. On the other hand, the C-terminal-to-C-terminal interactions are more stable in the parallel form of both mutant and wild type, leading for the residues 30–38 to a RMSF value of less than 1 Å (Figure 1). This suggests that this C-terminal-to-C-terminal interface is responsible for the increased stability that is observed experimentally for the parallel system of Aβ when compared to antiparallel Aβ. Note that the β1 region of both parallel systems (residues 18–22 in Figure 1) has an average RMSF of around 1.1 Å, which is more than the values observed in the antiparallel system. This is likely an artifact resulting from our truncation of the four ordered residues per peptide strand in the parallel model causing increased solvent exposure to normally buried residues.

Table I.

Average hydrophobic residues distance of the C-terminal-to-C-terminal interactions of β-sheets in adjacent layers measured in angstroms. The standard deviation (calculated from averaging over three trajectories for the last 100 ns of the simulation) is shown in parentheses.

C to C interface	Distance	Distance	Distance	Distance	Distance
Antiparallel Iowa mutant	Start	Average	Run 1	Run 2	Run 3
G29-E22′	10	13.4 (0.6)	13.5 (0.5)	14.4 (0.7)	12.5 (0.7)
I31-F20′	9.6	8.9 (0.4)	8.8 (0.3)	9.2 (0.4)	8.7 (0.4)
G33-V18′	9.9	8.31 (0.4)	8.6 (0.4)	8.1 (0.4)	8.3 (0.4)
M35-K16′	9.5	10.5 (0.5)	11.7 (0.5)	10.4 (0.4)	9.4 (0.6)
Antiparallel wild type	Start	Average	Run 1	Run 2	Run 3
G29-E22′	10.3	11.7 (0.6)	12.1 (0.5)	10.7 (0.5)	12.4 (0.7)
I31-F20′	10	8.6 (0.3)	9.2 (0.4)	7.8 (0.3)	8.7 (0.3)
G33-V18′	9.6	8.2 (0.4)	8.7 (0.4)	7.8 (0.4)	8.1 (0.4)
M35-K16	10.6	9.9 (0.4)	11.2 (0.4)	9.2 (0.4)	9.2 (0.5)
Parallel Iowa mutant	Start	Average	Run 1	Run 2	Run 3
I31-M35′	8.4	9.8 (0.3)	9.7 (0.4)	9.7 (0.3)	10.1 (0.3)
G33-G33′	7.2	8.1 (0.4)	8.2 (0.4)	8.0 (0.3)	8.3 (0.4)
M35-I31′	8.2	9 (0.3)	8.9 (0.4)	9.0 (0.3)	9.0 (0.3)
Parallel wild type	Start	Average	Run 1	Run 2	Run 3
I31-M35′	8.4	10 (0.4)	9.9 (0.3)	9.8 (0.3)	10.3 (0.5)
G33-G33′	7.4	8.4 (0.4)	8.0 (0.3)	8.2 (0.4)	9.1 (0.5)
M35-I31	8.2	9.2 (0.4)	9 (0.4)	9.1 (0.4)	9.6 (0.4)

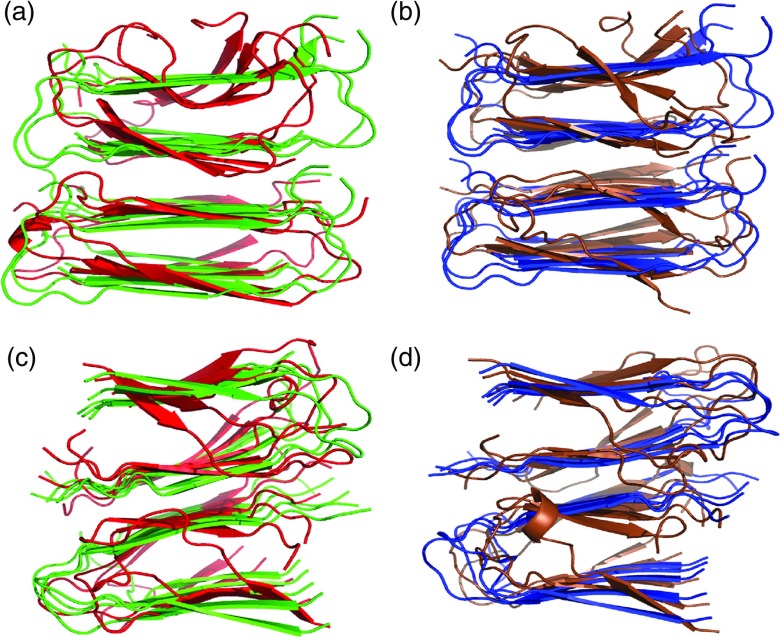
In all four cases, the oligomer models for the Aβ wild type and Iowa mutant keep the general characteristics and topologies of their initial conformation (Figure 2). The β-sheet-loop-β-sheet topology is stable in all chains of all oligomers and the hydrophobic interface between the U-shaped stacks stays intact throughout the simulation. However, the outer chains and the turn regions have an enhanced flexibility as shown in the above RMSF analysis. Hence, both parallel and antiparallel organizations are stable and therefore can contribute to the polymorphism during amyloid fibril formation. Previous simulations of the U-turn polymorphism of Aβ_17–42 by Miller et al.⁸ also showed that both parallel and antiparallel arrangements are stable and can contribute to a polymorphic population.

FIG. 2.

Overlay of the final and start configurations of Aβ wild type and Iowa mutant of one of the three independent trajectories of 300 ns for (a) the Iowa mutant antiparallel β-sheet; (b) the wild type antiparallel β-sheet; (c) Iowa mutant parallel β-sheet; and (d) wild type parallel β-sheet. Start configurations are marked in red for the mutant and in blue for the wild type; correspondingly red marks the final configuration of the mutant and tan for the wild type.

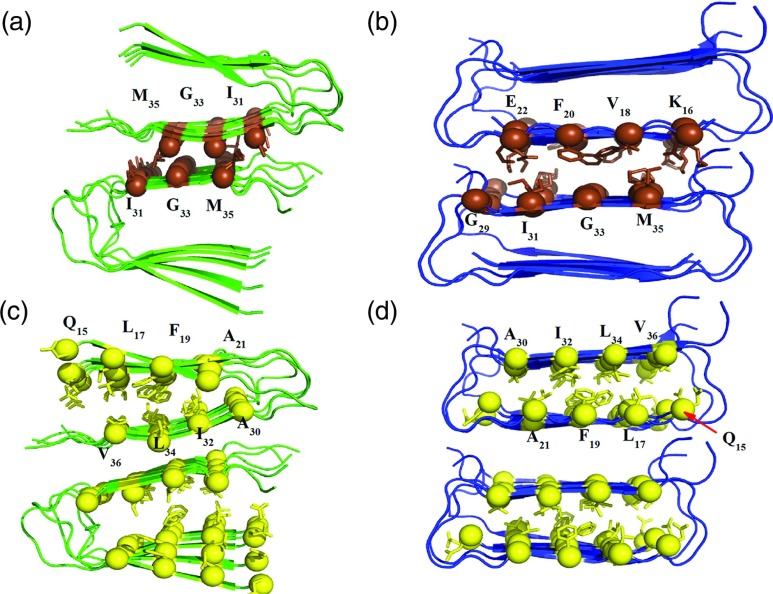
The above findings from visual and RMSF analysis are also confirmed by an analysis of side chain contacts, hydrogen bonds, and the secondary structure content. The fibril-like oligomers of both the Aβ wild type and Iowa mutant have tightly packed β-sheets with complementary side chains acting as a steric zipper^3,43 along the C-terminal interfaces of the double layer interface (see Figures 3(a) and 3(b)). We have monitored the distance between the Cα atoms complementary side-chains of the first β-sheet to the second β-sheet for the last 100 ns of the simulation in order to get further insight into their role in stabilizing the four different simulated oligomers. Our analysis of the data is shown in Table I. The distances between G₃₃–G₃₃, and M₃₅–I₃₁ residues in the parallel β-sheets are smaller than 9.5 Å, while the distance for the I₃₁–M₃₅ pair is slightly larger than 10.0 Å. These distances are close to the experimental values of 8–11 Å,³ indicating a good fit between the interacting amino acid side chains, which keeps the oligomer intact during the simulation. The contacts between the residues G₂₉–E₂₂ in the antiparallel β-sheet model are larger than the experimental value of 8–11³ and increase by about 2 Å during the simulation, indicating poor packing between these residues. However, the remaining pairs of residues that are involved in the C-terminal β-sheets interface have a tight inter-digitation, keeping the structure in both wild type and Iowa mutant stable.

FIG. 3.

Face-to-face interactions in decamers of Aβ wild type and Iowa mutant. The side-chains involved in the complementary interactions are shown as spheres, with yellow spheres representing the face-to-face interactions between β-sheets of the single fold residues and brown spheres representing C–C terminal side chain interactions between protein layers. Parallel systems are shown in green and antiparallel is shown in blue. (a) Side chain interactions along the C-terminal β-sheets interface residues I31/M35, G33/G33, and M35/I31 for the parallel β-sheet double fold; and (b) side chain interactions along the C-terminal β-sheets interface residues G29/E22, I31/F20, G33/V18, and M35/K16 for the antiparallel β-sheet double fold. Face-to-face interactions within β-sheets between the single fold residues Q15/V36, L17/L34, F19/I32, and A21/A30 are shown in (c) for the wild-type parallel β-sheet, and in (d) for the antiparallel β-sheet in the Iowa mutant.

Another type of interaction that is important for stabilizing the fibril-like oligomers is the face-to-face interactions between β-sheets in each single fold (see Figures 3(c) and 3(d)). Table II displays the results of the face-to-face interaction dynamics for the last 100 ns of the simulation. Among selected pairs of residues for both the parallel and antiparallel experimental oligomer models, the distances increase during the simulation for the antiparallel conformation more than for the parallel. The face-to-face contacts in the parallel structure tighten during the simulation by about 1 Å. This may be due to a better steric fitting of adjacent side chains in parallel conformations than in antiparallel ones that have been proposed by Antzutkin et al.⁴ Additional stability results from the ordering of residues 10–14 in the parallel structure while the same residues are disordered in the antiparallel structures.^12,14 As the face-to-face distance indicates how well the side chain packing is, our simulation points out differences between the two systems. These differences are not enough by themselves to establish differences in thermodynamic stability; however, they point to face-to-face interactions as an important factor contributing towards differences in stability. The looser fit between the side chains, as determined from the β-sheet to β-sheet distances at the interface (Table I) and the face-to-face interactions (Table II) leads to creation of a cavity in the anti-parallel aggregates that does not exist in the parallel form. We conjecture that the more efficient packing between β-sheets makes the parallel aggregates more stable than the antiparallel forms.

Table II.

Averaged sheet-to-sheet interactions measured in angstroms for the last 100 ns of the simulation. The standard deviation (calculated from averaging over three trajectories) is shown in parentheses.

Face to face interface	Distance	Distance	Distance	Distance	Distance
Antiparallel Iowa mutant	Start	Average	Run 1	Run 2	Run 3
Q15-V36	8.4	9.3 (0.7)	8.8 (0.7)	9.4 (0.6)	9.6 (0.7)
L17-L34	9.5	10.1 (0.5)	10.1 (0.4)	9.6 (0.5)	10.8 (0.5)
F19-I32	9.5	10.4 (0.5)	9.9 (0.4)	10.2 (0.4)	11.0 (0.6)
A21-A30	9.9	10.6 (0.5)	10.0 (0.5)	11.1 (0.5)	10.8 (0.6)
Antiparallel wild type	Start	Average	Run 1	Run 2	Run 3
Q15-V36	8.6	9.1 (0.6)	8.8 (0.6)	9.5 (0.6)	9.1 (0.7)
L17-L34	9.6	9.8 (0.5)	10.1 (0.5	9.7 (0.5)	9.7 (0.4)
F19-I32	9.6	9.9 (0.4)	10.3 (0.5)	9.8 (0.4)	9.7 (0.4)
A21-A30	10	10.6 (0.5)	10.3 (0.5)	11.1 (0.5)	10.3 (0.5)
Parallel Iowa mutant	Start	Average	Run 1	Run 2	Run 3
Q15-V36	14.7	12.9 (0.7)	12.7 (0.8)	13.9 (0.7)	12 (0.6)
L17-L34	13.9	12.0 (0.5)	12.9 (0.6)	11.2 (0.5)	11.9 (0.4)
F19-I32	12.3	12.0 (0.5)	12.0 (0.6)	11.7 (0.4)	12.4 (0.5)
A21-A30	11.5	11.1 (0.6)	10.4 (0.6)	11.7 (0.5)	11.3 (0.5)
Parallel wild type	Start	Average	Run 1	Run 2	Run 3
Q15-V36	14.5	13.5 (0.8)	13.8 (0.7)	14.2 (0.9)	12.5 (0.9)
L17-L34	13.3	12.1 (0.6)	12.9 (0.5)	12.5 (0.7)	11 (0.5)
F19-I32	12.3	11.9 (0.5)	12.1 (0.5)	11.6 (0.5)	12.1 (0.5)
A21-A30	11.5	10.5 (0.6)	11.2 (0.6)	9.2 (0.6)	11.2 (0.8)

Root-mean-square deviation and root-mean-square fluctuations differ by approximately 1 Å between the parallel and the antiparallel conformations. These differences, and the one in packing, indicate that the parallel conformation is only slightly more stable than the antiparallel conformation. However, our setup underestimates the stability of parallel aggregates as we have removed residues 9–14 of the parallel structure in order to have the same size in all our structures (simplifying our simulation setup). These residues are part of the ordered β-sheet in the parallel-structure fibril, but are disordered in and do not contribute to the stability of the antiparallel experimental structure. The presence of these additional five residues in the N-terminal region of the full-sized parallel fibril increases further the differences in stability between the two forms but is not accounted for in our simulations.

Another important factor in stabilizing the supra-molecular organization of amyloid peptides⁴⁴ is the arrangement of hydrogen bonds. We have analyzed the extent of hydrogen bonds in order to determine whether there is a difference between parallel or anti-parallel β-sheet organizations of the wild type and Iowa mutant oligomers. We find that the total number of hydrogen bonds is comparable for Iowa mutant and wild type in both parallel and anti-parallel systems. However, the number of backbone, side chain, and side chain-backbone (i.e., protein-protein) hydrogen bonds are slightly larger (by 18(8) bonds) in the antiparallel systems than the parallel systems (see Figure 4) of Aβ_15–40 and D₂₃N Aβ_15–40. On the other hand, the number of hydrogen bonds between the aggregate and the surrounding solvent is larger in the antiparallel configuration than in the parallel one by about the same amount (21.9(19) bonds). However, the error in the latter number is large and makes an interpretation difficult. No signal for a preference of one over the other configuration was found in the solvent-solvent hydrogen bonding. From these results, we conjecture that, in the experimentally determined structures, the four additional ordered residues in the parallel arrangement of Aβ_10–40 increase the number of hydrogen bonds and therefore stabilize this structure over that of the anti-parallel D₂₃N Aβ_15–40 oligomer. This is also in agreement with the experimental data and will make the parallel form more stable than the antiparallel form.^12,14

FIG. 4.

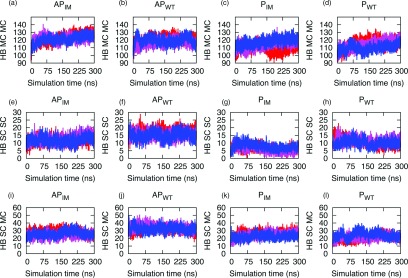
(a)–(l) Number of hydrogen bonds involving residues 15–40 plotted versus time for the Aβ wild type and Iowa mutant. Shown are in the first row the main chain to main chain hydrogen bonding (HB MC MC), in the second row the side chain to side chain hydrogen bonding (HB SC SC), and in the third row the main chain to side chain hydrogen bonding (HB SC MC) for the antiparallel Iowa mutant (AP_IM), the antiparallel wild-type (AP_WT), the parallel Iowa mutant (P_IM), and the parallel wild type (P_WT). The three independent runs are shown in red, blue, and pink.

Evidence for this conjecture is also found in our monitoring of the secondary structure during the simulation. Given that amyloid fibrils are composed mainly of β-sheets, this quantity provides information on the relation between interactions that involve the β-strand motif and the stability of the aggregates.⁴⁵ Table III lists the average secondary structure content from the DSSP analysis of the energy-minimized initial structure and the last 100 ns of each system. As a general tendency, we find lower β-sheet content in the decamers with parallel organization than in such with antiparallel structure. The increased β-sheet content in the latter case could contribute to the stability of the antiparallel organizations and could explain how this structural organization can compete with the parallel conformation.¹⁴ Qiang et al.¹⁴ have proposed that the difference in the number of ordered residues (50% of antiparallel versus 75% in parallel oligomers) is responsible for the thermodynamic preference of parallel over antiparallel structures. However, our simulation of Aβ_15–40 fibril-likes oligomer of Aβ wild type and Iowa mutants indicates that the antiparallel structure has a slightly larger percentage of β-sheet secondary structure. This difference may be due to limitations of our model, which considers only residues 15–40. While residues 1–15 are disordered in the experimentally determined antiparallel D₂₃N Aβ_15–40 fibril, in the Aβ wild-type fibril only residues 1–10 are disordered. We therefore would expect more β-sheet secondary structure in simulations than seen in the experimental Aβ_10–40 parallel β-sheet oligomer. Hence, our results suggest that the relative stability of parallel β-sheet over antiparallel β-sheet conformations depends on the larger number of ordered residues in the parallel β-sheet conformation.

Table III.

Secondary structure of the wild-type Aβ and Iowa mutant antiparallel and parallel sheet systems, measured for the energy minimized initial configurations and also averaged over the last 100 ns. The standard deviation between the three runs is shown in parentheses.

	Percentage of secondary structure of the				Percentage of secondary structure
	energy minimized initial configurations				averaged over the last 100 ns
System	Helix	Beta sheet	Turns	Random	Helix	Beta sheet	Turns	Random
Antiparallel Iowa mutant	0	49.59	13.11	37.30	1.1 (0.49)	51.65 (0.59)	16.96 (0.45)	30.29 (1.47)
Antiparallel wild type	0	47.48	15.87	36.65	0.56 (0.86)	50.01 (0.8)	18.41 (1.91)	31.01 (1.18)
Parallel Iowa mutant	0	46.33	14.26	39.41	1.3 (1.11)	44.43 (1.71)	18.41 (2.89)	35.87 (2.68)
Parallel wild type	0	46.28	14.96	38.76	2.82 (2.37)	44.68 (1.75)	19.90 (0.8)	32.59 (1.1)

Free energies of wild type and Iowa aggregates

Common paradigm is that the protein-aggregation landscape resembles a rugged valley with numerous close local minima corresponding to different polymorphic forms of fibrils. Multiple polymorphic aggregates can emerge during fibril formation, with different environmental conditions favoring different polymorphic forms over the others.^46,47 In order to gain further insight into the relative stability of our four oligomers, we have done MM-PBSA calculations of the oligomers allowing us to monitor their interactions⁴⁸ through calculating approximate binding free energies from molecular simulations.^49,50 While the MM-PBSA approach in general does not replicate the absolute binding free energy values,⁵¹ we chose this approach because it allows one to calculate quickly an estimate for differences in the free energy of binding, and because it usually exhibits a good correlation with experimental data.⁵² In the present study, the binding energy between the two β-sheets (that is between the pentamers that form the decamer) is estimated with the MM-PBSA methodology as implemented in AMBER12. Before starting the MM-PBSA analysis, all water molecules and ions were excluded from the trajectory. The dielectric constants used for the solute and surrounding solvent are 1 and 80, respectively. Multiple molecular dynamics runs relying on the all atom AMBER99SB force field and TIP3P water model were performed for each of the four double layer aggregate models and carefully equilibrated for 5 ns. Specifically, three trajectories of 40 ns were generated that unlike our production runs did not utilize mass-scaling. Such an approach is preferable over a single long time run as it leads to a more efficient sampling of phase space. The MM-PBSA single trajectory approach is used to calculate the binding energy. Snapshots are gathered at intervals of 40 ps during the 40 ns of simulation leading to 1000 equally spaced snapshots for each single trajectory from the three 40 ns MD trajectories. For our analysis we use the Python implementation of MM-PBSA as provided with AmberTools 12.⁵³ The results of the binding energy in Table IV are the average of the three calculations. Note that we did not account for entropic contributions to binding since we compare only systems that are very similar where these contributions could even raise the overall uncertainty in the calculated binding energies.⁵⁴ For a detailed discussion, see Refs. 55 and 56.

Table IV.

Binding energies and standard deviations as calculated with the MM-PBSA approach, including its components (Kcal/mol) for the four-fibril models. The standard deviation (calculated from averaging over three trajectories) is shown in parentheses.

System	ΔEvdw	ΔEele	ΔEPB	ΔESA	ΔEnon-polar	ΔEpolar	ΔGbinding	ΔΔGa
Parallel wild-type	−325.0(12.3)	−96.2(111.6)	187.6(89.2)	181.4(3.6)	−143.6(8.7)	91.4(22.6)	−52.2(26.5)	−21.6
Antiparallel wild-type	−351.1(18.1)	−307.23(36.7)	431.8(20.7)	195.7(7.9)	−155.3(10.2)	124.7(18.4)	−30.6(9.2)
Parallel Iowa mutant	−344.8(9.2)	−457.7(31.6)	546.1(42.8)	192.3(0.8)	−152.6(8.7)	88.3(17.3)	−64.3(24.2)	−23.4
Antiparallel Iowa mutant	−351.1(22.1)	−670.3(64.2)	782.8(60.3)	197.7 (10.0)	−153.4 (12.4)	112.5(24.4)	−40.9(14.4)

^aΔΔG is the difference in binding free energy ΔG_binding between the parallel and antiparallel conformation of Aβ wild type and Iowa mutant. The negative values indicate that parallel conformations are more stable than the corresponding antiparallel conformations. ΔG_binding = ΔE_vdw + ΔE_ele + ΔG_sol; ΔG_sol = ΔE_PB + ΔE_SA. Here, ΔE_vdw is van der Waals energy and ΔE_ele is the non-solvent electrostatic energy. The contributions to the solvation free energy are split into a nonpolar and polar part. E_SA is a nonpolar contribution to solvation free energy; ΔG_PB is electrostatic contributions to the solvation free energy calculated by the Poisson-Boltzmann equation. The nonpolar term (ΔE_non-polar) consists of the van der Waals interaction energies (E_vdW) and the nonpolar contribution to the solvation free energy (E_SA). The polar term (ΔE_polar) is the sum of Coulomb interaction energy (E_elec) and polar contribution to the solvation free energy (E_PB). Various entropic contributions are neglected in our MM-PBSA approximation.

The obtained binding energies listed in Table IV are in agreement with the experimental observation that the parallel Iowa mutant is more stable than the transient antiparallel structure¹⁴ and that, while there is experimental evidence for the possibility of wild type Aβ existing in an antiparallel form,¹⁵ all experimentally determined models of Aβ are built out of parallel β-sheets.¹² This high-energy difference predicted by our MM-PBSA calculation suggests that the conversion between parallel and antiparallel forms cannot be achieved by simple rearrangement (since it is a topological difference), but is most likely due to individual strands detaching from the less stable antiparallel form and assuming the more stable parallel β-sheet structure.^14,52,53

We have further analyzed the various components in order to identify the dominant factors in the binding affinity. The van der Waals (ΔE_vdw), electrostatic term (ΔE_ele), and nonpolar terms (ΔE_non-polar) favor complex formation in all cases. The nonpolar solvation (ΔE_SA), which describes the process of transferring a nonpolar molecule from vacuum to water including the creation of a cavity in water, is unfavorable in all cases. Similarly, the polar solvation term opposes the protein-protein binding due to polarization of the solvent environment by the solute. The electrostatic contribution (ΔE_ele) between the proto-filament pairs, which in an in-register parallel β-sheet structure is larger than in an anti-parallel β-sheet structure with its pairing of negatively and positively charged groups, is favorable but cancelled by the electrostatic solvation term (ΔE_PB).

For both the Iowa mutant and wild type Aβ, the binding energy of the two parallel and antiparallel conformations suggests a slightly higher thermodynamic stability of the parallel organization over that of the antiparallel one. While free energy perturbation and other free energy calculations methods are more accurate than the MM-PBSA approach we used,⁵⁷ this ranking of the stability could explain the experimental observation of the conversion of the less stable antiparallel Iowa mutant into the more stable parallel conformation fibril.^14,58 While our data are noisy with only small differences, they are supported by a recent theoretical study by Okamoto et al.⁵⁹ using the ab initio MP2/6-31G method that also found the parallel conformation in both the wild type and Iowa mutants more stable than the antiparallel ones.

CONCLUSION

We have investigated in silico the stability of decamers of Aβ wild type and its Iowa mutant that are reported to exhibit either an antiparallel or parallel β-sheet organization. Simulations with scaled mass are compared with such simulations where the physical masses are unchanged. Our data demonstrate that mass scaling leads to increased sampling efficiency by reducing the viscosity of the system. Similar to the more common raising of system temperature, this allows for an easier escape from local minima and therefore enhanced sampling while at the same time keeps deviations from the natural dynamics small. In some cases, we found that mass scaling led to improvements in sampling efficiency by factors of 15. There may be potential for further refinement of selective scaling to provide even greater yields in efficiency. Even with this increase in efficiency our simulations clearly do not cover the time scales on which the conversion of antiparallel to parallel forms is observed in experiments. However, signals for these transitions can be found by comparing the stability of wild type and mutant in the two forms. An analysis of the free energy of binding by MM-PBSA of our data, as derived from configurations that originated from these enhanced molecular dynamics simulations, indicates that the parallel forms of both wild type and Iowa mutant aggregates are the most stable, while the antiparallel aggregates are less stable for the Iowa mutant and least stable for the wild type. This ranking of stabilities is consistent with previous experimental results and is explained here with the dependency of the structurally important sheet-to-sheet interface interactions on the side chain complementarity. The direct alignment of hydrophobic interactions in the in-register parallel oligomers makes them more stable than the antiparallel aggregates. The parallel supra-molecular organization could be due to favorable stacking of residues allowing each adjacent residue to overcome potential repulsive interactions, which makes it energetically more favorable than the antiparallel aggregates.⁴ However, our data demonstrate that both parallel and anti-parallel β-sheet fibrils can exist under physiological conditions even though they have differences in thermodynamic and structural stability. Hence, both forms may contribute to the polymorphism of Aβ aggregates. Eisenberg and co-workers⁶⁰ utilizing the parallel β-sheet fibril models of an Alzheimer's peptide in combination with computer modeling have found several compounds that reduce amyloid toxicity. Our data suggest that using as templates for Aβ aggregation inhibitor design not only parallel but also anti-parallel β-sheet fibrils may lead to compounds that reduce toxicity even further.

The slightly higher thermodynamic stability of the Iowa mutant oligomer in its parallel organization over that of the mutant in antiparallel form is supported by previous experimental measurements showing slow inter-conversion of antiparallel aggregates into parallel ones. Our calculations indicate that this conversion is energetically costly. This suggests that the conversion is not a simple re-arrangement but rather involves the detachment of monomers from the less stable antiparallel form and re-aggregation into the more stable parallel structure. Future plans include computational studies that rely on novel sampling techniques currently under development in our lab.