Fluorescence lifetime plate reader: Resolution and precision meet high-throughput

Abstract

We describe a nanosecond time-resolved fluorescence spectrometer that acquires fluorescence decay waveforms from each well of a 384-well microplate in 3 min with signal-to-noise exceeding 400 using direct waveform recording. The instrument combines high-energy pulsed laser sources (5–10 kHz repetition rate) with a photomultiplier and high-speed digitizer (1 GHz) to record a fluorescence decay waveform after each pulse. Waveforms acquired from rhodamine or 5-((2-aminoethyl)amino) naphthalene-1-sulfonic acid dyes in a 384-well plate gave lifetime measurements 5- to 25-fold more precise than the simultaneous intensity measurements. Lifetimes as short as 0.04 ns were acquired by interleaving with an effective sample rate of 5 GHz. Lifetime measurements resolved mixtures of single-exponential dyes with better than 1% accuracy. The fluorescence lifetime plate reader enables multiple-well fluorescence lifetime measurements with an acquisition time of 0.5 s per well, suitable for high-throughput fluorescence lifetime screening applications.

I. INTRODUCTION

Fluorescence spectroscopy provides exceptional sensitivity for biological assays, because the fluorescence emission signal is readily separated from excitation and background fluorescence wavelengths, but its precision is limited by the inherent variability of fluorescence intensity.^1,2 Intensity-based measurements are subject to noise due to uncertainty in optical path length or assay volume, light scatter from surfaces or contaminating particulates, differences in local concentration of fluorophores, or presence of interfering fluorescent compounds.³ Nanosecond time-resolved fluorescence measurements provide a means to improve assay resolution and precision because the time-resolved signal is largely independent of intensity variations.⁴ The fluorescence lifetime (an observable related to the quantum yield) may be used to analyze fluorescence decay waveforms by methods including moment analysis,⁵ multi-exponential fitting,^6,7 or phasor analysis.⁸ Fluorescence lifetime detection is most useful in assays sensitive to probe environment, such as fluorescence quenching, resonance energy transfer, or intrinsic fluorescence.⁹ Lifetime-based assays have been used to measure macromolecular interactions,^8,10 distances,^11,12 and forces¹³ as well as enzyme activity and ligand binding.^14–16

High-precision lifetime measurements are typically performed with time-correlated single-photon counting (TCSPC),¹⁷ a digital method that employs low-intensity excitation at the expense of long acquisition times (typically seconds or longer to obtain signal-to-noise ≥ 100). The alternative method of direct waveform recording (DWR) acquires analog fluorescence decays in response to high-intensity pulsed excitation.¹⁸ DWR dramatically reduces acquisition time from ∼10 s to ∼0.1 ms, without sacrificing accuracy or precision, by exciting many probe molecules with a single pulse and detecting thousands of emitted photons.¹⁸ We have demonstrated that this technology enables the acquisition of hundreds of high signal-to-noise waveforms with nanosecond time resolution and kHz repetition rate following stopped-flow.^12,19 We have developed a new instrument to enable high-throughput sample preparation and detection in a 384-well microplate format. Here we present a description of the NovaFluor Plate Reader that has already been employed in high-throughput studies.^20,21 We show here that fluorescence lifetime measurement in this instrument dramatically improves measurement precision relative to fluorescence intensity, without sacrificing throughput, in addition to its benefits for signal resolution, in a fluorescence lifetime plate reader.

II. MATERIALS AND METHODS

A. Instrument

The NovaFluor plate reader (Fig. 1) was designed and built by Fluorescence Innovations, Inc. We performed 355 and 532 nm excitation with a 10 kHz pulse rate using an yttrium-aluminum-garnet microchip laser (JDS Uniphase) followed by a frequency multiplier and bandpass filter. We excited at 473 nm with a 5 kHz pulse rate using an FP2-473-3-5 microchip laser with LD-702 controller (Concepts Research Corporation). Excitation light passed through a neutral density filter and then through a pinhole in a collector mirror fixed beneath the moving stage. Fluorescence was gathered by the parabolic mirror for detection. Emission filters (470/20 nm band pass or 590/10 nm band pass) were placed before the detector, a H10270-20 photomultiplier tube (Hamamatsu) operating at 400 V except as noted. Detector current was converted to voltage at 50 Ω by a custom circuit board based on a 1 GHz analog transient waveform digitizer (ATWD version 3.1).²² Motors driving the X-Y stage, shutter, neutral density, and emission filters were controlled by a second custom board. All controllers were routed to USB using an RS-232 serial adapter. Instrument control and data acquisition were performed with custom software on a personal computer. We used an Ophir PD-10v2 power meter to calibrate neutral density filter position.

FIG. 1.

Fluorescence lifetime plate reader. The NovaFluor spectrometer uses an X-Y stage, pulsed laser, PMT, and digitizer for direct waveform recording (DWR) of fluorescence lifetime decays. Excitation light is focused through a pinhole to the center of each well of a microplate. Fluorescence emission is collimated by a parabolic mirror and focused on the PMT. Fluorescence decays are digitized and acquired for lifetime or moment analysis.

B. Fluorescent dyes

Solid dyes were dissolved to ∼1 mM in spectroscopic grade ethanol and stored at −20 °C, except EDANS (5-((2-aminoethyl)amino) naphthalene-1-sulfonic acid) which was dissolved in N,N-dimethyl-formamide. Working solutions were diluted to 1 μM (except as noted) in de-ionized water. Rhodamine B and 6G were excited at 473 nm, EDANS at 355 nm, and Rose Bengal at 532 nm. Fluorescence decays were acquired (Fig. 2) using a neutral density filter to adjust the peak signal to near 100 mV with 50–150 mV as an optimal range (1–3 mA peak output current of the PMT). We recorded decay waveforms with 640 samples at 0.2 ns resolution (128 ns total time). The signal delay was adjusted to allow at least 40 samples (8 ns) of pre-excitation data used to adjust the signal baseline.

FIG. 2.

Direct Waveform Recording (DWR) of Fluorescence Decays. The instrument response function (IRF, black squares) acquired from scattering in water is shown with fluorescence decay waveforms for rhodamine B (blue triangles) and rhodamine 6G (red circles). Waveforms acquired by DWR at 400 V with 0.2 ns resolution. Signal does not start at time zero because pre-excitation data were used to adjust the Y-axis baseline for each normalized waveform.

C. Microplate preparation

We loaded plates manually with a multichannel pipet (ThermoFisher) or automatically with a FlexDrop IV dispenser (PerkinElmer). We used well volumes of 50 or 100 μl in a 384-well glass-bottomed Greiner SensoPlate. Dye mixtures were dispensed in volumes with 5 μl increments. Plates were spun briefly (up to 300 rpm in Eppendorf rotor 5810R A-4-81) to remove air bubbles. The instrument response (IRF) was influenced by choice of laser, PMT voltage, and other factors and was acquired daily from a single well of de-ionized water with neutral density filter adjusted to a 100 mV peak signal.

D. Data analysis

Analysis of total fluorescence and first moment was performed in Microsoft Excel or Matlab (MathWorks). Total fluorescence was calculated as ${\sum }_{i}F\left(t_i\right)$, where F(t) was the signal intensity after baseline correction. Lifetime analysis used custom software to simulate exponential decays convolved with the measured IRF for fitting using nonlinear least-squares (Levenberg-Marquardt algorithm.) For single dyes, a lifetime model was used:

$$F\left(t\right)=A\exp \left(-\frac{t-\Delta }{\tau }\right),$$ (1)

where A was the amplitude of fluorescence, τ was fluorescence lifetime, and Δ was a parameter accounting for time shift between the signal and the IRF.

Mixtures were averaged across replicate wells and fit to

$$\begin{array}{ccc}\hfill F_j\left(t\right)& =& C_j\{x_j{A}_1\exp \left[-\left(t-\Delta \right)/{\tau }_1\right]\hfill \\ & & +\left(1-x_j\right)A_2\exp \left[-\left(t-\Delta \right)/{\tau }_2\right]\},\hfill \end{array}$$ (2)

where x_j was the mole fraction in the jth mixture and C_j was a scaling factor to account for intensity-dependent noise. Lifetimes τ₁, τ₂ were globally constrained⁷ to the values obtained for pure dye. Time shift Δ and amplitudes A₁, A₂ were globally fit. Amplitude terms reflected the combined effect of extinction coefficient and quantum yield in the two dyes and fraction x represented the ratio of dye molecules. We found constraining the start (x = 0) and end fractions (x = 1) using single dyes improved fit accuracy.

Raw first moments were defined as ${\sum }_i{t}_{i}F\left(t_i\right)/{\sum }_{i}F\left(t_i\right)$ and adjusted using exponential depression²³ to suppress noise at longer time intervals. We used the raw first moment μ⁰ to calculate a depression function, exp (−t/βμ⁰). Larger β values increased agreement of the moment and lifetime values, but decreased precision. We found β = 3 was sufficiently small to maintain precision. The adjusted first moment,

$$\mu =\frac{1+\beta }{\beta }\left[\frac{{\sum }_i{t}_i\exp (-t_i/\beta {\mu }^0)F\left(t_i\right)}{{\sum }_i\exp (-t_i/\beta {\mu }^0)F\left(t_i\right)}\right],$$ (3)

was calculated by assuming that F(t) was an exponential function (Eq. (1)). Integration of Eq. (3) by parts would then yield μ = τ in an ideal case where the IRF is infinitely steep.

III. EXPERIMENTAL RESULTS

The NovaFluor plate reader is a nanosecond time-resolved spectrometer that uses pulsed laser excitation, a high-speed digitizer, and a photomultiplier tube (PMT) detector to record fluorescence decays from each well of a microplate. The digitizer read time is approximately 1 ms per waveform for a 5 kHz laser source (interleaving over 5 pulses) and the transport time is 0.3 s per well. Typical acquisitions were averaged across 200 successive waveforms giving an acquisition rate of 0.5 s per well or 3 min per 384-well plate. We used single-lifetime dyes to determine the precision and resolution of the plate reader and to measure its signal-to-noise performance.

A. Lifetime compared with intensity

We used water-soluble dyes with a variety of lifetimes to measure instrument performance (Fig. 3). First we measured the instrument response function (IRF) in pure water. We then selected an appropriate emission filter and adjusted excitation power with a neutral density filter to give a peak signal of 50–150 mV. Total intensity was measured as the fluorescence decay integrated across all time points of the acquired waveform. Lifetime and moment were determined from the waveform (see Sec. II).

FIG. 3.

Fluorescence lifetime is more precise than fluorescence intensity. Intensity (black squares) and lifetime (red triangles) of rhodamine B (1 μM in water) were calculated from waveforms acquired in 192 wells of a 384-well microplate. Lifetime CV is 0.7% (coefficient of variation = SD/mean), 5-fold more precise than intensity CV (3.5%) for this short lifetime dye. Left axis is total intensity divided by mean and right axis is centered and scaled in proportion.

The plate reader acquired lifetime data with better than 1% precision for dye lifetimes of 1.6 ns and higher. Precision was measured as coefficient of variation (CV = SD/mean). Lifetime measurements were up to 25-fold more precise relative to the simultaneous measurement of total intensity. The ultra-short lifetime dye Rose Bengal fit to a single lifetime (0.04 ns) with low precision, although the standard deviation (11 ps) was comparable to that of other dyes.

We measured the precision of lifetime detection by uniformly dispensing dye into 384-well plates and measuring the DWR signal using the plate reader (Fig. 3). We fit the decays to a single exponential lifetime model (Eq. (1)). We found rhodamine B lifetime had 5-fold improved precision compared with total intensity, while the longer lifetime dyes rhodamine 6G and EDANS showed a 25-fold relative improvement in precision (Table I). We would expect DWR to have better precision for lifetimes that are long relative to the IRF (2.8 ns FWHM), and this is consistent with our results. In most cases we found that well-to-well precision improved when analyzing half of each plate (192 wells) due to systematic errors in volume of liquid dispensed.

Table I.

Comparison of precision for intensity, lifetime, and moment measurements. Dyes were dispensed in uniform volume in microplates to measure signal precision across wells. Lifetime precision (coefficient of variation, CV = SD/mean) is superior to intensity precision in all but the shortest lifetime dye. Further enhancement of precision is seen in the adjusted first moment.

	Intensity	Lifetime	Lifetime	Lifetime	Moment	Moment SD	Moment
	CV	(ns)	SD (ns)	CV	(ns)	(ns)	CV
Rose Bengal	7.17%	0.040	0.011	27.50%	1.187	0.004	0.34%
Rhodamine B	3.47%	1.566	0.010	0.67%	2.476	0.009	0.37%
Rhodamine 6G	6.99%	3.914	0.011	0.27%	3.357	0.008	0.25%
EDANS	2.74%	12.684	0.028	0.11%	10.197	0.014	0.14%

We also analyzed waveforms using first moment, a more direct analysis than the lifetime model. We found the raw first moment had poor precision and was sensitive to noise during the later fluorescence decay, even when we truncated the data. The adjusted first moment (Eq. (3)) had greater precision than was seen in the fitted lifetimes. The absolute value of the moment differed from the value of lifetime and was affected by experimental conditions such as PMT voltage.

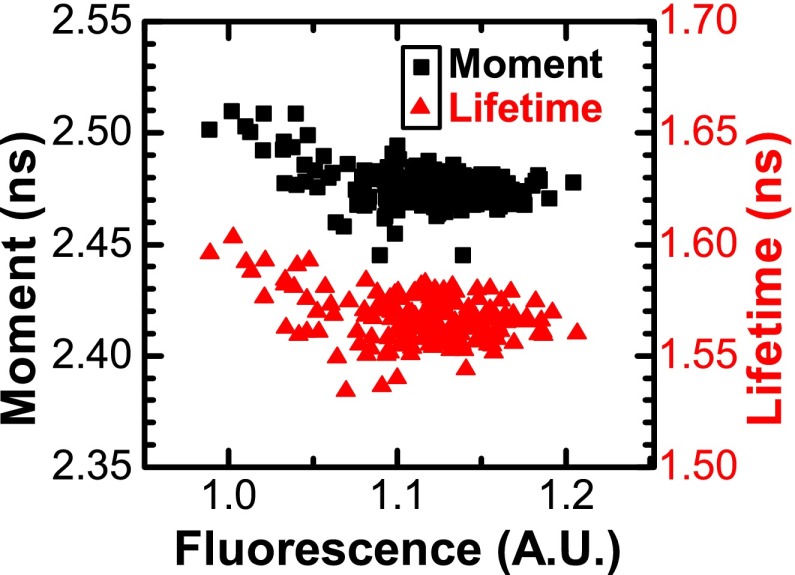
We examined variation between wells by comparing total intensity with lifetime and adjusted first moment (Fig. 4). Lifetime values for the dyes in Table I were mostly randomly distributed, showing weak correlation with intensity (Pearson's correlation coefficient r took values|r| ⩽ 0.5). Rhodamine 6G showed a moderately strong correlation (r = 0.87) with intensity, although the coefficient of variation remained less than 1%. We hypothesize that these correlations reflect a small nonlinear response in the detector and/or digitizer.

FIG. 4.

Lifetime and moment are precise across wells. Lifetime and adjusted moment of rhodamine B (1 μM in water) were calculated from the decay waveform in each well. CV was 0.67% (SD 10 ps) for lifetime and 0.22% (SD 9 ps) for moment. CV (coefficient of variation) = SD/mean. One fluorescence unit = total intensity given a peak signal of 100 mV.

B. Linearity of detection

Direct waveform recording requires fluorescence emission to be linearly related to signal intensity, since intensity-dependent variations could distort the waveform and fitted lifetime.¹⁸ We varied excitation power and sample concentration to determine whether nonlinearity affected instrument performance. First, we tested linearity of the total intensity measurement by reducing the excitation power in calibrated steps and measuring intensity of the ultra-short lifetime dye Rose Bengal, finding excellent agreement (Fig. 5). We defined an arbitrary unit of fluorescence as the total intensity of a given waveform with a 100 mV peak signal.

FIG. 5.

Linear dependence of fluorescence on excitation power. Incident power was varied by a neutral density filter to excite Rose Bengal (1 μM in water) in a single well. Total intensity (red squares) varied linearly (r² > 0.999; RMSD 0.90%). Black line is the predicted relationship, scaled to the unit intensity of a waveform at 100 mV peak signal.

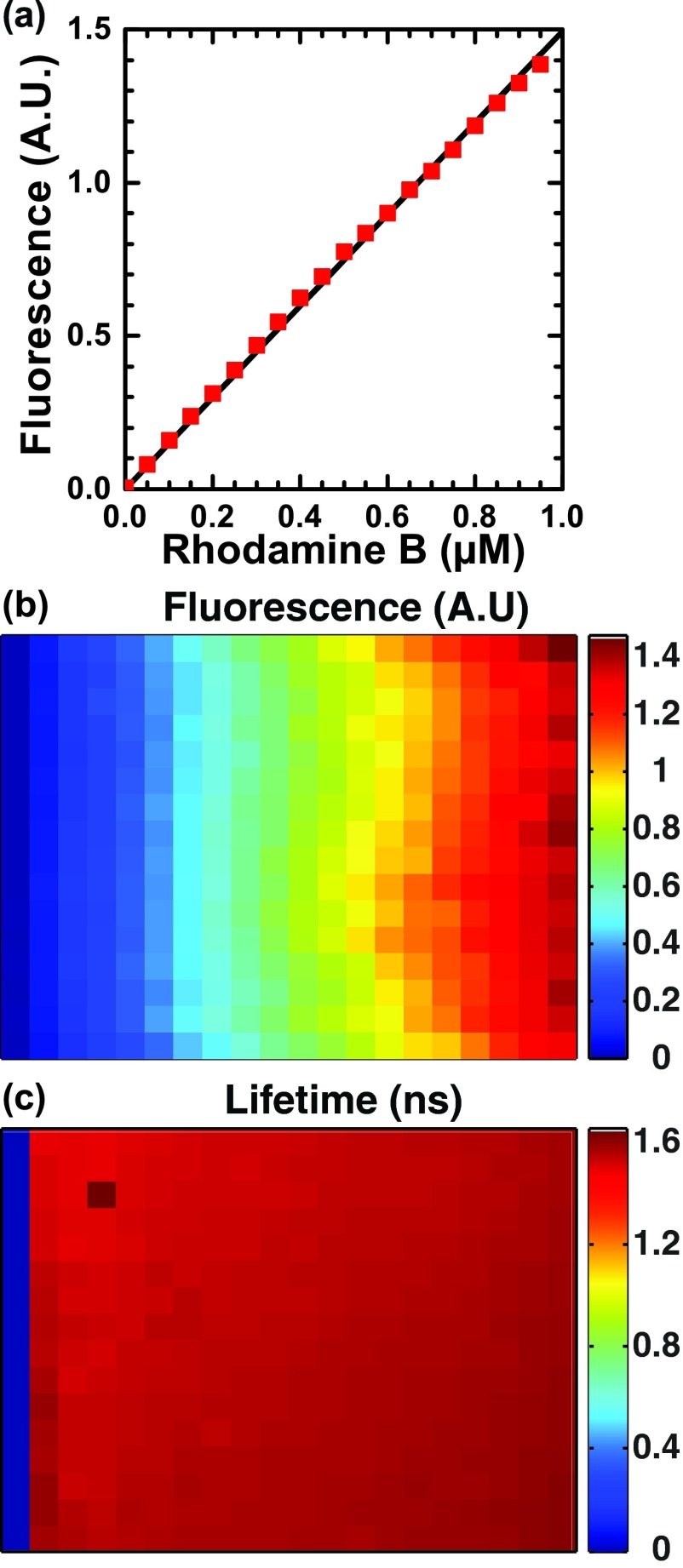
Next we tested how fluorescence intensity varied with concentration of the short lifetime dye rhodamine B over a 50–950 nM range (Fig. 6(a)) and found the expected linear relationship with a root-mean-squared deviation of 1.8%. For this experiment, each dye concentration was dispensed in 16 replicate wells. CV of intensity was 2%–6% in each set of replicates and CV of lifetime was 1.64% across all wells, varying from 2.08% at 50 nM to 0.87% at 950 nM.

FIG. 6.

Fluorescence is proportional to intensity. (a) Fluorescence total intensity (red squares) of rhodamine B (0–950 μM in water) varies linearly with concentration (r² > 0.999; RMSD 1.8% relative to expected relationship shown in black line). (b) Intensity map of plate shown in false color with dye concentration ranging from 0 (left column) to 950 μM (right column). (c) Lifetime map of the same plate, with wells empty of rhodamine assigned a lifetime of zero.

We further analyzed the effect of signal intensity on apparent lifetime by plotting lifetime and intensity for each well (Fig. 7). Lifetime values were increasingly variable below 0.5 A.U., while the instrument provided good precision for fluorescence signals in the range 0.5–1.5 A.U. The apparent lifetime showed a moderate positive correlation with intensity (r = 0.70) despite the overall low CV (1.6%). This correlation had minimal impact on precision when intensity variation was due to experimental error alone. For example, the data in (Fig. 4) span a range of ∼1.0–1.2 A.U. with a lifetime CV of 0.7%. The lifetime of rhodamine B (1.6 ns) was short compared to the IRF (2.8 ns) and thus was more affected by instrument nonlinearity than were the longer lifetime dyes.

FIG. 7.

Distribution of apparent fluorescence lifetime and intensity. Fitted lifetimes (red triangles) were precise (1.6% CV) across a range dye concentrations (50–950 μM rhodamine B in water). The apparent correlation of lifetime and intensity reflects detector nonlinearity. CV = coefficient of variation (SD/mean).

C. Signal quality

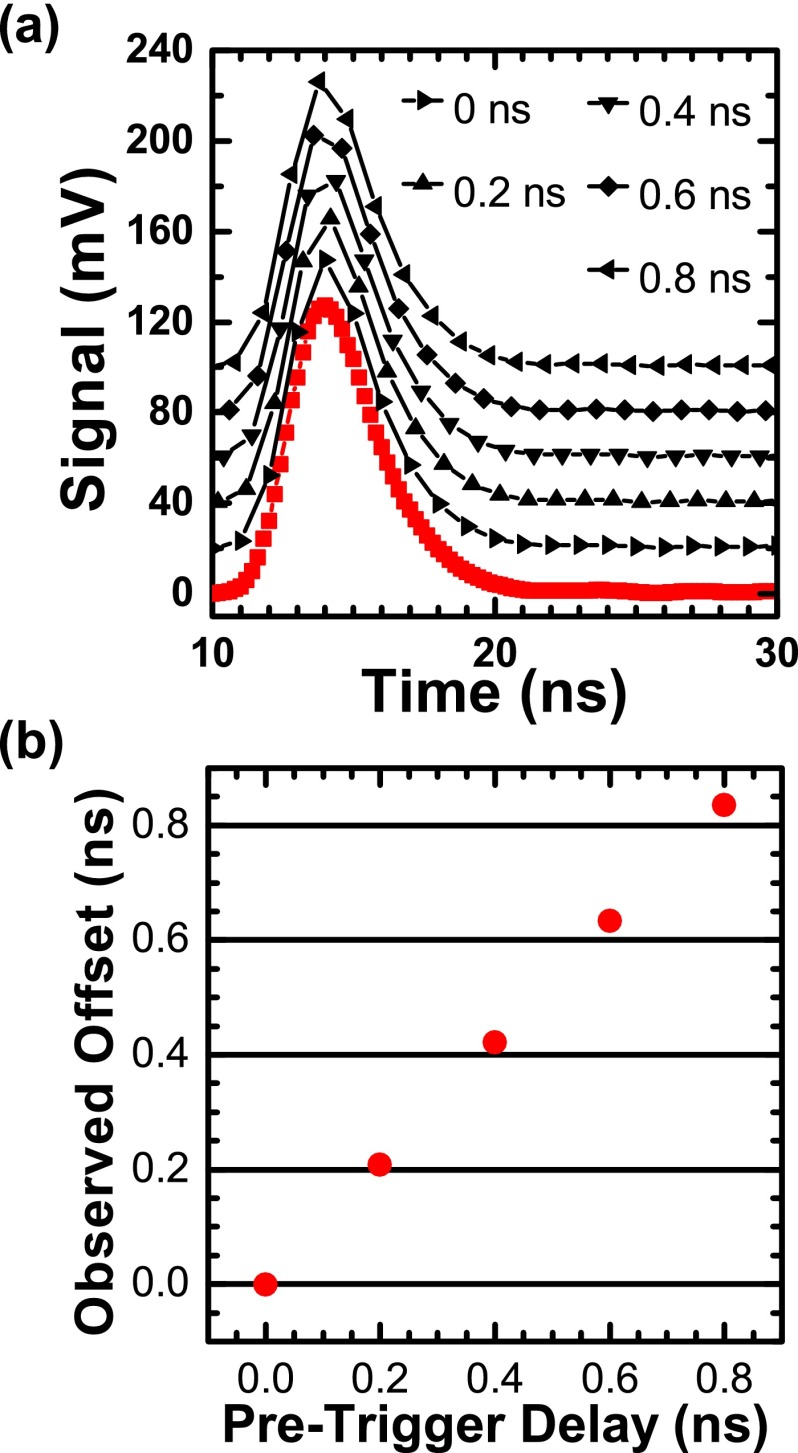
The instrument response function (IRF) had a measured FWHM of 2.3 ns (full width at half maximum) with 355 nm excitation and 2.8 ns with 473 nm excitation (Fig. 2). In all experiments we acquired waveforms at 1 GHz with the ATWD digitizer and increased the effective sample rate to 5 GHz by interleaving each cycle of 5 laser pulses (Fig. 8(a)). We calibrated a series of onboard pre-trigger delays in 0.2 ns steps so that the delay incremented with each laser pulse. We verified the delay calibration by recording 200 successive 5 GHz waveforms of a rhodamine B sample and extracting the 1 GHz waveforms. We then fit the time delay relative to the IRF for each waveform and calculated mean offset values (Fig. 8(b)). The observed offsets had better than 5% accuracy over 6 months compared with calibrated values.

FIG. 8.

Pulse interleaving increases effective sampling rate. (a) The ATWD digitizer was calibrated to use a series of pre-trigger delays (black symbols: 0, 0.2, 0.4, 0.6, and 0.8 ns) on successive laser pulses. Each sequence of five 1-GHz acquisitions was combined into a single 5-GHz interleaved waveform (red squares). (b) The true offsets (red circles) were measured by exponential fitting showing better than 5% agreement with calibrated values (X-axis), root-mean-squared deviation 2.8%.

The ability to precisely acquire lifetime data depends on the experimental signal-to-noise ratio (SNR), typically measured at the peak of the fluorescence decay.^4,18 We acquired 1000 signal-averaged waveforms from a sample of rhodamine 6G in order to estimate instrument noise from the variation in a single well. We calculated the SNR waveform (Fig. 9(a)) as the signal of one waveform divided by the standard deviation at each time point. Peak SNR was inversely related to the detector voltage. At the low PMT voltage (400 V, a detector gain of about 1000) SNR peaked at 580 and dropped to 360 at higher PMT voltage (500 V, a detector gain of about 5000). These values were far above the desired threshold for precise lifetime detection (SNR ≥ 100).

FIG. 9.

Direct waveform recording provides high SNR. Signal-to-noise ratio (SNR, defined as signal/SD) was measured for 1000 successive acquisitions with 0.2 ns resolution. (a) SNR waveform of rhodamine 6G (1 μM in water) acquired with 200 cycle averaging of each waveform; (b) Representative values of peak SNR of rhodamine 6G with varied number of cycles averaged. Peak SNR was highest (580) at low PMT voltage (400 V, black squares) and dropped to 360 at high PMT voltage (500 V, blue diamonds).

The maximum signal-to-noise ratio was affected by the PMT voltage and the number of cycles averaged (Fig. 9(b)). In the absence of averaging, SNR ranged from 40 at 400 V acquisition to 90 at 500 V. Averaging over 200 cycles per acquisition increased SNR better than 6-fold. Experimental sources of variation between wells had a large effect on lifetime precision relative to instrumental sources. We found a 384-well plate of rhodamine 6G that showed substantial well-to-well variation in observed lifetime (CV 1.62%) with 200 cycles of averaging showed nearly equal precision with 50 cycles of averaging (CV 1.64%) despite the nearly 50% decrease in SNR per well. Pulse interleaving had a modest effect in the presence of experimental noise. Interleaved waveforms (5 GHz) of the short lifetime dye rhodamine B were more precise across wells (CV 0.59%) than the same waveforms without interleaving (1 GHz, CV 0.87%).

D. Resolution of lifetimes

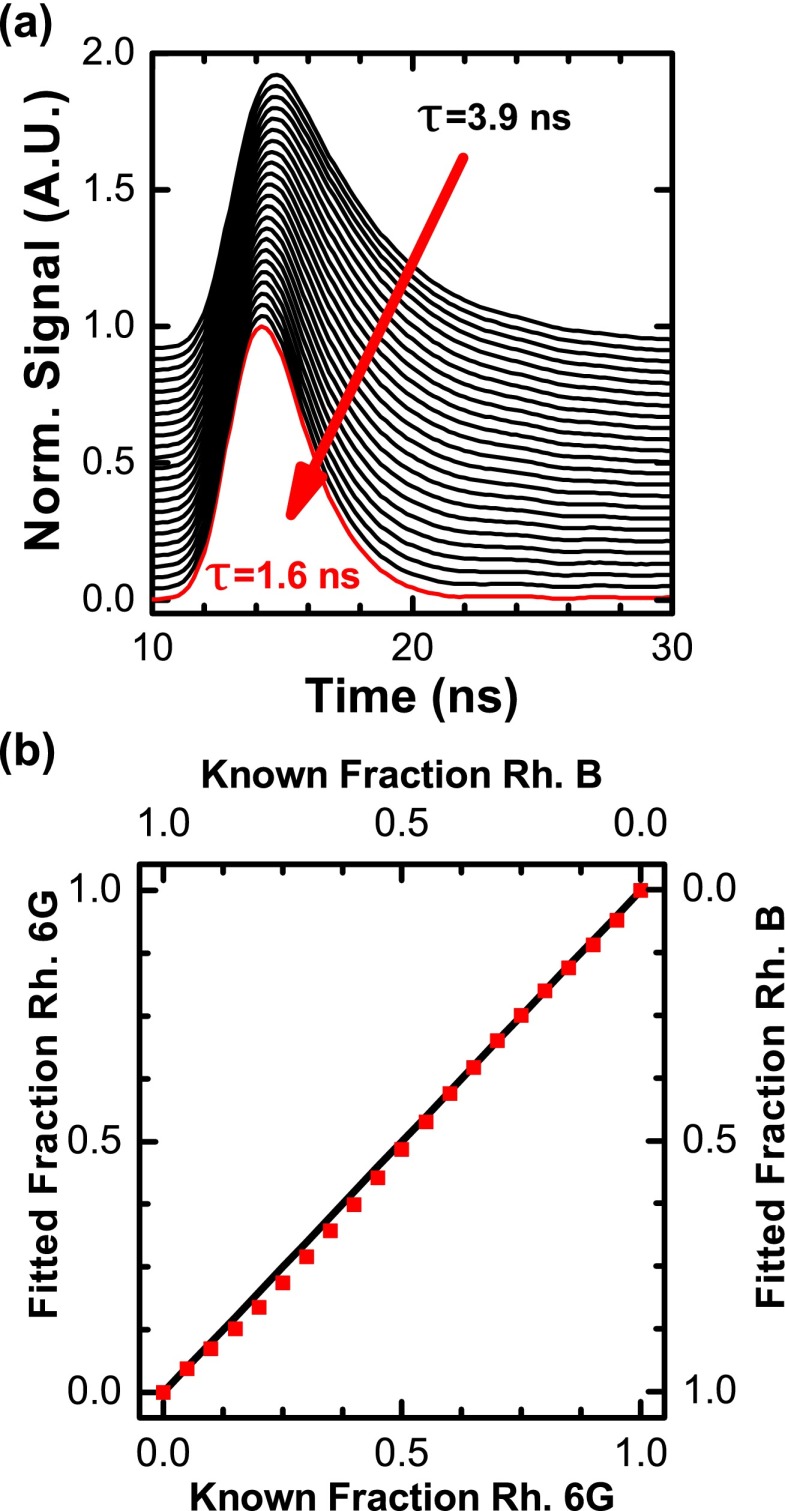
We tested the ability of the plate reader to resolve two dyes with similar lifetimes (1.6 ns for rhodamine B and 3.9 ns for rhodamine 6G) and overlapping emission spectra by mixing the dyes in 384-well plate, incrementing the volume of each dye by 5% in each column of wells to maintain a total concentration of 1 μM (Fig. 10). We averaged 16 replicate wells at each concentration and fit the relative fraction of dye using a two-component model (Eq. (2)). The fit recovered the true fraction with high accuracy (root-mean-squared deviation (RMSD) = 0.74% relative to the predicted mole fractions). The two-component mixture required averaging of replicate wells as fit results showed high variability (RMSD 2% or greater). Variability decreased to 1.08% RMSD with 4 replicates and 0.74% with 16. This result demonstrates the NovaFluor plate reader is capable of resolving changes in lifetime with high accuracy, a key requirement for lifetime-based assays.

FIG. 10.

Fluorescence lifetime quantitatively resolves dye mixtures. (a) Rhodamine 6G was mixed with rhodamine B in 5% volume steps (1 μM total, in water) for lifetime detection. (b) The mole fraction of rhodamine 6G was recovered with high accuracy by a two-component exponential fit (blue squares). Squared correlation coefficient r² > 0.999, root-mean-squared deviation 0.74% relative to the predicted relationship x = y (black line).

IV. DISCUSSION

Direct waveform recording (DWR) enables fluorescence lifetime acquisition in a microplate with a signal-to-noise ratio (SNR) of 400 or better while maintaining acquisition rates of 0.5 s per well. The plate reader acquires waveforms with high precision across a range of lifetimes, from short (1.6 ns, rhodamine B) to long (12.7 ns, EDANS). While there is great interest in developing long lifetime probes to improve the resolution of lifetime assays,¹⁵ the high precision of DWR permits the use of short lifetime probes as well. The per-well precision of lifetime measurement is routinely near 10 ps allowing us to resolve small changes in lifetime with high precision. The width of the IRF (2.8 ns) was not a barrier to analysis of short lifetimes, although the ultra-short lifetime dye Rose Bengal was unsuitable.

Fluorescence lifetime has a key advantage in high-throughput screening assays because it directly resolves interfering fluorescence signals²⁵ that are present in most screening compound libraries.²⁶ The use of multiple-exponential fits to resolve compound interference is firmly established.² We have shown (Fig. 10) that the DWR plate reader resolves the relative fraction present in a two-component mixture with better than 1% accuracy over a 20-fold concentration range, making it resistant to compound interference.

Acquisition rate has been a key limitation in applying fluorescence lifetime to high-throughput screening. We can compare DWR with photon counting methods of lifetime detection by comparing peak SNR in each. In photon counting,⁴ SNR increases as $\sqrt{N}$, while DWR measures SNR as signal/SD of successive waveforms.¹⁸ Photon counting applications have been optimized for a CV of 0.5% acquired in several hundred milliseconds.²⁴ If we assume a single 4 ns lifetime and 0.2 ns bins, this measurement would have a peak channel photon count of about 5000 corresponding to an SNR of 70. This is comparable to our performance with no signal averaging (Fig. 9) and at least 5-fold worse than our actual SNR performance in a 0.5 s acquisition. In another example¹⁶ a 5 MHz TCSPC instrument acquired 10 000 peak channel photon counts in 3 s, an SNR of 100. Increasing SNR to 400 would require ∼50 s acquisition in this example. DWR provides SNR of 400 or greater in 200 ms (200 cycles averaged), at least 100-fold faster when compared with TCSPC. The transport time of the microplate stage (0.3 s) limits our plate reader to a per-well acquisition time of 0.5 s (200 cycles averaged). With this limitation, the two methods are roughly comparable in speed.

Several factors affect the per-well acquisition time. Waveform averaging provides some protection against fluctuations in the fluorescence signal on the ms time scale, e.g., due to motion of contaminating particulates. We routinely average 200 waveforms per well. Averaging is not necessary as instrument noise is quite low (∼0.5 mV or less) providing high SNR. Reducing the number of waveforms to 50 modestly improves the acquisition time to 0.35 s, but may harm resolution. Similarly, pulse interleaving may be disabled to increase acquisition rate at a cost of decreased resolution of lifetime components. We are currently pursuing a rapid scan mode to decrease acquisition time to 0.1 s per well. Early results show SNR comparable to data acquired with 50 cycles averaged, a 3.5-fold improvement in speed.

Cost is another limitation in high-throughput screening assays. We have used costly glass plates in this study, but have tested plastic plates (polystyrene or cyclic olefin polymer) finding their precision to comparable. Plastic plates generate autofluorescence that hinders lifetime resolution. Assays that do not require resolution of component mole fractions may therefore benefit from plastic plates. We have begun development of a top-read format plate reader that enables use of lower cost polypropylene plates. Early results show comparable precision to that presented here (CV of lifetime better than 0.5%).

Direct waveform recording relies on the linearity of the analog current generated by the PMT. While the total intensity signal of our instrument is linear with excitation power (Fig. 5) and concentration (Fig. 6), nonlinearity results in a correlation of apparent lifetime with intensity. The nonlinearity is likely due to physical limitations in the PMT at high peak output current (2 mA for a 100 mV signal). High intensity signals produce slightly longer lifetimes as a result. The effect is small (∼50 ps per fluorescence unit, Fig. 7). We find nonlinearity has negligible effect when intensity varies due to experimental error alone (Fig. 4) as per-well precision (∼10 ps) becomes limiting. Assays requiring full dynamic range should consider the effect of nonlinearity on apparent lifetime. This effect is a subject of ongoing study.

Other approaches to improving resolution of fluorescence assays include homogeneous time-resolved fluorescence (HTRF) using long-lived lanthanide probes²⁷ or development of ratiometric assays that exploit changes in emission spectra, for example, the ratio of donor to acceptor emission in a FRET pair.²⁸ Both of these techniques limit the choice of probes available and do not eliminate the issue of signal precision common to intensity-based measurements. For applications requiring greater sensitivity and rejection of signal interference, enzyme-coupled bioluminescence assays remain the gold standard.^25,29

Fluorescence lifetime has been pursued for improvement of high-throughput screening assays for many years. The high precision of DWR has enabled development of new types of fluorescence assays including time-resolved transient kinetics¹⁹ and the recently reported time-resolved flow cytometry measurement of single cells.³⁰ The NovaFluor lifetime plate reader demonstrates that direct waveform recording achieves excellent signal-to-noise and per-well precision while providing fast acquisition rates suitable for drug screening and other high-throughput applications.