Quantum and Molecular Mechanical (QM/MM) Monte Carlo Techniques for Modeling Condensed-Phase Reactions

Abstract

A recent review (Acc. Chem. Res. 2010, 43:142–151) examined our use and development of a combined quantum and molecular mechanical (QM/MM) technique for modelling organic and enzymatic reactions. Advances included the PDDG/PM3 semiempirical QM (SQM) method, computation of multi-dimensional potentials of mean force (PMF), incorporation of on-the-fly QM in Monte Carlo simulations, and a polynomial quadrature method for rapidly treating proton-transfer reactions. The current article serves as a follow up on our progress. Highlights include new reactions, alternative SQM methods, a polarizable OPLS force field, and novel solvent environments, e.g., “on water” and room temperature ionic liquids. The methodology is strikingly accurate across a wide range of condensed-phase and antibody-catalyzed reactions including substitution, decarboxylation, elimination, isomerization, and pericyclic classes. Comparisons are made to systems treated with continuum-based solvents and ab initio or density functional theory (DFT) methods. Overall, the QM/MM methodology provides detailed characterization of reaction paths, proper configurational sampling, several advantages over implicit solvent models, and a reasonable computational cost.

Introduction

Simulating large, complex systems at the atomic level remains a challenge despite continual improvements in computational hardware. Combined quantum and molecular mechanical (QM/MM) methods provide an efficient approach to model bond making and breaking processes in organic and enzymatic reactions relative to QM alone.^1–6 In our method, the reacting system (or key parts) is treated using a QM method, solvent and protein environment encompass the MM region, solute-solvent interactions are modelled with charges and Lennard-Jones (LJ) interactions using force field parameters, and Monte Carlo (MC) statistical mechanics provides the configurational sampling. Adequate sampling requires hundreds of millions of QM calculations,⁷ as the energy and wave function for designated solutes or residues are obtained from single-point calculations upon each MC move of the solutes. Thus, highly efficient QM methods are needed. In our case, semiempirical QM (SQM) methods have been explored, though there are alternative approaches including the ONIOM, empirical valence bond (EVB), and EE-MCMM/MM methods.^8–15 This article summarizes the continued development of our QM/MM/MC methodology and its application to multiple organic and enzymatic reactions in the condensed-phase. Unique solvation challenges are also highlighted, including modelling “on water” and ionic liquid (room temperature molten salts) environments.

QM/MM/MC Methodology Details

Solvent and Atomic Charges

Solvent molecules are included explicitly using the OPLS-AA force field for non-aqueous solvents and the TIP4P model for water.¹⁶ Periodic boundary conditions are used for the organic reactions, while water caps are employed to solvate enzymes. Solute-solvent and solvent-solvent interactions are typically truncated using 12 Å residue-based cutoffs with smoothing applied over the last 0.5 Å. The energy and wave function for the QM region are obtained from single-point calculations upon each attempted Monte Carlo move of a QM element. The non-bonded potential energy between the QM and MM regions is given by Coulomb and Lennard-Jones interactions (eq 1). The σ and ε parameters are taken from the OPLS-AA force field along with the atomic charge q_i for MM atoms.

$$E_{\mathit{nonbond}}={\displaystyle \sum }_i{\displaystyle \sum }_{j>i}\{\frac{q_i{q}_j}{r_{\mathit{ij}}}+4{\epsilon }_{\mathit{ij}}[{(\frac{{\sigma }_{\mathit{ij}}}{r_{\mathit{ij}}})}^{12}-{(\frac{{\sigma }_{\mathit{ij}}}{r_{\mathit{ij}}})}^6]\}$$ (1)

Our work utilizes the Cramer-Truhlar CMx models¹⁷ for the calculation of charges on the QM atoms. The CMx models have been optimized for reproduction of gas-phase dipole moments. Based on tests for performance in solution, our choice for neutral molecules has been CM1A (AM1-based) or CM3P (PM3-based) charges scaled by ca. 1.14.^{18, 19} The 1.14*CM1A charges yield a mean unsigned error (mue) of 1.0 kcal/mol for free energies of hydration, while the mue is 0.7 kcal/mol with OPLS-AA charges. These choices provide a balanced treatment such that acceptable results are consistently obtained for free energies of hydration and medium effects on equilibria and reaction rates.^{1, 20, 21} All QM/MM computations are carried out with the BOSS and MCPRO programs for organic and enzymatic reactions, respectively.²²

Long-Range Electrostatics

Exhaustive simulations of the substrate, protein, and solvent molecules require a large amount of computer time for proper convergence, much of which is spent evaluating long-range electrostatics via Ewald summations. Ewald (or lattice) summation techniques can provide an accurate electrostatic treatment by using a cutoff distance for the quickly decaying short-ranged real-space summation and by performing a second long-ranged reciprocal-space summation.²³ However, as the number of particles, N, increases, a simple Ewald implementation can increase the simulation effort as O(N²). Optimization of the reciprocal-space summation with Fourier-based approaches, e.g., particle-mesh Ewald (PME), can scale lower, O(N log(N)).^24–26 Cutoff truncation artifacts can be reduced by the use of a linear scaling shifted potential scheme that provides a continuous shifting of the potential at all distances such that the value of the potential (or the value and first derivative for a shifted force potential) becomes zero at the cutoff distance.²⁷ In our recent work, a new method was developed, the shifted force 3^rd derivative (SF3), and examined on 59 unique ionic liquid combinations of 1-alkyl-3-methylimidazolium [RMIM] (R = M (methyl), E (ethyl), B (butyl), H (hexyl), and O (octyl)) and N-alkylpyridinium [RPyr] cations, along with Cl⁻, PF₆⁻, BF₄⁻, NO₃⁻, AlCl₄⁻, Al₂Cl₇⁻, and TfO⁻ anions.²⁸ The SF3 formalism is given in eq 2, where R_C is the cutoff distance and r_ij is the distance between particles. Monte Carlo simulations utilizing our custom OPLS-AA ionic liquid force field²⁹ and employing different pairwise alternatives with multiple cutoff distances and electrostatic damping values were compared to the energetics from full Ewald sums. The SF3 method provided a significant 8- to 9-fold speed-up in the calculation time and was found to be an accurate alternative to full Ewald sums.

$$V_{\mathit{SF}3}=\{\begin{array}{l}{q}_i{q}_j[\frac{i}{r_{\mathit{ij}}}-\frac{1}{R_C}+(r_{\mathit{ij}}-R_C\left)\right(\frac{1}{R_C^2})-{(r_{\mathit{ij}}-R_C)}^2(\frac{1}{R_C^3})+{(r_{\mathit{ij}}-R_C)}^3(\frac{1}{R_C^4}\left)\right],r_{\mathit{ij}}\le R_C\hfill \\ 0,r_{\mathit{ij}}>R_C\hfill \end{array}$$ (2)

Improved Semiempirical QM Methods

The most popular SQM choices, AM1³⁰ and PM3,³¹ were developed over 30 years ago and follow the MNDO³² formalism. However, these SQM methods suffer from multiple issues.^{30, 31} Common errors for molecules with small rings or adjacent heteroatoms could be attributable to both the valence-only sp basis sets and neglect of differential overlap (NDO). Recent efforts included reintroduction of the overlap matrix into the secular equations in MNDO yielding NO-MNDO,³³ and the addition of d-orbitals on the first row with MNDO and AM1. The mean unsigned error (mue) for heats of formation was reduced from 8.4 kcal/mol using MNDO to 6.8 kcal/mol with NO-MNDO for a diverse set of 622 neutral, closed-shell molecules containing C, H, N, and O atoms.³³ The addition of d-orbitals for 217 hydrocarbons reduced the mue for ΔH_f, excluding unacceptably large errors in alkynes, with MNDO from 9.3 to 6.8 and for AM1 from 5.3 to 3.8 with ring compounds improving from 7.1 to 4.5 kcal/mol. The problem for the alkynes was traced to overly repulsive 2-center resonance integrals for short d-d interactions, which may be ameliorated with a damping function.

$$\mathit{PDDG}(A,B)=\frac{1}{z_A+z_B}[{\displaystyle \sum }_{i=1}^2{\displaystyle \sum }_{j=1}^2(P_{\mathit{Ai}}+P_{\mathit{Bj}})\exp (-10{(R_{\mathit{AB}}-D_{\mathit{Ai}}-D_{\mathit{Bj}})}^2\left)\right]$$ (3)

Improvement of the core repulsion formula (CRF) yielded the most successful results. The main difference between AM1 and MNDO is the inclusion of additional Gaussians to the MNDO CRF. Starting with MNDO, the pairwise-distance-directed Gaussian (PDDG) expression in eq 3 was added, which uses 4 terms for an A-B interaction and 3 for A-A, where A and B are atoms separated by a distance R_AB. Each element requires a total of four optimizable parameters for the PDDG function, two preexponential factors, P_Ai and P_Bj, and two distances terms, D_Ai and D_Bj. This method, PDDG/MNDO, has fewer parameters than AM1, but upon optimization reduced the ΔH_f mue for the 622 molecule set from 8.4 (MNDO) and 6.7 (AM1) to 5.2 kcal/mol.³⁴ The mue with PM3 for the 622 compounds is 4.4 kcal/mol; however, this was surpassed with a mue of 3.2 by adding the PDDG terms to PM3 yielding PDDG/PM3. The PDDG methods were extended to the halogen elements and Si, P, and S.^{35, 36} Performance with the alternative SQM method, SCC-DFTB, was found to be intermediate between AM1 and PM3.³⁷ With PDDG/PM3, well-known problems with homologation and hydrocarbon branching were corrected, and results for diverse isomerization energies were found to be more accurate (mue = 1.6) than from B3LYP/6-31G(d) (mue = 2.3). Heats of reaction are significantly improved with PDDG/PM3 over B3LYP-based DFT methods; e.g., for the G3 dataset, the mues are 3.2 for PDDG/PM3 and 7.2 for B3LYP/6-311+G(3df,2p). Notably, the listed SQM methods all reproduce MP2/cc-pVTZ molecular geometries with average errors for bond lengths, bond angles, and dihedral angles of only ca. 0.01 Å, 1.5°, and 3°. However, a general weak point for SQM methods is the description of hydrogen-bonding; this issue is largely avoided in our QM/MM studies by the MM representation of the solvent and use of the CM1A charges for QM atoms.

Free Energy Perturbations (FEP)

Accurate calculation of free energy changes is essential for the characterization of chemical processes. Recent reviews on the FEP calculations and historical perspectives are available.^38–42 FEP uses the Zwanzig expression (eq. 4) to relate the free energy difference by constructing a nonphysical path connecting the desired initial (X) and final (Y) state of a system.⁴³ For application of eq 4 to the medium effect on the interconversion of two molecular entities, A and B, the thermodynamic cycle in Scheme 1 is used. The A to B FEP conversion is performed in both media, and the medium effect is given by eq 5. Single or double topology perturbations⁴⁰ can be made to convert one compound to another. In the single topology method, force field parameters, e.g., atomic partial charges, Lennard-Jones energy terms, force constants, and geometric changes describing the initial and final states, are linearly interpolated between X and Y. The double topology approach does not use interpolation of the force field parameters, but instead it interpolates the potential energy. In addition, both molecules, i.e., initial and final state, are present throughout the simulation while occupying the same volume. Both topology methods should in principle provide equally accurate results; however, for FEP methods it has been reported that the single topology approach is more efficient than the dual topology for all but very long simulations.⁴⁴ The < > brackets in eq 4 indicate that the bracketed quantity is averaged over all the configurations X can adopt from ΔG(X→Y) and are weighted by their Boltzmann probabilities. Configurations of X are generated using a molecular simulation, e.g., Monte Carlo (MC) statistical mechanics in our work, with the appropriate Boltzmann weights. A simple average of the exponential term is then performed over these configurations.

$$\mathrm{\Delta }\mathrm{G}(\mathrm{X}\to \mathrm{Y})=-{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\text{ln}<\exp [-({\mathrm{E}}_{\mathrm{Y}}-{\mathrm{E}}_{\mathrm{X}})/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]{>}_{\mathrm{X}}$$ (4)

$$\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_2-\mathrm{\Delta }{G}_1=\mathrm{\Delta }{G}_{\mathrm{B}}-\mathrm{\Delta }{G}_{\mathrm{A}}$$ (5)

Scheme 1.

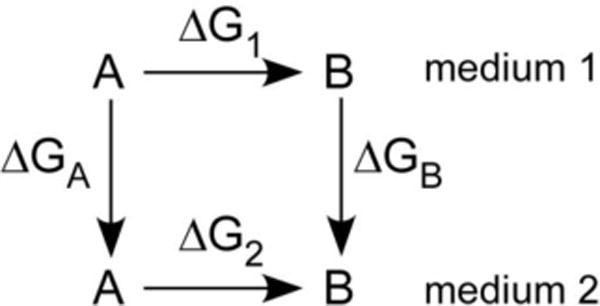
Thermodynamic cycle for mutation of A to B in two solvents.

Instead of chemical mutations, free energy changes may be computed as a function of some inter- or intramolecular coordinate, e.g. a bond distance or angle. The free energy surface along the chosen coordinate is known as a potential of mean force (PMF). In our implementation, the PMF reaction coordinate is broken into a series of “windows” that is characterized by a coupling parameter λ. A window entails an MC simulation at one point along the mutation coordinate λ, which interconverts two ligands or a geometrical variable as λ goes from λ_i to λ_j. The number of FEP calculations is determined by the range for the geometrical mutation and the increments, δλ, between them (grid spacing). The geometric perturbation of a distance must be small, δλ = 0.01 − 0.05 Å, to ensure adequate overlap between configurations (λ + δλ) which are combined to produce a one-dimensional (1-D) PMF. It is also possible to combine a PMF run along one reaction coordinate with a series of PMF runs along additional reaction coordinates to produce a multi-dimensional PMF.⁴⁵ For many reactions, two coordinates are sensible such as breaking and making bonds or the two forming bonds in a cycloaddition.

Condensed-Phase Organic Reactions

Substitutions and Additions

Substitutions have proven to be an excellent class of reactions for testing QM/MM methods.^46–50 Our recent review¹ highlighted multiple successful examples of SQM-based PDDG/PM3/MM calculations that have included S_N2 reactions of chloride ion with methyl, ethyl, and neopentyl chlorides,^{51, 52} the S_N2 methyl-transfer reactions of sulfonium and ammonium salts,⁵³ the S_NAr reaction of N₃⁻ + p-FPhNO₂,⁵⁴ and the NH₃ + CH₃Cl → CH₃NH₃⁺ + Cl⁻ Menshutkin reaction.¹⁴ An additional Menshutkin reaction between triethylamine and ethyl iodide (Scheme 2) was recently carried out using both the nonpolarizable OPLS and polarizable OPLS-AAP force fields.⁵⁵ The reaction energetics were computed using B3LYP and MP2 methods and a variety of basis sets containing small- and large-core energy-consistent relativistic pseudopotentials. Condensed-phase corrections in seven different solvents, i.e., cyclohexane, CCl₄, THF, DMSO, acetonitrile, methanol, and water (Figure 1), were applied from QM/MM simulations. The B3LYP/MIDI! theory level provided the best ΔG^‡ values with a mean absolute error (MAE) of 4.9 kcal/mol from experiment. However, the relative rates in cyclohexane, and to a certain extent CCl₄, were determined to be greatly underestimated when using the non-polarizable force field. For example, B3LYP/LANL2DZ with OPLS-AAP gave a ΔG^‡ in cyclohexane of 27.0 kcal/mol, which is in close agreement with the experimental value of 26.6 kcal/mol;⁵⁶ the unpolarized OPLS-AA version yielded a ΔG^‡ of 37.2 kcal/mol. In general, the nonpolarized ΔG^‡ MAEs were approximately 2 kcal/mol higher than the OPLS-AAP results regardless of the QM theory level employed. This emphasizes the need for a polarizable force field when computing solvent effects for highly dipolar transition structures in low-dielectric media.⁵⁷ Notably, the MAEs obtained with the PDDG/PM3 SQM method coupled to OPLS-AA and OPLS-AAP of 5.3 and 3.8 kcal/mol, respectively, provided comparable results to B3LYP at a small fraction of the computational cost.

Scheme 2.

Menshutkin reaction between triethylamine and ethyl iodide.

Figure 1.

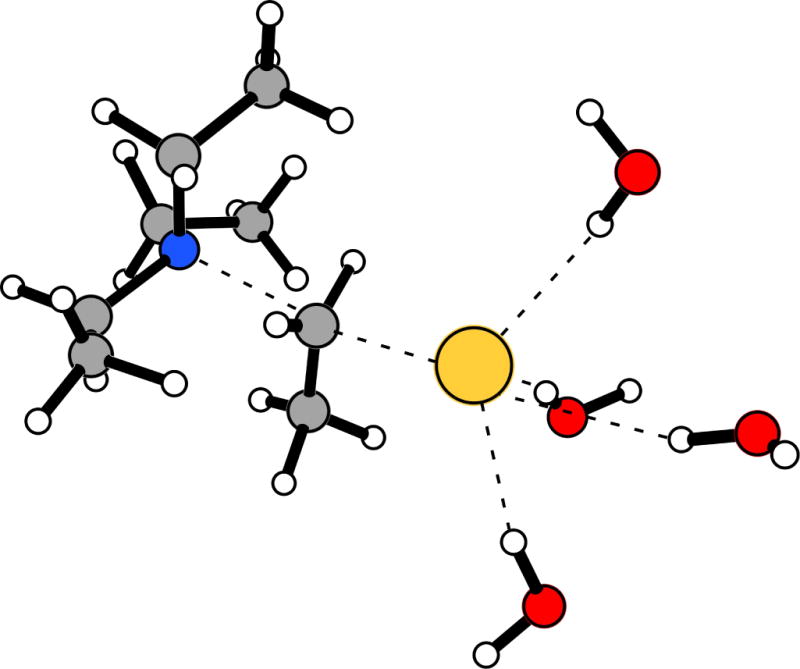
Typical configuration for the transition structure for the Menshutkin reaction between triethylamine and ethyl iodide in water. Nearby hydrogen bonding water molecules are shown.

While the PDDG/PM3 SQM method has generally provided excellent absolute or relative agreement with experimental energies,¹ the advent of RM1 – a modern reparameterization within the AM1 SQM framework,⁵⁸ provides an alternative SQM method to explore for QM/MM simulations. A good test is the NH₃ + CH₃Cl → CH₃NH₃⁺ + Cl⁻ Menshutkin reaction, as it has been extensively studied by a variety of computational methods implementing numerous aqueous solvation models, e.g., continuum, RISM, and QM/MM.^{14, 18} The Menshutkin reaction was carried out using a RM1/TIP4P-Ew procedure that gave a computed ΔG^‡ of 14.5 kcal/mol in aqueous conditions, which was underestimated compared to the PDDG/PM3/TIP4P value of 25.8 kcal/mol¹⁴ and other computational predictions that place the ΔG^‡ in the range of 16 – 31 kcal/mol.¹⁸ The RM1-based transition structure geometry and computed ΔG_rxn of −24.7 kcal/mol were found to be in close agreement with those obtained from a wide range of computational approaches; however, most ΔG_rxn calculations fall short of the experimental estimate of −36 ± 6 kcal/mol.⁵⁹ Additional study of different reaction classes will be required to assess the general accuracy of the use of RM1 in mixed QM/MM calculations.

As a valuable method for the synthesis of C-C and heteroatom-C bonds, addition reactions have been well-reproduced by the QM/MM methodology as highlighted by the ene reactions between 4-phenyl-1,2,4-triazoline-3,5-dione (PTAD) and tetramethylethylene,⁶⁰ and between singlet oxygen (¹O₂) and tetramethylethylene.⁴⁵ More recently, Henry reactions between (1) formaldehyde and nitromethane and (2) benzaldehyde and nitropropane (Scheme 3) were investigated using the AM1 SQM method in the QM/MM simulations.⁶¹ Free-energy barriers, ΔG^‡, of 6.7 and 14.1 kcal/mol were computed in the gas and aqueous phase, respectively, for the nitromethane anion and formaldehyde reaction; the calculated ΔG_rxn values were 2.2 in gas and 5.3 kcal/mol in water. The increased activation barrier in aqueous solution was attributed to poorer solvation for the more charge-delocalized transition structure than for the reacting anion. In the reaction between nitropropane and benzaldehyde, the resulting nitroalkoxide product contains two stereogenic centers. Accordingly, the calculations examined the two diastereomeric reaction pathways leading to the syn (R,R or S,S) and anti (R,S or S,R) transition states. Unsurprisingly, the reaction proceeded more slowly in water than in DMSO (Table 1). Yet, the barrier lowering by 2–3 kcal/mol in DMSO is relatively modest compared to the 6–7 kcal/mol shifts for some S_N2 reactions.⁵¹ While the intrinsic preference for having the sterically bulky ethyl and phenyl groups anti is consistent with the anti transition structure being favored over the syn alternative, the effect of solvent on this preference was found to be negligible.

Scheme 3.

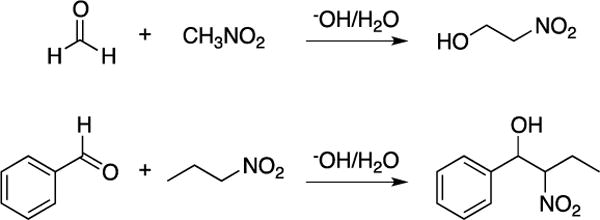
Henry reaction between formaldehyde and nitromethane and between benzaldehyde and nitropropane.

Table 1.

Free Energies of Activation, ΔG^‡ (kcal/mol), at 25 °C for the Henry Reaction between Nitropropane Anion and Benzaldehyde from QM/MM Simulations and Kinetic Studies.^a,b

	syn	anti	exptl
Gas	16.4	15.1	–
Water	24.8	22.7	17.5
DMSO	22.4	20.5	15.1

^aAM1 and MC/FEP.

^bRef. ⁶¹.

Decarboxylation and Eliminations

Excellent results from the PDDG/PM3 method were also found for QM/MM condensed-phase decarboxylation and elimination reactions including the Kemp decarboxylation of benzisoxazole-3-carboxylic acid,⁶² the decarboxylation of N-carboxy-2-imidazolidinone (a biotin model),⁶³ and the Cope eliminations of threo- and erythro-N,N-dimethyl-3-phenyl-2-butylamine oxide.⁶⁴ The computed energies and geometries were in close agreement with experiment and earlier computational decarboxylation studies.^{65, 66} More recently, the spontaneous decarboxylation of glycine in water to yield CO₂ and methylamine was explored using the QM/MM methodology.⁶⁷ The simulations showed a preference for a direct CO₂ departure with no specific assistance from an explicit water molecule. A computed ΔG^‡ of 45 kcal/mol was in good agreement with B3LYP and MP2 calculations coupled to a CPCM hydration model (44.5 and 42.8 kcal/mol, respectively) and within a reasonable range of an experimentally estimated ΔH^‡ of 39 ± 2 kcal/mol.⁶⁸

The Kemp elimination has also been of recent interest in both organic²⁹ and enzymatic^69–71 QM/MM studies. For example, the Kemp elimination ring-opening of benzisoxazole using piperidine as the base in the 1-butyl-3-methylimidazolium hexafluorophosphate [BMIM][PF₆] ionic liquid followed a concerted mechanism where the R_NO distance of the isoxazole ring in the transition structure is 2.06 Å while the R_NH and R_CH distances are 1.10 and 1.75 Å, respectively (Figure 2).²⁹ Computed changes in free energy yielded a ΔG^‡ value of 25.2 ± 1 kcal/mol. The experimental ΔG^‡ for the reaction under the same conditions is 22.6 ± 0.5 kcal/mol.⁷² The same PDDG/PM3 based QM/MM methodology was also successfully applied to examine the catalysis of the Kemp elimination of 5-nitrobenzisoxazole by catalytic antibody 34E4 and its Glu50Asp variant.⁷⁰ A predicted increase in the activation barrier by 2.4 kcal/mol for the mutant relative to wild-type 34E4 resulted from a small change in the positioning of the catalytic base and correlated well with the observed 30-fold rate reduction in k_cat at 20 °C.⁷³ The Kemp elimination of 5-nitrobenzisoxazole in catalytic antibody 4B2⁷¹ is discussed in greater detail in the “Biological Reactions” section.

Figure 2.

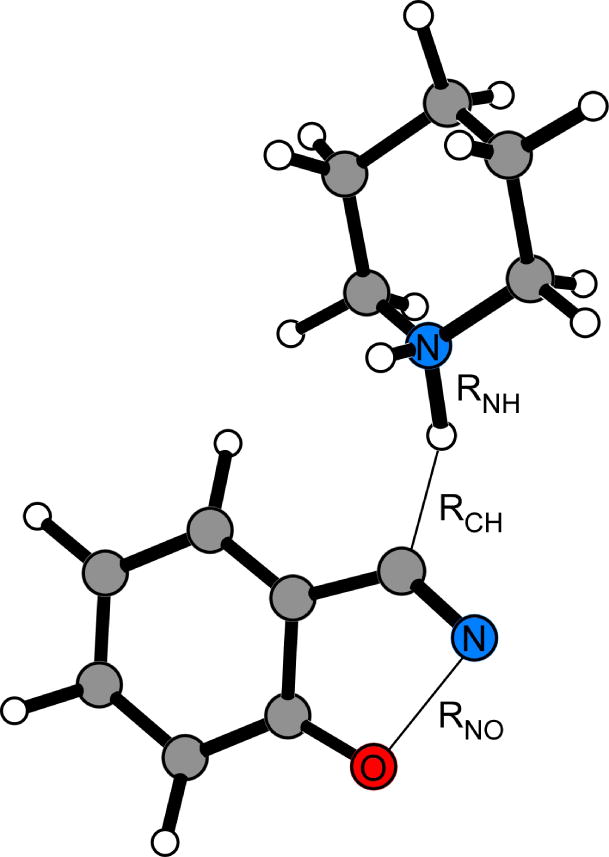
Reaction coordinates, R_NH – R_CH and R_NO, used to locate stationary points from free-energy maps obtained via PMF simulations for the Kemp elimination of benzisoxazole using piperidine. Illustrated structure corresponds to the transition state computed from QM/MM calculations.

QM/MM calculations have been carried out to determine the origin of the ionic liquid effect on a reported mechanism change for the β-elimination between 1,1,1-tribromo-2,2-bis(3,4-dimethoxyphenyl)ethane and the cyclic amines piperidine and pyrrolidine (Scheme 4).⁷⁴ D’Anna et al. proposed that the reaction occurs via an irreversible E1cB route in methanol, but via an E2 mechanism in the [BMIM][BF₄] and [BMIM][PF₆] ionic liquids.⁷⁵ Our PDDG/PM3-based simulations found that the ionic liquids did produce a reaction pathway change from an E1cB-like mechanism in methanol to a pure E2 route, which is consistent with the experimental observations. The origin of the ionic liquid effect has been found as: (1) a combination of favorable electrostatic interactions, e.g., bromine-imidazolium ion, and (2) π-π interactions that enhance the coplanarity between the solute β-phenyl rings maximizing the electronic effects exerted on the reaction route. The BMIM cations form a cage-like structure to favorably interact with the Br anion and β-phenyl substituents (Figure 3), which agrees with reports of liquid clathrate formation in 1-alkyl-3-methylimdazolium-based ionic liquids with aromatic compounds.

Scheme 4.

β-Elimination Reaction of 1,1,1-tribromo-2,2-bis(3,4-dimethoxyphenyl)ethane.

Figure 3.

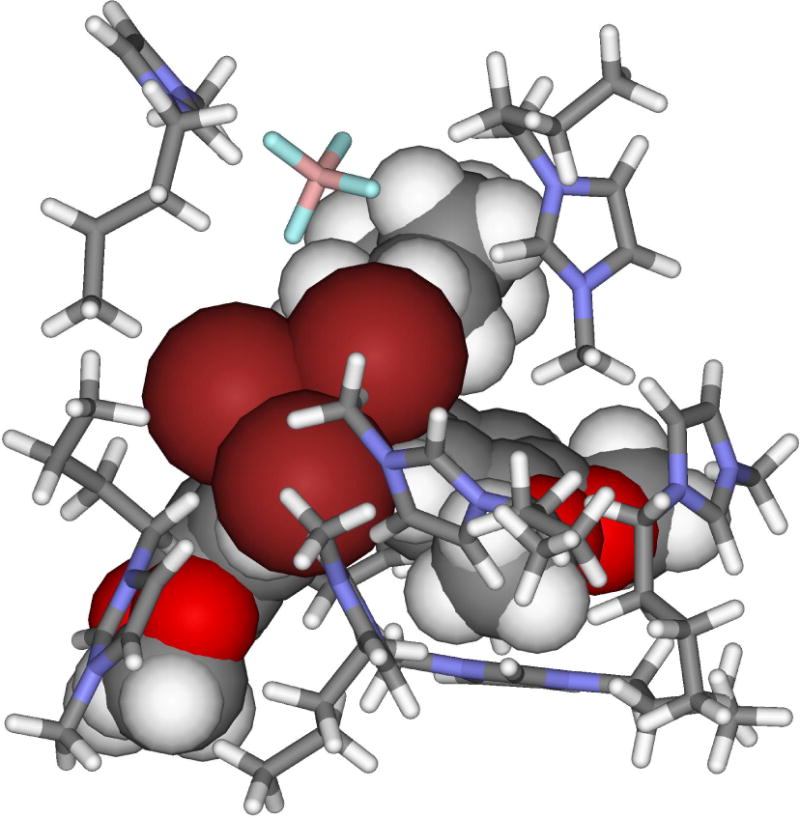
Illustration of the encapsulation of the β-elimination solute with piperidine transition state (given as a CPK space-filling model) by nearby ions from [BMIM][BF₄] (shown as sticks).

Pericyclic Reactions

PDDG/PM3/MM calculations were also applied to the Claisen rearrangement of allyl p-tolyl ether (R = CH₃ in Scheme 5A) and compared to experimental rates and thermodynamic parameters in 12 solvents of differing polarities.⁷⁶ While PDDG/PM3 overestimated the absolute ΔG^‡ values, which is common when applying SQM methods to pericyclic reactions,^{45, 77–79} the solvent effects were accurately reproduced (Table 2). Intriguingly, the solvent dependence of rates for the Claisen reaction is complex and did not show simple increases with increasing solvent polarity, e.g., rates in phenol and water were similar.⁸⁰ The simulations found the rate enhancements to be correlated to favorable electrostatic interactions between solvent and the dipolar transition structure, e.g., hydrogen bonding with the oxygen of the ether and π-π stacking between the aromatic rings in the case of p-chlorophenol. Notably, B3LYP/6-31G(d) calculations using the polarizable continuum model (PCM) failed to predict the correct order of reaction rates for the allyl p-tolyl ether rearrangement in solution.⁸¹ Substituent effects on the Claisen rearrangement were also studied by the inclusion of R = Br, CH₃, and OCH₃ groups in the allyl p-R-phenyl ether (Scheme 5A); the relative energies were in excellent agreement with experiment, e.g., computed ΔΔG^‡ values of 0.4, 0.0, and -1.1 kcal/mol compared to reported values of 0.5, 0.0, and -0.9 kcal/mol for the Br, CH₃, and OCH₃ reactions in water,⁸² respectively. Calculation of a second Claisen rearrangement featuring allyl naphthyl ether (Scheme 5B) in five solvents: water, methanol, acetonitrile, DMF, and toluene, were consistent with the qualitative representation of the rates and yields given by Sharpless and coworkers.⁸³

Scheme 5.

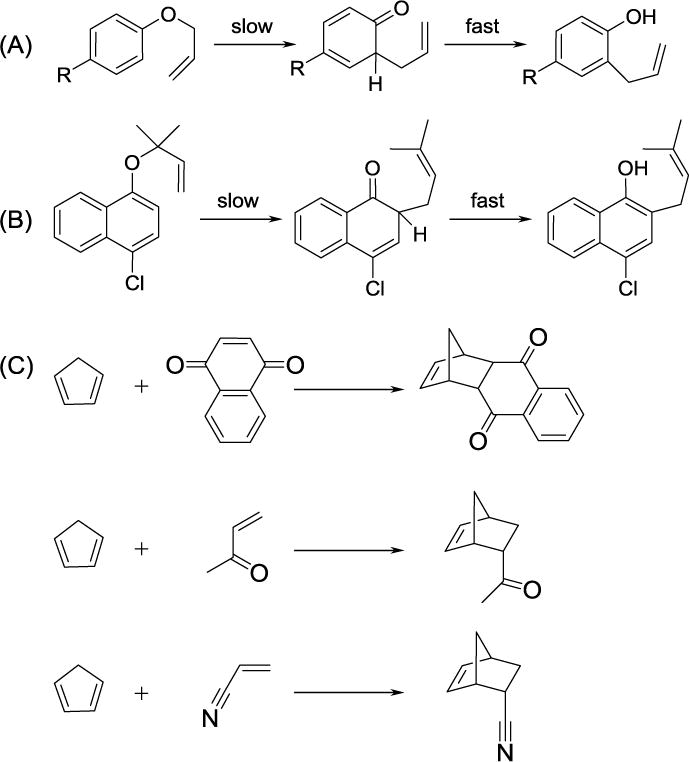
Claisen rearrangement of (A) allyl p-R-phenyl ethers, R = CH₃, Br, and OCH₃ and (B) allyl naphthyl ether; and (C) the Diels-Alder reaction between cyclopentadiene and 1,4-naphthoquinone, methyl vinyl ketone, and acrylonitrile.

Table 2.

Free Energy of Activation, ΔΔG^‡ (kcal/mol), at 25 °C for the Claisen Rearrangement of Allyl p-Tolyl Ether Relative to “In Water” using QM/MM.

	ΔΔG‡ (calc)a	ΔΔG‡ (exptl)b
p-chlorophenol	−0.8	−1.0
“in water”	0.0	0.0c
phenol	0.4	0.0
p-cresol	0.0	0.3
ethylene glycol	0.0	0.3
“on water”	0.9	–
2-aminoethanol	1.0	1.1
carbitol	1.3	1.5
sulfolane	1.8	1.9
adiponitrile	2.0	2.0
propylene carbonate	2.1	2.1
n-decylamine	2.7	2.7

^aPDDG/PM3 and MC/FEP.

^bRef. ⁸⁰, 170°C; Exptl. error for ΔG^‡ is ca. ± 0.3 kcal/mol.

^c28.5% EtOH-H₂O.

A novel application of our QM/MM methodology has been the calculation of the Claisen rearrangements (Schemes 5A and 5B) on the surface of water.⁷⁶ Sharpless has reported large rate increases and enhanced yields compared to organic solvents for a variety of reactions solely “on water.”^{83, 84} On water is defined as a reaction that proceeds in an aqueous organic emulsion prepared by vigorously stirring insoluble reactants with water, whereas “in water” the reactants are dissolved homogeneously in water.^83–88 The on water reactions were modeled in a similar fashion to the homogeneous solution-phase calculations except that periodicity was removed from the z-axis of an explicit water molecule box and the reactants were placed on the z-face (Figure 4). The equilibrated water slab used in the chemical reaction featured an NVT ensemble to prevent a very slow drift of the water molecules that reduces the exposed surface, i.e., stretch in the z-direction.

Figure 4.

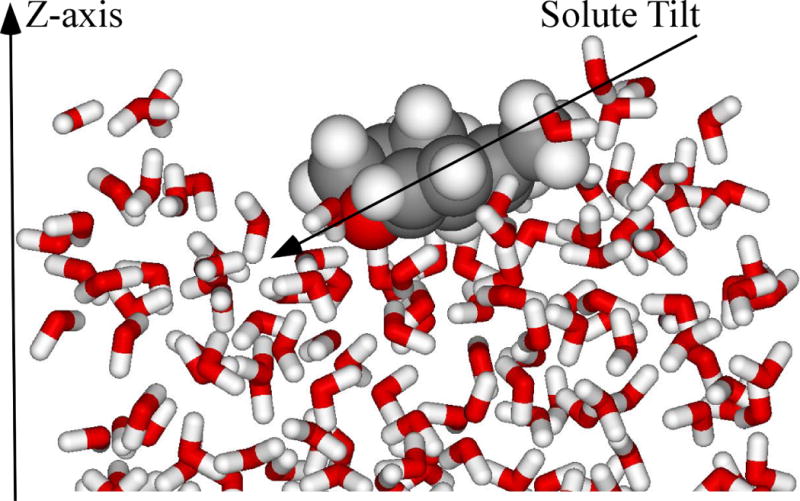
Illustration of the “on water” allyl p-tolyl ether transition structure from the QM/MM/MC Claisen rearrangement calculations. Figure originally published in ref. ⁷⁶.

An orientation analysis of the Claisen allyl p-tolyl ether rearrangement on the surface of the water slab found that the aromatic ring tended to lie essentially flat on the surface with a slight tilt towards the oxygen while the allyl side chain occupied the gas-phase (Figure 4). A similar orientation was found for allyl naphthyl ether, where the fused aromatic rings lay effectively flat on the surface of the water slab with a tilt towards the oxygen atom. Hydrogen bonding was found to be primarily responsible for the orientation, i.e., favorable interactions between water and the π-system of the aromatic ring and the oxygen. The addition of hydrophilic substituents on the phenyl ring, e.g., R = OCH₃ in the allyl p-R-phenyl ethers (Scheme 5A), strongly tilted the ring on the surface towards the substituent and as a result tilted the reacting oxygen away from the interfacial waters reducing the number of hydrogen bonds available. The ΔΔG^‡ for the on water reaction was predicted to be 0.9 and 0.6 kcal/mol higher in energy than the same reaction homogeneously dissolved in pure aqueous solution for the allyl p-R-phenyl ethers and allyl naphthyl ether, respectively.

The Diels-Alder reaction is of considerable interest both academically^{89, 90} and industrially.⁹¹ The cycloaddition has been extensively studied using our QM/MM methodology to elucidate the origin of solvent effects upon reported rate and stereoselectivity enhancements in conventional solvents^{77, 79, 92} and room temperature ionic liquids.⁷⁸ Three Diels-Alder reactions, cyclopentadiene with 1,4-naphthoquinone, methyl vinyl ketone, and acrylonitrile (Scheme 5C), were investigated in four different solvents including on water conditions.^{77, 79} The QM/MM methodology reproduced the large rate increases observed, up to 10,000-fold, when proceeding from aprotic solvents to water. For example, ΔG^‡ for the reaction between cyclopentadiene and 1,4-naphthoquinone is computed to increase upon transfer from water to methanol, acetonitrile, and hexane by 3.2, 4.1, and 5.1 kcal/mol, while the experimental values are 3.4, 4.0, and 5.0 kcal/mol (Table 3). The computed free energies of activation on the water surface are somewhat higher than for pure methanol, analogous to the results for the Claisen rearrangement. Similar differences in ΔΔG^‡ were shown for other dienophiles with cyclopentadiene on water and in methanol, respectively, e.g., 6.8 compared to 4.2 kcal/mol for methyl vinyl ketone and 4.0 versus 1.2 kcal/mol for acrylonitrile.^{77, 79} Since the density of water is reduced near the surface, the situation is comparable to a condition of higher temperature or lower pressure, which would diminish the solvent effects. About 1.0 – 1.5 kcal/mol of the ΔΔG^‡ values can be attributed to hydrophobic effects in water, but the remainder can be ascribed to the differences in hydrogen-bonding capacity for water and methanol. The calculations do not support the notion that a water surface is more effective than bulk water at catalyzing pericyclic reactions and contrast a conceptual model of an organic-aqueous interface with dangling OH bonds as responsible for substantial rate enhancements.⁹³ The experimental situation with the biphasic emulsions is somewhat different and could be better modeled by studying the reactions at the interface between water and a liquid hydrocarbon.

Table 3.

ΔΔG^‡ (kcal/mol) for Diels-Alder reaction between cyclopentadiene and 1,4-naphthoquinone.

	In water	On water	MeOH	MeCN	hexane
MP2/CPCMa	0.0	–	1.2	−0.2	1.7
PDDG/PM3b	0.0	3.7	3.2	4.1	5.1
exptl.c	0.0	–	3.4	4.0	5.0

^a6-311+G(2d,p) single-points on CBS-QB3 geometries.

^bQM/MM.

^cRef. ⁹⁸.

Condensed-Phase Biological Reactions

Catalytic Antibody 4B2

Catalytic antibody 4B2 possesses the ability to efficiently catalyze two unrelated reactions: the Kemp elimination of 5-nitrobenzisoxazole (k_cat/k_uncat = 18,000)⁹⁴ and the unrelated allylic rearrangement of α-cyclopent-1-en-1-yl-p-acetamidoacetophenone (k_cat/k_uncat = 1,500)⁹⁵ (Scheme 6). A general programmed base – Glu L34, is believed to catalyze both reactions and originated from the ‘bait-and-switch’ method of using of a charged hapten to induce a complementarily charged amino acid in the binding site microenvironment.⁹⁶ The promiscuity of the antibody is particularly surprising as 4B2 was elicited from a cyclic amidinium salt originally intended to generate antibodies with glycosidase activity.⁹⁷ In an effort to elucidate the reasons behind the significant rate enhancements reported for two very different reactions, a PDDG/PM3/MM MC/FEP mechanistic investigation of the system was carried out with particular emphasis on the active site residues and solvent molecules that play the largest roles in stabilizing the transition structures for the two reactions.⁷¹

Scheme 6.

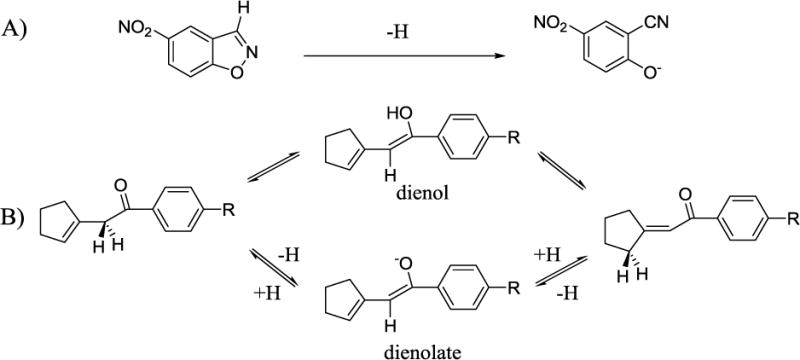
Antibody 4B2 catalyzed (A) Kemp elimination of 5-nitro-benzisoxazole, and (B) allylic rearrangement of α-cyclopent-1-en-1-yl-p-acetamidophenone (R = NHCOCH₃) via a dienol or dienolate intermediate.

The free-energy surface for the Kemp elimination of 5-nitro-benzisoxazole in antibody 4B2 via Glu L34 yielded a ΔG^‡ value of 17.1 ± 1 kcal/mol (Figure 5). The reaction follows a concerted mechanism where the N^⋯O distance of the isoxazole ring in the transition structure is 1.68 Å while the Glu-O^⋯H-solute and solute-H^⋯C-solute distances are 1.20 and 1.65 Å, respectively, for the proton abstraction. The experimental ΔG^‡ for the 4B2-catalyzed reaction is estimated at 19.7 kcal/mol from the reported conditions (k_cat = 3.5 ± 0.8 × 10² s⁻¹, pH 7.1, 1% CH₃CN, 40 mM phosphate buffer with 100 mM of NaCl, and 30 °C).⁹⁴ Proper positioning of the base in the binding pocket was controlled through a strong hydrogen bonding network between Glu L34 and nearby His and Trp residues. However, provision of extra room in an otherwise hydrophobic binding pocket for a few water molecules to rearrange into advantageous geometric orientations enabled a flexible microenvironment capable of delivering specific stabilization through hydrogen bonding to the emerging negative charges over the isoxazolyl nitrogen and oxygen atoms at the transition state.

Figure 5.

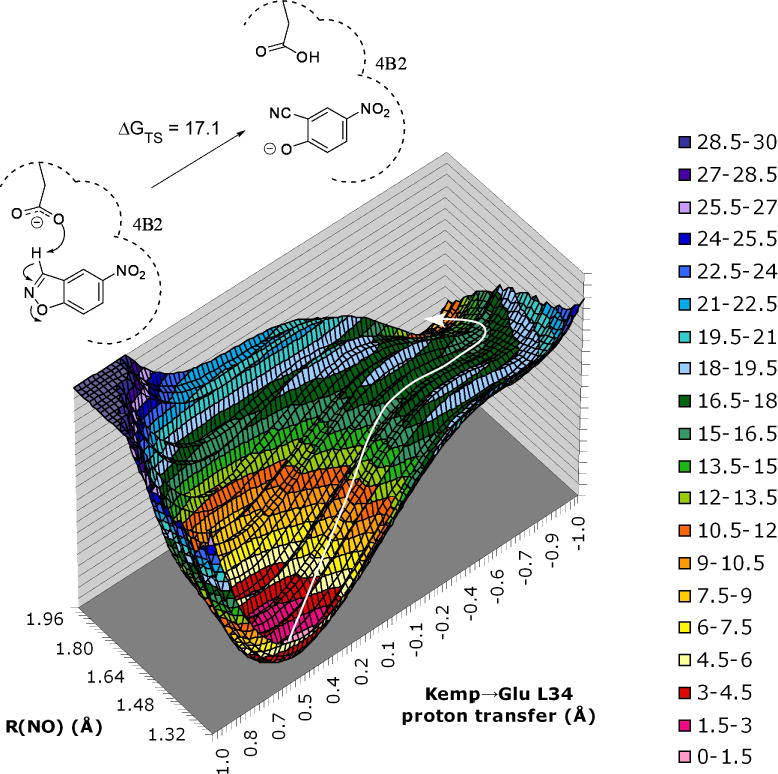
Free-energy profile (kcal/mol) for the Kemp elimination of 5-nitro-benzisoxazole in antibody 4B2. The reaction coordinate for the proton transfer is OH – CH with OH + CH = 2.85 Å. Maximum free-energy values truncated to 30 kcal/mol for clarity. Figure originally published in ref. ⁷¹.

The role of water was found to be more pronounced in the allylic isomerization with the mechanism predicted from QM/MM calculations to follow a stepwise path (Figure 6); the abstraction of the α-proton via Glu L34 leads to the formation of a neutral dienol intermediate which is rapidly reprotonated at the γ-position via a solvent hydronium ion. The H₃O⁺ catalyzes the first step of the mechanism by either donating a proton to or stabilizing the large developing negative charge on the carbonyl oxygen prior to formation of the intermediate. In addition, preferential channeling of a H₃O⁺ ion in the active site ensures a stereoselective proton exchange from the α- to the γ-position, in good agreement with observed deuterium exchange NMR and HPLC experiments and an extremely narrow pH versus k_cat/K_m efficiency range centered around a pH of 4.5.⁹⁵ Overall, the α-proton abstraction in the allylic isomerization is predicted to be catalyzed partially by desolvation effects on the Glu L34 base, similar to the Kemp elimination, and through a favorable microenvironment that allows a strong base and acid to occur simultaneously in the active site.

Figure 6.

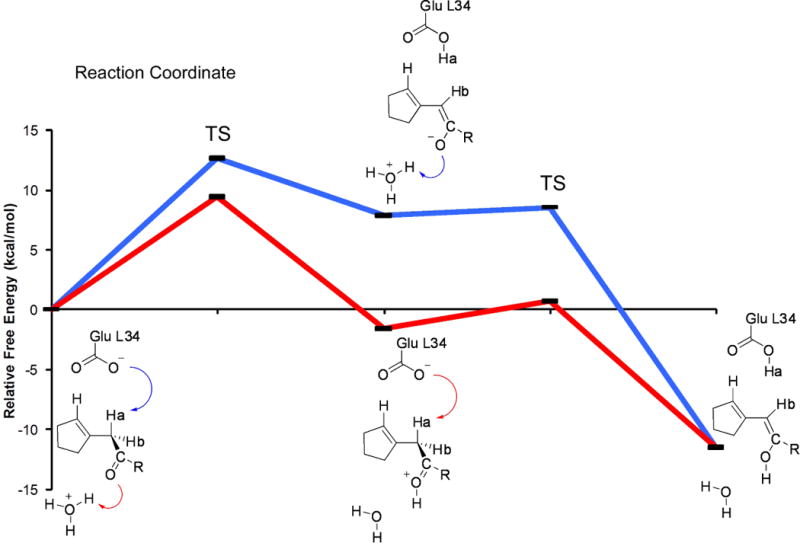
Computed free energies (kcal/mol) for competitive proton abstraction pathways towards dienol intermediate formation; R = phenyl-NHCOCH₃. Figure originally published in ref. ⁷¹.

Conclusion

This review highlighted numerous QM/MM calculations of organic reactions in multiple solvents and under enzymatic conditions. The PDDG/PM3 semiempirical method coupled to MC/FEP calculations was shown to be particularly effective at describing reaction paths and accurately reproducing activation barriers relative to experiment. In addition, the ability of the explicit solvent model to mimic unique solvent environments, such as on-water conditions and room temperature ionic liquids, provided a distinct advantage over that of ab initio and DFT based approaches coupled to implicit solvent models. Nevertheless, new advances in QM/MM methodology are necessary to expand towards larger and more varied chemical and biological environments. Some future and ongoing work include better descriptions of the QM/MM boundary effects, the inclusion of adaptive QM/MM methods – where molecules are allowed to enter and leave the QM region dynamically, improvements to the fast QM methods, and on-the-fly QM/MM calculations with ab initio and DFT methods.