Functional Design Space of Single-veined Leaves: Role of Tissue Hydraulic Properties in Constraining Leaf Size and Shape

Abstract

• Background and Aims Morphological diversity of leaves is usually quantified with geometrical characters, while in many cases a simple set of biophysical parameters are involved in constraining size and shape. One of the main physiological functions of the leaf is transpiration and thus one can expect that leaf hydraulic parameters can be used to predict potential morphologies, although with the caveat that morphology in turn influences physiological parameters including light interception and boundary layer thickness and thereby heat transfer and net photosynthesis.

• Methods An iterative model was used to determine the relative sizes and shapes that are functionally possible for single-veined leaves as defined by their ability to supply the entire leaf lamina with sufficient water to prevent stomatal closure. The model variables include the hydraulic resistances associated with vein axial and radial transport, as well as with water movement through the mesophyll and the leaf surface.

• Key Results The four parameters included in the model are sufficient to define a hydraulic functional design space that includes all single-veined leaf shapes found in nature, including scale-, awl- and needle-like morphologies. This exercise demonstrates that hydraulic parameters have dissimilar effects: surface resistance primarily affects leaf size, while radial and mesophyll resistances primarily affect leaf shape.

• Conclusions These distinctions between hydraulic parameters, as well as the differential accessibility of different morphologies, might relate to the convergent evolutionary patterns seen in a variety of fossil lineages concerning overall morphology and anatomical detail that frequently have evolved in linear and simple multi-veined leaves.

INTRODUCTION

‘Morphospaces, carefree and fun, are the light and life of any social gathering.’

C.K.B.

Morphological diversity provides an essential tool for understanding evolutionary patterns and processes. Patterns of morphological diversity have been quantified with discrete and continuous characters, mathematical approximations of shape, and growth algorithms. Changes in morphological diversity through time have been interpreted in terms of radiation and extinction dynamics, the progressive canalization of development over evolutionary time, and the evolution of key innovations (Foote, 1997; Thomas and Reif, 1993). Studies of morphological diversity in plants provide insight into the dynamics of character evolution during the early history of vascular plants (Knoll et al., 1984), morphological and taxonomic diversification during the angiosperm radiation (Lupia, 1999), and the evolution of developmental processes (Boyce and Knoll, 2002).

A potential limitation of such empirical studies is that they are based exclusively upon the range of morphologies that have been known to exist, without addressing the possibility of functionally efficacious morphologies that, due to developmental constraints, trade-offs associated with fulfilling multiple functions, or purely stochastic processes, were never occupied in the natural world (Foote, 1997; Swan, 2001). Furthermore, though the relationship between morphological characteristics and functional attributes under different environmental conditions is a central concern of ecophysiological and many paleontological and paleoclimatological studies, the morphological limits of what is functionally possible are usually poorly understood. Functional evaluation of morphological diversity was part of a ground-breaking study in which randomly evolved branching patterns were selected for structural stability, ability to disperse propagules, and light interception for photosynthesis (Niklas, 1997). However, in that and other theoretical studies of plant function (Roth and Mosbrugger, 1996; Roth-Nebelsick et al., 2001), morphologies are still determined independently and then evaluated in terms of their intrinsic physiological properties.

Here is presented a different approach, in which shape is not predefined, but rather the result of functional constraints. The range of functionally permissible leaf morphologies is determined by construction of a functional design space (McGhee, 1999) over a range of reasonable values for several hydraulic variables. To understand the general implications of this type of analysis, it has been applied to linear, single-veined leaves, such as those of most conifers. However, most of the conclusions drawn from this exercise can be generalized to more morphologically complex leaves without their variable details distracting from these generalities.

Considered broadly across the fossil and extant record, linear leaves range from millimetres to up to 1 m in length and several centimetres in width. In their role as photosynthetic organs, leaves must be able to maintain sufficiently favourable water potential to allow stomata to open for CO₂ uptake (Farquhar and Sharkey, 1982). This can only be achieved if the water supply across the entire leaf blade is sufficient to balance transpiration. Because water is supplied to the leaf at essentially one point, but lost to the atmosphere across its entire surface, the hydraulic parameters that determine the rate of water supply throughout the lamina may constrain the size and shape of the leaf blade. The specific hydraulic parameters considered here are the transport capabilities of the vasculature (vein axial resistance), the leakiness of the vasculature to the mesophyll (vein radial resistance), the ability within the mesophyll to redistribute water (mesophyll resistance), and the resistance to water loss from the leaf (leaf surface resistance which includes stomatal and cuticular resistance). The sensitivity of cell expansion to water availability (Jones and Rawson, 1979; Jones, 1980; Boyer, 1985; Dale, 1988; Van Volkenburgh, 1999) provides a basic mechanism by which leaves could adjust the growth of their photosynthetic area in relation to their capacity to supply this same surface with water. Although the basic architecture of the leaf's vascular system may be determined by hormonal and various poorly understood genetic controls during the earliest stages of development, overall leaf shape and size is markedly influenced by patterns of water availability during the period of leaf expansion (Zwieniecki et al., 2004). The analysis performed here is based upon the same imposition of size and shape constraints by hydraulic limitations.

Construction of functional design space

The maximum leaf sizes and geometries that could be supported by a single centrally located vein were determined over a range of hydraulic parameters using an iterative model. By approximating the continuous pressure distribution across the leaf as a set of pressures at discrete, regularly spaced points in the grid, explicit finite element analysis was used to generate water potential distributions across the leaf for each set of hydraulic parameters and preset boundary conditions, i.e. water potential at the petiole and vapour pressure deficit at the leaf surface. If the calculated water potential in any part of the leaf falls below a threshold value [assumed to reflect minimum water potential needed to support stomatal opening (Kramer and Boyer, 1995; Fredeen and Sage, 1999)], then a portion of the current leaf area with the lowest potential was removed and a new water potential distribution was generated. Iterations were halted when the calculated water potential throughout the entire leaf was above the threshold value.

In the model, the leaf is described as a flat surface of uniform thickness represented by a two-dimensional matrix D:

where each element a_ij encodes the identity of a specific part of the leaf, i.e. vein or mesophyll. The two leaf tissue types were distinguished in terms of the hydraulic resistances between adjacent elements: (a) vein, with parameters of axial and radial hydraulic resistance; and (b) mesophyll, with the same hydraulic resistance value between all adjacent tissue elements (Fig. 1). Each element of the leaf, regardless of tissue type, is subject to water loss to the atmosphere through a surface resistance that represents the parallel pathways of water movement through the stomata and the cuticle. All model runs assume constant parameter values for each tissue type regardless of position within the leaf. The basic assumptions of the model are given in Table 1.

Fig. 1.

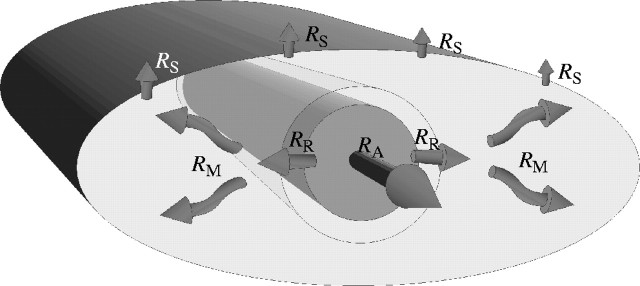
Schematic representation of the hydraulic parameters included in the model used to construct the design space of single-veined leaves. R_A = axial resistance of the vein; R_R = radial resistance of the vein (porosity or ‘leak’); R_M = mesophyll resistance (including both liquid and vapour flux); R_S = surface resistance (including both stomatal and cuticular resistance). The actual model is two dimensional, not three, but mesophyll tissue is shown above and below the vein in this schematic to acknowledge that the matrix elements that include the vein were allowed to transpire water at the same rate as exclusively mesophyll elements.

Table 1.

Basic model assumptions

Leaves are single-vein structures that can build tissue around the vein in a planar geometry.
Water potential must remain above set threshold for vein or mesophyll tissue to remain alive.
Water can enter the leaf only through the petiole. Pressure of water entering the leaf is held constant for all model runs.
Water can leave the system through any portion of the leaf in response to a constant evaporative demand.
Leaf hydraulic properties are described with four dimensionless parameters with realistic ratios:
Axial resistance of the vein RA
Radial resistance of the vein (porosity or leakage) RR
Resistance to water flow in the mesophyll RM
Surface resistance (stomatal and cuticular) RS
Overall leaf length and width are limited to 220 and 200 times the vein diameter. Vein length is limited to 200 times its diameter.

Flow is generated in the model by imposing evaporation on each element of the leaf grid at a rate prescribed as:

where T is transpiration, R_s is resistance of the leaf surface to diffusional water loss, and Δp is the vapour pressure deficit. Leaf to air vapour pressure deficit was held constant across all model runs. Water lost through evaporation must be replaced by flow from the petiole. The model calculates the water potential within each element of the leaf and the water fluxes between elements based on the hydraulic resistances (e.g. R_{i−1j → ij}) between elements of the matrix D. For a steady-state condition, it was assumed that there is no change in net volume of each element (a_ij) of matrix D, i.e. the sum of flows in and out from surrounding elements equals zero (J_{ij net} = 0). Each element of the leaf is allowed to exchange water only with the four adjacent (in-plane) elements and transpire water (out-of-plane) at a constant rate independent of the water potential in the leaf (Fig. 2).

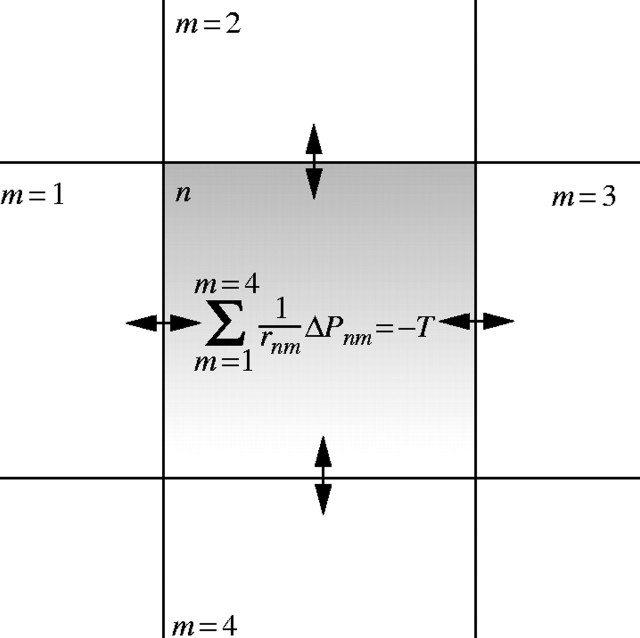
Fig. 2.

Representation of single mass flow equation from a single element of the matrix D. n = the element of interest; m = the four neighbouring elements with which exchange of water can occur; r_nm = hydraulic resistance between element n and m; ΔP_nm = hydrostatic pressure difference between element n and m; T = transpiration.

The general form of flow in/out of each element in matrix D is:

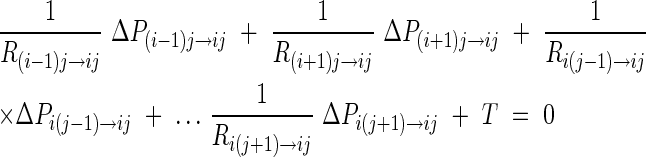The above equation can be rewritten as:

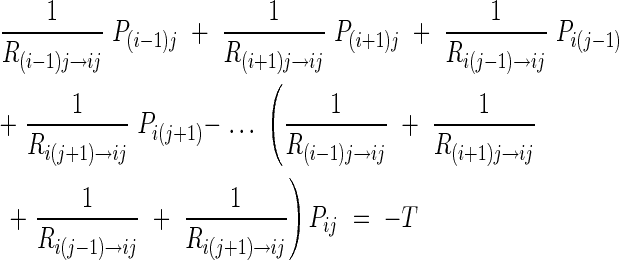allowing the creation of a complete set of simultaneous linear equations that can be used to determine the pressure in each element of matrix D. This set of simultaneous linear equations was then solved directly (using MatLab 5.0, MathWorks, MA, USA) with the creation of a coefficient matrix A based on the user-specified hydraulic resistances and a right-hand side vector b:

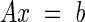where x is the vector of pressures in each element of the matrix D and b is the vector describing the exchange between elements and the atmosphere, which is here mathematically described as an out-of-plane sink.

After each calculation of the water potential distributions in matrix D, if there were elements of the matrix with potentials below the threshold value, then the elements which constituted the lowest 1 % of water potentials of all elements were eliminated from the leaf (mathematically equivalent to setting all of their hydraulic resistances to infinity). A new distribution of pressures was then calculated and the entire procedure repeated until all elements of matrix D were above the threshold value. Thus, the final size and shape of the leaf represents the maximum amount of tissue that can be hydraulically supported by a given set of hydraulic parameters.

In the model, the maximum size of the leaf was limited by the size of matrix D (220 × 200 elements) and vein length was limited to 0·9 length of the m dimension of matrix D. Resistance values for each hydraulic property span several orders of magnitude, which allows for the range of parameter ratios seen in living plants, including those reported for angiosperm leaves (Salleo et al., 2000; Sack et al., 2002). Hydraulic resistance ratios used in the model are shown in Table 2.

Table 2.

Resistances used in the calculations of the functional design space

RA axial	RR radial	RM mesophyll	RS surface
0·00001	0·001	0·001	1
0·0001	0·01	0·01	10
0·001	0·1	0·1	100
	1	1

In this model, transpiration is constant across the leaf surface, reflecting a single imposed vapour pressure deficit and a uniform surface resistance (R_s) that combines stomatal, epidermal and boundary layer resistance. The successive values here employed for R_s differ by an order of magnitude and thereby represent significant changes in surface properties that override the more subtle influences of boundary layer thickness that might result from changes to leaf size and shape. Similarly, the order of magnitude step sizes in other model parameters should guarantee that the relatively minor effects expected from the simplification of the leaf as a two-dimensional structure or the assumption of uniform hydraulic properties throughout the leaf will be overridden by any larger trends.

RESULTS

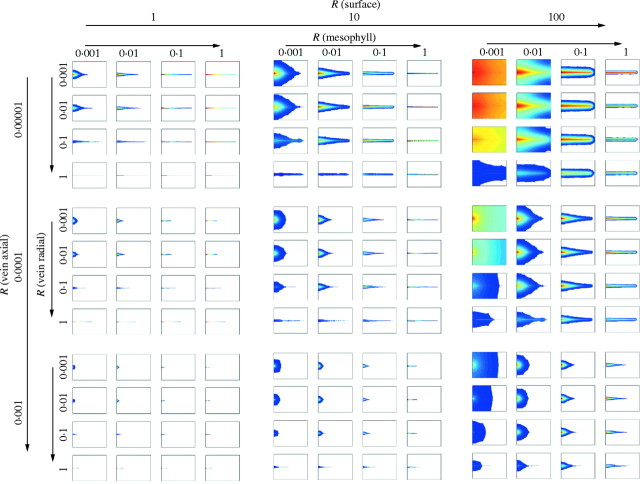
Several important observations derive from this exercise (Fig. 3). Despite a simple and invariant vascular architecture, modification of leaf hydraulic parameters results in a diverse set of morphologies encompassing all those found in plants with single-veined leaves. Rounded, scale-like structures are formed when hydraulic properties of the vein are similar to that of the mesophyll (effectively equivalent to the absence of a vein). Needle-like morphologies require very high ratios of radial to axial resistance in the vein, high ratios of mesophyll resistance to axial vein resistance, or both. However, these high radial resistances sometimes result in a ‘leaf’ with little or no tissue surrounding the vein. The formation of awl-like morphologies was more complicated, resulting from several alternative combinations of hydraulic parameters. The largest ratios of length to width found among fossil and extant plants are not produced here only because of the maximum vein length permitted in the model. The absence of some morphological details, such as the petiole constrictions of many conifers, reflects that the analysis only indicates the size and shape of the largest possible leaf under a particular set of hydraulic parameters; actual leaf shape will also be influenced by a variety of other developmental factors.

Fig. 3.

Functional design space of single-veined leaves created based on hydraulic properties of the vein, mesophyll and leaf epidermis. Colours reflect distribution of water potential in the leaf from 0 to −20 units with red reflecting values close to 0, yellow approx. −5, green approx. −10, light blue approx. −15, and dark blue −20.

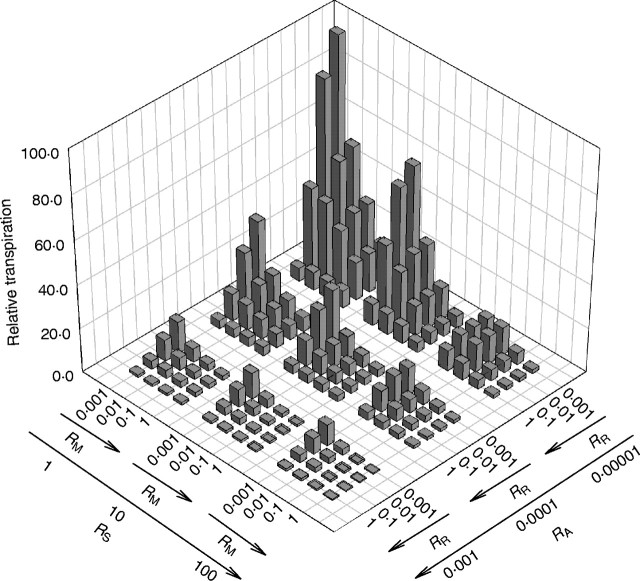
Contrary to the usual emphasis upon xylem and stomata in discussions of hydraulic function, changes in both radial vein resistance and mesophyll resistance appear to have more dramatic effects upon shape. Surface resistance has a more pronounced influence upon leaf size than leaf shape. This interaction between surface resistance and leaf size means that increases in leaf size are not necessarily associated with an increase in carbon gain. For example, a scale leaf that is able to support greater rates of water loss may have a higher total productivity than a much larger leaf that requires high surface resistances (Fig. 4).

Fig. 4.

Relative transpiration of each leaf hydraulic design. x and y axes correspond to Fig. 2.

DISCUSSION

All of the general classes of single-veined leaf morphologies (de Laubenfels, 1953) are represented in this hydraulic design space. Despite this overall correspondence, there are several important departures from the living world. First, many of the largest leaves predicted by the model are rarely seen in nature. This reflects the fact that these largest leaves require extremely low rates of water loss (high surface resistance) that would severely limit uptake and photosynthetic function. It is notable that these largest leaves resemble the fertile scales of a variety of groups including some conifers and fossil groups, which can function with the small water supply and low stomatal conductance necessary for these sizes since they perform little or no photosynthesis. Second, there is not a one-to-one correspondence between general classes of extant morphologies and clusters of similar morphologies in the morphospace. Needle morphologies require a combination of low axial resistance and high radial and mesophyll resistance, however awl-like leaves are produced by multiple discontinuous sets of character states.

In paleontology, particularly paleobotany, traditionally there has been a strong expectation of gradual, continuous morphological change through the course of evolution (Stidd, 1987). The analysis described here demonstrates that, though perhaps easy to present diagrammatically, these hypothetical, smoothly changing morphological transition states that are envisioned as examples of gradual evolution may be problematic due to the fact that small modifications to physiological parameters can result in large, abrupt changes in morphology. Continuous morphological change may require complicated changes to physiological parameters, such as tracheid number or diameters, whereas these physiological parameters may themselves vary continuously, due to their being more directly subject to hormonal and genetic control (Sachs, 1991; Stein, 1993). Therefore gradual evolutionary modification may better be considered in relation to gradual changes to development and physiology than in terms of gradual changes in overall morphology. It has been recognized that micromutations of genetic regulatory genes can result in large homeotic effects (Lewis, 1992). The present study suggests that large morphological shifts may also result from micromutations that cause minor ultrastructural changes, e.g. small changes to the size or density of tracheid wall pitting could result in substantial, discontinuous changes in leaf morphology.

The model descibed here suggests that radial resistance parameters, specifically vein leakiness and mesophyll hydraulic resistance, are the primary determinants of the range of possible leaf shapes, while the more obvious parameter of cuticular and stomatal resistance influences leaf size, but has no effect on shape. In the natural world, the common occurrence in single-veined leaves of a variety of relatively unusual anatomical features may be related to these parameters. It has been suggested that the endodermis surrounding conifer leaf veins plays a role in concentrating solutes (Canny, 1993), but it may also modify the radial resistance. Similarly the transfusion tissue found in many taxa (Hu and Yao, 1981) should drastically alter mesophyll resistances. Rather than suggesting aridity, resistance increasing superficial features, such as thick waxy layers, stomata only found in furrows, and a sclerotized hypodermis, may reflect necessities for permitting larger leaf sizes despite such limited venation.

A restricted range of morphologies is found in many conifer families, with the almost exclusive presence of scales in the Cupressaceae and longer, lanceolate to needle-like leaves in the Pinaceae, Taxaceae and Cephalotaxaceae. This might suggest that evolutionary transitions between morphologies may be limited, but Taxodiaceae and Araucariaceae/Podocarpaceae are more variable and range from scales to single-veined leaves 25 cm long and 3 cm wide in Podocarpus. A correlation between leaf width and shade tolerance in these morphologically flexible families may illustrate a responsiveness of leaf shape to evaporative demand (Brodribb and Hill, 1997). The intermediate, awl-shaped morphologies that can be achieved with a variety of opposing sets of resistance parameters are the first to appear in the fossil record of conifers (Carboniferous: de Laubenfels, 1953; Clement-Westeroff, 1988; Mapes and Rothwell, 1991), but needles up to 3 cm long in the Majoniaceae (Clement-Westeroff, 1987) and 8 cm long in the Ullmanniaceae were present by the Late Permian (Florin, 1944; reviewed in Taylor and Taylor, 1993). Scale leaves have been present among conifers throughout their preserved history, at least in association with reproductive structures, but may not have been vegetatively abundant until the Mesozoic Cheirolepidiaceae (Watson, 1988).

Linear leaf morphologies are also found in other seed plant lineages (such as fossil Ginkgoales and Czekanowskiales), as well as the sphenophytes, but nowhere is the range of morphologies more dramatic than in the lycopods. Lycopod microphylls typically exhibit scale to awl-shaped morphologies; however, Paleozoic arborescent lycopods possessed leaves 0·8 m (Lepidodendraceae) to 1·0 m (Sigillariaceae) long (Andrews and Murdy, 1958; Kosanke, 1979). The extreme stomatal arrangements found in these plants, with stomata only found sunken in two deep abaxial furrows flanking the vein (Reed, 1941), may have been necessary to achieve stomatal resistances high enough to allow single-veined leaves of such size, their swamp habitats notwithstanding.

It has been recognized that the longest leaves of the arborescent lycopods are found proximally on the plant (Chaloner and Meyer-Berthaud, 1983). This distal decline in leaf size has been linked to the size of the parent axis and the overall determinate architectures of these plants (Eggert, 1961); however, this may also reflect the increasingly negative water pressure associated with increased path length for water supply to the leaf as evidenced by recent studies (Koch et al., 2004; Woodruff et al., 2004). Changes in water supply to the leaf would have the same effect as changes to stomatal resistance for limiting leaf size. Such distal size shifts may be particularly pronounced in arborescent lycopods with limited wood production and unusually large leaves so close to the maximum possible sizes, but such hydraulics-induced size gradients may also be relevant to other lineages. Conifers often have different juvenile and adult morphologies (de Laubenfels, 1953) with the transition typically being from larger to smaller leaves. This may be largely due to other factors, such as establishment strategies and light availability to seedlings growing on a forest floor, but may also reflect changes in water availability as the path length of water transport to the leaf increases over the life of the plant. In many conifers, this transition from juvenile to adult foliage occurs while the individual is still quite small, suggesting control by factors other than hydraulics, but in other cases morphological transitions occur later in ontogeny or between the main axis and lateral branches, situations in which hydraulic limitations may be relevant.

Much of this discussion can readily be applied to leaves of more complex vascular architectures. The above discussion of lycopod leaf sizes is an extension of what has already been recognized in dicots concerning the effects of canopy placement on leaf size (Zwieniecki et al., 2004). Leaves with open dichotomous venation and marginal vein endings have either a uniform vein density with veins that follow parallel courses and remain roughly equidistant from their neighbours along their entire length (seen today in Ginkgo, broad leaved conifers, and some cycads), or they have a distally increasing vein density with veins that are widely spaced at their origins, but converge towards their marginal endings (seen today in many ferns). The vein densities resulting from such parallel and convergent vein patterns can be compared, respectively, to needle-like and triangular, awl-like morphologies in the current analysis. Parallel veins may therefore require a narrow range of high radial resistance values similar to those required of needles, whereas convergent venation may be possible under a broader range of resistance parameter values. In fact, parallel veined leaves often share many of the anatomical features common to conifer needles, such as transfusion tissue, an endodermis and a sclerotized hypodermis (Stopes, 1903; Hu and Yao, 1981). Multiple independent lineages that evolved laminate leaves during the Devonian and Carboniferous did so by first evolving parallel veins, a process linked to the evolution of underlying developmental mechanisms, and this was only later followed by the evolution of convergent venation (Boyce and Knoll, 2002). This divergent to convergent transition may equal an increase in developmental complexity that allowed for a more hydraulically permissible vascular architecture.