A Simple Method to Estimate Photosynthetic Radiation Use Efficiency of Canopies

Abstract

• Background and Aims Photosynthetic radiation use efficiency (PhRUE) over the course of a day has been shown to be constant for leaves throughout a general canopy where nitrogen content (and thus photosynthetic properties) of leaves is distributed in relation to the light gradient. It has been suggested that this daily PhRUE can be calculated simply from the photosynthetic properties of a leaf at the top of the canopy and from the PAR incident on the canopy, which can be obtained from weather‐station data. The objective of this study was to investigate whether this simple method allows estimation of PhRUE of different crops and with different daily incident PAR, and also during the growing season.

• Methods The PhRUE calculated with this simple method was compared with that calculated with a more detailed model, for different days in May, June and July in California, on almond (Prunus dulcis) and walnut (Juglans regia) trees. Daily net photosynthesis of 50 individual leaves was calculated as the daylight integral of the instantaneous photosynthesis. The latter was estimated for each leaf from its photosynthetic response to PAR and from the PAR incident on the leaf during the day.

• Key Results Daily photosynthesis of individual leaves of both species was linearly related to the daily PAR incident on the leaves (which implies constant PhRUE throughout the canopy), but the slope (i.e. the PhRUE) differed between the species, over the growing season due to changes in photosynthetic properties of the leaves, and with differences in daily incident PAR. When PhRUE was estimated from the photosynthetic light response curve of a leaf at the top of the canopy and from the incident radiation above the canopy, obtained from weather‐station data, the values were within 5 % of those calculated with the more detailed model, except in five out of 34 cases.

• Conclusions The simple method of estimating PhRUE is valuable as it simplifies calculation of canopy photosynthesis to a multiplication between the PAR intercepted by the canopy, which can be obtained with remote sensing, and the PhRUE calculated from incident PAR, obtained from standard weather‐station data, and from the photosynthetic properties of leaves at the top of the canopy. The latter properties are the sole crop parameters needed. While being simple, this method describes the differences in PhRUE related to crop, season, nutrient status and daily incident PAR.

INTRODUCTION

Net primary production has often been found to be linearly related to the photosynthetically active radiation (PAR) absorbed or intercepted by crops (Monteith, 1972; 1977). The slope of this relationship is the radiation use efficiency (RUE), and has been used to model plant growth, especially in crops where growth is not limited by water or nutrient shortage, or by other adverse climatic conditions that may decrease RUE (Stockle and Kiniry, 1990; Runyon et al., 1994; Ruimy et al., 1995). RUE differs between crops (Sivakumar and Virmani, 1984; Gosse et al., 1986; Prince, 1991), with plant nitrogen status (Green, 1987; Muchow and Davis, 1988; Sinclair and Horie, 1989) and with phase of the crop cycle (e.g. vegetative versus reproductive growth) among other factors (Trapani et al., 1992).

Linearity has also been found between net CO₂ assimilation of canopies, integrated over one day (‘daily’ assimilation), and daily absorbed or intercepted PAR, implying constant photosynthetic RUE (PhRUE) on a daily basis as reviewed by Sinclair (1991), Ruimy et al. (1995) and by Sinclair and Muchow (1999). However, instantaneous (i.e. hour or minute) canopy photosynthesis tends to saturate at high PAR, and instantaneous PhRUE varies with time of the day (Grace et al., 1995; Ruimy et al., 1995).

Theoretical studies predict that nitrogen content (and thus photosynthetic properties) of leaves is distributed in a canopy in relation to the light gradient in such a way that daily canopy photosynthesis is optimized in relation to light (Hirose and Werger, 1987); there is then a linear relationship between daily canopy photosynthesis and intercepted PAR (De Witt 1965; Charles‐Edwards, 1982; Kull and Jarvis, 1995). Haxeltine and Prentice (1996) and Dewar and co‐workers (Dewar, 1996; Dewar et al., 1998) have mathematically simulated this linearity. Their results imply that all leaves in a canopy have constant PhRUE over 1 d (daily PhRUE), independent of their canopy position and PAR exposure.

In these simulations, the PAR incident on the leaves was estimated with a modelling approach, which averaged light in space and/or time, and assumed optimal N allocation in the canopy based on the modelled PAR. Real leaves, however, can be sunlit or shaded and thus are exposed to a pattern of PAR which is more variable than predicted by such models. Patterns of PAR with time also change from day to day, due to weather conditions. These variations occur on a time scale which is too rapid for the acclimation of leaf photosynthetic capacity (De Pury and Farquhar, 1999). Further, averaging of PAR, whether in space or in time, leads to overestimation of photosynthesis (Sinclair et al., 1976; Spitters, 1986). Nonetheless, when daily photosynthesis of leaves was calculated using incident PAR measured in the field and measured photosynthetic properties of individual leaves in place of modelled values, Rosati and DeJong (2003) found that daily PhRUE was constant among leaves. Constant daily PhRUE resulted from the integration over the day of instantaneous PhRUE values, which varied with incident PAR.

Rosati and DeJong (2003) suggested that if all leaves have the same daily PhRUE, then the whole canopy has the same PhRUE and this can be represented by the PhRUE of a leaf at the very top of the canopy, which is exposed to above‐canopy incident PAR. Thus, calculations of daily PhRUE and modeling of canopy photosynthesis could be done simply from the photosynthetic properties of leaves at the top of the canopy and from the PAR data available from weather stations. However, weather‐station data are commonly available as hourly averages and not as minute‐by‐minute data used by the above authors. Whether averaging light data every hour results in correct estimation of PhRUE was not investigated by Rosati and DeJong (2003). In that study, due to equipment limitation, the light incident on individual leaves was measured over the course of several days in July and August and daily PhRUE was calculated for pooled data. This did not allow changes of daily PhRUE over the season, or in response to variations in day‐to‐day incident PAR to be modelled. Further, the above authors presented data only for one annual crop, aubergine. Other crops may have different patterns of incident light on individual leaves, which may not necessarily result in a linear relationship between daily photosynthesis and incident light.

The objective of this study was to validate the simple method of estimating daily PhRUE of leaves and canopies proposed by Rosati and DeJong (2003), on species with very different leaf size and canopy architecture: for this purpose the trees almond (Prunus dulcis), with small, narrow leaves and walnut (Juglans regia), with large and broad leaves, were chosen because of their canopy architecture compared with aubergine used by Rosati and DeJong (2003), which is an annual, herbaceous crop. In particular, we tested whether this simple method was sensitive to variations in daily PhRUE with changes in incident PAR from day to day, due to weather conditions and over the season.

Materials and methods

Plant material

The experiment was carried out in orchards of 8‐year‐old almond (Prunus dulcis (Mill) D.A. Webb ‘Nonpareil’) and 13‐year‐old walnut (Juglans regia L. ‘Tulare’) trees in Dixon, CA, USA. Tree spacing was 6 × 7 m for almond and 4·7 × 7·3 m for walnuts. Almonds were trained to an open vase while walnuts were mechanically hedged on alternate rows up to 2 and 3 years prior to the experiment (depending on the side of the row), but were not hedged the year before the experiment. The crops received routine horticultural care suitable for commercial production including fertilization, irrigation, weed and pest control, etc. Tree water status was monitored periodically to assure that they were not water stressed.

PAR measurements

Photosynthetically active radiation (PAR) incident during one day on individual selected leaves in the crop canopies was monitored with GaAsP photosensors (Hamamatsu, Japan), placed on the leaf adaxial surface (so that they were parallel to the leaf lamina). The lightweight (0·1 g) photosensors were connected by thin wires and kept in place by a narrow strip of surgical tape, placed across the wires just below the photosensors. This allowed them to move with the leaves if necessary, without influencing their natural position. The photosensors were previously calibrated with a quantum sensor (LI‐190; LI‐COR Inc., Lincoln, NE, USA). Data were logged every 60 s from 0500 to 2100 h with a battery‐operated datalogger (DL2e; Delta‐T Devices Ltd, Cambridge, UK). Measurements were made on days in May, June and July 2003, on about 50 leaves at a time.

Single leaf gas exchange and modelling of photosynthesis and PhRUE

Gas exchange was measured with a portable computerized open‐system IRGA (LI‐6400; LI‐COR Inc.). A cool light source (6400–02 LED) under software control was mounted on the leaf chamber as the source of variable light. All measurements were taken between 0900 and 1400 h. During this time, light‐saturated photosynthesis of leaves at the top of the canopy was relatively constant (i.e. it never varied by more than 2 µmol CO₂ m^–2 s^–1).

Instantaneous light‐saturated net photosynthesis (A_max) was measured on all selected (i.e. 50) leaves the day after the last day of PAR measurements for each period (i.e. once in May, once in June and once in July). It was assumed that leaf photosynthetic properties did not change during the few days of measurements within each period. In addition to A_max, the response of net photosynthesis to PAR was measured on six leaves ranging from the inner to the outer canopy. Leaves were exposed to high PAR (2000 µmol m^–2 s^–1) until photosynthesis was constant, then PAR was decreased in steps down to zero (2000, 1500, 1000, 500, 250, 100, 50, 25, 0 µmol m^–2 s^–1). The rate of CO₂ emission at zero PAR was assumed to be the dark respiration rate (R_d) of the leaf. From these data, a linear regression between R_d and A_max was calculated, separately for each period. The values for the curvature and the apparent quantum yield that best fitted all curves (non‐rectangular hyperbola: Thornley, 1976) were also determined by changing the parameters in steps of 0·05 (no dimension) and 0·005 (mol mol^–1), respectively, until the model fit the data. The values thus determined did not differ for the three periods, nor between the two species and were 0·8 (no dimension) and 0·05 (mol mol^–1), respectively.

The net photosynthetic response curve to PAR was then calculated with the Thornley (1976) model for each sampled leaf, using the measured A_max of the leaf, R_d estimated from its A_max and the curvature factor and apparent quantum yield that best fitted the measured curves. The photosynthetic response curves were then used with the measured incident PAR data of the corresponding leaf to estimate the instantaneous leaf photosynthesis. PAR data were not averaged in space or in time, but rather each single value of PAR (one every 60 s) was used to estimate the corresponding photosynthesis. Daily photosynthesis was then calculated as the integral (i.e. from 0500 to 2000 h) of the instantaneous values and was plotted against the PAR incident on the leaf, integrated over the same period (daily incident PAR). Daily PhRUE was then calculated as the slope of the linear regression with zero intercept between the two variables.

Hourly photosynthesis was obtained similarly for a subset of data (20 June), but in this case the instantaneous values of photosynthesis were integrated over each hour, rather than over the whole day, and plotted against the hourly PAR incident on the leaf.

Modelling of PhRUE with the simple method

To calculate daily PhRUE with the simple method proposed by Rosati and DeJong (2003), we assumed that if all leaves (and thus the whole canopy) have the same daily PhRUE, then a hypothetical leaf, placed at the very top of the canopy and thus exposed to the above‐canopy incident PAR, should also have similar daily PhRUE. A_max of this leaf would equal that of the leaves at the top of the canopy, which have the highest A_max in the canopy. Thus, we estimated the photosynthesis of this hypothetical leaf as for the actual leaves, but used a photosynthetic response curve based on the average A_max of the three leaves with the highest A_max of each period (i.e. leaves at the top of the canopy), using the PAR incident above the canopy (instead of PAR incident on an actual leaf). The PAR incident above the canopy was obtained from the CIMIS (California Irrigation Management Information System) data for the ‘Davis’ station (no. 6) which was located about 15 km away from the experimental site. CIMIS data (hourly averages) for incident global radiation (W m^–2) were converted into PAR (µmol m^–2 s^–1) based on a regression between global radiation data and our own measurements of incident PAR above the canopy, taken with a quantum sensor (LI‐190; LI‐COR Inc.) during 25 sample days in July and August. This regression had a very high coefficient of determination (r² = 0·98). The daily PhRUE of the hypothetical leaf (PhRUE_HL) was calculated as the ratio between its daily photosynthesis and the daily PAR incident above the canopy (i.e. weather‐station data), used to calculate the daily photosynthesis. This ratio (i.e. PhRUE_HL), which corresponds to the slope of a linear fit with zero intercept between daily photosynthesis and daily incident PAR, was compared with the daily PhRUE calculated with data from the 50 individual leaves (PhRUE_50L) for the same day. PhRUE_HL was calculated not only for the same days, when the PAR incident on individual leaves was measured, but also for each day in between these dates.

Results

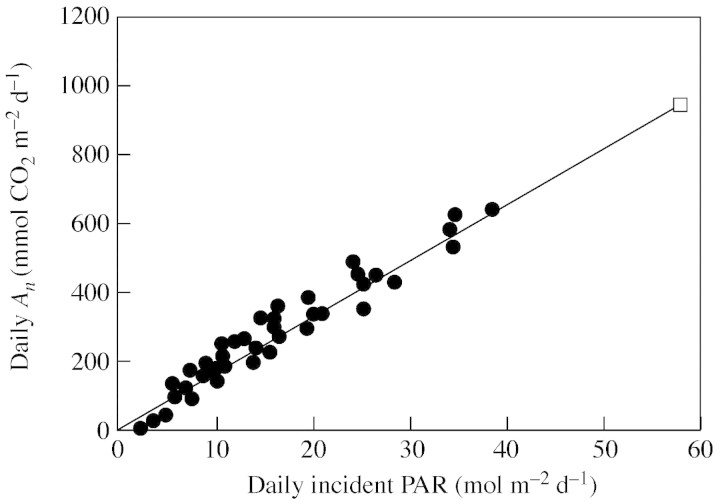
The net photosynthesis of individual leaves, integrated over 1 d (daily photosynthesis) was linearly related (average r² = 0·88; P < 0·001 for all regressions; r² range 0·73–0·97) to daily PAR incident on the leaves and the slope of these relationships (i.e. the PhRUE_50L) was within 5 % of the PhRUE calculated with the simple method (PhRUE_HL) except in five out of 34 cases. An example of this regression (data for almond on 20 June) is shown in Fig. 1 while all datasets are shown in Fig. 2, where the slopes obtained with both the 50 actual leaves (PhRUE_50L) and with hypothetical leaf (PhRUE_HL) are compared.

Fig. 1. Relationship between net CO₂ assimilation integrated over a day (daily A_n) and daily incident PAR of individual leaves (circles) and for a hypothetical leaf at the top of the canopy (open square). Data are for almond on 20 June 2003. The regression shown is for the hypothetical leaf: y = 17·2x. Comparison between slopes (PhRUE) for the hypothetical leaf and for individual leaves and relative statistics are shown in Fig. 2.

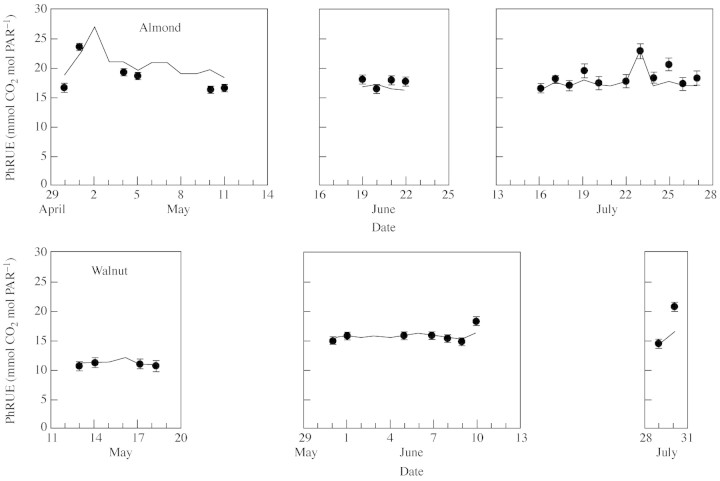
Fig. 2. Seasonal pattern of the slope (PhRUE) of the relationship between net CO₂ assimilation and incident PAR, both integrated over a day, for individual leaves of almond and walnut. The slopes were calculated both with data on all sampled leaves (PhRUE_50L, circles) and for a hypothetical leaf at the top of the canopy (PhRUE_HL, solid line). Bars indicate the 95% confidence limits of the slopes (i.e. PhRUE_50L).

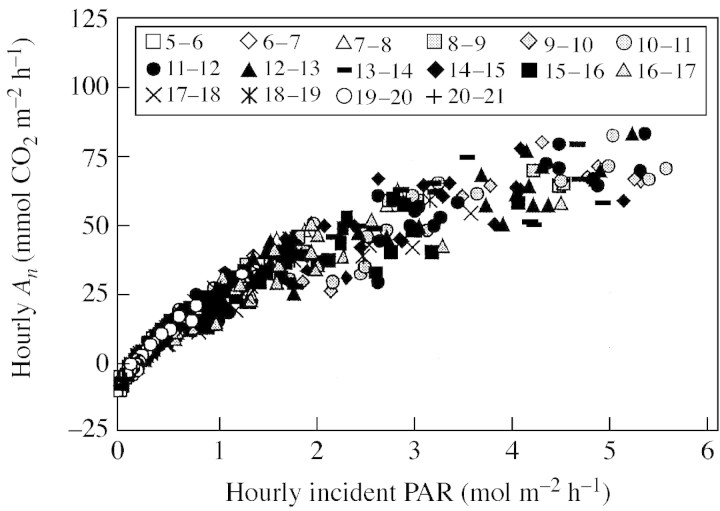
When hourly data of PAR and photosynthesis were used, the regressions were curvilinear (data for almond on 20 June, Fig. 3), showing that linearity (i.e. constant PhRUE) occurred only over a time scale greater than 1 h.

Fig. 3. Relationship between net CO₂ assimilation integrated over 1 h (hourly A_n) and hourly incident PAR of individual leaves, for the same data shown in Fig. 1 (almond on 20 June 2003). Data for each hour (i.e. 0600–0700 . . . 1900–2000 h) are plotted using different symbols. The regression (not shown for clarity of graphs) had a significant quadratic component (P < 0·001).

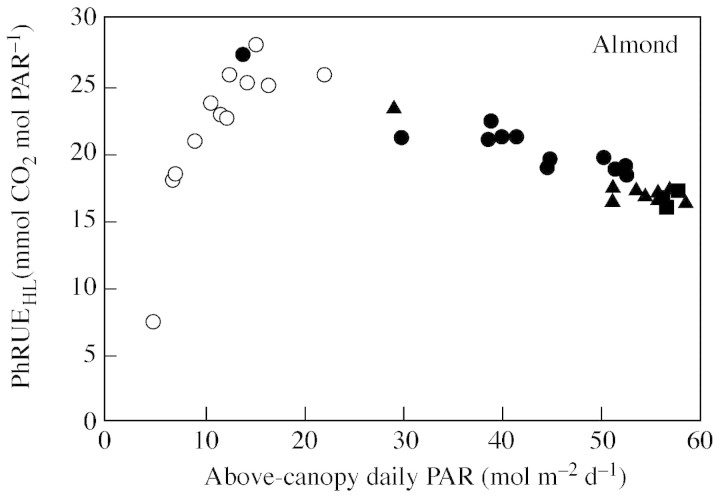
In walnut, PhRUE (both PhRUE_50L and PhRUE_HL) increased from about 11 mmol CO₂ mol PAR^–1 in May, to about 15 mmol CO₂ mol PAR^–1 in June and July (except on 30 July which was overcast, when PhRUE was higher; Fig. 2). This increase was associated with an increase in A_max from about 15 µmol CO₂ m^–2 s^–1 in May, to 24 and 21 µmol CO₂ m^–2 s^–1 in June and July, respectively. In almond, there were no obvious seasonal changes in PhRUE, and A_max also varied little (about 30 µmol CO₂ m^–2 s^–1 in May and 25 µmol CO₂ m^–2 s^–1 in June and July). In both crops, PhRUE was not constant within each period of measurement, but fluctuated from day to day, especially in the almond experiment where more overcast days occurred. The PhRUE_HL simulated the PhRUE_50L closely, often being within the 95 % confidence limits of the latter. These day‐to‐day variations of PhRUE were related to weather conditions (i.e. daily radiation) and a negative linear relationship was found between PhRUE_HL and the daily incident PAR above the canopy (Fig. 4). In almond this relationship was similar for all data sets, while in walnut the relationship was different for each period of measurement.

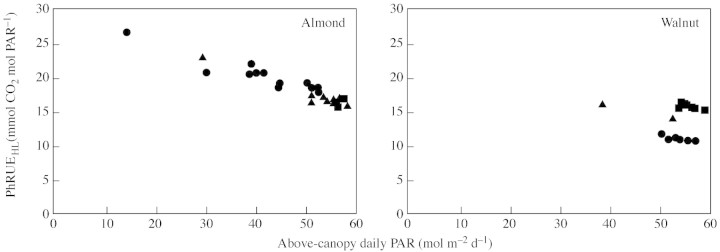
Fig. 4. Relationship between the PhRUE calculated with the simple method (PhRUE_HL) and the daily incident PAR above the canopy for almond and walnut. Data for each period (May, circles; June, squares and July, triangles) are plotted. A fit to all data for almond gave the following equation: y = –23x + 30, r²=0·91, P < 0·001. Fits for walnut data were not calculated since the range of the x values was too limited.

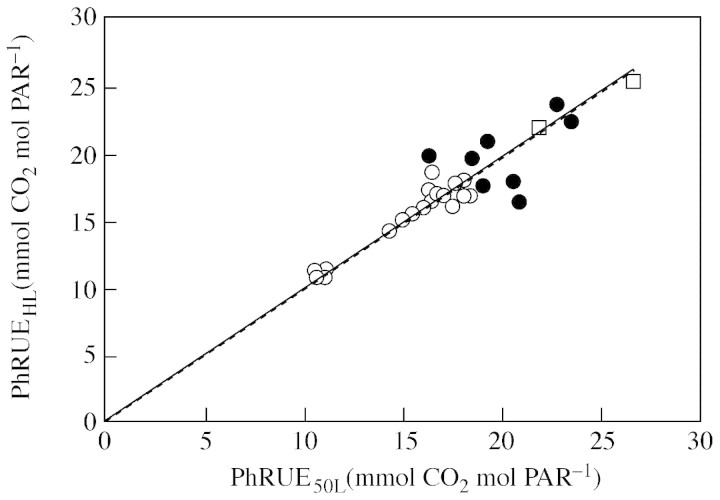
Plotting PhRUE_HL against PhRUE_50L for all datasets, including data on aubergine from Rosati and DeJong (2003) resulted in a linear regression with slope close to 1 (Fig. 5). Omitting data for overcast days improved the fit (r² increased from 0·81 to 0·91) but did not change the slope (0·982 for all data and 0·989 for clear days only).

Fig. 5. Relationship between the PhRUE calculated with the simple method (PhRUE_HL) and that calculated with data on actual leaves (PhRUE_50L). The dotted line (barely visible because it overlaps with the solid line) is a linear fit with zero intercept to all data on almond and walnut, including data for clear days (open circles), overcast days (closed circles) and data on aubergine (open squares) from Rosati and DeJong (2003). The solid line is a linear fit with zero intercept to all data except data on overcast days. The equation parameters are: y = 0·982x, r² = 0·81, P < 0·001 for all data and y = 0·989x, r² = 0·91, P < 0·001 for clear days only (including aubergine data).

Discussion

Validation of the simple method to estimate PhRUE

Rosati and DeJong (2003) proposed a simple method of estimating daily PhRUE of leaves and canopy from the photosynthetic properties of leaves at the top of the canopy and from the PAR incident above the canopy. This method is based on the assumption that all leaves in a canopy have the same PhRUE over a day, which was found to be the case in aubergine when incident PAR measured in the field together with the photosynthetic properties of individual leaves were used to calculate PhRUE. The present data show that PhRUE was also constant within canopies of walnut and almond trees (i.e. linear relationship with zero intercept between daily photosynthesis and daily incident PAR of individual leaves, Figs 1 and 2), despite their different canopy architecture and leaf size compared with aubergine. Thus, constant PhRUE within the canopy appears to be a widespread phenomenon. This is true only for daily integrated data since hourly data yield a curvilinear relationship between photosynthesis and incident PAR (Fig. 3), confirming previous findings (Rosati and DeJong 2003) that constant daily PhRUE results from integration of variable instantaneous PhRUE over the day. Detailed discussion on the mathematical aspects of this integration was reported in Rosati and DeJong (2003).

Another assumption of the proposed simple method to estimate PhRUE is that a hypothetical leaf, placed at the top of the canopy and thus exposed to above‐canopy incident PAR, would have the same PhRUE as all other leaves. While Rosati and DeJong (2003) have found this to be true for aubergine, they did not use PAR data from a weather station, but used their own minute‐by‐minute incident PAR measured above the canopy. Since averaging of light results in overestimation of photosynthesis and PhRUE, using weather station data (which is averaged hourly), might not allow for correct estimation of PhRUE. Our results, however, suggest that using weather station data produces accurate estimates of PhRUE with the simple method, as PhRUE_HL was very similar to PhRUE_50L (Figs 1, 2 and 5). This is probably because, being exposed to the above‐canopy PAR, the hypothetical leaf (as well as real leaves at top of the canopy) does not experience alternating sun and shade as in the case of leaves inside the canopy. Thus, hourly averaging of the above‐canopy light results in a daily pattern of incident PAR on the hypothetical leaf which is similar to the minute‐by‐minute (i.e. actual) data.

The slope of the relationship between PhRUE_HL and PhRUE_50L did not change when including the few overcast days, and remained very close to 1 (Fig. 5). This suggests that the simple method predicted PhRUE accurately for overcast days as well as clear ones. This was probably due to the fact that during overcast days, incident radiation did not change rapidly between clear and overcast, but rather slowly, so that hourly averages did not differ substantially from actual data. If overcast and sunny conditions were to alternate frequently (i.e. several times in an hour), averaging above‐canopy PAR hourly might overestimate photosynthesis and PhRUE.

Although the slope of the relationship between PhRUE_HL and PhRUE_50L did not change when including overcast days, the coefficient of determination did decrease, showing that the simple method was less accurate for overcast days (Fig. 5). The reason for this was probably the distance between the weather station and the experiment location (about 15 km). While total incident PAR varies very little between nearby locations during clear days, during overcast and especially partially overcast days, it can vary considerably. This is particularly true in our experimental site where clouds move in from the San Francisco Bay and dissipate in the Central Valley creating very different cloud cover between the relatively close locations. Given the strong relationship between daily PAR and PhRUE (Fig. 4), the need for accurate (i.e. local) PAR data for correct estimation of PhRUE is obvious.

Variations in PhRUE with daily incident PAR and over the season

Rosati and DeJong (2003) found that PhRUE did not change significantly between an overcast and a subsequent clear day. Those data appear to contrast with data in the literature, as well as with the results given here, which suggest that PhRUE (and RUE in general) increases when the daily incident PAR is small and there is a large fraction of diffuse light (De Witt, 1965; Horie and Sakuratani, 1985; Stirling et al. 1990; Norman and Arkebauer, 1991; Sinclair et al., 1992; Hammer and Wright, 1994; Bange et al., 1997). To study the reasons for this apparent contrast, we plotted PhRUE_HL against daily incident PAR, as in Fig. 4 (i.e. almond dataset), but included data for the most heavily overcast days we could find in the weather‐station datasets. Since there were only few and not heavily overcast days for the ‘Davis’ station, we included data for the most overcast days recorded for the ‘Oakland Foothills’ station (no. 149) in March and April (Fig. 6). The results show that with decreasing incident PAR, PhRUE_HL increases but then reaches a point at which PhRUE decreases rapidly. This relationship resembles closely the instantaneous PhRUE of a leaf, calculated as the ratio between instantaneous photosynthetic response to PAR and PAR, which was described by Hirose and Bazzaz (1998). These authors showed that at high PAR, instantaneous PhRUE decreases due to saturation while at low PAR it decreases due to the negative intercept of net photosynthesis at zero PAR. Instantaneous PhRUE is zero when PAR is at the compensation point. Our results (Fig. 6) represent daily integration of PAR and PhRUE rather than instantaneous values. This brings about some variability of daily PhRUE for a given daily PAR because the latter can be obtained with different combinations of PAR intensity and duration, which would slightly affect PhRUE. For instance, since days in April are shorter than in June, the same daily PAR must be achieved with brighter days in April, resulting in greater saturation of photosynthesis and lower PhRUE. Data shown in Fig. 6 explain why the daily PhRUE found in aubergine for an overcast day was similar, instead of greater, than for clear days: the overcast day used by Rosati and DeJong (2003) was a heavily overcast one (i.e. below 10 mol m^–2 d^–1) and at such low daily PAR, PhRUE tends to be small and can reach values similar to those obtained with clear days.

Fig. 6. Relationship between the PhRUE calculated with the simple method (PhRUE_HL) and the daily incident PAR above the canopy as in Fig. 4 (almond data only), but including the PhRUE_HL calculated for more heavily overcast days (open circles). For these days, the PhRUE_HL was calculated using the same A_max (29·9 µmol CO₂ m^–2 s^–1) for the hypothetical leaf, as used in May.

RUE‐based models have often considered RUE to decrease linearly with daily PAR. Our data (Fig. 6) show that at very low daily PAR this assumption leads to overestimation of PhRUE.

The variability of PhRUE with daily incident PAR agrees with model simulations of Haxeltine and Prentice (1996) and Dewar and co‐workers (Dewar, 1996; Dewar et al., 1998) which have often been misinterpreted in the literature as implying a linear relationship between canopy photosynthesis and incident PAR and thus constant PhRUE at any daily PAR. More correctly, their results imply that once the photosynthetic properties of leaves have adjusted to a given (and constant) daily pattern of PAR, then their daily PhRUE is constant (i.e. linear relationship between daily photosynthesis and daily light incident on individual leaves within a canopy). However, if daily light above the canopy changes faster than the leaf photosynthetic properties can be readjusted (e.g. two sequential days with different daily PAR), then the photosynthesis of a leaf responds curvilinearly to light. This results in a curvilinear response of canopy photosynthesis to incident PAR, though this is less curvilinear than for an individual leaf, and thus there is variation in canopy PhRUE as shown in Fig. 6. Our data suggest that with day‐to‐day changes in incident PAR, the slope (i.e. PhRUE) of the relationship between photosynthesis of, and light incident on, individual leaves changes, but the regression remains linear, allowing the calculation of PhRUE with the simple method proposed.

The RUE based on biomass varies during the season for a given crop (Trapani et al., 1992). This variability has been ascribed to both the different metabolic cost of the organic matter produced in different periods of the crop cycle and to different photosynthetic properties of the canopy. Our results are based on gas exchange data and therefore cannot be compared with biomass data. However, both PhRUE_50L and PhRUE_HL reflected changes in the photosynthetic properties of the canopy measured in the field. These changes are obvious in Figs 2 and 4 (walnut dataset) where PhRUE appeared lower in May, due to the lower A_max (about 15 µmol CO₂ m^–2 d^–1 compared with 24 in June and 21 in July). The lower A_max in May was related to the emergence of walnut leaves: none were fully expanded and their photosynthetic properties were different to those of mature laves. For almond, there were no seasonal changes in PhRUE. The occasionally higher values in May (Fig. 2) were related to the occurrence of overcast days (Fig. 4) rather than to changes in the photosynthetic properties, which did not alter as much between periods as they did in walnut. In fact, emergence in almond leaves occurred much earlier than in walnut and they were already mature and fully expanded in May. The slight decrease in A_max from May (30 µmol CO₂ m^–2 d^–1) to June and July (25 µmol CO₂ m^–2 d^–1), which tends to decrease PhRUE, was probably compensated by longer days in June and July, which tend to increase PhRUE for a given daily PAR, as explained earlier. Thus, although extremely simple, the proposed method of estimating PhRUE responds to changes in PhRUE with crop, daily light condition and with season, provided that the right incident PAR and seasonal photosynthetic properties of leaves at the top of the canopy are used as inputs in the calculations.

Final considerations

Since Monteith’s (1972, 1977) statement that RUE can be considered approximately constant, this parameter has been shown to vary with crop, season, nutrient (particularly nitrogen) status, daily incident PAR and percent of diffuse radiation. Our simple method to estimate daily PhRUE responds to all the above factors affecting PhRUE and is based on two easily collectable inputs: (1) photosynthetic properties of leaves at the top of the canopy, which reflect crop, season and nutrient status, and (2) daily pattern of incident light. We have shown that this simple method is accurate, producing estimates close to the values of PhRUE estimated with a more detailed model. This simplified method is attractive since it reduces calculation of canopy photosynthesis to a multiplication between the PAR intercepted by the canopy, which can be remotely sensed (Kumar and Monteith, 1981; Daughtry et al., 1983) and the PhRUE calculated using incident PAR from weather stations. The canopy photosynthesis can thus be calculated for each day, or for periods greater than a day, using average values of PhRUE calculated on representative days. The photosynthetic properties of leaves at the top of the canopy, which can often be derived from the literature, are the sole crop parameters needed.

While these characteristics allow for a simple method of estimating PhRUE and canopy photosynthesis, it may be worth noting that this approach has the limitations of all other models of this type, i.e. it is based on the leaf photosynthetic response to incident PAR and assuming no variation of these properties with temperature, water or other environmental stresses. Thus, these models are more accurate for cultivated crops where water and nutrients are supplied and incident PAR represents the main determinant of photosynthesis. However, there is evidence that on a canopy scale the effects of environmental constraints (e.g. temperature, VPD, etc.) are small, due to feedback mechanisms that develop within the canopy (McNaughton and Jarvis, 1991). Further, the environmental constraints that affect photosynthetic properties on a time‐scale longer than 1 d, may be easily included in our simple method by changing the hypothetical leaf properties in response to the stress. For example, Rosati and DeJong (2003) found that the simple method predicted the changes in PhRUE associated with N deficiency in aubergine. Comparison of PhRUE estimated with our approach and that measured by whole‐canopy gas exchange and whole‐canopy PAR interception in the field is desirable.

Received: 23 September 2003; Returned for revision: 6 November 2003; Accepted: 22 January 2004 Published electronically: 24 March 2004