Simulation of the Stomatal Conductance of Winter Wheat in Response to Light, Temperature and CO₂ Changes

Abstract

• Background and Aims The stomata are a key channel of the water cycle in ecosystems, and are constrained by both physiological and environmental elements. The aim of this study was to parameterize stomatal conductance by extending a previous empirical model and a revised Ball–Berry model.

• Methods Light and CO₂ responses of stomatal conductance and photosynthesis of winter wheat in the North China Plain were investigated under ambient and free‐air CO₂ enrichment conditions. The photosynthetic photon flux density and CO₂ concentration ranged from 0 to 2000 µmol m^–2 s^–1 and from 0 to 1400 µmol mol^–1, respectively. The model was validated with data from a light, temperature and CO₂ response experiment.

• Key Results By using previously published hyperbolic equations of photosynthetic responses to light and CO₂, the number of parameters in the model was reduced. These response curves were observed diurnally with large variations of temperature and vapour pressure deficit. The model interpreted stomatal response under wide variations in environmental factors.

• Conclusions Most of the model parameters, such as initial photon efficiency and maximum photosynthetic rate (P_max), have physiological meanings. The model can be expanded to include influences of other physiological elements, such as leaf ageing and nutrient conditions, especially leaf nitrogen content.

INTRODUCTION

Leaf stomata control plant CO₂ absorption through photosynthesis and water loss through transpiration. Their aperture regulates water use efficiency of crops and energy partitioning into sensible and latent heat. Therefore, parameterization of stomatal conductance is essential in the simulation of crop productivity and water‐use efficiency in agricultural ecosystems. As stomatal aperture is a balance between CO₂ assimilation and water loss, its conductance is related to photosynthesis and transpiration (Cowan, 1965). Stomatal opening affects photosynthesis by regulating intercellular CO₂ concentration, and thereby the biochemical processes in chloroplasts (Yu et al., 2001). The extent of stomatal opening is jointly determined by light intensity and water balance of the guard cells. Light intensity affects photosynthesis rate through light receptors which drive CO₂ fixation and lower intercellular CO₂ concentration, and the guard cells are conditioned jointly by the water balance of the bulk leaf tissue and the CO₂ concentration in the substomatal cavity.

In the simulation of stomatal conductance, the Jarvis model (Jarvis, 1976) has been applied widely to studies of evapotranspiration, land surface processes and the biogeochemical cycle (e.g. McMurtrie, 1992; Hanan and Prince, 1997; Cox et al., 1998). The model is a typical empirical one, which is characterized by multiplying by a series of correction coefficients each of which represents a factor. It does not include physiological feedbacks from changes in rates of photosynthesis and transpiration due to stomatal movements. A semi‐empirical model, the Ball–Berry model (Ball et al., 1987), has a solid experimental basis with a linear relationship between photosynthesis and stomatal conductance. But to take account of the feedback interaction between photosynthetic rate and stomatal conductance requires iteration of calculations. In this study, a hybrid stomatal model is proposed, based partly on those empirical and semi‐empirical models, which gives a direct calculation of stomatal conductance from solar radiation, temperature, humidity, CO₂ concentration of air, and soil water potential, but has physiological relationships similar to the Ball–Berry model.

The objective of this study was to construct a Jarvis‐type stomatal model with physiological relationships based on the Ball–Berry model, so as to enable the model to calculate the conductance directly from environmental variables, whilst maintaining a relevant physiological basis.

MATERIALS AND METHODS

Experiments were conducted at the Yucheng Comprehesive Experiment Station (36°57′N, 116°36′E, 28 m a.s.l.), Chinese Academy of Sciences, which is located in the North China Plain. The light and CO₂ responses of photosynthesis, transpiration, and stomatal conductance of winter wheat were measured in the field. The light and CO₂ response curves were measured in a leaf chamber. Each measurement was made over a short period. Flag leaves were used for all measurements, which were conducted at the bearing stage (from 16 April to 6 May 2003). Every 2 h over the course of a day, light and CO₂ response curves were generated by varying light (400–700 nm) intensity between 0 and 2000 µmol m^–2 s^–1, and CO₂ concentrations between 0 and 1400 µmol mol^–1. Thus, environmental conditions varied greatly in light, temperature and CO₂ concentration.

The infrared CO₂ analysis system LI‐COR 6400 (LI‐COR Inc., Lincoln, NE, USA) was used. The system was calibrated and found to give a stable performance. The wheat fields were routinely irrigated, according to soil water content, and were well fertilized. Irrigation water of about 70–100 mm was applied three times after the turning‐green stage. The area of cultivation was more than 20 ha. For a detailed description of management and environmental conditions, see Yu et al. (2002).

The model

There are five main environmental factors affecting stomatal conductance under natural conditions, i.e. solar radiation, air temperature, humidity, CO₂ concentration, and soil water potential. The actual stomatal conductance (g_s) can be obtained from the maximum conductance (g_max) under suitable conditions modified by correction coefficients for all the above factors (Jarvis, 1976):

g_s = g_max f(PPFD) f(T_a) f(C_a) f(VPD) f(ψ)(1)

in which I is absorbed photosynthetic photon flux density (PPFD), T_a is air temperature, C_a is CO₂ concentration, D is vapour pressure deficit and ψ is soil water potential.

Ball et al. (1987) proposed a semi‐empirical stomatal model in which the mathematical relationship between relative humidity at the leaf surface (h_s), CO₂ concentration (C_s) and photosynthetic rate (A_n) was represented by the following equation under conditions of ample water supply:

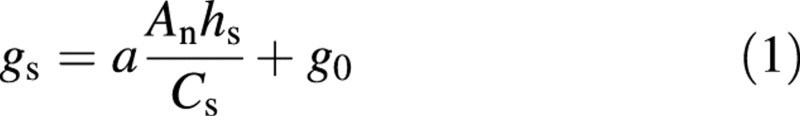
in which a is a constant, h_s is the relative humidity and C_s is the CO₂ concentration of air at the leaf surface, g_s is stomatal conductance, and g₀ is a parameter. Since it is the vapour pressure deficit from stomatal pore to leaf surface (D_s) which drives transpiration, D_s should replace h_s in the Ball–Berry model (Leuning, 1995). Here, the value of D in air is used instead of D_s, because D is a meteorological variable and can be easily obtained. Equation 2 is rewritten as

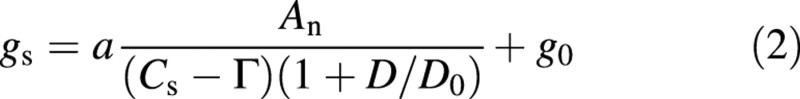
in which Γ is the CO₂ compensation point, and D₀ is a parameter reflecting characteristics of response of stomata to atmospheric D (Pa), which determines the curvature of humidity response curve of stomatal conductance.

As stomatal conductance begins to increase immediately with increasing light, even below the light compensation point, Yu et al. (2001) proposed gross assimilation rate should be used instead of net assimilation and, correspondingly, C_s – Γ should be replaced by C_s in eqn (3):

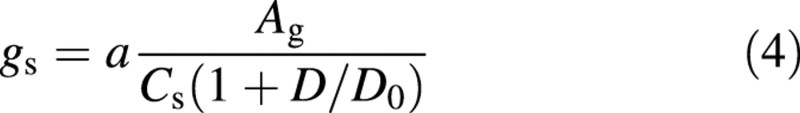
where A_g is the gross assimilation rate, and C_s is CO₂ concentration at leaf surface. In this expression, parameter g₀ in eqn 3 is taken as 0, because A_g and g_s go to 0 in the dark.

A_g is a function of environmental variables. A revision was adopted to take account of the limitation of photosynthesis by stomatal conductance:

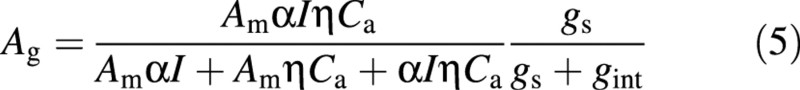
in which A_m is the maximum catalytic capacity of Rubisco per unit leaf area, α is initial photochemical efficiency, and ç is the initial slope of the CO₂ response curve [µmol m^–2 s^–1 (µmol mol^–1)^–1]. g_int is a parameter. If g_int → 0, g_s/ (g_s + g_int) = 1, and the equation shortens to the original light and CO₂ response curve.

A_m is a function of temperature with a maximum given by (Collatz et al., 1991):

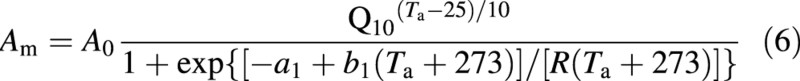
in which a₁, b₁ are parameters, A_m = A_{0 at} T_a = 25 °C and R is the universal gas constant.

It is assumed that g_s/(g_s + g_int) is determined chiefly by leaf or soil water status for a particular plant. Therefore, eqn (5) can be converted into the following:

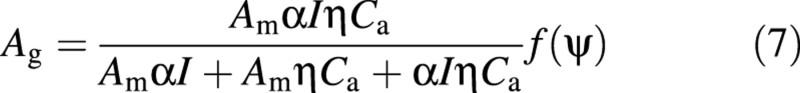
The water‐stress coefficient, f(ψ), is simply characterized by a linear relationship from the water potential at wilting point (ψ₀) to water potential at field capacity (ψ_m), i.e. relative extractable water (Lagergren and Lindroth, 2002). Therefore, by combining eqns (4) and (7), stomatal conductance can be expressed as a function of environmental variables in the following form:

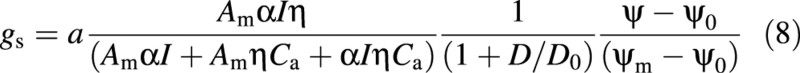
Stomata close in the dark, i.e. g_s is zero when I is zero, which is satisfied by eqn (8). Boundary conditions of stomatal response to light, D and water potential are also satisfied by eqn (8). The unit of a is the same as that of CO₂ concentration.

In conclusion, the stomatal conductance model (eqn 8) is based on both the relationship between stomatal conductance and gross photosynthesis (eqn 4; Yu et al., 2002) and that between photosynthesis and I (eqn 7; Thornley, 1976). The parameters α and A_m are related to biochemical processes, which are influenced by environmental factors. The model consists of two parts: (1) the relationship between stomatal conductance and photosynthesis (eqn 4), where the influences of light, temperature and CO₂ concentration on photosynthesis (eqns 6 and 7), and thereby on stomatal conductance, are integrated into one expression; and (2) the effects of evaporation demand (D) and soil water potential on stomatal conductance are included in this expression (eqn 8).

RESULTS

Relationship between stomatal conductance and photosynthetic rate in the model

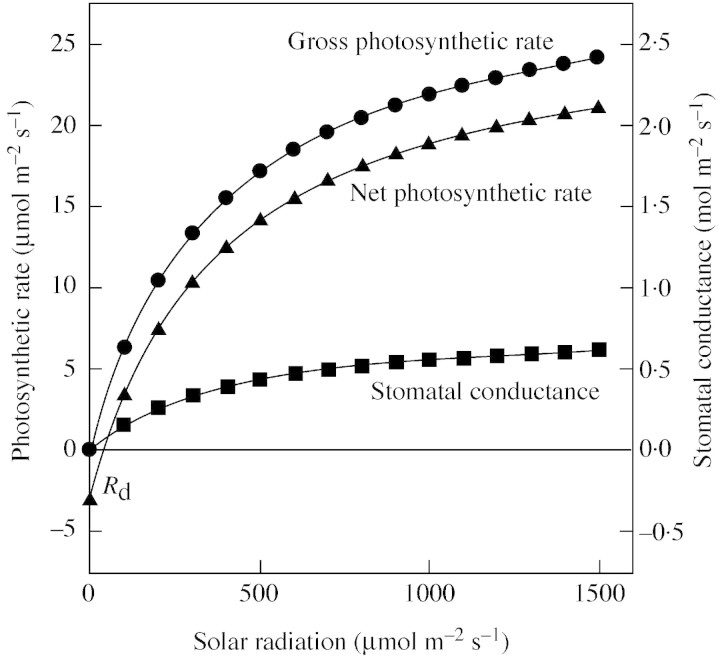
Figure 1 illustrates the responses of stomatal conductance, and net and gross photosynthetic rates to changes in light intensities. It is shown that both stomatal conductance and gross photosynthetic rate start from zero, which is a boundary condition of eqn (8). But net photosynthetic rate starts from a negative value representing dark respiration (–R_d), the value of which depends on air temperature and other variables. Therefore, the revised version of the Ball–Berry stomatal model (eqn 4), expressing the relationship between g_s and A_g instead of net assimilation, will give a stronger relationship between stomatal conductance and photosynthesis.

Fig. 1. Illustration of the relationship between stomatal conductance, net and gross photosynthetic rates and light intensity.

To fit eqns (2) and (4) with experimental data, the parameters reflecting the physiological characters in the equations, D₀ and Γ, should be given in advance. The CO₂ concentration point is assumed to be about 50 µmol mol^–1, and D₀ is adjusted so that the relationship between stomatal conductance and stomatal conductance index (algebraic formula on the right of equations including environmental and physiological elements) achieves the highest coefficient of correlation, which is taken as the best fit obtained.

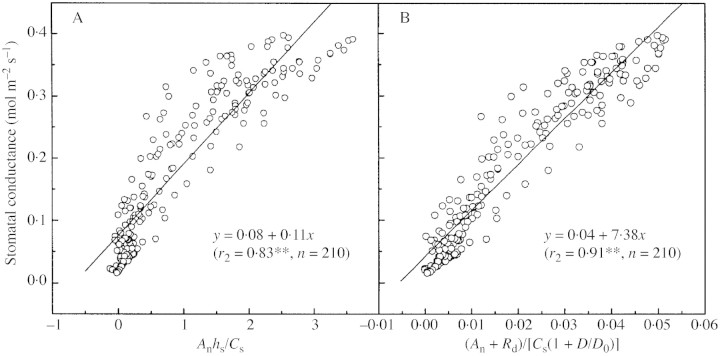
The relationship between stomatal conductance and stomatal conductance index in eqn (2) is significant (r² = 0·83, P < 0·01, n = 210) for the simulation of original Ball–Berry model in Fig. 2A. Equation 4 gives a much better correlation in Fig. 2B (r² = 0·91, P < 0·01, n = 210). There is a considerable improvement in the goodness‐of‐fit. The reason for this is that, since stomata respond to water loss, the relationship between rate of water loss and vapour pressure deficit is closer than that between water loss and leaf surface humidity (Sheriff, 1984; Aphalo and Jarvis, 1991).

Fig. 2. Simulation of stomatal conductance using (A) the original Ball–Berry model, and (B) its revised form, eqn 4 (Yucheng, 16 and 18 April 2003; **P < 0·01).

The dependence of photosynthetic rate on light and CO₂

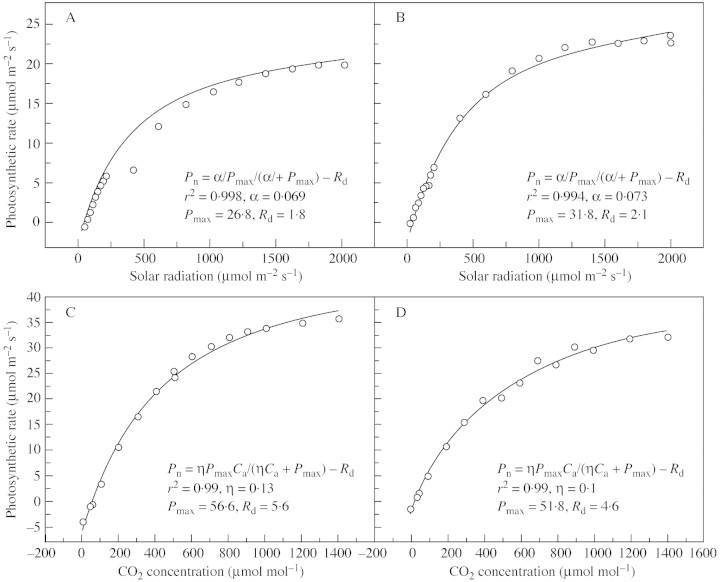
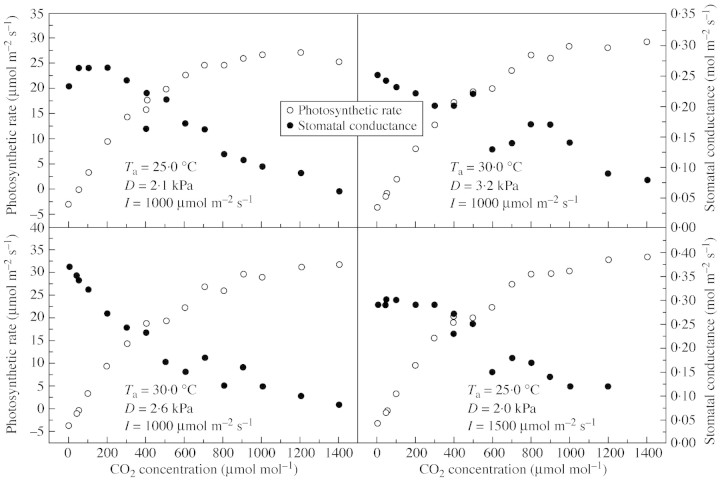
Light response curves of photosynthesis were fitted to data collected from leaves under changing light intensities when other factors were kept stable for each measurement. Figure 3(A and B) shows two typical light response curves of photosynthesis of wheat in which the photosynthetic rate was observed under different atmospheric conditions of temperature, humidity and CO₂ partial pressure. All light curves are similar in shape, but have different parameters due to differences in temperature and humidity. Temperature ranged from 25 to 30 °C over the period of observation, and relative humidity changed from 10 to 50 %.

Fig. 3. Fitted responses of photosynthesis to changes in light intensities and CO₂ concentrations (Yucheng, 16 and 21 April and 2 and 6 May 2003). (A and B) Typical light response curves. (C and D) Typical CO₂ response curves over the range 0–1400 µmol mol^–1.

Figure 3(C and D) shows the CO₂ response of photosynthesis to CO₂ concentration over the range 0–1400 µmol mol^–1. The scatter of points is wider than that of the light response. When photosynthetic rates and light intensity in the field are fitted by a rectangular hyperbola (Fig. 3), a good relationship is obtained. The initial slope of the fitted curve (α) is about 0·07 µmol CO₂ µmol^–1. For common crops, α is lower than its theoretical maximum (0·08), ranging from 0·04 to 0·07 under field conditions (Xu, 1984). The maximum photosynthetic rate is about 30·0 µmol m^–2 s^–1, which is basically the photosynthetic rate at the saturation point of light (Fig. 3). The maximum photosynthetic rate under field conditions varied between 25·0 and 35·0 µmol m^–2 s^–1, and stomatal conductance between 0·2 and 0·4 mol m^–2 s^–1; photosynthetic rate was higher and stomatal conductance lower under conditions of CO₂ enrichment.

Model validation

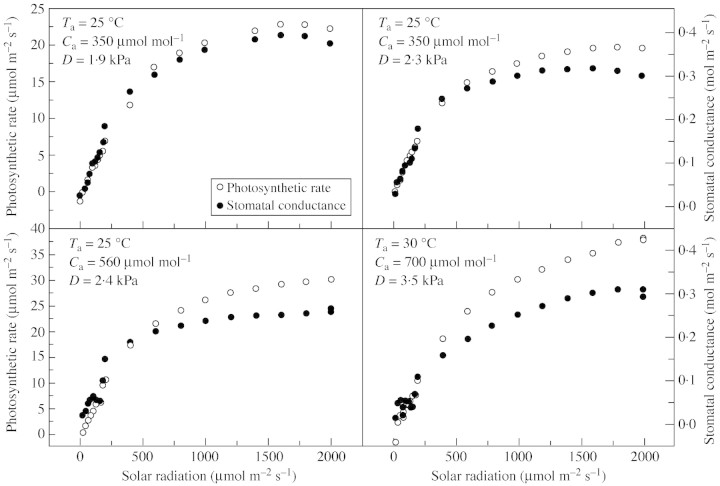
The data used in model validation are shown in the light and CO₂ responses (Figs 4 and 5). The response curve of photosynthetic rate to light intensity is a typical Michaelis–Menten curve (Fig. 4). Stomatal conductance corresponds well to photosynthesis in a changing light environment.

Fig. 4. Measured responses of photosynthesis and stomatal conductance to changes in light intensities (Yucheng, 16, 20 and 21 April 2003).

Fig. 5. Measured responses of photosynthesis and stomatal conductance to changes in CO₂ concentrations (Yucheng, 24 April and 6 May 2003).

Increased atmospheric CO₂ concentration will raise the intercellular CO₂, and hence photosynthetic rate. Stomatal conductance decreases with increased CO₂ concentration, whereas photosynthetic rate increases (Fig. 5).

As the experiment was conducted under ample water supply, the influence of water stress in eqn (8) is not included in the validation. The model was run with observational data of meteorological variables as inputs. After maximum carboxylation rate was obtained, the values of other parameters were adjusted according to previous studies (Collatz et al., 1991; Leuning, 1995; Yu et al., 2002), so that there is a very high coefficient of correlation between stomatal conductance and the index of stomatal conductance, i.e.

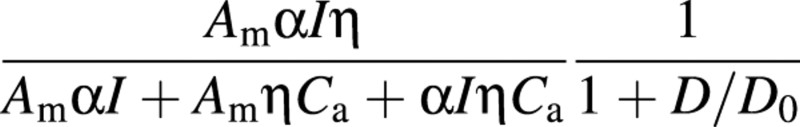
Then, the measured stomatal conductance was compared with the index. The parameters used were as follows: A_m = 60·0 µmol m^–2 s^–1, Q₁₀ = 2·4, a₁ = 220·0 kJ mol^–1, b₁ = 703·0 J mol^–1 K^–1, D₀ = 3·5 kPa, α = 0·06, η = 0·03. The constant R is 8·314 J mol^–1 K^–1.

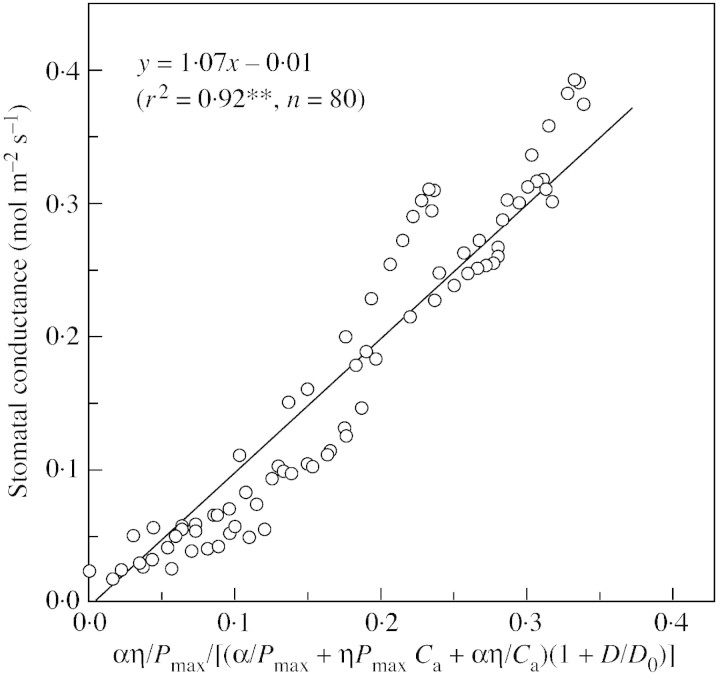
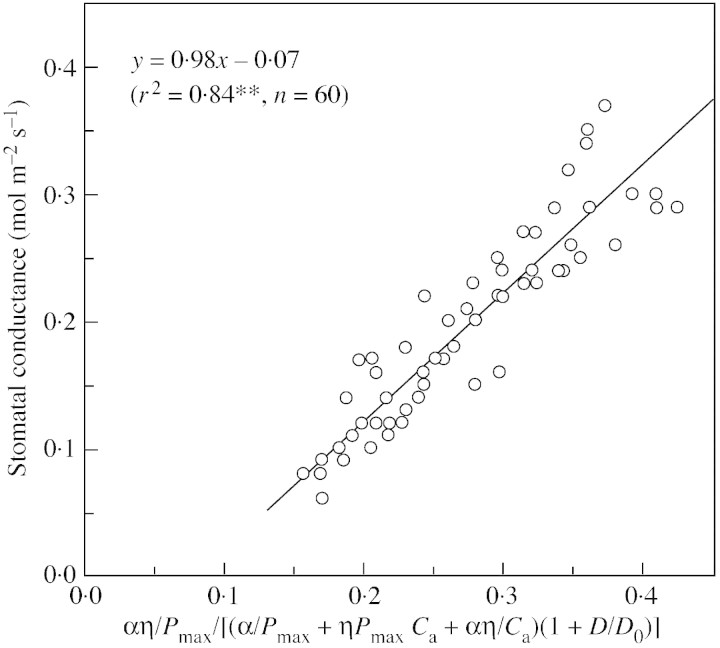
Figures 6 and 7 are comparisons between measured stomatal conductance and the stomatal conductance index under changing light intensities and CO₂ concentrations, respectively. Figure 6 shows that stomatal conductance agrees well with the index calculated from light, temperature, D and CO₂ concentration (Fig. 6). There is a good linear relationship between stomatal conductance and the index with a slope of 1·067, and the intercept on the y‐axis of simulated values is –0·01, which is very close to 0. That means that the model predicts stomatal conductance quite well. Agreement between measured stomatal conductance and predicted index under changing CO₂ concentration is also good, with the intercept also near to zero. However, the spread of points is slightly greater than that of the light response (Fig. 7).

Fig. 6. Measured stomatal conductance vs. calculated stomatal conductance index under changing light intensities (data from Fig. 4).

Fig. 7. Measured stomatal conductance vs. calculated stomatal conductance index under changing CO₂ concentrations (data from Fig. 5).

DISCUSSION

Plant transpiration is a physical process in which part of the net radiation energy is converted into latent heat, under physiological control by changes in stomatal aperture (Jarvis and McNaughton, 1986). In the Penman–Monteith evapotranspiration model based on energy balance, canopy resistance to water vapour diffusion is the sole factor reflecting physiological regulation (Thom, 1975). There fore, determination of resistance, the reciprocal of conductance, is a key topic in the simulation of evapotranspiration. In this study, a stomatal model is proposed as a function of solar radiation, CO₂ concentration and temperature, as well as D and soil water content. The mechanism of stomatal closure remains to be explored under conditions of changing climate, which is essential for the evaluation of primary production and water consumption. If it is not necessary to calculate photosynthesis, as in some hydrological models (Hatton, 1992; Gottschalck et al., 2001), the stomatal model can be directly applied to calculate evapotranspiration.

In addition to many relationships between stomatal conductance and atmospheric humidity or D_s, Monteith (1995), based on many experimental results, proposed that stomata respond to humidity in such a way that stomatal conductance decreases linearly with an increase in the rate of transpiration. This linear relationship between stomatal conductance and transpiration is identical to the non‐linear relationship between conductance and D_s (Leuning, 1995). Dewar (1995) has given thorough interpretations of stomatal conductance in relation to environmental factors, photosynthesis and transpiration in these stomatal models.

Parameters in empirical models do not have a clear physiological significance which changes with the specific plot or variety (Calvet, 2000), and the complexity of the determination of their values increases sharply with the number of parameters included. Application of the Jarvis model (eqn 1) usually includes some of the five environmental variables, i.e. light intensity, temperature, humidity, CO₂ concentration and soil water. Semi‐empirical models are based on physiological characteristics of the plant, although they are not theoretical expressions. Parameters used in semi‐empirical models with some physiological basis may extend the generality of the model. For example, P_max, α and η have physiological significance, which makes their values meaningful. Some parameters in the model may include the influence of other factors. For example, maximum photosynthetic rate is a function of leaf nitrogen content. As photosynthetic parameters are applied, the relationship between stomatal conductance and photosynthetic rate is included, and plant nutrition can be included in the parameter P_max.

There are many parameters in empirical stomatal models. The semi‐empirical model can reduce the number of parameters by means of theoretical analysis. For example, stomatal conductance and gross photosynthetic rate increase from zero, and this boundary condition suggests a constant ratio of the two quantities and the intercept, g₀, goes to zero (eqn 4). The introduction of a light and CO₂ response equation (Thornley, 1976) also reduces the number of parameters required when the effects of light and CO₂ are considered separately. Cannell and Thornley (1998) proposed that temperature and CO₂ were two important factors affecting P_n in the form of non‐rectangular hyperbolas. In this study, the simple rectangular hyperbola was used as the light response curve.

The model was validated by measurement of data under controlled conditions of light and CO₂ over a wide range, designed to verify its universality. The stomatal conductance model was validated by data over a wide range of temperatures, including diurnal variation, as well as light intensities and CO₂ concentration.

The climate in the North China Plain is characterized by high solar radiation and low humidity. The light response curve is no longer a hyperbola when the observation time is extended, as photosynthetic rate decreases with the increase in light intensity beyond a certain limit (Yu et al., 2002). In this study, the data were confined to a period from early morning to 1100 h each day. There was a significant decrease in photosynthetic rate with increasing light intensity after that hour due to photoinhibition, similar to the phenomenon reviewed by Leverenz (1994).

ACKNOWLEDGEMENTS

This work is supported by the Natural Science Foundation of China under project 40071008. We thank Dr Shucun Sun for the measurements and Dr Tim Green at USDA‐ARS Great Plains Systems Research Unit for his review of the manuscript. We thank Professor Shipley and Dr Thornley for their critical reviews and constructive suggestions.

Received: 28 May 2003; Returned for revision: 29 August 2003; Accepted: 8 December 2003; Published electronically: 23 February 2004