Acclimation of Photosynthesis to Light and Canopy Nitrogen Distribution: an Interpretation

Abstract

• Background and Aims Acclimation of photosynthesis to light and its connection with canopy nitrogen (N) distribution are considered. An interpretation of a proportionality between light‐saturated photosynthesis and local averaged leaf irradiance is proposed by means of a simple model.

• Model The model assumes (a) local irradiance drives synthesis of photosynthetic protein from metabolic N; (b) photosynthetic N is slowly degraded over approx. 5–7 d; (c) metabolic N is equally available through the canopy.

• Conclusions The kinetics of acclimation at different light levels may provide a way of parameterizing and testing the model. The model provides a rationale for the proportionality assumption mentioned above, which, while it is consistent with much experimental work, is valuable because it allows canopy photosynthesis to be calculated analytically.

INTRODUCTION

Leaf photosynthetic response to incident irradiance has been described by many models and equations, some totally empirical (e.g. see Thornley, 1976, table 4.1 for six equations) and others with variable mechanistic content (e.g. von Caemmerer, 2000). However, they all have, without exception, a light‐saturated asymptote denoted here by P_max. P_max can acclimate to several factors, which are, in approximate order of importance, light, nitrogen nutrition, ambient carbon dioxide concentration and temperature. Acclimated P_max values span a wide range, up to ten‐fold (Prioul et al., 1980a; Charles‐Edwards, 1981, p. 69; Evans and Terashima, 1988; Pettersson and McDonald, 1994; Hikosaka and Terashima, 1996; Walcroft et al., 1997; Kull and Niinemets, 1998; Meir et al., 2002). Acclimation may take 2–8 d, responding to average conditions over the period.

Many of the studies cited above address the problem of N distribution in the canopy, and whether it maximizes canopy photosynthesis. Leaf nitrogen (N) and photosynthesis are connected as most of the N in leaves is associated with photosynthetic machinery. However, there is no unanimity of view, partly because the experimental data are variable and do not tell the same story. Frak et al. (2002) state ‘There is presently no consensus about the factor(s) driving photosynthetic acclimation and the intra‐canopy distribution of leaf characteristics’. Hollinger (1996) summarizes another position, saying ‘In the meantime, modellers may wish to follow the pragmatic approach and allocate N as a linear function of the microsite PPFD’ (PPFD = photosynthetic photon flux density).

Assuming that P_max is proportional to leaf N, then Hollinger’s prescription of leaf N being proportional to irradiance is equivalent to a suggestion of Charles‐Edwards (1981, p. 70, equations 3.14 and 3.15) that P_max is proportional to irradiance. In this note, a simple interpretation of this relationship is proposed. Although more detailed mechanistic acclimation models by Thornley (1998a) and by Kull and Kruijt (1999) bear on the matter, neither paper spells out this possible inference (these two models are discussed below).

DEVELOPMENT OF THE MODEL AND DISCUSSION

With I denoting averaged local irradiance incident on foliage, then the equation suggested by Charles‐Edwards (1981, p. 70) and Hollinger (1996) amounts to

P_max = cI(1)

c is a constant. (In reality a running average for I is required, with a decay time of approx. 4 d, but dependent on conditions; here it is assumed that I is constant.) Charles‐Edwards made his assumption partly because he realized that the assumption greatly simplified calculations of canopy photosynthesis (which were needed for a tomato crop modelling program), and partly because his colleagues’ data were consistent with the assumption. Indeed, as the tomato plants were grown in glasshouses with partially controlled environments, the quality of the data compares well with much subsequent work. His assumption has had an unexpected durability and seen widening application, suggesting that a simple view of the hypothesis is pertinent.

Consider the scheme of Fig. 1. Assume metabolic or substrate nitrogen, N_s (possibly amino acids), is available throughout the foliage, and that N_s can be converted by a light‐driven reaction with rate constant, k, to photosynthetic nitrogen, N_ph. Photosynthetic nitrogen can be degraded according to linear kinetics with degradation rate constant k_d (time^–1). Assume that the same pool of substrate N (N_s) is equally available to the whole of the canopy and that the mean value of N_s is constant on the time scale of photosynthetic acclimation, which is much less than the timescale of seasonal changes. When the two pools are in equilibrium

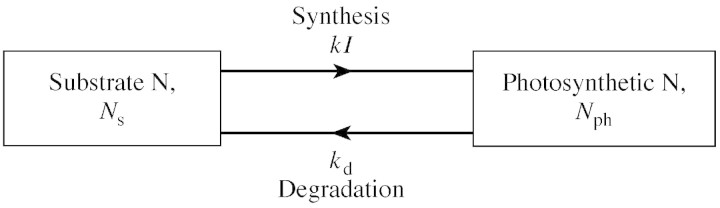
Fig. 1. Scheme for acclimation response of photosynthesis to leaf irradiance, I. k and k_d are constants.

kIN_s = k_d N_ph(2)

Hence

Assume that the light‐saturated photosynthetic asymptote, P_max, is proportional to photosynthetic N, N_ph, and eqn (1), the phenomenological equation of Charles‐Edwards (1981, p. 70) follows immediately.

Can eqn (2) be justified? Light absorption followed by photophosphorylation gives rise to ATP which is required for protein synthesis. This perhaps rationalizes the kI term as a reasonable first approximation. The plant circulation systems (phloem, xylem) are rapid compared with acclimation times. Whatever the details, it seems reasonable to assume that the whole of the foliage might experience the same concentration of available N substrate (N_s). This assumption may be invalid under some conditions: for instance in low‐fertility soils, or where key nutrients are transported in the xylem and transpiration streams which do not supply foliage uniformly. While different photosynthetic proteins doubtless have different turnover rates, applying a single specific turnover rate to all protein components of the photosynthetic machinery is a first approximation. This is consistent with the observation that foliage respiration rates are often proportional to foliage N content.

Can the rate constants of Fig. 1 be measured? In principle, yes. Assuming total N is constant at N_tot = N_ph + N_s, the kinetics of the scheme are described by

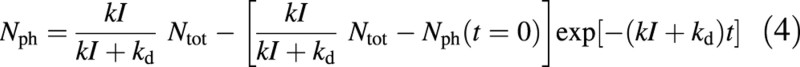
t is time. N_ph(t = 0) is photosynthetic N at zero time, t = 0. Acclimation rate depends on kI + k_d, and increases with the light to which photosynthesis is acclimating. However, this assumes that the Fig. 1 scheme is isolated from the rest of the plant. Other factors may well overwhelm an investigation based on such a simplified model. Data of Prioul et al. (1980b, table III) suggest tentatively that low light to high light acclimation occurs faster than the reverse. Photosynthetic acclimation has much in common, at least formally, with photosynthesis in fluctuating light [see figure 2 of Thornley (1974) and compare eqn (4) with equations 20 and 13 therein].

Figure 1 and eqn (3) suggest that complete acclimation and subsequent reacclimation are always possible. This is consistent with the findings of Prioul et al. (1980a, b) for grass, but may not be true for trees (Meir et al., 2002). Urban et al. (2003), investigating mango, reported an effect of nearby fruit on photosynthetic capacity. Leaf age can be also a factor in the relationships between light environment, N distribution and photosynthetic capacity (Kull et al., 1998; Dungan et al., 2003). Meir et al. (2002) reported a linear relationship with zero intercept between leaf nitrogen and P_max but with a positive intercept in the P_max : I relationship. A complex model would be required to address all these issues.

Equation (2) is a simplification of a more elaborate mechanistic scheme for acclimation proposed by Thornley (1998a, figure 2; henceforth, the T‐model). The more elaborate scheme has been incorporated into grassland and forest ecosystem models (Thornley, 1998b; Thornley and Cannell, 2000), where its performance to date has been satisfactory (stable, and predicting reasonable values of leaf N and upper canopy P_max). The elaborate scheme is needed when acclimation to other factors (such as soil fertility, CO₂ and temperature) is to be included, as required in a realistic ecosystem model. The mechanistic acclimation model of Kull and Kruijt (1999, figure 1; henceforth, the KK‐model) is at a similar level of complexity to that of the T‐model. However, there are important differences. In the T‐model, light drives synthesis of photosynthetic N (N_ph, Fig. 1) from shoot N substrate (presumably amino acids) alone. In the KK‐model, leaf N substrate and leaf C substrate drive N_ph synthesis using mass‐action kinetics. This seems not to allow for effects from photophosphorylation without accompanying carbon reduction, and could in principle provide a way of discriminating between the two approaches. Also there is a positive‐feedback effect in the KK‐model whereby increased P_max increases photosynthesis, thus boosting leaf C substrate and increasing N_ph and P_max yet further. The calculation of photosynthesis is based on Farquhar et al.’s model (Farquhar, 1980) and is not analytical. For these reasons, in the KK‐model a simple analytic deduction of consequences (such as in eqn 1) is difficult. Possibly a combination of the two approaches is required. Other aspects are treated similarly in the T‐ and KK‐models. However, in neither case do the authors make the simplification and draw the conclusions summarized here in eqn (3). For the T‐model, simplification to Fig. 1 and eqn (3) is direct. For the KK‐model, it is not obvious if eqn (3) can be extracted. Urban et al. (2003) describe an empirical acclimation model is which certain parameters of the Farquhar et al. (1980) photosynthesis model are related to leaf N per unit area.

Equation (1) with the proportionality of P_max to leaf N provides a useful view of light, photosynthesis and N relationships within crop canopies, consistent with many data (but see equation 8 of Anten and Hirose, 2001). It is valuable for ecosystem modellers because it allows canopy photosynthesis to be calculated analytically, even allowing for sun and shade effects (Thornley, 2002). Here, an interpretation is given in terms of a simple model (Fig. 1), extractable from a more complex mechanistic acclimation model (Thornley, 1998a). Thornley’s model (Thornley, 1998a) is discussed in relation to the mechanistic acclimation model of Kull and Kruijt (1999). Equation (4) indicates that the simple model might be parameterized with acclimation experiments performed at different light levels. The investigation also suggests that a detailed model, combining aspects of the models of Kull and Kruijt (1999) and Thornley (1974, 1998a), could aim to integrate the consequences of short‐ and longer‐term variations in light level for acclimation and photosynthesis.

ACKNOWLEDGEMENTS

This problem was suggested to me by the anonymous referee of an earlier but related investigation (Thornley, 2002). The work has been supported by the European Union through the MEGARICH project and is a contribution towards COST 619. It also contributes to work funded by the UK Department of Environment, Food and Rural Affairs under contract 1/1/64.

Received: 8 October 2003; Returned for revision: 11 November 2003; Accepted: 5 December 2003; Published electronically: 23 February 2004