Identification of Biomechanical Factors Involved in Stem Shape Variability between Apricot Tree Varieties

Abstract

• Background and Aims Stem shape in angiosperms depends on several growth traits such as elongation direction, amount and position of axillary loads, stem dimensions, wood elasticity, radial growth dynamics and active re‐orientation due to tension wood. This paper analyses the relationship between these biomechanical factors and stem shape variability.

• Methods Three apricot tree varieties with contrasting stem shape were studied. Growth and bending dynamics, mechanical properties and amount of tension wood were measured on 40 1‐year‐old stems of each variety during one growth season. Formulae derived from simple biomechanical models are proposed to quantify the relationship between biomechanical factors and re‐orientation of the stems. The effect of biomechanical factors is quantified combining their mechanical sensitivity and their actual variability.

• Key results Re‐orientations happened in three main periods, involving distinct biomechanical phenomena: (a) passive bending due to the increase of shoot and fruit load at the start of the season; (b) passive uprighting at the fall of fruits; (c) active uprighting due tension wood production at the end of the season. Differences between varieties mainly happened during periods (a) and (b).

• Conclusions The main factors causing differences between varieties are the length/diameter and the load/cross‐sectional area ratios during period (a). Wood elasticity does not play an important role because of its low inter‐variety variability. Differences during period (b) are related to the dynamics of radial growth: varieties with early radial growth bend weakly upward because the new wood layers tend to set them in a bent position. The action of tension wood during period (c) is low when compared with passive phenomena involved in periods (a) and (b).

INTRODUCTION

Stem shape and orientation are important components of the architectural diversity among trees. They control light interception and mechanical stability and are thus implicated in the adaptation of trees to their environment. For sylviculture and horticulture, they are major factors in product quality.

In the case of fruit trees, stem shape and orientation have a qualitative and quantitative impact on fruit production. The bending or tilting of stems typically reduces vegetative growth and modifies the branching pattern of the stems, and in some cases increases flowering. This phenomenon is called gravimorphism (Wareing and Nasr, 1961). In the case of apple trees, exploiting this reaction has led to training practices based on arching (Lakhoua and Crabbe, 1975; Lauri et al., 1997; Lauri and Lespinasse, 1999). To reduce fieldwork and increase productivity, breeding programmes now aim to select new varieties with stems that are naturally bent (Laurens et al., 2000). As tree shape is an integrated and multifactorial character, a better comprehension of the mechanisms involved in final stem shape was necessary, and was first tackled in apricot trees (Alméras, 2001).

The realization of a stem shape has previously been studied in the context of forestry and ecology, and is an important topic in tree biomechanics (Castera and Morlier, 1991; Fournier et al., 1991a, b, 1994b; Niklas, 1994). It depends on several factors related to growing habits. It initially depends on the orientation of the bud on its axis, and is modified by the growth direction of the apex during elongation. In addition to this primary orientation, important re‐orientations of the stems occur, related to both mechanical effects and secondary growth.

The increasing mass of wood, axillary shoots and fruits during growth causes the stem to bend. The intensity of this bending depends on the magnitude of the different loads and their location, on the dimensions of the stem and the mechanical properties of the wood. The bending can be predicted by the mechanical theory of beam bending which is classically used in an engineering context (Timoshenko, 1953).

The effect of cambial growth on stem shape is more complex. Its first effect is to increase stem diameter, and therefore stem rigidity and mass over time. Because of the variations in stem rigidity, stem shape depends not only on the amount of loading, but also on the relative dynamics of diameter growth and loading (Fournier et al., 1994b).

In addition to this ‘passive’ mechanical effect, which is related to the increase in stem rigidity, secondary growth plays an active role in stem shape. Maturation stresses occur at the end of cell differentiation in the new wood layers. When the distribution of these stresses is asymmetrical over the section, for example where reaction wood was formed, then active re‐orientation of the stem occurs (Archer, 1986).

In the present study, it was assumed that differences in stem shape and orientation observed between varieties of a given tree species result from variations in one or several of these biomechanical factors. The objective was to identify which of these factors have the most impact on stem shape changes in 1‐year‐old shoots.

The validity of the mechanical theories underlying the models was first checked independently for each biomechanical phenomenon (Alméras, 2001). This was performed for different stems, using detailed data obtained at various positions along the stems (Alméras et al., 2002). In this paper simplified models are presented designed to differentiate between the effects of the various biomechanical factors and to quantify their implication in the variability of stem shape. The models are evaluated and applied to the analysis of stem shape variability between apricot tree varieties.

MATERIALS AND METHODS

Most of the plant material and measurement methods used in this study have been presented in detail in a previous paper (Alméras et al., 2002).

Plant material

Three varieties of apricot trees of contrasting shapes were chosen for the study (Fig. 1): ‘Lambertin no. 1’ (upright shape), ‘Modesto’ (spreading shape) and ‘Palsteyn’ (weeping shape). The trees were planted in 1993 in the INRA experimental orchard in Melgueil, near Montpellier (France). They were grafted onto seedlings of ‘Manicot’ rootstock, and trained in a Y‐shape.

Fig. 1. Schematic shape of the three varieties studied: (A) ‘Lambertin no. 1’ (upright shape); (B) ‘Modesto’ (spreading shape); (C) ‘Palsteyn’ (weeping shape).

The flowering of apricot trees is located on 1‐year‐old stems, and blooming precedes the vegetative bud‐break. This is followed by an initial stage of fruit growth and development of leafy shoots (Costes et al., 1995). Radial growth starts later in the season (Costes et al., 2000). One‐year‐old stems are slender structures which are, for the first time, subject to marked axillary load from first‐fruiting. It was therefore considered that the second year of stem development was a key stage for stem shape realization in the apricot tree.

Trees were pruned at the beginning of 1998 to induce the development of long shoots. In early 1999 a representative sample of 40 1‐year‐old stems per variety was chosen for the study. The selected stems were composed of a single growth unit without any sylleptic branches, and their length was between 70 and 170 cm. Additional material was used to establish allometric relations between the dimensions and the weight of axillary production that developed on the sampled stems during the 1999 growing season. This material (axillaries from 20 additional 1‐year‐old stems and 150 additional fruits) was taken from the same tree, but on different branches throughout the season.

Dynamic observation of growth and bending

The stems were observed at bloom, 5 weeks after bloom and then every 3 weeks until the end of the 1999 growing season.

At each node, the vegetative bud either remained latent or developed as a leafy shoot. Two kinds of shoot were distinguished. Short shoots were composed of a single, preformed part and stopped growing very soon, with at most 12 short internodes and a maximal length of 10 cm. Long shoots developed a neoformed part with up to 30 elongated internodes and a maximal length of 50 cm. In addition to this vegetative growth, each node produced between zero and two fruits. Fruits and shoots that developed during the 1999 growing season will henceforth be denoted as ‘axillaries’.

The growth of each axillary was recorded by counting the number of leaves on the short shoots, the number of leaves and the length of long shoots, and the diameter of fruits. The weight of axillaries was calculated by the allometric relation based on a similar sample. Fruits and shoots from this sample were measured in the same manner as those in the survey, and were then weighted to within ±0·1 g. Power laws were used to obtain statistical relations between these measurements and the weight of the axillaries for each variety and each kind of axillary. Relations were statistically highly significant for all varieties, with R² between 0·83 and 0·87 for shoots and between 0·91 and 0·93 for fruits.

Diameter growth was quantified by measuring the diameter with digital callipers every 10 cm along the stems at each measurement date. The shape and orientation of the stems was recorded at the same dates by noting the 3D‐coordinates of fixed points every 10 cm along the stem. This was performed in situ using a magnetic digitizing device (Polhemus, 1993) and data acquisition software (Adam et al., 2000).

As the stage of full bloom was reached at different dates (mid‐February for ‘Lambertin’ and ‘Palsteyn’, end of February for ‘Modesto’), all dynamics were expressed as days after full bloom (DAFB). Results for growth dynamics are presented as mean behaviour of each variety. They were obtained by averaging data for all the stems of a given variety over each week. This sometimes masks inter‐individual variability. However, it was checked that growth events were generally synchronous between the stems of a given variety so that results presented are representative of behaviour on a variety level.

Measurement of other biomechanical factors

Mechanical properties of the stems were measured by evaluating the apparent modulus of elasticity of five stems per variety. This was performed by in situ elastic bending tests. Test methods and results have been described in detail in a previous paper (Alméras et al., 2002).

Stems were removed from the field at the end of the growing season, after the fall of the leaves. A sub‐sample of 15 stems per variety was used for anatomical studies and quantification of tension wood. Each stem was cut into three parts of equal length, and a 40 µm transverse section was cut through the middle of each part. Tension wood in the apricot tree is composed of typical G‐fibres. Sections were stained with safranine/astra blue to highlight tension wood areas. Safranine stains lignins red, and astra blue stains tissues composed of pure cellulose, such as G‐fibres. Sections were digitally scanned and annual rings and tension wood areas were delimited. The area of each identified zone was quantified using OPTIMAS® image analysis software.

The intensity of wood maturation strains was not measured in this material. Since this parameter is needed for biomechanical modelling of a growing stem, it was considered that the difference between maturation strains in normal wood and tension wood is 0·0025 m m^–1, which is consistent with growth strain data obtained for other deciduous tree species (Fournier et al., 1994a).

Biomechanical models: definition and evaluation

The biomechanical analysis involved three steps: (1) growth and bending dynamics were observed to identify the relevant periods of re‐orientation (i.e. when the differences in stem shape occur), and the biological phenomena related to these periods; (2) biomechanical models relative to each period were evaluated by comparing their predictions with the actual observations; (3) models were used to quantify and compare the effect of various biomechanical factors during each period.

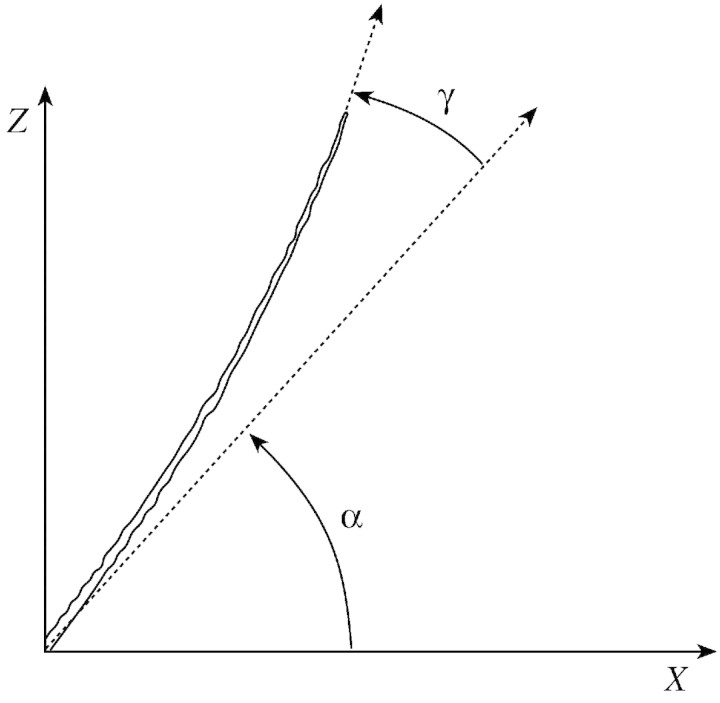
To quantify growth and bending phenomena, descriptors of the stems were computed from the data collected. Axillary growth was described by the total weight of fruits and shoots per stem, while diameter growth was described by the variations in mean diameter of the stem. Shape and orientation were described by the angle at the base (relative to the horizontal) and the ‘angular deviation’ of the stem, i.e. the difference between the angle at the base and the angle at the top (Fig. 2).

Fig. 2. Descriptors of stem shape: angle at the base (α) and angular deviation (γ).

Simple biomechanical formulae were established to model stem re‐orientations. Three different models were used depending on the biological phenomena involved. The formulae and mechanical assumptions on which they are based are detailed in the Appendix. They are all based on the beam theory (Timoshenko, 1953) and on the principles of its application to a growing tree (Fournier et al., 1991a, b).

Each model was reformulated so that the re‐orientations were expressed as a product of factors of biological significance. Factors were chosen to be as size‐independent as possible, and to reflect a single biological notion. The choice of factors will be discussed later. Their name, range and biological meaning are given in Table 1.

Table 1.

Definition of the factors of bending used in the three models (A, passive bending model; B, passive uprighting model; C, active uprighting model): relation to basic parameters, name, related biological concept, minimal and maximal values possible

Model	Factor	Name	Biological concept	Minimum value	Maximum value
A, passive bending	cosϕ	Initial leaning	Biomechanical history	0: vertical	1: horizontal
	L/D	Slenderness	Morphology of the stem	0: compact	+: slender
	M/D2	Relative load	Growth of shoots and fruits	0: no load	+: increasing load
	p	Position of loads	Distribution of growth	0: concentrated at the base	1: concentrated at the top
	1/E	Compliance	Wood quality	0: completely rigid	+: increasing compliance
B, passive uprighting	Δγ	Previous bending	Biomechanical history	0: no bending	π: maximal bending
	ΔM/M	Unloading rate	Fruit/shoot balance	0: not unloaded	1: completely unloaded
	D/(D + ΔD)	Diameter constancy	Delay between primary and secondary growth	0: high diameter growth when loaded	1: no diameter growth when loaded
C, active uprighting	sin(β/2)	Tension wood	Amount of tension wood	0: no tension wood	1: upper half full of tension wood
	ϵ	Maturation strains	Efficiency of tension wood	0: same maturation strain in tension and normal wood	+: higher maturation strain in tension wood
	L/(D + ΔD)	Slenderness	Morphology of the stem	0: compact	+: slender
	ΔD/(D + ΔD)	Diameter growth	Relative intensity of diameter growth	0: no diameter growth	+: increasing diameter growth

Model A.

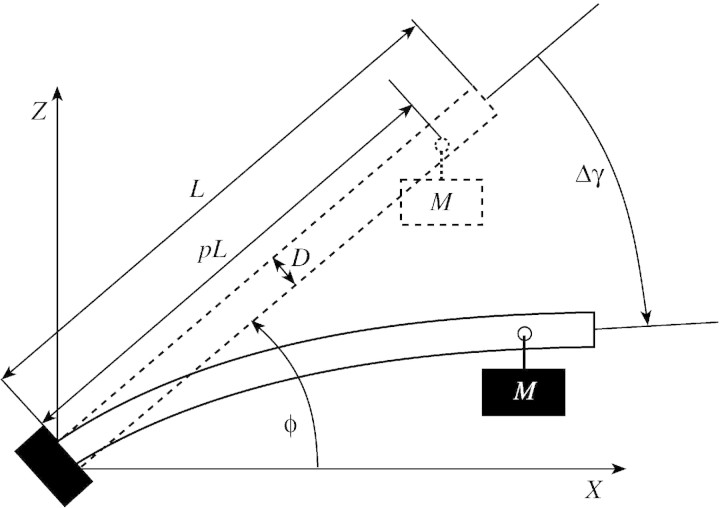
The first model predicts the bending of a loaded stem, while ignoring the effect of diameter growth. The variation in angular deviation, Δγ (in radians), can be expressed as a function of the length, L, of the stem, its diameter, D, its initial leaning, ϕ, the mass of loads, M, their relative position, p (i.e. the position of the centre of mass of the load along the stem, divided by the length of the stem to obtain a value between 0 and 1), and the modulus of elasticity of the material, E (Fig. 3). This model will be referred to as ‘the passive bending model’. It can be reformulated as:

Fig. 3. Bending of a straight beam of length, L, and diameter, D, initially leaning at an angle, ϕ, from the horizontal, subjected to a mass, M, at position, pL, from the base, resulting in variation of angular deviation, Δγ.

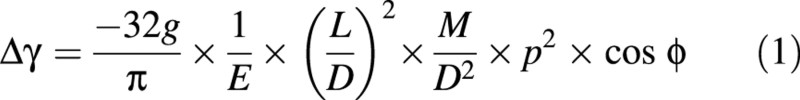
Model B.

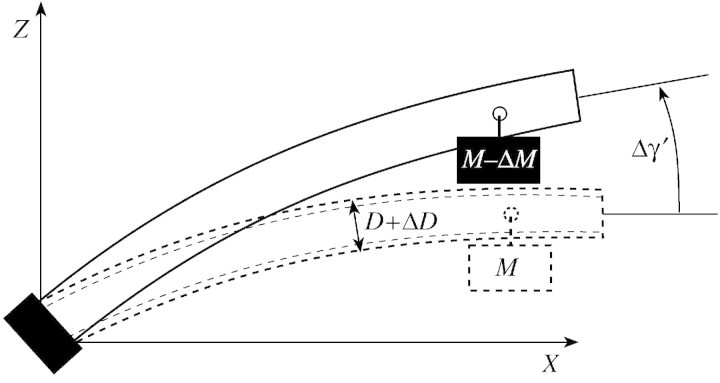
The second model predicts the uprighting of the stem at harvest, and takes into account the effect of diameter growth. This model assumes that the stem bends because of load increase, then grows in diameter without bending, and is finally partly unloaded. The variation in angular deviation can be expressed as a function of the initial diameter, D, of the stem, its diameter increment, ΔD, the initial load, M, and the reduction of load at harvest, ΔM (Fig. 4). This model will be referred to as ‘the passive uprighting model’. It can be reformulated as:

Fig. 4. Uprighting of a beam of diameter, D, subjected to a diameter increase, ΔD, and then unloaded of ΔM, resulting in a variation of angular deviation, Δγ′.

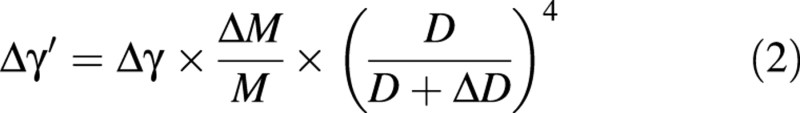
Model C.

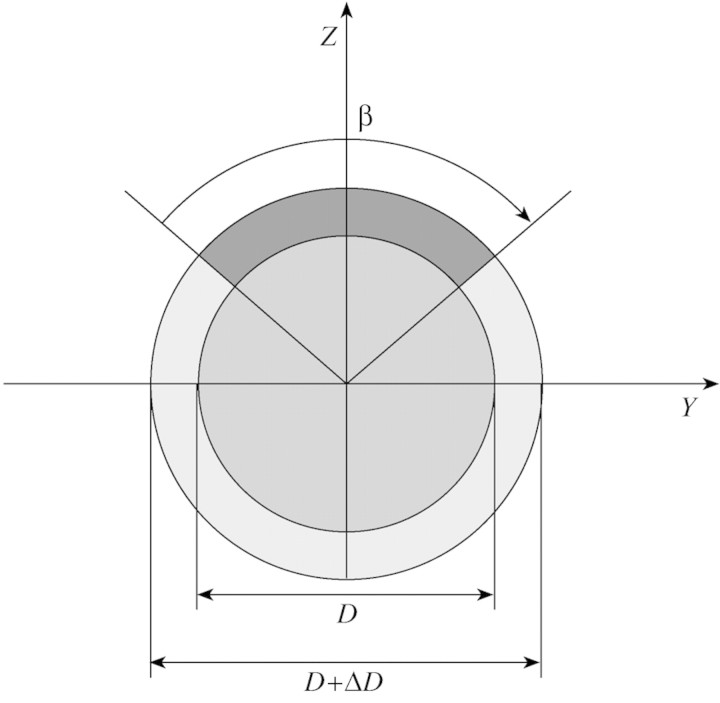
The third model predicts the uprighting of the stem due to the effect of tension wood, with the effect of loads being neglected. The variation in angular deviation can be expressed as a function of the length, L, of the stem, its initial diameter, D, its diameter increment, ΔD, the angular extension of tension wood, β (Fig. 5), and a parameter related to maturation strains, denoted, ϵ. This model will be referred to as ‘the active uprighting model’. It can be reformulated as:

Fig. 5. Schematic representation of a stem cross‐section of initial diameter, D, subjected to a diameter increase, ΔD, with a sector of tension wood in its upper part, characterized by its angular extension, β.

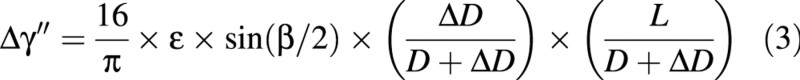
These models are based on strong assumptions (see the Appendix): they consider the effects of different biomechanical phenomena independently and are based on a very simple geometric description of the stems (most properties are considered to be uniform along it). To check the relevance of these models, each was evaluated prior to use in the analysis. For each model, the predicted variations in angular deviation were compared with those measured.

Biomechanical models were assessed using all stems for which data were available. Two criteria were used to evaluate their quality. The standard error of the model was computed as the square‐root of the mean quadratic difference between the observed and predicted values. This indicates the precision of the model for an individual level, i.e. its ability to predict the re‐orientation of a given stem. The mean difference between the predicted and observed values was also computed to quantify the global bias of the model. This indicates the error of the model when applied to a sample of stems.

Analysis of the biological causes of shape variability

It was assumed that variability in stem shape between varieties resulted from variability in biomechanical factors. To quantify and analyse the impact of each factor on stem shape at the level of the variety, biomechanical formulae were applied to mean values for both factors and variations of angular deviation. Biomechanical formulae were log‐transformed in order to obtain additive models. Each model can be written as:

log |Δγ∗| = Σ log(F_i)

where |Δγ∗| is the absolute predicted variation in angular deviation and F_i is the value of the ith biomechanical factor.

This equation quantifies a deterministic relation between the variation in angular deviation and the value of factors at the variety level. Assuming that theoretical means of log values for biomechanical factors are normally and independently distributed between varieties:

V[log |Δγ∗|] = Σ V[log(F_i)]

where V is the inter‐variety variance.

Stem shape variability between varieties was therefore quantified as the inter‐variety variance of the log of the variation in angular deviation, i.e. V[log |Δγ∗|]. This may be decomposed into the sum of the inter‐variety variances of the log of the factors. These parameters quantify the impact of each factor (i.e. their ability to explain stem shape diversity) integrating both their mechanical effect and their biological variability. They are expressed in an additive and size‐independent manner.

Comparisons between the factors were based on calculations of these parameters. As only three varieties were studied, it was not possible to check the assumptions made for the model of variance decomposition (i.e. normality and independence of factors between varieties). Thus, no statistical test was performed to check the significance of the differences between the variances of the factors. This point will be further expanded in the Discussion.

The analysis was performed over each growth period. The total re‐orientation during the year corresponds to the sum of the variations of angular deviation over all periods, whereas the decomposition of variance relative to each period is based on the log of the variations of angular deviation. Therefore, the effects of the log‐transformed variables are not additive between periods. As a consequence, our method cannot be directly used to analyse the sources of variability in total re‐orientations. This was analysed from a qualitative point of view, taking account of the relative importance of re‐orientation between periods and the impact of each factor in each period. A factor was considered to have an important overall impact if it had a strong impact in a period when major inter‐variety differences in stem re‐orientation occurred.

RESULTS

Morphology and growth dynamics

Average values and confidence intervals for stem parameters (i.e. those needed for biomechanical formulae) are given in Table 2 for each variety. These values relate to different key dates in the year: bud‐burst, harvest and end of the year. Data relative to harvest and end of the year are based on sub‐samples for which data were available (see Table 2 for detail).

Table 2.

Mean and 95 % confidence interval for the basic stem parameters measured over each period and for each variety.

	‘Lambertin’	‘Modesto’	‘Palsteyn’
Period T0–T1 (whole sample)
	n = 40	n = 40	n = 36
L (m)	1·16 ± 0·11	1·16 ± 0·08	1·26 ± 0·09
D (mm)	7·46 ± 0·39	6·53 ± 0·30	6·75 ± 0·54
M (g)	136 ± 15	122 ± 22	176 ± 41
p (%)	66·2 ± 3·0	76·1 ± 2·6	70·4 ± 2·6
E (Gpa)	5·49 ± 1·66	5·61 ± 0·63	4·99 ± 1·01
Period T2–T3 (stems with fruits)
	n = 24	n = 27	n = 9
L (m)	1·22 ± 0·14	1·22 ± 0·08	1·40 ± 0·10
D (mm)	7·57 ± 0·54	6·67 ± 0·34	7·22 ± 0·80
ΔD (mm)	1·40 ± 0·42	1·87 ± 0·43	0·74 ± 0·34
M (g)	284 ± 33	369 ± 70	230 ± 69
ΔM (g)	135 ± 26	200 ± 65	109 ± 43
Period T3–T4 (sub‐sample used for anatomy)
	n = 14	n = 15	n = 14
L (m)	1·29 ± 0·18	1·15 ± 0·13	1·33 ± 0·16
D (mm)	9·88 ± 1·25	9·98 ± 0·86	9·89 ± 1·45
ΔD (mm)	4·49 ± 1·52	2·37 ± 0·80	3·27 ± 0·86
β (°)	54 ± 12	103 ± 14	96 ± 11

n, Sample size; L, total length; D, mean diameter; M, axillary load; p, relative position of the mass centre of the loads along the stem; E, modulus of elasticity; ΔD, diameter increment; ΔM, load increment; β, angular extention of tension wood.

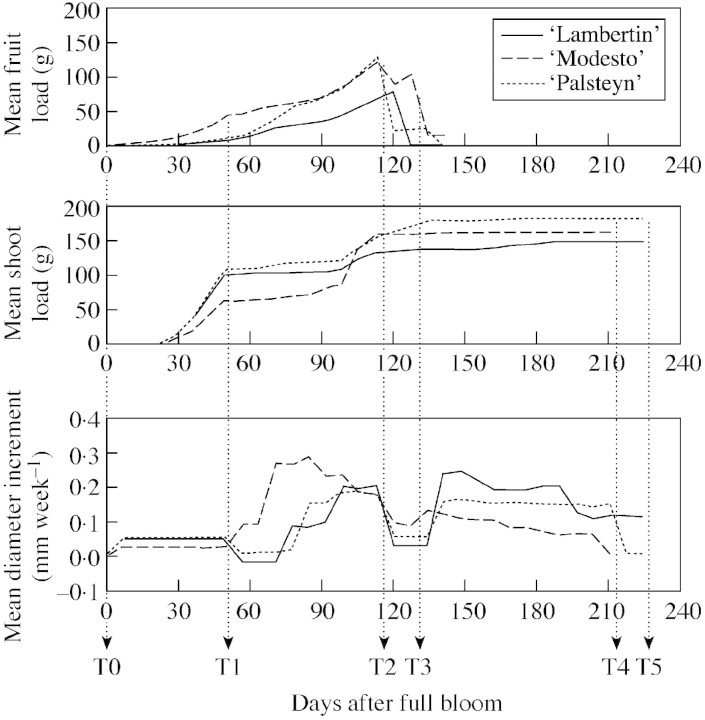
The mean number of fruits per stem was low (between two and four, depending on the variety), as conventionally observed in long 1‐year‐old stems. Most of the fruits were located on the top quarter of the stem. ‘Physiological’ drops were observed about 50 DAFB. Subsequently, the number of fruits per stem was constant until harvest for ‘Modesto’ and ‘Palsteyn’. For ‘Palsteyn’, the wind caused many fruits to drop 2 weeks before harvest. As a consequence, it was not possible to evaluate harvest uprighting for many stems in this variety. At harvest, 24 stems in ‘Lambertin’, 27 in ‘Modesto’ and nine in ‘Palsteyn’ were bearing fruits. Figure 6 shows the mean dynamics of fruit load for all the stems as resulting from the superposition of fruit growth and fruit drops.

Fig. 6. Mean dynamics of fruit load, shoot load and diameter increment for the three varieties studied, highlighting key dates in the year: T0 (bud‐break), T1 (physiological drops), T2 (before harvest), T3 (after harvest), T4 (end of growth) and T5 (fall of leaves).

Figure 6 shows the changes in mean shoot load per stem over the season. Vegetative bud‐break occurred 2 weeks after full bloom for all three varieties and led to the extension of the first growth unit (GU). This GU was mainly composed of short shoots located along the length of the stems, with a mean total load of 104 g for ‘Lambertin’, 65 g for ‘Modesto’ and 111 g for ‘Palsteyn’. Short shoots stopped growing 3 weeks after bud‐burst. A second GU grew about 2 months after the first and was mainly composed of long shoots located in a distal position, with a mean total load of 51 g for ‘Lambertin’, 103 g for ‘Modesto’ and 78 g for ‘Palsteyn’.

Figure 6 highlights the fact that mean weekly diameter increments were not evenly spread over the season. Diameter growth was very slow until 50 DAFB for all varieties, and occurred in two main periods afterwards. For ‘Lambertin’ and ‘Palsteyn’, the first period extended between 70 and 120 DAFB, and the second period (between 130 DAFB and the end of the season) was more intense than the first. For ‘Modesto’, the first period started earlier (50 DAFB) and was more intense than the second.

Other biomechanical factors

Apparent modulus of elasticity was evaluated in situ for only five stems per variety. Differences between the varieties were minor when compared with inter‐individual variability, and could not be evidenced statistically in such a small sample. The models nevertheless used mean values for the five stems since this gives the most accurate evaluation of inter‐variety differences in material properties. Mean modulus of elasticity was 5489 MPa for ‘Lambertin’, 5610 MPa for ‘Modesto’ and 4993 MPa for ‘Palsteyn’.

Tension wood was found in the second annual ring of all the sections analysed. This appeared as tangential bands, mostly located in the upper part of the section. Tension wood bands were found both in early and late wood. The amount of tension wood in a section was quantified as the total area of all tension wood bands in the second annual ring, divided by the total area of the ring.

The examination of sections taken at different points along the stems did not allow us to identify any specific pattern of longitudinal variations in the percentage of tension wood. Each stem was characterized by the mean percentage of tension wood in its sections. The mean percentage of tension wood was 15 % for ‘Lambertin’, 29 % for ‘Modesto’ and 27 % for ‘Palsteyn’. If the percentage of tension wood is τ, then its angular extension can be calculated as β = 2πτ, assuming that the amount of tension wood is constant along the radial direction within the ring and is located in the upper part of the section (see Fig. 5).

Identification of the re‐orientation periods

The dynamics of the different growth phenomena are presented in Fig. 6. This shows that for all three varieties, the changes in primary and secondary growth rhythm coincided with fruit drops (either physiological drops or harvest). Different periods were identified based on the growth phenomena involved. From bloom (denoted T0) to physiological drop (50 DAFB, denoted T1), fruits and shoots started to grow while diameter growth was still negligible. From T1 to fruit maturity (denoted T2), the fruits continued to grow along with a second vegetative growth unit and the start of intense diameter growth. The fruits were removed at harvest (T2–T3). From harvest to the end of the growing season (T4), the shoots showed negligible growth while diameter growth was intense. The leaves dropped at the end of the season (T5).

Figure 7 represents the ‘mean shape’ of stems for each variety at the reference dates, illustrating the mean angle at the base and mean angular deviation. For ‘Palsteyn’, no data concerning T2 were available due to wind drops. Data at 119 DAFB (i.e. 2 weeks before harvest) were used instead.

Fig. 7. Mean shape of the stems for each variety at each key date (T0–T5, starting with T0 at left with each successive stage indicated by the arrows), demonstrating the angle at the base and the angular deviation.

At T0, the stem orientation differed between varieties: ‘Palsteyn’ stems were already more tilted than the other varieties. Subsequent changes in stem orientation were mainly due to variations in angular deviation. A slight decrease in the angle at the base (<5°) was noted over the period T1–T2, but was balanced by an equivalent increase during T2–T3.

The mean change in angular deviation for each period is given in Table 3. Stems bent downward from T0 to T2, and upwards from T2 to T5. Most of the downward bending occurred during T0–T1, and most of the upward bending during T2–T3. A comparison between the means by variety and the overall mean (Table 3) showed that differences between the varieties mainly occurred during these periods: ‘Lambertin’ bent less than the other varieties during T0–T1, and ‘Modesto’ bent weakly upwards during T2–T3 (i.e. at harvest).

Table 3.

Mean by variety, and overall mean for the variation of angular deviation over each identified period

Time	‘Lambertin’	‘Modesto’	‘Palsteyn’	All varieties
T0–T1	–25·7°	–45·9°	–52·6°	–41·4°
T1–T2	–15·5°	–11·0°	–18·3°	–14·9°
T2–T3	+20·5°	+9·8°	+20·1°	+16·8°
T3–T4	+7·8°	+7·7°	+13·8°	+9·8°
T4–T5	+4·3°	+7·5°	+12·6°	+8·1°
T0–T5	–8·6°	–31·9°	–25·3°	–21·9°

Negative values indicate bending and positive values indicate uprighting.

On the basis of the identified period and related biological phenomena, the biomechanical model that was most suitable for the analysis of each period was selected. Diameter growth was negligible over the period T0–T1, so the passive bending model (model A) was used to model the bending due to the axillary growth load. During the period T1–T2 diameter growth occured together with load increase. When the mechanical interactions of these phenomena are taken into account, this leads to complex biomechanical models (e.g. Castera and Morlier, 1991; Fournier et al., 1991a, b). None of our simple biomechanical models was suitable here. Period T2–T3 corresponds to the instantaneous unloading of the stem at harvest time and was analysed using the passive uprighting model (model B). During the period T3–T4, axillary growth was low and diameter growth intense. Anatomical observations showed that most of the tension wood was produced during this period. The active uprighting model (model C) was used to analyse this period. Period T4–T5 corresponded to a period of passive uprighting due to the fall of the leaves. However, this was less important than T2–T3 from a quantitative point of view and was, therefore, not analysed specifically. Our biomechanical analysis therefore concentrated on the periods T0–T1, T2–T3 and T3–T4.

Evaluation of the models

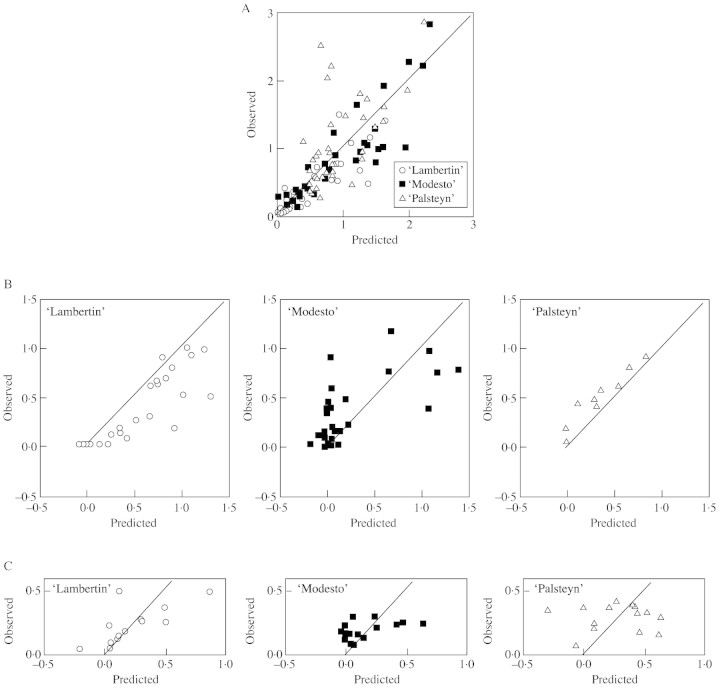
Predicted and measured values for variations of angular deviation are shown in Fig. 8 and are given for all stems sampled of each variety, at each period.

Fig. 8. Comparison between observed and predicted stem re‐orientations (in radians). (A) Period T0–T1 (whole sample); (B) period T2–T3 (sub‐sample with fruits); (C) period T3–T4 (sub‐sample for which anatomy was studied).

The passive bending model (Model A) was evaluated using the data from all 120 stems (Fig. 8A). The standard error of the model was 0·381 rad (i.e. 53 % of the mean observed variation in angular deviation). Despite an important error for some stems, the mean re‐orientation predicted by the model was only 3·6 % higher than the mean observed variation. This low bias was observed for all the varieties. Therefore, this mechanistic model gives a good estimation of the mean re‐orientation, provided it is applied at variety level.

The passive uprighting model (Model B) was evaluated using the data from all stems from which fruits were harvested (Fig. 8B). The standard error of the model was 0·309 rad (i.e. 77 % of the mean observed re‐orientation). When computed from the data obtained from all the stems, the errors mostly cancelled each other out and the global bias of the model was only –1·5 %. However, the error and bias were not identical in all the varieties. Uprighting was underestimated for most ‘Lambertin’ stems, and overestimated for ‘Palsteyn’ stems. The error was the greatest for ‘Modesto’ stems where uprighting was generally overestimated. Some stems in this variety showed a low negative value for uprighting (i.e. slightly accentuated bending) at harvest and this will be considered in the Discussion.

The active uprighting model (Model C) was evaluated using the data from all the stems involved in the anatomical study (45 stems). Figure 8C shows that the errors of prediction were often substantial at the individual level. The standard error of the model was 0·221 rad (i.e. 103 % of the mean observed re‐orientation). Re‐orientations were generally overestimated for low values, and underestimated for high values. This model was unable to predict uprighting at the individual level, but only gave an order of magnitude. When averaged for the sample, the errors partly cancelled each other out, and the global bias of the model was only +11·4 %. This bias was similar for all three varieties. Negative uprighting values (i.e. slightly accentuated bending) were observed for some stems in all varieties; this will be considered in the Discussion.

Analysis of the biological causes of shape variability

In this section, the factors affecting shape variability are first analysed independently for each period. Conclusions concerning the different periods are then considered together to analyse the main factors impacting on shape variability throughout the entire season.

The histograms in Fig. 9 illustrate the position of the varieties relative to each other for each factor. The values plotted correspond to the differences between the mean log values by variety and the overall mean log value. Each plot concerns a single factor for a single variety. A positive value indicates that this factor is associated with re‐orientation for this variety more than for other varieties. A negative value indicates that it prevents re‐orientation. For each factor, the mean by variety, the overall mean and inter‐variety variances are given in Table 4.

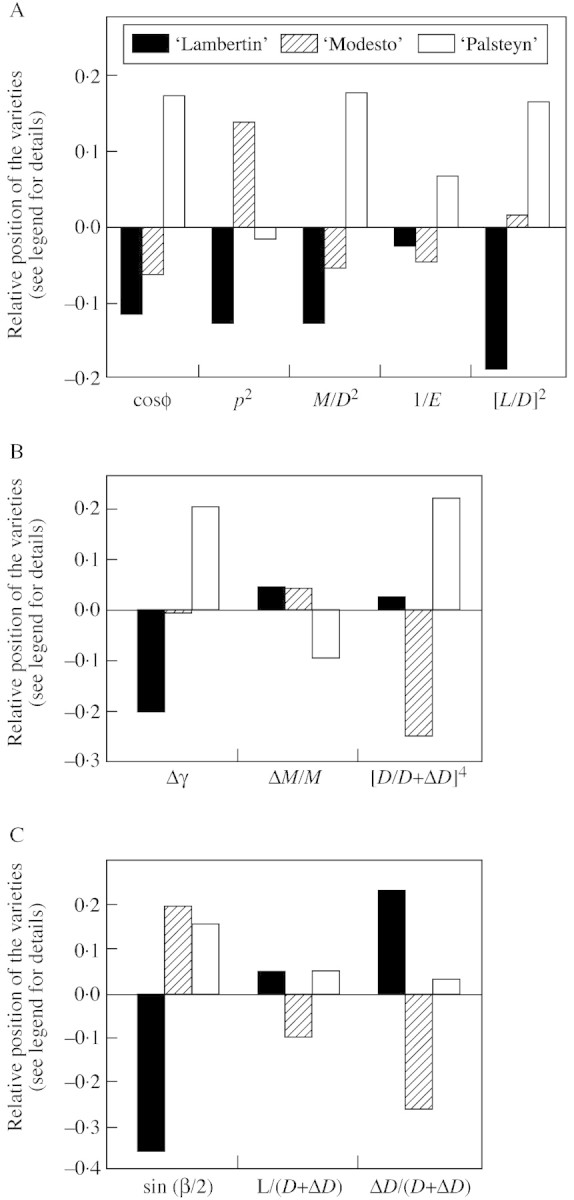
Fig. 9. Position of the varieties relative to each other for each re‐orientation factor. Each bar represents the difference between the mean log‐value for a given variety and the overall mean log‐value. (A) Period of passive bending (T0–T1); (B) period of passive uprighting (T2–T3); (C) period of active uprighting (T3–T4). A positive value means that the factor promotes reorientation for that variety more than for the other two varieties.

Table 4.

Overall mean, mean by variety and inter‐variety variance of the log‐transformed factors for each reorientation period (A, passive bending; B, passive uprighting; C, active uprighting)

Model	Factor	Unit	All varieties	‘Lambertin’	‘Modesto’	‘Palsteyn’	Variance
A, passive bending	Initial leaning cosϕ	–	–0·34	–0·49	–0·40	–0·11	0·0260
	Position of loads p2	–	–0·71	–0·85	–0·56	–0·72	0·0141
	Relative load M/D2	kg cm–2	–1·36	–1·45	–1·42	–1·19	0·0135
	Compliance 1/E	10–9 m2 N–1	–1·68	–1·70	–1·72	–1·61	0·0026
	Slenderness (L/D)2	m2 cm–2	1·06	0·83	1·11	1·26	0·0318
B, passive uprighting	Previous bending Δγ	–	–0·09	–0·41	0·012	0·453	0·1230
	Unloading rate ΔM/M	–	–0·84	–0·82	–0·82	–0·92	0·0023
	Diameter constancy [D/(D + ΔD)]4	–	–0·74	–0·63	–0·94	–0·42	0·0460
C, active uprighting	Tension wood sin(β/2)	–	–0·22	–0·39	–0·13	–0·14	0·0139
	Slenderness L/(D + ΔD)	m cm–1	0·10	0·11	0·06	0·13	0·0011
	Diameter growth ΔD/(D + ΔD)	–	–0·67	–0·56	–0·80	–0·65	0·0095

Model A.

Our passive bending model considers five biomechanical factors, denoted ‘initial leaning’, ‘position of loads’, ‘relative load’, ‘compliance’ and ‘slenderness’. Figure 9A shows that ‘Lambertin’ has low values for all factors, resulting in the lowest re‐orientation. In contrast, ‘Palsteyn’ has the highest values for almost all factors, and consequently the greatest re‐orientation. ‘Modesto’ has moderate to low values for most factors (except for ‘position of loads’) so that its re‐orientation is intermediate.

A comparison between the factors showed that ‘compliance’ was not an important cause of the bending variability since inter‐variety variance for this factor was lower than for the other factors which all play a substantial role. The two major factors are ‘initial leaning’ and ‘slenderness’, which have the highest inter‐variety variability. The two secondary factors are load intensity and position. The limited impact of these factors is related to the fact that, once standardized (the load is divided by the squared diameter and its position expressed between 0 and 1) their inter‐variety variance is low.

‘Initial leaning’ acts by increasing the lever arm of loads: the more tilted the stem prior to loading, the more it is going to bend. This factor depends on reorientations of the stem during its first year of development. This was not analysed here and will not be further considered.

Model B.

The incomplete recovery of the initial shape at harvesting can be analysed using the passive uprighting model. Results are shown in Fig. 9B and Table 4 (B). The three biomechanical factors involved in uprighting during this period correspond to ‘previous bending’, ‘unloading rate’ and ‘diameter constancy’. Previous bending was mainly achieved during T0–T1 and has been analysed above.

The ‘unloading rate’ (i.e. the mass of removed fruits divided by the total mass of axillaries) showed a low inter‐variety variability. Therefore, as demonstrated by inter‐variety variances (Table 4, B) the main factor explaining differences in uprighting is ‘diameter constancy’, i.e. the proportion of final diameter that had already been reached before loading. This proportion was high for ‘Lambertin’ and ‘Palsteyn’, explaining why these varieties show marked uprighting at harvest. ‘Palsteyn’ had the highest value for this factor, but this was partly offset by its relatively low unloading rate.

The ‘diameter constancy’ factor is related to the relative dynamics of diameter growth and loading. If diameter growth is late compared with loading, then the stem tends to recover its initial shape when unloaded (i.e. at harvest). If diameter growth starts early before harvest, as is the case for ‘Modesto’, then wood layers are produced while the stem is already bent. These layers tend to fix the stem in a bent position, and prevent uprighting. This factor is important because of its inter‐variety variability and it impacts to the power of 4 in the mechanical formula.

Model C.

Results concerning the period T3–T4 are shown in Fig. 9C and Table 4 (C). Three factors are considered: ‘tension wood’, ‘slenderness’ and ‘diameter growth’.

Differential diameter growth earlier in the season resulted in less pronounced differences in slenderness at this stage than during T0–T1. In addition, this factor only impacts with a power of 1 during T3–T4, whereas it was squared in the model of T0–T1. This explains why this factor has a weak impact during this period.

The main factor in the variability was ‘tension wood’, whereas ‘diameter growth’ was a complementary factor. ‘Lambertin’ produced the lowest amount of tension wood, but this was partly offset by a marked radial growth. ‘Modesto’ had the highest amount of tension wood, but its radial growth was low at this time of the season. This resulted in moderate uprighting for both varieties. ‘Palsteyn’ had a large amount of tension wood together with fairly pronounced radial growth. This explains why active uprighting was maximal for this variety.

Variability of maturation strains was not accounted in the analysis, since no data were available for this inter‐variety variability (an arbitrary constant value was used instead). This factor reflects on the efficiency of the tension wood, i.e. the ability of a given amount of tension wood to generate an uprighting movement. Since this factor was not measured, it is not known if it had any effect, but microscopic observations of cell dimensions and wall thickness (not presented in this paper) did not evidence any anatomical difference between the tension wood cells in the varieties studied.

Analysing the entire season.

Bending variability at the beginning of the season (T0–T1) was mainly affected by slenderness. As previously outlined (see Table 3), most of the variability in stem re‐orientation occurred during T0–T1. Therefore, it may be considered that slenderness is the main factor in re‐orientation variability. Other important factors are load mass and position (which play a secondary role during the main reorientation period) and the dynamics of diameter growth (‘diameter constancy’ factor, which has most impact in the second re‐orientation period, T2–T3).

Re‐orientations measured over period T3–T4 were small when compared with previous periods. Thus it may be stated that tension wood does not appear to be an important factor in shape variability. Moreover, this factor acts in moderating the differences in bending: the more a stem was bent earlier in the year, the more it produces tension wood and partly offsets this bending. However, this offsetting remains weak, suggesting that for the kind of shoots studied, tension wood is unable to play a major role in shape regulation.

DISCUSSION

In this section, a critical discussion of our methodology concerning the use of simplified biomechanical models and the quantification of re‐orientation factors is presented. The biological consequences of the results are then considered.

Biomechanical models

The models used were designed to be as simple as possible in order to highlight the role played by each parameter. Similar simple models, based on strong assumptions and a few parameters, are often used to compare the mechanical stability of different tree species (Niklas and Kerchner, 1984; Niklas, 1994). Our models are based on strong assumptions, and their application to biological material must be discussed.

Three biomechanical phenomena were considered independently: (i) the effect of axillary load; (2) the interaction between temporary loads and the dynamics of diameter growth; and (3) the active re‐orientations due to wood maturation. These phenomena were modelled independently by the passive bending model (A), the passive uprighting model (B) and the active uprighting model (C). In the study reported here, growth processes related to these phenomena occurred in almost distinct periods, except for T1–T2 which could not be analysed. All other periods were analysed using the model related to the main phenomenon, thus ignoring the effect of other phenomena. However, their negligibility is open to discussion: diameter growth was not completely absent during the period when model A was applied; the dynamics of loading and diameter growth were not as simple as assumed in model B; active re‐orientation occurred together with a slight increase in self load due to the new layers of wood, which was neglected in model C. These approximations have consequences on the quality of the predictions and may explain some discrepancies between the model and observations. For example, negative values for uprighting (i.e. accentuated bending) in models B and C cannot be explained without considering these neglected phenomena.

Moreover, the manner in which each single phenomenon was modelled can be discussed. For simplicity, most stem parameters were assumed to be uniform along the stem, whereas the biological reality is more complex. A real stem is tapered, with an irregular initial shape and distribution of loads. In the case of models A and B, complex mechanical phenomena (e.g. large displacements and visco‐elastic effects) are likely to play a role.

The application and evaluation of a mechanical model of stem bending accounting for these phenomena can be found in Alméras et al. (2002). That work showed that the quality of the predictions is improved slightly by the use of a more complex model. This kind of model is based on several parameters describing the local heterogeneity of the stems. It therefore could not be used for the purpose given here. Indeed, the variability analysis is based on a formulation with synthetic parameters, whose role and biological meaning are easily identified.

An evaluation step was developed to check the global validity of the models. It showed that substantial prediction errors may occur at the individual level, through violation of some model assumptions. These errors are underestimations for some stems and overestimations for others. They offset each other when averaged for the sample, resulting in a low global bias. Therefore, these models appear to be suited to the biomechanical study of stem populations, and are ‘robust’ in this context (i.e. little affected by the violation of the assumptions on which they are based).

For some situations, the validity of the model can be questioned. Indeed, model B showed marked bias when averaged for sub‐samples of varieties. This was due to the fact that the assumptions are not equally verified for all the varieties, so that the offsetting of errors between stems did not happen. The effect of large displacements was probably greater for ‘Lambertin’ because its stems were closer to the vertical (Alméras et al., 2002). This results in an underestimated re‐orientation for this variety. The effect of radial material heterogeneity (i.e. differences in elasticity between annual rings, or between early wood and late wood) may be more pronounced for ‘Modesto’ because its diameter growth starts earlier. This results in an overestimated re‐orientation for this variety. Therefore, the evaluation step is essential before using these models on new material.

Quantification and comparison of factors

The last step in the methodology consisted of analysing the origin of stem shape diversity. The effect of biomechanical parameters is usually studied using two methodological approaches. The first is rather theoretical and consists of building a model describing the biomechanical problem. The relationship between model output and input parameters is then studied to draw general conclusions about the mechanical constraints upon the plant (Niklas, 1994; Moulia and Fournier‐Djimbi, 1997). The second approach consists of measuring biomechanical parameters in different samples to demonstrate the effect of ontogenic (Rowe and Speck, 1996), genetic (Cilas et al., 2000) or environmental conditions. This approach quantifies the actual variability of biomechanical factors, but cannot compare the effects of different factors.

An original point in our approach is that the effect of each biomechanical factor was quantified by integrating its mechanical sensitivity and its inter‐variety variability. It is emphasized that both of these factors must be mixed to analyse the origin of stem shape diversity. A sensitive parameter will have a significant effect only if it is variable. Reciprocally, a biomechanical factor exhibiting a marked variability can be considered as a cause of shape diversity only if it is mechanically sensitive.

A very simple model of variance decomposition was used for this purpose. An additive model was obtained by applying the ‘log’ function to the mechanical formulas. This was possible because of the simplicity of the models. Factors with symmetrical multiplicative effects were identified in the formula. The signs of the factors and variations of angular deviation were known, so all the variables could be expressed as positive values and log‐transformed. This was not always possible. For example, we were unable to obtain such a symmetric formulation for a model including both diameter growth and load increase (period T1–T2).

The variance decomposition was based on strong assumptions concerning the distribution of factors between the varieties. As only three varieties were studied, these assumptions could not be checked statistically and need to be discussed. The log‐normality of the factors was compatible with the fact that they are positive variables and are based on dimension variables (length, diameter or mass).

More attention should be paid to the assumption of independence between factors. Basic parameters in the model (L, E, D, M, etc.) were grouped into ‘factors’. The reformulation was designed to be as close as possible to the assumption that the factors are independent. Dimension ratios were used because dimension variables are clearly not independent from one another (they are all subject to a size effect). For example, the correlation between the mass of loads, M, and the diameter, D, of the stem was 0·68. The correlation between M/D and D reduced to 0·54, and the correlation between M/D² and D reduced to 0·13. Therefore, M/D² was considered as the ‘most independent’ descriptor of the load. This choice is consistent with concepts introduced by other authors concerning the ratio of leaf surface area to the cross‐section of a branch in a forestry context (Shinozaki et al., 1964) or the equilibrium between fruit load and the size of the branch in a horticultural context (MAFCOT, 2000). Similar arguments can be given for factors that are dimension ratios. Other factors were chosen to describe distinct biological processes, where the biological control of each is expected to be as independent as possible from that of the others.

The main limit to the application of the variance decomposition model is the small number of varieties studied. Independence between factors could not be checked in this context, and the estimation of inter‐variety variances based on only three varieties may be questioned. However, it should be noted that the varieties were chosen to be representative of the diversity of the species.

Conclusions for tree architecture

Our results suggest that slender stems, heavy load (fruit and leaves) and early diameter growth are the main causes of natural bending. However, these results are based on the analysis of a single type of organ: the long shoots during their second year of growth. The differences in shape at the beginning of the year (Fig. 7) result from the first year of growth, when other phenomena such as primary re‐orientations (i.e. changes in the growth direction of the apex) may play an important role. Moreover, in the case of older stems, the relative impact of the different factors may depend on the ontogenetic evolution of physiological and morphological stem characters (Barnes et al., 1994; Rowe and Speck, 1996; Mansour and Defay, 1998). Differences in modulus of elasticity, amount of tension wood or intensity of maturation strains could play an accentuated role in older stems.

The fact that the shape of a stem depends not only on the amount of diameter growth and load, but also on the relative dynamics of these phenomena was previously highlighted by Fournier et al. (2001). The consequences are particularly important for fruit trees, because they hold an abundant and temporary fruit load. Even small differences between the dynamics of these phenomena can have major biomechanical consequences, suggesting that more attention should be paid to the dynamics of the growth processes and to the physiological relationships between primary growth and cambial activity (Barnola and Crabbé, 1993).

Through this phenomenon, phenology has an impact on tree shape. The diversity of morphological and phenological factors observed in the same genotype at different sites (Fournier et al., 2001) may partly explain why they exhibit different shapes (Audergon, 1985). For example, if a given genotype starts its diameter growth earlier at one site than at another while the dynamics of loading are similar at both sites, the first variety will tend to have a lower uprighting rate and appear more bent.

The methodology presented in this paper may be applied to other categories of stems as well as to other genotypes to clarify the relationships between growth processes and stem shape. More generally, it can be used to compare populations based on any criterion, such as comparing different growth conditions for the same genotype.

APPENDIX: MECHANICAL FORMULAE

Three simple mechanical models were built to predict the re‐orientations of a growing stem. They model independently the effect of different biomechanical phenomena. The ‘model of passive bending’ predicts the bending of a stem due to an addition of load, assuming the stem is not growing in diameter. The ‘model of passive uprighting’ predicts the incomplete uprighting of an unloaded stem, assuming diameter growth occurred between the loading and the unloading phase. The ‘model of active uprighting’ predicts the reorientation of a stem due to the maturation of new wood layers.

Models are based on beam theory and on the principles of its application to a growing tree (Fournier, 1991a, b). In this section, an application of these principles is presented in very simple cases. The stem and biomechanical stimuli are represented by a small number of parameters, leading to simple analytic formulae where the meaning and the influence of each parameter can be easily identified.

Model A: passive bending

Let us consider a cylindrical beam of length, L, and diameter, D, perfectly embedded at its base and initially leaning at an angle, ϕ, from horizontal (Fig. 3). This beam is made of a homogeneous elastic material characterized by its modulus of elasticity, E. A load increment of mass M is attached to it at a distance, pL, from the base (p is the relative position of the load along the beam).

The change in orientation, Δγ, due to the bending of the beam is the sum of local curvature variations along the beam. Variation in curvature at curvilinear abscissa, s (from the base) is given by beam theory:

Δc(s) = Δm(s)/k(s)

where Δm(s) is the variation of bending moment at abscissa, s, and k(s) is the flexural rigidity of the beam at abscissa, s. As diameter and material properties of the beam are assumed to be uniform, the rigidity is constant along it. For a circular cross‐section, it is given by:

k(s) = πED⁴/64

The bending moment at abscissa, s, depends on loads attached to the downward beam portion, i.e. the part of the beam located between s and the free extremity. From the base to abscissa, pL, it is given by:

Δm(s) = w(s) δ_x(s)

where w(s) is the weight of the downward beam portion and δ_x(s) is the lever arm of the weight. The weight of the load is given by:

w(s) = –gM

where g is the gravity constant.

The lever arm depends on the position of the load relative to s. In a ‘small displacements’ formulation, we ignore the variations of ϕ during deformation. The lever arm is then given by:

δ_x(s) = (pL – s)cosϕ

From abscissa, pL, to the top of the beam, the bending moment is null because the downward mass is null. Therefore, local variations in curvature are given by:

Δc(s) = –64gM(pL – s)cosϕ/(πED⁴)    for s < pL

Δc(s) = 0 for s ≥ pL

Integrating Δc(s) from 0 to L allows the expression of Δγ as:

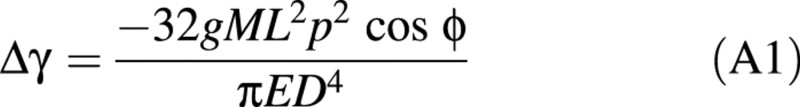
Model B: passive uprighting

Equation A1 is a simple model to predict the bending of a stem when diameter growth is negligible. Let us now assume that this stem is growing in diameter after being loaded. Let ΔD denote the diameter increment in the bent position, assumed to be uniform along the stem. Let us ignore the joint effect of the load and maturation strains due to the new wood layer, so that the shape of the stem is supposed constant during diameter growth. Finally, let us assume that a part of the initial load (ΔM > 0) is removed (Fig. 4).

The problem of re‐orientation during the unloading operation is analogous to the problem of passive bending, considering a negative load –ΔM and the total diameter D + ΔD. Assuming that the material properties in the new wood layers are the same as in the old wood layer, the change in orientation of the top (Δγ′) is given by:

It can be simply expressed as a function of previous bending Δγ:

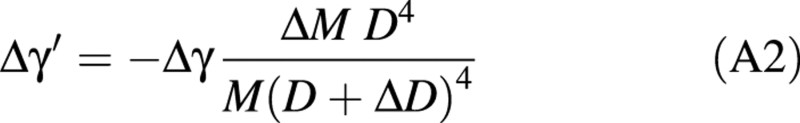
Model C: active uprighting

Equation A2 is based on the assumption that the shape of the stem does not vary during diameter growth. However, in most deciduous tree species, the production of tension wood on the upper part of the stem creates an asymmetrical field of maturation stresses, which generates stem uprighting. Let us assume that tension wood is located in the upper part of the section as a radial band of angular extension, β (Fig. 5).

The curvature variation at abscissa, s, is given by:

Δc(s) = Δm*(s)/k(s)

where k(s) denotes the flexural rigidity of the stem and Δm*(s) the bending moment due to wood maturation at abscissa, s. It is given by:

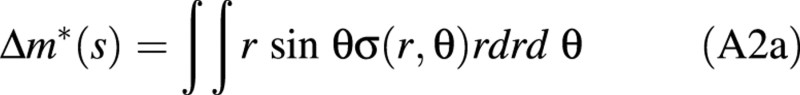
where σ(r,θ) denotes the intensity of maturation stress at any position in the section (r is the distance to the centre of the section and θ is the polar angle).

Let us assume that the modulus of elasticity, E, is uniform over the section and that the intensity of maturation stress only depends on the nature of the wood. Let σ_NW = Eϵ_NW denote its value in normal wood and σ_TW = Eϵ_TW its value in tension wood. Due to axisymmetry of the problem, uniform values of stress (e.g. normal wood everywhere) would not induce any bending moment. Therefore, only the contrast between tension wood and normal wood plays a role:

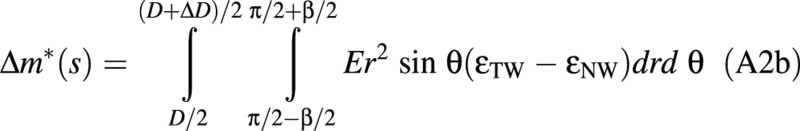
Assuming small variations of diameter (ΔD << D), this expression can be integrated as:

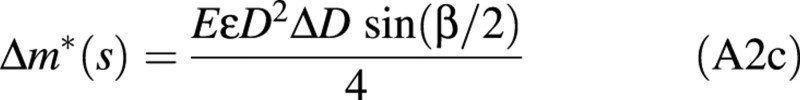
where ϵ = ϵ_TW – ϵ_NW denotes the difference in maturation strains between normal and tension wood.

The change in orientation of the top of the stem is therefore given by:

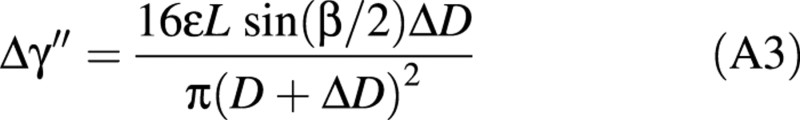
Received: 31 July 2003; Returned for revision: 3 November 2003; Accepted: 3 December 2003; Published electronically: 23 February 2004