Size‐Dependent Growth and the Development Of Inequality in Maize, Sunflower and Soybean

Abstract

Links were investigated between allometry of plant growth and dynamics of size structure of well‐fertilized, irrigated crops of soybean (Glycine max L.), sunflower (Helianthus annuus L.) and maize (Zea mays L.) grown at standard plant‐population densities (D), as in commercial crops (D = 30, 6 and 8·5 plants m^–2, respectively), and at high densities (2D). Patterns of size‐dependent growth of shoot and seed mass accumulation were distinctly different among species. In soybean and sunflower, non‐linear relationships between size and subsequent growth led to strong hierarchical populations in terms of both shoot and seed biomass. Curvilinear (soybean) and sigmoid (sunflower) size‐dependent growth determined strongly asymmetrical (soybean) and bimodal (sunflower) frequency distributions of shoot biomass indicating predominantly size asymmetrical competition among individuals. In comparison, a lower plant‐to‐plant variation coupled with a typical linear allometry of growth to plant size indicated symmetrical two‐sided plant interference in maize. Despite the weak development of hierarchies in shoot biomass, a strong inequality in reproductive output developed in crowded populations of maize indicating an apparent breakage of reproductive allometry.

INTRODUCTION

Interactions among neighbouring individuals in populations lead to size inequality and can restrict the reproductive outcome and/or survival of suppressed individuals (Yoda et al., 1963; Mohler et al., 1978; Kikuzawa, 1999). Interactions among neighbours bring about changes in the dynamics of size structure of populations over time (Koyama and Kira, 1956). While development of hierarchies is more marked in populations of wild plants, it is also common in crops despite the comparatively uniform age and genetics of the individuals, and agronomic practices that often aim to supply amply resources.

Empirical and theoretical studies—mainly in the field of plant population ecology—have contributed to our knowledge of the growth of individuals (Warren Wilson, 1981; Hara, 1986b) and the size structuring of populations (Koyama and Kira, 1956; Hara, 1984). However, underlying mechanisms and links between these two processes are poorly understood (Hara, 1986b; Kikuzawa, 1999). Some authors have claimed that the relationship between initial plant size and subsequent growth determines the size structuring in plant populations (Westoby, 1982; Hara, 1984b). Notwithstanding its ecological significance, few studies have been framed against this concept (Weiner and Thomas, 1992; Thomas and Bazzaz, 1993; Schwinning, 1996; Berntson and Wayne, 2000; Suzuki and Hara, 2001).

In crop physiology, studies dealing with the analysis of individuals or the development of size hierarchies are limited to a very small number of examples. For instance, analyses based on individual plants growing within crops were used to build relationships between yield or its components (seed number and mass) and growth (Edmeades and Daynard, 1979; Vega et al., 2001). Interestingly, the individual plant‐based approach demonstrated that allocation of dry matter to reproduction, quantified as harvest index or seed number per unit of growth, is size‐dependent, possibly reflecting the condition of stressed individuals in the population. While allometric analysis in species of economic importance has been useful for modelling yield‐related processes, it has rarely been used to improve our understanding of how neighbouring plants within crops interact, and how these interactions affect crop yield and its stability.

The objective of this work was to improve understanding of the dynamics of size structuring in crop species, analysing its connection with size‐dependent growth. The experimental framework is based on three main components. First, a case study is presented for three species (soybean, sunflower and maize) that differ in physiological and morphological traits, including growth habit (determinate vs. indeterminate), canopy structure (erect vs. horizontal leaves) and plant location of reproductive sinks (apical vs. axillary). Secondly, dynamics of the population structure are analysed by following growth of the same individual plants using a non‐destructive method (Vega et al., 2001). And thirdly, attention is focused on the development of size inequality and its relationship with reproductive success.

MATERIALS AND METHODS

Experiments

Soybean, sunflower and maize crops were sown at Balcarce, Argentina (37°45′S, 58°18′W) on optimal planting dates and at two plant densities: standard, as in commercial crops (D = 30, 6 and 8·5 plants m^–2, respectively), and high (2D). In each species, treatments were laid out in randomized blocks with three replications. Target plant densities were achieved by modifying the distance between plants within rows that were 15 m long and 0·7 m apart. All crops were sown by hand, fertilized and irrigated; weeds and insects were controlled effectively. Shoot and reproductive biomass of tagged individuals was determined non‐destructively four times during vegetative and reproductive growth stages, and destructively at maturity. Details of the non‐destructive technique are presented elsewhere (Vega et al., 2001). Briefly, destructive plant samplings (n ≌ 60, including both plant densities) were performed at each growth stage to derive allometric relationships between biomass and morphometric variables of plant (height, basal stem diameter, number of branches in soybean) and reproductive structures (diameter and length of ears in maize and head diameter in sunflower). Using these relationships, shoot and reproductive biomass of tagged individuals (258 > n > 322) were determined non‐destructively at each growth stage. At maturity, shoot biomass, yield and its components were recorded for each individual. In soybean, a species characterized by complete leaf shedding at maturity, final biomass did not include leaves. Plant growth rate during the most critical period for seed number determination, i.e. flowering ± 15 d in sunflower and maize, and from flowering to the start of seed filling or to mid‐seed filling in indeterminate soybean (Andrade et al., 2000), was calculated as the ratio between accumulated biomass and the duration of the period. Plants that completely failed to set seed—although not necessarily with null reproductive output—were considered barren plants. As a measure of reproductive partitioning at maturity, the harvest index was estimated for each individual as the ratio between seed mass and total shoot biomass (Vega et al., 2000).

Analytical approach

Research on plant‐to‐plant variation and its relationship with key processes, such as type and degree of interference among individuals and development of size hierarchies, relies on the analysis of frequency distributions of plant size variables, e.g. biomass, height and stem diameter. Although statistical descriptors such as the moments around the mean (standard deviation, skewness, kurtosis) give valuable information, their interpretation is not always straightforward (Benjamin and Hardwick, 1986; Wyszomirski, 1992). Moreover, statistical descriptions at one moment contribute little to the understanding of underlying processes (Weiner and Thomas, 1992). Descriptors of size hierarchies have been debated widely (Bendel et al., 1989). For example, it has been argued that size hierarchy could be better analysed using measures of size inequality, including the Lorenz curve and the Gini coefficient (Weiner and Solbrig, 1984), rather than using measures of size asymmetry (i.e. skewness). Theoretical models often predict size bimodality (which indicates the co‐existence of subgroups within the same density function), but empirical evidence for bimodality remains elusive owing, in part, to the lack of direct statistics for its evaluation (Ford and Diggle, 1981; Westoby, 1982; Wyszomirski, 1992). Some descriptors have been associated with bimodality, i.e. negative kurtosis (platykurtosis) of non‐transformed or log‐ or Box–Cox‐transformed variables (Ford, 1975; Wyszomirski, 1992; Nagashima et al., 1995). However, interpretation of bimodality through kurtosis is difficult and may be misleading, particularly when frequency distributions are strongly asymmetrical or leptokurtic (Wyszomirski, 1992).

In this study a series of descriptors (i.e. mean, standard deviation, skewness and kurtosis) was applied to non‐transformed data. In addition, the theoretical approach developed by Westoby (1982) and Hara (1984) was explored. These authors proposed that population dynamics are driven by particular patterns of size‐dependent growth, and introduced the concept of distribution‐modifying functions (DMF; Westoby, 1982) or growth functions [G(t, x); Hara, 1984], which relate initial plant size to subsequent growth. Hereafter we refer to this relationship as size‐dependent growth. The type of DMF or G(t, x) during a time interval affects the population size structure at the end of the time interval. The authors indicated that DMF or G(t, x) would range from the simplest linear model to curvilinear and sigmoid functions. As significant terms are included in these functions, the moments around the mean and, thus, the shape of frequency distributions (normal or asymmetrical) will be affected. For example, DMF with a significant cubic term would affect the four moments and yield bimodal frequency distributions (Westoby, 1982).

To analyse and contrast size inequality in terms of shoot and reproductive biomass at maturity, Lorenz curves were built as proposed by Weiner and Solbrig (1984).

RESULTS

Development of asymmetry in plant biomass and height

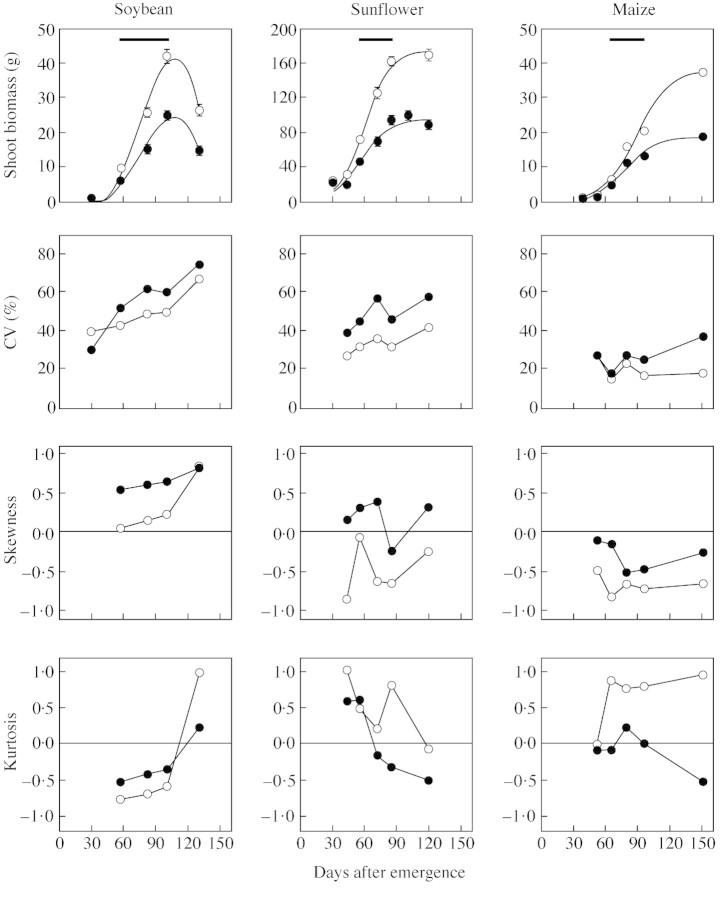
Accumulation of shoot biomass in the average plant was accompanied by dynamic changes in plant‐to‐plant variation within populations (Fig. 1). In comparison with standard plant population density, high density increased plant‐to‐plant variation but did not affect the time‐course of either skewness or coefficient of variation (CV). Plant‐to‐plant variation (skewness and CV) was largest in soybean and smallest in maize. The trend for positive skewness in shoot biomass, which leads to L‐shaped frequency distributions, was large in soybean and moderate in sunflower at high plant density. In maize, frequency distributions of shoot biomass were predominantly normal or negatively skewed (J‐shaped).

Fig. 1. Evolution of the mean and its standard error, the coefficient of variation (CV), skewness and kurtosis of biomass per plant in soybean, sunflower and maize grown at two plant population densities: standard (D = 30, 6 and 8·5 plants m^–2, respectively; open symbols) and high (2D; closed symbols). Horizontal bars in the upper panel indicate the critical period for seed set. In soybean, typical leaf shedding accounted for the decrease in biomass at maturity.

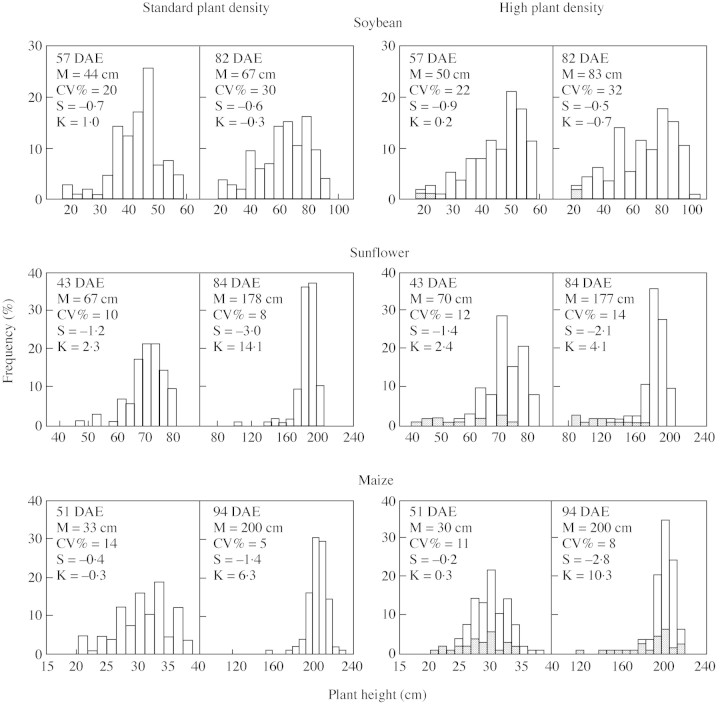
Plant height structures were negatively skewed both at standard and at high plant densities (Fig. 2). Among species, soybean had the largest plant‐to‐plant variation and a trend for negative kurtosis (flat‐topped structure). Sunflower and maize developed strongly J‐skewed and leptokurtic populations. These traits were coupled with reduced plant‐to‐plant variation (8 > CV% > 14) and a large proportion of individuals reaching the canopy modal height (Fig. 2). Stem elongation rates per unit of growth during a 15‐d period prior to flowering, i.e. in the early phase of the critical period for seed set were negatively associated with plant height in sunflower (y = 441e^–0·04x, R² = 0·8) and maize (y = 517 e^–0·03x, R² = 0·7). In sunflower, barren individuals (Fig. 2) were, on average, 35 % shorter than the mode, and ceased stem elongation at the beginning of the critical period for seed set. Some of these individuals senesced shortly after flowering, accentuating both skewness and kurtosis of plant height at maturity. In contrast, barren maize individuals were found in all height categories with no evidence of self‐thinning. Bimodality in height, a trait indicative of the coexistence of two canopy levels within the same population (Nagashima et al., 1995), was not evident in these three species. In soybean, however, negative kurtosis both in non‐ (Fig. 2) and Box–Cox‐transformed (not shown) final height data is an indirect indicator of a trend for bimodality (Wyszomirski, 1992). Similar trends were confirmed in an independent set of soybean experiments (C. R. C. Vega, unpubl. res.).

Fig. 2. Frequency distributions of plant height measured during vegetative and reproductive stages in soybean, sunflower and maize plants grown at standard and at high plant population densities. DAE, Days after crop emergence; M, mode; CV, coefficient of variation; S, skewness; K, kurtosis. Grey bars indicate position of ultimately barren individuals.

Population structure during the critical period for seed set

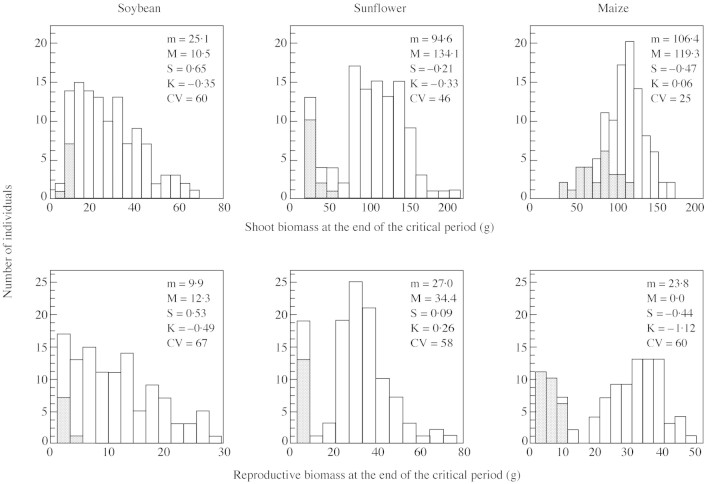
At the end of the period for seed set, the frequency distribution of shoot biomass was L‐shaped in soybean, bimodal in sunflower and normal in maize. These patterns were found at both standard (only shown as moments around the mean in Fig. 1) and high plant population densities (Fig. 3), and persisted in mature populations (Fig. 4). Soybean was additionally distinguished by extended ranges of shoot biomass on both tails of the frequency distributions, supporting the notion of a greater development of size hierarchies in relation to the other species (see also CV in Fig. 1). Size structures for repro ductive output closely mirrored those of shoot biomass at standard plant population density (not shown) but displayed parallelism only in soybean and sunflower at high density (Fig. 3). In high‐density maize populations, a bimodal frequency distribution of reproductive biomass contrasted with a rather normal distribution for shoot biomass. Bimodality in reproductive output in maize and sunflower was largely associated with barren individuals (Fig. 3), which developed reproductive structures but did not set seed. In sunflower, anticipated harvest of early senescing individuals (most of them barren) allowed for quantification of bimodality in shoot biomass at maturity (Fig. 4).

Fig. 3. Frequency distributions of plant shoot and reproductive biomass at the end of the critical period for seed set in crowded populations of soybean (n = 114), sunflower (n = 111) and maize (n = 105). m, Mean; M, mode; CV, coefficient of variation; S, skewness; K, kurtosis. Grey bars indicate position of ultimately barren plants.

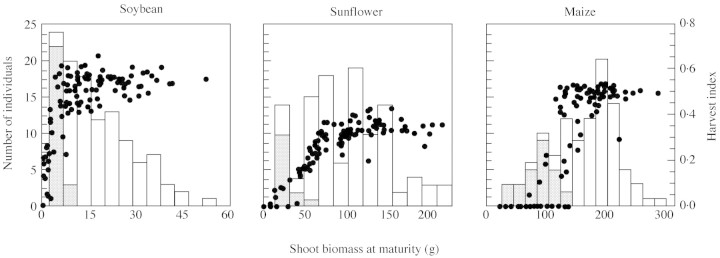
Fig. 4. Frequency distributions of plant shoot biomass in crowded populations of soybean, sunflower and maize at maturity. Moments of the frequency distributions are presented in Fig. 1. Grey bars indicate barren individuals, and closed circles indicate plant harvest index, i.e. seed mass/total shoot mass (adapted from Vega et al., 2000).

Size‐dependent growth and the development of hierarchies

The development of size hierarchies around the critical period of seed set reflected distinctive patterns of size‐dependent growth in each species: curvilinear in soybean, sigmoidal in sunflower and linear in maize (Fig. 5; Table 1).

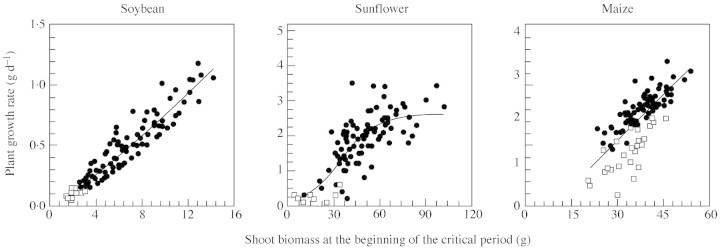
Fig. 5. Relationships between plant growth rate during the critical period for seed set and initial biomass in crowded populations of soybean, sunflower and maize. Fitted models are presented in Table 1. Open squares indicate barren individuals.

Table 1.

Models for the relationship between plant growth rate during the critical period for seed set (G_C) and initial shoot biomass per plant (S_P) in soybean, sunflower and maize crops grown at high plant population density (56·5, 10·3 and 16·9 plants m^–2)

Species	Model type	Parameters ± s. e.	R2*	n †
Soybean	GC = a*SPb	a = 0·053 ± 0·005	0·89	114
		b = 1·15 ± 0·046
Sunflower	GC = a/{1+ exp [–(SP – b)/c]}	a = 2·60 ± 0·138	0·68	111
		b = 35·12 ± 1·861
		c = 11·15 ± 1·878
Maize	GC = a + bSP	a = –0·58 ± 0·222	0·57	105
		b = 0·07 ± 0·006

* Coefficient of determination; all models and parameters were significant at P < 0·0001 except for parameter a in maize (P < 0·01).

^† Number of individuals.

A polynomial with a significant positive quadratic term (P < 0·0001) fitting size‐dependent growth rate in soybean, closely predicted the ability of relatively few large‐ and medium‐sized plants to more than proportionally increase plant growth rate in response to initial size. Similar curvilinear size‐dependent growth was observed during early growth, i.e. during the period from flowering to the beginning of seed set (G = 0·03M^1·3, where G is plant growth rate and M is initial shoot biomass; P < 0·0001). Such a plastic response of soybean would have boosted the divergence between small and large individuals and intensified the development of strongly asymmetrical populations (Figs 1 and 4).

Individuals at both tails of the sigmoid pattern of size‐dependent growth had major consequences for the size‐structure of sunflower populations (Fig. 5). First, plants with an initial shoot mass between approx. 50 and 120 g had similar growth rates during the critical period of seed set; their contribution to increasing skewness was therefore less than that of larger plants in soybean populations. Secondly, impaired growth of most individuals with initial shoot mass below 40 g led to bimodality. This process caused a rather abrupt drop in skewness and kurtosis (Fig. 1) and prevented the population from being strongly asymmetrical. Removing these slow‐growing, mostly barren individuals from the analysis yielded a positively skewed frequency distribution of shoot biomass, i.e. skewness shifted from –0·21 to 0·64, and kurtosis from –0·33 to 0·37. The trend for bimodality in sunflower shoot biomass was observed during the whole growth cycle before self‐thinning occurred at both standard (data not shown) and, more intensively, at high plant population densities (Fig. 4).

The absence of bimodality or L‐asymmetry in shoot biomass (Fig. 3) or plant growth rate (not shown) was conspicuous in maize populations. Two features of maize populations are worthy of special consideration in this regard: (1) the absence of strongly suppressed, extremely small individuals; and (2) the weak size hierarchies compared with those of other species. Only a few individuals had an impaired growth rate during the early stages of the critical period of seed set (plant growth rates close to or less than 1 g d^–1; Fig. 5). Importantly, when plant growth rate was plotted against initial shoot biomass (Fig. 5), datapoints for barren plants were consistently below the general relationship. Linear models fitted to fertile and sterile individuals had different intercepts (approx. 0 vs. –0·78 ± 0·34), but similar slopes (0·06 ± 0·001 vs. 0·06 ± 0·01). Although less marked than in sunflower, the uncoupling of plant growth rate and initial size in barren maize plants was a major factor underlying the drop in skewness in shoot biomass around the critical period (Fig. 1). The comparatively small reduction in growth rate of sterile plants did not allow for the development of bimodality in mature maize populations. However, the fall in kurtosis and increase in CV at high plant population densities (Fig. 1) revealed the segregation of fertile and barren individuals with contrasting abilities to accumulate biomass (Fig. 4). Removal of barren plants from the analysis of shoot mass at maturity increased skewness from –0·26 to 0, kurtosis from –0·5 to 0·4, and decreased CV from 37 to 22.

Inequality in reproductive output of crops grown at high plant density

At maturity, frequency distributions of plant seed mass closely paralleled those of reproductive biomass at the end of the critical period: L‐asymmetrical in soybean, and bimodal in sunflower and maize (Table 2). Bimodality in seed number per plant, the main yield component, was apparent in all three species, although it was stronger in maize as indicated by negative kurtosis (Table 2). In all three species, individuals belonging to the lowest categories of shoot biomass exhibited decreasing efficiency in terms of harvest index (Fig. 4). Such a pattern was associated with bimodal (sunflower and maize) or strongly asymmetrical (soybean) frequency distributions of harvest index (Table 2).

Table 2.

Coefficient of variation (%) and moments of the frequency distributions of seed mass (Y_p; g per plant), seed number per plant (N_S) and harvest index per plant (H, dimensionless) in soybean, sunflower and maize crops grown at high plant population densities (56·5, 10·3 and 16·9 plants m^–2, respectively)

	Soybean			Sunflower*			Maize
	Y p	N S	H	Y p	N S	H	Y p	N S	H
Mean ± s. e.	7·8 ± 0·6	52 ± 3·7	46 ± 1·4	29·7 ± 1·9	861 ± 44·4	25 ± 1·2	59·8 ± 4·2	240 ± 17·0	33 ± 2·1
Skewness	0·85	0·60	–1·44	0·29	–0·09	–0·94	–0·32	–0·29	–0·71
Kurtosis	0·28	–0·59	1·24	–0·80	–0·66	–0·34	–1·35	–1·49	–1·33
CV	82	77	33	67	53	50	72	73	66
Median	6·5	43	51	28·4	868	31	75·4	308	47
Mode	0·08	1	57	0	0	0	0	0	0

* Early‐senesced plants were excluded from the analysis at maturity.

Lorenz curves summarize and compare the development of size inequalities in shoot and seed biomass (Fig. 6). Departures from the 1 : 1 line, which indicates perfect equality among individuals (Weiner and Solbrig, 1984), ranked soybean > sunflower > maize in inequality. Soybean and sunflower, while developing strong hierarchies in terms of shoot biomass, showed a close parallel between shoot and seed biomass inequality in mature populations. Conversely, maize had the weakest hierarchical structure in terms of shoot biomass, and the strongest bimodality in reproductive output. From Lorenz curves, bimodality can be assessed as two linear sections representing modes (Weiner and Solbrig, 1984). Accordingly, bimodality in seed mass in maize was apparent in Lorenz curves (Fig. 6) as two sections joining at x ≌ 30 (antimode of the bimodal frequency distribution of seed mass).

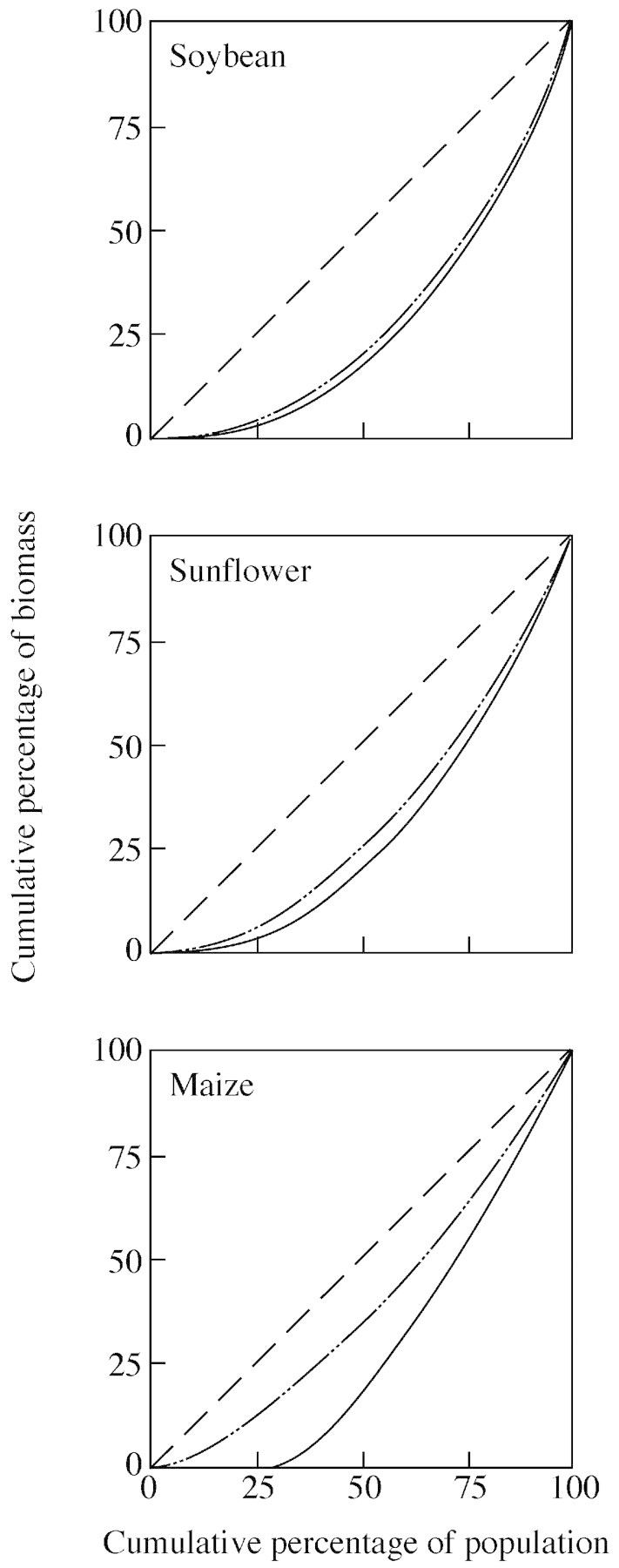
Fig. 6. Lorenz curves for plant shoot biomass (– ··) and seed yield (—) at maturity in high‐density populations of soybean, sunflower and maize (56·5, 10·3 and 16·9 plants m^–2, respectively). The 1 : 1 line (– –) indicates perfect equality among individuals.

At this point, the relative contribution of individuals to shoot and seed biomass in maize can be assessed as follows. The smallest 30 % of individuals accounted for 25 % of the population’s shoot biomass at the beginning of the critical period for seed set (data not shown), 16 % of shoot biomass at maturity, and only 1 % of seed mass (Fig. 6). The heaviest 65 % of individuals, comprising the second linear portion of the seed mass curve, exhibited a normal frequency distribution of seed mass, with mean ± s. e. = 90 ± 2·2 g per plant. In comparison, the smallest 30 % of sunflower individuals accounted for 15 % of the population’s shoot biomass at the beginning of the critical period (data not shown), and 9 % of shoot biomass and 5 % of seed mass in mature populations. As in maize, Lorenz curves were useful at detecting bimodality in seed mass in sunflower. With the exception of seed number (Table 2), evidence for bimodality in soybean was not apparent from frequency distributions (Figs 3 and 4) or from Lorenz curves (Fig. 6). Strong asymmetry in seed yield, however, could have obscured bimodality in soybean.

DISCUSSION

Allometry of individual plant growth and development of size hierarchies

Interactions among individuals and plant‐to‐plant variation both increase with ontogeny and plant population density (Fig. 1; Koyama and Kira, 1956; Thomas and Bazzaz, 1993). There is substantial evidence that strong interactions among neighbouring plants lead to populations with L‐shaped frequency distributions of biomass, i.e. few large and many small individuals (Koyama and Kira, 1956; Harper, 1977). In this study, such a response was analysed in three crop species that differ in their ability to tolerate crowding, i.e. with increasing plant density, yield per unit of surface responds in an asymptotical (soybean and sunflower) or parabolic (maize) fashion (Valentinuz, 1996).

Soybean and sunflower crops showed traits typical of markedly hierarchical populations, including large range, high plant‐to‐plant variation and positive skewness of plant size (Fig. 1; Ford, 1975; Harper, 1977; Hara, 1984; Weiner and Solbrig, 1984). Such a development of hierarchies has frequently been associated with asymmetrical competition for resources, with large individuals acquiring a disproportionate share of resources in relation to small ones (Ford, 1975; Weiner and Fishman, 1994; Schwinning and Weiner, 1998). Light‐mediated interactions among neighbouring plants, including early signals involving changes in the spectral composition of light and trophic effects of competition for radiation (Ballaré et al., 1994) are probably relevant in the well‐fertilized, irrigated crops used in this study. Owing to radiation being a pre‐emptable resource, it could be inferred that asymmetrical interference was intensified with increasing crowding (Hara, 1988; Weiner, 1990; Schwinning, 1996; Berntson and Wayne, 2000). Size asymmetry was stronger in soybean than in sunflower. In the former, frequency distributions rapidly shifted to L‐ (shoot biomass) or flat‐shaped (height), indicating that a large proportion of individuals was restricted to small size categories. Possibly, early events such as differences in microenvironment or emergence time led to small differences in growth among plants and these were compounded over time (Benjamin and Hardwick, 1986). Importantly, the high phenotypic plasticity of soybean may underlie the ability of a few large individuals to increase growth exponentially and, hence, to accentuate the strong skewness of shoot biomass (Fig. 5).

In sunflower, measurement of shoot biomass asymmetry over time allowed the detection of bimodality (Figs 3 and 5), an apparently transitional phenomenon prior to self‐thinning of slow‐growing individuals (Kikuzawa, 1999). Develop ment of bimodality in shoot biomass is rather infrequent in plant populations, although statistical constraints limit its detection (Wyszomirski, 1992). Bimodality can result from the development of a lower canopy (Nagashima et al., 1995; Yokozawa and Hara, 1995), the co‐existence of sub‐groups of individuals having different relative plant growth rate (Ford, 1975), or from strong, asymmetrical competition for resources. In our study, bimodality of shoot biomass in high‐density sunflower populations can be detected visually (Figs 3 and 4) and statistically through a rather abrupt decrease in skewness and kurtosis around the critical period for seed set (Fig. 1). Importantly, we provide evidence indicating that bimodality could result from a breakage of growth allometry in the smallest individuals (those with plant growth rates between 0 and 1 g per plant; Fig. 5). Impaired growth of these individuals was coupled with early cessation of stem elongation (Fig. 2), reduced reproductive partitioning (Fig. 3) and early senescence. A sigmoidal pattern of size‐dependent growth emerged when the complete population was considered (Fig. 5). We thus provide empirical evidence supporting Westoby’s (1982) proposal that bimodal frequency distributions result from sigmoid growth dependence.

In contrast to sunflower and soybean, maize displayed rather normal or J‐shaped frequency distributions of shoot biomass (Figs 3 and 4). These results were striking, and indicated that interference among neighbouring plants was not enough to drive processes leading to the development of strong size hierarchies, even at a plant population density twice that normally used by commercial growers. In comparison with the other species, reduced development of asymmetry in maize was also evident for plant height, a key trait for radiation interception, efficiency in photosynthesis per unit of biomass and success in crowded stands (Ballaré et al., 1994; Weiner and Fishman, 1994; Berntson and Wayne, 2000; Anten and Hirose, 2001). Frequency distributions of plant height, which were normal at early growth stages and remarkably leptokurtic at more advanced stages, were coupled with low plant‐to‐plant variation (Fig. 2). Daynard and Muldoon (1983) found similar patterns in height structure of maize populations grown at densities of up to 20 plants m^–2. In this study, the ability of most individuals to reach the canopy height showed that growth was hardly impaired in small, shorter plants. Although very few (≌ 10 %) plants could not attain the canopy height (mode ± 10 % mode), these shorter individuals had greater rates of stem elongation per unit of growth than tall individuals, probably reflecting their ability to respond phenotypically to the stimulus of an altered light environment (Ballaré et al., 1994). Importantly, since growth was not completely suppressed even in the smallest individuals, self‐thinning and bimodality would be less frequent in maize than in soybean and sunflower. Although bimodality was not evident for shoot biomass, it is worth noting some indirect responses of shoot biomass that are indicative of a slight trend towards developing distinct groups of plants at high population density: (1) the abrupt drop in skewness around the critical period; and (2) the negative kurtosis at maturity. Bimodality at maturity would be more likely to occur since the larger biomass accumulation in fertile than in barren plants during the seed filling period shifts the shoot biomass mode to the right of the density function. Maize seed can account for up to 100 % of biomass accumulation after flowering (Fig. 1; Valentinuz, 1996). In contrast, barren plants would not continue to accumulate biomass at similar rates to fertile plants owing to impaired photosynthesis or assimilate translocation, limited ability of alternative sinks to store assimilates and feedback control of photosynthesis (Sadras et al., 2000a). Import antly, our results highlight how static interpretation of bimodality in shoot biomass, e.g. at maturity, may obscure the mechanisms of size hierarchy development.

In summary, close‐to‐normal frequency distributions of shoot biomass were associated with linear size‐dependent growth in maize. Non‐linear growth allometries, i.e. curvilinear in soybean and sigmoidal in sunflower, triggered the development of skewness and bimodality. These results closely fit predictions by theoretical models (Ford and Diggle, 1981; Westoby, 1982; Hara, 1984). The temporal drop in skewness in four out of six cases in our study (Fig. 1) has also been observed in other studies (Gates et al., 1983; Hara, 1986b). There is no clear biological explanation for the decrease in skewness, although it has been associated with self‐thinning (Mohler et al., 1978). In our study, the decline in skewness was not causally associated with self‐thinning or with barrenness, since it was also observed at standard plant densities. Importantly, however, it was associated with an apparent trend for the development of a second mode of slow‐growing individuals. At high plant population densities, most small individuals showed impaired or null reproductive output (sunflower and maize) or senesced early during the reproductive phase (sunflower).

Reproductive allometry

Soybean and sunflower showed a close similarity between shoot and seed mass inequality, possibly reflecting the similar strategy (high phenotypic plasticity) of the species (Connor and Sadras, 1992). In maize grown at high population density, a strong hierarchical population in terms of reproductive growth sharply contrasted with a rather normal frequency distribution of shoot biomass. Barrenness was the main source of bimodality in maize reproductive output. Thus, in this species, reproductive inequality at the population level would be only weakly associated with shoot biomass inequality. Although the likelihood of sterility decreased with the size of the individual, barrenness was not restricted to lighter or shorter individuals (Figs 2 and 3). Daynard and Muldoon (1983) consistently found bimodal frequency distributions of seed yield in maize crops grown at high plant population density, and demonstrated the potential for barrenness of individuals belonging to most size categories. Our work adds evidence that alterations in partitioning of biomass to reproductive structures may lead to a breakage of reproductive allometry in maize (Daynard and Muldoon, 1983; Vega et al., 2001).

Such a breakage in reproductive allometry highlights the uncoupling of vegetative and reproductive growth, and possibly relates to strong apical dominance in this monoecious species (Doebley et al., 1997). At the population level (Fig. 6), the breakage of reproductive allometry could account for the low tolerance of maize to high plant population densities. In this species, genotypic variation in response to high plant population densities has often been reported, but the underlying mechanisms are still poorly understood (Duvick, 1992). Based on the present results, it is hypothesized that tolerance to high plant population densities in maize is associated with the ability of hybrids to preserve reproductive allometry during the critical period of seed set.

Consistent with Donald’s (1981) concept of ‘weak competitor’ as an ideotype for monocultures, negative associations have been found between yield potential and sensitivity to competition in wheat and sunflower (Reynolds et al., 1994; Sadras et al., 2000b). Zhang et al. (1999) blended Maynard Smith’s (1982) concept of an evolutionary stable strategy, and Donald’s concepts of ideotype and communal plants, and showed that optimal resource partitioning maximizing crop yield is evolutionary unstable, with large growth redundancy in modern crop plants. In the light of the theories of Donald and Zhang, the present results for maize indicate that low competitive ability could be necessary, but not sufficient, to ensure high yield potential as breakage of reproductive allometry could negate the benefits of low sensitivity to intraspecific interference. Experiments comparing the stability of allometric relationships and sensitivity to competition in crops of contrasting maize hybrids could increase understanding of these traits and their potential use in breeding for yield potential.

Mechanisms controlling size structure

Patterns of plant‐to‐plant variation reveal the effects of species adaptive behaviour on use of resources and growth of individuals within populations. Soybean and sunflower displayed traits typical of populations undergoing asymmetrical competition for resources (Ford and Diggle, 1981; Weiner, 1990). In maize, a comparatively low plant‐to‐plant variation coupled with a linear size‐dependent growth indicated a less asymmetrical interference among individuals or, alternatively, a greater size symmetry for resource acquisition (Yokozawa and Hara, 1992; Berntson and Wayne, 2000). Importantly, these results, which are in agreement with those of other authors (Yokozawa and Hara, 1992), do not support the assumption that competition for light is always asymmetrical (Ford and Diggle, 1981; Hara, 1988; Weiner, 1990). Traits contributing to differences among species in symmetry of radiation capture include those related to canopy geometry, radiation interception and radiation‐use efficiency (Hara, 1986a, b; Yokozawa and Hara, 1992, 1995). Theoretical studies demonstrate that species with broad or horizontal leaves, with foliage mass located mainly in upper layers, with high light‐extinction coefficients and low radiation‐use efficiency are more likely to develop asymmetrical frequency distributions of plant biomass as crowding increases (Hara and Yokozawa, 1994; Yokozawa and Hara, 1995). In agreement with this, the present work showed that skewness of shoot biomass was lowest in maize, a species with more erect leaves, a lower light‐extinction coefficient and a higher efficiency in terms of plant growth rate per unit biomass (Andrade et al., 2000) than sunflower and soybean. In comparison, the trend for asymmetry was higher in soybean and sunflower, species with high light‐extinction coefficients particularly during the early phases of growth (Flénet et al., 1996; Andrade et al., 2000). Other traits that might be involved include: shoot and root morphological features that determine the foraging capacity for light and nutrients (dicots > monocots) (Grime, 1988); phenotypic plasticity (soybean > sunflower > maize); sensoring systems for eliciting shifts in allometric responses (Weiner and Thomas, 1992; Ballaré et al., 1994; Weiner and Fishman, 1994); and light compensation points for photosynthesis (maize > soybean and sunflower). Importantly, the nature and interactions among limiting factors influence the dynamics of growth and biomass allocation (Hara and Yokozawa, 1994; Schwinning, 1996), thus affecting the predominant mode of competition (Ford and Diggle, 1981; Weiner, 1990; Schwinning and Weiner, 1998). For example, competition for soil resources is mainly symmetrical (Casper and Jackson, 1997; Berntson and Wayne, 2000), whereas intraspecific competition for light in even‐aged populations shifts from asymmetrical to mainly symmetrical two‐sided as soil resources are depleted or crowding decreases (Hara, 1986a; Hara and Yokozawa, 1994; Schwinning, 1996; Anten and Hirose, 2001).

The study of growth allometry of individual plants and its consequences for key population traits opens new areas for research in agronomic studies. Donald’s (1981) concept that breeding for high yield potential favours plant types with reduced responsiveness to intraspecific competition needs to be linked to Zhang et al.’s (1999) theories on growth redundancy to investigate the dynamics and regulation of size structure as affected by species, genotype and their interactions with the environment. Insight from experiments designed against this conceptual framework would contribute to crop management (i.e. grain yield response to plant density and spatial pattern), and breeding for yield potential.

ACKNOWLEDGEMENTS

We thank Professor M. Westoby for helpful comments on our work, and thank INTA, UNMdP and CONICET for financial support. C.R.C.V. is a postdoctoral fellow of CONICET, the Research Council of Argentina and V.O.S. is funded by the Australian Grain Research and Development Corporation of Australia.

Received: 15 October 2002; Returned for revision 19 December 2002; Accepted 4 February 2003    Published electronically: 3 April 2003