What can we learn from learning models about sensitivity to letter-order in visual word recognition?

Abstract

Recent research on the effects of letter transposition in Indo-European Languages has shown that readers are surprisingly tolerant of these manipulations in a range of tasks. This evidence has motivated the development of new computational models of reading that regard flexibility in positional coding to be a core and universal principle of the reading process. Here we argue that such approach does not capture cross-linguistic differences in transposed-letter effects, nor do they explain them. To address this issue, we investigated how a simple domain-general connectionist architecture performs in tasks such as letter-transposition and letter substitution when it had learned to process words in the context of different linguistic environments. The results show that in spite of of the neurobiological noise involved in registering letter-position in all languages, flexibility and inflexibility in coding letter order is also shaped by the statistical orthographic properties of words in a language, such as the relative prevalence of anagrams. Our learning model also generated novel predictions for targeted empirical research, demonstrating a clear advantage of learning models for studying visual word recognition.

In the last decade a large number of studies have consistently reported that readers are surprisingly tolerant to letter transpositions. This aspect of visual word recognition, often labeled as “The Cambridge University effect” (an alleged study conducted at Cambridge University showing that readers don’t care about the order of letters), has been the focus of extensive research, heated debates, and impressive modeling efforts. Overall, studies that experimentally examined the impact of manipulating letter-order on reading performance have shown a very small cost of letter-transpositions in terms of reading time, along with robust priming effects when primes and targets share all of their letters but in a different order (e.g., jugde-JUDGE; Duñabeitia, Perea, & Carreiras, 2007; Johnson, Perea, & Rayner, 2007; Kinoshita & Norris, 2009; Perea & Carreiras, 2006a,b, 2008; Perea & Lupker, 2003, 2004; Rayner, White, Johnson, & Liversedge, 2006; Schoonbaert & Grainger, 2004). Transposed-letter (TL) effects were reported in a variety of European languages such as English (e.g., Perea & Lupker, 2003), French (Schoonbaert & Grainger, 2004), and Spanish (Perea & Carreiras, 2006a,b), but also for non-European alphabetic languages such as Basque (Duñabeitia, Perea & Carreiras, 2007), and Japanese Katakana (Perea & Perez, 2009).

The apparent indifference of readers to letter order converged with experimental findings such as relative position priming (Humphreys et al., 1990), and subset priming (Peressotti & Grainger, 1999), and was consequently taken to be a hallmark of reading. Its implications to modeling visual word recognition resonated with mounting theoretical discussions regarding the alignment problem (Davis, 1999), according to which, words are recognized irrespective of the absolute position of their letters (e.g., CAT, TREECAT), so that their letter identification must be context-sensitive and (relatively) position invariant. Because prior computational models of orthographic processing encoded letter positions in rigid and absolute terms (e.g., the Interactive Activation Model, IAM, McClelland & Rumelhart, 1981) and models of orthographic-to-phonological correspondences made similar peripheral assumptions about rigid orthographic coding (e.g., the Dual-Route Cascaded model, DRC, Coltheart et al., 2001; the Connectionist Dual Process Model, CDP, Zorzi, Houghton, & Butterworth, 1998; Plaut, McClelland, Seidenberg, & Patterson, 1996), they were taken to miss a critical component of orthographic processing— fuzziness in coding letter-position. This limitation led the way for a new generation of models that focused on producing letter-coding schemes and computational solutions that were non-rigid (e.g., the SERIOL model, Whitney, 2001; the SOLAR model, Davis, 1999; the Spatial Coding model, Davis, 2010; the Bayesian Reader model, Kinoshita & Norris, 2009; the Overlap model, Gomez, Ratcliff, & Perea, 2008).

The new models of reading naturally differ in their initial aims and in the scope of phenomena they describe. However, recent discussions regarding their descriptive adequacy have centered to a large extent on their relative ability to reproduce and fit the growing body of empirical data regarding readers’ resiliency to letter-jumbling, given different types of distortion in the sequence of letters. While this approach has advanced us in outlining the possible constraints imposed on the front-end of the reading system, it also had a critical disadvantage. From an empirical perspective, consistent findings have shown that TL priming effects are not universal but restricted to a family of languages (Frost, 2012a). For example, reading in Semitic languages such as Hebrew and Arabic is characterized by extreme letter-coding precision (Velan & Frost, 2007, 2009, 2011; Perea, Abu Mallouh, & Carreiras, 2010)¹. Thus, transposing the prime’s letters in Hebrew or Arabic does not yield a strong facilitation of target recognition as in Indo-European languages, and sometimes even hinders it (Velan & Frost, 2009, 2011)². Similarly, presenting sentences that contain TL words in rapid serial visual presentation results in strikingly poor reading performance in Hebrew but not in English (Velan & Frost, 2007). Recent studies from Korean (Lee & Taft, 2009, 2011) also indicate that letter-transposition effects are not obtained in the alphabetic Korean Hangul as they are in European languages. These cross-linguistic differences regarding the impact of letter-transpositions are critical for understanding visual word recognition and should be taken as important constraints while modeling it. Because most recent models of reading have exclusively focused on languages that show insensitivity to transposed letter effects, they miss the well-established cross-linguistic variability in positional encoding necessary in a general account. More important, from a theoretical perspective, understanding the source of differences in sensitivity to letter-position is critical for assessing the explanatory adequacy of any model of reading (see Frost, 2012a for an extensive discussion).

In the case of TL effects, the debate has centered on what it is that determines (or allows for the emergence of) insensitivity to letter order. For many recent modelers of visual word recognition the working hypothesis was that this reflects a hardwired neurobiological constraints in coding position of sequentially aligned visual stimuli given the inherent noise characteristic of the visual processing system (see Szwed et al., 2012; Grainger et al., 2012; Norris & Kinoshita, 2012). For example, in open-bigram models (e.g., Whitney, 2001), it is claimed that the brain encodes words based on the presence of all ordered combinations of two letters appearing in a given word (e.g., encoding the word ‘form’ as the collective bigrams ‘fo’, ‘or’, ‘rm’, ‘fr’, ‘om’, and ‘fm’). By this view, TL priming effects mirror the way in which the human brain encodes the position of letters in printed words in any language (e.g., Whitney, 2001; Grainger & Whitney, 2004; Dahaene et al., 2005), where letters are often taken as two-dimensional objects processed by the visual system (e.g., Grainger et al., 2012; Norris & Kinoshita, 2012). In contrast, in a recent review of TL effects across writing systems, Frost (2012a) has argued that the overall findings regarding letterposition insensitivity cannot be described and explained simply by assuming a predetermined characteristic of the brain’s neurocircuitry that processes orthographic information. Rather, it is an emergent particular consequence of the neural system’s interaction with the linguistic properties of European languages, reflecting an efficient optimization of encoding resources. By this account, in European languages printed words generally (albeit with some exceptions) differ by the identity of their constituent letters, so that different sets of letters are assigned to different words. Consequently, printed words can still be easily recognized even when their letters are transposed. In contrast, in Semitic languages, words are formed by inserting a tri-consonantal root into fixed phonological word-patterns (see Frost, Forster, & Deutsch, 1997, for a detailed description), and the root letters are the initial target of orthographic processing (e.g., Frost, Kugler, Deutsch, & Forster, 2005). Because many roots share a subset of three letters but in a different order, words often differ by the order of these letters rather than by their mere identity. This cross-linguistic difference is reflected by the differential prevalence of anagrams in European versus Semitic languages: Whereas in English, French, or Spanish anagrams are mostly incidental exceptions, in Hebrew or Arabic many words are anagrams because they are printed with the same set of letters but in a different order (Velan & Frost, 2011).

This account provides a very different theoretical explanation to TL effects. It shifts the cause of insensitivity to letter-order from a hard-wired and fixed neurobiological constraint of the visual/orthographic information processing system, to an emergent property of the interaction of the neurobiological constraints with a domain-general computational system that is tuned to the distributional characteristics of the linguistic environment. By this view, since for efficient reading, the statistical properties of letter distributions of the language (root vs. word-pattern letters) and their relative contribution to meaning have to be detected, readers of Semitic languages become sensitive to letter order. In contrast, readers of European languages simply do not require such sensitivity and are thus affected by the neurobiological noise involved in processing letters. Indeed, Velan and Frost (2011) have shown that even within one language, Hebrew, TL effects can be made to appear or vanish given the linguistic properties of the printed words that are presented as stimuli (see footnote 2). In that study, the authors demonstrated that when native speakers of Hebrew are presented with Hebrew printed words of non-Semitic origin, which resemble base words in European languages, the typical TL effects observed in European languages are obtained. The approach of some recent models of reading that essentially hardwire letter-position insensitivity given the general noise involved in processing visual stimuli (e.g., directly motivating positing open bigrams as a computational mechanism to produce relative-position priming effects; Grainger & Whitney, 2004, p. 58) is inevitably blind to these cross-linguistic and cross-stimuli differences, and does not explain how and why cross-linguistic differences are observed.

This brings us to the potential advantage of the approach advocated by proponents of learning models. Learning models are developed from the outset to gradually learn a mapping between representations via domain-general learning mechanisms (see McClelland et al., 2010). Thus, in such models, a specific behavior emerges instead of being hardwired. This approach de-emphasizes the tailoring of the model’s architecture and processing mechanisms, and instead focuses on how representations and processing principles interact with the statistical regularities in the environment during learning (see Rueckl, 2010, for a detailed review). The significant advantage of learning models in the context of understanding visual word recognition and letter-order effects seems evident. First, the emphasis on generic learning mechanisms is compatible with a broad range of learning and processing phenomena in general, including but extending well beyond the challenge of learning to read. Second, languages differ on many statistical properties, such as the distributions of orthographic and phonological sub-linguistic units, their adjacent and non-adjacent dependencies, the systematic correlations between graphemes and phonemes (or syllables), and the type of correlations between form and meaning through morphological structure (Frost, 2012a). Native speakers can pick up on these characteristics implicitly through statistical learning procedures (e.g., Frost et al., 2013). A model of reading that is built using this same set of principles has, therefore, the potential to capture, explain, and predict empirical phenomena observed in any language, and more specifically the observed cross-linguistic differences in TL effects.

Recently, Baayen (2012) has used a related approach to examine how the linguistic environment shapes sensitivity to letter order. Using Naïve Discriminative Learning (NDL, Baayen et al., 2011), Baayen compared the sensitivity to letter order in English versus biblical Hebrew, for cases in which words from the two languages were aligned with their meanings. Baayen (2012) demonstrated that pairs of contiguous letters (correlated with order information in the model) had a much greater functional load than single letters in Hebrew relative to English, thereby showing that greater sensitivity to letter order emerges in Semitic languages, when nothing but abstract discriminant learning principles are considered. Although Baayen’s modeling approach does not make explicit claims about bigrams as representational units, this choice of input representations does include some explicit relative position information, rather than allowing this property to be learned. More importantly, given the concatenated morphology of English, and because transpositions typically involve middle letters rather than initial or final ones, bigram representations naturally preserve morphological information for English (e.g., the plural suffix), more than for Hebrew. This could be a contributing factor to the higher loads of bigrams to meaning in English relative to Hebrew. A critical question, therefore, is whether language-specific letter-transposition effects would emerge during learning in a neural network, and if so, how and why?

From this perspective, learning models are akin to any empirical investigation. Considering TL effects, the modeler manipulates the statistical properties of the input scheme, aiming to examine whether sensitivity or insensitivity to letter-order emerges given implemented changes in the linguistic environment. The present paper offers such an investigation. Our aim was to produce a simple and readily-generalizable neural network model that demonstrates how differences in the statistical properties of the language naturally lead to differences in TL effects as a result of simple error-driven learning. In the following, we describe a multi-layer neural network that maps orthographic inputs to semantic outputs. The use of a relatively generic architecture here was intentional to emphasize that the results we obtained do not depend on a highly-tailored set of learning, representation, and processing principles, that have been developed for capturing a specific and narrow set of data. In so doing, we have implemented a fundamentalist model of reading-skills acquisition that intentionally eliminates irrelevant complexity and focuses only on the effects of letter identity and letter position (see Kello & Plaut, 2003; McClelland, 2009 for a discussion of this approach). This model was trained on Hebrew orthography or English orthography and its “behavior” was then tested in response to new pseudo-words that diverged from the original ones by means of letter transpositions or letter substitutions. Two different versions of these simulations were run. In Simulation 1, input words were represented using a coding scheme that orthogonalized the identity and position information. Accordingly, we treated each letter and its position as independent features of a word, and simulated noise in the positional units by making the positional information less readily available than the identity information. This representation scheme allowed us to directly investigate some of the characteristics of the network’s solutions – in particular, its different treatment of position and identity information – when learning the orthography-to-semantic mapping. In Simulation 2, we replicated these findings using the well-known, biologically-driven coding scheme of the overlap model (Gomez et al., 2008) to demonstrate that the outcome of the simulations is not input-code dependent but, rather, reflects general learning principles. Each of these two simulations was further divided to two different examinations: the first used highly simplified words that allowed us to examine the model’s behavior under tightly controlled settings, whereas in the second, the same network was tested on real Hebrew and English words, thus allowing the examination of the model in realistic settings that mimic the true linguistic environments of English and Hebrew.

Simulation 1: Word representations with independent identity and position information

Simulation 1a: Artificial words

To evaluate whether differences in word structure in Semitic versus European languages shape sensitivity to letter order, we began our examinations with a set of artificially created words. These words were intentionally simplified to allow us to focus on the main linguistic difference between Hebrew and English which we presume lie in the heart of letter order sensitivity: The statistical properties of letter distributions that differentiate between words. Two sets of words were therefore created: an “English-like” set and a “Hebrew-like” set. In the English-like set, there were no anagrams, and each “word” was comprised of its own unique random combination of letters. In the Hebrew-like set, a given combination of letters occurred in two orders in two different words, resulting in a substantial number of anagrams. Taken together, these simulations were aimed at investigating the differential influence of identity and position information that emerges when the same network architecture learns to map orthography to semantics in the two different languages.

Methods

Network architecture

In this simulation, the network architecture maps separate position and identity orthographic input representations onto semantic output representations. The specific architecture of this network was inspired by the well-known architecture of Rumelhart and Todd (1993; see also McClelland & Rogers, 2003). In particular, the architecture allowed for the pre-processing of input representations of the identity and position of a word’s letters in two separate 200-unit hidden layers before this information was combined in a second 200– unit hidden layer, which ultimately feeds into a 200-unit semantic output layer (see Figure 1a). This architecture, as in the original Rumelhart and Todd model, allows for the separate examination of the hidden representations that emerge in the first hidden layers (‘Identity representation layer’ and ‘Position representation layer’ in Figure 1a) prior to their intermixing in the ‘Integration layer’. Note that our choice of architecture, which separates identity and position coding, is not an explicit claim regarding a separate encoding of these two sources of information (see Simulation 2 for results using a more biologically plausible architecture without such an explicit separation). Rather, this separation was intended to provide clearer insight into the relative contribution and effects of the two sources of information, letter-identity and letter-position, under the constraints imposed by the structure of the two different languages.

Figure 1.

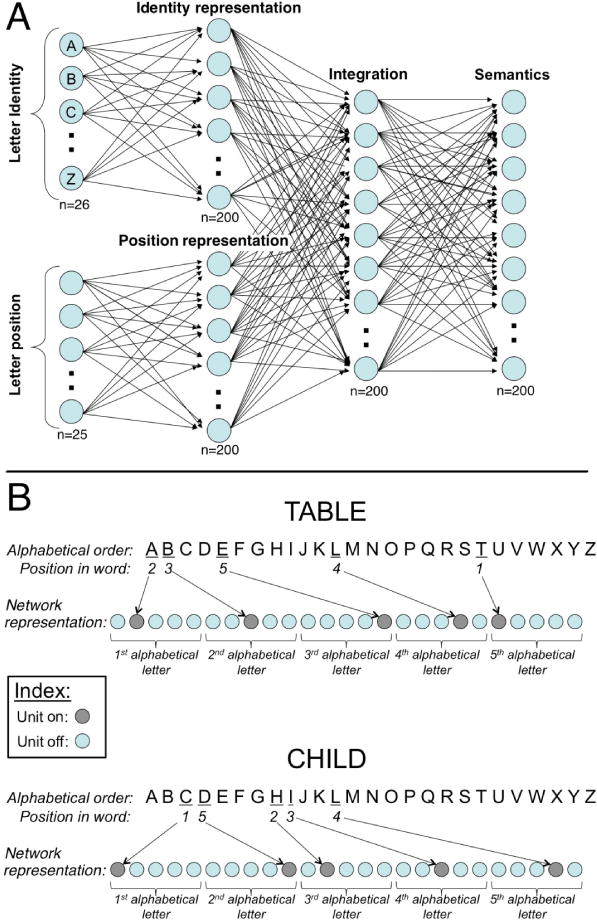
A) Model architecture employed in Simulation 1 using artificial words. B) Examples of two representations illustrating how letter-position information was coded.

In this simulation and in all subsequent simulations, the net input of each unit in a layer in the network was the sum of the activity of the units connected to it in the previous layer, as well as that of a bias connection, multiplied by the connection weights between these units. A unit’s output was a sigmoidal function of its net input.

Training Patterns

Orthographic and semantic representations were generated for 1000 five-letter “words” for each of the two languages. Five-letter words were chosen here because they correspond, approximately, to a typical word length across experiments studying TL effects in both languages (e.g., Velan & Frost, 2009; Perea & Lupker, 2004). In the English-like set, each word was comprised of 5 different letters chosen randomly with equal probability. Critically, no two words in this set of 1000 contained exactly the same set of letters—that is, there were no anagrams. In the Hebrew-like set, an initial set of 500 words was created per the same generation procedure as for English, but the remaining 500 words were created by shuffling the letter order of each of the initial 500 words to generate an anagram. Note that this choice of input was deliberately designed to highlight the main difference of interest between the languages; it therefore drastically simplified all other characteristics of real English and Hebrew words, such as different word lengths, specific statistical regularities of vowels and consonants, or the existence of letter repetitions (all these are included in Simulation 1b which is trained on real words).

For each word in the training vocabulary, the visible (i.e., input and output) representations were generated as follows: The identity input representation contained 26 units, one for each letter in the alphabet (including for the Hebrew-like stimuli. The true number of Hebrew letters – 22 – is captured in later. See the Supplementary Materials for discussion of simulations showing orthographic density is not driving the effects). The representation of a word’s letters in the identity layer consisted of clamping the activation of each letter that was present in a word to 1 and clamping all of the other units to 0. For example, in the word ‘table’, the units representing the letters t, a, b, l, and e would assume the value 1, while the rest of the units would be silent.

Coding of letter-position was designed such that it prevents the input from artificially biasing the network into finding orthographic-to-semantic mappings that make use of identity-position dependencies. As such, any dependencies found by the network by the end of training would necessarily result from the need to accomplish the mapping task rather than due to an initial bias in the input. To accomplish this, we have used a coding scheme that completely orthogonalizes the position information from the identity information (in contrast to several previous methods of orthographic coding, such as bigrams or trigrams.). The position input representation contained 25 units, and its coding was based on the alphabetical order (A, B, C, D, E…). To generate a word’s position representation, the five letters in each word were first arranged according to their order in the alphabet. Each letter was then assigned a rank based on its position in the word. For instance, in the word ‘table’, a is the earliest alphabetical letter within the existing letters and is positioned at location 2, b is the second and positioned at location 3, and so on (See Figure 1b for examples). Therefore, the letter order for the word ‘table’ is coded as 2-3-5-4-1. Conversely, in the word ‘bleat’, containing the same letters, the order is coded as 4-1-3-2-5. This code was then translated to a binary representation of letter position in five five-unit “slots”, each of which coded for the position of one of the letters in the word. The coding of a specific position was accomplished by clamping on the unit whose position in the five-unit slot corresponded to the desired analog position, while clamping all other units off. For example, ‘5’ was coded as 00001 in the five-unit slot, ‘4’ was coded as 00010, and so on. This coding system separates the letter identity information and the letter position information in a non-redundant way.³

The input representation of each word was associated with a 200-unit semantic output representation that reflects the arbitrary nature of orthographic-to-semantic coding. The semantic representations consisted of sparse semantic representation organized per a categorical structure (see Plaut, 1997). Specifically, an initial set of 40 category prototypes were created, each with 15% of the semantic units turned on. Each of these prototype representations were then distorted by regenerating each semantic feature with a probability of 0.15 using the same initial 15% sparsity, under the constraints that each semantic pattern needed to be different from every other semantic pattern by at least three features, and that every pattern needed to have exactly 15% of its units turned on (this reduces irrelevant variability across exemplars). The same set of semantic representations was used for both the Hebrew and English items.

Noisy Positional En coding

The input patterns, as described so far, are structured such that identity and position information are equally accessible to the network. Independent neurobiological evidence indicates, however, that position information is fuzzier than identity information for any language, due to inherent characteristics of the visual system (e.g., Martelli, Burani, & Zoccolotti, 2012; Perea & Carreiras, 2012; see Gomez et al., 2008, for discussion). Thus, the contribution of identity information should outweigh, to some extent, that of position information, for all languages, because of simple reliability considerations. Therefore, in all of the following simulations we ensured that the letter-position information would be less reliable than letter-identity information. In simulation 1, this was achieved by directly scaling down the contribution of the position representation by 80% relative to the identity representation (i.e., instead of a binary 0/1 input, the position layer now contained a binary 0/0.2 input). The choice of the specific scaling value was arbitrary as our goal here was simply to investigate the qualitative impact of reducing the contribution of positional information in the two languages. Such scaling down partially corresponds to the ‘letter position uncertainty’ previously suggested by other studies (e.g., Davis, 2010; Gomez et al., 2008) because in biologically-realistic settings containing noisy conditions, a lower degree of signal inherently becomes more susceptible to coding error.⁴ It can also be thought of as representing a lower degree of attention given to the position of letters in a word compared to their identity (see Servan-Schreiber, Printz, & Cohen, 1990, for a related proposal. For additional control simulations with other noise implementations and without noise altogether, see Supplementary Materials).

From the computational perspective, we hypothesized that because English can essentially rely on identity information alone to activate a correct semantic representation, the network will primarily learn to rely on this stronger source of information when mapping from orthography to semantics. This is because the activation of units in the network, and by proxy, the magnitude of the weight-adjustments during error-driven learning, are made in proportion to the input that they receive from other units (see Rumelhart et al., 1986). If the contribution of positional information is scaled down, the network will primarily activate a semantic representation based on letter identity, and will make weight adjustments that primarily improve the mapping of the identity input onto the semantic output. Effectively, this will cause the network to rely more on identity information, making it less sensitive to transpositions. In contrast, we hypothesized that in Hebrew, the network would learn to rely more strongly on positional information despite the initial scaling down of the activation of the positional input representation (reflecting neurobiological noise). This is because error-driven learning will fundamentally not be able to learn to correctly activate a semantic representation for Hebrew words without the information from the position input, due to the fact that many words are anagrams. Consequently, the only way by which error will be reduced for the pairs of words that form an anagram is by adjusting the weights in the network to place a greater reliance on positional information in activating semantics. Thus, we expected that over the course of training in Hebrew, the network would learn to overcome, to some degree, the reduced contribution of positional information (i.e., it would functionally reduce the neurobiological noise in its internal representations). Such a finding would be in line with the general claim that Hebrew readers implicitly learn to encode relatively precise letter-position given the statistical structure of their linguistic environment (Frost, 2012a, Velan et al., 2013).

Procedure

Training

All weights in the network were initialized to small random values drawn from a uniform distribution of range [−0.01 0.01]. The mean of the distribution for the bias connections was set to −1.73 so that the mean semantic activation at the onset of training was 0.15, corresponding to that in the target semantic representations (Armstrong & Plaut, 2008).

The training method followed standard procedures used in prior modeling investigations (e.g., Plaut, 1997; Plaut & Gonnerman, 2000). The network was trained by presenting each input and allowing activation to feed forward to activate a semantic output. This semantic output was then compared to the target output for that word and error was calculated using cross entropy (Hinton, 1989). Error was accumulated across all of the words in the training corpus and weights were adjusted based on the accumulated error after a full sweep through the corpus. Weights adjustment was based on the delta-bar-delta variation of the back-propagation algorithm (Jacobs, 1988; Rumelhart, Hinton, & Williams, 1986), using a global learning rate of 0.0001, momentum of 0.9 and decay of 0.00001. The local learning rate for each weight was initialized to 1.0 and adjusted over training with an additive increment of 0.1 and multiplication decrement of 0.9 (see Plaut, 1997). The network was trained until a homeostatic stopping criterion was reached, wherein the effects of weight decay were effectively cancelling out the effects of error-driven learning (Armstrong, 2012; Armstrong, Joordens, Cree, & Plaut, in revision). Per this criterion, training stopped once two criteria were met: First, each word’s orthographic inputs activated a semantic representation for which each semantic unit was within 0.5 of its target value. Thus, the semantic representation produced by the network was always most similar to the correct semantic output for each word than it was to the semantic representation of the other words in the training corpus. Second, the slope of the error function was required to be near-zero (when the average error reduction across two successive batches of 100 sweeps through the training corpus was less than 5%). Approximately 9,000 sweeps through the training corpus were required to reach homeostasis in English, and 9,800 sweeps in Hebrew.

Testing

Testing involved freezing the network’s weights and examining the trained network’s output when exposed to two main kinds of novel inputs: nonwords created from the training words either via letter-transposition or letter-substitution(s). In the letter-transposition case, two of the internal letters (letters 2, 3, or 4) in a randomly chosen word from the training set switched locations⁵. In the letter-substitution case, one or two of the internal letters in a word were replaced with different letters (see Velan & Frost, 2009). The letter substitutions were constrained to not involve repeating any letter from the original word. All of the test stimuli that were created were unique and not part of the training set. A total of 1000 inputs were randomly constructed as described above for each of the three testing sets (transposition, 1-letter substitution, 2-letter substitution).

After presenting each testing item to the network, we calculated the correlation between the semantic output activated by this testing item and the one activated by the base item in the training set from which the testing item was derived (e.g., the correlation between the outputs to ‘table’ and ‘talbe’). This correlation was taken to reflect the degree of facilitation that the modified word would induce on the original word (see Perea & Lupker, 2003, for the effect of letter-transpositions on semantic activation, and Seidenberg & McClelland 1989 for the parallel between reaction times and similarity measures).⁶ TL priming effects were calculated as the difference between the mean correlations of the letter-transposition condition and the mean correlations of the 1-letter substitution condition that served as baseline (using the 2-letters substitution condition as baseline does not significantly change any of our results). The whole procedure was carried out twice to assure robustness of the results to any differences stemming from randomization of word stimuli or initial weights (similar to Plaut, 2002). All reported results are averaged over these two runs of the simulation.

Results

Mean correlations between the semantic representations activated by the English or Hebrew words and those activated by the same words with either letter-transpositions, 1-letter substitutions, or 2-letters substitutions are presented in Table 1 (‘Artificial words’). As hypothesized, dramatic cross-linguistic differences emerged in the letter transposition condition, with the English-like inputs being less sensitive to the transposition manipulation compared to the Hebrew-like inputs. In contrast, there was almost no difference between the languages in either of the substitution conditions.⁷ The TL priming effects, calculated as the difference in the mean correlation between the letter-transposition condition and the letter-substitution condition with a single substitution (e.g., Velan & Frost, 2011) are plotted in Figure 2, showing much stronger priming in English compared to Hebrew. It is especially notable that TL primes in the English-like set are producing semantic outputs that are extremely similar to those produced by the original word stems (r > 0.99), indicating that the network has learned to be virtually insensitive to such transpositions. This result fits well with masked priming experiments demonstrating similar priming effects for identity versus TL priming (e.g., Forster et al., 1987), as well as the ease by which subjects are able to read full English paragraphs made up almost exclusively of transposed-letter words (the “Cambridge University effect”; see Velan & Frost, 2007, for related results using a RSVP paradigm).

Table 1.

Correlations between primes and targets, and the TL priming effect, for English-like and Hebrew-like stimuli in Simulation 1a (artificial words) and Simulation 1b (real words).

		Letter transposition	1-Letter substitution	2-Letter substitution	TL priming effect
Simulation 1a: Artificial words	English-like	0.99	0.16	0.06	0.83
	Hebrew-like	0.59	0.16	0.07	0.43
Simulation 1b: Real words	English words	0.87	0.13	0.05	0.74
	Hebrew words	0.53	0.09	0.03	0.44

Figure 2.

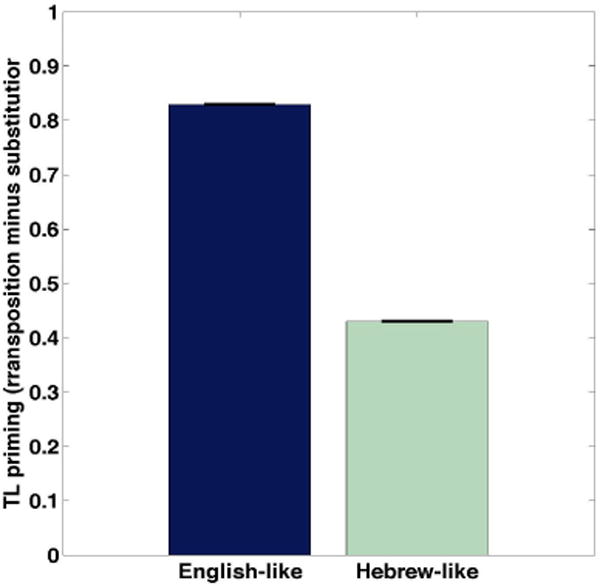
TL priming effects in the model trained on artificial words (Simulation 1a). Priming effects were calculated as differences in average co rrelation coefficients between the transposed and 1-letter substitution conditions. The error bars in this figure and all subsequent figures represent the standard error of the mean, averaged across the two runs of the simulation.

Representational differences between id entity and position

To further understand why the default and noisy conditions produced differential TL effects across English and Hebrew, we conducted additional investigations that contrasted other network properties. In particular, we focused on how well the network was able to distinguish between the different words in the two linguistic environments based on its internal representations of word identity and position, as coded in the identity and position hidden layers.

To probe the network’s ability to differentiate between words based on either identity or position information, we measured how far apart the internal representations of identity – and, separately, of position – were from each other. This was accomplished by calculating the mean Euclidian distance between the hidden representations of identity and position across all pairwise comparisons of the words in the training corpus. The larger the distance, the more distinct each representation is, and thus the better it serves as a source of “input” for the subsequent layers to use in activating a particular semantic output. First, as a baseline, we calculated the mean pairwise distances in the position and identity representation layers before training, and established that these distance scores were near-zero in all cases (a logical outcome, given that the strong negative bias led to only small mean levels of activation for all words in the hidden layers, and prior to training, the differences between hidden representations are due strictly to the random initial weights). We then repeated these computations at the end of training to see its impact. The results are plotted in Figure 3.

Figure 3.

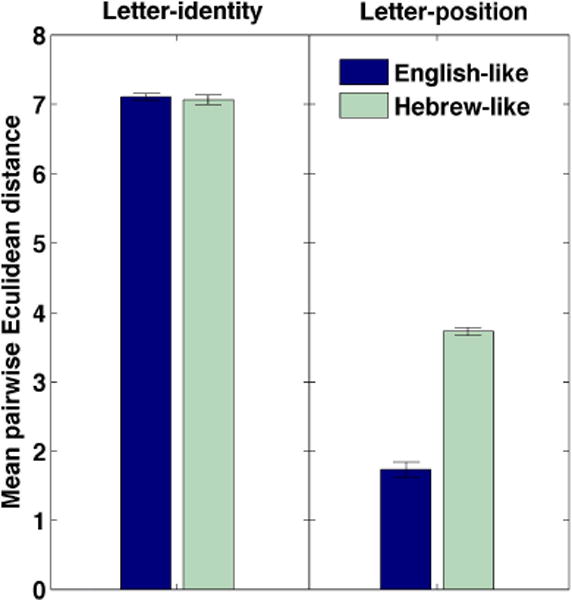
Mean pairwise Euclidean distances between the representations formed for identity and position. The error bars represent the standard error of the mean across the two runs of the simulation.

As can be seen in the figure, both English and Hebrew show similarly separate internal representations of identity. In contrast, there were major differences in the mean distances between the position representations for English versus Hebrew. This is attributable to the fact that different position representations must be generated for at least the anagrams, so the network must develop distinct (and reasonably distant) internal position representations in Hebrew. In contrast, in English, the position representation is not necessary to complete the mapping because each word has a unique identity input representation. Consequently, rather than a necessity, position information is no more than just a helpful but optional input for facilitating the mapping. Because the reduced position input leads to a reduced error signal being back-propagated to the position input representation, learning to use position information is much slower (i.e., harder) than simply solving the input-output mapping via the identity pathway (where learning is fast due to the large input activations and correspondingly large back-propagated errors). Therefore, the network favors the identity pathway and does not learn to differentiate well between the position representations. To sum up, the results show that when position information of English words is fuzzy (i.e., reduced), it is not represented well in the network; in contrast, position information of Hebrew stimuli is always represented reasonably well (see Supplementary Materials for more details).

Discussion

Whereas English- and Hebrew-like inputs were effectively identical in the magnitude of the priming that they generated in letter-substitution conditions, the TL condition produced substantially greater priming in English than in Hebrew. This is consistent with our hypothesis that simple variations between the statistical properties of English and Hebrew words, as extracted by a simple learning model, are sufficient to produce qualitatively similar effects to the ones observed in behavioral TL priming experiments (e.g., Velan & Frost, 2011; Perea & Lupker, 2003). Thus, our results support the notion that increased position sensitivity emerges during learning when the linguistic environment requires it.

Simulation 1a was focused on simple artificial vocabularies that qualitatively capture the fact that in English, there are virtually no anagrams, whereas in Hebrew, anagrams are highly frequent. However, while enabling us to examine the premises of our approach by focusing on the key network properties that underlie TL effect, this simulation used relatively small vocabularies made of highly controlled sets of artificial words that do not fully reflect the richness and complexity of English and Hebrew. In the next simulation we turn to a more stringent test of our theoretical claims by using inputs with greater ecological validity.

Simulation 1b: Real words

In Simulation 1b, we extended our model to investigate TL effects obtained for real Hebrew and English words in linguistic environments that mimic those of English and Hebrew. Thus, the words chosen for the simulation were sampled to reflect the actual statistical properties of English and Hebrew on a number of metrics (e.g., word length, frequency), but most importantly in terms of the real distribution of anagrams as a function of word length in the two languages. In so doing, this simulation allowed us to investigate two important additional issues. First, it allowed us to evaluate whether the effects observed in Simulation 1a are not due to some artifact related to the simple and relatively small vocabulary used; thus, Simulation 1b generalized our findings to the real statistical properties of Hebrew and English. Second, the simulation enabled more direct comparisons between our findings and empirical TL effects by allowing us to compare the stimuli used to produce TL effects in English and in Hebrew on factors such as word length and word frequencies that could bias the empirical (and computational) results.

Methods

Training patterns

English and Hebrew words used in the simulation

We selected two large corpora from which to draw the English and Hebrew stimuli. The English words were taken from the SUBTL word frequency database (Brysbaert & New, 2009). The Hebrew words were taken from the Plaut and Frost database (http://word-freq.mscc.huji.ac.il/index.html). Effectively, these corpora sample the full span of words that are used in both of the languages, including words in singular and plural form, inflected words with prefixes and suffixes, and so on. To avoid introducing very low-frequency words that are not known by many native speakers of English and Hebrew, we then filtered these corpora so that they only contained words with frequencies greater than or equal to one per million. This left 17,530 English words and 61,383 Hebrew words as our base lists from which we drew the samples to train the models.⁸ The number of anagrams in these base lists was computed separately for each word length, in number of letters, in each of the languages. Additional details regarding the distribution of anagrams as a function of word length are discussed later and presented in Figure 5b.

Figure 5.

a) Transposed-Letter Priming of English and Hebrew words as a function of word-length. b) Proportion of anagrams relative to all words of a given length for English and Hebrew.

Training vocabularies for Hebrew and English consisted of 3000 words each that were randomly sampled from the base lists, ensuring that the sample sets had the same proportion of anagrams as the base lists. This was accomplished by sampling the corresponding proportion of occurrence of anagram pairs (e.g., ‘act’, ‘cat’), anagram triplets (e.g., ‘are’, ‘ear’, ‘era’) and so on, as well as the occurrence of words without anagrams at all, separately for each word length (with total number of words of a given length proportional to its prevalence in the base list). The likelihood of sampling a specific word without any anagrams was proportional to the frequency of the word; similarly, in the case of anagrams, the likelihood of sampling a specific set of anagrams was proportional to the multiplication of the frequencies of all of the anagram words in this set (e.g., the frequencies of ‘cat’ multiplied by the frequency of ‘act’ were evaluated compared to multiplications of the frequencies of other anagram pairs, such as ‘dog’ and ‘god’, etc.).⁹ Note that the final samples had a mean word frequency of 250.31 per million in English and 92.16 per million in Hebrew. This difference stemmed from the fact that individual Hebrew words are less frequent than English words because of their morphological complexity (e.g., there are separate words that mean “he sat” and “she sat” in Hebrew, whereas in English this meaning would be communicated via two words and the word “sat” would have its frequency incremented when both “he sat” and “she sat” are encountered). However, because both networks were trained to the same homeostatic criterion (i.e., all words had to be well known and the mean error in the network was stable) this mean difference is superficial and irrelevant to the analyses of the trained network (see Supplementary materials for additional analysis of the effect of word frequency in our model).

Network architecture and representations

The network architecture was, in abstract, identical to that employed in Simulation 1a, although some minor changes were necessary to accommodate the representations of real words, which were more numerous and varied on a number of properties (e.g., word length). These changes were as follows: First, to accommodate the larger training corpus, all the hidden layer sizes were increased to 500 units. Second, the letter-identity input layer was slightly modified to allow it to accurately reflect the actual letter-identity properties in English and in Hebrew (26 letters in English, 22 letters In Hebrew). Additionally, to allow for the representation of repeated letters, the unit activations in this layer could be set to integer values (i.e., 0/1/2/3/etc. instead of only 0/1) that reflected the number of times a letter occurred in a word. For example, in ‘nanny’, the units representing ‘a’ and ‘y’ would have their activations set to 1, as before, whereas the unit representing ‘n’ would have its activation set to 3. Note that this change also allowed the identity input to have a different identity representation for words like ‘end’ and ‘need’, which otherwise contained the same letters but for which the number of occurrences of each letter are different. Similarly, the letter-position input layer was modified to allow for the representation of repeated characters and varied word-length. This was accomplished as follows: Instead of having 25 units as in the previous simulations (i.e., 5 slots * 5 units), the letter-position input consisted of 256 units (16 slots *16 units, per the maximum word length in English; in Hebrew, the longest word contained 14 letters so the last two slots were never used). Multiple appearances of a letter were coded by setting all units corresponding to the positions of this letter in the designated slot as active, and the rest silent. For example, the letter n in the word ‘nanny’ was coded with the 16-unit slot 1011000000000000 (corresponding to n appearing in the 1^st, 3^rd, and 4^th positions). In unused slots for words with fewer than 16 letters, all unit activations were set to 0. Finally, as in Simulation 1a, position information was scaled down from 0/1 to 0/0.2.

The target semantic outputs for the words were generated using the same method described for Simulation 1a; only the number of category prototypes was increased from 40 to 120, proportional to the increased size of the training set.

Procedure

Training

The training and testing procedures were identical to those described in Simulation 1a, with the exception that during training, the error for each word was scaled proportionally to log₁₀(word frequency + 1) (see Seidenberg & McClelland, 1989, Plaut et al., 1996, for related approaches). The English network reached the training criterion after approximately 23,000 epochs and the Hebrew network reached the training criterion after approximately 25,000 epochs.

Testing

Test stimuli for both the letter-transposition and letter-substitution conditions were created by modifying internal letters within a word and only for words with four letters or more (words with three or fewer letters do not contain enough letters to generate internal-letter transpositions). Facilitation effects were computed as in Simulation 1a. Also similarly to Simulation 1a, the whole procedure – including the creation of the training and testing samples and initialization of the weights – was repeated twice and the reported results reflect average over the two runs.

Results and Discussion

Facilitation effects for letter transposition and substitutions are presented in Table 1 (‘Real words’). The results indicate that the same qualitative effects observed in Simulation 1a with artificial words were reproduced when the network was trained on real words. The same was also true for the magnitude of TL priming effects and the Euclidian distances between the identity representations and position representations (see Figure 4).

Figure 4.

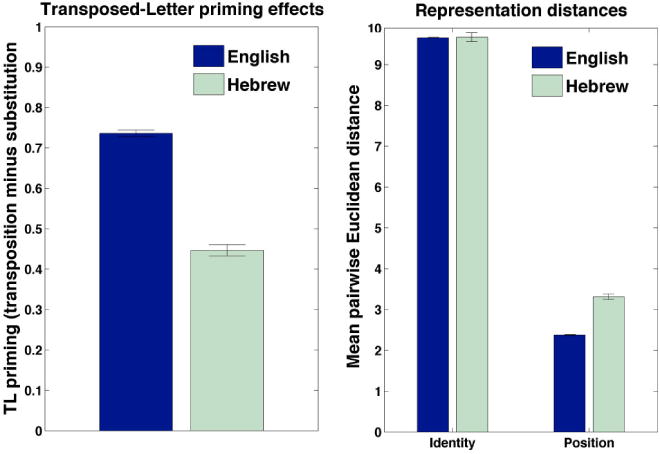
Transposed-letter priming and pairwise Euclidean distances between representations for the real English and Hebrew words used in Simulation 1b.

We next examined the priming effect separately for words of different lengths. There were two main reasons for performing this analysis: First, the Hebrew stimuli list was mostly comprised of words with four to eight letters whereas in English, words with nine letters or more were also relatively abundant. Consequently, we wanted to make sure that this difference was not responsible for the different TL priming effects observed across languages. Second, it is known that TL priming is stronger for long words compared to short ones (and, in fact, is typically only studied in words with five or more letters; see Forster et al., 1987; Schoonbaert & Grainger, 2004). We therefore examined whether this interaction between TL effects and word length was present in our simulated data. To investigate this issue, we computed the TL priming effects separately for words with different numbers of letters. The results are plotted in Figure 5a. As can be seen, the difference in priming between Hebrew and English was not due to word length since the same qualitative difference is apparent for each word length condition in isolation. In addition, the figure shows that TL priming indeed increased for longer words, consistent with other results in the literature (Schoonbaert & Grainger, 2004). Moreover, the magnitude of the TL priming effect interacted with word length and language: For shorter words, the TL priming effect was moderately large in English but very small in Hebrew, whereas both languages show relatively stronger TL priming effects for very long words (although, importantly, the effects always remained smaller in Hebrew relative to English). To our knowledge, this 3-way interaction represents a novel finding that emerges from the simulations reported here, which has not been yet addressed in empirical cross-linguistic studies.

The simulation also allowed us to examine to what extent the cross-linguistic differences between Hebrew and English in TL priming could be due, to some extent, to a word-length confound across studies. Examining the common word lengths used in empirical studies in the past, we found that, indeed, some differences are evident: studies of TL effects in English have generally used words with lengths ranging from 5 to 10 letters (Davis & Bowers, 2006; Forster et al., 1987; Lupker & Davis, 2009; Perea & Lupker, 2003; Schoonbaert & Grainger, 2004), whereas analogous studies in Hebrew have mostly used somewhat shorter words with lengths of 5–6 letters (e.g., Velan & Frost, 2011). We therefore examined how these differences in average word length in empirical studies of English and Hebrew TL effects may have impacted the magnitude of the TL effect differences between languages in our simulations. To do so, we computed length-restricted TL priming effects for English words that contained 5–10 letters, and Hebrew words that contained 5–6 letters. These length-restricted TL priming effects showed a slightly stronger cross-linguistic difference than those reported earlier: there was a 0.75 TL priming effect in English but only a 0.41 TL priming effect in Hebrew. Our simulations, therefore, suggest that the variations in typical word-lengths across studies in the two languages do contribute to the differences in TL priming effects, but are not the main cause of cross-linguistic differences in TL priming.

To understand the cause of this interaction between TL priming effects, word length, and language, we conducted additional analyses of the statistical properties of English and Hebrew stimuli, motivated by the results of Simulations 1a. Recall that in those simulations, word length was fixed and so the only way in which the stimuli could differ was in terms of the different orthographic input structure that we introduced by creating an anagram for every Hebrew word and not allowing any anagrams for English words. We therefore hypothesized that the three-way interaction between TL priming effects, word length, and language in Simulation 1b could be due to a large difference in number of anagrams between English and Hebrew for short words and a much smaller difference for longer words. To probe this issue, we examined how the proportion of anagrams out of the total number of words of a given length varied as a function of word length in each language. A plot of these data is included in Figure 5b based on the training stimuli (which, to reiterate, were designed to accurately capture anagram proportions as a function of word length in the full-scale English and Hebrew corpora). This plot shows that in both languages there are more anagrams for shorter words than for longer words. However, the relative difference in number of anagrams as a function of word length between English and Hebrew is largest for short words and virtually disappears for very long words. Taken together, the results observed in Simulation 1a and 1b seem to indicate that, indeed, the relatively large number of anagrams in Hebrew words and the relative paucity of anagrams in English words modulate the cross-linguistic differences between TL effects in English and in Hebrew.

Taken together, the second simulation successfully extends the first simulation to real words, showing that the effects observed with artificial stimuli remain robust in the context of the realistic linguistic environments of Hebrew and English. Furthermore, the present results highlight an important interaction between word length, the likelihood of anagrams due to increased orthographic density, and the magnitude of the cross-linguistic differences in TL effects.

Simulation 2: Word representations using the Overlap Model

In Simulation 1, we have shown how the linguistic environment determines the magnitude of the TL effect in a neural network that learns to map words into semantic outputs. In order to outline how the network differently exploits letter position and letter identity, we used a representational scheme that explicitly separated between these two types of information. However, the position of letters in visually presented words is intertwined with their identity, unavoidably affecting their retinotopic representation and, as suggested by intracellular recordings from monkeys’ V1, may also continue to take effect in adjacent receptive fields further down the visual processing stream as long as no discrimination training is applied (Crist, Li & Gilbert, 2001; Kapaida, Ito, Gilbert, & Westheimer, 1995). The aim of Simulation 2 was therefore to replicate the findings of Simulation 1 using a more biologically plausible representation of words in which the information about the position and identity of letters is intertwined at the input level. To this end, we represented words using the coding scheme of the overlap model (Gomez et al., 2008), a highly influential model of orthographic coding in that 1) it does not separate position and identity; 2) it includes noise in position coding that is biologically inspired; and 3) it takes under consideration physical properties of position, such that if the same letter appears in proximal locations within two words, its corresponding representations will be more correlated compared to when the two locations are distant, amongst other strengths. In this model, letter representation is depicted as a Gaussian activation function over several possible positions, with peak activity in the ‘true’ position of the letter and reduced activity in the neighboring positions.

Simulation 2a: Artificial Words

As in simulation 1a, we started our investigations using simplified word-like stimuli that allowed us to examine our hypothesis under well-controlled settings.

Methods

Training Patterns, Network Architecture and Procedure

Words were coded using the scheme described by Gomez and colleagues for the overlap model (2008). Specifically, each letter was represented by 19 units that corresponded to different locations in the word, with unit 1 corresponding to the start of the word and unit 19 to the end of it (we used 19 units because this was the longest number of letters in a word in the real-word vocabulary in Simulation 2b and this guarantees a sufficient resolution to distinguish between all locations in this word. However, qualitatively similar results are obtained with higher and lower numbers of units). When a letter was present in a word, these units assumed Gaussian activation values with peak activity around the unit reflecting the relative position of the letter in the word. For example, in the word ‘cat’, the letter ‘c’ had a Gaussian activation with a peak around unit 4, ‘a’ had a peak around 10 and ‘t’ around 16 (see Figure 6B; see also Figures 1 and 7 in Gomez et al, 2008). Following Gomez, the exact activation values of a certain letter for a given word were computed as following: The 19 units representing this letter were considered to encompass the full length of the word regardless of its length, and a value representing the location of the peak was computed based on the relative location of the letter in the word. For example, for the letter ‘a’ in the word ‘cat’, the location of the peak was in the middle of the range 0–19, that is, 9.5. A Gaussian distribution centered on the “true” location of each letter was then spread across 19 equal bins across the 0–19 range. The standard deviation of the activation function was set to the range of the Gaussian (and see Supplementary Material for additional simulations showing how the width of the Gaussian noise distribution impacts performance). These activations were then scaled by the total area such that the total activation of all units equaled 1, corresponding to a probability function. For simplicity, the Gaussian activation functions of all letters had the same variance. Units of letters that did not appear in the word had 0 activation.

Figure 6.

a) Model architecture employed in Simulation 2. b) Examples of a word representation illustrating the overlap Model’s coding scheme used in the Simulation.

Figure 7.

TL priming effects for the English-like and Hebrew-like words used in Simulation 2a. ‘Eng’: English; ‘Heb’: Hebrew. The number besides the label ‘Heb’ refers to the number of anagrams per letter string in the Hebrew-like condition. Error bars represent the standard error of the mean across the two runs of the simulation

Initial training vocabularies were selected using the same methods as for Simulation 1a. In additional simulations, we investigated how competition between different positions of the same letter affects the results by manipulating the number of anagrams per letter string in the Hebrew-like set (2,4 or 8 anagrams).

The network architecture contained three layers (Figure 6A): the input, one hidden layer with 400 units, and a semantic output (only one hidden layer was used because there was no separation of identity and position information as in Simulation 1). The global learning rate was set to 1/10^th that of Simulation 1a based on pilot simulations aimed at achieving positive gradient descent linearity during training. The outgoing weights from the input layer were also scaled down by a factor of 30 to reduce the saturation (all 0’s or 1’s in the first hidden layer), which slows learning. In all other respects, training and testing of this simulation was identical to the methods reported for Simulation 1a.

Results and Discussion

Transposed letter priming for the various conditions is presented in Figure 7, and the values obtained for letter substitution and letter transposition for the simulation of the English-like stimuli and the Hebrew-like stimuli using 8 anagrams per letter string are presented in Table 2 (‘Artificial words’). Similar to Simulation 1, TL priming was substantially higher for the English-like stimuli than the Hebrew-like stimuli. The effect increased with number of anagrams per letter-string in the Hebrew-like set, confirming, once again, that it is the existence of anagrams that pushes the network to develop sensitivity to letter position.

Table 2.

Correlations between primes and targets, and the TL priming effect, for the artificial English-like and Hebrew-like words in Simulation 2a (Hebrew-like condition with 8 anagrams per letter string) and English and Hebrew in Simulation 2b (real words).

		Letter transposition	1-Letter substitution	2-Letter substitution	TL priming effect
Artificial words	English-like	0.99	0.16	0.06	0.83
	Hebrew-like	0.6	0.13	0.06	0.47
Real words	English words	0.90	0.08	0.03	0.82
	Hebrew words	0.68	0.06	0.01	0.62

Unlike Simulation 1, we could not investigate network representations separately for identity and position due to the intertwined nature of the input. Instead, we examined the representations formed in the hidden layer by presenting the network with pairs of random 5-letter nonwords (letter strings that the network has not been exposed to during training) and examined the Euclidean distance between them. Pairs could either have the same letters in different order or they could include completely different letters. This way, we could examine to what degree the network in each language condition tends to separate representations that are differentiated based on letter-order alone compared to those that are differentiated based on identity and order. Figure 8 shows the results (averaged over 1000 random repetitions for each condition and each of the two simulation runs). It is clear that while the average distance between representations of words with different letters was not strongly modulated by language, the distance between representations of words with the same letter strings in different positions was. Specifically, the English-like set produced smaller average distances than the Hebrew-like set, an effect that became stronger the more anagrams the Hebrew set included.

Figure 8.

Mean Euclidean distances between pairs of hidden representations of non-words differing from each other by letter position or letter identity in Simulation 2a. ‘Eng’: English; ‘Heb’: Hebrew. The number besides the label ‘Heb’ refers to the number of anagrams per letter string in the Hebrew-like condition. The error bars represent the standard error of the mean across the two runs of the simulation. Some error bars are too tiny to be identifiable.

Simulation 2b: Real words

Our final simulation examined the network using the overlap model’s representations with real words as inputs, to confirm, once again, that our results generalize to the actual statistics of the two languages.

Methods

Training Patterns, Network Architecture and Procedure

Stimuli were real English and Hebrew words chosen from the same two databases as in Simulation 1b, under the restriction of a frequency higher than 1 word per million. Once again, words were sampled while maintaining equivalent anagram statistics to that of the full database. The training vocabularies contained 10000 words, both to increase the validity of our results, as well as to increase the probability of each letter occurring in various positions over the entire set of stimuli, without requiring overly extensive computational resources (see the Supplementary Materials for further analysis of how training-sample size affect TL priming in our model). The network consisted of 3000 units in the hidden layer (keeping the relative number of units to input samples roughly equal to the previous simulations). As before, the network was trained twice using different stimuli samples and different initial conditions. We also repeated the analysis of hidden representations (using non-words pairs of various lengths, but keeping the same length within a pair) as well as the analysis presented in Simulation 1b regarding priming effects as a function of word length. In this last analysis, we examined only transpositions of adjacent letters, to avoid biases caused by the fact that long words can have transpositions of very distant letters whereas short words cannot (this was not an issue in Simulation 1 because the coding scheme used in that simulation does not differentiate between close and distant transpositions).

Results and Discussion

Table 2 (‘Real words’) presents the effects of letter transposition and letter substitution for each language. The overall TL priming effect of the two languages, its dependency on word length, and the corresponding differences in average Euclidean-distance between representations are displayed in Figure 9. Replicating the findings of Simulation 1b, TL priming was stronger for English compared to Hebrew, a difference that was most strongly pronounced for short words. Similar to Simulation 2a, smaller representational distances were found in English compared to Hebrew for pairs of transposed non-words, but not for pairs of non-words with different letters. Combining the results of Simulations 2a and 2b together, it is evident that the more anagrams a language has, the stronger the sensitivity to letter position it produces, resulting in more separable representations of words with the same letters in different positions and, consequently, higher TL priming. Thus, Simulation 2 replicates the central findings of Simulation 1, showing the robustness of this mechanism across different network architectures and input coding schemes.

Figure 9.

TL priming effects and average Euclidean distances between hidden representations in Simulation 2b.

General Discussion

In the present study we investigated how a simple learning architecture that maps orthography to meaning performs in tasks such as letter-transposition and letter substitution when it had learned to process words in the context of different linguistic environments. The results of our investigation are clear cut: Despite inherent neurobiological noise in position coding, emergent flexibility (or a lack thereof) in coding letter order is strongly shaped by the statistical properties of the linguistic environment (c.f. Grainger & Whitney, 2004; Norris & Kinoshita, 2012). Specifically, our simulations show that when the words of the language are often differentiated by the order of their constituent letters (e.g., Hebrew, Arabic), relative rigidity of letter-position coding naturally emerges through learning when mapping a visual word form onto its meaning. In contrast, when words in a language differ mainly by the identity of their constituent letters (e.g., English, French, Spanish), the insensitivity to letter-position due to the neurobiological noise in early visual representations is passed forward throughout the network and the system learns to recognize words primarily based on letter identity. This basic phenomena has not been previously addressed or explained in prominent popular modeling frameworks (e.g., Grainger & Whitney, 2004; Davis, 2010; Norris, 2010; but see Baayen, 2012).

Our findings suggest that an important statistical property that shapes sensitivity or insensitivity to the order of letters, and thereby predicts cross-linguistic differences in TL effects, is the proportion of anagrams in the language. This is well demonstrated by the strong relationship between the number of anagrams in Hebrew versus English at various letter-lengths, and the cross-linguistic differences in TL effects. Our modeling approach also allowed us to examine the structure of the internal representations that develop during learning. This reveals that the model learns not only to rely more strongly on positional information in a linguistic environment that requires it, but that it also learns more distinct (i.e. separated) representations of position information. This work therefore extends a recent investigation by Baayen (2012) using NDL, showing stronger loadings for positional information in biblical Hebrew relative to English. Our model, however, provides a mechanistically-detailed account of what a “higher loading” implies: it is not (only) that the network learns to rely more on positional information, but that it develops, through the process of learning, internal representations that encode positional information more distinctly. Relatedly, this account offers a developmentally plausible learning theory of reading similar in principle to that of NDL, but that offers additional detailed insight into how and why particular internal representations emerge during learning. Consequently, the present approach can, in principle, trace clear developmental predictions regarding how reading and its supporting representations are shaped in a given language through exposure to larger and larger corpora of words. In turn, this type of approach can capture how readers gradually derive the statistical properties of their language, thereby determining their reading behaviour (see Yermolayeva & Rakison, 2013, for additional discussion related to the connectionist modeling of development).

Our findings speak to the heart of a recent heated debate regarding what drives TL priming effects (see Frost, 2012a,b). Some views have considered flexibility in letter position coding and its subsequent behavioural effects as stemming from the hardwired neurobiological property of the visual system (e.g., Whitney, 2001; Grainger & Hannagan, 2012). Some recent literature has gone even further to argue that TL effects are observed also with primates, thereby proposing that the front-end of reading is supported by neural mechanisms that are non-linguistic in nature (Grainger et al., 2012; Ziegler et al., 2013; but see Frost & Keuleers, 2013, for a discussion of TL effects in Baboons). Our simulations speak directly to this controversy. Assuming that there is indeed an inherent neurobiological noise in registering letter position as compared to letter identity (as instantiated in our various simulations), what eventually permits flexibility or inflexibility in letter position coding is the structure of the linguistic environment.

The present study highlights the clear benefit in developing models of word recognition that are not tailored to fit specific sets of data from a specific language, and that are not based on ad hoc hardwired constraints. The potential limitations of such models is best exemplified by considering the Open Bigram approach outlined in the SERIOL model (Whitney, 2001). Although the original model targeted effects such as relative position priming (e.g., Peressotti & Grainger, 1999), its subsequent developments (e.g., Grainger & Whitney, 2004; see Whitney & Cornelissen, 2008, for a discussion) were mainly set to account for TL effects in English and posited open bigrams as the computational mechanisms that produce this specific behavior. The model was then evaluated in terms of whether its hypothesized organization indeed resulted in the behavior it was designed to describe (for example, whether it produced the various TL effects revealed in English). Finally, once it did, its architecture became a theoretical construct for explaining behavior; Open bigram representations in the brain were postulated to explain insensitivity to letter-order, without recurrence to independent empirical support (e.g., Dahaene et al., 2005).

This state of affairs and its limitations have been described in detail by Rueckl (2012), who labeled this type of modeling as the “reverse engineering approach to cognitive modeling”. In the context of reading research, rather than inform us about what underlies reading behavior and how it is shaped by the characteristics of the writing system, the outcome of the game with these models is more or less predetermined. Instead of searching for the full scope of constraints that underlie a particular behavior, modelers explicitly incorporate their own hypothesized constraints into their model, which then serves as a post hoc existence-proof for its capacity to describe the narrow set of data specifically selected by the modelers. This strategy runs the risk of producing models that provide a highly precise fit (and by proxy, an apparent explanation) of the empirical research, simply because they overfit a well-specified and selected array of findings (see Woollams, Lambon Ralph, Plaut, & Patterson, 2010, and Coltheart et al. 2010, for a discussion). Perhaps more importantly, this approach often fails to explore and predict new types of phenomena that could emerge from general computational principles that a model instantiates (McClelland, 2009; McClelland et al., 2010). Therefore, the success of the model in simulating the desired behavior does not necessarily teach us something interesting about the source of that behavior.

Here, we offer an alternative approach to understanding reading and, in particular, cross-linguistic differences in reading. Our study emphasizes the critical insight gained by employing simple and general learning, processing, and representation mechanisms and examining how they learn the statistical characteristics of different linguistic environments. Our approach, therefore, closely resembles standard experimental methods of studying reading, in that we experiment on the model to understand both how and why it learns to performs the way it does.

An apparent limitation of this approach is that it does not produce a model that generates detailed quantitative fits for the wide range of behavioral phenomena characterizing reading in various orthographies. However, this was explicitly not the goal of the current endeavor. Accounting for a wide set of phenomena (e.g., including the specific priming conditions in which Hebrew primes generates inhibitory effects; Velan & Frost, 2010) would naturally require more extensive architectural complexity, more sophisticated representations, and very large training vocabularies. Without denying that quantitatively accurate models have important contributions (e.g., PMSP; Plaut et al., 1996), these models also suffer from a complexity that often obfuscates the mechanisms that drive specific effects. Our aim in the present study was not to build yet another complex model of visual word recognition. Rather, we opted to use a widely accepted set of modeling principles to experimentally probe what drives cross-linguistic differences in TL effects. This enabled us to make our central theoretical conclusion that TL effects emerge from the interaction of neurobiological noise and the linguistic environment. By shaving off unnecessary complexity, we also were able to show that these main theoretical constructs are both necessary and sufficient to explain a set of phenomena which have rarely been addressed by computational model to date that have reported quantitative fits of data in English (e.g., Grainger & Whitney, 2004; Norris & Kinoshita, 2012; cf. Baayen, 2012). This is a key strength of the fundamentalist approach that we have adopted, and serves to highlight the critical importance of modeling cross-linguistic TL effects.

In light of the present findings, it is therefore clear that any comprehensive model of visual word recognition must address the empirical effects highlighted in the present work. It is therefore worth considering how some other influential models could, potentially, be able to capture these phenomena. For example, the precursors to the Spatial Coding model (Davis, 2010)—although not the Spatial Coding model itself—did instantiate a learning mechanic. It is therefore possible that a revised Spatial Coding model that contains a similar learning mechanic may become sensitive to the statistics of a language as a function of experience, much as the current model does. Following a different vein, the Bayesian Reader model (Kinoshita & Norris 2009) focuses on processing as opposed to learning dynamics, assuming that certain basic statistical information can, in principle, be extracted from the environment. From this basic statistical information, it is also possible that more complex effects, such as those related to cross-linguistic differences in TL effects, can emerge as the representations of the environment interact with the model’s processing dynamics. For instance, in this model, visual word recognition is viewed as a gradual process that is terminated when sufficient evidence regarding the identity of the word has accumulated. Because such a process is sensitive to neighbourhood effects, the statistical properties of a language, such as anagram frequency, could influence the number of competing neighbours that the recognition process needs to overcome in order to terminate successfully. Consequently, the model may require that more precise information, particularly with respect to letter-position, be accumulated before generating a response. Resultantly, this model might exhibit some cross-linguistic TL effects (although see our simulations reported in the Supplementary Materials, indicating that simple manipulations of orthographic density may not be enough to account for the present effects).

It is important to note, however, that models often behave in complex and non-intuitive ways well beyond the scope of simple verbal postulations — indeed, such behaviour is one of the core reasons why models are valuable tools in psycholinguistic research. Consequently, our conjectures regarding other models must be evaluated via explicit simulations to establish the actual capacities of these frameworks, to better understand the computational principles that may give rise to cross-linguistic TL effects, and to contextualize the modeling approach in relation to reverse-engineering (Rueckl, 2012).

In conclusion, the success of a fundamentalist learning model in producing cross-linguistic effects in orthographic processing gives promise to producing a universal learning model of reading that explains a broad set of findings assembled from different languages and different orthographic systems (Frost, 2012b). It also shifts research on orthographic processing towards theories that focus on general modeling principles that simultaneously consider how a model learns about the environment, how it represents the environment, and how it processes information. In so doing, it elucidates how learning, representation, and processing principles interact with the statistical properties of a given linguistic environment to capture, explain, and predict a range of empirical phenomena that force a re-consideration of the core phenomena that a model of written word recognition should explain, and of the place of fundamentalist modeling in subsequent theoretical advances.

Highlights.

• We examined letter-position coding and transposed-letter effects in a connectionist model.

• We used a fundementalist strategy producing a simple and readily-extendable model.

• We show how noise and the statistics of the language determine transposed-letter effects.

• Our model generated novel predictions for targeted empirical research.

• This demonstrates a key strength of learning models for studying visual word recognition.