An integrated approach to patient-specific predictive modeling for single ventricle heart palliation

Abstract

In patients with congenital heart disease and a single ventricle (SV), ventricular support of the circulation is inadequate, and staged palliative surgery (usually 3 stages) is needed for treatment. In the various palliative surgical stages individual differences in the circulation are important and patient-specific surgical planning is ideal. In this study, an integrated approach between clinicians and engineers has been developed, based on patient-specific multi-scale models, and is here applied to predict stage 2 surgical outcomes. This approach involves four distinct steps: (1) collection of pre-operative clinical data from a patient presenting for SV palliation, (2) construction of the pre-operative model, (3) creation of feasible virtual surgical options which couple a three-dimensional model of the surgical anatomy with a lumped parameter model (LPM) of the remainder of the circulation and (4) performance of post-operative simulations to aid clinical decision making. The pre-operative model is described, agreeing well with clinical flow tracings and mean pressures. Two surgical options (bi-directional Glenn and hemi-Fontan operations) are virtually performed and coupled to the pre-operative LPM, with the hemodynamics of both options reported. Results are validated against postoperative clinical data. Ultimately, this work represents the first patient-specific predictive modeling of stage 2 palliation using virtual surgery and closed-loop multi-scale modeling.

1. Introduction

Single ventricle (SV) circulations encompass a wide range of abnormalities in cardiac anatomy leading to one ventricle being poorly or non-functional. The aim of surgery is to bypass the non-functioning ventricle by connecting the systemic venous return to the pulmonary arterial (PA) system, leading to a circulation in series powered by a SV (Fontan and Baudet 1971). Typically, this is performed as three, staged procedures over the first few years of life, in order to provide adequate systemic oxygen delivery without severe volume overloading of the ventricle.

Stage 1 surgery (Figure 1(a)) occurs as a neonate. The aim is to provide an unrestrictive systemic outflow tract with unrestricted venous return to the ventricle. Balanced flow to the pulmonary circulation is provided through a systemic-to-pulmonary shunt or PA banding depending on the anatomy. In the first few months, pulmonary vascular resistance (PVR) decreases and lung surface area increases (Bardo et al. 2001), thus stage 2 surgery may be performed. At about 6 months, the shunt is taken down or PA is ligated, and the superior vena cava (SVC) is attached to the PA vasculature to provide pulmonary flow. This may be via a Glenn [Figure 1(b), SVC to right pulmonary artery (RPA)] or hemi-Fontan procedure (Figure 1(c), SVC remains connected to the right atrium with a homograft patch redirecting its flow to the PAs). The proportion of systemic venous return from the lower body (LB) increases with age; therefore at stage 3, the Fontan procedure, the inferior vena cava (IVC) is connected to the pulmonary vasculature.

Figure 1.

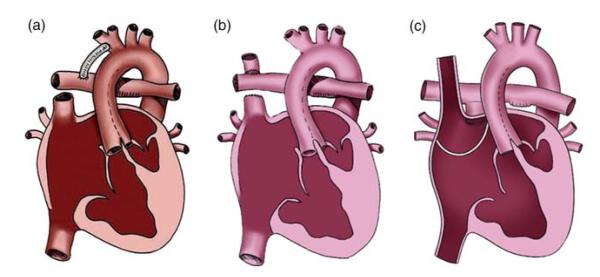
SV palliation surgical procedures: (a) stage 1, (b) stage 2 Glenn, (c) stage 2 hemi-Fontan. (a) republished with kind permission from Springer Science and Business Media, originally published in Dillman et al. (2010, p. 264, Figure 4) illustration by Anne Phillips, University of Michigan Health System, Department of Radiology Media Services; Figure (b),(c) produced by Carolyn Nowak, University of Michigan Health System, Department of Radiology Media Services.

Patients requiring SV surgery comprise a small, but highly complex population. There is wide variation in anatomy and physiology between individuals, with several alternative surgical procedures at each stage. In addition, patient-specific decisions are required to plan the timing and type of surgery. Differences in local hemodynamic effects with different procedures may affect global parameters such as pulmonary flow distribution and systemic oxygen delivery, but these are difficult to predict clinically.

Patient-specific surgical planning involves the implementation of a pre-operative computational model that accurately reproduces patient hemodynamics, and the comparison of different surgical options through computational fluid dynamics (CFD) analysis. Several prior studies have shown the potential clinical application of virtual techniques for congenital heart disease (CHD) surgeries (Pekkan et al. 2008; Haggerty et al. 2009; Marsden et al. 2009; Vignon-Clementel, Marsden, et al. 2010), although two critical issues are the reproduction of the surgeon’s anatomical manipulation and the prescription of model boundary conditions (BCs). Recently, an interactive tool for surgical planning of CHD has been developed combining cardiovascular magnetic resonance (CMR) imaging and CFD allowing free-form manipulation of anatomy with systematic geometric and hemodynamic optimization (Pekkan et al. 2008). Pre-operative blood flow rates have been adopted as inlet BCs while different pulmonary flow splits were imposed as outlet BCs (Pekkan et al. 2005; de Zelicourt et al. 2006, 2011). The limitation of this type of modeling is the inability to describe interactions with the rest of the circulation in post-operative scenarios since BCs are statically enforced without any two-way coupling to the rest of the circulation.

‘Multi-scale’ or ‘multi-domain’ models couple a three-dimensional (3D) model of the surgical region to a lumped parameter model [LPM or zero-dimensional (0D)] or a one-dimensional model of the peripheral circulation (Laganà et al. 2002; Vignon-Clementel et al. 2006; Vignon-Clementel, Figueroa, et al. 2010; Vignon-Clementel, Marsden, et al. 2010). This gives information about local fluid dynamics with changes in anatomical features, plus hemodynamic variables up or downstream. Presently, this approach has been applied in either a closed-loop model where the LPM (with detailed description of entire cardiovascular circulation) is coupled with geometrically simplified 3D models (Laganà et al. 2005; Bove et al. 2008; Corsini et al. 2011), or in an open-loop model that combines realistic 3D reconstructions with simple resistance BCs (Vignon-Clementel et al. 2006; Marsden et al. 2007; Spilker and Taylor 2010; Vignon-Clementel, Figueroa, et al. 2010). In these studies, while proper outflow impedances are applied to simulate the lung vasculature without assuming a flow split, the inlet BC is typically prescribed as velocity, potentially following a certain time-varying flow rate.

For patient-specific virtual planning it is essential that the 3D model and the LPM are customized based on pre-operative clinical data. The 3D model and LPM should be coupled in a closed-loop to avoid imposing BCs that would not account for the considerable circulatory changes postoperatively. A patient-specific, closed-loop, multi-scale approach has been applied to stage 3 virtual planning (Baretta et al. 2011), but an equivalent model for the earlier stage 2 is missing to date.

The role of virtual surgical prediction in CHD is to aid clinicians’ decision-making for customized patient-specific treatments; however, it requires considerable interaction between clinicians and engineers. This study describes in detail a step-by-step integrated approach that could be applied to patient-specific virtual surgical planning of SV stage 2 or 3 operations. The workflow is illustrated for a patient undergoing stage 2 surgery. Two surgical options, Glenn and hemi-Fontan procedure, are compared, and both local and global hemodynamic effects are assessed using the coupled 3D-LPM approach. Model predictions are discussed on the basis of a number of clinical data collected post-operatively. This approach may be used as a workflow for future patients with CHD.

2. Materials and methods

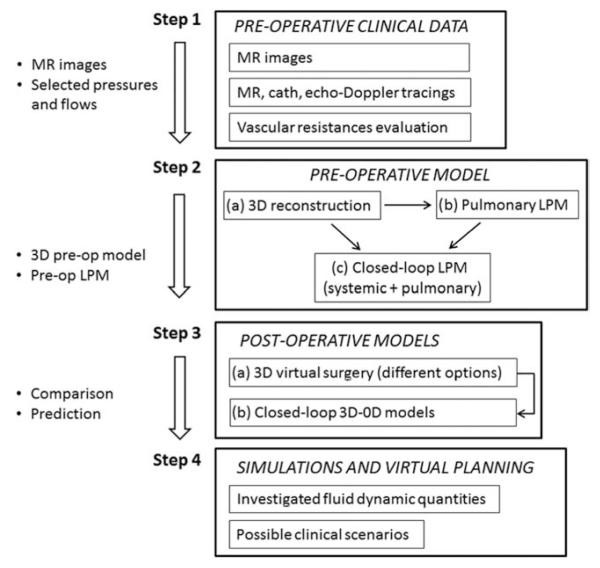
The workflow (Figure 2) for virtual surgical planning presented in this study is comprised of four main steps. The first one is the collection and selection of pre-operative clinical data, based on its consistency and reliability. The processed anonymised data is submitted to a secure online data repository for analysis at multiple centers. The second step is the implementation of the pre-operative model, including the 3D patient-specific anatomical reconstruction to build the pulmonary LPM, and the coupling of the pulmonary and systemic LPMs in a closed-loop fashion. The third step is the virtual surgery for post-operative model construction of possible surgical options, i.e. a number of virtual 3D reconstructions based on the pre-operative anatomical model. The complete post-operative multi-scale model is then constructed by replacing the surgical domain in the LPM with the 3D surgical reconstruction, thus allowing coupling of the virtual 3D reconstruction with the LPM. The final step is to perform simulations of different scenarios for virtual surgical planning. Potentially, a number of different postoperative scenarios corresponding to different physiological states (e.g. exercise in older children, crying in younger children) may be analysed. All steps involve a strong interaction between surgeons, physicians and engineers, although the first step is mainly performed by clinicians and the others are engineer-led.

Figure 2.

Workflow of the modelling process.

The above summarised approach includes several sub-steps that will be described in detail using a case study: stage 2 surgical planning for a baby with a previously constructed systemic-to-pulmonary shunt.

2.1 Pre-operative clinical data

Clinical data for the case study were collected at the University of Michigan C.S. Mott Children’s Hospital (Ann Arbor, MI, USA), after institutional review board approval at the University of Michigan. Informed consent was obtained from the subject’s parents. At the time of data collection, the patient was a 6-month old infant weighing 6.9 kg with a body surface area (BSA) of 0.34m². The baby was born with pulmonary atresia with intact ventricular septum (hypoplastic right heart), not suitable for a two ventricle circulation. On the 5th day of life, the patient underwent surgical placement of a 3.5 mm central shunt, from the ascending aorta (AoA) to the main pulmonary artery (MPA). The patent arterial duct was divided at the time of the procedure.

Pre-operative echocardiogram was performed 5 weeks prior to surgery, under sedation with chloral hydrate, using commercially available equipment (iE33, Philips, Best, Netherlands) and routine clinical protocols. Particular attention was paid to spectral Doppler signals in the superior and IVC, central shunt and branch PAs.

CMR was performed under general anesthesia immediately prior to surgery, on a commercially available 1.5 T scanner (Philips Intera Achieva, Best, Netherlands). Cine images were obtained with a breath-hold, electrocardiographic (ECG)-gated, segmented k-space, steady-state free precession sequence. Flow measurements were obtained in the AoA and descending aorta (AoD), transverse aortic arch, branch PAs, pulmonary veins, superior and inferior venae cavae, using an ECG-gated, free-breathing, cine-phase contrast velocity-encoded pulse sequence, and commercially available cardiac analysis software (ViewForum, Philips). Anatomy was assessed with a contrast-enhanced CMR angiography sequence, following the administration of 0.2 mmol kg⁻¹ of gadoteridol (Prohance, Bracco, Princeton, NJ, USA). Blood pressure was recorded throughout the CMR using an automated blood pressure cuff applied to the right arm.

Cardiac catheterization for pre-operative testing was performed under conscious sedation, including meperidine, midazolam and ketamine, 3 days prior to surgery, using routine clinical protocols. The procedure was performed in a biplane fluoroscopy suite (Siemens Medical Solutions USA, Inc., Malvern, PA, USA). Hemodynamic assessment with intracardiac and vascular pressure measurements was obtained using a fluid filled catheter system and Witt Biomedical Calysto Series IV software (Philips Medical Systems, Best, Netherlands).

From the mean values of clinical flows and pressures collected, the patient-specific PVRs, and systemic vascular resistances of the upper and lower body (UBSVR and LBSVR, respectively) were calculated as follows:

$$\begin{array}{cc}\hfill \mathrm{P}& \mathrm{VR}=\frac{P_{\mathrm{PA}}-P_{\mathrm{SA}}}{Q_{\mathrm{PA}}}\hfill \\ \hfill & \mathrm{UBSVR}=\frac{P_{\mathrm{SysA}}-P_{\mathrm{SA}}}{Q_{\mathrm{UBA}}}\hfill \\ \hfill & \mathrm{LBSVR}=\frac{P_{\mathrm{SysA}}-P_{\mathrm{SA}}}{Q_{\mathrm{LBA}}},\hfill \end{array}$$ (1)

where P_PA, P_SA, P_SysA are the common pulmonary arterial pressure, single atrium pressure and systemic arterial pressure, while Q_PA, Q_UBA, Q_LBA are the flows in the pulmonary arteries, in the upper body (UB) arteries and in the LB arteries, respectively.

2.2 Pre-operative geometry reconstruction

The patient’s anatomy was reconstructed from CMR data using commercial software (Mimics, Materialise NV, Leuven, Belgium). After selection of the vasculature of interest, based on the geometric constraints that might affect the surgical procedure, a 3D volume was obtained for each of the components, following operations of segmentation and region-growing described in detail elsewhere (Armillotta et al. 2007; Schievano et al. 2007).

2.3 Pre-operative open-loop multi-scale pulmonary model

A 3D rigid-walled sub-model of the PA vasculature (Figure 3(a)) was extracted from the reconstructed anatomy. This model included an inlet (i.e. the shunt) and a number of outlets (pulmonary branches) depending on the CMR images resolution, and was discretized using commercial mesh generation software (MESHSIM, Simmetrix, Inc., Clifton Park, NY, USA) into an isotropic finite-element mesh. The pulmonary vasculature downstream each outlet was represented by reduced models, built based on pre-operatively measured CMR and catheterisation data. Namely, the inflow (total pulmonary flow) was imposed in an open-loop configuration, while the flow split between the right and left lungs and the transpulmonary pressure gradient between the inlet of the 3D model and the left atrium were used as the target quantities. A resistance BC (Figure 3(a)) was computed for each outlet by an automatic tuning algorithm necessitating several 3D steady simulations (Troianowski et al. 2011). For each outlet, the resistance led to the localization of the branch within a morphometric PA tree, and thus to the definition of the corresponding arterial sub-tree (Figure 3(b)). An impedance consisting of two resistances and one compliance (RCR block) was then inferred from the Womersley-based impedance of this sub-tree (Figure 3(c)) (Spilker et al. 2007; Troianowski et al. 2011). Since the arterial side of pulmonary vasculature comprises only 20% of the total compliance (Dawson et al. 1988; Presson et al. 1998), compliance values were multiplied by a factor of four to account for the capillary and venous distensibility. The obtained values of resistances and compliances were used as initial values for additional tuning of the LPM described below (see Section 2.4). All simulations were performed using a custom version of the finite element Navier–Stokes solver released with SimVascular (http://simtk.org) and assuming blood as a Newtonian fluid with a density of 1060 kg m⁻³ and a dynamic viscosity of 0.004 Pa s, with a monolithic coupling between the 3D and 0D models (Vignon-Clementel et al. 2006; Vignon-Clementel, Figueroa, et al. 2010).

Figure 3.

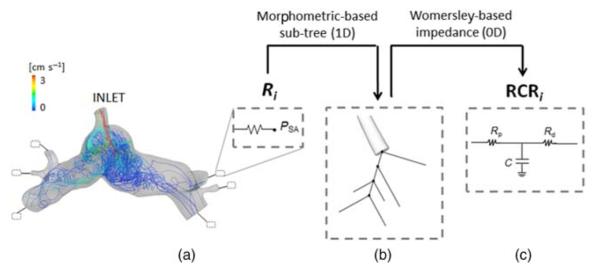
Pre-operative pulmonary LPM generation. A resistance R_i is computed for each ith outlet of the 3D model (a) by means of steady simulations (velocity-colored pathlines are displayed); R_i is first converted in a morphometric-based sub-tree (b), then in the corresponding Womersely-based impedance RCR_i (c). P_SA = single atrium pressure; R_p = proximal resistance; R_d = distal resistance; C = compliance.

2.4 Pre-operative closed-loop LPM of the patient’s cardiovascular system

2.4.1 Model layout

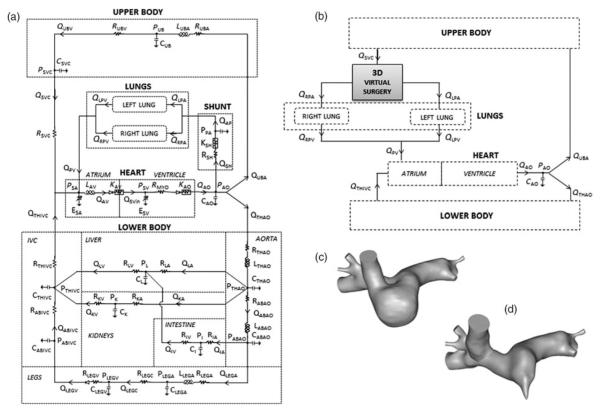
An LPM of the pre-operative SV cardiovascular system was used (Figure 4(a)) (Baretta et al. 2011). The model layout was derived from Snyder and Rideout (1969) who focused the lumped parameter representation on the LB circulation, especially the venous side, including the abdominal organs and the respiration. The LPM, indeed, was designed to be suitable for virtually planning stage 3 surgeries, i.e. when exercise conditions, combined with respiratory effects, and hepatic flow distribution to the lungs may become interesting to study. The detailed description of the LB allows one to alter only those parameter values that belong to specific regions of the body (e.g. legs for vasodilation due to exercise, and thorax/abdomen for respiration).

Figure 4.

Detailed scheme of (a) pre-operative stage 1 LPM; (b) post-operative 3D model of the virtual surgery coupled to the LPM; 3D virtual surgery of (c) hemi-Fontan and (d) bi-directional Glenn.

The network comprised five main blocks to model the heart, the systemic UB and LB circulation, and the right and left lung circulation (see Appendix for equations). For the sake of simplicity and in absence of any clinical information, coronary circulation, gravity and respiratory effects were neglected in the present case study.

The heart was described by two time-varying elastances, representing the single atrium (SA) and the SV, as well as atrio-ventricular (AV) and aortic valves. The contractions of the two cardiac chambers were ruled by two activation functions, properly shifted in time, so that the ventricular activation function starts when atrial activation function reaches zero value. AV and aortic valves were described by non-linear diodes that allow unidirectional flow and exhibit resistances.

In the LB three abdominal organs (kidneys, liver and intestine) and legs vasculature were modelled; a venous valve was included by means of a diode in the leg venous block. Cerebral and brachial circulations were not distinguished within the UB portion of the model.

For the lungs, a number of RCR blocks, arranged in parallel, were used corresponding to the outlets of the 3D model, as described in Section 2.3. A resistive block mimicking the systemic-to-pulmonary shunt was added, including linear and non-linear components accounting for both distributed and concentrated energy dissipations.

The LPM resulted in a set of algebraic and ordinary differential equations, solved using a 4th order Runge–Kutta algorithm with an adaptive step, implemented in the software Simnon® (SSPA Maritime Consulting, Göteborg, Sweden) (version 3.00.011, 1998, Sweden).

2.4.2 Model parameters

The lumped parameter values included in the LPM were obtained after a manual tuning starting from ‘first attempt’ values. The systemic-to-pulmonary shunt parameters were not tuned, but were expressed as functions of the shunt diameter (Migliavacca et al. 2001 – see Appendix).

The ‘first attempt’ values were differently defined according to the different area in the LPM: the RCR values obtained at the end of ‘Section 2.3′ for the lungs, the data reported in Migliavacca et al. (2001) for the heart, while a scaling method was adopted for the systemic parameters. The scaling method is divided in two parts: (i) starting from a reference LPM of a healthy adult, based on the model by Snyder and Rideout (1969), differential scaling was applied according to the patient’s BSA (Pennati and Fumero 2000) and (ii) the parameters obtained were then modified to account for the patient-specific vessels and organs development.

The model resulting from the first part of the method represents a generic subject with BSA equal to that of the considered patient (BSA*). Differential scaling was applied to derive the parameter values x_{i− BSA*} (with x = resistance, compliance, inertance and i denoting the model block) with the following equation:

$$x_{i-{\mathrm{BSA}}^{\ast }}=x_0\cdot {\left(\frac{{\mathrm{BSA}}^{\ast }}{{\mathrm{BSN}}_0}\right)}^b,$$ (2)

where x₀ and BSA₀ are the generic parameter and the BSA, respectively, of the reference adult LPM, and b is a constant coefficient depending on the parameter type (i.e. resistance, compliance, inertance) and on the organ/vessel (Baretta et al. 2011). Indeed, this BSA-based scaling approach enables one to account for the different organ/vessel growths with age (thus BSA), according to the region of the body (e.g. head, torso, legs) where the organ/vessel is located. Passing from an adult model (BSA₀) to a child one (BSA*), the values of the UB and LB systemic vascular resistances become representative of the BSA of the patient (UBSVR_BSA* and LBSVR_BSA*), automatically giving the flow repartition between the UB and LB typical for a baby.

In the second part of the scaling method, each model resistance R_{i− BSA*} of the systemic circulation was modified (R_i with i denoting the model block) to obtain the global patient-specific resistance values UBSVR and LBSVR, as calculated in Equation (1), using the following equations: depending on whether the resistance belongs to the UB or LB, respectively. Furthermore, the patient-specific compliances C_i (with i denoting the model block) were obtained accordingly to the change of R_i:

$$\begin{array}{cc}\hfill R_i& =R_{i-{\mathrm{BSA}}^{\ast }}\cdot \frac{\mathrm{UBSVR}}{{\mathrm{UBSVR}}_{{\mathrm{BSA}}^{\ast }}}\text{or}\hfill \\ \hfill & {\mathrm{R}}_i={\mathrm{R}}_{i-{\mathrm{BSA}}^{\ast }}\cdot \frac{\mathrm{LBSVR}}{{\mathrm{LBSVR}}_{{\mathrm{BSA}}^{\ast }}}\hfill \end{array}$$ (3)

where C_{i− BSA*} being the generic compliance of the systemic circulation. The adopted power expresses the dependence of resistances and compliances on vessel length and diameter (Pennati and Fumero 2000; Baretta et al. 2011). Since the cause of different development of the individual impedances is unknown, the repartition of resistances and compliances among the organs and vessels within the UB and LB was assumed to be the same in both parts of the method.

Once the ‘first attempt’ values were obtained for all the areas of the LPM, manual tuning was performed through a sequential process. First, the flow resistance of the 3D pulmonary model had to be represented in the closed-loop LPM, as disregarding this additional resistive term would provide a PVR and, potentially, a left/right pulmonary flow split different from the clinical ones. Therefore, the 3D contribution to the PVR was accounted for by properly increasing the total resistances of the lung blocks. Manual tuning was then applied to match the clinical cardiac output (CO) and the clinical time tracings available. In particular, the ventricular elastances were tuned to obtain the correct ventricular-circulatory coupling, verifying that the ventricle model worked at reasonable volumes and that the clinical atrial pressure was reproduced. This tuning enabled to reproduce the desired mean flow distribution among the various blocks and the mean pressures throughout the model. Furthermore, the atrial elastances and the venae cavae parameters were tuned to match the SVC and IVC flows, the aortic parameters to match aortic tracings (both flows and pressures), the lung distal-to-total resistance ratio and compliance to match the PA flow pulsatility. The tuning of the heart and circulatory parameters was based on a sensitivity analysis previously performed, showing the influence of different parameters on flow and pressure tracings (Pennati and Fumero 2000). The matching was not evaluated comparing values at any given time, but considering the morphology of the tracings (e.g. number of peaks, presence of reverse flow …) and a number of quantitative features of clinical interest (e.g. peak values, peaks ratios …).

2.5 Virtual reconstruction of different post-operative options

Using the same 3D volume generated to build the pre-operative model, various anatomies were virtually designed according to possible surgical options and to the geometric constraints given by the organs and vessels surrounding the region of the future cavo-pulmonary connection(s), e.g. the heart, aorta, SVC and IVC.

2.6 Post-operative closed-loop multi-scale models

The post-operative 3D models were then coupled to the pre-operative LPM, as depicted in Figure 4(b). Since the post-operative 3D models include the SVC and the first PA branches (as those in the 3D pre-operative model), the SVC resistance was removed from the LPM and each proximal resistance of the lung blocks (evaluated at the end of Section 2.4, ‘Final LPM’ in Table A2) was decreased to remove the resistive contribution of the 3D arterial branches from the 0D representation of the pulmonary vasculature.

Each of the post-operative 3D models was discretized using MESHSIM and a custom stabilized finite-element method with a rigid-wall assumption was used to solve the incompressible Navier–Stokes equations. Neumann BCs were prescribed in the 3D domain at the interfaces (i.e. inlets and outlets) with the LPM, and pressures were passed from the 0D domain to the 3D domain at the interfaces. The LPM equations were solved using a 4th order Runge–Kutta time-stepping scheme. Computed flows from the 3D domain were used as input parameters in solving the LPM equations, thus completing the two-way iterative coupling between the 3D and 0D domains. Coupling was performed using a stable and efficient semi-implicit algorithm, implemented in a custom solver, with negligible additional computational cost compared to the 3D simulation alone (Esmaily Moghadam et al. 2012). Backflow stabilization was applied at each of the inlets and outlets, to prevent simulation divergence (Esmaily Moghadam et al. 2011). The assumptions regarding fluid properties were the same as for the pre-operative model.

2.7 Simulations and virtual planning

The post-operative simulations were performed using the models from Section 2.6. In this case study we have concentrated on a resting physiological state in order to illustrate the methodology. In predictive modelling the post-operative heart rate (HR) was unknown, therefore was assumed to be the same as the average during pre-operative data collection. This was used to set the cardiac cycle length for the simulations. Peripheral vascular parameters were assumed to be unchanged from the pre-operative situation.

In order to ensure clinical relevance, the reported simulation outputs were selected in conjunction with the clinicians. Global circulatory outputs were represented as both mean values and time tracings. The hemodynamic outputs most relevant to the clinicians were flow ratios, such as pulmonary-to-systemic flow and flow split to each lung, and parameters related to the heart, including CO, ejection fraction and pressure volume loops to estimate cardiac work and efficiency. Local effects were studied using 3D velocity and pressure maps at certain time instants of the cardiac cycle, maps of average wall shear stress (WSS) per cardiac cycle, and local energy losses.

The local power dissipation due to the hemodynamics in the surgical region was calculated as the difference between the inlet and the outlet energy fluxes of the 3D model, accounting for the potential and kinetic terms (Marsden et al. 2007). The local efficiency was defined as the ratio between the outlet and inlet energy fluxes.

3. Results

3.1 Pre-operative clinical data

Clinical data collected are listed in Table 1, underlining those selected for modelling. There was a normal HR range during acquisition of Doppler and CMR data (112–132 bpm). However, HR during catheterisation was higher and had greater variability, due to varying degrees of agitation during the procedure, necessitating repeated doses of sedation. For this reason, modelling was performed using the HR of 120 bpm, selected as an average of CMR and Doppler HRs, and representing a resting clinical state. The average mean blood pressure as measured by cuff on either arm during the CMR was 43 mmHg. Aortic oxygen saturation was 69% during catheterisation. The CMR flows and catheter measurements represent averaging of several cardiac cycles and therefore respiratory influences were negligible.

Table 1.

Clinical data pre-operatively collected from the patient.

	Magnetic resonance		Cardiac catheterization
	Flow rate (cm3 s−1)	HR (bpm)	Pressure (mmHg)	HR (bpm)	Other data
AoA	24.4	117	N.A.	N.A.	74/28 (43) a
Transverse aorta	10.6	116	N.A.	N.A.
AoD	5.7	132	102/56 (82)b	N.A.
SVC	9.8	115	9	143	3.06c
IVC	7.3	118	N.A.	N.A.	1.15c
RPA	4.8	116	13 d	135 ÷ 170e
LPA	2.7	115	12d	134
Right pulmonary vein	7.4	117	N.A.	N.A.
Left pulmonary vein	4.8	115	N.A.	N.A.
Right atrium	N.A.	N.A.	6	143
Left atrium	N.A.	N.A.	5	136
SV	N.A.	N.A.	103/6b	167

Notes: Flow and pressure values are averaged over several cardiac cycles. Values in italic are those selected for modeling.

^aMax/min (mean) brachial cuff pressure in mmHg.

^bMax/min (mean).

^cAbsolute value of the non-dimensional venous flow index S/A.

^dMeasured as pulmonary venous wedge pressure.

^eRange covered by the right venous wedge pressure measured in three different locations. 1 mmHg = 133.32 Pa.

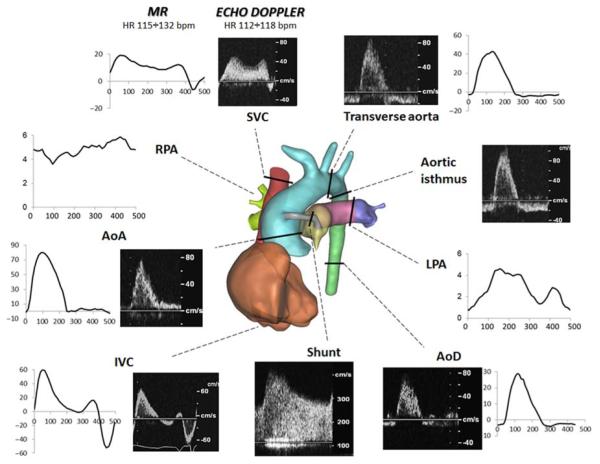
Given the selected mean values of pressures and flows (Table 1), the PVR, UBSVR and LBSVR were calculated as described in Equation (1), obtaining 1.10, 3.39 and 6.67 mmHg s cm⁻³, respectively. The UBSVR and LBSVR were calculated using the mean cuff pressure (see ‘Other data’ column in Table 1) as a measure of P_SysA, since the aortic pressure recorded during cardiac catheter-isation did not correspond to a resting condition for the reasons explained above. The collected clinical CMR flow rates and echo-Doppler tracings are shown in Figure 5.

Figure 5.

Pre-operative data: 3D reconstructed anatomy (centre), clinical MR (cm³ s⁻¹ vs. ms) and echo-Doppler (cm s⁻¹ vs. time) tracings. AoA/AoD, ascending/descending aorta; SVC/IVC, superior/inferior vena cava; RPA/LPA, right/left pulmonary artery.

From the CMR and angiographic data collected, the shunt presented a non-circular area with a variable cross-section along the axis (diameter range: 2.3–3.0 mm), which was smaller than the original size of the shunt implanted at surgery (3.5 mm).

3.2 Pre-operative model

The reconstructed anatomy (Figure 5, centre) included: the aortic arch, the AoD), the main, RPA and left pulmonary artery (LPA) and pulmonary branching up to the second bifurcation, the right atrium, the SVC and the central shunt.

In the 3D sub-model used for the calculation of the downstream pulmonary impedances, the inlet was the distal part of the central shunt, and six outlets were included. The model was meshed with 7.15 × 10⁵ elements. Figure 3(a) shows the resulting local hemody-namics in terms of pathlines when imposing an inlet flow equal to 7.5 cm³ s⁻¹, with a 64% flow to the right lung. The obtained values of pulmonary lumped parameters, corresponding to a transpulmonary pressure gradient of 8 mmHg (in agreement with Table 1), are reported in Table A2 (see ‘Morphometric’ columns).

In the pre-operative closed-loop LPM each resistance of the lung blocks derived from ‘Section 2.3’ was increased to obtain the clinical PVR (1.10 mmHg s cm⁻³), thus corresponding to 30% PVR increase from the value calculated (Equation (1)) when neglecting the 3D additional resistance. The lumped parameter values of the whole pre-operative LPM, evaluated after the manual tuning which is described in Section 2.4, are listed in the Appendix (Table A1, for the heart and systemic parameters, and Table A2 – ‘Final LPM’ columns, for the pulmonary parameters).

Concerning the shunt lumped parameters, it was not straightforward to evaluate their values using the equation in the Appendix, due to the variable diameter along shunt length. Hence, they were determined with the measured difference between the mean systemic and PA pressures (i.e. 43–13 = 30 mmHg), and the shunt flow rate (i.e. 7.5 cm³ s⁻¹). The corresponding diameter of the shunt was calculated to be 2.65 mm.

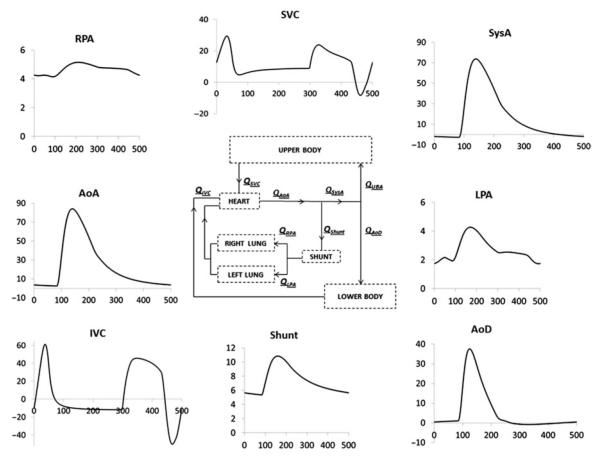
The LPM developed for the pre-operative circulation produced the flow tracings reported in Figure 6. A good agreement between clinical and model tracings can be observed comparing Figures 5 and 6: minimum and maximum flow values as well as the flow waveforms of the clinical tracings were acceptably reproduced by the model. In both clinical and model tracings, the aortic flow upstream of the shunt (AoA) showed positive values throughout the whole cardiac cycle, while the flow in the systemic arteries downstream the shunt (SysA) was positive during systole and negative in diastole, approaching values close to zero in the AoD at the end of the cardiac cycle, as reported by the CMR tracings.

Figure 6.

Flow time tracings (cm³ s⁻¹ vs. ms) resulting from the final pre-operative LPM (scheme in the centre). AoA/AoD, ascending/descending aorta; SVC/IVC, superior/IVC; RPA/LPA, right/left pulmonary artery; SysA, systemic artery.

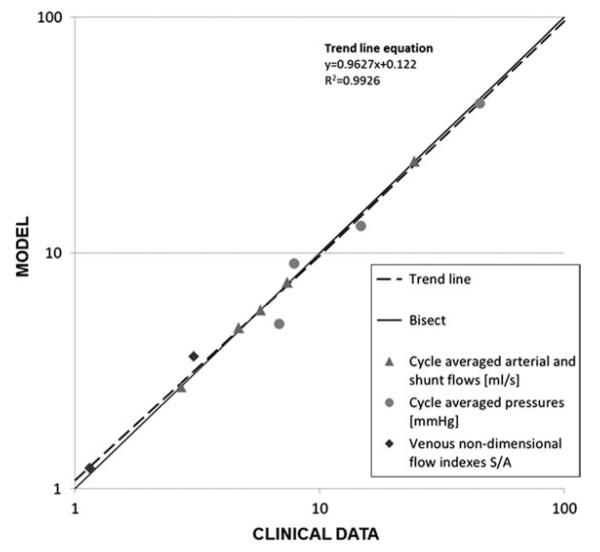
Cycle-averaged flow values differed <4% from the clinical ones. Because of the different conditions of data acquisition during catheterisation (i.e. agitation, sedation and variable HR), averaged pressure values showed higher discrepancies (<28%) than flow values, but on the whole the clinical tracings were reasonably matched by the model. In Figure 7 the simulated results of flows, pressures and non-dimensional venous flow indexes are plotted against clinical data. The non-dimensional index (S/A) is the ratio between the S-wave (corresponding to ventricular systole) and the A-wave (corresponding to atrial contraction) of the SVC and IVC flow tracings. The satisfactory agreement between clinical and model data is clearly visible.

Figure 7.

LPM results vs. clinical data: time-averaged (over cardiac cycle) arterial and shunt flows, pressures, SVC and IVC non-dimensional venous flow indexes S/A (calculated as the ratio between the S-wave and the A-wave during atrial contraction). The trend line (dashed) is obtained by best fitting the LPM results. The x- and y-axes are shown in a logarithmic scale.

3.3 Post-operative models

For the case study, the hemi-Fontan and bi-directional Glenn were virtually performed (hF and bG geometry, respectively). For the hF geometry, a portion of the atrium was removed from the 3D volume so to create the ‘bulging patch’ typical of this surgical configuration, the size of which was determined in agreement with the surgical team who performed the operation. This volume was attached to the MPA and merged into a new, unique volume. The final anatomical model is shown in Figure 4(c). In the case of the bG geometry, the SVC–RPA anastomosis was recreated by virtually resecting the SVC from the atrium and adjoining it with minimal movement to the RPA. The two volumes were merged into a single one, as shown in Figure 4(d). In both cases, the central shunt was removed from the virtual models, to simulate the shift from stages 1 to 2 physiology.

The hF and bG model meshes used for simulation had a maximum edge size of 0.3 mm, containing 1.30 × 10 and 8.64 × 10⁵ linear tetrahedral elements, respectively. The hF and bG geometries were coupled to the pre-operative LPM, as shown in detail in Figure 4(b).

3.4 Simulations and virtual planning

For both the hF and bG multi-scale simulations, 12 cardiac cycles were simulated with a time step size of 1 ms. A value of 120 bpm was used as the HR in the simulations, for the reason explained above (see Section 3.1). The results from the last cycle, after the pressures had stabilized, were used in the analysis.

For the case study, a number of results from the simulations carried out with the two post-operative models are reported below. Figures and numerical values are shown side by side to allow for comparison.

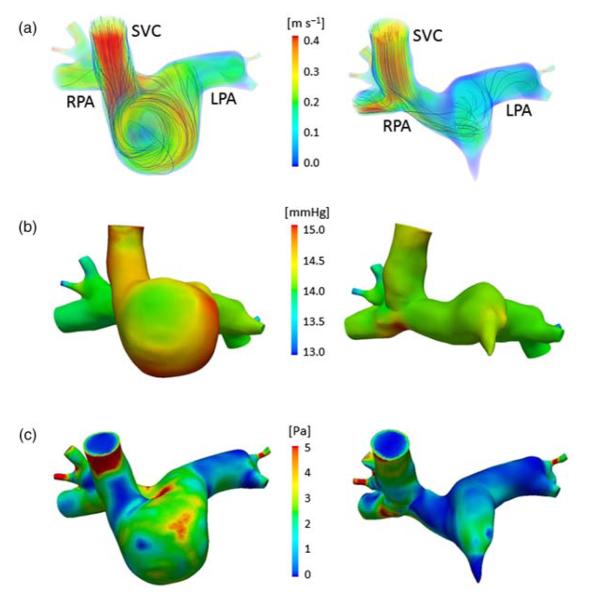
Figure 8(a) shows the time-averaged, volume-rendered flow velocities in the hF and bG geometries. The color map represents the velocity magnitude and the lines represent the velocity streamlines. In the hF geometry, the SVC inflow swirls along the side of the cavopulmonary junction, forming a vortex and maintaining a higher velocity (compared to that in the bG) before entering the PAs. In the bG geometry, the flow impacts the bottom of the RPA after entering from the SVC, and splits into the left and right directions.

Figure 8.

Comparison of the hemodynamics in the hF (left) and bG (right) models: (a) volume-rendered velocities at peak flow with streamlines, (b) wall pressure at peak flow, (c) time-averaged (over cardiac cycle) WSS magnitude. 1 mmHg = 133.32 Pa.

In Figure 8(b) the pressure maps show higher values at the inlet for hF model compared to the bG model. Moreover, in both models areas of high pressure occur where the SVC flow impacts the vessel wall.

Figure 8(c) shows the time-averaged WSS magnitude in the hF and bG geometries. An area of high WSS close to the model inlet is present in both models, due to entrance effects and vessel curvature (in particular in the hF geometry). Moreover, in the hF model the area of high WSS persists throughout most of the surgical junction, due to the presence of a swirling vortex. Conversely, in the bG model a more limited area of high WSS is concentrated at the bottom of the RPA in the region where the inflow from the SVC impacts. The mean WSS in the hF and bG is 2.11 and 1.48 Pa, respectively. These values are a little higher than those reported for older bG (Troianowski et al. 2011), but fall in the lower range of previously reported values of WSS in large arteries (Alevriadou and McIntire 1995; Tang et al. 2010).

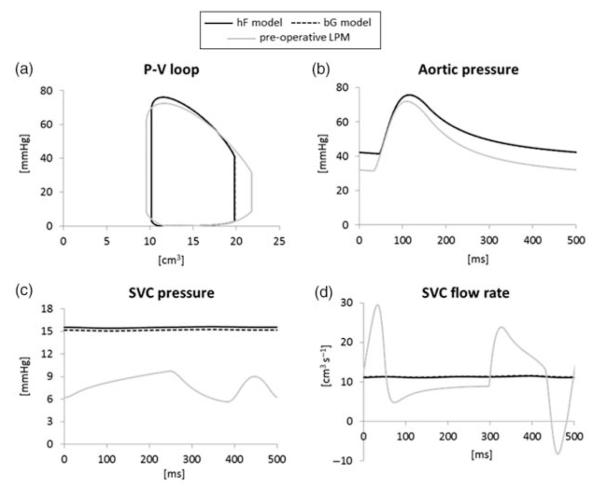
The hemodynamics of the global circulation in the two post-operative configurations are very similar, and both are distinct from the pre-operative one (Figure 9). Only the SVC pressure shows slight differences between the hF and bG models, in agreement with the pressure maps in Figure 8. Similar considerations are found by examining the time-averaged flows, pressures, power losses and efficiencies obtained from the simulations (Table 2).

Figure 9.

Comparison of the simulation results of the pre-operative LPM (grey lines) and post-operative hF (solid lines) and bG (dashed lines) models: (a) ventricular pressure-volume loop, (b) aortic pressure, (c) SVC pressure, (d) SVC flow rate. Except in graph (c), hF and bG curves overlap.

Table 2.

Time-averaged flows, pressures and power losses of the post-operative models.

	hF model	bG model
SVC flow rate (cm3 s−1)	11.3	11.4
IVC flow rate (cm3 s−1)	7.89	7.87
LPA flow rate (cm3 s−1)	4.21	4.17
RPA flow rate (cm3 s−1)	7.07	7.21
SVC pressure (mmHg)	15.4	15.1
Aortic pressure (mmHg)	53.1	53.1
Atrial pressure (mmHg)	2.43	2.48
3D power loss (mW)	1.26	0.61
3D potential term (mW)	1.29	0.62
3D kinetic term (mW)	−0.03	−0.01
3D efficiency (−)	0.95	0.97
Ventricular power (mW)	166	166

Note: SVC/IVC, superior/inferior vena cava; LPA/RPA, left/right pulmonary artery. 1mmHg = 133.32 Pa.

Comparing the post-operative and the pre-operative simulations (Figure 9), regardless of surgical option: (a) stroke volume (i.e. the CO, assuming no change in HR) significantly decreases (21%) together with a slight increase in the systolic pressure, thus reducing (12%) the ventricular work; (b) aortic pressure increases in the mean value (from 43.3 to 53.1 mmHg) as in both systolic and diastolic values; (c) mean SVC pressure roughly doubles (from 7.9 to about 15.3 mmHg) while damping its pulsatility and (d) SVC flow pulsatility is highly reduced, although its mean value does not significantly change from the pre-operative one.

Table 2 shows that the surgical junction power loss in the bG model (0.61 mW) is roughly half of that in the hF model (1.26 mW), with a higher contribution of the potential term compared to the kinetic term (0.62 vs. −0.01 mW for bG, 1.29 vs. −0.03 mW for hF). These values are in the same range as previously reported power loss values in the stage 2 junctions and consistent with previous observations that bi-directional Glenn tends to exhibit lower power loss compared to hemi-Fontan (Pekkan et al. 2009). High efficiencies were obtained, in the same range as in Troianowski et al. (2011). However, under resting conditions the power loss of both surgical junctions is very small in comparison to the inlet and cardiac powers: it is only 3% (in bG) and 5% (in hF) of the time-averaged power calculated at the inlet (22.6 mW in bG and 23.1 mW in hF), and <0.8% of the ventricular power (166 mW in both models). Hence, the surgical junction geometry has very little impact on the behaviour of the overall circulation at rest, with differences in flows and pressures resulting from the two models not exceeding 2%.

4. Discussion

This study reports the first, patient-specific predictive modelling of SV palliation using virtual surgery, closed-loop multi-scale modelling and an integrated approach between clinicians and engineers. Our approach involves four distinct steps: collection of clinical data, creation of the pre-operative model, creation of feasible virtual surgical options, and modification of the LPM for postoperative simulations to aid clinical decision making. This approach is generally applicable to stages 2 and 3 of SV surgery. In this study, we applied our predictive surgical planning to patient-specific stage 2 surgery in order to demonstrate the applicability of the approach.

4.1 Pre-operative clinical data

Predictive modelling of stage 2 surgery represents a demanding challenge as patients at this stage have complex physiology. Patient physiological parameters are complex, difficult to acquire simultaneously, and the clinical equipment has inherent limitations in measurement accuracy. Hence, the clinical data set is not suitable for direct implementation into the pre-operative model. Discrepancies in each measurement might result in an inconsistent system unlikely to obey the law of conservation of mass. Despite these limitations such simulations need to work for ‘real-world’ clinical problems, emphasizing the importance of the interaction between clinicians and engineers to guide the selection of suitable data and ensure suitably representative and reproducible models. Identifying and excluding portions of clinical data where the patient’s physiology has changed significantly, and finding alternative methods of confirming less reliable measurements is essential for a meaningful and consistent model.

In this case study, there was uncertainty about the accuracy of the pre-operative shunt geometry measured by CMR, which was used for the reconstruction of the pre-operative 3D model. While the original shunt used in surgery was 3.5 mm in diameter, quantifying the shunt size to 2.65 mm (see Section 3.2) in the pre-operative model agreed with the loss of luminal diameter observed in the CMR (diameter ranging from 2.3–3.0 mm along the length of the shunt, see Section 3.1). The small dimensions of the conduit and the turbulent nature of the flow inside it resulting in non-optimal signal resolution could cause underestimation of the shunt diameter from CMR data. Nevertheless, using shunt measurements from cardiac angiography, as a quality control measure, confirmed a generalized reduction in shunt lumen compared to original size at the time of surgery, consistent with neointimal proliferation and endothelialization of the tube graft following surgery.

4.2 Pre-operative model

An open-loop multi-scale model was used as the initial step to account for hemodynamics that are challenging to model. In fact, a closed-loop model is not necessary to evaluate the pulmonary model because the inlet flow is known and this simplifies the process of tuning the downstream impedances to the clinical data, yet taking into account 3D effects. Owing to the shunt and the ligated PA, the hemodynamics in the 3D models are particularly complex, with a jet coming from the shunt, impinging on the wall and leading to downstream complex flow structures (Figure 4(a)). It is imperative that the pre-operative model accounts for as many anatomical features of the surgical region and fluid dynamic variables of the remaining vasculature as possible. However, clinical investigations and bedside data are not intended, nor designed, for precise mathematical modelling, but to provide guidance to patient management. Therefore, the adaptation of clinical data in modelling studies, such as ours, can be challenging due to inconsistencies and a lack of precision. Moreover, the added complexity of the abnormal cardiovascular system in congenital heart defects makes lumped parameter identification and model simulations ever more difficult.

Pre-operative open-loop multi-scale modelling allows the lung vasculature to be adequately described. Closed-loop LPM allows fast tuning of parameters accounting for the whole system. In the present case study, the values of pulmonary impedances were modified during the tuning process (i.e. changing the distal-to-total resistance ratio and compliances) to reproduce the clinical pulmonary flow pulsatility.

In the LPM used in this study, respiratory effects have not been included since the pre-operative CMR and catheter data were averaged by cardiac cycle thereby removing respiratory variation. Doppler traces e.g. IVC, SVC could be used to indicate variation in flow with respiration, although timing of inspiration and expiration needs to be measured. The influence of respiration could be effectively implemented in the LPM as intra-thoracic and intra-abdominal pressure modulation due to diaphragm movement (Baretta et al. 2012), provided that enough respiratory data in the pre-operative analysis have been acquired.

The effect of gravity has not been included in the current model, although this is likely to be of most importance after stage 3 surgery.

In our approach, most of the tuning of the lumped parameters was done manually, starting from a LPM previously developed and the clinical data available; however, automatic tuning methods have already been implemented, such as the method presented by Spilker and Taylor (2010) that enables systematic optimisation of the LPM used as outlet BCs of 3D blood flow models (e.g. patient-specific abdominal aorta) in order to achieve the desired features of pressure and flow waveforms.

4.3 Post-operative models and virtual planning

The use of post-operative closed-loop multi-scale models is necessary to study different surgical options at the global and local scale. Constructing the possible postoperative surgical options is difficult since the exact reconstruction a surgeon will perform is unknown. In this case study, two options were considered (i.e. bi-directional Glenn and hemi-Fontan), after consulting several surgeons to ensure the reconstructions were technically feasible and realistic. In the future, it would be possible to consider several geometries of a similar theme for each option, e.g. a Glenn with different anastomosis locations or angles.

The post-operative 3D models were provided with appropriate BCs simulating the patient-specific circulation at the time of surgery. However, the potential change of cardiovascular parameters due to vascular self-regulation and adaptation to new local hemodynamics following the operation was not taken into account, posing a severe threat to reliability of virtual surgical predictions (Pennati et al. 2011). Moreover, the effects of different surgical options on the global hemodynamic variables were here compared only at rest (i.e. a clinically stable postoperative state), whereas extending the modelling to more extreme physiological states (e.g. crying in younger children, exercise in older children) would allow clinicians to catch differences in surgical options not apparent at rest.

4.4 Validation

The pre-operative LPM produced a good agreement between the modelled flows and clinical tracings (Figures 5 and 6). Qualitatively, the flow waveforms and maxima and minima were well reproduced, with <4% difference from the clinical data in average flow. Pressures in this case were less well matched (<28% difference); however, qualitatively the clinicians accepted the model as representative of the pre-operative state of the patient.

The patient investigated in this study underwent a hemi-Fontan procedure. Systemic arterial pressure was non-invasively monitored (brachial cuff pressure) throughout their entire hospital stay. This meant we could perform a direct comparison with our model using brachial cuff pressure. However, it was difficult to quantify an indicative value for mean arterial pressure since the baby experienced fluctuations according to the time of day, physical state (e.g. awake, asleep, crying) and drug administration. Overall, the patient had a substantial increase in mean arterial blood pressure compared to the pre-operative values, as correctly predicted by the hF model under resting conditions.

In the last 5 days while the patient was in hospital, systolic blood pressure was 73 to 116 mmHg (average 94 mmHg) and diastolic between 30 to 76 mmHg (average 52 mmHg), with a HR between 96 to 130 bpm (average 113 bpm). Assuming HR equal to 120 bpm as in the pre-operative conditions, the hF simulation produced results (systolic and diastolic pressures of 78 and 42 mmHg, respectively – Figure 9(b)) consistent with the lower range of values from the clinical data. This suggests a reasonable predictive capability of the model since the pre-operative model is based on measurements that were obtained under sedation and general anaesthesia when blood pressure is expected to be lower than when fully conscious. However, the challenges of modelling transient autonomic changes (Vignon-Clementel, Marsden, et al. 2010; Pennati et al. 2011) still need to be faced in order to more accurately predict hemodynamics when the patient is awake.

SVC pressure in the patient was 10–17 mmHg (average 13 mmHg), in good agreement with the model result (15.4 mmHg – Table 2). Moreover, the predicted SVC flow tracing (Figure 9(d)) showed damping of its pulsatility, matching the post-operative Doppler tracing (data not shown).

4.5 Modelling for clinical decision support and future directions

In this case study, we have performed a direct comparison between two surgical options – bi-directional Glenn and hemi-Fontan. The results of these simulations have shown that clinically there is little difference in the global performance of the two geometries at rest. However, there has been a significant change in both surgical options from the pre-operative state (i.e. decreased stroke volume, higher blood pressure and lower ventricular work) as would be expected with volume unloading of the ventricle with stage 2 surgery. There are some differences in local hemodynamics between the hF and bG geometry; however the clinical relevance of this is not known.

The potential benefits of using this type of modelling are both patient-specific and generalizable to all SV patients. Patients with specific geometric problems such as PA stenosis may undergo predictive modelling of different options, concentrating on local hemodynamics to aid clinician decision making about the extent of the operation. Global hemodynamics are useful in cases where it is uncertain whether a patient would even be a suitable candidate for SV palliation.

One of the primary issues of this study is the clinical data acquisition. SV patients represent a particularly challenging population to study given the young age range, unstable nature of their physiology, and the small number of patients with the condition thereby limiting the numbers of potential participants. Ideally, all clinical data would be collected simultaneously ensuring identical physiological states and simplifying the construction of the pre-operative model. In practice, this is impossible with the technology available. Even measurements that are temporally close have errors due to the limitations of equipment such as fluid-filled catheters and the constantly changing physiology of the patient. Therefore, clinical data are often conflicting, incomplete, and limited. A major part of the collaboration between clinicians and engineers is in developing strategies to deal with the clinical data based on the experience of clinicians and engineers in their respective fields. Constant communication between the two fields is essential so that clinicians can help engineers to understand what can be modelled and what data are suitable for modelling, and engineers can perform clinically feasible and sensible simulations. While current state of the art in predictive modelling remains in the assessment of local flow dynamic variations between different surgical reconstructive options, the present methodology allows the evaluation of detailed, clinically-relevant global systemic effects in context of patient-specific simulations. To further affect the translation of this new modelling paradigm to the bedside, future work will focus on establishing a ‘minimum’ set of data that can be implemented to allow reliable and meaningful simulation results that can support clinical decision-making.

5. Conclusions

Multi-scale modelling of a patient-specific SV pathway is shown to effectively predict post-operative results for a patient approaching stage 2 palliation for SV heart disease. The complex process of utilizing clinical data appropriately to create pre-operative models, and using those models to test virtual operations, relies on comprehensive collaboration and integration between engineers and clinicians.

Appendix

The equations describing the pre-operative LPM (Figure 4(a)) are reported below. All constant parameters are listed in Tables A1 and A2.

Heart equations

The heart is described by two time-varying elastances, a SA and a SV respectively, whose contraction is ruled by two activation functions (AA(t) and AV(t), respectively). Both AA(t) and AV(t) are sinusoidal shape functions consecutive in time (Figure A1(a)), with duration of t_SAs and t_SVs, respectively.

Atrium

Blood flow across the atrial elastance:

$$C_i=C_{i-{\mathrm{BSA}}^{\ast }}\cdot {\left(\frac{R_i}{R_{i-{\mathrm{BSA}}^{\ast }}}\right)}^{-4∕3},$$ (4)

$$\frac{\mathrm{d}{V}_{\mathrm{SA}}}{\mathrm{d}t}=Q_{\mathrm{PV}}+Q_{\mathrm{SVC}}+Q_{\mathrm{THIVC}}-Q_{\mathrm{AV}}$$

Ventricle

Blood flow across the ventricular elastance:

$$\begin{array}{cc}\hfill \mathrm{SA}& \text{pressure}:P_{\mathrm{SA}}=P_{\mathrm{SA},\text{active}}\cdot \mathit{AA}\left(t\right)+P_{\mathrm{SA},\text{passive},}\text{with}\hfill \\ \hfill & P_{\mathrm{SA},\text{active}}=\frac{1}{C_{\mathrm{SA}}}\cdot (V_{\mathrm{SA}}-V_{\mathrm{SA}0})\text{and}\hfill \\ \hfill & P_{\mathrm{SA},\text{passive}}=c_{\mathrm{SA}}\cdot \{{\mathrm{e}}^{[{\mathrm{d}}_{\mathit{SA}}-V_{\mathit{SA}0})]}-1\}.\hfill \end{array}$$

$$\frac{\mathrm{d}{V}_{\mathrm{SV}}}{\mathrm{d}t}=Q_{\mathrm{AV}}-Q_{\mathrm{AO}}$$

The pressure effectively generated by the SV is reduced by the viscous term due to the myocardium fibers: P_SVeff = P_SV − R_MYO · Q_AO.

Valves

The AV and aortic (AO) valves are described by non-linear diodes, reproducing flow unidirectionality and resistance, with inertances accounting for inertial effects of blood flow (AO valve inertance is not present in the following equations because is included in the downstream arterial inertances L_UBA and L_THAO).

• AV valve

Pressure drop across the AV valve: $P_{\mathrm{SV}}-P_{\mathrm{AO}}=R_{\mathrm{MYO}}\cdot Q_{\mathrm{AO}}+K_{\mathrm{AO}}\cdot Q_{\mathrm{AO}}^2$

Therefore, blood flow across the AV valve can be expressed by the following equations:

$$\begin{array}{cc}\hfill \mathrm{SV}& \text{pressure}:P_{\mathrm{SV}}=P_{\mathrm{SV},\text{active}}\cdot \mathrm{AV}\left(t\right)+P_{\mathrm{SV},\text{passive},}\text{with}\hfill \\ \hfill & P_{\mathrm{SV},\text{active}}=a\cdot {(V_{\mathrm{SV}}-V_{\mathrm{SV}0})}^2+b\cdot (V_{\mathrm{SV}}-V_{\mathrm{SV}0})\text{and}\hfill \\ \hfill & P_{\mathrm{SV},\text{passive}}=c_{\mathrm{SV}}\cdot \{{\mathrm{e}}^{[{\mathrm{d}}_{\mathrm{SV}}-V_{\mathrm{SV}0})]}-1\}.\hfill \end{array}$$

• AO valve

Pressure drop across the AO valve: $P_{\mathrm{SA}}-P_{\mathrm{SV}}=L_{\mathrm{AV}}\cdot (\mathrm{d}{Q}_{\mathrm{AV}}∕\mathrm{d}t)+K_{\mathrm{AV}}\cdot Q_{\mathrm{AV}}^2$

Therefore, blood flow across the AO valve can be expressed by the following equations:

$$\begin{array}{c}\hfill Q_{\mathrm{AV}}=0,\text{if}{Q}_{\mathrm{AV}}<0\hfill \\ \hfill \frac{\mathrm{d}{Q}_{\mathrm{AV}}}{\mathrm{d}t}=\{\begin{array}{cc}0,\hfill & \text{if}{P}_{\mathrm{SA}}<P_{\mathrm{SV}\mathrm{eff}}\text{and}{Q}_{\mathrm{AV}}\le 0,\hfill \\ \frac{P_{\mathrm{SA}}-P_{\mathrm{SV}}-K_{\mathrm{AV}}\cdot Q_{\mathrm{AV}}^2}{L_{\mathrm{AV}}},\hfill & \text{elseware}.\hfill \end{array}\phantom{\}}\hfill \end{array}$$

Systemic and pulmonary circulation equations

The systemic and pulmonary circulation is represented by RC and RL blocks, described by the following equations expressed for the generic resistance R_i, compliance C_i and inertance L_i of the block i.

RC blocks (Figure A1(b))

$$Q_{\mathrm{AO}}=\{\begin{array}{cc}\frac{\sqrt{R_{\mathrm{MYO}}^2+4K_{\mathrm{AO}}(P_{\mathrm{SV}}-P_{\mathrm{AO}})-R_{\mathrm{MYO}}}}{2K_{\mathrm{AO}}},\hfill & \text{if}{P}_{\mathrm{SV}}>P_{\mathrm{AO}},\hfill \\ 0,\hfill & \text{if}{P}_{\mathrm{SV}}<P_{\mathrm{AO}}.\hfill \end{array}\phantom{\}}$$

$$\begin{array}{cc}\hfill & P_{i-1}-P_i=R_i\cdot Q_i,\hfill \\ \hfill & Q_i-Q_{i+1}=C_i\frac{\mathrm{d}{P}_i\left(t\right)}{\mathrm{d}t}\hfill \end{array}$$

RL blocks (Figure A1(c))

$$P_{i-1}-(P_i+R_i\cdot Q_i)=L_i\cdot \frac{\mathrm{d}{Q}_i}{\mathrm{d}t}.$$

Leg venous valve

A venous valve was included by means of a diode in the leg venous block. The following equation describes the flow Q_LEGV through the valve, with (P_LEGV − P_ABIVC) being the pressure drop across the valve and R_LEGV the resistance of leg veins:

$$Q_{\mathrm{LEGV}}=\{\begin{array}{cc}\frac{P_{\mathrm{LEGV}}-P_{\mathrm{ABIVC}}}{R_{\mathrm{LEGV}}},\hfill & \text{if}{P}_{\mathrm{LEGV}}>P_{\mathrm{ABIVC}},\hfill \\ 0,\hfill & \text{if}{P}_{\mathrm{LEGV}}<P_{\mathrm{ABIVC}}.\hfill \end{array}\phantom{\}}$$

Shunt equation

The expression for the pressure drop across the shunt is the following:

$$\Delta P=R_{\mathrm{SH}}{Q}_{\mathrm{SH}}+K_{\mathrm{SH}}{Q}_{\mathrm{SH}}^2=\frac{k_1}{D^4}{Q}_{\mathrm{SH}}+\frac{k_2}{D^4}{Q}_{\mathrm{SH}}^2,$$

where R_SH and K_SH are the linear and non-linear terms, respectively, of shunt resistance, and Q_SH is the shunt flow. R_SH and K_SH can be expressed as functions of the shunt diameter D, with k₁ and k₂ being proportionality constants previously evaluated (Migliavacca et al. 2001).

Figure A1.

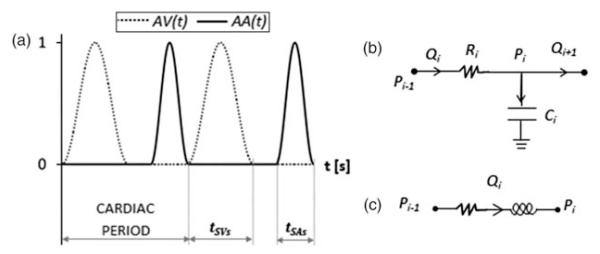
(a) Atrial and ventricular activation functions; (b) RC block; (c) RL block.

Table A1.

Parameter values for the heart and systemic circulation.

LPM blocks	Parameters	Values
Heart
Atrium	CSA	0.50
	cSA	0.30
	dSA	0.40
	VSA0	1.63
	tSAs	0.12
Ventricle	a	−0.115
	b	12
	cSV	0.14
	dSV	0.22
	VSV0	3.80
	tSVs	0.28
	RMYO	4.03 × 10−2
Valves	LAV	2.64 × 10−5
	KAV	7.02 × 10−4
	KAO	7.39 × 10−5
UB	RUBA	8.43 × 10−1
	LUBA	6.47 × 10−4
	CUB	1.81
	RUBV	2.46
	CSVC	2.26 × 10−1
	RSVC	9.35 × 10−2
LB
Aorta	CAO	1.41 × 10−1
	RTHAO	2.23 × 10−1
	LTHAO	2.20 × 10−3
	CTHAO	2.96 × 10−2
	RABAO	1.70
	LABAO	2.20 × 10−3
	CABAO	6.26 × 10−2
Legs	RLEGA	4.63
	LLEGA	2.20 × 10−3
	CLEGA	3.04 × 10−2
	RLEGC	10.9
	CLEGV	6.20 × 10−1
	RLEGV	2.55
IVC	CABIVC	3.22 × 10−1
	RABIVC	4.67 × 10−2
	CTHIVC	9.65 × 10−1
	RTHIVC	3.64 × 10−2
Liver	RLA	26.5
	CL	7.79 × 10−1
	RLV	1.66 × 10−1
Kidneys	RKA	18.7
	CK	3.24 × 10−1
	RKV	1.75
Intestine	RIA	41.0
	CI	1.94 × 10−1
	RIV	7.45 × 10−1

Note: R [mmHg s cm⁻³], C [cm³ mmHg⁻¹], L [mmHg s² cm⁻³], K [mmHg s² cm⁻⁶], V [cm³], a [mmHg cm⁻⁶], b [mmHg cm⁻³], c_SA and c_SV [mmHg], d_SA and d_SV [cm⁻³], t_SAs and t_SVs [s].

Table A2.

Parameter values for the pulmonary RCR blocks.

	Morphometric			Final LPM
Block	Rp + Rd (mmHg s cm−3)	Rd/(Rp + Rd) (−)	C (cm3mmHg−1)	Rp + Rd (mmHg s cm−3)	Rd/(Rp + Rd) [−]	C (cm3mmHg−1)
Right lung
1	9.64	0.87	1.53 × 10−2	12.5	0.83	6.48 × 10−2
2	37.9	0.92	3.14 × 10−3	49.3	0.89	1.33 × 10−2
3	1.61	0.73	1.43 × 10−1	2.09	0.67	6.03 × 10−1
Left lung
1	49.5	0.93	2.39 × 10−3	64.3	0.98	1.01 × 10−2
2	21.0	0.89	5.90 × 10−3	27.3	0.98	2.49 × 10−2
3	2.69	0.82	7.41 × 10−2	3.50	0.96	3.14 × 10−1

Notes: ‘Morphometric’ values are obtained from the Womersley-based impedances of the morphometric PA sub-trees (see Section 2.3). ‘Final LPM’ values are obtained after the manual tuning (see Section 2.4), i.e. correction of the total resistance (R_p + R_d), compliance C and distal-to-total resistance ratio R_d/(R_p + R_d).