Coupling 3D Monte Carlo light transport in optically heterogeneous tissues to photoacoustic signal generation

Abstract

The generation of photoacoustic signals for imaging objects embedded within tissues is dependent on how well light can penetrate to and deposit energy within an optically absorbing object, such as a blood vessel. This report couples a 3D Monte Carlo simulation of light transport to stress wave generation to predict the acoustic signals received by a detector at the tissue surface. The Monte Carlo simulation allows modeling of optically heterogeneous tissues, and a simple MATLAB™ acoustic algorithm predicts signals reaching a surface detector. An example simulation considers a skin with a pigmented epidermis, a dermis with a background blood perfusion, and a 500-μm-dia. blood vessel centered at a 1-mm depth in the skin. The simulation yields acoustic signals received by a surface detector, which are generated by a pulsed 532-nm laser exposure before and after inserting the blood vessel. A MATLAB™ version of the acoustic algorithm and a link to the 3D Monte Carlo website are provided.

1. Introduction

The generation of photoacoustic (PA) signals for imaging objects within tissues is dependent on how well light can penetrate to and deposit energy within light-absorbing objects. For light-scattering tissues, the task of light delivery to an absorbing object, such as a blood vessel within the dermis, is usually the key bottleneck. Stress waves generated in the object can more easily return to an acoustic detector at the surface than can optical perturbations caused by the object. When light first enters a tissue, the local background absorption by the tissue creates a strong PA signal that initially reaches the detector. The PA signal from the deeper vessel arrives later, and hence can be distinguished from the background signal.

The field of PA sensing and imaging has a long history, with explosive growth in the last couple decades (see reviews [1–3]). PA signals have been used to detect the momentum transfer during laser ablation of tissues [4], to specify tissue optical properties [5,6] and to detect buried objects within light-scattering medium [7,8]. Patrikeev et al. [9] used a Monte Carlo simulation of light transport, coupled to an acoustic calculation, to model the photoacoustic signals generated in a jugular vein by a pulsed light source.

This paper revisits the coupling of light transport to acoustic signal generation by presenting a 3D Monte Carlo simulation of light transport in an optically heterogeneous tissue, which is coupled to a calculation of stress wave generation and transport to a detector at the tissue surface. This calculation simulates how an impulse of energy deposition generates the time-resolved velocity potential reaching a detector, and then converts the velocity potential into the time-resolved pressure signal seen by the detector. This “forward” calculation allows prediction of signals from complex tissues seen by an acoustic detector on the tissue surface. The goal is to provide an example that instructs students beginning their work in photoacoustic imaging and detection, and a tool for approaching complex tissues during design of photoacoustic imaging devices. However, the program does not account for heterogeneous acoustic properties in a tissue, nor for acoustically mismatched boundaries.

Descriptions of the signals generated by absorbing particles, e.g. by small spheres, Diebold et al. [10], and spheroids, Li et al. [11], can be convolved against spatial distributions of absorption in more complex tissues. Ermilov et al. [12] and Yaseen et al. [13] coupled Monte Carlo simulations to photoacoustic signal generation. They used an N-shaped impulse response to each voxel of energy deposition, and coherently added the pressure waves from all voxels that reached a detector. Treeby and Cox [14] published a k-wave computation of photoacoustic signal generation that accounts for heterogeneous acoustic and optical tissue properties, and one can couple Monte Carlo simulations of energy deposition to this k-wave computation. Hence, there are alternatives to the simple acoustic model of this paper.

2. Materials and methods

2.1. 3D Monte Carlo

A 3D Monte Carlo program (mcxyz.c) has been developed [15], based on previous work [16,17], that creates a 3D Cartesian grid of voxels and assigns a tissue type to each voxel. Each tissue type has a unique set of optical properties (absorption coefficient μ_a [cm⁻¹], scattering coefficient μ_s [cm⁻¹], anisotropy of scattering g), appropriate for a particular wavelength of light. A MATLAB™ program allows the user to (1) create an input file that defines the parameters of the simulation (number of bins, bin size, etc.) and the optical properties of the desired tissue type (e.g. 1 = water, 2 = pigmented epidermis, 3 = blood-perfused dermis, 4 = whole blood), and (2) create a binary input file holding a 3D array T(y, x, z) that defines the tissue structure, where T holds integers (e.g. 1–4) that specify the desired tissue type in each voxel. The C-code mcxyz.c program reads the input files, executes the simulation, and saves a file that holds the spatial distribution of deposited energy, W(y, x, z) [J/cm³ per J delivered] or [1/cm³].

The current version of mcxyz.c uses a common refractive index for all tissue types, which is a limitation. Photons launch with a weight of 1.0, which is progressively attenuated as energy is deposited in the W(y, x, z) voxels after each photon step. Each photon propagates by steps of s [cm] or dimensionless step sμ_s. As a photon propagates and its stepsize s [cm] crosses from one voxel to the next, it jumps to the boundary between the voxels using some of its dimensionless step, deposits a portion of its current weight into the current voxel based on its partial step to the boundary, adjusts its optical properties for the next voxel, and continues to use its remaining dimensionless step based on the μ_s in the new voxel. Once all of the photon's stepsize is utilized, the photon's trajectory is changed by a scattering event, a new stepsize is assigned, and the process repeats. As photons are launched, the spatial pattern of energy deposition in W(y, x, z) accumulates. After a total of N photons have been launched, the program normalizes W by the voxel volume (dV = dx dy dz) and by N to yield W in units of [J/cm³ per J delivered] or [1/cm³]. This W [1/cm³] is converted to [1/m³] for use in the acoustic computation. This final W(y, x, z) is the pattern of energy deposition that will elicit thermoelastic expansion and launch the stress wave to be detected by a detector (see Section 2.1.1).

The example of this paper implements delivery of a pulsed 532-nm laser (pulse duration < bin size/speed of sound = 20 × 10⁻⁶ m/1500 m/s = 13 ns) delivered orthogonally onto the skin as an 800-μm-dia. circular flat-field collimated beam. Directly beneath the beam is a 500-μm-dia. blood vessel centered at 1 mm below the surface and extending along the y-axis (see Fig. 1A). The properties of the tissues are listed in Table 1.

Fig. 1.

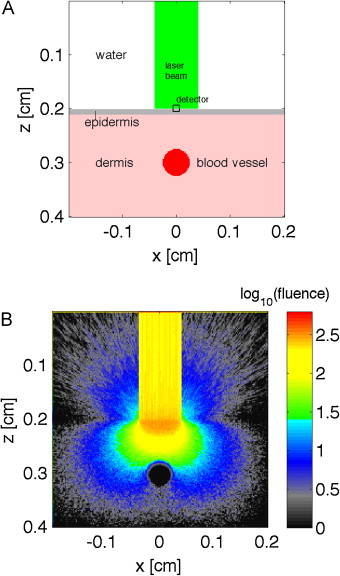
(A) Skin model, with epidermis, dermis and 500-μm-dia. blood vessel centered 1 mm below the skin surface, and a water layer on the surface boundary at z = 0.2 cm. (B) Fluence [J/cm² per J delivered] or [1/cm²], displayed as log₁₀(fluence). Above surface, the fluence escaping into the water is shown.

Table 1.

Optical properties of tissue types used in Monte Carlo simulations.

	μa [1/cm]	μs [1/cm]	g
Watera	3.56 × 10−4	100	1.0
Pigmented epidermis	16	376	0.90
Dermis (with 0.2% bloodb)	0.46	357	0.90
Blood vessel	231	94	0.90

^aWater is assigned a low absorption but a high scattering coefficient with g = 1.0, so that the photon steps through the water with no scattering and deposits energy to allow calculation of the escaping fluence in the water.

^bThe apparent average dermal blood volume fraction based on diffuse reflectance spectra. This tutorial model does not attempt to distinguish the superficial venous plexus in the papillary dermis and the reticular dermis.

2.1.1. Stress wave generation and detection

The method of calculating the stress wave that reaches the detector is based on the velocity potential, ϕ [m²/s] per J delivered to the tissue, which is related to the spatial distribution of energy deposition, W. At each time point after the impulse of energy deposition, a spherical shell of deposited energy, W_shell [1/m³], with a radius r = c_st centered on the detector will have launched a stress wave that arrives at the detector at time t. The value −ϕ(t) is positive and is calculated:

$$-\varphi (t)=\frac{\beta }{4\pi \rho C_p}\frac{1}{dt}{\int }_{r-dr/2}^{r+dr/2}\frac{W_{shell}}{r}4\pi r^{2}dr$$ (1)

where

• r = c_st, the distance from shell to detector at time t [m];

• t = time of stress wave arrival at detector [s];

• dt = time step of integration, dt = dz/c_s (bin size dz = 20 μm, dt = 1.33 ns);

  W_shell = the average energy deposition in shell [J/m³ per J delivered] = [1/m³];

and

• c_s = speed of sound in tissue ≈ 1500 m/s;

  ρ = density ≈ 1000 [kg/m³];

  C_p = specific heat ≈ 4180 [J/(kg °C)];

  β = thermal $\text{expansivity}=\Gamma C_p/\rho c_s^2\approx 2.57\times {10}^{-4}$ [°C⁻¹], such that

  Γ = Grüneisen $\text{coefficient}=\beta c_s^2/C_p\approx 0.138$ [dimensionless] at skin temperature.

The parameter W_shell is calculated discretely using the Monte Carlo array W(z, x, y):

• W_shell = sum(W(y, x, z)B_shell)/N_shell [1/m³] average energy deposition in shell;

• B_shell = shell-shaped 3D Boolean array that satisfies abs(R − r) < c_sdt/2 & R within tissue;

• R = sqrt((x − x_d)² + (y − y_d)² + z²), 3D array of distances from voxels to detector at x_d, y_d, z_d = 0;

• N_shell = sum(B_shell), the number of voxels in the shell.

Hence, the magnitude of the velocity potential arriving at time t, −ϕ(t), is proportional to the energy deposited in the shell, W_shell, at a distance r from the detector. The pressure P [Pa] per J delivered, is related to ϕ:

$$P=-\rho d\varphi /dt$$ (2)

Consider a medium with homogeneous deposition of energy, W, and negligible acoustic attenuation. The shell size grows as r² but the amplitude of a propagating acoustic wave attenuates as 1/r, so the signal from the shell reaching the detector grows as r = c_st, and hence −ϕ(t) at the detector grows linearly with time:

$$-\varphi (t)=\frac{\beta c_s^2}{\rho C_p}{W}_{shell}t=\frac{1}{\rho }\Gamma W_{shell}t$$ (3)

The pressure (Eq. 2) is therefore constant at ΓW, since W_shell = W in this case of homogeneous energy deposition. See Appendix for an illustration of this example.

Once the time-resolved pressure of the stress wave, P(t), is obtained, the frequency dependent attenuation of acoustic waves can be considered. The fast Fourier transform (FFT) of P(t) yields P(f), where f is frequency [Hz]. A frequency-dependent attenuation, α(f) [dimensionless], appropriate for a given tissue, can then scale the frequencies in the pressure wave, α(f)P(f). A typical expression for attenuation of pressure wave amplitude is α(f) = α₀(f/1 MHz)^b α₀ ≈ 90 dB/m, f is frequency [MHz], and b ≈ 1.1 for soft tissues (Table 4.16 in [18]). An inverse Fourier transform, iFFT(αP), will return the signal to the time domain, with the higher frequencies of the pressure waves appropriately attenuated.

The appendix lists the MATLAB™ program get_tVP() for implementing the above equations in a discrete calculation. The energy deposition in each voxel of the shell, U_shell(z, x, y), equals B_shellW(y, x, z)dV, where dV = dx dy dz. The total energy deposition in the shell is sum(B_shellW_shell)dV, where B_shell is the boolean array with values of 1 in voxels within the shell and within the tissue. The shell is spherical, W_shell4πr²dr, to allow response to an irregularly shaped tissue. The detector is in the middle of the grid and accepts signals from all directions. For the special case where the detector is on the skin surface with the outside boundary filled with water, the energy deposition in the water above the skin surface is very low and contributes negligibly to the generated pressure. The detector can be selected to be an isotropic detector, or a cosine-dependent detector that approximates a flat detector placed on the skin surface. The response of a true detector must consider the size and shape of the detector, as discussed in Queirós et al. [19]. A 3D array cosANG(y, x, z) encodes the cosine of the angle of detection from each voxel (cosANG = 1 for isotropic detector), and this array scales the contribution from the shell, U_shell(z, x, y)cosANG(y, x, z). The total energy deposition in the shell, sum(B_shellW_shell), weighted by cosANG is calculated as U_t = sum(U_shell cosANG). To ameliorate an approximate ±4.5% coefficient of variation due to the discrete nature of the voxels in the calculation, this U_t is adjusted by the ratio of an ideal shell volume, 2πr²dr, to the discrete shell volume, sum(B_shell)dV. The value of P is then calculated: P = −ρ gradient(ϕ)/dt. The use of the MATLAB™ function gradient( ) is less noisy than using simple differences, (−ϕ[it] − (−ϕ[it − 1]))/dt.

3. Results

Fig. 1 shows the skin model and how the 800-μm-dia. laser beam delivered at the skin surface quickly disperses into a distributed fluence (Fig. 1B). Fig. 2 shows the energy deposition in the skin without (Fig. 2A) and with (Fig. 2B) the 500-μm-dia. blood vessel centered at 1 mm depth below the skin surface. The pigmented epidermis and blood content of the dermis elicited superficial deposition of energy. The penetrating light that reached the blood vessel elicited strong energy deposition in the superficial layers of the blood vessel. Little optical energy penetrated to the center of the vessel.

Fig. 2.

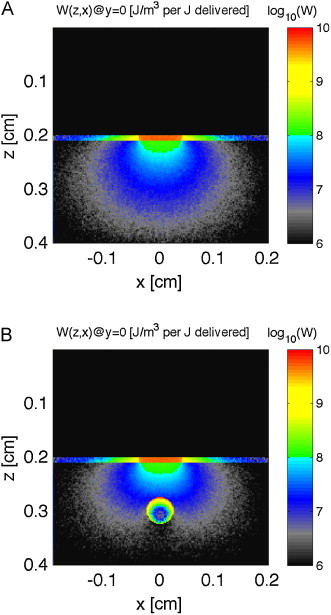
Monte Carlo simulation. Images show energy deposition, W [J/m³ per J delivered] or [1/m³], in skin (pigmented epidermis, dermis with 0.002 blood volume fraction) with overlaying water layer, induced by a very short pulsed 532-nm-wavelength laser (800-μm diameter). (A) No vessel. (B) 500-μm-dia. vessel centered at 1 mm depth. Skin structure and vessel extend along y-axis.

Fig. 3 shows the time courses of velocity potential and pressure arriving at the detector after the laser pulse. Two types of detectors are used. An isotropic detector collects equally from all angles. A Lambertian detector collects light proportional to the cosine of the angle between the line connecting a voxel to the detector and the normal to the surface. This Lambertian detector would mimic the behavior of a piezo detector laying flat on the skin surface. There is an initial response to the superficially deposited energy, followed by a delayed signal from the blood vessel.

Fig. 3.

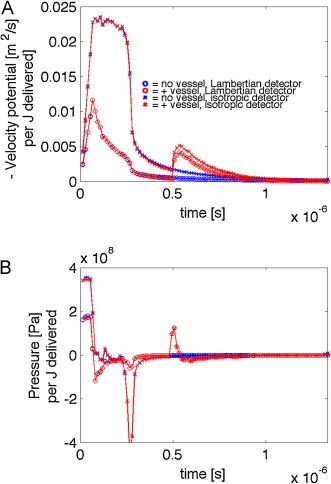
Velocity potential (−ϕ) and pressure (P) per J delivered to the skin with 500-μm-dia. blood vessel centered at 1 mm depth below the skin surface. (A) The time courses of the magnitude of velocity potential, −ϕ(t), for four cases, skin ± a vessel and detector collection either isotropic or Lambertian (detector flat on skin surface). (B) The pressure P(t) for the four cases. After the initial response to the superficial deposition of energy in the pigmented epidermis (370 Pa) and the blood-perfused dermis, the delayed signal from the vessel arrives at 0.5 μs. The isotropic detector is sensitive to the epidermal melanin, and there is a strong negative pressure due to the edge of the 0.8-mm-dia. beam of irradiation. The Lambertian detector is insensitive to this edge effect in the epidermis. The vessel pressure signal is the same for both isotropic and Lambertian detectors.

4. Discussion

The example simulations in this report used one wavelength (532 nm), but photoacoustic measurements of a blood vessel can be conducted at two wavelengths, allowing the oxygen saturation of the hemoglobin in the vessel to be determined. For example, dual-wavelength measurements of a vein draining a tissue or organ will reveal the oxygen extraction by the tissue. Simulations at two wavelengths can indicate the sensitivity of a dual-wavelength photoacoustic measurement to the oxygen saturation of a blood vessel.

The Monte Carlo simulations shown in this report used a 10-min computation. Since the shell of integration to yield W_shell averages out noise, the duration of the Monte Carlo run can be relatively short. As GPU-implemented Monte Carlo simulations become able to model a large grid of tissue heterogeneity, the simulations should be ∼1000-fold faster.

A limit of the model presented here is the sophistication of the stress wave calculation. There was no attempt to properly account for changes in the sound velocity of different tissue types. Deán-Ben et al. [20] have suggested the modification of the integration shell to account for small speed-of-sound variations in tissues. The model does not account for changes in the attenuation of acoustic signal by different tissue types, for reflectance at interfaces with sharply different acoustic impedance, nor for potential reflected waves off the tissue structure that might reach the detector. For example, attempting to model pressure waves generated in superficial brain tissue that escapes through the skull to reach a topical detector requires more care to model changes in attenuation and sound velocity through the skull, and to model reflected pressure waves internally reflecting from the air/skin surface and encountering the skin/skull and skull/brain interfaces to reflect back toward the detector. Nevertheless, it is hoped that mcxyz.c and get_tVP() will be useful to students beginning to work on photoacoustic signals in complex tissues.

Conflict of interest

The author declares that there is no conflict of interest.

Biography

Steven L. Jacques, Ph.D., received a B.S. degree in Biology at M.I.T., and an M.S. degree in Electrical Engineering and Computer Science and a Ph.D. degree in Biophysics and Medical Physics from the University of California-Berkeley (1984). His postdoctoral work was at the Wellman Center for Photomedicine at Massachusetts General Hospital, rising to the position of Lecturer in Dermatology/Bioengineering, Harvard Medical School. In 1988, he joined the University of Texas M.D. Anderson Cancer as an Assistant Professor of Urology/Biophysics, later achieving a tenured position as Associate Professor. In 1996, he joined the Oregon Health & Science University in Portland, Oregon, where he now serves as Professor of Biomedical Engineering and Dermatology.

Appendix.

The 3D Monte Carlo heterogeneous-tissue simulation (mcxyz.c) yields an array of energy deposition, W(z, y, x) [1/m³], where a bin size for the voxels (binsize [m]) and the position of the detector (xd,yd,zd [m]) are arguments for the function. A Boolean factor detector is assigned 0 to request isotropic collection by the detector, or assigned 1 to request a cosine-dependent collection by the detector, which is appropriate for a flat detector placed on the skin surface.

To illustrate the get_tVP() algorithm, the following MATLAB™ code creates a uniform distribution of 10⁶ J/m³ and places an isotropic detector at the center of the grid, then calls the algorithm. Plotting the resulting −ϕ (mVP) versus t, and P versus t, yields Fig. 4A and B. The result is a constant pressure of 0.138 MPa.

Fig. 4.

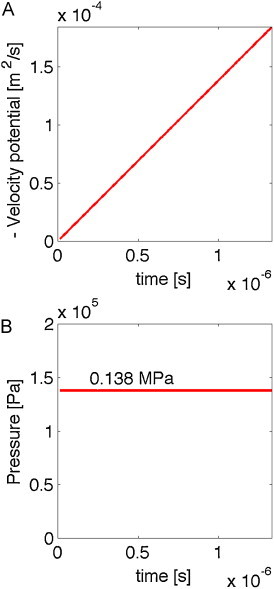
Demonstrating the algorithm for the case of a detector in the middle of an infinite medium with uniform energy deposition (10⁶ J/m³) at time zero, and a Grüneisen coefficient of Γ = 0.138. (A) The minus velocity potential (−ϕ) versus time. (B) The pressure versus time is constant.