Coexistence and relative abundance in plant communities are determined by feedbacks when the scale of feedback and dispersal is local

Summary

1. Negative plant-soil feedback occurs when the presence of an individual of a particular species at a particular site decreases the relative success of individuals of the same species compared to those other species at that site. This effect favors heterospecifics thereby facilitating coexistence and maintaining diversity. Empirical work has demonstrated that the average strengths of these feedbacks correlate with the relative abundance of species within a community, suggesting that feedbacks are an important driver of plant community composition. Understanding what factors contribute to the generation of this relationship is necessary for diagnosing the dynamic forces that maintain diversity in plant communities.

2. We used a spatially explicit, individual-based computer simulation to test the effects of dispersal distance, the size of feedback neighbourhoods, the strength of pairwise feedbacks and community wide variation of feedbacks, community richness, as well as life-history differences on the dependence of relative abundance on strength of feedback.

3. We found a positive dependence of relative abundance of a species on its average feedback for local scale dispersal and feedback. However, we found that the strength of this dependence decreased as either the spatial scale of dispersal and/or the spatial scale of feedback increased. We also found that for spatially local (i.e. relatively small) scale interaction and dispersal, as the mean strength of feedbacks in the community becomes less negative, the greater the increase in abundance produced by a comparable increase in species-specific average feedback. We found that life-history differences such as mortality rate did not generate a pattern with abundance, nor did they affect the relationship between abundance and average feedback.

4. Synthesis. Our results support the claim that empirical observations of a positive correlation between relative abundance and strength of average feedback serves as evidence that local scale negative feedbacks play a prominent role in structuring plant communities. We also identify that this relationship depends upon local scale plant dispersal and feedback which generates clumping and magnifies the negative feedbacks.

Introduction

Increasing evidence supports the idea that plant-soil feedbacks structure plant community composition. Aside from the important role plant-soil feedbacks play in determining the success of invaders (Klironomos, 2002; Wolfe and Klironomos, 2005; Reinhart and Callaway, 2006; Pringle et al., 2009) and driving successional changes (Kardol et al., 2007; Middleton and Bever, 2012), they may play a dominant role in facilitating coexistence among competitors (Bever, 2003; Klironomos, 2002; Kulmatiski et al., 2008; Petermann et al., 2008; Bever et al., 2010). Plant-soil feedbacks can be positive, negative or neutral. Positive feedback can occur when species-specific mutually beneficial plant-soil interactions promote the growth of soil microbes on which the host plant performs better than its competitors. Alternatively, it can occur when the responsiveness of a plant to soil microbes is positively correlated with its effectiveness as a host (Bever et al., 2012). In either case, the presence of an individual of a particular species at a particular site increases the relative success of other individuals of the same species at or near the site. While positive feedbacks can play an important role in community dynamics, such as invasion (Stinson et al., 2006; Levine et al., 2006; Vogelsang and Bever, 2009), we will focus on negative feedbacks in this study. Negative feedback occurs when the presence of an individual decreases the success of other individuals of the same species at or near the same site. The decreased success can be the result of the accumulation of species-specific parasites and herbivores. Empirical evidence suggests that pathogens are a main driver of feedback in plant communities (Packer and Clay, 2000; Bell et al., 2006; Mangan et al., 2010; Bever et al., 2012), favoring heterospecifics and thereby facilitating coexistence and maintaining diversity.

Perhaps the strongest empirical evidence of the role negative feedbacks play in structuring plant communities has been the observation that the average strengths of these feedbacks correlate with the relative abundance of species within a community. In temperate grasslands (Klironomos, 2002; Diez et al., 2010), temperate forests (Johnson et al., 2012), and tropical forests (Mangan et al., 2010; Comita et al., 2010), plant species that experience less negative feedbacks on average tend to be more abundant. While more work is needed to ascertain the generality of this empirical pattern (e.g. see absence of correlation in (Reinhart, 2012)), these published patterns suggest that negative feedbacks are an important driver of plant community composition. This suggestion is supported by theoretical work that shows negative feedback can generate a positive correlation between average feedback and relative abundance (Mangan et al., 2010; Chisholm and Muller-Landau, 2011). A more thorough theoretical understanding of the factors affecting the correlation between strength of feedback and relative abundance is necessary for diagnosing the dynamic forces that maintain diversity in plant communities. Here we focus on several candidate factors (life history differences, the spatial scale of dispersal, the spatial scale of feedback interactions, the strength of negative feedbacks across communities, and the variation of average feedbacks for species within a community) that could contribute to the generation of a dependence of relative abundance of plant species on the strength of its average feedback.

One potential problem with interpreting the correlation between average feedback and relative abundance as evidence that negative feedbacks are important drivers of plant community composition is that colonization/mortality rates might correlate with soil feedbacks. Empirical studies have shown that early successional species, which have relatively high colonization and mortality rates (Huston and Smith, 1987), tend to have more negative feedbacks than later successional species (Van der Putten et al., 1993; Kardol et al., 2006; Middleton and Bever, 2012). Therefore, in successional communities and communities where life history trade-offs between colonization and mortality rates drive community composition, the colonization/mortality rates could co-vary with average feedback and abundance. This could potentially confound the observed correlation between feedback and abundance. How these life-history trade-offs interact with feedback interactions to structure plant communities remains unclear.

The spatial scale of dispersal, or the distance at which plants are dispersal limited when colonizing open sites, as well as the spatial scale of feedback interactions, or the distance from the focal plant that negative competitive effects can be detected through reduced growth of neighboring plants, may also affect the correlation between average feedback and relative abundance. The common observation of poor seedling recruitment in local proximity of conspecific adults (Janzen, 1970; Packer and Clay, 2000; Mangan et al., 2010; Johnson et al., 2012) serves as evidence that the spatial scale of negative feedback can be very local, or within a few multiples of the size of the adult focal individual's canopy. Previous simulations have shown that spatial patterns generated by negative feedback can depend on the relative scale of dispersal and feedback (Molofsky et al., 2002; Levine et al., 2006). Furthermore, the previous theoretical work showing a positive relationship between strength of average negative feedback and relative abundance has been either spatially explicit (Mangan et al., 2010) or implicit (Chisholm and Muller-Landau, 2011). In neither of these was the scale of the feedback investigated. Meanwhile, a recent non-spatial model failed to find a relationship between average feedback and abundance (Mack, 2012), which suggests that the correlation could depend on the spatial dynamics of the feedback interactions being local. Despite this, the extent to which the relationship between average feedback and abundance depends on local spatial dynamics and what type of spatial dynamics, dispersal limitation and/or interaction distance limitation, has not been investigated.

The strength and variability of species-specific pairwise feedbacks may also affect the dependence of relative abundance on average feedback. Studies of theoretical food webs have demonstrated that the strength and variability of interactions play an important role in determining the dynamics of a community (McCann et al., 1998; Berlow, 1999; Berlow et al., 2004). Since the maintenance of diversity is one of the major consequences attributed to negative feedbacks, the role of species richness on the feedback/abundance relationship might be important. Work done on ecological networks has shown that communities may become less stable as community richness increases (Thébault and Fontaine, 2010). Theoretical results of Bonanomi et al. (2005) showed that as the strength of negative feedbacks became more negative or species richness decreased, the oscillatory dynamics of species coexistence driven by feedbacks also increased. Oscillatory dynamics make finding a correlation with abundance at any single time point difficult. Therefore, the correlation between abundance and feedback in communities with either very negative average community feedback, or relatively few species may be difficult to measure despite the dynamic importance of feedbacks in structuring community composition. However, the importance of interaction strengths, as well as the impact of species richness on the feedback/abundance relationship remains unknown despite the fact that negative feedbacks would be expected to promote coexistence (Bever 2003) and therefore increase richness.

Here we used a spatially explicit, individual-based computer simulation to test the extent to which the strength and slope of the correlation between average feedback and relative abundance depend on local spatial dynamics. In addition to the scale of dispersal and feedback, which in this model we will refer to as the dispersal neighbourhood size and the feedback neighbourhood size, we manipulated species-specific feedback strengths and variability, and community richness. We also incorporated life-history trade-offs in order to assess how confounding their co-variance with feedbacks and abundances are to determine how confident we can be with attributing the feedback-abundance relationship to soil feedbacks as opposed to life-history differences. Specifically we tested these hypotheses: i) if differences in species-specific average feedback do exist in a community and they are important drivers of community composition, then there will be an effect on abundance despite the inclusion of life-history trade-offs, ii) if the relationship between feedback and abundance is dependent on local spatial dynamics, then as we relax the localness of these effects in our model, the correlation will disappear, iii) if increased oscillatory dynamics reduce the signal of the relationship between abundance and feedback, then as the strength of average community feedback becomes more negative and species richness decreases, the strength of the relationship between abundance and feedback will decrease.

Materials and methods

The simulation

We extended the spatially explicit stochastic cellular automata computer simulation presented in Mangan et al. (2010). Each cell on a 100×100 torus grid was randomly assigned a plant species identity. Population dynamics were determined by choosing a focal cell at random for replacement 2 million times. The new occupant of the focal cell was chosen stochastically from a pool of dispersants weighted by the probability of establishment. The dispersant pool was comprised of all species occupying cells a specified distance from the focal cell, or within the focal individual's dispersal neighbourhood. Plants were assumed to disperse evenly over their dispersal neighbourhood. The prior occupancy of the focal cell and the composition of the cells a specified distance from the focal cell, which we call the interaction or the feedback neighbourhood, determines the soil microbial composition of the focal cell and therefore the establishment probability of each species. The probability of establishment for species i (e_i) was determined by the following:

$$e_i=(p_i{F}_i)/{\sum }_{i=1}^s{p}_i{F}_i$$ 1

where p_i is the proportion of that species in the dispersal neighbourhood, and F_i is the contribution of feedback. The contribution of feedback was determined by:

$$F_i=\left({\sum }_{d=1}^D\overline{f_i^d}\right)/D$$ 2

where D is the radius of the feedback neighbourhood, and the average growth effect from these cells on species $i(\overline{f_i^d})$ was determined by:

$$\overline{f_i^d}={\sum }_{j=1}^s\left(P_j^d{f}_{ij}\right)$$ 3

where f_ij is the influence of soil biota associated with species j on the growth of species i and $P_j^d$ is the proportion of soil biota influenced by species j at distance d from the focal cell. In this term, d weights this proportion with distance so that the strength of feedback is assumed to be scaled by root density, which will be highest immediately adjacent to an adult plant and taper in relative abundance with increasing distance. Pair-wise plant response measurements (f_ij) were generated by randomly assigning conspecific plant response values between a set minimum and maximum value to approximate experimentally obtained values and randomly assigning heterospecific responses between the conspecific maximum and a higher heterospecific maximum in order to ensure negative average feedback for all species. A new random establishment matrix was generated for each replication. Average feedback for each species was calculated following Bever (1994) as the average of the individual pairwise interaction coefficients (e.g. I_ij = f_ii − f_ij −f_ji + f_jj). The negative pairwise interaction coefficient is required for coexistence by negative feedback (Bever et al 1997). Average plant performance was standardized to 1 so that all abundance differences were the result of feedback differences only. Unless specifically manipulated, all communities consisted of 6 plant species as previously modeled in Mangan et al. (2010), mortality was uniform across species, the conspecific minimum was 0.4, the conspecific maximum was 0.7, the heterospecific maximum was 0.9, the dispersal neighbourhood size was the nearest 25 cells, the interaction neighbourhood size was the 8 nearest cells, and each treatment combination was replicated 5 times. All simulations were done using MATLAB 7.1 (The Mathworks, Inc.). All statistical analyses were done using SAS 9.2 (SAS Institute, Cary, NC USA).

Life-history trade-offs

We manipulated one component of life history trade-offs by introducing variation in each species mortality and establishment rates. The probability of mortality (m) for species i was determined by the following:

$$m_i=(P_i{M}_i)/{\sum }_{t=1}^s{P}_i{M}_i$$ 4

where P_i is the proportion of that species in the population, and M_i is its per capita adult mortality rate. In simulations in which species were assumed to have uniform mortality rates, M for all species was set to 1. We ran simulations with four different relationships between feedback and mortality. For the first manipulation, we introduced varied mortality and establishment rates, but kept average feedbacks uniform across species (-0.5). For these runs, establishment rates were inversely proportional to mortality rates for each species. A uniform average feedback across species was necessary to maintain coexistence since without feedbacks, the species coexist only neutrally and drift to extinction. For the second manipulation, mortality rates were set equal to the absolute value of each species' average feedback, thereby making mortality proportional to average negative feedback in each species. This relationship between negative feedback and mortality might be expected if, for example, fast growing plants invested less in defense which therefore allowed accumulation of host-specific pathogens resulting in negative feedbacks (Van der Putten 2003). For the third manipulation, mortality rates were set equal to 1 minus the absolute value of each species' average feedback, thereby making mortality inversely proportional to average negative feedback. For the fourth manipulation, mortality rates varied while both establishment rates and average feedbacks were kept uniform across species. The mortality differences generated a competitive hierarchy which would not allow coexistence without negative feedbacks. Communities consisted of 10 plant species. We analyzed the data using a GLM with each of the three relationships between mortality and feedback as a predictor of relative log-abundance.

Spatial structure

We manipulated the size of the dispersal neighbourhood from the nearest 8 cells in the 3 × 3 cell neighbourhood to the nearest 441 cells in a 21 × 21 neighbourhood. We also manipulated the size of the feedback neighbourhood from only the focal cell up to the nearest 361 cells in a 19 × 19 neighbourhood. All combinations of dispersal and feedback neighbourhood sizes were run in a fully factorial design. We used the AIC to find the best model fit and then performed a regression analysis using that model. Besides the size of the dispersal neighbourhood, the size of the feedback neighbourhood and their interaction, the squared terms were also tested. The best model included only dispersal neighbourhood size, feedback neighbourhood size, and the interaction term between them.

Magnitude and variance of feedbacks and community richness

We manipulated the magnitude and variance of the randomly assigned pairwise interaction measurements. Eight combinations of conspecific minimums and maximums (which set the heterospecific minimums thereby assuring negative average feedbacks) and heterospecific maximums were chosen to represent a spectrum of interaction strengths. The combinations of conspecific minimum, maximum, and heterospecific maximums used were; (0.1, 0.2, 0.3), (0.1, 0.2, 0.6), (0.1, 0.2, 0.9), (0.1, 0.5, 0.9), (0.1, 0.8, 0.9), (0.3, 0.5, 0.7), (0.4, 0.5, 0.6), (0.7, 0.8, 0.9) respectively. These combinations generated communities whose community level average feedback ranged from -0.12 to -0.86. After random values were assigned within the confined parameter space, the within species mean and variance of the difference between heterospecific pairwise interaction coefficients and the conspecific coefficients were then calculated as a measure of the strength of feedbacks in each community. We also manipulated the community richness from 5 species up to 10. We analyzed the results using a GLM using each level of species richness as a predictor of the slope of the relationship between relative log-abundance and average feedback.

Results

Life-history trade-offs

We manipulated one aspect of life history trade-offs by introducing variation in each species' mortality and establishment rates. We found that species-specific variation in mortality rates produced no detectable relationship with relative log-abundance when establishment rates were inversely proportional (F_(1,18) = 0.00, ns). Though there were species-specific differences in abundance, they appeared to be stochastic. Regardless of whether mortality was proportional or inversely proportional to average feedback, relative log-abundance was best predicted by average feedback and the relationship between them was positive (average feedback: F_(1,18) = 80.34, P < 0.0001, mortality: F_(1,18) = 0.02, ns). When coexistence was maintained by uniform negative feedbacks and mortality was allowed to vary independent of establishment, mortality rate strongly correlated with abundance (R² = 0.8609).

Spatial structure

We manipulated the size of the dispersal neighbourhood as well as the size of the feedback neighbourhood. We found a significant positive interaction between size of dispersal neighbourhood and feedback neighbourhood (interaction coefficient = 0.04, P = 0.008, Fig. 1a). The effect changing the size of the feedback neighbourhood has on the slope of the relationship between average feedback and relative abundance is dependent on size of the dispersal neighbourhood. We also found that as the scale of dispersal increased, the slope of the relationship between average feedback and relative log-abundance decreased (regression coefficient = -0.44, P < 0.0001, Fig. 1b). Likewise, we found that in general as the size of the feedback neighbourhood increased, the slope of the relationship between average feedback and relative log-abundance decreased (regression coefficient = -0.28, P = 0.006, Fig. 1c).

Fig 1.

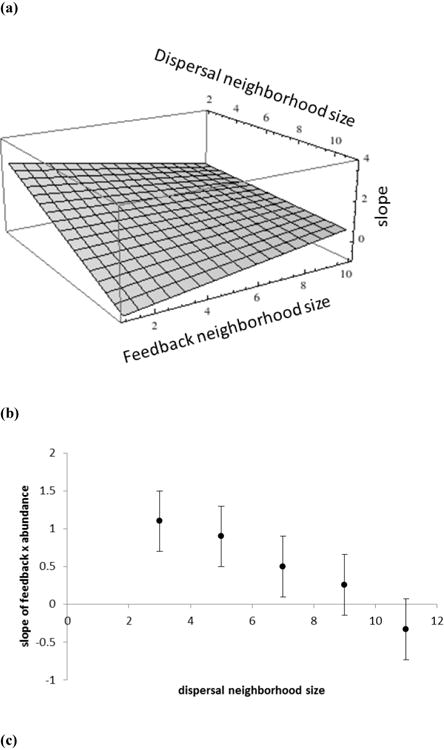
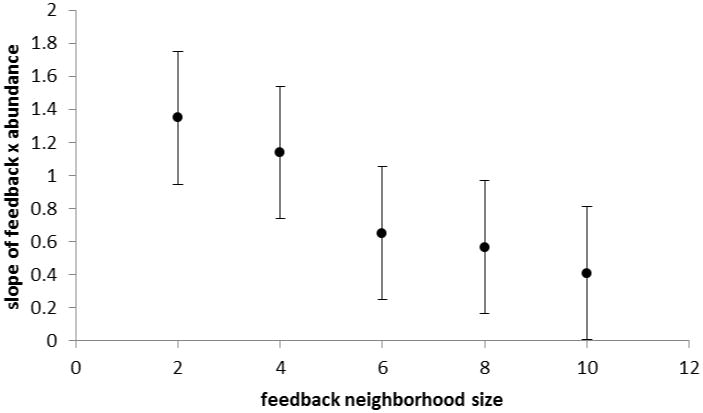
The relationship between dispersal and feedback neighbourhood size and the slope of the relationship between feedback and abundance. (a) The interaction effect between the size of dispersal and feedback neighbourhoods on the mean slope of the correlation between average feedback and relative log-abundance. The plane plotted represents estimates derived from the statistically significant regression model. (b) Mean slope of the correlation between average feedback and relative log-abundance as a function of the radius of the dispersal neighbourhood measured in cells between the focal cell and the maximum dispersal distance. (c) Mean slope of the correlation between average feedback and relative log-abundance as a function of the radius of the dispersal neighbourhood measured in cells between the focal cell and the maximum dispersal distance. Points are the least square means from a GLM analysis and bars represent standard errors for the model.

Strength and variance of feedbacks and community richness

We manipulated the strength and variance of the randomly assigned pairwise interaction measurements. We found that the slope of the relationship between relative log-abundance and average feedback is predicted by mean strength of feedback across a community (regression coefficient = 5.91, P < 0.0001). As the mean strength of feedback across communities became less negative the slope increased (Fig. 2).

Fig 2.

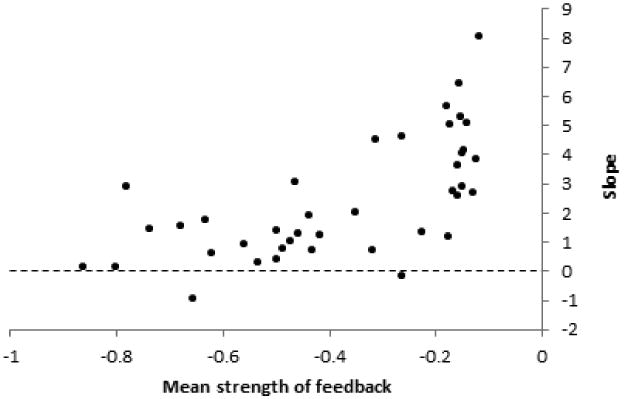
Plot of the slope of the relationship between abundance and species-specific average feedback as a function of average community feedback. As mean strength of feedback in a community becomes less negative, the slope of the correlation between species-specific average feedback and relative log-abundance increases.

We manipulated the community richness from 5 species up to 10. We were unable to detect a species richness effect on the abundance-feedback relationship, though the effect was marginally significant (regression coefficient = 0.22, P = 0.08). However, since we forced strict negative feedback on every species in the community, this lack of signal may have been the result of how we randomly chose pairwise interaction values.

Discussion

We find strong support for a deterministic dependence of plant relative abundance on strength of negative feedback when dispersal and interaction neighbourhoods are local (i.e. relatively small) and negative feedbacks structure plant communities. Tilman (1994) predicted that communities structured by competition and colonization and mortality rate trade-offs should show a correlation between longevity and abundance. Taken with the fact that feedbacks have been shown to correlate with successional stage (Van der Putten et al., 1993; Kardol et al., 2006; Middleton and Bever, 2012), which in turn correlate with colonization and mortality rates (Huston and Smith, 1987), it is possible that the observed correlation between feedback and abundance is actually the result of life-history differences. However, variation in mortality, regardless of whether it was proportional to or inversely proportional to average feedback, did not alter the dependence of relative abundance on average feedback in communities in which coexistence is mediated by negative feedbacks. Further work is necessary to investigate potential covariance between feedback and the competition and colonization trade-off which may also lead to coexistence. Our result is consistent with the observations of Comita et al (2010) who found that two measures of successional stage, shade tolerance or wood density, were not correlated with relative abundance, while relative abundance was correlated with measures of conspecific density dependence which may be due to negative feedback. Our result also supports the suggestion that the observation of a positive relationship between relative abundance and strength of feedback is evidence that negative feedback is an important driver of community structure (Mangan et al 2010).

That said, even the failure of a plant community to produce a positive correlation between species-specific average feedback and abundance, as recently observed by Reinhart (2012), does not necessarily rule out feedbacks as an important driver of community structure. In the model we know that coexistence is being driven by negative feedback. Yet, when the scale of plant dispersal is large and/or the scale of feedback interactions are large, the slope of the relationship between feedback and abundance becomes insignificantly different from zero (Fig. 1). Therefore, our results identify an important asymmetry in interpretation of field patterns, as observation of a positive relative abundance-strength of feedback correlation provides evidence of an important role of feedbacks in nature, but the lack of a signal between abundance and feedback is not sufficient reason to reject feedbacks as being important in the system. Notice that when the dispersal neighbourhood is very large, the slope of the relationship becomes insignificant from zero (Fig. 1a,b). This is consistent with results from recent mean field analyses examining diverse communities structured by feedbacks which found no dependence of species frequency on average feedback (Mack, 2012).

The shift of the abundance-feedback relationship with both the spatial scale of dispersal and the scale of feedback is consistent with previous observations of a dynamical dependence of competitive and frequency dependent interactions on spatial scale (Bolker et al., 2003; Eppstein et al., 2006,). The increase in the slope of the abundance-feedback relationship with both local dispersal and local interactions may result from an amplification of the penalty of negative feedback imposed by local scale interactions. The local scale dispersal generates clumped species distributions and a larger portion of the offspring of locally abundant species experience the negative consequence of prior occupancy with local scale negative feedbacks. This effect is analogous to the increased likelihood of coexistence with local scale competitive interactions in aggregated communities because of the enhanced importance of intraspecific competition (Bolker and Pacala, 1999). Notice however that the decay in slope is most rapid when the scale of feedback is limited and dispersal is not, a condition which intuitively should be more common than limited dispersal and global feedback (Fig. 1a). Also note that when the dispersal neighbourhood is very large, increasing the size of the feedback neighbourhood may increase the slope of the relationship between feedback and abundance. If the dispersal neighbourhood is large, then the likelihood of colonization due to dispersal for each species is essentially equal to its relative abundance and the distribution of species will be basically uniform without the clumping that results from local dispersal. In that case, having a small feedback neighbourhood may inhibit the effectiveness of the negative feedback to generate differences in relative abundance, thus reducing the slope of the relationship between abundance and feedback.

The slope of the abundance-feedback relationship also appears to flatten out with stronger community average negative feedbacks (Fig. 2). Previous theoretical work has shown that communities with stronger negative feedbacks produce larger population oscillations than communities with less negative feedbacks (Bonanomi et al., 2005). It is possible that the flattening of the relationship with stronger average feedbacks results from greater variation introduced by oscillatory abundance dynamics in communities with more negative community average feedbacks. Another possibility is that the differential penalty imposed by local scale negative feedbacks on clumped species distributions is reduced among more strongly negative values of negative feedback. Further work is necessary to identify the mechanism underlying this relationship.

In conclusion, our results show that a positive correlation between relative abundance of a plant species and the average strength of feedback for that species can represent a signature of negative feedbacks driving coexistence, but only when negative feedbacks occur on a local scale and plant dispersal is also limited. We note that these conditions may be commonly met as feedbacks through the soil community are very likely to be in proximity of root systems and hence very local (Bever et al 2012) and plant dispersal has frequently been noted as being largely limited (Clark et al., 1999). While a strength of this modeling approach was our ability to test the effect these mechanisms have on the relationship between abundance and feedback in isolation, in nature these processes would all be acting simultaneously with other factors, which could interact in ways not captured here. That said, given accumulating evidence of a positive feedback/abundance relationship across a diversity of plant communities (Klironomos, 2002; Diez et al., 2010; Mangan et al., 2010; Comita et al., 2010; Johnson et al., 2012), our results make a strong case for the importance of local scale plant-soil feedbacks as a dominant force structuring plant communities.