Abstract
Background
How aging, being unfavourable for the individual, can evolve is one of the fundamental problems of biology. Evidence for aging in unicellular organisms is far from conclusive. Some studies found aging even in symmetrically dividing unicellular species; others did not find aging in the same, or in different, unicellular species, or only under stress. Mathematical models suggested that segregation of non-genetic damage, as an aging strategy, would increase fitness. However, these models failed to consider repair as an alternative strategy or did not properly account for the benefits of repair. We used a new and improved individual-based model to examine rigorously the effect of a range of aging strategies on fitness in various environments.
Results
Repair of damage emerges as the best strategy despite its fitness costs, since it immediately increases growth rate. There is an optimal investment in repair that outperforms damage segregation in well-mixed, lasting and benign environments over a wide range of parameter values. Damage segregation becomes beneficial, and only in combination with repair, when three factors are combined: (i) the rate of damage accumulation is high, (ii) damage is toxic and (iii) efficiency of repair is low. In contrast to previous models, our model predicts that unicellular organisms should have active mechanisms to repair damage rather than age by segregating damage. Indeed, as predicted, all organisms have evolved active mechanisms of repair whilst aging in unicellular organisms is absent or minimal under benign conditions, apart from microorganisms with a different ecology, inhabiting short-lived environments strongly favouring early reproduction rather than longevity.
Conclusions
Aging confers no fitness advantage for unicellular organisms in lasting environments under benign conditions, since repair of non-genetic damage is better than damage segregation.
Electronic supplementary material
The online version of this article (doi:10.1186/s12915-014-0052-x) contains supplementary material, which is available to authorized users.
Keywords: computational modelling, mathematical modelling, senescence, aging, asymmetry, cell division
Background
Aging is detrimental; it is therefore hard to explain why it evolved [1]. Aging clearly occurs in those multicellular organisms that evolved a division of labour between germ line and soma, rendering the soma disposable [1,2]. Due to extrinsic mortality, natural selection may favour early reproduction at the cost of a reduced chance of reproduction later in life [3]; similarly early reproduction is also favoured when populations expand [4,5]. This leads to a trade-off in resource allocation between maintaining and repairing the disposable soma versus investing in reproduction, suggesting that evolution selects for an optimal investment in repair and hence optimal longevity, at least in multicellular organisms with a germ line [1].
For unicellular bacteria in particular, it was commonly believed that such a division of labour into germ line and soma and therefore aging does not occur, although in fact aging was long known to occur in a eukaryotic unicellular organism, the budding yeast Saccharomyces cerevisiae [6]. Budding yeast may have been seen as a special case not relevant to bacteria, although budding and other forms of asymmetric division also occur in bacteria [7]. Moreover, regarding the evolutionary benefits of aging, it should not matter whether the organism is eukaryotic (e.g. a yeast) or prokaryotic (e.g. a bacterium); it should only matter whether it is unicellular (including cancer cell lines) or multicellular. Regarding molecular mechanisms, aging would also require some form of asymmetric division in unicellular organisms. Whatever the reason, the idea of aging as a universal hallmark of life, even affecting bacteria, was considered but dismissed in the 1950s and 1960s [8–13].
It was the discovery of aging in the fission yeast Schizosaccharomyces pombe [14], which divides apparently symmetrically by binary fission like many bacteria, and then the discovery of aging in the asymmetrically dividing bacterium Caulobacter crescentus [15] that rejuvenated the idea that aging may be a universal hallmark of life. This view was cemented further by the discovery of a limited degree of aging in the model bacterium Escherichia coli by Stewart and co-workers in 2005 [16]. They showed that while cell division in E. coli was morphologically symmetric, it was not functionally symmetric: the old-pole cell, i.e. the daughter cell inheriting the older pole of the mother cell, grew more slowly and the new-pole cell grew faster than the mother cell, suggesting that the older pole was associated with more damage. This demonstrated the possibility of division of labour between daughter cells even if cells appear to divide symmetrically.
Since then, the evidence for aging in unicellular organisms in the sense of reduced growth rate of the old-pole cell has become less clear: some further studies supported a limited degree of aging in the bacteria E. coli [17], Bacillus subtilis [18], Mycobacterium spp. [19], and the diatom Ditylum brightwellii [20], while others found no evidence of aging in E. coli [19,21,22] and other bacteria [22] or the unicellular eukaryotic alga Euglena gracilis [23]. Chao and co-workers [24,25] pointed out that age, in the sense of the damaged fraction of cells, could reach a steady state in growing cells where damage accumulation would be balanced by damage dilution such that ‘age’ would not increase with time, and that this was the case in the studies of [16,21]. Repair was not considered, but could be an additional process that removes damage. In such a steady-state age, damage would keep being formed, but the growth rate and condition of the cell would not deteriorate over time, nor would lifespan be reduced. This differs strongly from what is observed in the budding yeast [6,26] and in C. crescentus [15]. However, Wang and co-workers [21] found that growth rates of E. coli old-pole cells grown in channels of a microfluidic device did not change over 200 generations, suggesting lifespan to be long. On the other hand, they also found that the probability of sudden events, such as death or filamentation (elongation into long filaments due to growth without cell division), increased with age, suggesting that at least some kind of damage accumulated during this apparent steady state. This is difficult to reconcile with the interpretation that these cells grew in a steady state of age. Moreover, different experimental conditions such as the presence of damaging agents or the expression of fluorescent proteins might also explain differences between studies [27]. Adding a further note of caution, we know nothing of aging in Archaea, multicellular bacteria or those spherical bacteria that do not conserve the ‘old pole’ over consecutive divisions since their division plane cycles through orthogonal directions [28].
Most recently, the fission yeast was shown not to age under benign conditions in a study that included following individual cells for at least 30 consecutive divisions [29]. The two studies following cells for a large number of generations under benign conditions suggest that the growth rates of old-pole cells of E. coli [21] and of the fission yeast [29] may fluctuate but do not decline. Rather, death may become more likely with age in wild-type E. coli approaching the probability of death of an SOS repair deficient lexA3 mutant [21]. In the fission yeast, death also appears to be a sudden and random event triggered by accidental partitioning of protein aggregates during cell division, rather than an active mechanism of damage segregation [29].
In the wake of [16], some mathematical models have been specifically developed to address the evolutionary question of the fitness benefits of aging in unicellular organisms [5,24,30–32]. These models differ in their assumptions and their treatment of key processes, making it difficult to describe them and their predictions briefly yet accurately; we will therefore discuss differences and the extent of experimental support for the various assumptions later. Taken together, these models predicted asymmetric division and absence of repair to be the fittest strategy, placing unicellular organisms into the division of labour terrain just like multicellular organisms. Note, however, that these models predicted complete asymmetry combined with complete absence of repair to be the fittest strategy. Neither predictions are correct [24,27]: asymmetry is often very limited [16–20] or absent [19,21,22,27,29] whilst dedicated molecular systems for the repair of damage are ubiquitous. Further, these repair mechanisms are inducible and deletions reduce fitness [33,34].
Given the confusing experimental evidence and the incorrect predictions of previous mathematical models developed to explore consequences of aging, we revisit this question using iDynoMiCS, a generic individual-based model of the growth of unicellular organisms [35]. iDynoMiCS and its precursors have been applied to a range of problems and its aging-independent elements, such as the simulation of the chemostat environment as well as growth and cell division, have thereby been validated. By adding the processes of accumulation, repair and segregation of damage, where the damage is either inert or toxic, we have extended iDynoMiCS to develop UnicellAge. Three differences from previous models are central: (i) inclusion of costly repair, (ii) continuous growth of individual cells catalysed by undamaged components of the cell, making any decrease of these catalytically active components by damage accumulation or increase by repair immediately effective, and (iii) growth rate dependence on resource concentration, leading to resource competition in dynamic environments.
We find that repair is always beneficial when damage accumulation is above a baseline rate. Further, there is an optimal investment in repair. In contrast, damage segregation is only beneficial in addition to damage repair if the damage accumulates at a high rate and is toxic and repair is inefficient. This suggests that repair should occur in all unicellular organisms, while damage segregation should be limited to toxic damage that cannot be repaired at reasonable cost. This is well in line with experimental evidence for many unicellular organisms where aging is either absent or minimal, at least under benign conditions. However, our model predictions are in contrast to the considerable degree of aging found in the budding bacterium C. crescentus and the budding yeast. We suggest that budding functions as a mechanism of cell division that facilitates damage segregation. The evolution of aging in these budding organisms can be explained by their ecology, as they are living in transient habitats where longevity is of little advantage. Overall, taking account of all experimental evidence in the light of the predicted fitness benefits clearly shows that the idea that aging is beneficial for unicellular organisms and therefore universal is overly simplistic.
Results
Model development
We have embedded the three aging-related processes of damage accumulation, repair and segregation in iDynoMiCS [35], a general individual-based model of the growth of microbial cells immersed in a given environment. Together with its predecessors, iDynoMiCS has been applied to colony [36] and biofilm growth [37,38], evolution of cooperation [39], lag phase [40], metabolic switching [35] and plasmid transfer [41], and thereby tested relatively well. We refer to our new iDynoMiCS-based aging model as UnicellAge as it is a general model for aging in all unicellular organisms, or unicells for short. iDynoMiCS and UnicellAge are open-source programs, which are freely available from [42]. An overview of UnicellAge is given in Figure 1. The complete set of equations is in Additional file 1, a figure showing the qualitative behaviour of the kinetics used is in Additional file 2, and the symbols used are in Additional file 3.
Figure 1.
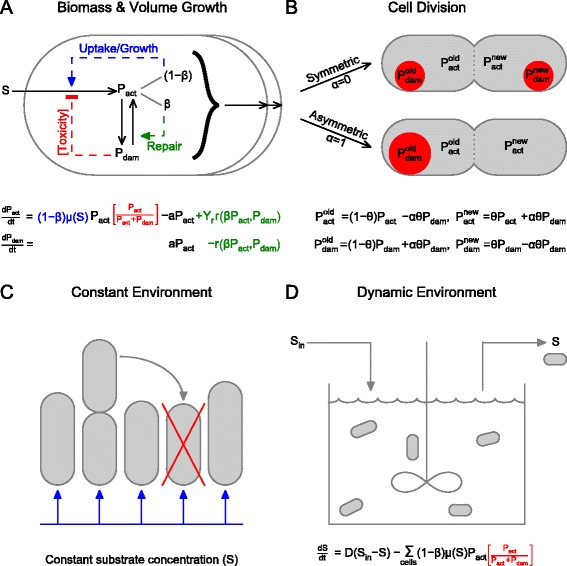
Schematic of the model. (A) The continuous processes of growth, damage accumulation and repair. Substrate (S) is taken up and converted into active protein (P act). The substrate concentration may be either constant or dynamic, depending on the environment. This autocatalytic growth process is catalysed by the ‘growth machinery’, a fraction (1 − β) of active protein, producing more active protein. Active protein is converted at damage accumulation rate a into damaged protein (P dam), which may inhibit the growth process if it is toxic. Damaged protein may also be repaired according to Equation 1 by the ‘repair machinery’, the other fraction of active protein (β). Protein represents the entire biomass. (B) The discontinuous process of cell division. Both daughter cells inherit the same amounts of total biomass on average, specified by the variable θ that is chosen from a truncated normal distribution with mean 0.5, standard deviation 0.025. They may acquire the same proportions of active and damaged protein (symmetric division) or the old-pole cell may take on all (or as much as possible) of the damaged protein (asymmetric division). These are the two extreme cases of a continuum denoted by the variable α. (C) In a constant environment, a cell is randomly replaced by a new cell formed upon cell division; this models external mortality. Substrate is taken up by the cells but its concentration does not change. (D) In a dynamic environment, substrate at concentration Sin is fed into the system, and cells and substrate at concentration S leave the system, all in proportion to the dilution rate D. Removal of cells is a form of extrinsic mortality. See Additional files 1,3 for more details.
In UnicellAge, cells grow by taking up nutrients from the environment, which automatically leads to competition for limiting resources. For example, cells with a strategy of damage repair can compete against cells with a strategy of damage segregation. Fitness emerges from this interaction rather than being defined by some arbitrary measure, such as population size after a certain time. The fitter strategy wins the competition significantly more frequently.
Modelling growth
Each individual cell in the model is composed of just two types of biomass, both referred to simply as ‘protein’ [43]: intact, active protein Pact and damaged protein Pdam (Figure 1A). Only active protein catalyses biomass growth: the consumption of substrate resulting in the production of more catalytically active biomass. Note that this autocatalytic nature of growth leads to an exponentially increasing rate of biomass growth of a damage-free cell. Such exponential growth of single cells during their cell cycle is empirically well supported by most studies of unicellular organisms [21,44–47]. However, some studies of the fission yeast [48,49] and E. coli [50] provided evidence for bilinear growth. Nevertheless, bilinear growth can be approximated by exponential growth. We have also examined linear growth for comparison with previous models that make this assumption [5,24,32] (Additional file 1). To describe the dependence of growth rate on substrate concentration we chose Monod kinetics (Additional file 2B) as appropriate for a non-toxic, sole growth-limiting substrate, e.g. growth of E. coli on glucose [51].
Modelling damage accumulation and repair
Active protein is converted to damaged protein at an environmentally determined, constant rate of damage accumulation a, in line with those previous models based on continuous time processes [5,24,32]. We assume that once damaged, material can be repaired by a lumped repair process requiring resources and specialised proteins, such as chaperones and proteases, known as ‘repair machinery’. Cells have evolved sophisticated mechanisms of repair that can be induced in response to stress [33,34,52–55]. For example, misfolded proteins can be refolded by ATP-dependent chaperones or failing that degraded by ATP-dependent proteases. Chaperones also prevent misfolding. Oxidatively damaged proteins can be degraded by proteases although the formation of cross-links may impede proteolysis [34]. If the capacity for such repair is exceeded, e.g. during stress, misfolded proteins aggregate temporarily to become later disaggregated and preferentially refolded or alternatively degraded by bi-chaperone systems [33,34]. Elevated expression of proteasome or disaggregase activities can prevent the accumulation of aggregates and hence aging of budding yeast [56]. Similarly, elevated expression of superoxide dismutase in E. coli reduces formation of protein aggregates to below wild-type levels [57].
Importantly, repair processes, defences against e.g. reactive oxygen species, and their expression levels could evolve to adapt to recurring stresses provided this would increase fitness. For this reason, we do not prescribe details and expression levels of repair and defence processes as we are asking an evolutionary question. What is essential is to consider the costs of repair, and there are two types of cost in UnicellAge: (i) protein dedicated to repair cannot contribute to growth, so that the conversion of substrate into new active biomass, and thus growth rate, becomes reduced in proportion to β, the fraction of protein dedicated to repair (Additional file 2C); (ii) some material has to be consumed in the repair process to generate the required resources, such as energy and building blocks. Refolding requires less energy than proteolysis plus re-synthesis, but even proteolysis will release intact monomers that can be recycled in the synthesis of new polymers. Hence, the efficiency of converting damaged material into new material should be higher than the efficiency of converting a single type of monomer, the growth substrate glucose, into all monomers required [58]. In summary, the efficiency of repair should be higher than the efficiency of growth (known as the growth yield) on glucose of 44% [59] but lower than 100%. By default we assume an efficiency of 80%.
Repair and growth machineries are considered to be equally susceptible to damage. For simplicity, we assume that the rate of repair, r, is proportional to the concentration of damage and proportional to the concentration of repair machinery (Additional file 2D), and that this rate saturates similar to Michaelis–Menten enzyme kinetics as some maximal rate of repair cannot be exceeded. This gives
| 1 |
as the simplest kinetics satisfying these assumptions. Some previous models have not included repair at all [24], while others have assumed that damage decays with a certain, fixed rate [5,32]. The difference between repair in our model and damage decay in previous models is twofold: (i) decay is assumed to follow first-order kinetics like spontaneous, radioactive decay, i.e. decay is not catalysed by repair machinery; (ii) in decay, the material is lost while in repair some of the material is recycled.
Modelling toxicity of damaged material
While it is known that some types of damaged material have some inhibitory or toxic effects [54,60], the empirical evidence for an overall toxic effect of damage is weak. If damage were inert, one would expect the specific growth rate of a cell to be proportional to the fraction of catalytically active material it contains. As a corollary, specific growth rate should decline linearly with the fraction of damage, i.e. the age of the cell. The decline of reproductive output or specific growth rate with age appears to be approximately linear in C. crescentus [15,61] and, albeit to a much lesser extent, in E. coli [16,17] and B. subtilis [18]. If damage were toxic, one would expect the specific growth rate of the cell to decline more strongly than linear, resulting in a concave quadratic relationship (Additional file 2A). Such a concave quadratic relationship was found to be statistically significant only in some experiments with C. crescentus [31], but the deviation from a linear dependency was rather small. The small deviation from a linear relationship observed could be due to a residual activity of damaged material compensating a stronger toxic effect, or due to efficient repair of the damage masking the true rate of toxic damage accumulation. For these two reasons, toxicity may only appear to be absent. As the evidence is not conclusive, we compare both cases, inert versus toxic damage, in UnicellAge. In previous models, toxicity has either been neglected or included in various ways (Table 1).
Table 1.
Summary of assumptions and predictions of various aging models
| Assumptions | Predictions | |||
|---|---|---|---|---|
| Growth & Division | Effect of damage | Removal of damage | Environment | |
| Watve et al. (2006) [30]: Leslie matrix model with multiple cellular components of different ages | ||||
| Growth rates of cellular components decline with their age. Cells divide after a fixed time without any restriction on daughter cell sizes. Cells die if they are in the oldest age class and no longer contribute to population growth | ‘Toxicity’ considered by assuming oldest and slowest growing components to be growth rate limiting | Repair converts oldest into newest components without growth rate cost | Constant | Asymmetric division increases population growth rate over the symmetric case if older components in the latter are ‘toxic’ and decline of growth rate with age is above minimal. Repair increases population growth rate since repair turns old into new components at no growth rate cost |
| Ackermann et al. (2007) [31]: evolutionary model where survival depends on damage and repair | ||||
| Cells do not grow, yet divide after a fixed time | Damage decreases survival probability | Repair removes damage, at cost of decreased survival probability | Constant, extrinsic mortality | Repair is only beneficial in symmetrically dividing cells. The best strategy is complete asymmetry without any repair |
| Erjavec et al. (2008) [32]: metabolic model of growing cells | ||||
| Growth of cells linear; cells divide once active protein reaches a threshold | Damage toxic | No repair but decay of active and damaged protein; decay without cost, no recycling of damaged into active protein | Constant | Asymmetry of damage partitioning beneficial, the stronger the asymmetry, the higher the benefit. Symmetry beneficial if offspring are smaller unless damage accumulation rate too high |
| Chao (2010) [24]: damage affects time between divisions | ||||
| Cells acquire active and damaged protein at linear rates; cells divide once active protein reaches a threshold | Damage toxic by linearly decreasing growth rate | Repair absent | Constant, extrinsic mortality | Complete asymmetry has highest mean fitness apart from a narrow region of intermediate damage accumulation rates where the fittest strategy is slightly below complete asymmetry |
| Rashidi et al. (2012) [5]: energy budget model | ||||
| Cells grow and prevent damage accumulation depending on energy allocated to growth and prevention, with a fixed total energy budget for the cell | No effect on growth or division, but can trigger instant cell death if above threshold | Damage is degraded but not repaired (recycled) | Constant | Asymmetry ensures survival of the population at high damage accumulation rates in the absence of degradation. Symmetrically dividing cells invest just enough into damage prevention to avoid instant death |
| UnicellAge: metabolic model of growing and repairing cells competing for resources | ||||
| Cells grow exponentially by consuming resource; cells divide once total protein reaches a threshold | Damage inert or toxic | Repair by active protein that does not contribute to growth; repair recycles material with a certain efficiency | Constant or dynamic, extrinsic mortality | Repair better than asymmetry unless damage accumulation rate high, damage toxic and efficiency of repair low |
Modelling time
All processes in UnicellAge occur continuously and concurrently, apart from discrete events such as cell division. As a consequence, any formation of new damage will decrease, and any repair of damage will increase, the specific rate of growth with immediate effect rather than once per generation. Another consequence of continuous time processes is that cells do not have to be divided after a certain, fixed generation time as in [30,31]. Rather, cells with different amounts of damage will grow at different rates and divide at different times in UnicellAge, as in [5,24,32]. Recent high-precision measurements in E. coli confirm the assumption made in UnicellAge that cell division is triggered by cell size rather than a timing mechanism [62].
Modelling cell division
Regarding division of volume, cells are assumed to divide instantly into roughly equally sized daughter cells upon reaching a threshold volume (Figure 1B). Limited random variation of daughter cell sizes around the average 50:50, models the imprecision of cell division and leads to desynchronisation of cell divisions amongst offspring (see Additional file 1 for details). Since age-related changes of cell size at division have either not been noticed [15,17,18,21,22 for E. coli31] or if noticed have been small [16,22 for Methylobacterium extorquens], we assume that the volume triggering cell division is the total volume of the cell regardless of how much of it is active or damaged material. However, we change this assumption for comparison with [32] in Additional file 1.
Regarding damage segregation, we follow the scheme of [32] for partitioning active and damaged material between the old-pole and new-pole inheriting daughter cells at division (Figure 1B). This scheme employs an asymmetry parameter α that can take any value between 0 for completely symmetric division (i.e. no damage segregation) leading to identical offspring and 1 for completely asymmetric division where one daughter cell takes all the damage (up to the capacity of the cell). The daughter cell inheriting more of the damage represents the daughter cell inheriting the older cell pole from the mother. We simulated complete symmetry, complete asymmetry and various intermediate asymmetries.
Modelling a constant environment
To compare our results more directly with all previous models, which have not included any competition for dynamic resources, we have also implemented a constant environment. For this case, substrate concentration is kept constant and the total population size is maintained at 1,000 cells by removing an individual at random each time a division occurs (Figure 1C). This implements extrinsic mortality, which is important since extrinsic mortality is the reason why early reproduction is favoured by natural selection [3]. Note that only some models include extrinsic mortality (Table 1).
Modelling a dynamic environment
The constant environment is clearly unrealistic, so we have followed the tradition of using the chemostat to assess experimentally or theoretically the fitness of different strategies competing for the same limiting resource. A chemostat is an open, well-mixed system where fresh resources are supplied, and cells and left over resources are removed, with a constant dilution rate D (Figure 1D, see Additional file 1 for more details). This system reaches a steady state where growth is balanced by dilution. Since specific growth rate in the chemostat will become equal to the fixed dilution rate in the steady state, growth rate cannot be used to assess fitness. Rather, the steady-state substrate concentration can be used to assess the fitness of single strategies in isolation because the ability to grow as fast as the dilution rate at a lower substrate concentration confers higher fitness [63,64]. Note that dilution is a form of extrinsic mortality, so both environments feature extrinsic mortality.
Determination of fitness
Specific growth rate in the constant environment, or substrate concentration sustaining sufficient growth rate in the steady state of a chemostat, are important contributing factors to fitness, but ultimately, fitness cannot be determined in single-species cultures since it emerges from the interactions between strategies. Therefore, fitness has to be evaluated by competition of two strategies in a given environment, counting how often a strategy becomes extinct or fixed in the population, as described in Methods.
Repair is fitter than damage segregation
We compared the fitness of damage repair and damage segregation strategies, assuming damage to be either inert or toxic, and varying all aging-related parameters: the investment in repair, the efficiency of repair, the degree of asymmetry and the rate of damage accumulation. All strategies were evaluated in two well-mixed environments, with constant or dynamic resources, as well as in isolation (pure culture) and in competition (mixed culture). Apart from very low damage accumulation rates, the fittest strategy was repair of damage but not damage segregation (Table 2).
Table 2.
Overview of which strategy is fittest depending on conditions
| Damage accumulation rate (h −1 ) | Environment | Damage inert | Damage toxic |
|---|---|---|---|
| 0.01 | Constant | N | SO |
| Dynamic | SO | SO | |
| 0.05 | Constant | SO | SO |
| Dynamic | SO | SO | |
| 0.10 | Constant | SO | SO |
| Dynamic | SO | SO | |
| 0.15 | Constant | SO | SO |
| Dynamic | SO | SO | |
| 0.20 | Constant | SO | SO |
| Dynamic | SO | SO | |
| 0.25 | Constant | SO | SO |
| Dynamic | SO | SO |
Damage accumulation rate and environment were varied for inert and toxic damage that was repaired at a certain optimal investment in repair determined beforehand. Fitness was evaluated by competition. Strategies were: (N) non-repairers regardless of the damage segregation strategy when the latter had insignificant effects on fitness; (S) symmetric division and (O) optimal repair.
If damage was inert, fitness differences between strategies were minute (Figure 2A,C; Additional files 4A,C and 5). Nevertheless, these minute differences were large enough to result in statistically significant differences in competitiveness in most cases, particularly between strategies that repair but differ in damage segregation. Indeed, the only set of conditions under which the fitnesses of the higher-ranked strategies were found to be indistinguishable was the most benign, i.e., when damage was inert and accumulated at the lowest rate of 0.01 h−1 in the constant environment. Under all other sets of conditions tested, there was a clearly superior strategy (Table 2; Additional file 5).
Figure 2.
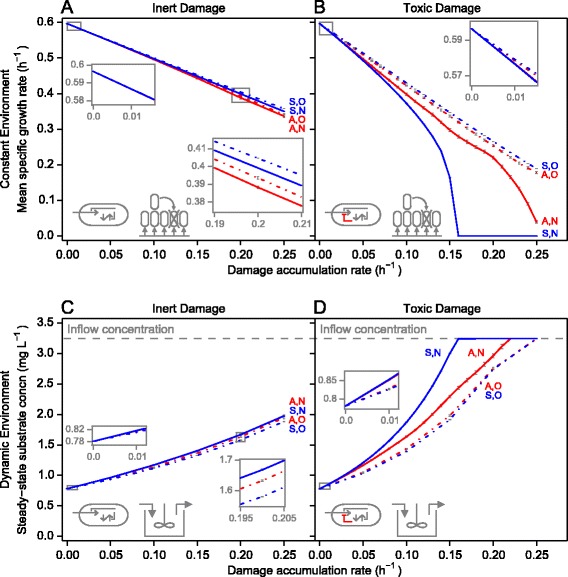
Fitness of damage repair and segregation strategies with increasing damage accumulation rates. The fitness of both the completely symmetric (S, blue) and completely asymmetric (A, red) damage segregation strategies increased when combined with repair (solid lines with no repair, N, dash-dotted lines with optimal repair, O). As expected, optimal repair was always fittest, and in this combination symmetric was best. Fitness differences were much smaller when damage was inert (A, C) than when it was toxic (B, D). Note that in the constant environment (A, B), single-strategy fitness is determined by specific growth rate, while in the dynamic environment (C, D), it is determined by the ability to persist at the lowest substrate concentration. Error bars show standard deviations (n = 400). concn, concentration.
If damage was toxic, the fitness differences between strategies were more apparent, becoming very strong at high damage accumulation rates (Figure 2B,D; Additional file 4B,D). Nevertheless, there were still a few instances of statistically insignificant differences in competitiveness of lower ranked strategies at low damage accumulation rates (Additional file 5).
Optimal investment in repair machinery
An optimal investment in repair machinery is expected given that repair is both beneficial, by turning damaged protein into active protein, and costly. This would suggest that strategies become well adapted to their long-term environmental conditions. Indeed, an optimal, positive investment in repair existed for all damage segregation strategies and environments (Figure 3; Additional files 4,6,7). These optima were often quite broad (Figure 3), suggesting that investment in repair remains almost optimal for small changes in environmental conditions. The optima were broader for asymmetrically dividing cells and this might give these strategies an advantage if damage accumulation rates fluctuate. One would also expect that the optimal investment in repair increases in proportion to the damage accumulation rate, and this was more or less the case (Additional file 7). With optimal repair, fitness never declined sharply at high damage accumulation rates (Figure 2B) since cells remained rather young even at the highest damage accumulation rate (Additional file 8B). In the chemostat, optimal repair slightly decreases growth yield for inert damage, but increases growth yield for toxic damage (Additional files 1,9). As mentioned, experimental studies have rarely found growth rate to decline more strongly than linearly, although one would expect this if damage were non-catalytic and toxic. Our results suggest that optimal repair, which led to a linear decline of growth rate even if damage was toxic, can effectively mask toxic effects (Figure 2B; Additional file 4B).
Figure 3.
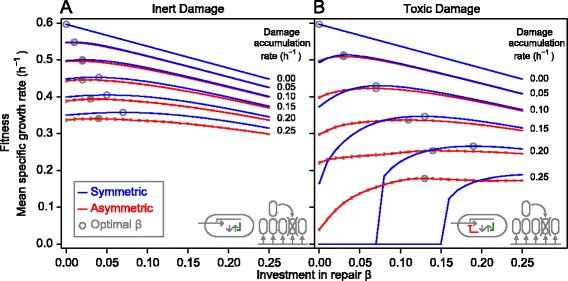
Existence of optimal investment in repair for both symmetric and asymmetric damage segregation strategies. The dependence of the mean specific growth rate on the level of investment in repair β is shown for completely asymmetric (red) and completely symmetric (blue) segregation strategies over a range of damage accumulation rates. Optimal investment in repair β is indicated by circles. The optimum was at a higher β for symmetric division. Fitness at the optimal β for symmetric division was higher than the fitness at the optimal β for asymmetric division. Repair was more beneficial if damage was not segregated. Damage is assumed to be (A) inert or (B) toxic. The environment is constant. Error bars show standard deviations (n = 400).
Interaction between repair and segregation
Since repair of damage was found to be beneficial, the next question was whether it is best to repair and segregate damage or just repair damage. In both environments and for inert and toxic damage, the fittest strategy was to repair damage optimally but not to segregate it (Figures 2,3; Additional files 4,5,6). An intermediate degree of segregation (mid-symmetric) resulted in an intermediate fitness (Additional file 6). While repair was always beneficial, this benefit was more pronounced if the damage was not also segregated. As a corollary, the less damage was repaired the more beneficial it became to segregate it: if damage was inert and not repaired, asymmetric division became about as fit as symmetric division; if damage was toxic and not repaired, asymmetric division was fitter than symmetric division (Figures 2,3; Additional files 4,5), in line with results of previous models [5,24,30–32].
Benefits of repair
Another question was why the benefits of repair outweighed the costs. As a consequence of investment in repair being optimal, optimally repairing cells had a higher fraction of active protein than those investing too little in repair (Additional file 8). Those investing too much in repair had a higher fraction of active protein than those investing optimally. However, optimally repairing cells did have more active protein that was dedicated to growth (recall that repair machinery cannot contribute to growth). If damage was toxic, this led to an additional benefit: optimally repairing cells also contained less damage hindering growth.
Population age structure
Firstly, we followed a single asymmetrically dividing cell over consecutive divisions. The specific growth rate of an old-pole cell, the cell that inherited all of the damaged protein at each division, declined from generation to generation (Figure 4A). In this example, old-pole cells of non-repairers grew at a lower specific growth rate than optimally repairing cells, already after the first cell division. Only the new-pole cells of non-repairers grew at higher specific growth rates than cells repairing damage optimally. Another advantage of repair was that it increased the number of generations over which an old-pole cell remained viable (Figure 4A). Note that this benefit of an extended lifespan of the old-pole cell could be reduced by extrinsic mortality, as present in the simulations, so that cells were unlikely to survive into old age (Figure 4C,D).
Figure 4.
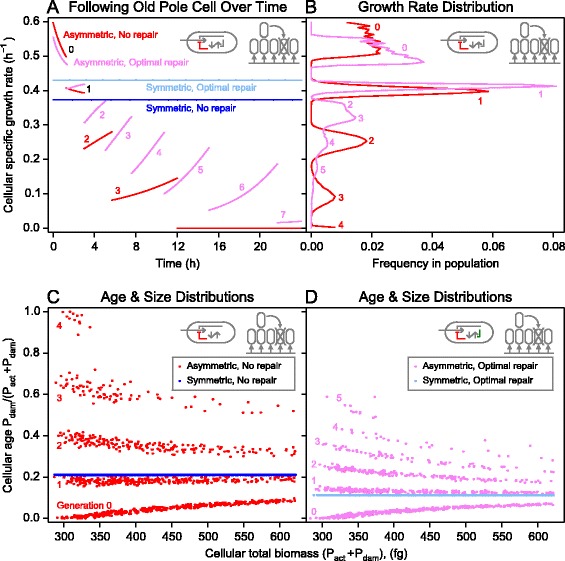
Effect of repair on specific growth rate. (A) Following asymmetrically dividing single cells over consecutive cell divisions, indicated by numbers, in which they repeatedly inherited all damage (old-pole cells), shows that the specific growth rate of a cell without repair (red) starts higher but decreases faster than that of a cell with optimal repair (magenta, β = 0.07). Specific growth rates of symmetrically dividing cells do not change at division giving horizontal lines: lower without repair (blue) than with optimal repair (cyan, β = 0.07). (B) Specific growth rate distribution in steady-state populations of asymmetrically dividing cells. Only new-pole cells grow faster without repair (red) than with optimal repair (magenta). (C, D) Snapshots of age and size distributions in the population without repair (C) or with optimal repair (D). Each dot represents a cell with a certain mass and age. Age is constant, i.e. in a steady state, in symmetrically dividing cells, and reduced with optimal repair. In asymmetrically dividing cells, young cells grow older during the cell cycle while the damage that older cells have inherited can become diluted by growth, which decreases age during the cell cycle. Cells are younger with optimal repair. (A-D) The environment was constant and damage toxic, accumulating at a rate of 0.1 h−1.
Secondly, we examined the benefits of repair for asymmetrically dividing cells at the population level, i.e. where an ancestor produced a lineage of offspring, leading to a clonal population with age structure (Figure 4C,D). The snapshots of the population age structures show several generations and in each generation cells in different phases of their division cycle (from approximately 300 to 600 fg dry mass). Age during the division cycle can increase due to damage accumulation, or decrease because of dilution of damage due to growth. The former is more likely if the cell has initially little damage and vice versa. Due to extrinsic mortality, there are fewer cells in older generations. With optimal repair, there are more generations and the ages are younger and closer together as the increase of age during the division cycle is reduced. The youngest age cohort of non-repairers was the only one growing at a faster specific rate than optimal repairers. For all other ages, optimal repairers grew faster, and the difference increased the older the cells became (Figure 4B).
Symmetrically dividing cells, in contrast, were all of equal age (Figure 4C,D), i.e. containing the same fraction of damage, and therefore growing at the same specific growth rate (Figure 4A). In this case, the specific growth rate was higher if damage was repaired optimally than if it was not repaired, for all cells (Figure 4A). In summary, optimal repair contributed most to fitness, while symmetry provided an additional advantage, in all cases (Figure 3; Additional file 5).
When repair is not beneficial
In the absence of measurements, we have so far assumed that 80% of the mass of the damaged material being repaired can be recycled into undamaged material, allowing for a small energy requirement for refolding denatured proteins and a larger energy requirement for degrading and re-synthesising those that are not refolded. The default parameter of 80% comes from assuming that recycling is about twice as efficient as de novo synthesis from glucose, but this is only an estimate so we have tested lower repair efficiencies as well.
If damage was inert, the optimal investment in repair fell to zero if the recycling efficiency was reduced to 60% or 40%. In this case, fitness of symmetric or asymmetric damage segregation was not significantly different (Additional file 10). If damage was toxic, the optimal investment in repair was lower but remained above zero in all cases, even if the efficiency of repair was lower than de novo synthesis. In combination with optimal repair, symmetric division was fitter at low damage accumulation rates. Damage segregation, in combination with optimal repair, became the fittest strategy at high enough damage accumulation rates (Additional file 10).
When asymmetry is better than repair
Looking at results from the perspective of the advantages of asymmetric division rather than the advantages of repair, the range of aging parameters under which asymmetry is advantageous can be made explicit. Damage segregation was beneficial at sufficiently high damage accumulation rates provided that damage was toxic and repair inefficient (Figures 2,3; Table 2; Additional files 4,10). If damage was inert and repair optimal but inefficient, the fitnesses of symmetric and asymmetric damage segregation were not significantly different (Additional file 10).
Dependence of predictions on model assumptions
So far, we have evaluated the sensitivity of results to changes of all aging parameters (damage accumulation rate a, investment in repair β, damage segregation α, efficiency of repair Yr and toxicity of damage) and examined this in two environments. Now we look at the sensitivity of results towards structural changes in the model, i.e. changing assumptions and equations rather than parameters (see Additional file 1 for more details). In particular, we examine the effect of replacing our assumptions with those made in a previous model that did not include repair and assumed damage to be toxic, but otherwise followed the same approach of letting cells grow and accumulate damage continuously and dividing cells when they reach a threshold size [32].
The model in [32] differs in three respects. Firstly, it includes decay rather than repair. In UnicellAge, whether or not spontaneous decay of active and damaged material was included, asymmetric division was beneficial at higher damage accumulation rates in the absence of repair and damage being toxic, in agreement with [32] (Additional files 11,12). Therefore decay, which requires no investment in repair machinery but does not recycle any material, is no replacement for repair. Secondly, the model in [32] lets division be triggered by active mass rather than total mass reaching a threshold. In UnicellAge, this had no effect on results for cells growing exponentially, but did change results completely if cells followed a linear growth law (Additional files 11,12). As growth of microbial cells is genuinely or approximately exponential, (see Modelling growth), it would generally not matter whether cell division is triggered by total or active mass. Thirdly, the model in [32] assumes cells grow linearly rather than exponentially. In UnicellAge, results are qualitatively the same whether the cells grow linearly or exponentially, but only if the division is triggered by active mass, otherwise, there is no advantage in damage segregation with linear growth (Additional files 11,12). This suggests that assumptions that one might regard as peripheral can affect conclusions. We have confirmed the results of [32] that damage segregation is beneficial if the damage accumulation rate is high, the damage is toxic and repair does not occur.
Minimal aging
The results of UnicellAge suggested that all damage should be repaired rather than segregated, if repair is biochemically possible, optimal and sufficiently efficient (Figure 3, Additional file 10). Now we compare these predictions with data (Figure 5A) that suggest minimal aging does occur in some unicells such as E. coli. Note, however, that not all studies found evidence for aging in E. coli or some other unicells. Nevertheless, let us assume that, for whatever reason, a fraction of the damage arising may not be repaired before cell division. This should be a small fraction, perhaps about 10% of the total damage accumulated during a generation. For such recalcitrant damage, UnicellAge predicts that it should indeed be completely segregated if it is toxic (see the case of zero investment in repair in Figure 3). If it were inert, the effect would be very small (Figures 2,3), and presumably impossible to detect experimentally. Let us further assume that not all of this recalcitrant and toxic damage can be as perfectly segregated as it should, e.g. because the segregation of a few large protein aggregates is quite stochastic [65], so asymmetry would be somewhat below perfect.
Figure 5.
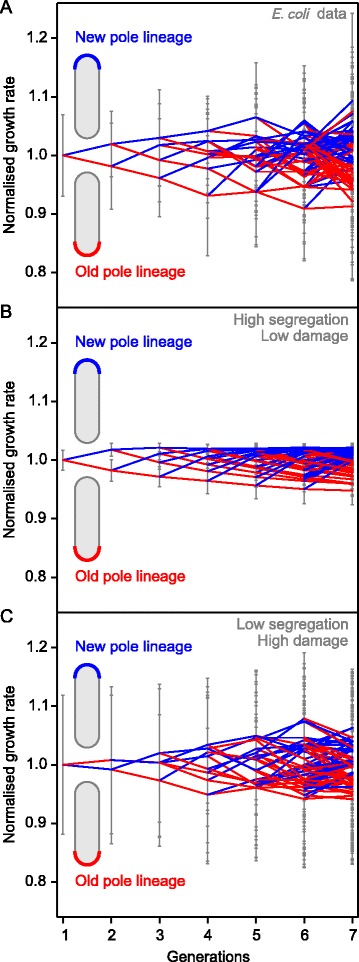
Comparison with some experimental results for E. coli . Mean growth rates of new-pole cells (blue) and old-pole cells (red), normalised by generation. Error bars show standard deviation. (A) Measured growth rates of E. coli as published in [16] but without removing rates from lower quality fits (n = 2 to 30). (B,C) Results of UnicellAge lineage simulations mimicking the experimental set-up of (A). The standard deviation of asymmetry was 0.25 and coefficients of variation were 0.05 for both the cell radius triggering division and mass fractions of daughter cells; see Figures S6,S7 for the effect of changing the extent of stochasticity in these processes. (B) Simulation assuming a high degree of segregation (α = 0.75) of low amounts of damage (a = 0.04 h−1) (n = 26 to 30). (C) Simulation assuming low degree of segregation (α = 0.05) of high amounts of damage (a = 0.35 h−1) (n = 30). Both scenarios (B, C) are consistent with the data (A), but only (B) is consistent with predictions of UnicellAge.
Figure 5B shows that this scenario of largely complete segregation of small amounts of non-repairable, toxic damage can explain the observed specific growth rate reduction of old-pole cells of E. coli (compare with Figure 5A showing unfiltered data from the study of [17]). Additional files 1, 13 and 14 show that stochastic variation of asymmetry only had a strong effect if asymmetry was small and that stochastic variation of other parameters had little, if any, effect. Note that we were not fitting the model to the data, since these data do not provide sufficient information for fitting key parameters such as the rates of damage accumulation and repair. Importantly, the alternative scenario shown in Figure 5C of minimal segregation of larger amounts of damage can also explain the experimental data, demonstrating that at least two aging scenarios are consistent with these data, while only the first scenario is consistent with predictions of UnicellAge.
Discussion
We explain why key results between models differ and examine which models’ assumptions and predictions are empirically better supported. Figure 6 shows the conceptual structure of the various models: the components considered and the processes that produce or remove or interconvert components, apart from the model of Watve et al. [30], which is conceptually too different to be described in this framework. Table 1 also describes the latter model, and summarises assumptions and predictions for all.
Figure 6.
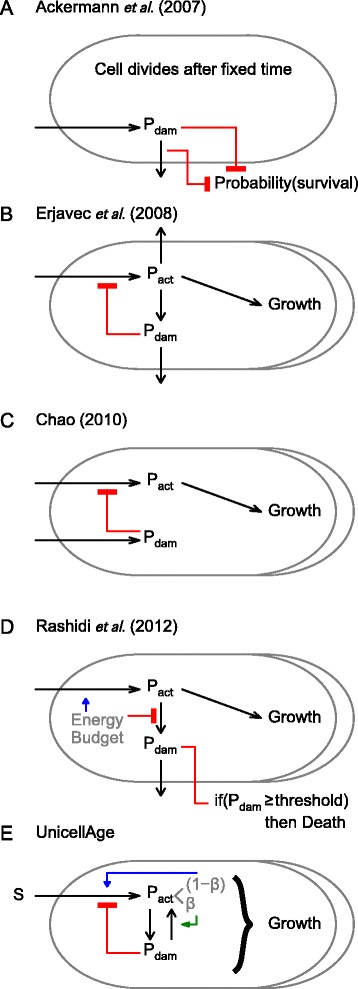
Comparison of the models. The components and processes producing, removing or interconverting the components in various mathematical models, apart from Watve et al. [30], which does not fit into this framework. See Table 1 for a description of the assumptions and predictions of these models, including [30].
Repair is beneficial if costs and benefits immediately affect growth
Overall, previous models have supported the notion that repair of damage is not beneficial, but as assumptions vary, results also vary (Table 1). If repair has been considered at all, it has either been implemented as removal of damage rather than return to active protein (with or without cost), or conversion of oldest components into newest without any cost (Figure 6, Table 1). How these differences lead to different predictions is best explained comparing UnicellAge with the conceptually clear and simple model of Ackermann et al. [31]. They assumed that repair removes a certain amount of damage from the cell. Since cells in their model are vehicles of damage without size or catalytically active protein, adding or removing damage cannot affect cell growth and division. Hence, repair cannot immediately improve growth rate by turning damaged material into active material as in UnicellAge. Instead, the benefits of repair are delayed as cells with less damage are more likely to survive after cell division. Costs of repair were implemented by linearly reducing the probability of survival into the next generation with increasing investment in repair [31]. They found that repair is not beneficial if damage can be segregated; the best strategy is complete asymmetry without repair. The absence of an autocatalytic growth process leading to cell division as soon as a critical size is reached prevents the immediate advantage that repair has in UnicellAge. Note that this immediate advantage is not forced in the model, but an emergent effect deriving from the interactions of damage repair and growth.
None of the previous models has implemented repair in such a way that both costs and benefits are realistically accounted for. If repair has no growth rate cost, it is always beneficial [30]. If repair has no immediate benefit on growth rate, it either does not improve fitness [31], or the bare minimum is employed to avert sudden death [5]. If repair is simply decay [32] it has no fitness benefit, as we showed by re-implementing their model (see Additional file 1). Only if repair has both immediate benefits and costs as in UnicellAge, is there an optimal investment in repair machinery that depends on environmental conditions. Such optimal repair is predicted to improve fitness in the environments we tested, i.e. in long-lasting steady-state environments with random external mortality with or without resource competition. Key features of the model and results are summarised in Figure 7.
Figure 7.
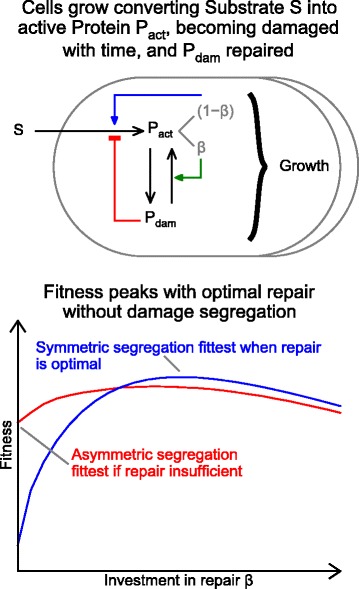
Summary of UnicellAge and key findings. Repair benefits growth immediately despite certain costs by returning damaged protein into active protein. This leads to an optimal investment in repair β, which is higher if damage is not segregated, leading to higher fitness of repairing but not aging cells.
Evidence supports the prediction that repair is beneficial
Importantly, all organisms studied in this regard have evolved active mechanisms to prevent the formation of, and to repair, various types of non-genetic damage: superoxide dismutases, catalases and reactive oxygen species scavengers prevent oxidative damage, various chaperones prevent misfolding or refold misfolded proteins, bi-chaperone systems disaggregate aggregates of misfolded proteins, and various proteases degrade proteins too damaged to be refolded [34,52]. Sophisticated defence and repair systems have obviously evolved despite their consumption of ATP and other resources, suggesting that the fitness benefits outweigh the costs, exactly as predicted by UnicellAge. Costs have been reduced in the course of evolution by making the systems inducible [34] such that their expression is more or less optimal under given environmental conditions. This suggests that the optimal investment in repair identified in UnicellAge will typically be realised in vivo.
Further support for the predictions of UnicellAge comes from the following findings: damage reduces fitness in a dosage-dependent manner [55]; repair mutants have reduced fitness [54]; a repair mutant had an increased rate of aging [33] and overexpression of defence systems (superoxide dismutase) [57] or overexpression of disaggregase activity reduces the amount of protein aggregates [56]. Experimental evidence, therefore, supports the prediction of UnicellAge that optimal repair evolved to be the major mechanism to deal with damage.
Aging under benign conditions in the laboratory is pronounced in some unicells that inhabit transient environments (Table 3). We will discuss this in depth later, but mention it here because it suggests that such unicells invest less in repair than other unicells such as E. coli that show minimal aging. This highlights that organisms can evolve to deal with damage by segregation or repair, and have done so depending on their ecology. The minimal damage segregation due to sufficient investment in repair observed in E. coli, and other unicells living in lasting environments, confirms the prediction of UnicellAge for stable environments.
Table 3.
Summary of experimental evidence
| Organism | Key experimental findings | ||
|---|---|---|---|
| Name | Phylogeny | Ecology | |
| Cell division by budding facilitating damage segregation | |||
| Saccharomyces cerevisiae | Ascomycota | Spoils environment | Limited number of generations of mother cell, sharp increase of generation time of mother cell starting a few generations before death (benign) [26], protein aggregates tethered to organelles that remain in mother cell enabling segregation of unrepaired damage [66] |
| Caulobacter crescentus | α-Proteobacteria | Attached to short-lived surfaces | Marked decline of growth rate of mother cell over time (benign) [15,31,61] |
| Cell division by binary fission | |||
| Schizosaccharomyces pombe | Ascomycota | Spoils environment | No apparent decline of growth rate over ≥30 generations (benign), sudden death of mother cell when aggregates accumulate under stress [29] |
| Methylobacterium extorquens | α-Proteobacteria (Gram-negative) | Plant leaves, relatively long-lived but seasonal | No decline of growth rate over five generations (benign) [22] |
| Escherichia coli | γ-Proteobacteria (Gram-negative) | Grows in relatively long-lived colon, survives outside host | No decline of growth rate over three generations (benign) [22] |
| No difference in growth rates between old- and new-pole siblings (benign) [67] | |||
| No decline of growth rate (benign) but decline in the presence of streptomycin [27] | |||
| Slow decline of growth rate over seven generations in the presence of FPs [16,17] | |||
| No decline of growth rate over approximately 200 generations in microfluidic device in the presence of FPs, but increased probability of sudden death [21] | |||
| Stronger aging after mild heat shock or in a repair mutant (chaperone clpB deletion) (in presence of FPs) [33] | |||
| Reduced protein aggregate formation if superoxide dismutase overexpressed [57] | |||
| Bacillus subtilis | Firmicutes (Gram-positive) | Grows in soil while nutrients present, then sporulates | Similar to E. coli, slow decline of growth rate over four generations under fluorescence microscope [18] |
| Mycobacterium spp. | Actinobacteria (Gram-positive) | Pathogen remaining inside host cells for years | Complex growth pattern: alternating polar growth of cell wall, cycling between fast and slow growth, age of pole different from age of sidewall and rest of cell, minimal decline of growth rate with age of sidewall in the presence of FPs [19] |
Phototrophic organisms have been excluded from this table since they are less well studied whilst their diurnal life cycle is more complicated. Cells growing in the absence of external stresses and damaging agents, such as streptomycin and not expressing fluorescent proteins (FPs), were considered to grow under benign conditions. Any other conditions are indicated explicitly. For an in-depth discussion of the ecology of the organisms see Additional file 1.
Damage segregation on top of repair is beneficial under stress
Collectively, previous models have shown damage segregation to be more advantageous than repair, but not always under all conditions (Table 1). Note that Erjavec et al. [32] concluded that damage segregation is fittest when division leads to equally sized offspring, but that symmetry may be advantageous when offspring are smaller, as in the budding yeast. This conclusion is in conflict with evidence of aging in the budding rather than fission yeast and may be a consequence of not including repair as an alternative mechanism of dealing with damage.
We found that optimal repair plus segregation of damage was the fittest strategy under severe conditions, i.e. if damage was toxic and accumulated at a high rate whilst repair was inefficient. Under more benign conditions, optimal repair without damage segregation was the best strategy in the steady-state environments examined. Thus, UnicellAge results suggest that unicellular organisms growing in benign and lasting conditions should not age. Aging should be limited to stressful conditions or short-lived environments. This prediction will now be compared with evidence.
Aging is not for all
Compiling all the evidence on aging for relatively well-studied unicellular organisms, three aspects appear to be crucial for aging: (i) the presence of stress in the experiments, (ii) the cell division mechanism and (iii) the ecology of the organism (Table 3). There appear to be two different life expectancy groups: short-lived and long-lived unicells. The short-lived unicells are Caulobacter crescentus and Saccharomyces cerevisiae. These are the only unicells that show considerable aging without stress. Their cell biology has little in common, but both produce daughter cells by budding, a process where the non-diffusible components of the daughter cell are made de novo. They also live in temporary habitats: for an in-depth discussion of the ecology of all organisms we have to refer the reader to Additional file 1. We argue that the combination of budding as a facilitating mechanism and inhabiting short-lived environments, giving damage segregation an evolutionary advantage, explains why only these two prokaryotic and eukaryotic unicells age. The fission yeast has a similar ecology to the budding yeast but divides by binary fission and does not age in the absence of stress [29].
In short-lived environments, early reproduction becomes much more advantageous, also because these environments enable population expansion [4]. Producing offspring quickly as soon as the habitat has arisen is more beneficial than maintaining cellular function to reproduce late when the environment is short lived, in contrast to the long-lasting environment assumed in UnicellAge. Figure 4B shows that populations of asymmetrically dividing, non-repairing cells contained a fraction of cells that were younger and faster growing than populations of cells that segregated but also repaired damage. The ecology of model organisms is rarely considered, but it turns out to be crucial for understanding why only certain unicells age considerably. A recent analysis of lifespan in birds and mammals came to the similar conclusion that extrinsic mortality, influenced by the ecology and life history of the organisms, can explain the observed variation in life expectancy [68].
Minimal aging in lasting environments
According to our model predictions, unicells living in lasting environments are not expected to segregate damage under benign conditions as this would not increase their fitness. Some experimental studies, however, suggest a small degree of damage segregation in long-lived unicells, apparently in the absence of stress. Rang et al. [27] have argued that studies using fluorescent proteins in fact apply an extrinsic damage agent or stress, and that this is required for aging to be observed. However, many studies using fluorescent proteins have not detected any fitness effects, e.g. [17,21], so the level of stress may be quite small or, as UnicellAge predicts, effects may be masked by repair processes efficiently dealing with most of the damage. Note that C. crescentus [15] and S. cerevisiae [26] do age even if fluorescent proteins are not used. In any case, the studies showing minimal aging of long-lived unicells under no more than small degrees of stress require further consideration.
Let us first consider the extent to which studies showing minimal aging are consistent with the predictions of UnicellAge. As an example study, we chose [17] because it is a follow-up study of [16] revealing the contribution of protein aggregates to the growth rate decline. This study should be representative of all that found a similarly small extent of growth rate decline in: E. coli [16], B. subtilis [18], Mycobacterium smegmatis [19] and the diatom D. brightwellii [20]. When growth rate does decline with age, it is clear that some damage was not repaired, but inherited by the old-pole cell. UnicellAge predicted that there is an optimal investment in repair, provided that repair is sufficiently efficient at returning damaged to active material. This suggests that repair of some damage might not be efficient enough. Indeed, some damage might be too difficult or costly to repair, especially damage that organisms do not usually encounter such as the protein aggregate binding chaperone IbpA fused to the fluorescent protein YFP [17]. Moreover, even if the cell has invested in what would normally be the optimal amount of repair machinery, the rate of repair is never infinite so some residual damage will be present during cell division. Results of UnicellAge also suggest that the effect of a small amount of inert damage on the growth rate is too small to be detectable experimentally. Together, this means that any observed extent of aging should be due to the presumably small fraction of non-repaired, toxic damage. Such damage might be associated with protein aggregates, which have been shown to localise at the cell poles due to passive Brownian motion combined with size exclusion by the nucleoid, resulting unavoidably in preferential location at the old-pole [33,65]. This scenario was simulated in Figure 5B, which shows a similar extent of growth rate decline as in the experiments (Figure 5A). However, other scenarios not consistent with UnicellAge predictions (Figure 5C) can also explain the experimental findings. In summary, the observations of minimal aging in long-lived cells neither contradict nor support the predictions of UnicellAge, while the studies finding no aging support the predictions of UnicellAge (Table 3).
Longer-term studies
The most decisive studies should be those that have followed old- and new-pole cells over the largest number of generations. A recent study by Coelho et al. [29] of the fission yeast followed old- and new-pole cells over more than 30 generations and found fluctuations of growth rate but no clear trend in time under benign conditions. Applying oxidative or heat stress, aging in the sense of an increased time between divisions and probability of death was observed and due to the formation and inheritance of large protein aggregates [29].
Wang et al. [21] used the same E. coli strain with fluorescent protein expression as Stewart et al. [16], but trapped old-pole cells in a microfluidic cul-de-sac environment. They followed the growth of these cells for about 200 generations. The specific growth rates of these old-pole cells fluctuated but did not decline over time, while the probability of sudden death increased, although to a low level of 0.02 per cell and per generation. Interestingly, a lexA3 SOS stress response mutant had a constant, higher death probability of 0.027 per cell and per generation. Compare undiminished growth over 200 generations to the less than 30 generations of life expectancy of budding yeast where growth rate drops sharply in the last few generations [6,26,69]. Rang et al. [25] suggested that the old-pole cells tracked by Wang et al. [21] had reached a steady-state age. However, as explained in the Background section, this steady-state hypothesis is inconsistent with the observed increase of the probability of death. In summary, the reasons for the various differences between experimental systems remain unclear and it cannot currently be decided whether aging in the group of long-lived unicells only occurs in the presence of external damage agents or whether minimal yet significant aging also occurs under benign conditions. The latter case would suggest that some toxic damage is not efficiently repairable but can instead be ‘automatically’ segregated by a passive, diffusion-based mechanism.
More evidence supporting the predictions of UnicellAge
There is more empirical backing for the predictions of UnicellAge than the existence of active repair machinery in all organisms studied and the limited extent of aging in some bacteria and fission yeast under benign conditions. Firstly, if aging would in fact be beneficial for all unicellular organisms, either in place of repair or in addition to repair, unicellular organisms dividing by binary fission should have evolved mechanisms for active segregation of damage. However, to our knowledge no active damage segregation mechanisms have been discovered in these organisms, and accumulating evidence is now strongly in favour of passive segregation of protein aggregates in E. coli [33,65]. This supports the view that active damage segregation mechanisms have not evolved in unicells dividing by binary fission, while budding to facilitate damage segregation is not very common. In budding yeast, damage segregation is now thought to result from tethering of protein aggregates to organelles [66,70].
Secondly, the fact that some unicells show considerably less (if any) aging than Caulobacter and the budding yeast under similar stress-free laboratory conditions, implying similar damage accumulation rates, suggests that these minimally aging organisms have invested more in repair than budding cells, in line with expectations from our results for steady-state environments (Figure 7).
Conclusions
Assumptions made in UnicellAge abstract from the details of real unicellular organisms for generality, yet capture the essence of empirical knowledge better than previous models. Most importantly, UnicellAge combines damage segregation and repair, includes realistic costs of repair and allows damage accumulation or repair to have immediate effects on autocatalytic growth. UnicellAge predicts that active repair mechanisms should exist in all unicells but segregation mechanisms should not, or only as a stress response if large amounts of damage accumulate suddenly. Decline of growth rate with age should be absent under benign conditions, or where present, minimal and due to the small amounts of damage that cannot be efficiently repaired whilst segregating passively, due to stochastic rather than active mechanisms. These predictions are much better supported by evidence than previous models’ predictions of complete asymmetry and absence of repair. However, some unicells do age considerably without stress. We argue that this can be explained by the ecology and cell biology of these organisms: all inhabit short-lived environments and evolved a budding mechanism for cell division, which facilitates damage segregation. Distinguishing between (a) benign versus stressful conditions, (b) inhabiting lasting versus ephemeral environments, and (c) morphologically symmetric versus budding mechanisms of cell division resolves many of the discrepancies in the literature. Aging is not beneficial for unicellular organisms in well-mixed, lasting and benign environments.
Methods
Simulation protocol
For simulations of the constant environment, the substrate concentration was set fixed to the half-saturation constant KS, and populations were initialised either with 1,000 cells of one strategy or with 500 each of two competing strategies. To assess the fitness of a single population following a given strategy in isolation, the mean specific growth rate of all cells in the population was sampled once a day after a stochastic steady state had been reached (over the final 400 days of a 500-day simulation), and the mean of these calculated. For the dynamic environment, populations were seeded either with 2,000 cells of one strategy or with 1,000 each of two competing strategies. As with mean specific growth rate in the constant environment, substrate concentration was recorded daily after reaching steady state, over the final 400 days of a 500-day chemostat simulation, and averaged.
For the lineage simulations replicating the experiments of Lindner et al. [17], the population was first simulated in a constant environment to mimic inoculation from a pre-culture growing under the same conditions. Parameters used in these simulations were: maximum growth rate μmax = 3 h−1 and constant substrate concentration S = 5.64 mg L−1 to reflect the experiments. Fifteen cells were randomly selected from the final output of the pre-culture, i.e. at steady state, and the two immediate offspring of each of these 15 used as progenitors (i.e. 30 progenitor cells) for a simulation with identical parameters but without removal of cells from the population. These simulations ran until the total population reached 8,000 to ensure that all cells underwent at least six divisions, from which the lineage trees were constructed. Growth rates were normalised by generation and averaged, as in [17].
Statistical analysis of competitions
The fitnesses of aging strategies were initially ranked based on simulations of single strategies in isolation. To verify these rankings, we then performed pairwise competitions between strategies next in rank, which most of the time confirmed the initial rankings but not always. For deciding competitiveness, we tested the null hypothesis that the binomial probability of each of the two competing strategies being washed out was equal, i.e. 50:50. If this had to be rejected, then the strategy washed out less often was considered to have a significant competitive advantage. Results of all competitions are provided in Additional file 5. Additional file 15 contains all data shown in figures. For detecting an effect size of 10% (i.e. probability of washout 40:60) at a significance level of 5% (two-sided) and a power of 90%, up to 518 pairwise competitions between the strategies were required. If the effect was larger, fewer competitions were simulated. Note that not all competitions led to washout within the 500-day maximum simulated time; these draws were ignored.
Software and hardware used
UnicellAge (included as Additional file 16) is free open-source software written in Java™ version 1.6 and based on iDynoMiCS [35] version 1.1, and was run on both a High Performance Computing Cluster and a Dell Precision T1500 PC with 8 GB RAM under a Linux operating system. Custom analysis scripts were written in Python [71] and are included in the UnicellAge repository accessible from [42]. All figures were produced using the Python module Matplotlib [72].
Acknowledgements
We thank Bhima Auro, Kevin Foster, Laurence Hurst, Ariel Lindner and Thomas Kirkwood for helpful discussions. We are grateful to Anthony Pemberton for technical support with running the simulations on the High Performance Computing Cluster (HPCC). We are indebted to Ariel Lindner and Alice Demarez for access to their data, to Bree Aldridge and Sarah Fortune for theirs, and Marija Cvijovic for further information on parameters used in [32]. RJC was supported by a PhD studentship from the Natural Environment Research Council, UK (NERC grant NE/I528218/1). RJD gratefully acknowledges the support of the University of Birmingham’s Systems Science for Health initiative.
Additional files
Supplementary text. Complete model description and equations, and supplementary results and discussions including structural robustness of the model, comparison with the model of Erjavec et al. [32], and the role of ecology in aging.
Explaining the qualitative behaviour of various elements of the model equations. (A) Specific growth rate declines with age, defined as the fraction of damaged material. This decline is either linear for inert damage (black) or concave quadratic for toxic damage (red). (B) Specific growth rate increases with substrate concentration, μ(S), following saturation (Monod) kinetics (solid line), reaching half its maximal rate at a substrate concentration of K S (dotted line). (C) Specific growth rate decreases linearly with investment in repair since the fraction of protein involved in repair does not contribute to growth. (D) The specific repair rate is Equation 10 (in Additional file 1) divided by total protein, making it a function of β and age. The specific repair rate initially increases with increasing age since damaged protein is the substrate of the repair process, but since the amount of enzyme for the repair process is proportional to active protein, the specific repair rate then declines as age tends to one. Increasing investment in repair increases the specific rate of repair and also increases the age at which this rate peaks.
List of variables and parameters used. The parameter values were taken from measurements of Escherichia coli growing on glucose as the limiting nutrient wherever possible. *The protein amount triggering division is based on total protein, i.e. P act + P dam. Note that 621 fg is equivalent to a spherical radius of 0.8 μm (volume approximately 2 μm3) as dry biomass density is 290 g L−1 [73].
Fitness of damage repair and segregation strategies with increasing damage accumulation rate. This figure adds fixed investment into repair and the mid-symmetric strategy, which had intermediate fitness, to Figure 2. The fitness of the symmetric (blue), mid-symmetric (green) and asymmetric (red) damage segregation strategies increased when combined with repair (solid lines without repair, dashed lines with repair fixed at β = 0.01). Optimal investment in repair was always fittest (dash-dotted lines), most of all in the absence of segregation. Fitness differences were much smaller when damage was inert (A, C) than when it was toxic (B, D). Note that in the constant environment (A, B) fitness is determined by specific growth rate, while in the dynamic environment (C, D) fitness is determined by the ability to persist at the lowest substrate concentration. Error bars show standard deviations (n = 400).
Competition spreadsheet. Competitions were performed as described in the Methods section. All competition results are listed in this spreadsheet (xlsx format), organised into the following sheets: Const Inert – constant environment, damage is inert; Const Toxic – constant environment, damage is toxic; Chemo Inert – dynamic environment (chemostat), damage is inert; Chemo Toxic – dynamic environment (chemostat), damage is toxic.
Existence of an optimal investment in repair for symmetric, mid-symmetric and asymmetric damage segregation strategies. This figure adds the mid-symmetric damage segregation strategy to Figure 3 showing that intermediate asymmetry results in an intermediate specific growth rate response. The dependence of the mean specific growth rate on the level of investment in repair β is shown for completely asymmetric (red), mid-symmetric (green) and completely symmetric (blue) segregation strategies at a damage accumulation rate of 0.1 h−1. Optimal investment in repair β is indicated by circles. The less damage was segregated, the more beneficial it became to repair it, such that repair without segregation reached the highest fitness overall. Damage is assumed to be (A) inert or (B) toxic. The environment is constant. Error bars show standard deviations (n = 400).
The optimal investment in repair (β) increased with damage accumulation rate. Asymmetric (red), mid-symmetric (green) and symmetric (blue) damage segregation strategies showed similar trends. Abrupt deviations from a smooth increase were due to older age classes becoming extinct at certain damage accumulation rates and also imprecise determination of optimal values of β due to broad optima. The increase of the optimal investment in repair with damage accumulation rate was much lower for inert damage (A, C) than for toxic damage (B, D). Trends were similar within the same environment, whether constant (A, B) or dynamic (C, D).
Mean age increased with damage accumulation rate. Age, defined as the fraction of damaged protein, increased with damage accumulation rate, regardless of whether the environment was constant (A, B) or dynamic (C, D) or whether damage was inert (A, C) or toxic (B, D). Asymmetric (red), mid-symmetric (green) and symmetric (blue) damage segregation strategies showed similar trends, but there were notable differences between repair strategies: strategies without repair (solid lines) were oldest, strategies with fixed repair were intermediate (dashed lines, β fixed at 0.01), and strategies with optimal investment in repair were youngest (dash-dotted lines). Surprisingly, strategies with optimal investment in repair had a lower age when damage was toxic than when it was inert. Note that age cannot exceed one and that populations may become extinct if they are too old to grow fast enough. Error bars show standard deviations (n = 400).
Growth yield decreased due to repair if damage was inert but increased if toxic. The asymmetric (red), mid-symmetric (green) and symmetric (blue) segregation strategies without repair (solid lines), with fixed repair (β = 0.01, dashed lines) and with optimal repair (dash-dotted lines) are shown. Yields mostly decreased with increasing damage accumulation rate, much more so if the damage was toxic (B). Only if damage was inert and repair absent, did yield remain constant (A). Repair had two effects on growth yield: it converted damaged into active biomass with some loss of mass, therefore reducing yield, but it enabled more cells to grow sufficiently fast to remain in the system despite dilution. The latter effect appeared to be stronger if the damage was toxic. Growth yields could only be determined in the dynamic environment where substrate concentration was not kept constant. Where values are not shown, the population had been washed out. Error bars show standard deviations (n = 400).
Repair efficiency affects which strategy is fittest. Damage accumulation rate and repair yield (repair efficiency) were varied for inert and toxic damage. Fitness was evaluated by competition in the constant environment. Strategies were: (N) non-repairers regardless of the damage segregation strategy when the latter had insignificant effects on fitness; (SO) symmetric with optimal repair and (AO) asymmetric with optimal repair.
Exponential growth with toxic damage in a constant environment without repair. Mean specific growth rates (per arbitrary time unit) of different damage segregation strategies when growth is exponential (Additional file 1: Equations 21 and 22): asymmetric (red), mid-symmetric (green) and symmetric (blue). (A, B) Division is triggered by total protein, the default for UnicellAge. (C, D) Division is triggered by active protein only, as in [30]. (A, C) Without degradation (k = 0.00), the default for UnicellAge. (B, D) With degradation (k = 0.69), as in [32]. (A)–(D) should also be compared with the corresponding panels in Additional file 12 for linear growth. Conditions and assumptions for panel (A) are equivalent (although with different units and parameters) to those made in UnicellAge; see Additional file 4B. Results for UnicellAge under these conditions are qualitatively the same as the results from the re-implemented model [32]. Error bars are standard deviations (n = 400).
Linear growth with toxic damage in a constant environment without repair. Mean specific growth rates (per arbitrary time unit) of different damage segregation strategies when growth is linear as in [32] (Additional file 1: Equations 20 and 22): asymmetric (red), mid-symmetric (green) and symmetric (blue). (A, B) Division is triggered by total protein, the default for UnicellAge. (C, D) Division is triggered by active protein only, as in [32]. (A, C) Without degradation (k = 0.00), the default for UnicellAge. (B, D) With degradation (k = 0.69), as in [32]. (A, B) Symmetric division had a minimally but not significantly higher specific growth rate than mid-symmetric division. (A)–(D) should also be compared with the corresponding panels in Additional file 11 for exponential growth. Error bars are standard deviations (n = 400). For comparison with the results of [32], panel (E) reproduces their Figure 3A with permission (© 2008 The National Academy of Sciences of the USA). Their parameter re (retention of damage) is equivalent to α in UnicellAge, with 0 indicating symmetric division.
Effect of stochasticity in damage segregation. Lineages were simulated using the same method as in Figure 5 and Additional file 14; see also Simulation protocol. The standard deviation of the damage segregation parameter α increases from row to row: (A, B) α dev = 0.00; (C, D) α dev = 0.25 as in Figure 5B,C; (E, F) α dev = 0.50. The left column (A, C, E) shows the scenario of low segregation of high damage (α = 0.05, a = 0.35 h−1) showing that the spread of mean growth rates and standard deviations increases with increasing α dev. The right column (B, D, F) shows the scenario of high segregation of low damage (α = 0.75, a = 0.04 h−1) showing the opposite effect. All other parameters were fixed and the same as in Figure 5B,C: division radius CV = 0.05 and baby mass fraction CV = 0.05. Error bars show standard deviations (n = 17 to 30).
Effect of stochasticity in size at division and daughter cell sizes. Lineages were simulated using the same method as in Figure 5 and Additional file 13; see also Simulation protocol. For the top row, the threshold radius triggering division was deterministic (division radius CV = 0) (A) or allowed to vary (division radius CV = 0.1) (B). For the bottom row, the mother’s total material is divided deterministically into identically sized daughter cells (baby mass fraction CV = 0) (C) or stochastically, leading to somewhat differently sized daughter cells (baby mass fraction CV = 0.1) (D). The other CVs had default values of 0.05 as in Figure 5C and Additional file 13C. The effect of stochasticity in size at division and daughter cell sizes was negligible, especially when compared with the effect of varying α dev in Additional file 13. Error bars show standard deviations (n = 30).
Results spreadsheet. All data used in Figures 2, 3, 4 and 5 and Additional files 4, 6, 7, 8, 9, 11, 12, 13 and 14 are listed in this spreadsheet.
UnicellAge source code. The full source code of UnicellAge, written in Java™, along with analysis scripts, written in Python. We recommend exploring the source code in an integrated development environment (IDE) such as Eclipse [74].
Footnotes
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
RJC participated in the design of the study, conducted the research, participated in the statistical analysis and wrote the manuscript. RJD participated in the design of the study and helped write the manuscript. JUK conceived of the study, participated in its design and statistical analysis, and helped write the manuscript. All authors read and approved the final manuscript.
Contributor Information
Robert J Clegg, Email: rjc096@bham.ac.uk.
Rosemary J Dyson, Email: r.j.dyson@bham.ac.uk.
Jan-Ulrich Kreft, Email: j.kreft@bham.ac.uk.
References
- 1.Kirkwood TBL. Understanding the odd science of aging. Cell. 2005;120:437–447. doi: 10.1016/j.cell.2005.01.027. [DOI] [PubMed] [Google Scholar]
- 2.Kirkwood TBL, Cremer T. Cytogerontology since 1881: a reappraisal of August Weismann and a review of modern progress. Hum Genet. 1982;60:101–121. doi: 10.1007/BF00569695. [DOI] [PubMed] [Google Scholar]
- 3.Medawar PB. An Unsolved Problem of Biology. HK Lewis & Co: University College London; 1952. [Google Scholar]
- 4.Ratcliff WC, Hawthorne P, Travisano M, Denison RF. When stress predicts a shrinking gene pool, trading early reproduction for longevity can increase fitness, even with lower fecundity. PLoS One. 2009;4:e6055. doi: 10.1371/journal.pone.0006055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rashidi A, Kirkwood TBL, Shanley DP. Evolution of asymmetric damage segregation: a modelling approach. In: Breitenbach M, Jazwinski SM, Laun P, editors. Aging Research in Yeast. Amsterdam: Springer Verlag; 2012. pp. 315–330. [DOI] [PubMed] [Google Scholar]
- 6.Mortimer RK, Johnston JR. Life span of individual yeast cells. Nature. 1959;183:1751–1752. doi: 10.1038/1831751a0. [DOI] [PubMed] [Google Scholar]
- 7.Angert ER. Alternatives to binary fission in bacteria. Nat Rev Micro. 2005;3:214–224. doi: 10.1038/nrmicro1096. [DOI] [PubMed] [Google Scholar]
- 8.Hughes WH. The inheritance of differences in growth rate in Escherichia coli. J Gen Microbiol. 1955;12:265–268. doi: 10.1099/00221287-12-2-265. [DOI] [PubMed] [Google Scholar]
- 9.Powell EO. Growth rate and generation time of bacteria, with special reference to continuous culture. J Gen Microbiol. 1956;15:492–511. doi: 10.1099/00221287-15-3-492. [DOI] [PubMed] [Google Scholar]
- 10.Powell EO. An outline of the pattern of bacterial generation times. J Gen Microbiol. 1958;18:382–417. doi: 10.1099/00221287-18-2-382. [DOI] [PubMed] [Google Scholar]
- 11.Schaechter M, Williamson JP, Hood JR, Koch AL. Growth, cell and nuclear divisions in some bacteria. J Gen Microbiol. 1962;29:421–434. doi: 10.1099/00221287-29-3-421. [DOI] [PubMed] [Google Scholar]
- 12.Powell EO, Errington FP. Generation times of individual bacteria: some corroborative measurements. J Gen Microbiol. 1963;31:315–327. doi: 10.1099/00221287-31-2-315. [DOI] [PubMed] [Google Scholar]
- 13.Marr AG, Harvey RJ, Trentini WC. Growth and division of Escherichia coli. J Bacteriol. 1966;91:2388–2389. doi: 10.1128/jb.91.6.2388-2389.1966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Barker MG, Walmsley RM. Replicative ageing in the fission yeast Schizosaccharomyces pombe. Yeast. 1999;15:1511–1518. doi: 10.1002/(SICI)1097-0061(199910)15:14<1511::AID-YEA482>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 15.Ackermann M, Stearns SC, Jenal U. Senescence in a bacterium with asymmetric division. Science. 2003;300:1920. doi: 10.1126/science.1083532. [DOI] [PubMed] [Google Scholar]
- 16.Stewart EJ, Madden R, Paul G, Taddei F. Aging and death in an organism that reproduces by morphologically symmetric division. PLoS Biol. 2005;3:e45. doi: 10.1371/journal.pbio.0030045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lindner AB, Madden R, Demarez A, Stewart EJ, Taddei F. Asymmetric segregation of protein aggregates is associated with cellular aging and rejuvenation. Proc Natl Acad Sci USA. 2008;105:3076–3081. doi: 10.1073/pnas.0708931105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Veening J-W, Stewart EJ, Berngruber TW, Taddei F, Kuipers OP, Hamoen LW. Bet-hedging and epigenetic inheritance in bacterial cell development. Proc Natl Acad Sci USA. 2008;105:4393–4398. doi: 10.1073/pnas.0700463105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Aldridge BB, Fernandez-Suarez M, Heller D, Ambravaneswaran V, Irimia D, Toner M, Fortune SM. Asymmetry and aging of mycobacterial cells lead to variable growth and antibiotic susceptibility. Science. 2012;335:100–104. doi: 10.1126/science.1216166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Laney SR, Olson RJ, Sosik HM. Diatoms favor their younger daughters. Limnol Oceanogr. 2012;57:1572–1578. doi: 10.4319/lo.2012.57.5.1572. [DOI] [Google Scholar]
- 21.Wang P, Robert L, Pelletier J, Dang WL, Taddei F, Wright A, Jun S. Robust growth of Escherichia coli. Curr Biol. 2010;20:1099–1103. doi: 10.1016/j.cub.2010.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bergmiller T, Ackermann M. Pole age affects cell size and the timing of cell division in Methylobacterium extorquens AM1. J Bacteriol. 2011;193:5216–5221. doi: 10.1128/JB.00329-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Goto K, Beneragama CK. Circadian clocks and antiaging: do non-aging microalgae like Euglena reveal anything? Ageing Res Rev. 2010;9:91–100. doi: 10.1016/j.arr.2009.09.003. [DOI] [PubMed] [Google Scholar]
- 24.Chao L. A model for damage load and its implications for the evolution of bacterial aging. PLoS Genet. 2010;6:e1001076. doi: 10.1371/journal.pgen.1001076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rang CU, Peng AY, Chao L. Temporal dynamics of bacterial aging and rejuvenation. Curr Biol. 2011;21:1813–1816. doi: 10.1016/j.cub.2011.09.018. [DOI] [PubMed] [Google Scholar]
- 26.Egilmez NK, Jazwinski SM. Evidence for the involvement of a cytoplasmic factor in the aging of the yeast Saccharomyces cerevisiae. J Bacteriol. 1989;171:37–42. doi: 10.1128/jb.171.1.37-42.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rang CU, Peng AY, Poon AF, Chao L. Ageing in Escherichia coli requires damage by an extrinsic agent. Microbiology. 2012;158:1553–1559. doi: 10.1099/mic.0.057240-0. [DOI] [PubMed] [Google Scholar]
- 28.Turner RD, Ratcliffe EC, Wheeler R, Golestanian R, Hobbs JK, Foster SJ. Peptidoglycan architecture can specify division planes in Staphylococcus aureus. Nat Commun. 2010;1:26. doi: 10.1038/ncomms1025. [DOI] [PubMed] [Google Scholar]
- 29.Coelho M, Dereli A, Haese A, Kühn S, Malinovska L, DeSantis ME, Shorter J, Alberti S, Gross T, Tolić-Nørrelykke IM. Fission yeast does not age under favorable conditions, but does so after stress. Curr Biol. 2013;23:1844–1852. doi: 10.1016/j.cub.2013.07.084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Watve M, Parab S, Jogdand P, Keni S. Aging may be a conditional strategic choice and not an inevitable outcome for bacteria. Proc Natl Acad Sci USA. 2006;103:14831–14835. doi: 10.1073/pnas.0606499103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ackermann M, Chao L, Bergstrom CT, Doebeli M. On the evolutionary origin of aging. Aging Cell. 2007;6:235–244. doi: 10.1111/j.1474-9726.2007.00281.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Erjavec N, Cvijovic M, Klipp E, Nyström T. Selective benefits of damage partitioning in unicellular systems and its effects on aging. Proc Natl Acad Sci USA. 2008;105:18764–18769. doi: 10.1073/pnas.0804550105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Winkler J, Seybert A, König L, Pruggnaller S, Haselmann U, Sourjik V, Weiss M, Frangakis AS, Mogk A, Bukau B. Quantitative and spatio-temporal features of protein aggregation in Escherichia coli and consequences on protein quality control and cellular ageing. EMBO J. 2010;29:910–923. doi: 10.1038/emboj.2009.412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tyedmers J, Mogk A, Bukau B. Cellular strategies for controlling protein aggregation. Nat Rev Mol Cell Bio. 2010;11:777–788. doi: 10.1038/nrm2993. [DOI] [PubMed] [Google Scholar]
- 35.Lardon LA, Merkey BV, Martins S, Dötsch A, Picioreanu C, Kreft J-U, Smets BF. iDynoMiCS: next-generation individual-based modelling of biofilms. Environ Microbiol. 2011;13:2416–2434. doi: 10.1111/j.1462-2920.2011.02414.x. [DOI] [PubMed] [Google Scholar]
- 36.Kreft J-U, Booth G, Wimpenny JWT. BacSim, a simulator for individual-based modelling of bacterial colony growth. Microbiology. 1998;144:3275–3287. doi: 10.1099/00221287-144-12-3275. [DOI] [PubMed] [Google Scholar]
- 37.Kreft J-U, Picioreanu C, Wimpenny JWT, van Loosdrecht MCM. Individual-based modelling of biofilms. Microbiology. 2001;147:2897–2912. doi: 10.1099/00221287-147-11-2897. [DOI] [PubMed] [Google Scholar]
- 38.Picioreanu C, Kreft J-U, van Loosdrecht MCM. Particle-based multidimensional multispecies biofilm model. Appl Environ Microbiol. 2004;70:3024–3040. doi: 10.1128/AEM.70.5.3024-3040.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kreft J-U. Biofilms promote altruism. Microbiology. 2004;150:2751–2760. doi: 10.1099/mic.0.26829-0. [DOI] [PubMed] [Google Scholar]
- 40.Dens EJ, Bernaerts K, Standaert AR, Van Impe JF. Cell division theory and individual-based modeling of microbial lag: Part I. The theory of cell division. Int J Food Microbiol. 2005;101:303–318. doi: 10.1016/j.ijfoodmicro.2004.11.016. [DOI] [PubMed] [Google Scholar]
- 41.Merkey BV, Lardon LA, Seoane JM, Kreft J-U, Smets BF. Growth dependence of conjugation explains limited plasmid invasion in biofilms: an individual-based modelling study. Environ Microbiol. 2011;13:2435–2452. doi: 10.1111/j.1462-2920.2011.02535.x. [DOI] [PubMed] [Google Scholar]
- 42.iDynoMiCS. In ᅟ. [http://www.idynomics.org]
- 43.Lindner AB, Demarez A. Protein aggregation as a paradigm of aging. Biochim Biophys Acta. 2009;1790:980–996. doi: 10.1016/j.bbagen.2009.06.005. [DOI] [PubMed] [Google Scholar]
- 44.Koch AL. The growth kinetics of B. subtilis. A van Leeuw. 1993;63:45. doi: 10.1007/BF00871731. [DOI] [PubMed] [Google Scholar]
- 45.Godin M, Delgado FF, Son S, Grover WH, Bryan AK, Tzur A, Jorgensen P, Payer K, Grossman AD, Kirschner MW, Manalis SR. Using buoyant mass to measure the growth of single cells. Nat Methods. 2010;7:387–390. doi: 10.1038/nmeth.1452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mir M, Wang Z, Shen Z, Bednarz M, Bashir R, Golding I, Prasanth SG, Popescu G. Optical measurement of cycle-dependent cell growth. Proc Natl Acad Sci USA. 2011;108:13124–13129. doi: 10.1073/pnas.1100506108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cooper S. Schizosaccharomyces pombe grows exponentially during the division cycle with no rate change points. FEMS Yeast Res. 2013;13:650–658. doi: 10.1111/1567-1364.12072. [DOI] [PubMed] [Google Scholar]
- 48.Baumgärtner S, Tolić-Nørrelykke IM. Growth pattern of single fission yeast cells is bilinear and depends on temperature and DNA synthesis. Biophys J. 2009;96:4336–4347. doi: 10.1016/j.bpj.2009.02.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Horváth A, Rácz-Mónus A, Buchwald P, Sveiczer A. Cell length growth in fission yeast: an analysis of its bilinear character and the nature of its rate change transition. FEMS Yeast Res. 2013;13:635–649. doi: 10.1111/1567-1364.12064. [DOI] [PubMed] [Google Scholar]
- 50.Reshes G, Vanounou S, Fishov I, Feingold M. Cell shape dynamics in Escherichia coli. Biophys J. 2008;94:251–264. doi: 10.1529/biophysj.107.104398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lendenmann U, Snozzi M, Egli T. Growth kinetics of Escherichia coli with galactose and several other sugars in carbon-limited chemostat culture. Can J Microbiol. 1999;46:72–80. doi: 10.1139/w99-113. [DOI] [PubMed] [Google Scholar]
- 52.Visick JE, Clarke S. Repair, refold, recycle: how bacteria can deal with spontaneous and environmental damage to proteins. Mol Microbiol. 1995;16:835–845. doi: 10.1111/j.1365-2958.1995.tb02311.x. [DOI] [PubMed] [Google Scholar]
- 53.Dougan DA, Mogk A, Bukau B. Protein folding and degradation in bacteria: to degrade or not to degrade? That is the question. Cell Mol Life Sci. 2002;59:1607–1616. doi: 10.1007/PL00012487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.González-Montalbán N, Carrió MM, Cuatrecasas S, Arís A, Villaverde A. Bacterial inclusion bodies are cytotoxic in vivo in absence of functional chaperones DnaK or GroEL. J Biotechnol. 2005;118:406–412. doi: 10.1016/j.jbiotec.2005.05.024. [DOI] [PubMed] [Google Scholar]
- 55.Geiler-Samerotte KA, Dion MF, Budnik BA, Wang SM, Hartl DL, Drummond DA. Misfolded proteins impose a dosage-dependent fitness cost and trigger a cytosolic unfolded protein response in yeast. Proc Natl Acad Sci USA. 2011;108:680–685. doi: 10.1073/pnas.1017570108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Andersson V, Hanzén S, Liu B, Molin M, Nyström T. Enhancing protein disaggregation restores proteasome activity in aged cells. Aging. 2013;5:802–812. doi: 10.18632/aging.100613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Maisonneuve E, Ezraty B, Dukan S. Protein aggregates: an aging factor involved in cell death. J Bacteriol. 2008;190:6070–6075. doi: 10.1128/JB.00736-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Stouthamer AH. The search for correlation between theoretical and experimental growth yields. In: Quayle JR, editor. International Review of Biochemistry. Baltimore: University Park Press; 1979. pp. 1–47. [Google Scholar]
- 59.Neijssel OM, de Mattos MJT, Tempest DW. Growth yield and energy distribution. In: Neidhardt FC, Curtiss R III, Ingraham JL, Lin ECC, Brooks Low K, Magasanik B, Reznikoff WS, Riley M, Schaechter M, Umbarger HE, editors. Escherichia coli and Salmonella Typhimurium: Cellular and Molecular Biology. Washington, DC: ASM Press; 1996. pp. 1683–1692. [Google Scholar]
- 60.Nyström T. Role of oxidative carbonylation in protein quality control and senescence. EMBO J. 2005;24:1311–1317. doi: 10.1038/sj.emboj.7600599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ackermann M, Schauerte A, Stearns SC, Jenal U. Experimental evolution of aging in a bacterium. BMC Evol Biol. 2007;7:126. doi: 10.1186/1471-2148-7-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Robert L, Hoffmann M, Krell N, Aymerich S, Robert J, Doumic M. Division in Escherichia coli is triggered by a size-sensing rather than a timing mechanism. BMC Biol. 2014;12:17. doi: 10.1186/1741-7007-12-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tilman D. Resource Competition and Community Structure. New Jersey: Princeton University Press; 1982. [PubMed] [Google Scholar]
- 64.Kreft J-U. Mathematical modeling of microbial ecology: spatial dynamics of interactions in biofilms and guts. In: Jaykus LA, Wang HH, Schlesinger LS, editors. Food-Borne Microbes: Shaping the Host Ecosystem. Washington, DC: ASM Press; 2009. pp. 347–377. [Google Scholar]
- 65.Coquel A-S, Jacob J-P, Primet M, Demarez A, Dimiccoli M, Julou T, Moisan L, Lindner AB, Berry H. Localization of protein aggregation in Escherichia coli is governed by diffusion and nucleoid macromolecular crowding effect. PLoS Comput Biol. 2013;9:e1003038. doi: 10.1371/journal.pcbi.1003038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Spokoini R, Moldavski O, Nahmias Y, England JL, Schuldiner M, Kaganovich D. Confinement to organelle-associated inclusion structures mediates asymmetric inheritance of aggregated protein in budding yeast. Cell Rep. 2012;2:738–747. doi: 10.1016/j.celrep.2012.08.024. [DOI] [PubMed] [Google Scholar]
- 67.Lele UN, Baig UI, Watve MG. Phenotypic plasticity and effects of selection on cell division symmetry in Escherichia coli. PLoS One. 2011;6:e14516. doi: 10.1371/journal.pone.0014516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Healy K, Guillerme T, Finlay S, Kane A, Kelly SBA, McClean D, Kelly DJ, Donohue I, Jackson AL, Cooper N. Ecology and mode-of-life explain lifespan variation in birds and mammals. Proc R Soc B. 2014;281:20140298. doi: 10.1098/rspb.2014.0298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lin S-J, Austriaco N. Aging and cell death in the other yeasts, Schizosaccharomyces pombe and Candida albicans. FEMS Yeast Res. 2014;14:119–135. doi: 10.1111/1567-1364.12113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Unruh JR, Slaughter BD, Li R. Quality control: putting protein aggregates in a bind. Curr Biol. 2013;23:R74–R76. doi: 10.1016/j.cub.2012.12.005. [DOI] [PubMed] [Google Scholar]
- 71.Python Software Foundation: Python Language Reference, version 2.7. In ᅟ. ; 2010 [http://www.python.org]
- 72.Hunter JD. Matplotlib: a 2D graphics environment. Comput Sci Eng. 2007;9:90–95. doi: 10.1109/MCSE.2007.55. [DOI] [Google Scholar]
- 73.Shuler ML, Leung S, Dick CC. A mathematical model for the growth of a single bacterial cell. Ann NY Acad Sci. 1979;326:35–52. doi: 10.1111/j.1749-6632.1979.tb14150.x. [DOI] [Google Scholar]
- 74.Eclipse. In ᅟ[http://www.eclipse.org/]


