Contrast Sensitivity Perimetry and Clinical Measures of Glaucomatous Damage

ABSTRACT

Purpose

To compare conventional structural and functional measures of glaucomatous damage with a new functional measure—contrast sensitivity perimetry (CSP-2).

Methods

One eye each was tested for 51 patients with glaucoma and 62 age-similar control subjects using CSP-2, size III 24-2 conventional automated perimetry (CAP), 24-2 frequency-doubling perimetry (FDP), and retinal nerve fiber layer (RNFL) thickness. For superior temporal (ST) and inferior temporal (IT) optic disc sectors, defect depth was computed as amount below mean normal, in log units. Bland-Altman analysis was used to assess agreement on defect depth, using limits of agreement and three indices: intercept, slope, and mean difference. A criterion of p < 0.0014 for significance used Bonferroni correction.

Results

Contrast sensitivity perimetry-2 and FDP were in agreement for both sectors. Normal variability was lower for CSP-2 than for CAP and FDP (F > 1.69, p < 0.02), and Bland-Altman limits of agreement for patient data were consistent with variability of control subjects (mean difference, −0.01 log units; SD, 0.11 log units). Intercepts for IT indicated that CSP-2 and FDP were below mean normal when CAP was at mean normal (t > 4, p < 0.0005). Slopes indicated that, as sector damage became more severe, CAP defects for IT and ST deepened more rapidly than CSP-2 defects (t > 4.3, p < 0.0005) and RNFL defects for ST deepened more slowly than for CSP, FDP, and CAP. Mean differences indicated that FDP defects for ST and IT were on average deeper than RNFL defects, as were CSP-2 defects for ST (t > 4.9, p < 0.0001).

Conclusions

Contrast sensitivity perimetry-2 and FDP defects were deeper than CAP defects in optic disc sectors with mild damage and revealed greater residual function in sectors with severe damage. The discordance between different measures of glaucomatous damage can be accounted for by variability in people free of disease.

Perimetric testing is used clinically to detect visual field abnormalities and to monitor change during the course of management of patients with glaucoma as well as diseases of the retina and visual pathway. However, test-retest variability is high in glaucomatous defects,1,2 limiting the ability to detect progression. Agreement between perimetric measures and optic nerve examination gives the clinician greater confidence in diagnosis and grading severity of the disease, but perimetric and imaging measures have poor agreement in a substantial subset of patients.3–5

Our laboratory has analyzed sources of poor agreement and variability by recording responses of primate retinal ganglion cells,6 performing neural modeling,7–10 and conducting clinical research.8,11,12 This led to the use of sinusoidal stimuli, referred to as contrast sensitivity perimetry13,14 (CSP) to achieve low variability in glaucomatous defects and improve agreement between perimetric and structural measures of glaucomatous neuropathy.15 Studies from our laboratory confirmed these predictions in a pilot study of CSP that used a fixed stimulus size,15 and then developed a second-generation method (CSP-2) using stimuli varying in size with visual field location16 and resistant to effects of peripheral defocus17 and pupillary miosis.18

For low stimulus contrasts the firing rate of primate retinal ganglion cells shows a linear increase with contrast, then at higher contrasts, the firing rate increases more and more slowly as contrast increases, an effect called saturation.6 Contrast thresholds in eyes free of disease are highly variable for the size III stimulus used in conventional automated perimetry (CAP), and the nature of this variability is consistent with the effects of ganglion cell saturation causing CAP to overestimate loss in more severely damaged areas.19 Furthermore, in visual field regions with severe damage, the size III stimulus may not be seen even at the highest contrast available, whereas size V20 and CSP-115 have been found to reveal residual function. In an effort to reduce the effects of saturation and provide a better assessment of the amount of ganglion cell loss than CAP, we designed CSP-2 to use stimuli at least as large as size V and with much lower contrast thresholds in control subjects than for size III. The purpose of the current study is to assess whether CSP-2 performed as designed, in terms of agreement with clinical measures.

METHODS

Subjects

Subjects were participating in a multicenter longitudinal study at three different university clinics, in Manhattan (State University of New York [SUNY]), Indianapolis (Indiana University [IU]), and Bloomington (IU). The research for this study adhered to the tenets of the Declaration of Helsinki and was approved by the institutional review boards at SUNY College of Optometry and at IU. Informed consent was obtained from each participant after explanation of the procedures and goals of the study, before testing began.

Fifty-one patients with glaucomatous field loss and glaucomatous optic neuropathy and 62 age-similar control subjects completed baseline testing for the longitudinal study. Ages ranged from 45 to 84 years (mean [±SD], 64 [±9] years) for patients and 46 to 84 years (mean [±SD], 62 [±9] years) for control subjects. Mean deviation for CAP ranged from −23 to +1.2 dB (mean, −5.4 dB) for patients and −2.9 to +1.5 dB (mean, −0.3 dB) for control subjects.

Inclusion and Exclusion Criteria

Common inclusion criteria for both groups were best-corrected visual acuity of 20/20 or better (20/25 for those older than 70 years), spherical equivalent within −6 to +2 diopters (D) (so that lenses for perimetry at 33 cm would range from −3 to +5 D), cylinder correction within 3 D, clear ocular media, and absence of known eye disease during a comprehensive eye examination within 2 years (except for glaucoma in the patient group).

Common exclusion criteria for both groups were ocular or systemic disease known to affect the visual field (e.g., diabetic retinopathy, prior vein occlusion, macular degeneration, degenerative myopia, and migraines), except glaucoma in the patient group; history of intraocular surgery (except uncomplicated cataract surgery more than 1 year before enrollment, or glaucoma surgery in the patient group); usage of medications known to affect vision; inability to yield optical coherence tomography images free of segmentation errors or low signal strength; and inability to produce reliable perimetric data (>15% false positives, >20% fixation losses unless eye tracker information demonstrated high fixation accuracy). Perimetric reliability criteria were used to exclude subjects based on repeatedly exceeding these criteria but were not applied to individual visits. Subjects were recruited based on past performance on perimetry and imaging; many had been participating in prior studies and all had prior clinic visits. This determined the 119 people who completed baseline testing. Six of these 119 people were removed during the course of the study because of repeated lack of reliability on perimetry, yielding the 113 in the study. Of the remaining 113, if the baseline visit had data that did not meet the reliability criteria for all four tests (retinal nerve fiber layer [RNFL], CAP, frequency-doubling perimetry [FDP], and CSP-2), then data for that visit were replaced with data from the next later visit in which all four tests met the reliability criteria. In the end, there were two patients for which no visit had all four tests with reliable indices, so data from the baseline visits were retained; these visits had initially been rejected because of false-positive scores of 19 and 28% on CAP.

Additional exclusion criteria for control subjects were a self-reported first-degree relative with glaucoma and intraocular pressure greater than 21 mm Hg for two or more clinic visits. An additional exclusion criterion for patients was intraocular pressure greater than 30 mm Hg at a clinic visit during the longitudinal study.

Study Definition of Glaucoma

Diagnosis of glaucoma was made by the treating clinician (Drs Malinovsky, Dul, Sutton, or Torbit), based on a complete ophthalmic examination including medical history, refraction, best-corrected visual acuity, slit lamp biomicroscopy (including gonioscopy), applanation tonometry, dilated fundoscopy, stereoscopic ophthalmoscopy of the optic disc, stereo photographs of the optic nerve, and optic nerve imaging. All patients had prior experience with perimetry and had a history of reliable visual fields. A glaucomatous visual field was defined as a reproducible defect (in at least two consecutive reliable visual fields) of two or more contiguous points with p < 0.01 loss or greater, or three or more contiguous points with p < 0.05 loss or greater, or a 10-dB difference across the nasal horizontal midline at two or more adjacent points in the total deviation plot,21 in the presence of clinical glaucomatous optic neuropathy. One patient has only one abnormal location for CAP, a nonseeing point at (−3,3) in the right eye, and corresponding rim thinning in the inferior temporal (IT) sector of the optic disc (“macular vulnerability zone”).22

An executive committee composed of five clinicians was established to review the diagnoses. Three members were from the clinics where the patients were recruited (Drs Malinovsky, Dul, and Torbit) and two were external clinicians (Drs Malik and Garway-Heath). Dr Malik visited each clinic and reviewed the records of patients recruited for the longitudinal study, to ensure that patients and healthy control subjects met the inclusion/exclusion criteria for the study, with consensual clinical agreement for ambiguous cases. Diagnosis of glaucoma was queried in nine patients, and a consensus was reached; two patients with comorbid disease were excluded.

Perimetric and Imaging Tests

Conventional automated perimetry testing was performed using the Humphrey Visual Field Analyzer II (Carl Zeiss Meditec, Inc, Dublin, CA), using the 24-2 SITA Standard. Frequency-doubling perimetry testing was performed with the Humphrey Matrix using the 24-2 test pattern. Retinal nerve fiber layer testing was performed with optical coherence tomography (Stratus OCT 3, Model 3000, Carl Zeiss Meditec, Inc) to obtain measurements of thickness of the peripapillary RNFL using the RNFL 3.4 Scan protocol.

Contrast sensitivity perimetry-2 testing was performed using custom testing stations based on 21-inch cathode-ray tube displays driven by a visual stimulus generator (ViSaGe; Cambridge Research Systems, Ltd, Rochester, Kent, UK) that provided a resolution of 800 by 600 pixels with a 14-bit control of each phosphor. A photometer with calibration software (Opti-Cal; Cambridge Research Systems, Ltd) was used to measure luminance versus voltage values for each phosphor, calculate transfer functions, and produce red-green-blue (RGB) gamma correction look-up tables. The monitors were Radius PressView 21SR (Miro Displays, Inc, Germany) with a frame rate of 152 Hz and Diamond Pro 2070SB (Mitsubishi Digital, Irvine, CA) with a frame rate of 140 Hz.

Contrast sensitivity perimetry-2 uses a custom-built motorized headrest for control of head position, with a 33-cm test distance so that the display subtended 51 degrees by 42 degrees of visual angle, displaying a total of 57 locations across the central visual field. Custom 50-mm spherical lenses were held in place by magnets to correct refractive error and test distance. The metal rim was a cue to head and eye position (a plain glass lens was used when no spherical correction was needed). The patient’s head was placed in an X-Y motorized chinrest and positioned so that their pupil was centered in the corrective lens (checked with Webcam) that was centered on the fixation target at a distance of 33 cm.

Subjects were corrected for refractive error (spherical equivalent) and the 33-cm test distance. The appropriateness of the correction was checked by measuring acuity in the apparatus at the 33-cm test distance before testing. For the clinical devices, the manufacturer’s recommendations were followed: for CAP, an average age-determined near correction for the perimetric test distance; and for FDP, the subject’s distance glasses.

All results were reviewed individually for artifacts. Perimetry results were reviewed for lid or lens artifacts. Optical coherence tomography scans had three circles per scan using the fast RNFL 3.4 Scan protocol with 256 scan points, and specialized software was used to extract data for each circle. Circles were rejected if there was decentration, low signal strength, or segmentation error. Scans were repeated when these factors were apparent during the study visit (the specialized software was used after all visits had been completed). Acceptable circles from repeated scans on a single visit were averaged to get mean RNFL thickness for IT and superior temporal (ST) sectors.

Perimetric Stimuli

Conventional automated perimetry presented a single stimulus at 54 locations: the size III stimulus, a 0.43-degree circular white luminance increment on a 10-cd/m² background at Weber contrasts from 10% (“35 dB”) to 31,746% (“0 dB”). Frequency-doubling perimetry presented a single stimulus at 54 locations: a vertical 0.5 cycle/degree (cpd) sinusoidal grating in a 5- by 5-degree square window, on a 100-cd/m² background, at Weber contrasts from 2% (“35 dB”) to 100% (“0 dB”). Contrast sensitivity perimetry-2 presented different stimuli at 57 locations, on a 40-cd/m² background at Weber contrasts from 0.7 to 71%. The CSP-2 stimuli17 were Gabor grating patches with magnification varying by location: spatial frequency was 0.5 cpd at fixation and decreased to 0.14 cpd at 21 degrees, based on spatial scale.16 These Gabor patches were horizontal gratings in sine phase within a two-dimensional Gaussian window whose size was increased as spatial frequency decreased so that stimuli were simply magnified as spatial frequency decreased (SD times spatial frequency = 0.25, yielding a spatial bandwidth of 2.25 octave). The 57 stimulus locations were selected from a recent study of structure-function correlations,23 the 24-2 test locations for the Humphrey Field Analyzer, and by superimposing the visual field on a nerve fiber layer map.24 Fig. 1 shows the locations of CAP, FDP, and CSP-2 stimuli. Conventional automated perimetry stimuli were presented with a 200-millisecond rectangular flash, FDP stimuli were presented with 18 Hz counterphase square-wave flicker, and CSP-2 stimuli were presented with 3 cycles of 5 Hz counterphase square-wave flicker.

FIGURE 1.

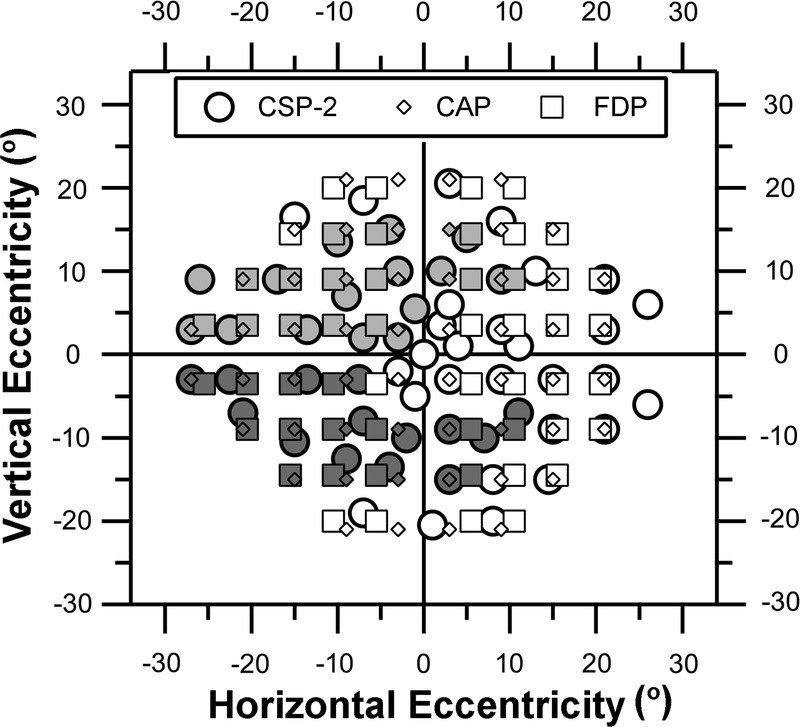
Visual field locations for CSP-2, CAP 24-2, and FDP 24-2. Grayscale identifies those locations assigned to the IT and ST optic disc sectors.25 Light gray (top) is for IT, dark gray (bottom) is for ST, and white is for locations assigned to neither sector.

For all three perimetry tests, sensitivities were measured by having the subject fixate a target in the center of the display and click a button whenever a stimulus was seen, as stimuli were presented at the different visual field locations on a uniform gray background, in a darkened room. For CAP, sensitivity was assessed with the SITA-Standard algorithm.26 For CSP-217 and FDP, sensitivity was estimated with a ZEST algorithm.27,28 Further details on strategies for assessing and managing fixation loss, false positives, false negatives, and other artifacts are described elsewhere.15,16

All four tests were performed on a single visit. First, the three perimetry tests were performed with the order counterbalanced and then the RNFL measurement was performed after perimetry.

Analysis

For each data set from an individual patient or control, arithmetic means were computed for ST and IT optic disc sectors, for either corresponding perimetric sensitivities or corresponding RNFL thicknesses. Fig. 1 identifies the perimetric locations associated with these sectors. For perimetric data, this required that sensitivities were converted from dB units, using 10^(dB/10) for CAP, 10^(dB/20) for FDP, and 10^logCS for CSP-2 (these transformations for CAP and FDP were previously used in analysis of ganglion cell data).6 For a given test and sector, the mean for the 62 control subjects was computed, and then for sectors of individual patients, the defect depth was computed as log difference from this mean (i.e., the logarithm of the ratio of the patient’s value divided by the mean value for the control group). Computation of defect depth in this way allowed measurements from the four tests to be compared in the same metric.

Use of defect depth as log difference from mean for control subjects is common in perimetry, clinical psychophysics, and electrophysiology, but not for RNFL thickness. The rationale for use of log difference from mean for control subjects is that expected between-subject variability in RNFL thickness is high, so that once a score of p < 0.01 has been reached, there are not many more micrometers to lose before thickness reaches values found in blind eyes.29 The use of log difference from mean for control subjects contracts the normal range and expands the range between mean of the control group and mean for blind eyes, just as it does for perimetry. We refer to log difference from mean for control subjects as “defect depth” expressed in log units for RNFL, CAP, FDP, and CSP.

Predictions were assessed with linear regression on Bland-Altman plots of defect depth,30 and 95% limits of agreement (±1.96 SD) were computed from SDs of residuals for these fits. The Bland-Altman limits of agreement were assessed for consistency with between-subject variability in control subjects.

Bland-Altman analysis was used with the null hypothesis that the two tests are in agreement for three indices: mean difference, intercept, and slope. For Bland-Altman analysis, the mean difference is the average of the difference in defect depth across all patients, the slope assesses whether the average difference varies with defect depth, and the intercept assesses whether mild defects have similar depths for both tests. The primary analysis was with a strict criterion: Bonferroni correction for the 36 possible tests, two-tailed p < 0.00138, t > 3.39. Exploratory analysis used one-tailed p < 0.05, t > 1.68, to determine whether associated comparisons trended in the same direction as the comparisons that met the strict criterion.

Bland-Altman analysis assumes that ranges of possible defect depths are similar for the two tests to be compared. However, CAP can produce defects as deep as −3 log units whereas FDP and CSP-2 cannot produce defects deeper than −1.5 log units. If not corrected for, this difference could produce a statistical artifact that caused rejection of the null hypothesis for CAP versus FDP or CSP. Therefore, we imposed a lower limit, or “floor” of −1.3 log units for depth of defect for comparisons among CAP, CSP-2, and FDP. For comparisons with RNFL, a floor of −0.5 was used. In secondary analyses, effects of these choices were evaluated by varying floor from −1.0 to −3.1 log units for comparisons among CSP, FDP, and CAP, and from −0.4 to −0.7 log units for comparisons with RNFL.

Variability in the control group was compared for CSP versus CAP and FDP, using an F test with the SDs. The prediction was that CSP would have lower variability for both sectors, and a strict criterion of p < 0.025 (F > 1.66) was used for significance by applying a Bonferroni correction assuming IT and ST were not independent.

RESULTS

Table 1 shows means and t values for the three indices from Bland-Altman analysis. The intercepts indicated that when CAP was at mean normal, CSP-2 and FDP were below mean normal; this finding reached the strict criterion for IT with both CSP-2 and FDP (t > 4, p < 0.0005), and exploratory analysis found the same result for ST (t > 2.4, p < 0.02). The slopes indicated that as sector damage became more severe, CAP defects deepened more rapidly than defects with CSP-2 and FDP; this finding reached the strict criterion with CSP-2 for both IT and ST sectors (t > 4.3, p < 0.0005) and exploratory analysis found the same trend with FDP for both sectors (t > 1.82, p < 0.04). This pattern of results persisted in secondary analyses with alternate floors from −1.0 to −3.1 log units.

TABLE 1.

Results of Bland-Altman analysis

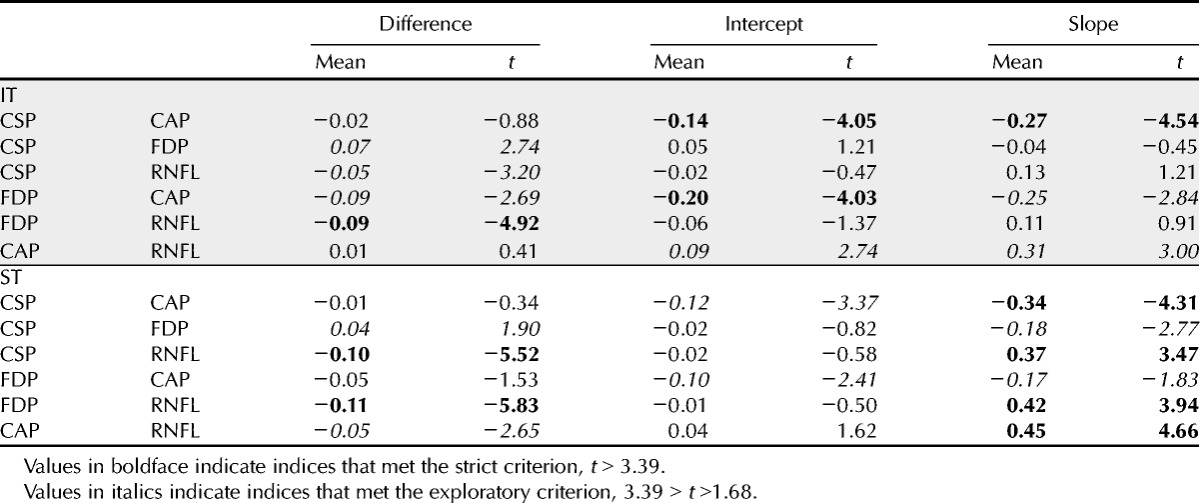
Fig. 2 illustrates these two findings with CSP-2 versus CAP for the IT sector. The finding about the intercept is illustrated by the Bland-Altman fit (thick gray line) being −0.13 log units when the mean is 0.0 log unit. This means that a CSP-2 value 0.065 log units below mean normal corresponds to a CAP value 0.065 log units above mean normal. The finding about the slope is illustrated by the fact that the Bland-Altman line shifts to positive values when the mean is below −0.5 log units.

FIGURE 2.

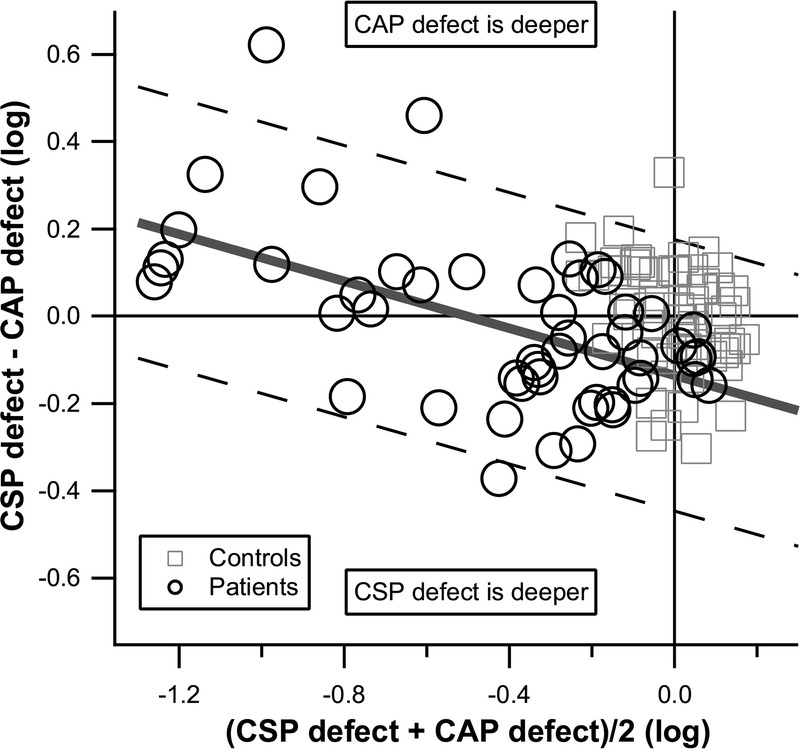
Bland-Altman graph of CSP-2 versus CAP defects for the IT sector, for patient data, with a floor of −1.3 log units. Control data are shown for reference and were not used in the Bland-Altman analysis, which yielded mean (solid diagonal line) and limits of agreement (dashed diagonal lines). The intercept was negative, signifying that CSP-2 defects were on average deeper than CAP defects in sectors with mild damage. The slope was negative, such that in sectors with severe damage, CAP defects were deeper than CSP-2 defects.

The mean differences indicated that perimetric defects were on average deeper than RNFL defects. This finding reached the strict criterion with FDP for both sectors and with CSP-2 for the ST sector (t > 5.4, p < 0.0001); exploratory analysis found the same trend with CSP-2 for the IT sector (t = 3.16, p < 0.002) and with CAP for the ST sector (t = 2.65, p < 0.006). For ST, the slopes reached the strict criterion with CSP, FDP, and CAP versus RNFL, indicating that as sector damage became more severe, perimetric defects deepened more rapidly than RNFL defects; exploratory analysis found the same trend for IT with CAP versus RNFL. This pattern of results persisted in secondary analyses with alternate floors from −1.0 to −3.1 log units. Fig. 3 illustrates these findings with CSP-2 versus RNFL for the ST sector (t = 3.49, p < 0.0006).

FIGURE 3.

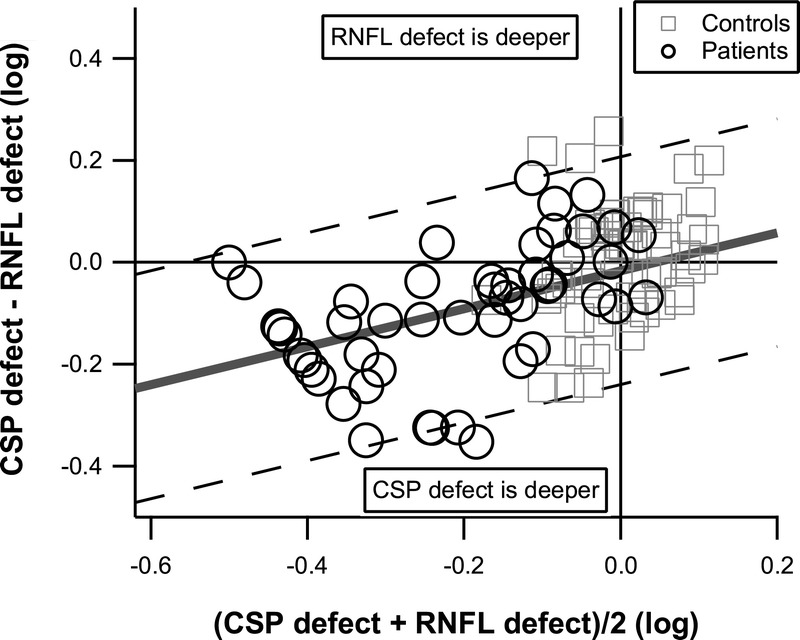
Bland-Altman graph of CSP-2 versus RNFL defects for the ST sector, for patient data, with a floor of −0.5 log units. Control data are shown for reference and were not used in the Bland-Altman analysis, which yielded mean (solid gray line) and limits of agreement (dashed diagonal lines). The mean difference reached the strict criterion, signifying that on average CSP-2 defects were deeper than RNFL defects The slope reached the strict criterion, whereas the intercept was near zero, signifying that the two tests were on average in agreement when the sector was not damaged, and CSP-2 defects were deeper than RNFL defects in damaged sectors.

Means and SDs of the data from control subjects are shown in Table 2; for both sectors, CSP-2 had lower variability than CAP (F > 1.68, p < 0.02) and FDP (F > 2.26, p < 0.001). Table 3 compares ranges for the 95% limits of agreement for patients as well as predictions from SDs of the data from control subjects. The variability in the control subjects was a good predictor of the variability in the patients: the mean ± SD of the differences between measured and predicted limits of agreement was −0.04 ± 0.10 log units.

TABLE 2.

Mean and SD for control subjects, in log units of contrast sensitivity (CAP, CSP, FDP) and micrometers (RNFL)

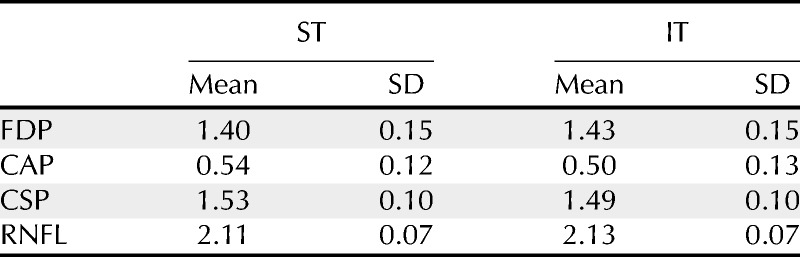
TABLE 3.

Range, in log units, of the 95% limits of agreement derived from patient data and predicted from control data, and the difference (measured minus predicted)

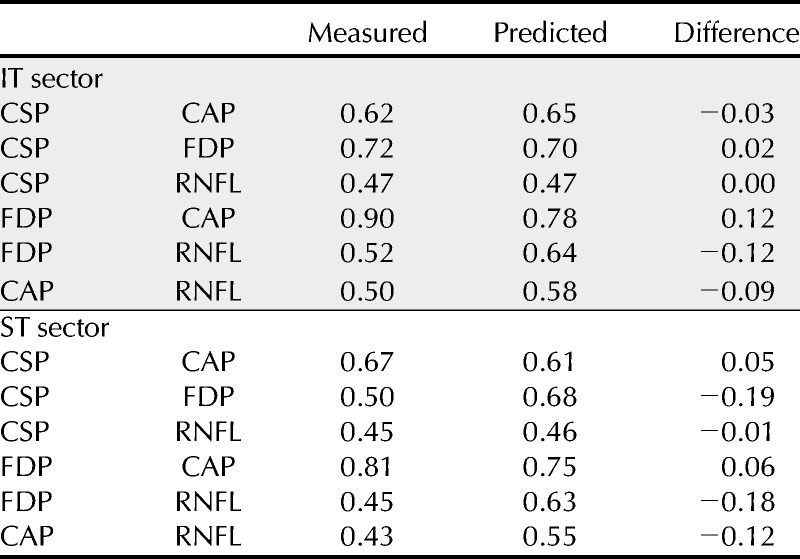
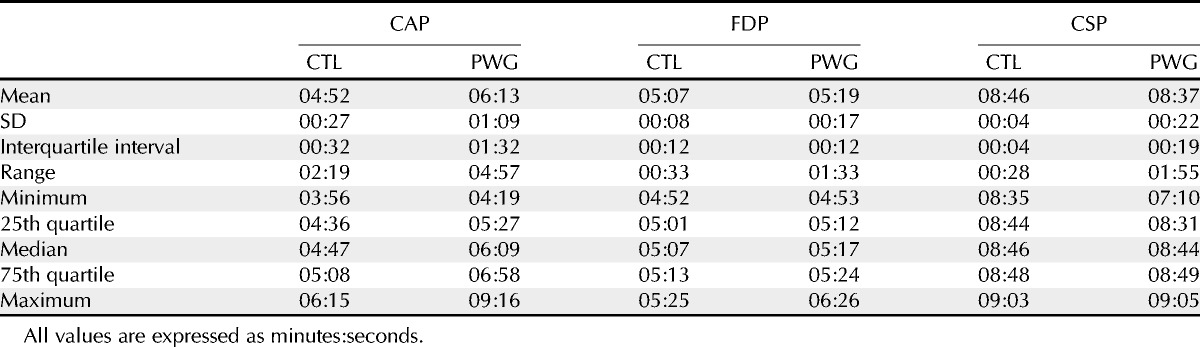
Fig. 4 shows defect depths for all four tests for ST (left) and IT (right) sectors, with FDP and CAP data represented by x and y location, CSP-2 data represented by symbol size, and RNFL data represented by grayscale. Most of the data points that had p < 0.05 for both FDP and CAP (below and to the left of the gray lines) also had RNFL and CSP-2 with p < 0.05. Table 4 shows descriptive statistics for test duration for the three tests. For CAP, test duration was on average 82 seconds longer for patients than control subjects. For FDP, test duration was on average 12 seconds longer for patients. For both CAP and FDP, 22% of patients had longer test durations than the longest duration for control subjects. For CSP-2, test duration was on average 9 seconds shorter for patients than control subjects and no patient had a duration longer than the longest duration for control subjects.

FIGURE 4.

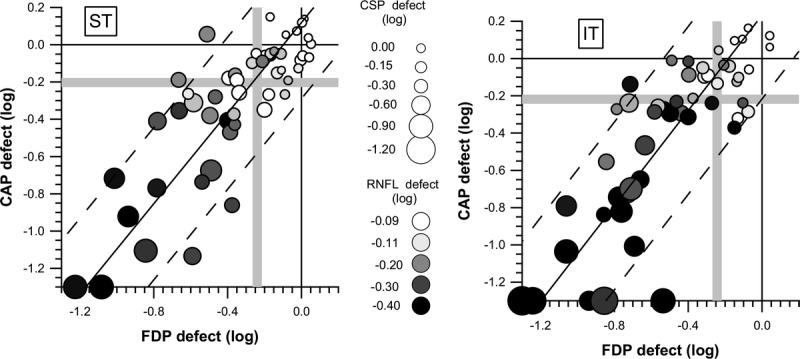
Depth of defect for the patients with glaucoma, with all four tests, for ST (left) and IT (right) sectors. The x and y positions of each symbol reflect defect depth for FDP and CAP, as indicated on the axes. Symbol shade represents RNFL defect depth with a grayscale, where white is within normal limits, light gray is borderline (−0.11 log units is p < 0.05), medium gray is well below normal limits (−0.20 log units is p < 0.005), dark gray is even deeper (−0.30 log units is p < 0.0001), and black is near the floor. Symbol size represents depth of CSP-2 defect, where −0.16 log units is p < 0.05 and −0.30 log units is p < 0.005. The solid diagonal line represents the Bland-Altman line for mean agreement between CAP and FDP, and parallel dashed lines represent the 95% limits of agreement. Gray vertical and horizontal lines show limits for abnormality used in exploratory analyses with p < 5% for defect depth, for FDP and CAP, respectively.

TABLE 4.

Statistics for test duration for the three tests, for the control (CTL) and patient (PWG) groups

DISCUSSION

The long-term goal of research on CSP is to develop sound principles for designing perimetric tests with low variability that are more representative of ganglion cell loss than existing clinical tests. These design principles lead to a revised version, CSP-2, which functioned as designed in the current study. These principles can guide interpretation of clinical tests and can be used to develop stimuli and strategies other than CSP-2 or use of sinusoids. The fundamental goals are greater knowledge and understanding of the interpretation of existing perimetric and structural data and the development of improved perimetric methods. We used sinusoids as a tool for assessing design principles, but these stimuli have no inherent value over more conventional stimuli such as Goldmann size V, as long as the design principles are applied.

The design principles arose from prior studies that used quantitative modeling to investigate how the pathophysiology of glaucomatous retinal ganglion cell damage relates to perimetric measures of glaucomatous visual field loss.6–11 This modeling led to the use of sinusoids to reduce test-retest variability in patients with glaucoma.15 Further studies on spatial scale,16 blur,17 and retinal illumination31 led to the design of a second generation of CSP, referred to as CSP-2. Here, we compared results for CSP-2 with results for three clinical tests, in terms of glaucomatous damage associated with ST and IT sectors of the optic disc. Contrast sensitivity perimetry-2 performed as designed, with lower normal between-subject variability than FDP and CAP, and better ability to detect residual visual function than CAP.

Results of prospective longitudinal studies have found that between-subject variability in structural and functional measurements32 will result in some patients showing anatomical damage before visual field damage and other patients showing visual field damage before anatomical damage.33 The current study included only patients with both perimetric and anatomical damage and found that the limits of agreement derived from the data for these patients were consistent with between-subject variability of the control subjects (Table 3). This supports the conclusion that the primary source of poor agreement between structural and functional measures in patients with glaucoma is normal between-subject variability, that there is little shared variance across measures, and that the disease process does not contribute substantially to poor agreement.32 If this conclusion is valid, then methods for reducing between-subject variability may improve agreement between structural and functional measures of glaucomatous damage.

As shown in Table 2, between-subject variability in the control group for CSP-2 was smaller than that for CAP or FDP, and SDs for CSP and RNFL did not exceed 0.1 log units. An SD of 0.1 log units corresponds to 95% of data points falling within ±0.2 log units, which in linear terms is from 64 to 157% of the mean for the control group. This is consistent with reports on expected between-subject variability in ganglion cell number34,35 and was lower than the between-subject variability for CAP and FDP. Our choice to design CSP-2 to be resistant to effects of nonneural factors (peripheral defocus, pupillary miosis, and lens aging) may have also played a role in reducing variability relative to CAP and FDP. Perimetric methods that reduce the effects of nonneural factors on normal between-subject variability have the potential to allow earlier detection of damage to optic disc sectors by reducing the normal range.

Our ZEST algorithm may also have contributed to low within-subject and between-subject variability, because it reduced confounding effects of test duration by allowing a narrow range of test durations, from 7.1 to 9.1 minutes across the 113 participants. Frequency-doubling perimetry had a similarly narrow range at 4.9 to 6.4 minutes. The range was much wider for CAP, from 3.9 to 9.2 minutes, with longer test durations in patients and especially in patients with more severe field defects (R² = 0.42 for duration vs. mean deviation). Variability can be increased by use of long testing sessions15; hence, the wide range of test durations for CAP may have been a confounding factor. This potential confound is reduced for CSP-2 and FDP with narrower ranges of possible durations.

CSP-2 was developed as a research tool rather than as a new clinical tool; thus, the emphasis was low test-retest variability rather than short test time. Clinical testing requires short test durations to screen both eyes of patients with minimal fatigue, whereas longitudinal research can perform perimetry only on the study eye and use a longer test duration. Pilot data with CSP-2 indicated that test-retest variability in glaucomatous defects was lower for an algorithm with a test duration of 8 to 9 minutes than for a faster algorithm with a test duration of 5 to 6 minutes. Higher variability was seen in wider limits of agreement for FDP, which also had a narrow range of durations and used shorter durations than CSP-2.

As sector damage became more severe, CAP defects became deeper than defects with CSP-2 and FDP. This is consistent with the predicted effects of ganglion cell saturation: at high contrasts, ganglion cell responses do not increase with contrast, resulting in overestimates of the true damage.6 There were eight patients where one of the sectors was at the floor (−1.3 log units) for CAP, six for IT, and two for ST. Frequency-doubling perimetry was at the floor for only two of these sectors, and CSP-2 was not at the floor for any of them. For these eight sectors, the mean (±SD) defect was −1.03 (±0.18) log units for CSP-2 and −1.06 (±0.27) log units for FDP. Four of these 8 sectors were at the floor (−0.5 log units) for RNFL, with a mean (±SD) of −0.44 (±0.08) log units. This is consistent with findings that increasing stimulus size to Goldmann size V can reveal remaining vision in locations where size III is not detected20,36 and a similar finding with the initial version of CSP.15 This result, combined with the finding that CSP-2 and FDP tended to have defects at least as deep as CAP defects in sectors with mild damage, supports the use of stimuli larger than size III. Size V has been shown to be just as sensitive to defect and more resistant to blur than size III.37 The principles used to design CSP-2 would propose that size V may perform similarly to FDP and CSP-2 if the contrasts used were restricted to 1.5 log units contrast range. Our design principles also support varying size rather than the use of high contrasts, as in size threshold perimetry37 and the Heidelberg Edge Perimeter when using size III.

Fig. 5 illustrates these findings in “dB” units, where 10 dB equals 1.0 log unit for all three tests, with no floor beyond that imposed by the devices. This is the meaning of “dB” on CAP; FDP uses 20 dB equal to 1.0 log unit; hence, dB units on the two machines are not directly comparable. The diagonal line shows equality: sectors falling above the line have deeper CAP defects, and sectors falling below the line have more shallow CAP defects. This shows that when CAP defect is not deeper than −5 dB, defect depths are similar for all three tests except that CAP tends to be not as deep (more often below the diagonal line). It also shows that when CAP defect is deeper than −10 dB, FDP and CSP defects were similar to each other but were not as deep as CAP defects.

FIGURE 5.

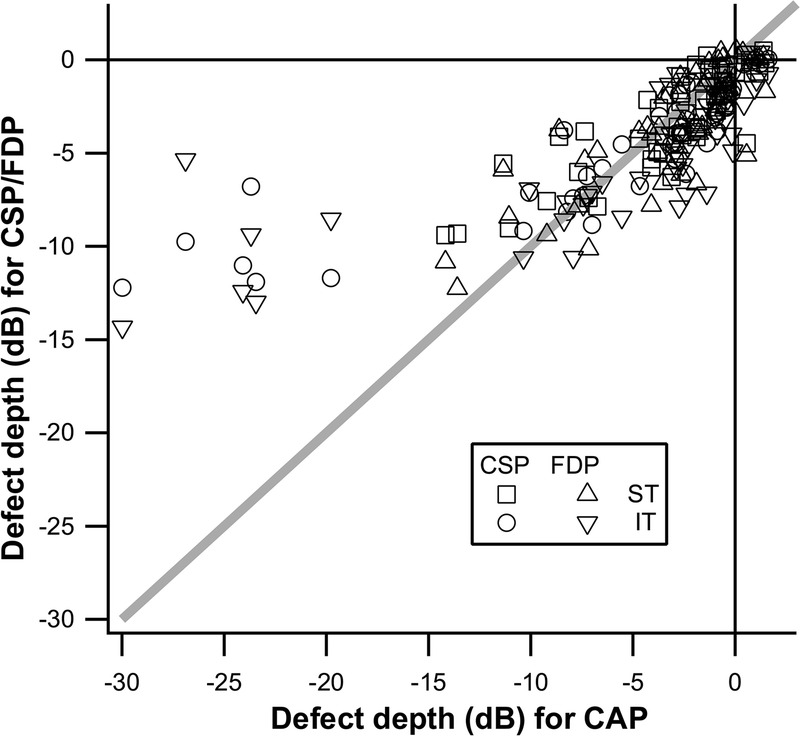
Scatterplot of perimetric defect depth for IT and ST sectors with CAP as the reference. Contrast sensitivity perimetry-2 and FDP data were transformed into units with 1 dB = 0.1 log units, without imposing a floor. The diagonal line represents equality of defects.

Bland-Altman analysis was used to avoid spurious results owing to lack of an independent variable.38 Bland-Altman analysis requires similar measures for different tests; thus, we expressed the data in terms of defect depth: the severity of damage for a given test, for a given optic disc sector in a given patient’s eye, was quantified by comparing the patient’s data with the mean for the control group for that sector, on a logarithmic scale. Bland-Altman analysis also requires similar ranges across tests; hence, we imposed a lower limit (a “floor”) to equate ranges. For CSP-2 and FDP, the use of flicker means that the stimulus cannot have a Weber contrast greater than 100%, yielding a floor for defect depth. For CAP, which uses luminance increments, there is no theoretical maximum for Weber contrast, and industrial engineers in the 1970s chose a maximum of 31,746% contrast. This 31,746% contrast has become the clinical maximum stimulus, referred to as “less than 0 dB,” which may (erroneously) be interpreted clinically as “nonseeing.” This can be scored as 3 log units below mean expected value (“−30 dB”) from an age-similar control group. However, on a later test, this same location may be scored as just 1 log unit below mean expected value (“−10 dB”)1,37; thus, a floor of −1.3 log units is not unreasonable for CAP and was consistent with the possible contrast ranges for CSP and FDP. For RNFL thickness, we used a floor of −0.5 log units because the most severe RNFL defect in our patients was −0.7 log units for IT and −0.6 log units for ST. We repeated the analyses with different choices for floors and found the same pattern of results.

Perimetric defects were on average deeper than RNFL defects, and the difference tended to be greater in sectors with more severe damage. This is consistent with RNFL having a substantial nonneural component (glial cells and blood vessels) that does not decline as the sector is damaged.5,39,40 The floor of −0.5 dB would represent a nonneural component that was 32% of the mean normal thickness, consistent with prior studies.5 For all three perimetric tests, the slopes were steeper for ST than IT; hence, the nonneural components may be different for these two sectors.

An unexpected finding was that, in sectors with mild damage, Bland-Altman analysis inferred that defects were on average deeper for CSP-2 and FDP than for CAP. This is unlikely to be attributed to different ganglion cell types being tested, because CAP and FDP stimuli are both potent stimuli for the magnocellular pathway.6 This is more likely to reflect effects of peripheral defocus on the control data used to compute defect depth. We estimated that peripheral defocus can cause CAP sensitivity to be reduced by as much as 0.3 log units at some locations in some control subjects.17 The mean for the control group will include varying degrees of peripheral defocus across control subjects and so will underestimate what mean sensitivity would be when the stimuli are in focus. Peripheral defocus will have greater effects on CAP than CSP-2 or FDP17; thus, some of the control subjects may have had locations where sensitivity for CAP was reduced because of peripheral defocus. For a patient with less impact of peripheral defocus than the average impact for the control subjects, defect depth will be underestimated by CAP but not by FDP or CSP because they are more resistant to blur. This would cause a small shift in Bland-Altman intercept for CAP, and the range of −0.2 to −0.1 log units for intercept is consistent with a subset of patients having reduced impact of peripheral defocus. It is also possible that differences in stimulus locations and sizes across CAP, CSP-2, and FDP could play a role (Fig. 1), as could differences in algorithms.

In summary, analysis of agreement for data from CSP-2 and data from clinical devices yielded results that were consistent with the goals and assumptions involved in the design of CSP-2: to cause less ganglion cell saturation than CAP, to be less influenced by optical blur than CAP, and to be less affected by reduced retinal illumination than FDP. The reduction in effects of ganglion cell saturation was reflected in the finding that CSP-2 yielded milder defects than CAP for sectors with severe damage; the reduction in effects of peripheral defocus was reflected in the finding that CSP-2 yielded deeper defects than CAP for sectors with mild damage. The reduction in effects of pupil and lens was reflected in the finding that between-subject variability was lower for CSP-2 than for FDP.

These findings are in alignment with the goal of our neural modeling, to provide analysis methods and perimetric tests that improve agreement between structural and functional methods. Improved agreement between structural and functional measures of the effects of glaucoma may assist clinicians in making earlier and more valid decisions regarding the status of their patients. Improved agreement may also reduce uncertainty early in the disease, where clinicians frequently are confronted with poor agreement between results obtained with clinically available structural and functional devices.