Vatalanib population pharmacokinetics in patients with myelodysplastic syndrome: CALGB 10105 (Alliance)

Abstract

Aims

Vatalanib is an oral anti-angiogenesis agent that inhibits vascular endothelial growth factor receptor tyrosine kinases, which in patients showed auto induction of metabolism and variability in pharmacokinetic (PK) disposition. The objective was to characterize the population PK and time-dependent change in vatalanib clearance and assess exposure–toxicity relationship in patients with myelodysplastic syndrome (MDS).

Methods

This was an open-label phase II study of vatalanib in MDS patients receiving 750–1250 mg once daily in 28-day cycles. Serial blood samples were obtained and plasma vatalanib concentrations measured by HPLC. Population PK analysis was performed using nonmem 7.2 with FO estimation since FOCE failed. The final model was evaluated using goodness-of-fit plots, bootstrap analysis, and visual predictive check.

Results

Pharmacokinetic data were complete for 137 patients (86 M, 51 F), of median age 70 years (range 20–91). A one-compartment model with lagged first-order absorption and time-dependent change in oral clearance was fitted to the vatalanib plasma concentration versus time data. The population means for pre-induction and post-induction oral clearance were 24.1 l h^–1 (range: 9.6–45.5) and 54.9 l h^–1 (range: 39.8–75.6), respectively. The apparent oral clearance increased 2.3-fold, (range: 1.7–4.1-fold) from first dose to steady state. Our data did not identify a significant relationship of the predefined covariates with vatalanib pharmacokinetics, although power to detect such a relationship was limited.

Conclusions

Vatalanib pharmacokinetics were highly variable and the extent of auto induction was not determined to correlate with any of the pre-defined covariates.

What is Already Known about this Subject

• Vatalanib pharmacokinetics has been described, but using noncompartmental analysis in patients with solid tumours.

• Previous clinical studies suggest that vatalanib can induce its own metabolism, resulting in decreased systemic exposure after multiple oral doses.

What this Study Adds

• This study is the first to characterize vatalanib population pharmacokinetics in patients with myelodysplastic syndrome.

• This study reinforces the autoinduction and time-dependent pharmacokinetics of vatalanib using a population pharmacokinetic approach and provides a comprehensive population pharmacokinetic model to aid dose adjustment for vatalanib treatment.

Introduction

Angiogenesis has been suggested to play an important role in the pathophysiology of several haematological malignancies [1,2]. Vascular endothelial growth factor (VEGF) is a specific angiogenic factor required for tumour neovascularization [3,4]. Vascular endothelial growth factor is produced by the malignant clone in myelodysplastic syndrome (MDS) and appears to stimulate both angiogenesis and growth of the malignant clone. Several reports indicate that angiogenesis is markedly increased in the bone marrow in acute myelogenous leukaemia [5–8]. Inhibition of VEGF receptor tyrosine kinases may have both an anti-angiogenic and a direct antileukaemic effect, thus providing the rationale for a phase II clinical trial of a VEGF inhibitor in MDS.

Vatalanib is an oral amino-phthalazine derivative that inhibits the VEGFR1 (Flt-1), VEGFR2 (KDR) and VEGFR3 (Flt-4) receptor tyrosine kinases as well as the platelet-derived growth factor receptor-β (PDGFRB) and c-kit kinases [9]. Vatalanib is rapidly absorbed following oral administration, with time to peak concentrations (T_max) occurring ∼2 h after dosing and a mean terminal half-life of 4–6 h. Mass balance data and metabolism studies indicate that vatalanib is extensively metabolized by the cytochrome P450 (CYP) enzyme CYP3A4, although it is also a substrate of CYP2D6 and CYP1A2, resulting in two major (inactive) metabolites, as well as a minor active metabolite [10,11]. The parent drug is ∼98% bound to plasma proteins, presumably primarily bound to alpha-1-acid glycoprotein. Early clinical trials revealed substantial vatalanib pharmacokinetic variability that is further increased by autoinduction of its metabolism [10–12]. Following oral administration, systemic exposure to vatalanib decreased by ∼50% between day 1 and day 7 of therapy, then remained relatively constant throughout a 28 day treatment cycle [12].

To date, the population pharmacokinetics of vatalanib in MDS has not been evaluated. The objective of this component of the clinical study was to use a population pharmacokinetic approach to model the pharmacokinetics of oral vatalanib, to attempt to identify clinically relevant covariates associated with variability in its disposition and to assess the vatalanib exposure–toxicity relationship.

Methods

Study design

This was an open-label, prospective study. Adult patients with primary or therapy-related (secondary) MDS who were enrolled in the Cancer and Leukemia Group B (CALGB) 10105 study (Alliance), a multicentre, phase II clinical study of vatalanib in MDS, were included in our analysis. The study protocol was approved by the local institutional review board (IRB). Vatalanib was administrated orally as a daily dose of 1250 mg over 28 days; a subsequent protocol modification allowed starting doses of 750 mg, as described previously [13]. No other drugs for MDS were used during the study. Patients were instructed to take vatalanib either on an empty stomach or at least 30 min after breakfast, and to avoid grapefruit and grapefruit juice. Patients were monitored for toxicity during follow-up visits after day 7. Toxicity was graded according to the National Cancer Institute (NCI) Common Terminology Criteria for Adverse Events (CTCAE) version 3.0.

Pharmacokinetic sampling schedule

Each participant signed an IRB-approved, protocol-specific informed consent, indicating that blood samples could be collected and used for research. Serial blood samples were obtained at the following time points: on study day 1, immediately prior to the first oral dose (0 h), between 15 and 45 min postdose, between 1 and 3 h postdose and between 4 and 6 h postdose; in addition, two blood samples were drawn at least 1 h apart between days 7 and 14 after initiation of treatment, and one sample was taken prior to initiation of a second cycle on day 28. The venous blood samples (3 ml) were collected in heparinized tubes, mixed well and immediately placed in an ice bath prior to centrifugation for 10 min at 2000g at 4°C. Aliquots of plasma were transferred into an appropriately labelled polypropylene tube and stored at or below −18°C until analysis.

Measurement of vatalanib plasma concentrations

Vatalanib plasma concentrations were determined using a high-performance liquid chromatography assay with ultraviolet detection at the wavelength of 315 nm by AAIPharma (Wilmington, NC, USA). The lower limit of quantification of the assay was 5 ng ml⁻¹. The linear range was 5–5000 ng ml⁻¹. The coefficient of variation (CV%) for the lower limit of quantification was <8.5% for all calibration curves. The CV% for the quality control values ranged from 1.7% for the 3500 ng ml⁻¹ calibrator to 5.1% for the 15 ng ml⁻¹ calibrator. Values less than the lower limit of quantification were assigned a value of 0 ng ml⁻¹.

Population pharmacokinetic analysis

Nonlinear mixed-effects modelling was performed using nonmem version 7.2 (ICON Development Solutions, Ellicott City, MD, USA) with a Gfortran Compiler (Free Software Foundation, Boston, MA, USA). A first-order (FO) estimation method was used to fit models because estimation with a first-order conditional estimation (FOCE) method failed to converge with plausible estimates for various parameters of interest. nonmem outputs were processed using Pdx-Pop 5.0 (ICON Development Solutions) and Xpose version 4.1.0 (Uppsala University, Uppsala, Sweden). R version 2.15.1 (Free Software Foundation, Boston, MA, USA) was used for statistical analysis and plot generation.

Model selection was based on the following criteria: plausibility and precision of parameter estimation; goodness-of-fit plots, the likelihood ratio test, measures of model stability (i.e. condition number <1000 and successful convergence). The likelihood ratio test was performed using the minimal objective function value (MOFV) test for any significant improvement in fit [ΔMOFV >3.84; P < 0.05; degree of freedom (d.f.) = 1] between nested models.

Base model building

One-compartment or two-compartment models with lagged first-order absorption and time-dependent clearance were fitted to the data. Time-dependent clearance was modelled with a first-order induction function, as follows:

where CL_induced/F represents apparent oral clearance at steady state postinduction, ΔCL/F represents the difference between apparent oral clearance at steady state postinduction and the pre-induction oral clearance, and K_induct represents the first-order induction rate constant. Alternative clearance autoinduction models, including enzyme turnover models, and differing K_induct values were also tested. In addition, other absorption models were also assessed, including first-order absorption, zero-order absorption, parallel dual first-order absorption, single Weibull absorption and transit compartment absorption. Interindividual variability (IIV) was modelled by assuming that the individual pharmacokinetic parameters followed a log normal distribution around the population mean values as follows: P_i = P_pop × exp(η_i), where P_i is the parameter estimate for individual i, P_pop is the mean parameter estimate of the population, and η_i represents the deviation of P_i from P_pop. The covariance between pharmacokinetic parameters was tested, found to be insignificant and therefore not included in the final model. Residual variability (RV) was modelled using an additive error model for natural logarithm-transformed data as follows: ln C_ij = ln C_pred,ij + ε_ij, where C_ij represents the jth observed vatalanib concentration for the ith individual, C_pred,ij represents the model predicted jth concentration for the ith individual, and ε_ij represents the residual error for the jth observation of the ith individual. Attempts to model residual variability using a proportional plus additive error model with untransformed concentration data yielded essentially negligible estimates for the magnitude of the additive component, suggesting that the residual error variability could be described adequately without an additive component.

Data were initially analysed in adapt II [Biomedical Simulations Resource (BMSR), University of Southern California, Los Angeles, CA, USA], and the pharmacokinetic (PK) parameter estimates from adapt (see Table S1) were used as initial values for the nonmem analysis.

Covariate model development

After the base model was determined, covariate modelling was conducted to identify covariates that have a significant effect on the variability of key pharmacokinetic parameters (clearance and volume terms). Patient demographic characteristics, including bodyweight, ideal bodyweight, dosing weight, height, body surface area, sex, race, age, liver function tests, total bilirubin and aspartate aminotransferase, were assessed. Ideal bodyweight and dosing weight were calculated using standard equations. Screening for potentially significant relationships between covariates and parameters was performed by a preliminary graphical analysis, which plotted parameter estimates vs. covariates or Eta values (IIV) vs. covariates. In addition, the generalized additive model in Xpose software was also used for covariate screening. Findings from the covariate screening process as well as the physiological plausibility of potential covariate–parameter relationships were considered in identifying the relationships to be tested for statistical significance directly through nonlinear mixed-effects modelling. Covariates were tested for statistical significance in the model using a stepwise model-building process, including forward addition and backward elimination. The criterion for covariate inclusion was P < 0.05 for forward addition, with P < 0.01 for backward elimination. Highly correlated covariates, e.g. bodyweight and body surface area, were selected based on physiological plausibility or highest significance.

Categorical covariates were evaluated as dichotomous dummy variables (0 or 1) using a fractional change function, as follows: P = θ₁ × (θ₂)^COV, where θ₁ represents the parameter estimate for an individual with COV coded as 0, and θ₂ represents the fractional change multiplier for θ₁ when COV is coded as 1. Continuous covariates were scaled on their median values and modelled using a power function, as follows:

where θ₁ represents the parameter estimate for subjects with their COV equal to the median values, and θ₂ represents the change in parameter estimate related to the difference between COV and COV_median.

Evaluation of model fit

The goodness of fit of the model was assessed by the following diagnostic plots: observations vs. population predictions, observations vs. individual predictions, weighted residuals vs. population predictions and weighted residuals vs. time. In addition, bootstrap analysis of 1000 resamples with replacement was performed to evaluate the precision of parameter estimation. Condition number was used to assess model stability, where a model with condition number <1000 was considered to be stable. Visual predictive check with 1000 simulations was used to assess the predictive performance of the final model by comparing the 5th and 95th percentiles of the simulated concentrations with the observations.

Assessment of systemic exposure–toxicity relationships

Toxicities determined to be attributable to vatalanib were used for evaluation of the systemic exposure–toxicity relationship. Logistic regression was performed, with toxicity grades, defined by NCI CTCAE version 3.0, as the outcome variable and steady-state area under the concentration–time curve (AUC) as the predictor variable. Owing to the sparse nature of our data set, other response variables, such as peak or trough concentration, were difficult to assess and not used. Steady-state AUC was calculated as the dose divided by steady-state clearance, i.e. postinduction clearance. Multinomial logistic regression with clinical toxicity grades ranging from 1 to 5 was used, as well as simple logistic regression with toxicity grades dichotomized to two categories (grade <3 and ≥3).

Results

Database description

The database for vatalanib pharmacokinetic analysis was comprised of 137 patients contributing a total of 564 vatalanib plasma concentration measurements. A total of 66.5% of the vatalanib concentration data points were obtained within 24 h of initial dosing. The other two clusters of sampling times between days 7 and 14 after initiation of treatment and prior to initiation of the second cycle on day 28 consisted of 26.6 and 6.9% of the data points, respectively. Patient demographic and clinical data are summarized in Table 1.

Table 1.

Patient characteristics

Characteristic	Value [median (range)]
Age (years)	70 (20–91)
Weight (kg)	80 (48–128)
Height (cm)	170 (149–193)
Body surface area (m2)	1.91 (1.46–2.46)
Total bilirubin (mg dl−1)	0.7 (0.2–2.0)
Asparate aminotransferase (IU l−1)	23 (7–92)
Body mass index (kg m−2)	26.8 (17.8–41.8)
	[n (%) of patients]
Sex
Male	86 (62.8)
Female	51 (37.2)
Race
Caucasian	128 (93.4)
Other	9 (6.6)

Model development

When the data were modelled using first-order absorption and time-dependent clearance, a two-compartment model did not improve the model fit compared with a one-compartment model. Time-dependent clearance was modelled with a first-order induction function as shown in the model section:

Enzyme turnover models as alternative clearance autoinduction models failed to converge, probably owing to the limited number of data points per patient. In addition, a one-compartment model with lagged first-order absorption resulted in less bias in goodness-of-fit plots than models with alternative absorption processes. An objective function value reduction of 88.7 was observed by using the lagged first-order absorption model compared with the first-order absorption model.

The base model was parameterized in terms of the rate constant of the lagged first-order absorption (K_a), the absorption lag time (A_lag), the apparent volume of distribution (V_d/F), the apparent clearance at steady state postinduction (CL_induced/F), the difference between apparent clearance at steady state postinduction and the pre-induction clearance (ΔCL/F) and the rate constant for the first-order autoinduction process (K_induct).

The effects of covariates on pharmacokinetic parameters assessed during the covariate modelling step included weight (actual bodyweight, ideal bodyweight and dosing weight) on CL_induced/F, weight on V_d/F, sex on CL_induced/F, age on CL_induced/F, total bilirubin on CL_induced/F, and aspartate aminotransferase on CL_induced/F. However, none of the covariate effects was significant after the stepwise covariate model-building process. Therefore, the base model was determined to be the final model. The final model nonmem parameter estimates and relative standard errors are shown in Table 2. Several secondary parameters were calculated using the primary parameter estimates, as follows: the apparent pre-induction oral clearance (CL_initial/F) was calculated as CL_induced/F − ΔCL/F; and the dose-adjusted apparent pre-induction AUC (AUC_initial) and postinduction steady-state AUC (AUC_induced) were calculated as 1250/CL_initial/F and 1250/CL_induced/F, respectively. The rationale for using dose-adjusted pre- and postinduction AUC values is that the doses were not the same for all subjects. Table 2 summarizes these secondary parameters. Both Wilcoxon signed rank tests for CL_initial/F vs. CL_induced/F and AUC_initial vs. AUC_induced were statistically significant (P value < 0.001). Boxplots showing the differences for these parameters before and after induction are in Figure 1. The IIV value associated with ΔCL/F was fixed to zero due to extremely small estimate and failure of convergence of the covariance step.

Table 2.

Parameter estimates

Parameter	Estimate (95% CI)	% RSE
CLinduced/F (l h−1)	54.9 (42.5, 67.2)	11.7
ΔCL/F (l h−1)	30.1 (14.8, 45.4)	27.6
Vd/F (l)	53.8 (38.4, 69.1)	14.9
Ka (h−1)	0.172 (0.141, 0.203)	9.2
Alag (h)	0.178 (0.136, 0.220)	11.7
Kinduct (h−1)	0.023 (fixed)*	–
Interindividual variability	% CV	% RSE
IIV for CLinduced/F	22.8	36.7
IIV for Vd/F	84.4	20.3
IIV for Ka	35.4	24.1
IIV for Alag	137.1	76.1
Residual variability	Variance	% RSE
σ2additive	0.596	17.8
Secondary parameters	Median (range)	% RSE
CLinitial/F (l h−1)	23.6 (9.6–45.5)	–
AUCinitial (mg h l−1)	52.9 (27.5–129.7)	–
AUCinduced (mg h l−1)	23.3 (16.5–31.4)	–

CL/F = CL_induced/F − ΔCL/F × exp(−K_induct × t). CL_initial/F = CL_induced/F − ΔCL/F. The 95th percentile confidence intervals (CIs) and relative standard error (RSE) estimates were derived from bootstrap analysis.

^*K_induct was fixed at 0.023 due to the fact that maximal clearance induction was reached on day 7.

CI, confidence interval; CV, coefficient of variation; IIV, inter-individual variability; RSE, relative standard error.

Figure 1.

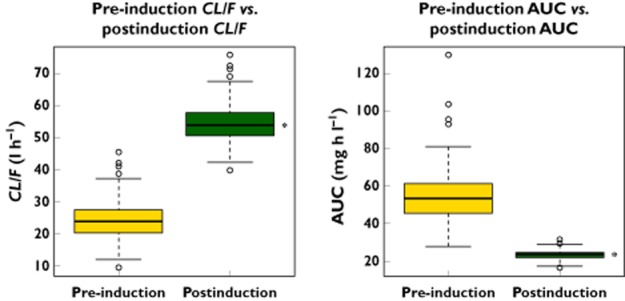
Boxplots of apparent oral clearance and dose-normalized area under the concentration–time curve (AUC) (pre-induction vs. postinduction). *P value < 0.001 for both using the Wilcoxon signed rank test

Evaluation of model fit

Goodness-of-fit plots for vatalanib are given in Figure S1. The 95% confidence intervals and relative standard errors obtained from 1000 bootstrap runs are given in Table 2. Minimization was successful in 99.7% of the 1000 bootstrap runs. All the estimates of parameters from the final model fell within the 95% bootstrap confidence intervals. The condition number of the final model, 459.5 (<1000), suggested reasonable model stability. Moreover, the visual predictive check result (Figure 2) shows that only 8.5% of observations were outside of the 90% prediction interval, indicating reasonable predictive power of the final model. A typical concentration–time profile is shown in Figure 3.

Figure 2.

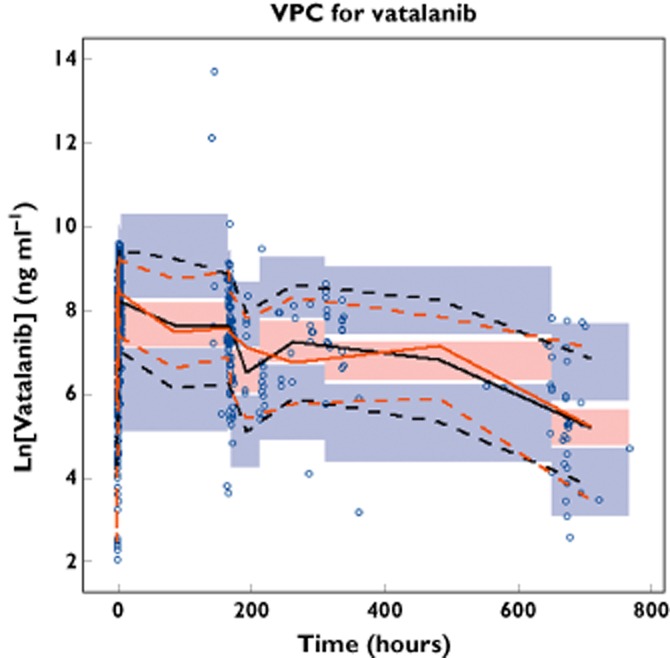
Visual predictive check (VPC) plot for the final model. Open circles represent observed vatalanib concentrations on day 1 and later. The black continuous line represents the median of the simulated concentrations. The black dashed lines represent the 5th and 95th percentiles of the simulated concentrations. The red continuous line represents the median of the observed concentrations. The red dashed lines represent the 5th and 95th percentiles of the observed concentrations. The shaded areas represent the 90% confidence intervals for the prediction percentiles

Figure 3.

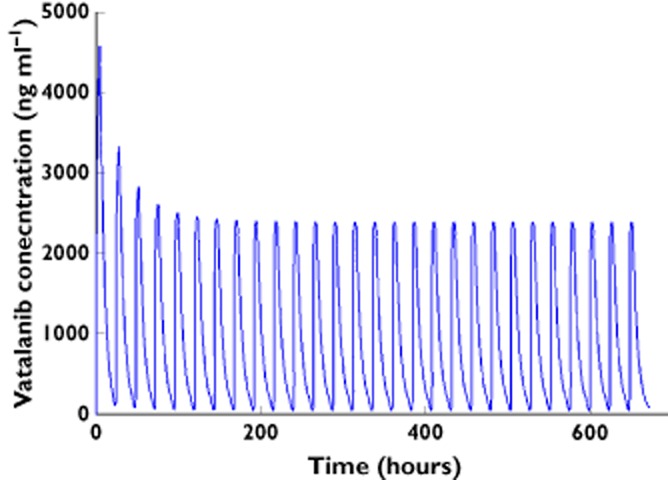
Typical vatalanib concentration–time profile for a myelodysplastic syndrome patient based on model parameter estimates at a dosage of 1250 mg daily

Assessment of systemic exposure (AUC)–toxicity relationship

Both multinomial logistic regression of five toxicity grades (grades 1–5) on steady-state AUC and simple logistic regression with toxicity grades dichotomized to two categories (grade <3 and ≥3) on steady-state AUC were performed. Chi-square tests were used to test whether the coefficients of the predictor variables were significantly different from zero. However, statistical testing revealed no significance, with all P values > 0.5, indicating that there was no correlation between systemic vatalanib exposure and the grade of toxicity. A scatter plot of toxicity grade and steady-state AUC (AUC_induced) is shown in Figure S2. Clinical toxicity data were graded using the NCI CTCAE and are summarized in Table 3.

Table 3.

Summary of toxicities

Toxicity category	Number of patients		Total (%)†
	Grade <3*	Grade ≥3*
Allergy/immunology	1	0	1 (0.8)
Auditory/ear	1	0	1 (0.8)
Blood/bone marrow	16	75	91 (71.7)
Cardiac arrhythmia	3	2	5 (3.9)
Cardiac general	12	4	16 (12.6)
Coagulation	2	2	4 (3.1)
Constitutional symptoms	63	36	99 (80.0)
Death	0	1	1 (0.8)
Dermatology/skin	12	2	14 (11.0)
Gastrointestinal	80	24	104 (81.9)
Haemorrhage/bleeding	17	8	25 (19.7)
Infection	8	12	20 (15.7)
Lymphatic	6	0	6 (4.7)
Metabolic/laboratory	48	9	57 (44.9)
Musculoskeletal/soft tissue	8	3	11 (8.7)
Neurology	56	20	76 (59.8)
Ocular/visual	6	0	6 (4.7)
Pain	28	9	37 (29.1)
Pulmonary	1	0	1 (0.8)
Pulmonary/upper respiratory	25	3	28 (22.0)
Renal/genitourinary	8	1	9 (7.1)
Sexual/reproductive function	1	0	1 (0.8)
Vascular	1	0	1 (0.8)

^*Defined by National Cancer Institute Common Terminology Criteria for Adverse Events grade.

^†Percentage was calculated using total number of patients with toxicities determined to be attributable to the study drug, which is 127.

For each patient, the toxicities with highest grade are summarized in this table.

Discussion

In the present study, a population pharmacokinetic model incorporating time-dependent clearance was developed for oral vatalanib using limited sampling over a 28 day period in adult patients with MDS. This model consisted of a one-compartment model with lagged first-order absorption and time-dependent clearance that changed over the first 7 days of therapy and remained constant thereafter. Mean apparent oral clearance increased from 24.1 to 54.9 l h⁻¹ over the course of therapy. The change in apparent oral clearance resulted in a corresponding reduction in the AUC, from 52.9 to 23.3 mg h l⁻¹ on day 1 and after at least 7 days of treatment, respectively. Moreover, the relative increase in apparent oral clearance varied over a 2-fold range, further increasing the variability seen in plasma vatalanib concentrations. The estimates for apparent oral pre-induction and postinduction clearance based on our data analysis are similar to those previously reported in patients with solid tumours receiving vatalanib who were heavily pretreated and had liver metastases (mean ± SD, 37 ± 45 l h⁻¹ for pre-induction clearance and 67.2 ± 57.9 l h⁻¹ for postinduction clearance) [12].

The exact mechanism responsible for the declining vatalanib concentrations over time is not clear at present. The most likely mechanism would be the autoinduction of its metabolism over time, which has been reported in previous studies [14,15]. Results from in vitro studies in human liver slices and hepatocytes showed that vatalanib could induce CYP3A4 at ∼40% of the positive control, rifampin, supporting the hypothesized explanation that autoinduction of CYP3A4 is the most plausible mechanism for the time-dependent change in vatalanib PK. The autoinduction of drug metabolism has been reported for a number of drugs, including carbamazepine [16–18], midostaurin [19,20], ifosfamide [21,22], phenobarbital [23], cyclophosphamide [24], ritonavir [25], efavirenz [26], nevirapine [27], aprepitant [28] and methadone [28]. Amongst these drugs, one of the most well-known and well-described drugs demonstrating autoinduction of metabolism is carbamazepine. In a study in human volunteers, a decline in plasma carbamazepine concentrations was observed following repeated doses. A model with a first-order enzyme induction was fitted to the plasma carbamazepine concentrations to obtain model parameter estimates of the initial clearance, the final clearance and the first-order rate constant for enzyme induction. The first-order rate constant characterized the time course of autoinduction and was able to raise the clearance from the initial value to its final steady-state value [16]. A similar model was employed to describe the time-dependent pharmacokinetics of methadone in opiate users [29]. Alternative models of enzyme autoinduction have been reported, including more complex models based on turnover of CYP450 enzymes [20,22,24,30]. In these complex models, an enzyme compartment was introduced to be linked to the drug model by drug concentrations either simulating the enzyme production or inhibiting the enzyme degradation, and the enzyme concentration/activity affected the drug clearance. These enzyme turnover models are more physiological and mechanistic. Additional possibilities for this relative increase in apparent oral clearance include a time-dependent change in F or a time-dependent change in protein binding. However, rich data profiles are necessary for developing such complex models. In the present analysis with limited sparse sampling data, the simpler model with first-order enzyme induction was shown to fit the vatalanib plasma concentration data reasonably well and appropriately characterize the time-dependent pharmacokinetics of this drug. Similar models incorporating a closed-form equation to account for time-dependent PK parameters have been previously reported [16,29]. A first-order rate constant K_induct was introduced into our model to characterize the autoinduction and time-dependent clearance over time. However, the fact that there are samples only on day 1 and after day 7 makes it very difficult to estimate this rate constant accurately; therefore, K_induct was fixed to an empirical value to ensure that maximal induction was reached on day 7 based on previous results (data not shown).

Although CYP3A4 autoinduction has been determined to be the most plausible mechanism for the decreased exposure of vatalanib over time, the exact mechanism for such autoinduction is still unclear. Autoinduction of vatalanib metabolism could be achieved either by upregulation of CYP3A4 expression via activation of the pregnane X receptor and/or the constitutive androstane receptor, which are important xenobiotic-activated transcription factors, or by decreased CYP3A4 protein degradation as a result of interaction of vatalanib with catalytic enzymes of CYP3A4 protein [31,32]. A recent study showed that sunitinib, which is a VEGFR tyrosine kinase inhibitor, induced CYP1A1 in breast cancer Michigan Cancer Foundation-7 cells by activating the aryl hydrocarbon receptor, suggesting another possible mechanism by which autoinduction of drug metabolism can occur [33]. In addition, the potential likelihood that autoinduction of CYP3A4 occurs not only in the hepatocyte but also in the gastrointestinal epithelium cannot be excluded, and this would result in increased presystemic clearance and decreased bioavailability.

Our results suggest that there is no exposure–toxicity relationship. However, we cannot rule out the possibility that the present study was insufficiently powered to identify such a relationship. In addition, even when the pharmacokinetic exposure in the plasma is the same, there might still be differences in pharmacodynamic response between patients. Therefore, the lack of an exposure–toxicity relationship needs to be interpreted carefully and may not be extrapolated.

In conclusion, in the present study we attempted to describe the time course of the time-dependent pharmacokinetics of vatalanib. A stable, predictive population PK model for vatalanib in adults with MDS, which fitted our data and accounted for clearance autoindution, was established for the first time. The mean apparent vatalanib oral clearance increased by 125% after 7 days of therapy, resulting in a concomitant mean decrease in vatalanib systemic exposure of 58%. None of the defined covariates was found to influence vatalanib pharmacokinetics significantly in the present study. Given our relatively narrow age range and measures of body size (i.e. body surface area, weight, etc), it is not unexpected that there was no significant covariate relationship with vatalanib pharmacokinetics. Additional studies might be needed to evaluate further the covariate effects on vatalanib pharmacokinetics, because this phase II study may not provide adequate power to detect any significant influence of the predefined covariates on vatalanib PK. The results of the present study suggest that no vatalanib dose adjustment needs to be made based on body size, gender or race. However, dose adjustment might be necessary for repeated doses to maintain vatalanib plasma concentration in the therapeutic range owing to decreased exposure caused by autoinduction of vatalanib metabolism. Simulation using our established population PK model can help to predict vatalanib concentrations following different dosage regimens and help guide dosage adjustments. This may be particularly important as additional information on the optimal therapeutic range becomes available. The relatively high intra-individual variability associated with the present model could probably be ameliorated in future studies through inclusion of more extensive sampling during the day 1–7 time period. Inclusion of such samples would probably allow for successful modelling of more complex representations of metabolism induction, including specific effects of such induction on bioavailability, as well as any variability among patients for such effects. Accounting more fully for such effects could, in turn, result in less unexplained within-subject residual error.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: no support from any organization for the submitted work; no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years; no other relationships or activities that could appear to have influenced the submitted work.

The research for CALGB 10105 (Alliance) was supported, in part, by grants from the National Cancer Institute (CA31946) to the Alliance for Clinical Trials in Oncology (Monica M. Bertagnolli, MD, Chair) and to the Alliance Statistics and Data Center (Daniel J. Sargent, PhD, CA33601). The content of this manuscript is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute. XW is supported in part by a University of Iowa Presidential Fellowship. XW and DJM are supported by CA47642; KO and FM are supported by CA33601; PG is supported by CA16450; RAL and MJR are supported by CA41287; AAM and DH are supported by CA03927; LDL is supported by CA04326; and RV is supported by CA77440.

Supporting Information

Additional Supporting Information may be found in the online version of this article at the publisher's web-site:

Figure S1

Vatalanib goodness-of-fit plots. Red dashed lines are smoothing lines. Black continuous lines are lines of identity. Concentrations are natural log transformed

Figure S2

The relationship between steady-state AUC (AUC induced) and toxicity grade is shown. There was no relationship between toxicity grade and steady-state AUC

Table S1

Parameter estimates from adapt and nonmem analysis