Improved prediction of tacrolimus concentrations early after kidney transplantation using theory-based pharmacokinetic modelling

Abstract

Aims

The aim was to develop a theory-based population pharmacokinetic model of tacrolimus in adult kidney transplant recipients and to externally evaluate this model and two previous empirical models.

Methods

Data were obtained from 242 patients with 3100 tacrolimus whole blood concentrations. External evaluation was performed by examining model predictive performance using Bayesian forecasting.

Results

Pharmacokinetic disposition parameters were estimated based on tacrolimus plasma concentrations, predicted from whole blood concentrations, haematocrit and literature values for tacrolimus binding to red blood cells. Disposition parameters were allometrically scaled to fat free mass. Tacrolimus whole blood clearance/bioavailability standardized to haematocrit of 45% and fat free mass of 60 kg was estimated to be 16.1 l h⁻¹ [95% CI 12.6, 18.0 l h⁻¹]. Tacrolimus clearance was 30% higher (95% CI 13, 46%) and bioavailability 18% lower (95% CI 2, 29%) in CYP3A5 expressers compared with non-expressers. An E_max model described decreasing tacrolimus bioavailability with increasing prednisolone dose. The theory-based model was superior to the empirical models during external evaluation displaying a median prediction error of −1.2% (95% CI −3.0, 0.1%). Based on simulation, Bayesian forecasting led to 65% (95% CI 62, 68%) of patients achieving a tacrolimus average steady-state concentration within a suggested acceptable range.

Conclusion

A theory-based population pharmacokinetic model was superior to two empirical models for prediction of tacrolimus concentrations and seemed suitable for Bayesian prediction of tacrolimus doses early after kidney transplantation.

What is Already Known about this Subject —

• Several population models have been developed to characterize the pharmacokinetics of tacrolimus following kidney transplantation and to identify covariates for individual dose selection.

• The published models generally used empirical approaches to covariate identification, and external evaluations have not supported the models for initial dosing or Bayesian dose predictions early after kidney transplantation.

What this Study Adds —

• A population pharmacokinetic model for tacrolimus was developed based on theoretically expected relationships between tacrolimus whole blood concentrations and haematocrit, fat free mass, CYP3A5 genotype and prednisolone dose.

• The model was externally evaluated and appears suitable to aid in prediction of initial and Bayesian revised tacrolimus doses to improve achievement of a tacrolimus target concentration early after kidney transplantation.

Introduction

Tacrolimus is an immunosuppressive agent widely used following kidney transplantation. Tacrolimus has a narrow therapeutic index and displays large pharmacokinetic variability 1. Individualizing the tacrolimus dosage regimen to optimize the therapeutic effect and minimize adverse effects is essential 2. The dose required to achieve targeted whole blood concentrations of tacrolimus varies considerably between patients, as well as with time after transplantation 1,3. Two distinct challenges exist for individualizing tacrolimus dosing in transplant recipients: Predicting the initial dose of tacrolimus prior to any known concentration–time data on a particular patient and adjusting the doses over time after transplantation.

Information needed for dosage individualization can be obtained through population pharmacokinetic modelling 4. An appropriate population pharmacokinetic model can be used to assist in predicting the optimal initial dose, prior to any available concentration–time measurements, based on population standard values and identified covariates. Furthermore, a population pharmacokinetic model can be used to assist with dosage adjustments by using Bayesian revised dosage predictions based on known concentration–time data in each individual 5. Numerous population pharmacokinetic models have been developed to characterize the pharmacokinetics of tacrolimus in adult kidney transplant recipients 6–16. However, the suggested covariates and their functional forms in the models are inconsistent between studies, leading to uncertainty as to which covariates are clinically important and how tacrolimus dosage should be adjusted with different covariate values. Passey et al. 10 proposed a model for initial dosing that was found to be imprecise during external evaluation 17,18. Models externally evaluated for Bayesian dose adjustments have been found imprecise in the first weeks post-transplant 19,20. Six of the available models were evaluated for their ability to predict the tacrolimus area under the concentration–time curve in independent patients and were found unacceptably imprecise unless at least two individual concentrations within the dosing interval were known 21. The available models to date have identified covariates mainly through empirical investigation.

Combining data from multiple studies to increase the number of subjects for population pharmacokinetic modelling may improve our ability to detect reliable and clinically useful covariate influences 22. Furthermore, including covariate effects based on theoretical mechanisms rather than empirically identifying relationships should lead to more consistent results. Mechanism- or theory-based covariate selection differs from empirical covariate selection in that it allows incorporation of relationships linking the parameters and covariates based on a fundamental understanding of pharmacokinetic processes rather than on the available data alone. Such models are expected to improve predictive performance in patients independent of the model building dataset 23.

In this study, we combined data from two previous studies, which independently developed population pharmacokinetic models of tacrolimus in adult kidney transplant recipients in Australia 6 and Norway 7. The primary aim of this study was to use the combined data to develop a new population pharmacokinetic model using a theory-based approach to covariate inclusion in contrast to the empirical approaches in the previous studies. The secondary aim was to evaluate the predictive performance of the theory-based model and the previous models in an independent patient cohort during the first 21 days post-transplant.

Methods

Patients and dataset combination

Data were combined from two previous population pharmacokinetic analyses, involving 242 adult kidney transplant recipients. Of these, 173 subjects were from the Princess Alexandra Hospital in Brisbane, Australia 6 and 69 subjects were from Oslo University Hospital Rikshospitalet in Oslo, Norway 7. A total of 3100 whole blood tacrolimus concentration–time points were available for model development: 791 (26%) were obtained as part of full pharmacokinetic profiling (>eight concentrations per dosing occasion), 1277 (41%) were obtained as part of limited pharmacokinetic profiling (four–five concentrations per dosing occasion) and 1032 (33%) represented trough concentrations measured as part of routine clinical practice (one concentration per dosing occasion). Data were predominantly from the first 3 months post-transplant (median 20 days, range 4 days to 15 years). There was a median of eight tacrolimus concentrations per patient (ranging from 4 to 52).

For the external model evaluation dataset, tacrolimus trough concentration–time points from the first 3 weeks post-transplant were obtained from 72 patients who underwent kidney transplantation at Oslo University Hospital Rikshospitalet in 2011/2012. A total of 837 tacrolimus measurements were collected retrospectively from patient medical records. The exact time of drug intake was not known, and it was assumed that doses were taken every 12 h with trough concentrations measured immediately pre-dose. Patients were excluded if they received multiple organ transplants, received grapefruit juice or if required covariate data were missing.

Demographic, clinical and pharmacogenetic characteristics of the participants involved in model development and external evaluation are shown in Table 1. Collection and analysis of data in Brisbane was approved by the Princess Alexandra Hospital and University of Queensland Ethics Committees and in Oslo by the Norwegian Regional Committee for Medical Research Ethics. All participants gave written informed consent.

Table 1.

Demographic, clinical and pharmacogenetic characteristics of participants

	Model development				External evaluation
	Number	Mean	Median	95% observation interval	Number	Mean	Median	95% observation interval
Patients (Oslo / Brisbane)	69 / 173				72 / 0
Sex (Male / Female)	165 / 77				50 / 22
CYP3A5 genotype (*1/*1, *1/*3, *3/*3)*	3 / 33 / 205				0 / 14 / 58
Age (years)		48	48	23–71		53	56	26–74
Height (cm)		173	175	152–193		175	175	159–192
Total body weight (kg)		82	80	51–121		77	77	50–99
Predicted fat free mass (kg)		57	59	35–80		56	59	35–71
Haematocrit (%)†		33	33	25–43		33	33	27–43
Serum albumin (g l−1)†		36	36	24–45		–	–	–
Total serum bilirubin (μmol l−1)†		11	10	4–21		–	–	–
Aspartate aminotransferase (IU l−1)†		23	20	9–53		–	–	–
Alanine aminostransferase (IU l−1)†		33	26	11–91		–	–	–
Alkaline phosphatase (IU l−1)†		72	64	35–149		–	–	–
Prednisolone dose (mg day−1)		21	20	5–36		20	20	15–31
Sampling time (days post-transplant)†		267	20	5–2591		11	11	9–13
Total tacrolimus samples (Oslo / Brisbane)	3100 (1546 / 1554)				837 (837 / 0)
Tacrolimus samples per patient (Oslo / Brisbane)		13 (22 / 8)	8 (24 / 8)	4–40 (8–40 / 4–16)		12	12	9–15
Tacrolimus dose (mg twice daily)† (Oslo / Brisbane)		5.8 (3.0 / 6.9)	6.0 (3.0 / 7.0)	1.0–10.0 (1.0–6.0 / 1.5–10.0)		3.0	3.0	1.8–5.0
Tacrolimus concentration (μg l−1)‡ (Oslo / Brisbane)		11.0 (7.0 / 15.0)	8.4 (6.1 / 13.1)	2.9–31.0 (2.5–16.6 / 4.2–35.9)		5.3	4.9	2.2–10.2

Brisbane, Brisbane dataset; CYP3A5, cytochrome P450 3A5; Oslo, Oslo dataset.

^*Frequency of CYP3A5 genotype was in Hardy–Weinberg equilibrium (Table S1). CYP3A5 genotype was established for all patients except one who was assigned to the most frequent genotype.

^†Calculated from average within each patient.

^‡Concentrations converted to liquid chromatography-tandem mass spectrometry equivalents if measured with immunoassay, see main text.

Immunosuppressive drugs

Patients received immunosuppressive therapy according to local clinical protocols. All subjects received oral tacrolimus from the day of surgery. Tacrolimus was started at a dose of 0.075 mg kg⁻¹ twice daily (Prograf®, Janssen-Cilag, MacQuarie Park, Australia) in Brisbane and 0.04 mg kg⁻¹ twice daily (Prograf®, Astellas Pharma, Dublin, Ireland) in Oslo. Subsequent tacrolimus doses were generally adjusted to achieve whole blood trough concentrations of 7–8 μg l⁻¹ in Brisbane and 3–7 μg l⁻¹ in Oslo during the first 3 months post-transplant (in selected patients who were considered to be at increased risk of organ rejection, the target concentration was adjusted up to a maximum of 12 μg l⁻¹ according to local protocols). At both centres, induction therapy generally consisted of high dose intravenous methylprednisolone (250 or 500 mg) and intravenous basiliximab (20 mg on the day of transplant and on the fourth day post-transplant). The maintenance immunosuppressive regimen included tacrolimus as described, fixed dose oral mycophenolate mofetil (1 g twice daily in Brisbane and 0.75 g twice daily in Oslo) and oral prednisolone, initiated at a dose of 0.3 mg kg⁻¹ ideal body weight daily (maximum 30 mg daily) in Brisbane and 20 mg daily (up to 80 mg in selected patients) in Oslo. Prednisolone dosage was tapered with time after transplantation as outlined previously 6,7.

Tacrolimus measurement and assay conversion

In the Brisbane dataset, all tacrolimus concentration measurements were made using liquid chromatography-tandem mass spectrometry assay (LC-MS/MS) 24. In the Oslo dataset, 80% of concentrations were measured with chemiluminescent microparticle immunoassay (CMIA, analyzed on the Architect® instrument, Abbott Laboratories, Abbott Park, IL 25), 11% with LC-MS/MS 26 and 9% with microparticle enzyme immunoassay (MEIA, analyzed on the IMx® instrument, Abbott Laboratories 27). In the external evaluation dataset, all concentrations were measured with CMIA. Concentrations (C) measured with CMIA and MEIA were converted to corresponding LC-MS/MS equivalents using an equation derived from linear regression as described previously (Equation 1) 7:

(1)

The LC-MS/MS assay used in Brisbane was linear over the range between 0.5 to 50 μg l⁻¹. The imprecision coefficient of variation (CV) was 5%. The LC-MS/MS assay used in Oslo had a lower limit of quantification (LLOQ) of 1.1 μg l⁻¹ and a CV of 5.2%. The CMIA had a LLOQ of 1.0 μg l⁻¹ and CVs of 9% at 2.3 μg l⁻¹ and 6% at 7.0 μg l⁻¹. The MEIA had a LLOQ of 3.0 μg l⁻¹ and CVs of 13% at 5 μg l⁻¹ and 7% at 23 μg l⁻¹.

CYP3A5 genotyping

To determine the cytochrome P450 3A5 (CYP3A5) genotype (rs776746; NG_007938.1:g.12083G>A) in subjects included for external evaluation, DNA was extracted from EDTA anti-coagulated whole blood by the MagNA Pure instrument (Roche Applied Science, Penzberg Germany), and genotyping performed by real-time polymerase chain reaction and melt curve analysis with hybridization probes on the LightCycler® 480 instrument (Roche Applied Science, Penzberg, Germany). The methods used to determine CYP3A5 genotype in subjects in the model building datasets have been described previously 6,7. Deviation from Hardy–Weinberg equilibrium was examined using Pearson’s χ²-test.

Population pharmacokinetic modelling

Population pharmacokinetic modelling was performed using the first order conditional estimation method with interaction (FOCE-I) in NONMEM 28 with the aid of Wings for NONMEM 29 for executing model runs, bootstrapping and results management. Statistical and graphical analyses were performed using R 30.

A two compartment model with first order absorption and a lag time was used to describe the pharmacokinetics of tacrolimus 1,6,7,14,15. Although whole blood concentrations were measured the model was parameterized in terms of plasma concentration based disposition parameters (see below for theory). Parameters estimated included tacrolimus apparent clearance (CL_p/F), apparent central volume of distribution (V1_p/F), apparent intercompartmental clearance (Q_p/F), apparent peripheral volume of distribution (V2_p/F), absorption rate constant (k_a), absorption lag time (t_lag) and bioavailability (F) relative to a population standard value defined as 1. Between subject variability (BSV) and between occasion variability (BOV) were estimated for all parameters, except t_lag, and were assumed to be log normally distributed. Proportional and combined proportional and additive structures were tested to describe the residual unexplained variability.

Theory-based and empirical covariate modelling

The following factors were evaluated as covariates: patient body size (total body weight, fat free mass, normal fat mass), age, sex and CYP3A5 genotype, prednisolone dose, time after transplantation, haematocrit, serum creatinine, aspartate aminotransferase, alanine aminotransferase, serum bilirubin, serum albumin and alkaline phosphatase. Covariates were preferably included based on known theoretical relationships as described below or investigated empirically through linear, piecewise linear, sigmoid or power functions. Binary covariates were evaluated by estimating the parameter fractional change in one group compared with the other.

Pharmacokinetic disposition parameters were related to body size based on allometric scaling theory (Equation 2) 31:

(2)

where P is the pharmacokinetic parameter, P_std is the standard parameter for a patient with standard size (SIZE_std), SIZE is the allometric size descriptor that gives the best fit with the allometric exponent b, fixed to theory-based values of ¾ for clearances and 1 for volumes of distribution. The theory-based exponents for clearance and volume have been confirmed experimentally with a large data set spanning a wide range of sizes 32. Body size was based on fat free mass predicted from total body weight, height and sex 33. To evaluate the effects of body composition, all pharmacokinetic disposition parameters were related to fat free mass and then any additional contribution of fat mass was estimated 34.

Tacrolimus exhibits extensive distribution into red blood cells, showing a haematocrit- and concentration-dependent whole blood to plasma ratio ranging from 4 to 114 1. Pharmacokinetic disposition parameters were estimated from the model-predicted plasma concentrations (C_p) rather than measured whole blood concentrations (C_wb) under the assumption that disposition is determined by unbound drug concentration, and that C_p is proportional to unbound concentration (assuming no saturation of plasma proteins). C_wb was related to C_p and haematocrit expressed as a fraction (f_HCT) (Equation 3).

(3)

where B_max is the maximum binding concentration expressed per volume of erythrocytes and K_D is the equilibrium dissociation constant. Values for these parameters were obtained from the literature (B_max = 418 μg l⁻¹ erythrocytes, K_D = 3.8 μg l⁻¹ plasma) 35.

Corticosteroids are known inducers of CYP3A enzymes and P-glycoprotein in the small intestine and/or liver 36, theoretically leading to altered tacrolimus F and/or CL_p. We tested different approaches to describe an effect of prednisolone induction on tacrolimus pharmacokinetics. In one approach (Equation 4), the pharmacokinetic parameter (P) of interest (i.e. F or CL_p) was modelled as a function of the prednisolone dose (Pred) and the standard parameter (P_std) for a patient not receiving prednisolone. The term Ind in Equation 4 represents the induction function relating P to Pred by either a linear (Equation 5) or a non-linear (Equation 6) function. In an alternative approach, P was related to the model-predicted CYP3A4 amount (Equation 7). The time course of CYP3A4 amount relative to a nominal baseline was modelled using a turnover model (Equation 8), assuming an inducible zero-order production rate (R_in) and a first order turnover rate (k_out × CYP3A4) 37. The turnover rate constant k_out was fixed using a turnover half-life of CYP3A4 obtained from the literature (70 h) 38.

(4)

(5)

(6)

(7)

(8)

In Equations 5 and 6, Pred is the prednisolone dose in mg assumed to be proportional to the average unbound prednisolone concentration responsible for induction, Slope is a linear parameter for the effect of prednisolone dose, Pred_max is the maximum change in P, Pred₅₀ is the prednisolone dose causing half maximum induction and Hill is the sigmoid shape coefficient. In addition, the influence of methylprednisolone single dose administration on CL_p and F was evaluated as a binary covariate (received vs. not received) because of the small range of distinct doses used.

Model selection was guided primarily by theory and biological plausibility, parameter imprecision obtained from non-parametric bootstrap 39 (100 replicates during model development and 500 replicates for the final model) and prediction-corrected visual predictive checks (pcVPCs) 40. Change in objective function value (ΔOFV) was calculated to assess the statistical significance of each covariate and to differentiate between theoretically equivalent models 28. However, statistical significance was not an absolute requirement for including a covariate if it had a clear pharmacological or biological basis and if pcVPCs were improved. In agreement with the modelling strategy, covariates that led to a statistical decrease in OFV without a known biological basis were not included in the model.

Model evaluation

The final theory-based model and the two previous empirical models were externally evaluated by examining their predictive performance using a Bayesian forecasting procedure. The first measured tacrolimus concentration after transplantation for each patient in the independent cohort was predicted based on the actual given dose, population pharmacokinetic standard values and covariates. The second measured tacrolimus concentration after transplantation for each patient was predicted based on continued dosing information, updated covariate values and revised individual pharmacokinetic parameters estimated from balancing population standard values and feedback from the first measured concentration. The n + 1^th measured concentration was predicted as described for the second concentration, but by using information from the first to n^th concentrations. For parameters with an estimated value of BOV, occasion-specific parameters from the last known occasion were used for prediction of the next concentration.

The ability of each model to predict the next tacrolimus concentration was assessed by calculating the median percentage prediction error (MPE%, measure of bias and imprecision) 41 as follows, where Conc_pred is the model-predicted concentration and Conc_obs is the observed concentration (Equation 9):

(9)

To compare prediction error at different time points after transplantation, eleven time bins were defined, including day 1, 2–3, 4–5, 6–7 and so on to day 20–21 post-transplant. If an individual contributed more than one concentration to a single bin, the prediction error was initially averaged for the individual to prevent undue individual influence. The 95% confidence intervals (CI) of the MPE% were generated from the 2.5^th to 97.5^th percentile of the medians in 10 000 non-parametric bootstrap replicate datasets.

In order to evaluate the previously developed population models, some model modifications needed to be made. One of the identified covariates in the Brisbane model (unbound prednisolone concentration on apparent central volume of distribution (V1/F)) was removed because this information was not available in the external evaluation group. The Brisbane model was then rerun to obtain parameters estimates without the prednisolone covariate effect (ΔOFV +16.7, estimated typical value of V1/F decreased from 107 l to 98 l, BSV in V1/F increased from 46% to 69% and BOV in V1/F increased from 114% to 121%). In the Oslo model, parameter estimates were originally based on immunoassay concentrations, and the model was therefore rerun to obtain parameter estimates based on LC-MS/MS-equivalent concentrations as described in Equation 1.

Evaluation of dosing strategies

Three dosing strategies were evaluated by simulating the concentration-time profiles of 1000 subjects during the first five days post-transplant with covariate values sampled from the original dataset. For each simulated subject, doses were based on (i) total body weight (0.04 mg kg⁻¹ 12 h^–1), (ii) typical population pharmacokinetic parameter values and covariates in the final population model and (iii) as (ii), but with BSV tapered to zero over the first 5 days without a change in BOV. Dosing strategy (iii) was designed to imitate the effect of Bayesian dose adaptation on prediction of individual parameters.

Calculation of model-based doses required a target concentration to aim for (Appendix S1). A likely appropriate target concentration was obtained from a recent study involving 150 kidney transplant recipients. This study reported that an average tacrolimus 12 h area under the concentration–time curve (AUC(0,12 h)) of 124 μg l⁻¹ h was achieved when tacrolimus trough concentrations of 3–7 μg l⁻¹ were targeted in the first 3 months post-transplant 3. This AUC(0,12 h) corresponds to an average concentration (C_ave = AUC(0,12 h)/12 h) of 10.4 μg l⁻¹. Patient haematocrit values were not reported in the aforementioned study, but assuming they were similar to the average in our study (33%), the corresponding concentration standardized to a haematocrit of 45% (Cstd_HCT45) would be 14.2 μg l⁻¹ (10.4 × 45%/33% 7, Figure S1). A range of 80% to 125% around the target concentration was considered to be safe and effective 42, giving an acceptable range of 11.4 μg l⁻¹ to 17.8 μg l⁻¹. The average steady-state Cstd_HCT45 for each simulated subject was predicted from individual whole blood apparent clearance standardized to a haematocrit of 45% (CL_{wb, HCT45}/F) and the tacrolimus dose on day 5 (Dose × F/CL_{wb, HCT45} × 12 h). For each dosing strategy, the percentage of average steady-state Cstd_HCT45 within the suggested acceptable range was calculated.

Results

Population pharmacokinetic modelling

A two compartment model with first order absorption and a lag time described the data adequately. The following random effects parameters were removed from the full model because their bootstrap 2.5^th percentile approached zero (<0.1%): BSV in k_a, BSV in V2_p/F, BOV in the disposition parameters and the additive residual error term. BOV associated with F (ΔOFV −606, P < 0.001) and k_a (ΔOFV −209, P < 0.001) were estimated. The final model parameter estimates and bootstrap results for the theory-based model are shown in Table 2.

Table 2.

Parameter estimates and bootstrap results for the theory-based population model

Parameter	Final model estimate*	Mean bootstrap estimate	RSE %	Bootstrap 95% CI†
CLwb/F (l h−1) (HCT 45%, FFM 60 kg)	16.1	15.7	10%	12.6, 18.0
V1wb/F (l) (HCT 45%, FFM 60 kg)	125	122	11%	95.8, 145
Qwb/F (l h−1) (HCT 45%, FFM 60 kg)	23.8	23.2	13%	17.4, 28.9
V2wb/F (l) (HCT 45%, FFM 60 kg)	636	623	16%	453, 834
ka (h−1)	1.01	1.03	9%	0.87, 1.22
tlag (h)	0.41	0.41	3%	0.39, 0.44
Covariates effects on clearance
CYP3A5 expresser‡ (factor)	1.30	1.29	7%	1.13, 1.46
Covariates effects on bioavailability (F)
CYP3A5 expresser‡ (factor)	0.82	0.83	8%	0.71, 0.98
Time, early
Fday 2 (factor)	2.68	2.69	8%	2.28, 3.09
Prednisolone dose
Predmax (%)	−67	−66	19%	−41, −89
Pred50 (mg)	35	33	40%	7, 50
Between subject variability
CLwb/F (CV %)	40	40	7%	35, 46
V1wb/F (CV %)	54	53	11%	42, 64
Qwb/F (CV %)	63	64	13%	46, 81
Fday2 (CV %)	57	57	14%	42, 71
Correlations
CLwb/F ∼ V1wb/F	0.43	0.41	23%	0.21, 0.59
CLwb/F ∼ Qwb/F	0.62	0.66	18%	0.40, 0.87
Between occasion variability
F (CV %)	23	22	7%	20, 25
ka (CV %)	120	122	7%	107, 140
Residual error
Proportional error (%)	14.9	14.9	4%	13.6, 16.3

CI, confidence interval; CL_wb/F, apparent whole blood clearance; CV, coefficient of variation; CYP3A5, cytochrome P450 3A5; F_day2, the increase in F the day after transplantation; FFM, fat free mass; HCT, haematocrit; k_a, absorption rate constant; Pred_max, maximum change in F with increasing prednisolone dose; Pred₅₀, the prednisolone dose with half maximum effect on F; Q/F_wb, apparent whole blood intercompartmental clearance; RSE, relative standard error; t_lag, absorption lag time; V1/F_wb, apparent whole blood central volume of distribution; V2/F_wb, apparent whole blood peripheral volume of distribution.

^*Standardized to CYP3A5 non-expresser with haematocrit of 45% and fat free mass of 60 kg not receiving prednisolone.

^†95% confidence interval generated from the 2.5^th to 97.5^th percentiles obtained from 500 non-parametric bootstraps replicates.

^‡CYP3A5 expressers included patients expressing one or two ^*1 alleles. The disposition parameters are presented standardized to a haematocrit of 45%, generated by dividing the plasma concentration based parameters in the model by the expected blood:plasma concentration ratio at a haematocrit of 45%. The original model was as follows:

CL_p/F = 811 × (FFM/60)^3/4 × 1.30 (If CYP3A5 expresser) l h⁻¹

V1_p/F = 6290 × FFM/60 l

Q_p/F = 1200 × (FFM/60) l h⁻¹

V2_p/F = 32100 × FFM/60 l

F = 1 × [1 – (0.67 × Prednisolone dose)/(35 mg + Prednisolone dose)] × 2.68 (If first day post-transplant) × 0.82 (If CYP3A5 expresser)

C_rbc = f_HCT × C_p × 418/(3.8 + C_p)

C_wb = C_p + C_rbc,

where CL_p/F is the apparent plasma clearance, V1_p/F is the apparent plasma central volume of distribution, Q_p/F is the apparent plasma intercompartmental clearance, V2_p/F is the apparent plasma peripheral volume of distribution, FFM is the fat free mass, F is the bioavailability relative to 1, C_rbc is the tacrolimus concentration in red blood cells, C_p is the tacrolimus plasma concentration, C_wb is the tacrolimus whole blood concentration and f_HCT is the haematocrit fraction.

The influence of patient body size on the disposition of tacrolimus was best described by allometric scaling based on fat free mass rather than total body weight for all the pharmacokinetic disposition parameters. An additional effect of fat mass was not identified (bootstrap averages of the fat contribution parameters were 0.01 [95% CI −0.35, 0.44] for apparent clearances (CL_p/F and Q_p/F) and −0.12 [95% CI −0.55, 0.45] for apparent volumes of distribution (V1_p/F and V2_p/F).

A model that accounted for differences in tacrolimus whole blood concentrations due to haematocrit variation via estimation of C_p was superior to one that estimated tacrolimus pharmacokinetic parameters based on whole blood concentrations alone (ΔOFV −106, P < 0.001).

A sigmoid E_max model describing an effect of prednisolone dose on F (Equations 4 and 6) reduced the OFV by −35.1 points (P < 0.001) and was superior to a linear model (ΔOFV −12.7, Equation 5) and a turnover model (ΔOFV −2.1, Equations 7 and 8). A model with the effect on F was slightly better than a model with the equivalent effect on CL_p (ΔOFV −28.0). The maximum reduction in F (Pred_max) caused by use of prednisolone was estimated to be −67% (95% CI −41%, −89%), and the prednisolone daily dose exerting half maximum effect (Pred₅₀) was estimated to be 35 mg (95% CI 7 mg, 50 mg). The Hill coefficient in Equation 6 was not significantly different from 1 (95% CI 0.97, 6.95) and the function was therefore simplified to an E_max model (Hill = 1, ΔOFV +1.5).

Because of the low number of CYP3A5 *1/*1 carriers in the dataset (n = 3), these subjects were grouped with CYP3A5 *1/*3 carriers (n = 33) during covariate analysis. CL_p was estimated to be 30% higher (ΔOFV −46.0, P < 0.001) and F 18% lower (ΔOFV −2.9, P = 0.09) in this group compared with patients not expressing functional CYP3A5 enzyme (*3/*3 carriers). Although an independent effect on F in addition to the effect on CL_p was not statistically supported at the significance level of 0.05 during covariate inclusion, effects on both parameters were retained because both CL_p and F should theoretically be altered in patients with functional CYP3A5 enzyme in their liver and intestines 43.

F was estimated to be 2.68 (95% CI 2.28, 3.09) times higher on the first day after transplantation (ΔOFV −209, P < 0.001) compared with any other time, an effect that could not be attributed to any of the measured covariates. This effect was retained in the model due to the large decrease in OFV, despite lack of a clear theoretical basis. Allowing BSV in the effect of the first day after transplantation improved the model further (ΔOFV −19.9, P < 0.001).

In addition to these covariate effects, F was found to significantly increase with age (F increasing by 1.4% per year in patients >45 years, ΔOFV −21.8, P < 0.001). However, age was not included in the final model due to the empirical nature of this covariate. No relationships were identified between tacrolimus pharmacokinetics and patient sex or biochemical measurements. The parameter estimates of the final model were close to bootstrap averages and were precisely estimated (relative standard error < 25%) except for Pred₅₀ (relative standard error 40%). In the final model, all retained covariates caused a significant increase of the OFV upon removal, including CYP3A5 genotype on F (ΔOFV +3.9, P = 0.046).

Model evaluation

Figure 1 shows pcVPCs of the Brisbane, Oslo and final theory-based model. The 5^th, 50^th and 95^th percentiles of the observations were within the 95% CI of the corresponding prediction percentiles for the theory-based model only. PcVPCs also indicated that the theory-based model described the trend in observed tacrolimus concentrations over the range of covariates (fat free mass, haematocrit, prednisolone dose) as well as over time after transplantation (Figure 2).

Figure 1.

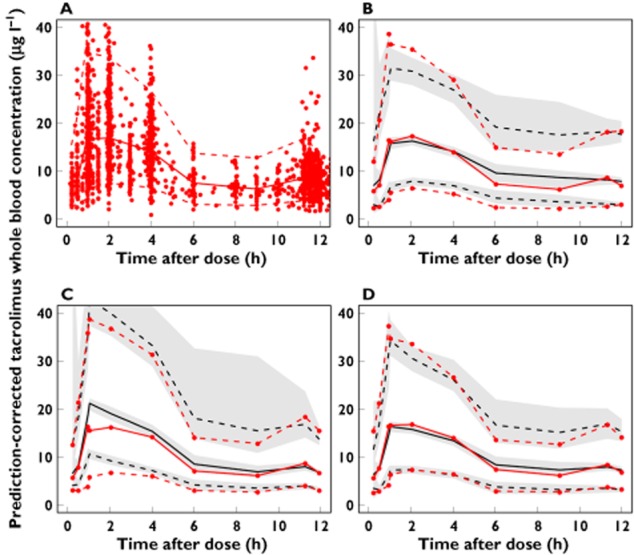
(A) Observed tacrolimus concentrations (n = 3100) in 242 patients (prediction-corrected). Prediction-corrected visual predictive checks using (B) the Brisbane model, (C) the Oslo model and (D) the theory-based model. Red solid line median observed concentration; red dashed lines 5^th and 95^th percentiles of the observed concentrations; black solid line median predicted concentration in 100 simulated subsets of total dataset; black dashed lines 5^th to 95^th percentiles of the predicted concentrations. Grey-shaded areas represent 95% confidence intervals of the prediction percentiles

Figure 2.

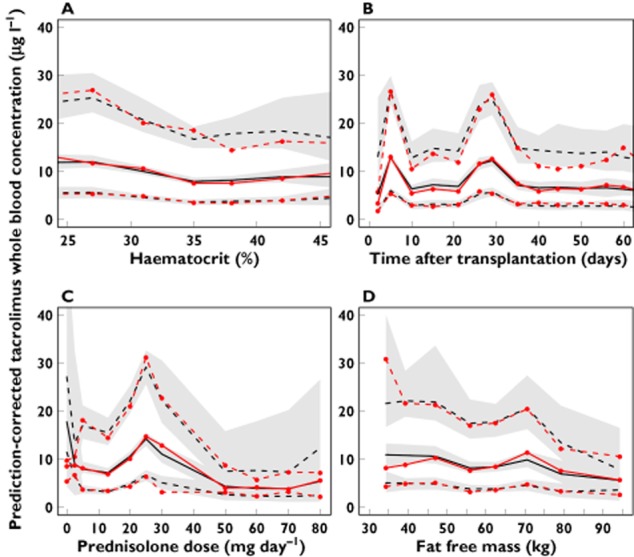
Prediction-corrected visual predictive check of tacrolimus concentrations using the theory-based model, shown over the range of the covariates; (A) haematocrit, (B) time after transplantation, (C) prednisolone dose and (D) fat free mass. Red solid line median observed concentration; red dashed lines 5^th and 95^th percentiles of the observed concentrations; black solid line median predicted concentration in 100 simulated subsets of total dataset; black dashed lines 5^th to 95^th percentiles of the predicted concentrations. Grey-shaded areas represent 95% confidence intervals of the prediction percentiles

Table 3 summarizes the MPE% of the entire external evaluation dataset for each model. All models were overall unbiased (95% CIs of the MPE% included zero). The MPE% and the 90% prediction error intervals in each time bin are shown in Figure 3. Whereas all three models under-predicted the first concentration (measured on the first day after transplantation), the under-prediction was larger for the empirical Brisbane (−66%, 95% CI −72%, −58%) and Oslo models (−40%, 95% CI −46%, −23%) than the theory-based model (−12.6%, 95% CI −26%, 8.0%). The theory-based model was superior in predicting concentrations measured throughout the first 14 days post-transplant, with MPE%s consistently closer to zero and with narrower prediction error intervals than the two empirical models. After day 14, the models showed equal predictive performance.

Table 3.

Median prediction errors and 90% prediction error intervals for each model summarized over all the 837 predictions the first 21 days post-transplant

	Prediction error
Model	Median (%) (95% CI)	5th percentile (%) (95% CI)	95th percentile (%) (95% CI)
Empirical model (Oslo)	+1.6 (−1.2, 3.7)	−44 (−47, −36)	+57 (51, 67)
Empirical model (Brisbane)	+1.3 (−0.7, 3.8)	−57 (−66, −44)	+73 (62, 79)
Theory-based model	−1.2 (−3.0, 0.1)	−38 (−42, −32)	+47 (42, 53)

CI, confidence interval.

Figure 3.

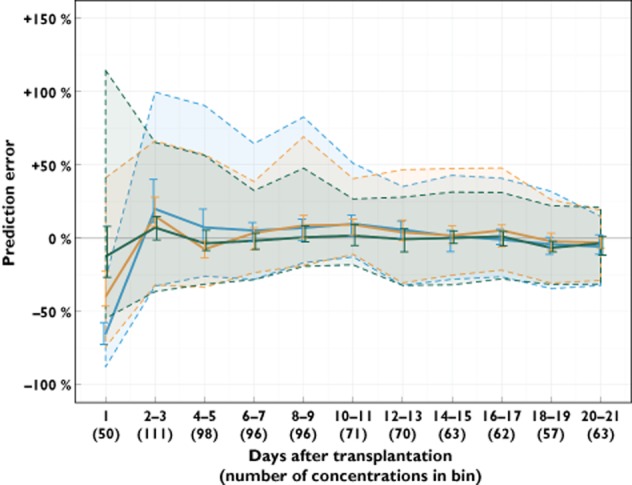
Prediction error of the tacrolimus concentrations in the external evaluation dataset over time after transplantation, using the empirical Brisbane and Oslo models and the combined theory-based model. Time in days after transplantation are binned: The first bin reflects day 1 after transplantation, while the subsequent ten bins are generated from day 2–3, 4–5 and so on until day 20–21. The median prediction error in each bin (solid lines) is shown with 95% confidence interval (vertical lines). The shaded areas represent the interval covering 90% of the individual prediction errors in each bin (5^th to 95^th percentiles). () Brisbane model, () Oslo model, () theory-based model

Evaluation of dosing strategies

Standard weight-based dosing (Strategy i) and covariate-based dosing (Strategy ii) led to 32% (95% CI 29%, 35%) and 37% (95% CI 34%, 40%) of simulated average steady-state concentrations within the suggested acceptable range, respectively (Figure 4A). With Bayesian dose adaptation (Strategy iii), 65% (95% CI 62%, 68%) of simulated average steady-state concentrations were within the suggested acceptable range (Figure 4B).

Figure 4.

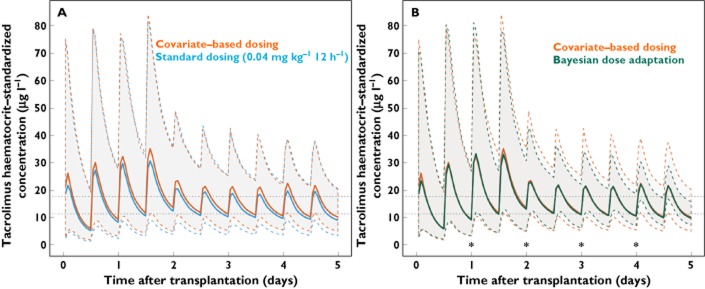
(A) Concentration–time profiles in 1000 simulated individuals using covariate-based dosing (red) and the current standard initial dose regimen in Oslo (0.04 mg kg⁻¹ twice daily, blue). (B) Concentration–time profiles in 1000 simulated individuals using covariate-based dosing (red) and covariate-based dosing with Bayesian dose adaptation (green). All concentrations are standardized to a haematocrit of 45%, and the simulation includes higher bioavailability on the day of transplantation (day 0) and the day after transplantation (day 1). Thick lines median predicted concentration; dashed, coloured lines 5^th to 95^th percentiles of the predicted concentrations; dotted, horizontal lines suggested acceptable range for average steady-state concentration values, standardized to a haematocrit of 45% (11.4 to 17.8 μg l⁻¹); stars times of concentration measurement, Bayesian feedback and reduction in between subject variability

Discussion

Achieving and maintaining desired tacrolimus concentrations in the first weeks after kidney transplantation remains a challenge 44. Although several pharmacokinetic models have been developed for tacrolimus to aid in the prediction of initial and revised doses in kidney transplant recipients, those that have been externally evaluated have generally been found to be imprecise 17,18,20,21 and most are not reported to be in clinical use. The published models included covariate relationships established through empirical investigation. Empirical models without a mechanistic basis are more likely to show poor predictive performance in patients not included in model development 45. To test this expectation, we present a model using mainly theory-based covariate relationships: Allometric scaling to fat free mass, accounting for binding of tacrolimus to red blood cells, altered clearance and bioavailability in CYP3A5 expressers and reduced tacrolimus bioavailability through an inductive effect of prednisolone on CYP3A/P-glycoprotein expression. The model was externally evaluated for its predictive performance and was found superior to two previously published empirical models for prediction of tacrolimus concentrations immediately following kidney transplantation. The theory-based model was developed from a larger dataset, which may also have contributed to the improved predictive performance.

A novel characteristic of our model is that the pharmacokinetic parameters are estimated from implicit plasma concentrations rather than from the measured whole blood concentrations. This approach is appealing because it reduces the confounding effect of haematocrit variability in predicting tacrolimus concentrations 7,46. Tacrolimus plasma clearance/bioavailability (CL_p/F) was estimated to be 811 l h⁻¹ for a CYP3A5 non-expresser with 60 kg fat free mass, which may be compared with previously reported values based on measured plasma concentrations in liver transplant recipients (695 l h⁻¹ 47 and 473 l h⁻¹ 35) for 70 kg total body weight patients. A higher CL_p/F estimate in our study is consistent with previous studies showing that kidney transplant recipients have higher clearance and lower bioavailability of tacrolimus compared with liver transplant recipients 1. The estimated CL_p/F corresponds to a whole blood apparent clearance (CL_wb/F) of 16.1 l h⁻¹ based on a standard haematocrit value of 45%. As expected this is somewhat lower than values previously published for kidney transplant recipients because haematocrit is typically lower than 45% in this population. Based on a haematocrit of 33% (average in the study population), the corresponding CL_wb/F was 21.7 l h⁻¹, comparable with previously published values (ranging from 21 to 38 l h⁻¹ 8–11,13).

On the first day post-transplant, we estimated tacrolimus bioavailability to be nearly three times higher than on any subsequent time. This observation may be related to the methylprednisolone bolus given to all patients during surgery, as methylprednisolone may inhibit CYP3A/P-glycoprotein, decreasing the presystemic metabolism and efflux of tacrolimus 36. However, a similar bioavailability increase was not seen in seven patients in this study who received methylprednisolone later after transplantation for treatment of acute rejection. Other events that may theoretically increase tacrolimus bioavailability post-operatively include surgery-related inflammation, anaesthesia or opioids affecting gut motility and/or reduced food intake 48. Although we could not establish a single theoretical explanation, accounting for this observation when using the first measured concentration as feedback for dose revision was important. A model that ignored this factor during external evaluation significantly underpredicted the tacrolimus concentrations measured on the first day post-transplant and overpredicted the subsequent revised concentration. We present this as an empirical association to stimulate further exploration for a mechanistic explanation of factors affecting bioavailability around the time of transplantation.

Several reports have described time-dependent changes in tacrolimus pharmacokinetics 3,12,15. The empirical models evaluated in this study used ‘time after transplantation’ as an independent covariate on CL_wb or F. However, subsequent to the initial prediction during external evaluation, both empirical models tended to overpredict tacrolimus concentrations until day 14, indicating that the empirical use of ‘time after transplantation’ as a covariate does not extrapolate well to new patients. In contrast, our theory-based model incorporated haematocrit and prednisolone dose, two factors known to change systematically with time post-transplant, and appeared to perform well in new patients. In addition, the pcVPCs indicated that the theory-based model performed well over the range of different covariates (Figure 2). A pattern of increasing tacrolimus whole blood concentration predictions with increasing haematocrit was however not seen in the pcVPC (Figure 2A). This is likely to be due to the design differences in the Brisbane and Oslo study. The subjects transplanted in Brisbane were sampled more frequently during the early post-transplant week when haematocrit tends to be low 6. Moreover, these subjects were sampled mainly during the first 4 h after dose. Thus, the observed and predicted concentrations at the lower end of the haematocrit range are over-represented by concentrations measured close to the peak. In contrast, the concentrations in the Oslo data were mainly trough concentrations, and the influence of haematocrit increases would therefore have been masked by the early Brisbane observation design. The corresponding pcVPCs stratified by centre show an increase in whole blood concentration as a function of haematocrit in the Oslo data (Figure S2).

A more complex covariate-based initial dosing strategy only slightly improved achievement of concentrations within the suggested acceptable range (37%) compared with simpler, weight-based dosing (32%) (Figure 4A). Bayesian dose adaptation would be expected to improve target achievement further, and did so (65%). However, BOV ultimately determines the percentage of concentrations that can be expected to lie within an acceptable range even when the optimal individual dose is used. We estimated BOV in bioavailability to be 23%, similar to the estimate of 22% in a previous study 16. To devise a dosing regimen that achieves at least 90% of concentrations within an 80–125% range, variability in BOV needs to be 13.6% or less 42. BOV in bioavailability estimated in this study is clearly too large for this to be achieved. Based on estimated BOV, 65% of tacrolimus concentrations will in theory lie within an 80–125% range. This is consistent with the 65% value calculated during the Bayesian dose adaptation simulation.

During external evaluation of the theory-based model, the 90% prediction error interval remained stable between −18 to −32% and +22 to +32% at time points subsequent to day 7 post-transplant (Figure 3), a persistent error likely to be mostly due to BOV in bioavailability. The error was however somewhat smaller than what would be expected from the estimated BOV. This might be because each concentration was predicted using the occasion-specific individual parameters updated from the previous occasion, indicating that the bioavailability is likely to vary less between two consecutive dosing occasions within a patient. There is currently a general interest in establishing genetic variables that may further characterize pharmacokinetic variability associated with tacrolimus therapy 17,43,49. While genetic information may be useful in improving prediction of initial doses, it can only help to explain BSV, which is also readily accounted for by feedback from measured concentrations. Future studies should aim to understand and predict BOV associated with tacrolimus oral bioavailability.

A limitation of our study was that the external evaluation dataset consisted only of retrospectively observed trough concentrations. Individual pharmacokinetic parameter values estimated from trough concentrations alone will likely shrink towards population mean values 50, reducing the ability to identify patients with pharmacokinetic parameters that deviate greatly from standard values. Taking a second sample within the dosing interval should improve individual parameter estimation and subsequent dosing prediction. Another limitation was that the exact time of dose administration relative to the time of drug concentration measurement was not known. Trough concentrations collected from the patient medical records were assumed to be measured 12 h after dose, but may have been measured after intake of the subsequent morning dose in some cases. Moreover, there was no way to confirm whether the patients were adherent to their prescribed dosage regimen. Tacrolimus concentrations were measured using multiple analytical methods. Converting immunoassay concentrations to corresponding LC-MS/MS values may have introduced uncertainty into the analysis.

The theory-based model included concentration-dependent binding of tacrolimus to erythrocytes. Removing the non-linear part of the current model (i.e. reducing Equation 3 to C_wb = C_p + C_p × B_max × f_HCT/K_D) increased the OFV by 2.7 (P = 0.10), providing no supportive evidence for non-linearity in the range of observed tacrolimus concentrations. A simple method to account for haematocrit differences in the interpretation of tacrolimus whole blood concentrations is to standardize concentrations to a haematocrit (HCT) of 45%: (Cstd_HCT45 = C_wb × 45%/HCT 7). Haematocrit-standardized concentrations maintain a stable ratio with therapeutically active unbound concentrations (assumed proportional to C_p) no matter what the haematocrit fraction (Figure S1). Including concentration-dependent binding of tacrolimus to erythrocytes in the modelling allows us to account for haematocrit differences in the interpretation of tacrolimus whole blood concentrations without the need to measure tacrolimus plasma concentrations.

During simulations we used a target haematocrit-standardized average concentration of 14.2 μg l⁻¹ to examine various dosing strategies, a value derived from observed tacrolimus AUC(0,12 h) in kidney transplant recipients. It should however be noted that there are currently no randomized controlled trials to support the recommendation of a specific tacrolimus target concentration or AUC(0,12 h) 3,51. In the Oslo and Brisbane cohorts, the average tacrolimus concentration standardized to a haematocrit of 45% on day 7 post-transplant was 12.2 and 19.9 μg l⁻¹, respectively (calculated from individual CL_{wb, HCT45}/F estimates, haematocrit values and actual doses), illustrating local differences in targeted tacrolimus exposure. The population model described here may be used to control haematocrit-independent tacrolimus exposure during a randomized concentration-controlled trial and potentially help to further characterize a target concentration.

In conclusion, we evaluated population pharmacokinetic models of tacrolimus in kidney transplant recipients using an external dataset and found that a model including theory-based covariates led to improved predictive performance as compared with two previously developed empirical models. The model appeared suitable to aid prediction of initial and Bayesian revised tacrolimus doses to achieve a tacrolimus target concentration independent of changes in haematocrit early after kidney transplantation. However, even with ideal dose adjustment with an average concentration exactly on target, 35% of concentrations in a typical patient will be outside the suggested acceptable range. To reduce this out of range percentage, efforts should be directed to reducing the between occasion variability associated with the oral bioavailability of tacrolimus.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: NHGH had salary support from University of Auckland, ES had salary support from the South-Eastern Norway Regional Health Authority and SH, TKB, StB, SaB, KM, AÅ and CS have nothing to disclose. There are no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.

The authors wish to thank the transplantation staff at Oslo University Hospital, Rikshospitalet and Princess Alexandra Hospital, Brisbane for their assistance. Elisabet Størset received grants from The Norwegian Pharmaceutical Society, Shipowner Tom Wilhelmsens Foundation and University of Queensland Summer Research Scholarship.

Author contributions

ES contributed to acquisition of data, analyzed and interpreted data, participated in study design and drafted the manuscript.

NH, SH and CES analyzed and interpreted data, participated in study design and revised the manuscript.

TKB, AÅ and KM contributed to acquisition of data, participated in study design and revised the manuscript.

SaB and StB performed pharmacological and genotyping analyses and revised the manuscript.

All authors approved the final version to be published.

Supporting Information

Additional Supporting Information may be found in the online version of this article at the publisher’s web-site:

Figure S1

Theoretical tacrolimus concentration as a function of haematocrit (HCT). Red line plasma concentration (C_p) (constant at 0.30 μg l⁻¹); green solid line whole blood concentration (C_wb) calculated from literature values of binding to red blood cells: [C_wb = C_p + C_p × HCT (fraction) × B_max/(C_p + K_D)], where B_max = 418 μg l⁻¹ and K_D = 3.8 μg l⁻¹ [35]; green dashed line haematocrit-standardized concentration (C_std) (C_std = C_wb × 45%/HCT)

Figure S2

Observed concentrations (prediction-corrected) and prediction-corrected visual predictive checks over the range of haematocrit, stratified by centre. (A) Observations and simulations based on the Brisbane dataset, (B) Observations and simulations based on the Oslo dataset. Red solid line median observed concentration; red dashed lines 5^th and 95^th percentiles of the observed concentrations; black solid line median predicted concentration in 100 simulated subsets of total dataset; black dashed lines 5^th to 95^th percentiles of the predicted concentrations. Grey-shaded areas represent 95% confidence intervals of the prediction percentiles

Table S1

Test for deviation from Hardy–Weinberg equilibrium of CYP3A5 genotype (rs776746), n = 241

Appendix S1

Supplementary equations