Abstract
Synchronizing movements with a beat requires rapid compensation for timing errors. The phase-correction response (PCR) has been studied extensively in finger tapping by shifting a metronome onset and measuring the adjustment of the following tap time. How the response unfolds during the subsequent tap cycle remains unknown. Using motion capture, we examined finger kinematics during the PCR. Participants tapped with a metronome containing phase perturbations. They tapped in ‘legato’ and ‘staccato’ style at various tempi, which altered the timing of the constituent movement stages (dwell at the surface, extension, flexion). After a phase perturbation, tapping kinematics changed compared to baseline, and the PCR was distributed differently across movement stages. In staccato tapping, the PCR trajectory changed primarily during finger extension across tempi. In legato tapping, at fast tempi the PCR occurred primarily during extension, whereas at slow tempi most phase correction was already completed during dwell. Across conditions, timing adjustments occurred primarily 100-250 ms into the following tap cycle. The change in movement around 100 ms represents the time to integrate information into an already planned movement and the rapidity suggests a subcortical route.
Keywords: sensorimotor synchronization, phase correction, motion capture, timing, movement kinematics
Synchronizing movements with a beat requires precise temporal integration of perception and action, and rapid adjustment of movement timing when deviations from synchrony occur. This timing adjustment or phase correction has been studied extensively in finger tapping by measuring the response to a synchronization error after shifting a metronome onset (e.g., Hary & Moore, 1987; Madison & Merker, 2004; Michon, 1967; Praamstra et al., 2003; Repp, 2001, 2002, 2005, 2008; Repp, Keller & Jacoby, 2012; Studenka & Zelaznik, 2011).
In the phase-perturbation paradigm, participants synchronize their finger taps with a metronome that contains unexpected timing perturbations. An unexpected delay or advance creates a large tap-to-target asynchrony, and is compensated for by adjusting the timing of the following tap (e.g., Repp, 2002; Repp & Keller, 2004). This adjustment is automatic and is called the phase-correction response (PCR) (e.g., Repp, 2005). The size of the PCR relative to the perturbation gives an estimate of the phase correction parameter, α, an important metric in many phase-correction models (e.g., Mates, 1994; Pressing, 1998; Semjen et al, 1998; 2000; Vorberg & Wing, 1996). An α of 1 indicates perfect phase correction (i.e., 100% of the metronome perturbation is corrected on the following tap). However, α is usually considerably lower than 1, indicating that only a portion of the error is corrected on the following tap. Vorberg and Schulze (2002) argue that it is not optimal to correct fully when a relatively large portion of each asynchrony arises from motor noise (faster tempi have a higher proportion of motor to timekeeper variance). Phase correction increases at slower tempi, and perfect phase correction (i.e., α = 1) can occur at very slow tempi (> 1000 ms inter-onset intervals (IOI)), (Repp, 2008). Increased PCR at slow tempi could reflect a decreased tendency to maintain the tapping rhythm (Repp, 2008) and/or the increased time available to integrate the perceptual information into the upcoming action.
To date, phase perturbation studies (and models of phase correction) typically consider only the time of tap contact (i.e., only the end point of each movement cycle). However, the entire movement trajectory can add insight into the dynamics underlying movement and perception-action integration. For example, continuous trajectories of hand movements can reveal underlying cognitive dynamics (Spivey, Grosjean, & Knoblich, 2005); and the kinematics of hand trajectories when observing moving or stationary stimuli can reveal interactions between concurrent perception and action (Grosjean, Zwickel & Prinz, 2009; Welsh & Elliott, 2004). Movement kinematics can provide a richer understanding of underlying processes, and are especially relevant for time-critical processes such as phase correction. In this study we examine the kinematics of finger trajectories to investigate the time course of the phase correction response.
Previous studies show a tight connection between movement kinematics and timing. In finger tapping, the movement trajectory breaks down into constituent movement stages: dwell at the surface, upward extension, and downward flexion to the target. Flexion times to the target are typically shortest (e.g., Doumas & Wing, 2007; Hove & Keller, 2010; Krause, Pollok & Schnitzler, 2010; Torre & Balasubramaniam, 2009). Relatively short flexion times and faster movements to the target are associated with more precise timing (Balasubramaniam, Wing & Daffertshofer, 2004; Brenner, van Dam, Berkhout & Smeets, 2012; Krause, Pollok & Schnitzler, 2010). At slower tempi, extension times and velocities change considerably more than flexion, which remain relatively stable across tempi (Doumas & Wing, 2007; Hove & Keller, 2010). Consistently high velocity flexion would produce a salient timing cue potentially important for synchronization timing (Balasubramaniam, 2006; Elliot, Welchman & Wing, 2009). Movement trajectories affect movement timing.
Little previous work has examined movement trajectories in relation to phase correction. In a few tapping studies with isochronous metronomes, movement trajectories correlated with timing errors. In a motion-capture study of finger tapping (with isochronous visual metronomes), movement trajectories differed systematically after relatively early versus late taps (Hove & Keller, 2010). For example, after a late tap, the following movement cycle had shorter extension and dwell times, but flexion time did not change. Similarly, when tapping without surface contact, late taps were compensated for by shortening the following extension stage (Torre & Balasubramaniam, 2009). This correlational evidence for the workings of phase correction can be examined more systematically by tracking finger kinematics when synchronizing with sequences containing timing perturbations.
Previous phase-perturbation studies examined the temporal evolution of the phase correction response in two-handed tapping and circle drawing. In one experiment, highly trained musicians tapped with various two-interval (short-long) rhythms using two hands in alternation (Repp, 2011). By shifting the timing of the rhythm's ‘earlier’ tone, phase correction could be examined on the rhythm's ‘later’ tap. When the later tap was 100 ms after the metronome shift, that tap displayed no phase correction response. But when the later tap was 150 ms after the metronome shift, that tap showed a discernable phase correction response. As the ‘early-late’ rhythm interval increased from 150 ms to 300 ms, the PCR on the later tap increased. Together the absence of a PCR 100 ms after a shift and its emergence by 150 ms indicates that phase correction starts to emerge slightly after 100 ms. This represents the time needed to change the temporal goal of an incipient action (Repp, 2011), and could relate to the window for perceptual-motor integration and the synchronization-rate limits of around 125 ms IOI (Repp, 2005; 2011).
In a phase perturbation study with circle drawing, Repp and Steinman (2010) examined the phase correction response at the four cardinal points around the circle. After a metronome perturbation, the phase correction response emerged gradually over the first cycle: very little PCR occurred at one-quarter cycle (i.e., 150 or 200 ms into the 600 or 800 ms cycle); the PCR started to emerge by halfway around the cycle (300 or 400 ms); and the PCR continued to increase throughout the cycle. Complete correction can take several cycles in circle drawing (Studenka & Zelaznik, 2011). The PCR in circle drawing is considerably weaker than in tapping (Repp & Steinman, 2010), and it is unclear how the time course of phase correction compares for continuous circle drawing and discrete tapping. The time course of the phase-correction response in standard unimanual tapping has not been examined to our knowledge.
In the current finger-tapping phase perturbation study, we use motion capture to examine the kinematics of baseline-finger tapping and phase correction responses. Participants tapped their index finger along with an auditory metronome at various baseline tempi (400, 500, 600 & 700 ms IOI). The metronome contained unexpected early and late timing perturbations (± 50, 40, 30, 20, & 10 ms). Responses to these perturbations were analyzed by comparing movement kinematics after a perturbation to baseline kinematics. Participants tapped in a smooth legato or short staccato manner, which manipulated the relative timing of dwell, extension, and flexion stages, and thus can provide additional information about the time course (or distribution) of the phase correction response. These manipulations allow us to determine whether the PCR occurs after an absolute amount of time or at a relative time that depends on the stage of the movement cycle. For example, if the PCR occurs at an absolute time point, then this may be located at a different movement stage for the two styles (e.g., dwell for legato vs. extension for staccato, especially al slow tempi).
Experiment
Methods
Participants
Eleven right-handed volunteers (3 women) aged 20 to 39 years (M = 26.3) participated in the experiment. The majority of participants had extensive musical experience. Musical training ranged from 6-31 years (M = 16). Musical training did not correlate with phase correction response, r = .24, p = .18.
Materials and procedure
Participants tapped their right index finger on a table surface in time with auditory sequences that contained occasional phase-shifted onsets. The sequences consisted of sine tones at 1400 Hz lasting 40 ms. Tones were presented in each trial at a constant baseline IOI of 400, 500, 600, or 700 ms. Each trial contained 10 phase perturbations that ranged from -50 ms (early) to +50 ms (late), in increments of 10 ms. These perturbations were “phase shifts”, meaning that a perturbation shortened or lengthened one IOI (e.g., IOIs = 500 500 450 500 500 ms). Phase perturbations were presented in random order and separated by a variable number of tones that ranged from 4-7. Each trial started with 5-8 tones at the trial's constant baseline IOI. Eight trials (each of the 4 tempi presented twice in random order) constituted a block.
Blocks alternated between “Legato” and “Staccato” tapping. Participants were instructed to tap in a legato or staccato manner, which manipulated the time of finger contact on the surface. Legato tapping is essentially standard finger tapping, and kinematics were quite similar to our earlier motion-capture investigations of tapping. Staccato tapping had shortened surface contact (similar to short staccato musical articulation). The experiment consisted of 10 blocks each containing 8 trials for 80 total trials (800 total perturbations), and lasted approximately 1 hour. The experiment was run from a PC using Presentation (Neurobehavioral Systems). Stimuli were presented from over Sennheiser circumaural headphones.
Data acquisition
The kinematics of participants' finger movements were tracked by a Vicon motion capture system with a 200 Hz sampling frequency. Reflective markers were attached to the tip of the index finger for kinematics and on the stationary hand and wrist for reference positions. Three-dimensional coordinates of marker position were saved on a separate PC. This PC also received information from the parallel port of the Presentation PC about target-onset times.
Additionally, the impact thuds produced by the taps were recorded with a microphone on the left channel of a stereo audio file (Audacity program at 8000 Hz sampling rate) on a separate computer. The right channel of the same audio file recorded the metronome beeps from the Presentation PC. Microphone recordings provided quality assurance: they were highly consistent with the motion-capture data and will not be reported here for brevity.
Analyses
Motion-capture data
Movement timing and kinematics were computed from the finger-motion data. The data were smoothed with a first-order Savitsky-Golay filter (window size = 11 samples). Metronome onsets and phase-perturbation information were extracted from the stimulus triggers recorded via the parallel port. An example movement trajectory is displayed in Figure 1.
Figure 1.
Example of the movement trajectory during finger tapping. The finger-tip amplitude (in mm) is plotted on the y-axis, and time (in ms) is plotted on the x-axis. Dwell, extension and flexion stages are labeled in this legato trial at 500 ms IOI. Metronome onsets are plotted as ticks along on the bottom of the figure; the perturbed metronome occurs at 1960 ms (40 ms earlier than expected). The dark line represents the trajectory of the phase correction response.
The phase-correction response (PCR) indexes the system's response to timing errors. The PCR was calculated by subtracting the trial's baseline IOI from the inter-tap interval (ITI) immediately following a perturbation. For example, in a 600 ms IOI trial, if the ITI following a delayed target was 645 ms, the PCR would equal 45 ms. PCRs larger than 100 ms were filtered out (∼1.5% of all PCRs). PCRs were averaged for each perturbation magnitude at each IOI duration for each participant (separately for legato and staccato conditions). These mean PCRs were regressed onto perturbation magnitude. The slope of this regression line gives an estimate of the error correction parameter, α.
We analyzed the trajectories of baseline tapping and the phase correction response. During finger tapping on a surface, three distinct stages arose in each movement cycle: extension away from the surface, flexion to the surface, and dwell time at the surface.1 To determine each cycle's extension, flexion, and dwell stages, an algorithm extracted each cycle's time of surface contact, surface release, and the local amplitude maximum as in previous studies (e.g., Balasubramaniam, Wing & Daffertshofer, 2004; Hove & Keller, 2010; Krause, Pollok & Schnitzler, 2010). Movement amplitude was measured as the difference between the surface-dwell position and the local maximum of the finger.
For each movement cycle, we calculated individual trajectory components (dwell time, extension time, flexion time, and amplitude). We examined these components' absolute magnitudes for each PCR, and their magnitudes relative to the 3 taps prior to each perturbation. Relative magnitudes represent the change in trajectory in response to a phase-shifted target and are used as the primary index of the PCR.
Results
First we report baseline synchronization performance and movement kinematics for the three taps prior to each perturbation. For each of the eight conditions (4 tempi × 2 legato/staccato tapping styles), each participant had 300 baseline taps, which are used in the following analyses.
Tap-to-target asynchronies during baseline tapping
Mean and standard deviation of tap-to-target asynchronies were analyzed in 4 (tempo) × 2 (legato vs. staccato) ANOVAs (Table 1). Overall, participants tapped slightly before the targets (grand mean asynchrony = -5 ms). Taps occurred earlier in the slower tempi, F(3,30) = 8.34, p < .001, ηp2 = .455. Mean asynchronies did not differ between legato and staccato tapping, p > .8, nor was there a tempo × style interaction, p > .5.
Table 1.
Mean tap-to-target asynchrony (and standard deviation of asynchronies) in ms by tempo and condition.
| Tap style | Tempo | |||
|---|---|---|---|---|
|
| ||||
| 400 | 500 | 600 | 700 | |
| Legato | 1.9 (19.8) | -5.2 (20.4) | -9.0 (22.9) | -9.7 (25.9) |
| Staccato | 4.6 (18.8) | -5.4 (20.5) | -10.5 (25.3) | -9.5 (26.6) |
The variability (SD) of tap-to-target asynchronies was higher at slower tempi, F(3,30) = 46.38, p < .001, ηp2 = .823. The variability of asynchronies did not differ between legato and staccato, p > .9; nor was there a tempo × style interaction, p > .2.
Movement kinematics during baseline tapping
We examined the baseline movement times of dwell, extension, and flexion stages. Legato and staccato tapping differed most clearly during the dwell stage, with shorter dwell in staccato. Three participants however showed no discernable shortening of dwell (or other trajectory difference) in the staccato condition (e.g., their respective dwell times averaged 185, 229, and 304 ms in the slowest staccato condition, compared to an average of 55 ms for the other 8 participants). These three participants did not tap in a staccato manner, therefore their staccato runs were not included in the following staccato analyses leaving n = 8. Their data were retained for the legato runs (n = 11).
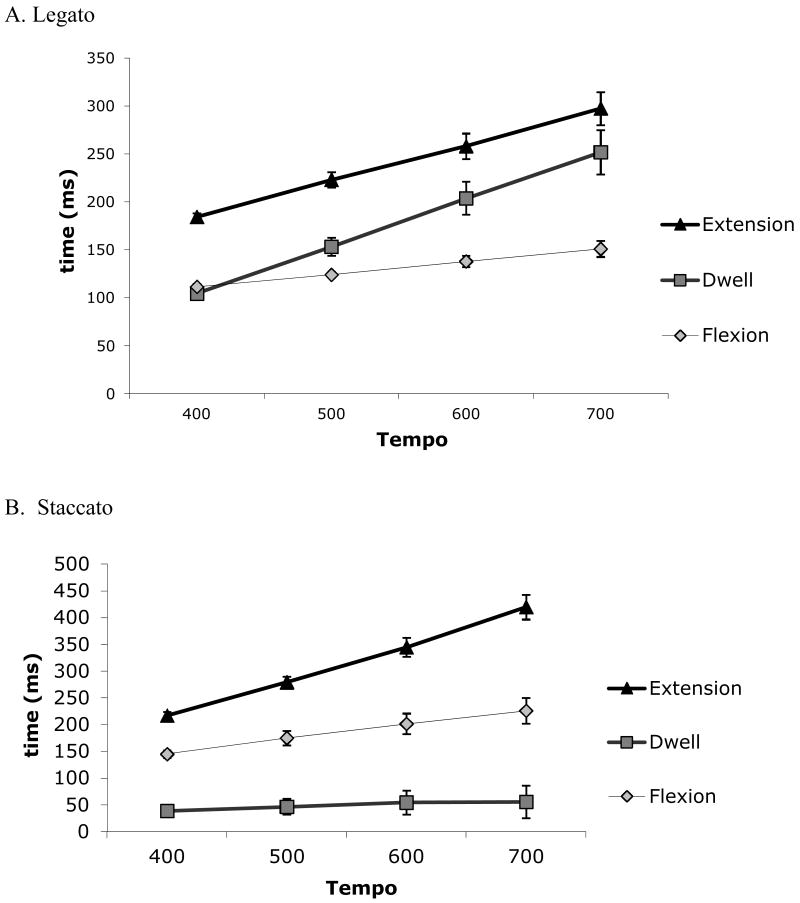
Baseline dwell, extension, and flexion times were compared in 3 (movement stage: dwell, extension, flexion) × 4 (tempo: 400, 500, 600, 700 ms IOI) repeated-measures ANOVAs separately for legato and staccato. In legato (Figure 2a), the movement times differed between stages, F(2,20) = 19.84, p < .001, ηp2 = .665, and pairwise comparisons showed that extension times were longest (ps < .05), and flexion times were the shortest (ps < .05). As tempi slowed, the extension and dwell times increased considerably more than the relatively consistent flexion times, as captured by the significant Stage × Tempo interaction, F(6,60) = 4.86, p < .001, ηp2 = .327.
Figure 2.
Average time of each movement stage (dwell, extension, flexion) during (pre-perturbation) baseline tapping by tempo for a) legato and b) staccato tapping.
In staccato (Figure 2b), movement times differed between stages, F(2,14) = 54.10, p < .001, ηp2 = .885; Extension times were the longest (ps < .001), and dwell times were the shortest (ps < .01). As tempi slowed, extension increased considerably more than dwell or flexion, as captured by the significant Stage × Tempo interaction, F(6,42) = 16.91, p < .001, ηp2 = .707.
The peak amplitude of the index finger averaged 42.3 mm (Table 2). We compared the amplitude between tapping style (legato, staccato) and tempo (400, 500, 600, 700 ms IOI) in a repeated-measures ANOVA. Finger amplitude was higher at slower tempi, F(3,21) = 12.17, p < .001, ηp2 = .635. The finger amplitude was higher in staccato than legato, F(1,7) = 5.93, p = .045, ηp2 = .459. No Style × Tempo interaction occurred, p > .6.
Table 2.
The baseline finger amplitude (in mm) by condition and tempo.
| Tap style | Tempo (in ms IOI) | |||
|---|---|---|---|---|
|
| ||||
| 400 | 500 | 600 | 700 | |
| Legato | 36.7 | 38.3 | 40.0 | 41.3 |
| Staccato | 44.1 | 44.8 | 46.2 | 47.3 |
Phase Correction Response
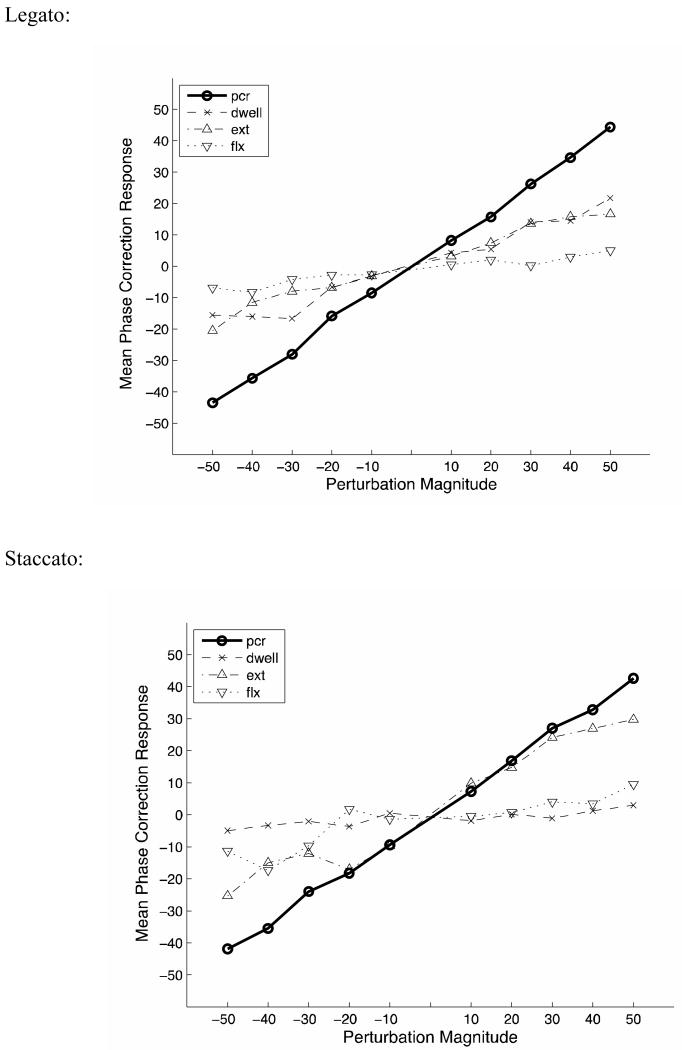
The PCR for each perturbation magnitude is displayed for legato and staccato in Figure 3. Points on the thick line represent the next movement cycle's overall PCR. The broken lines represent how the PCR breaks down into its component movement stages (i.e., the change in dwell, extension, and flexion times after a perturbation).
Figure 3.
Phase correction response on the following tap (in ms) for various metronome perturbation magnitudes (in ms) for Legato (3a) and Staccato (3b) conditions. The overall PCR is depicted in a solid black line, and the PCR for each stage of movement (dwell, extension and flexion) are depicted in a broken lines.
For legato, the overall PCR regression slope was 0.87 (indicating that 87% of the phase perturbation was corrected). Breaking this down by movement stage, the PCR slope in dwell was 0.39, extension was 0.36, and flexion was 0.12. Thus, the majority of the phase correction response in legato occurred during dwell and extension phases.
For staccato, the overall PCR regression slope was 0.84. Breaking this down by movement stage, the PCR slope in dwell was 0.06, extension was 0.58, and flexion was 0.21. Thus the majority of the staccato PCR occurred during extension.
Overall, the PCR slopes were similar for legato and staccato. No difference between legato and staccato occurred in a 2 (legato, staccato) × 4 tempo (400, 500, 600, 700 ms IOI) ANOVA, F(1,7) = 2.84, p = .14, ηp2 = .288, nor was there an interaction, F(3,21) = 0.34, p > .7, (Table 3).
Table 3. Phase correction response slope by tempo and style.
| Tap Style | Tempo | |||
|---|---|---|---|---|
|
| ||||
| 400 | 500 | 600 | 700 | |
| Legato (n=11) | 0.82 | 0.86 | 0.95 | 0.85 |
| Staccato (n=8) | 0.80 | 0.86 | 0.85 | 0.87 |
The effects of tempo and movement stage on PCR are examined separately for legato and staccato. PCRs were distributed differently across movement stages for legato and staccato, as shown in Figures 4a and 4b. PCR slopes were entered into 3 (movement stage: dwell, extension, flexion) × 4 (tempo: 400, 500, 600, 700 ms IOI) repeated-measures ANOVAs.
Figure 4.
The mean PCR slope of each movement stage (dwell, extension and flexion) during legato tapping (4a) and staccato tapping (4b).
In Legato, the PCR was distributed differently among the movement stages, F(2,20)= 5.94, p = .009, ηp2 = .373. The PCR during dwell and extension were considerably larger than during flexion (pairwise ps < .01); extension and dwell PCRs did not differ, p > .7. The PCR tended to differ between tempi, F(3,30) = 2.89, p = .052, ηp2 = .224, with generally larger PCRs at slower tempi (peaking at .95 in the 600 ms IOI tempo). The significant Movement Stage × Tempo interaction, F(6,60) = 10.90, p < .001, ηp2 = .521, indicates that the PCR was distributed across movement stages differently by tempi. At fast tempi, phase correction occurred primarily during extension; whereas at slow tempi, most phase correction was already completed during dwell. This indicates that the PCR is not distributed throughout the next cycle, but instead occurs during a limited time window during the next cycle.
In Staccato, PCR was also distributed differently among the movement stages, F(2,14)= 12.75, p = .001, ηp2 = .646. The PCR was largest during extension (ps < .05), and did not differ between dwell and flexion (p > .2). There was no main effect of tempo, F(3,21) = 0.53, p > .6, nor a significant Movement Stage × Tempo interaction, F(6,42) = 1.95, p = .099, ηp2 = .216. This indicates that the staccato PCR occurred primarily during extension across tempi.
Additionally, we analyzed the change in finger amplitude of the PCR (relative to the 3 prior taps) for the ten perturbation magnitudes in separate repeated-measures ANOVAs for legato and staccato. The change in finger amplitude differed between perturbation magnitudes for Legato, F(9,90) = 5.05, p < .001, ηp2 = .335, and for Staccato conditions F(9,63) = 2.25, p = .032, ηp2 = .241. The finger amplitude was slightly lower than baseline when responding to an early perturbation (Fig. 5). A change in amplitude was more apparent for early than late perturbations. However, the amplitude differences were very small: PCR amplitudes were typically within 0.5 mm of the baseline amplitude (mean baseline amplitude across conditions = 42.3 mm).
Figure 5.
The change in finger amplitude (relative to the three prior taps) in response to the various metronome perturbations.
Discussion
Movement Kinematics During Baseline Tapping
In this experiment we recorded finger kinematics while tapping with metronomes that contained unexpected timing perturbations. Baseline (i.e., pre-perturbation) tapping consisted of distinct movement stages: dwell, extension, and flexion. Movement trajectories differed considerably between legato and staccato tapping. Most notably, staccato tapping had short dwell times, consistent with the short tone durations in staccato musical articulation.
The three movement stages were distributed asymmetrically. In legato tapping, extension times were longest, dwell times were intermediate, and flexion times were shortest. As tempi slowed, each movement stage lengthened, but flexion times were relatively stable across tempi. In staccato tapping, extension times were the longest. As tempi slowed, extension lengthened most, whereas dwell and flexion were relatively stable across tempi.
Asymmetries between extension and flexion have been reported previously (Balasubramaniam, Wing, & Daffertshofer, 2004; Hove & Keller, 2010; Krause, Pollok & Schnitzler, 2010, Torre & Balasubramaniam, 2009). Flexion times to the target are shorter in standard tapping. But when participants were instructed to extend on-the-beat, extension was shorter; indicating that the extension-flexion asymmetry does not stem from biomechanical constraints (Balasubramaniam, 2006). Faster movements to the target have often been associated with more precise timing (Balasubramaniam, Wing, & Daffertshofer, 2004; Brenner, van Dam, Berkhout & Smeets, 2012; Krause, Pollok & Schnitzler, 2010). Extension-flexion asymmetries might help decrease the temporal variability of tapping (Torre & Balasubramaniam, 2009). Fast, quasi-ballistic movements might decrease variability by minimizing the time that inherent motor noise can accrue (Hove & Keller, 2010). Fast movements also provide increased sensory information, which could assist timing (Balasubramaniam, 2006; Goebl & Palmer, 2008). In a study comparing discrete tapping with continuous sinusoidal finger movements (which produce less force), the discrete tapping had better synchronization and a more robust phase-correction response to metronome perturbations (Elliott, Welchman & Wing, 2009). The authors suggest that the greater force in discrete tapping provides more salient asynchrony information, which could be used for phase correction in synchronization (Elliott, Welchman & Wing, 2009). Compared to the highly salient sensory feedback from a discrete tap, continuous movements (like circle drawing) lack a clear sensory feedback from the target time, and this likely contributes to poorer synchronization and error correction in continuous movements. Adding tactile feedback to continuous circle drawing can improve the phase correction response to perturbed metronomes (Studenka & Zelaznik, 2011).
Clear and reliable sensory information from movement is important for accurate synchronization and error correction. However, modulating sensory feedback (or flexion velocity) is unlikely utilized in the error correction process. Previous work showed that timing asynchronies did not correlate with changes in the following flexion phase (which would alter sensory feedback); but instead asynchronies correlated with changes during extension and dwell (Hove & Keller, 2010; Torre & Balasubramaniam, 2009). These correlations suggest that phase correction was implemented during the extension and dwell stages. In the current experiment, we extended this correlational evidence by introducing perturbations to create timing errors and using various tempi to alter the absolute time of each movement stage.
Time Course of the Phase Correction Response
We perturbed metronome onsets to examine how the motor system integrates sensory information and implements phase correction. After a metronome perturbation, the introduced error was partly corrected on the following tap cycle. This phase correction response was distributed unequally over the next movement cycle. In legato tapping, the majority of the phase correction occurred during dwell and extension, with little change in flexion. The distribution of PCR depended on tempo: at fast tempi, most phase correction occurred in extension, whereas at slow tempi, most phase correction was already completed during dwell. In staccato tapping, most phase correction occurred during extension across tempi.
Various factors could contribute to the phase correction differences by movement stage and tempo. First, the small PCR during flexion could reflect flexion's relative stability across tempi and quasi-ballistic movement profile. Stable flexion trajectories would be less adaptable and less likely to respond to timing errors. A second possibility relates to the relative time available: flexion times constitute a relatively small portion of the entire tap time (as do dwell times in staccato), so there is relatively little time to implement correction, which results in a relatively small PCR. However, if the relative movement time would drive relative PCR, the pattern of movement times (Figures 2a & 2b) should parallel the pattern of PCR across tempi (Figures 4a & 4b). The patterns clearly differ, so this ‘relative’ time explanation is unlikely. As tempi slow in legato, movement times increase similarly for dwell and extension (Figure 2a), whereas the PCR increases in dwell, but decreases in extension (Figure 4a). This reversal of PCR from extension to dwell indicates that the absolute time after a perturbation is critical in phase correction.
Closer examination of this extension-dwell reversal elucidates the time course of the phase correction response. In the fast trials (400 ms IOI), dwell occurs during the first 100 ms, and captures very little of the PCR; the PCR occurs mainly during the extension stage (100-300 ms post-perturbation). At the 500 ms tempo, dwell occurs during the first 150 ms, and now captures a similar proportion of the PCR as extension (150-370 ms post-perturbation). At the 600 ms tempo, dwell occurs during the first 200 ms, and now captures most of the PCR. By the 700 ms tempo, dwell occurs during the first 250 ms, and captures most of the PCR with little occurring during extension (250-550 ms post-perturbation). Thus in standard legato tapping, PCR appears to occur in a window between 100 and 250 ms post-perturbation.
In staccato tapping, this ‘triangulation’ technique is less insightful because this critical 100-250 ms window contained only extension (extension lasted from 40-260 ms at the fastest tempo, and from 55-465 ms at the slowest tempo). Across tempi, the PCR occurred primarily during extension, which contained the 100-250 ms window where phase correction was observed in legato.
The motion-capture evidence that phase correction occurred largely 100-250 ms post-perturbation aligns with a previous phase-correction study with two-handed tapping (Repp, 2011). Using a short-long rhythm, Repp (2011) showed that phase correction starts to appear around 100 ms after the shifted earlier tone. These results (in addition to results from two follow-up experiments, Repp, 2011) are consistent with a phase-resetting hypothesis: phase correction and tap timing in general are based on the most recent tone(s) and the tendency to maintain the tapping rhythm (Hary & Moore, 1987; Repp, 2005; 2008; 2011). Phase resetting of the next tap could be based on a dynamic competition between the preceding tone and the preceding tap. The 100-200 ms delay constitutes the time to integrate the new sensory information into an already planned and initiated movement (Repp, 2011).
Studies of grasping and reaching to visual targets whose positions shift unexpectedly indicate changes in hand and arm movements 100-200 ms after the shift (e.g., Brenner & Smeets; 1997; Hansen & Elliott, 2009; Paulignan et al., 1991; Soechting & Lacquaniti, 1983). This time window is similar to that observed in audio-motor phase correction, and further supports the time window for integrating newly acquired perceptual information into an initiated movement.
Movement kinematics provide a glimpse into the underlying neural dynamics. A change in trajectory only 100 ms after the perturbation is noteworthy, and suggests that phase correction might be too rapid to be implemented through the classical auditory cortical pathway. Mismatch negativity response to metronome timing perturbations occurs in the auditory cortex about 150 ms after a perturbation (e.g., Ford & Hillyard, 1983); thus this cortical memory trace occurs after the observed adjustments of movement timing. MEG work showing M100 responses to (sub- and supraliminal) metronome perturbations have been taken to suggest that auditory cortex might contribute directly to synchronize motor output (Tecchio et al., 2000; cf. Praamstra et al. 2003); but this M100 response is concurrent with the observed change in motor output. EEG recordings indicate that the early evoked response in the auditory cortex (not registering a ‘change’) occurs at a latency around 50 ms (e.g., ten Donkelaar & Kaga, 2011) [and direct recordings in macaques indicate that the response latency for tones to primary auditory cortex is around 25-35 ms (Camalier et al., 2012)]. This latency, combined with transmission time from auditory cortex to premotor and motor cortex along the postero-dorsal stream (Rauschecker & Scott, 2009), and the latency of the cortico-spinal tract to finger, suggest that this auditory cortex-motor cortex-effector pathway is possibly too slow to drive phase correction. Instead, a more rapid subcortical pathway might be involved in phase correction
Recent work suggests dual auditory pathways: the classical sensory pathway to the auditory cortex encodes fine details of sound and is relatively slow; whereas a rapid cerebellar pathway (via the brainstem's dorsal cochlear nucleus) encodes event onsets, and can rapidly transmit the temporal structure of a sound to thalamic and cortical targets (Schwartze & Kotz, 2013). This rapid route with highly accurate temporal precision could be critical in sensorimotor integration and phase correction (Schwartze & Kotz, 2013). Indeed, auditory stimuli that are encoded clearly in the cochlea and produce a clear burst of spikes on the auditory nerve yield a more robust phase correction response (Hove et al., 2014). The subcortical/cerebellar pathway for timing is supported by repetitive transcranial magnetic stimulation (rTMS) studies of phase correction. Selectively inhibiting motor and premotor cortex with rTMS did not alter phase correction after a phase shift (Doumas, Praamstra & Wing, 2005); whereas rTMS over the cerebellum impaired the phase correction response (Bijsterbosch et al., 2011).
Our present results are in line with earlier work looking at trajectory formation in timed rhythmic sequences (Balasubramaniam et al, 2004; Torre & Balasubramaniam, 2009 & Doumas & Wing, 2005). In general it appears that phase correction is implemented in the dwell and extension phases of the movement. The flexion phase of the movement appears invariant across all our experimental manipulations. It is likely that this relative constancy in flexion movement time provides the nervous system with the stability that it needs for planning each motor response, while being able to accommodate phase and period correction through other phases of the movement. Following Balasubramaniam et al (2004), we argue that this is indicative of an important adaptive feature of movement trajectories during voluntary timing tasks where error corrections have to be rapidly employed in the course of the response following a perturbation.
The principles of motor control underlying movement trajectory formation might extend beyond the human nervous system. Recent work suggests that monkeys time the pause duration during a synchronization-continuation task and not the durations of the movement (Donnet et al 2014). However, in that study they did not parse the movement cycles into their various phases based on position or velocity. To the best of our knowledge there is no evidence for the phase correction response in non-human species, although it is now apparent that auditory rhythmic entrainment might be more widespread in the animal kingdom (Patel et al., 2009; Cook et al. 2013).
In conclusion, the phase-correction response to a timing perturbation can be observed in adjustments of movement kinematics from 100-250 ms into the following tap cycle. Little timing adjustment occurred during flexion, which remains fast perhaps to produce perceptual information for timing (Balasubramaniam, 2006). Adjustments occurred primarily during dwell and extension phases, and vary based on tapping style and tempo. The change in movement starting around 100 ms represents the time to integrate information into an already planned movement and the rapidity suggests a subcortical route. Results also indicate the phase correction responses are completed fairly early (∼250 ms) into the following cycle. Thus imperfect phase correction at moderate tempi (< 800 ms IOI) is not due to the limited amount of time to implement phase correction, and perfect phase correction at slow tempi (>1000 ms IOI) does not emerge simply due to additional time to process and implement the correction. Together our findings suggest that the phase correction response is an automatic adjustment in movement timing that is constrained primarily by the time taken to integrate auditory and motor information at the subcortical level.
An important question to consider is how findings about phase correction obtained in finger-tapping studies generalize to less constrained forms of movement coordination with external rhythms, as in dancing to music or playing in a musical ensemble. These activities involve relatively large-scale movements, often involving the whole body. Further, to the extent that dance and ensemble performance take place in social contexts, these behaviors potentially involve mutual phase correction between individuals. One source of evidence for generalization to large-scale movements comes from the finding that the phase correction response occurs in synchronization of lower limbs (Chen, Wing, & Pratt, 2006). Examining the time course of phase correction may therefore improve understanding the mechanism underlying the effectiveness of rhythmic auditory stimulation in gait rehabilitation (e.g., Hove et al., 2012). It is also likely that phase correction responses at one timescale, such as the beat in music, affect movements at other timescales. Research on dancing to music has shown that body movements reflect multiple levels of periodicity in the music's hierarchical temporal structure (Toiviainen, Luck, & Thompson, 2010) and work with piano duos has demonstrated systematic relations between interpersonal coordination at the level of small-scale finger movements and large-scale body sway (Ragert, Schroeder & Keller, 2013). Moreover, recent research has addressed interpersonal phase correction in complex movements directly by examining how musicians adjust for mutual errors when playing together in string quartets (Wing et al., 2014). Such extensions of the phase correction paradigm highlight its potential to be applied to a range of human motor behaviors, thus providing a foundation for understanding the bases of the exceptional human ability for precise and flexible sensorimotor synchronization in socially embedded contexts.
Acknowledgments
We thank Bruno Repp for feedback in the early stages of this project. This work was partially supported by the Max Planck Society, and by funding to MJH from The Erasmus Mundus Auditory Cognitive Neuroscience program, and National Institute of Mental Health Grant T32-MH16259.
Footnotes
A fourth phase, hold at the top of the cycle sometimes occurs during very slow tempi. However, in our data set a hold phase was not very apparent, and we did not explicitly extract a separate hold phase. Future work could consider a hold phase based on position or velocity criteria.
References
- Balasubramaniam R. Trajectory formation in timed repetitive movements. In: Latash ML, Lestienne F, editors. Motor Control and Learning. Springer; US: 2006. pp. 47–54. [Google Scholar]
- Balasubramaniam R, Wing AM, Daffertshofer A. Keeping with the beat: Movement trajectories contribute to movement timing. Experimental Brain Research. 2004;159(1):129–134. doi: 10.1007/s00221-004-2066-z. [DOI] [PubMed] [Google Scholar]
- Bijsterbosch JD, Lee KH, Hunter MD, Tsoi DT, Lankappa S, Wilkinson ID, Barker AT, Woodruff PW. The role of the cerebellum in sub-and supraliminal error correction during sensorimotor synchronization: evidence from fMRI and TMS. Journal of Cognitive Neuroscience. 2011;23(5):1100–1112. doi: 10.1162/jocn.2010.21506. [DOI] [PubMed] [Google Scholar]
- Brenner E, van Dam M, Berkhout S, Smeets JB. Timing the moment of impact in fast human movements. Acta Psychologica. 2012;141(1):104–111. doi: 10.1016/j.actpsy.2012.07.002. [DOI] [PubMed] [Google Scholar]
- Brenner E, Smeets JB. Fast responses of the human hand to changes in target position. Journal of Motor Behavior. 1997;29(4):297–310. doi: 10.1080/00222899709600017. [DOI] [PubMed] [Google Scholar]
- Camalier CR, D'Angelo WR, Sterbing-D'Angelo SJ, Lisa A, Hackett TA. Neural latencies across auditory cortex of macaque support a dorsal stream supramodal timing advantage in primates. Proceedings of the National Academy of Sciences. 2012;109(44):18168–18173. doi: 10.1073/pnas.1206387109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen HY, Wing AM, Pratt D. The synchronisation of lower limb responses with a variable metronome: the effect of biomechanical constraints on timing. Gait and Posture. 2006;23(3):307–314. doi: 10.1016/j.gaitpost.2005.04.001. [DOI] [PubMed] [Google Scholar]
- Cook P, Rouse A, Wilson M, Reichmuth C. A California sea lion (< em> Zalophus californianus</em>) can keep the beat: Motor entrainment to rhythmic auditory stimuli in a non vocal mimic. Journal of Comparative Psychology. 2013;127(4):412–427. doi: 10.1037/a0032345. [DOI] [PubMed] [Google Scholar]
- Donnet S, Bartolo R, Fernandes JM, Cunha JPS, Prado L, Merchant H. Monkeys time their pauses of movement and not their movement-kinematics during a synchronization-continuation rhythmic task. Journal of Neurophysiology. 2014;111(10):2138–2149. doi: 10.1152/jn.00802.2013. [DOI] [PubMed] [Google Scholar]
- Doumas M, Praamstra P, Wing AM. Low frequency rTMS effects on sensorimotor synchronization. Experimental Brain Research. 2005;167:238–245. doi: 10.1007/s00221-005-0029-7. [DOI] [PubMed] [Google Scholar]
- Doumas M, Wing AM. Timing and trajectory in rhythm production. Journal of Experimental Psychology: Human Perception and Performance. 2007;33:442–455. doi: 10.1037/0096-1523.33.2.442. [DOI] [PubMed] [Google Scholar]
- Elliott MT, Welchman AE, Wing AM. Being discrete helps keep to the beat. Experimental Brain Research. 2009;192(4):731–737. doi: 10.1007/s00221-008-1646-8. [DOI] [PubMed] [Google Scholar]
- Ford JM, Hillyard SA. Event-related potentials (ERPs) to interruptions of a steady rhythm. Psychophysiology. 1981;18:322–330. doi: 10.1111/j.1469-8986.1981.tb03043.x. [DOI] [PubMed] [Google Scholar]
- Goebl W, Palmer C. Synchronization of timing and motion among performing musicians. Music Perception: An Interdisciplinary Journal. 2009;26(5):427–438. [Google Scholar]
- Grosjean M, Zwickel J, Prinz W. Acting while perceiving: Assimilation precedes contrast. Psychological Research. 2009;73:3–13. doi: 10.1007/s00426-008-0146-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen S, Elliott D. Three-dimensional manual responses to unexpected target perturbations during rapid aiming. Journal of Motor Behavior. 2009;41(1):16–29. doi: 10.1080/00222895.2009.10125917. [DOI] [PubMed] [Google Scholar]
- Hary D, Moore GP. Synchronizing human movement with an external clock source. Biological Cybernetics. 1987;56(5-6):305–311. doi: 10.1007/BF00319511. [DOI] [PubMed] [Google Scholar]
- Hove MJ, Keller PE. Spatiotemporal relations and movement trajectories in visuomotor synchronization. Music Perception: An Interdisciplinary Journal. 2010;28(1):15–26. [Google Scholar]
- Hove MJ, Suzuki K, Uchitomi H, Orimo S, Miyake Y. Interactive rhythmic auditory stimulation reinstates natural 1/f timing in gait of Parkinson's patients. PLoS ONE. 2012;7(3):e32600. doi: 10.1371/journal.pone.0032600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hove MJ, Marie C, Bruce I, Trainor LJ. Superior time perception for lower musical pitch explains why bass-ranged instruments lay down musical rhythms. Proceedings of the National Academy of Sciences. 2014 doi: 10.1073/pnas.1402039111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krause V, Pollok B, Schnitzler A. Perception in action: The impact of sensory information on sensorimotor synchronization in musicians and non-musicians. Acta Psychologica. 2010;133(1):28–37. doi: 10.1016/j.actpsy.2009.08.003. [DOI] [PubMed] [Google Scholar]
- Madison G, Merker B. Human sensorimotor tracking of continuous subliminal deviations from isochrony. Neuroscience Letters. 2004;370:69–73. doi: 10.1016/j.neulet.2004.07.094. [DOI] [PubMed] [Google Scholar]
- Mates J. A model of synchronization of motor acts to a stimulus sequence: I. Timing and error corrections. Biological Cybernetics. 1994;70:463–473. doi: 10.1007/BF00203239. [DOI] [PubMed] [Google Scholar]
- Michon JA. Timing in temporal tracking. Assen, The Netherlands: van Gorcum; 1967. [Google Scholar]
- Patel AD, Iversen JR, Bregman MR, Schulz I. Experimental evidence for synchronization to a musical beat in a nonhuman animal. Current Biology. 2009;19:827–830. doi: 10.1016/j.cub.2009.03.038. [DOI] [PubMed] [Google Scholar]
- Paulignan Y, MacKenzie C, Marteniuk R, Jeannerod M. Selective perturbation of visual input during prehension movements. Experimental Brain Research. 1991;83(3):502–512. doi: 10.1007/BF00229827. [DOI] [PubMed] [Google Scholar]
- Praamstra P, Turgeon M, Hesse CW, Wing AM, Perryer L. Neurophysiological correlates of error correction in sensorimotor-synchronization. Neuroimage. 2003;20(2):1283–1297. doi: 10.1016/S1053-8119(03)00351-3. [DOI] [PubMed] [Google Scholar]
- Pressing J. Error correction processes in temporal pattern production. Journal of Mathematical Psychology. 1998;42:63–101. doi: 10.1006/jmps.1997.1194. [DOI] [PubMed] [Google Scholar]
- Ragert M, Schroeder T, Keller PE. Knowing too little or too much: the effects of familiarity with a co-performer's part on interpersonal coordination in musical ensembles. Frontiers in Psychology. 2013;4 doi: 10.3389/fpsyg.2013.00368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauschecker JP, Scott SK. Maps and streams in the auditory cortex: nonhuman primates illuminate human speech processing. Nature Neuroscience. 2009;12(6):718–724. doi: 10.1038/nn.2331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Repp BH. Phase correction, phase resetting, and phase shifts after subliminal timing perturbations in sensorimotor synchronization. Journal of Experimental Psychology: Human Perception & Performance. 2001;27:600–621. [PubMed] [Google Scholar]
- Repp BH. Automaticity and voluntary control of phase correction following event onset shifts in sensorimotor synchronization. Journal of Experimental Psychology: Human Perception & Performance. 2002;28:410–430. [PubMed] [Google Scholar]
- Repp BH. Sensorimotor synchronization: A review of the tapping literature. Psychonomic Bulletin & Review. 2005;12:969–992. doi: 10.3758/bf03206433. [DOI] [PubMed] [Google Scholar]
- Repp BH. Perfect phase correction in synchronization with slow auditory sequences. Journal of Motor Behavior. 2008;40:363–367. doi: 10.3200/JMBR.40.5.363-367. [DOI] [PubMed] [Google Scholar]
- Repp BH. Temporal evolution of the phase correction response in synchronization of taps with perturbed two-interval rhythms. Experimental Brain Research. 2011;208(1):89–101. doi: 10.1007/s00221-010-2462-5. [DOI] [PubMed] [Google Scholar]
- Repp BH, Keller PE. Adaptation to tempo changes in sensorimotor synchronization: Effects of intention, attention, and awareness. Quarterly Journal of Experimental Psychology. 2004;57A:499–521. doi: 10.1080/02724980343000369. [DOI] [PubMed] [Google Scholar]
- Repp BH, Keller PE, Jacoby N. Quantifying phase correction in sensorimotor synchronization: Empirical comparison of different paradigms and estimation methods. Acta Psychologica. 2012;139:281–290. doi: 10.1016/j.actpsy.2011.11.002. [DOI] [PubMed] [Google Scholar]
- Repp BH, Steinman SR. Simultaneous event-based and emergent timing: Synchronization, continuation, and phase correction. Journal of Motor Behavior. 2010;42(2):111–126. doi: 10.1080/00222890903566418. [DOI] [PubMed] [Google Scholar]
- Schwartze M, Kotz SA. A dual-pathway neural architecture for specific temporal prediction. Neuroscience & Biobehavioral Reviews. 2013;37(10):2587–2596. doi: 10.1016/j.neubiorev.2013.08.005. [DOI] [PubMed] [Google Scholar]
- Semjen A, Schulze HH, Vorberg D. Timing precision in continuation and synchronization tapping. Psychological Research. 2000;63:137–147. doi: 10.1007/pl00008172. [DOI] [PubMed] [Google Scholar]
- Semjen A, Vorberg D, Schulze HH. Getting synchronized with the metronome: Comparisons between phase and period correction. Psychological Research. 1998;61:44–55. [Google Scholar]
- Soechting JF, Lacquaniti F. Modification of trajectory of a pointing movement in response to a change in target location. Journal of Neurophysiology. 1983;49(2):548–564. doi: 10.1152/jn.1983.49.2.548. [DOI] [PubMed] [Google Scholar]
- Spivey MJ, Grosjean M, Knoblich G. Continuous attraction toward phonological competitors. Proceedings of the National Academy of Sciences. 2005;102(29):10393–10398. doi: 10.1073/pnas.0503903102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Studenka BE, Zelaznik HN. Synchronization in repetitive smooth movement requires perceptible events. Acta Psychologica. 2011;136(3):432–441. doi: 10.1016/j.actpsy.2011.01.011. [DOI] [PubMed] [Google Scholar]
- ten Donkelaar HJ, Kaga K. The Auditory System. Berlin, Heidelberg: Springer Berlin Heidelberg; 2011. pp. 305–329. [Google Scholar]
- Tecchio F, Salustri C, Thaut MH, Pasqualetti P, Rossini PM. Conscious and preconscious adaptation to rhythmic auditory stimuli: A magnetoencephalographic study of human brain responses. Experimental Brain Research. 2000;135(2):222–230. doi: 10.1007/s002210000507. [DOI] [PubMed] [Google Scholar]
- Torre K, Balasubramaniam R. Two different processes for sensorimotor synchronization in continuous and discontinuous rhythmic movements. Experimental Brain Research. 2009;199(2):157–166. doi: 10.1007/s00221-009-1991-2. [DOI] [PubMed] [Google Scholar]
- Toiviainen P, Luck G, Thompson M. Embodied meter: hierarchical eigenmodes in music-induced movement. Music Perception. 2010;28:59–70. [Google Scholar]
- Vorberg D, Schulze HH. Linear phase-correction in synchronization: Predictions, parameter estimation, and simulations. Journal of Mathematical Psychology. 2002;46(1):56–87. [Google Scholar]
- Vorberg D, Wing A. Modeling variability and dependence in timing. In: Heuer H, Keele SW, editors. Handbook of perception and action. Vol. 2. London: Academic Press; 1996. pp. 181–262. [Google Scholar]
- Welsh TN, Elliott D. Movement trajectories in the presence of a distracting stimulus: Evidence for a response activation model of selective reaching. The Quarterly Journal of Experimental Psychology. 2004;57A:1031–1057. doi: 10.1080/02724980343000666. [DOI] [PubMed] [Google Scholar]
- Wing AM, Endo S, Bradbury A, Vorberg D. Optimal feedback correction in string quartet synchronization. Journal of the Royal Society Interface. 2014;11(93):20131125. doi: 10.1098/rsif.2013.1125. [DOI] [PMC free article] [PubMed] [Google Scholar]