A Role for Mixed Corollary Discharge and Proprioceptive Signals in Predicting the Sensory Consequences of Movements

Abstract

Animals must distinguish behaviorally relevant patterns of sensory stimulation from those that are attributable to their own movements. In principle, this distinction could be made based on internal signals related to motor commands, known as corollary discharge (CD), sensory feedback, or some combination of both. Here we use an advantageous model system—the electrosensory lobe (ELL) of weakly electric mormyrid fish—to directly examine how CD and proprioceptive feedback signals are transformed into negative images of the predictable electrosensory consequences of the fish's motor commands and/or movements. In vivo recordings from ELL neurons and theoretical modeling suggest that negative images are formed via anti-Hebbian plasticity acting on random, nonlinear mixtures of CD and proprioception. In support of this, we find that CD and proprioception are randomly mixed in spinal mossy fibers and that properties of granule cells are consistent with a nonlinear recoding of these signals. The mechanistic account provided here may be relevant to understanding how internal models of movement consequences are implemented in other systems in which similar components (e.g., mixed sensory and motor signals and synaptic plasticity) are found.

Introduction

Internally generated motor corollary discharge (CD) signals and proprioceptive feedback represent separate sources of information either of which could, in principle, be used to distinguish between external versus self-generated sensory input. However, there are few cases in which it has been possible to directly investigate the respective roles of CD and proprioception (Farrer et al., 2003; Cullen, 2004; Crapse and Sommer, 2008; Wurtz, 2008). One problem is the methodological difficulty of isolating CD and proprioception at the level of neural responses. Another is the difficulty of understanding how these signals actually contribute to sensory cancellation at the neural circuit level. Here we address this question in an advantageous model system—weakly electric mormyrid fish—in which CD and proprioception can be isolated and neural mechanisms for cancelling self-generated inputs are relatively well understood.

Weakly electric mormyrid fish possess an electric organ in their tail that generates an electric field, known as an electric organ discharge (EOD), and electroreceptors on their skin that are exquisitely sensitive to distortions of the field caused by nearby objects in the environment. However, the ability of the fish to use this active electrosensory system to detect and localize objects is complicated by the fish's own movements. Movements alter the position of the electric organ relative to electroreceptors and result in changes in the electric field that are as large, or larger, than those attributable to behaviorally relevant stimuli (Bastian, 1995; Chen et al., 2005; Sawtell and Williams, 2008; Fotowat et al., 2013). Previous studies suggest that this problem is solved in the electrosensory lobe (ELL)—the first central stage of electrosensory processing (Bell, 2001; Bol et al., 2011). ELL principal cells integrate somatotopically organized input from electroreceptors with input from a mossy fiber–granule cell–parallel fiber system that conveys a wide variety of information, including both CD and proprioceptive feedback related to movements (Bell et al., 2008). Evidence from in vivo, in vitro, and modeling studies of mormyrid fish suggest that anti-Hebbian synaptic plasticity at parallel fiber synapses generates negative images that serve to cancel out components of the principal cell response that are predictable based on signals conveyed by parallel fibers (Bell, 1981; Bell et al., 1997b; Roberts and Bell, 2000; Kennedy et al., 2014).

Although separate studies have provided evidence for negative images based on CD alone and proprioception alone (Sawtell and Williams, 2008; Requarth and Sawtell, 2014), little is known about how negative images are generated under conditions resembling self-generated movements, in which both streams of information are available. Here we show that ELL neurons can form approximately equivalent negative images based on either CD or proprioception and that, under conditions approximating self-generated tail movements, both are used. We develop a network model that explains unexpected features of negative images by assuming that plasticity acts on random, nonlinear mixtures of CD and proprioception. Finally, we provide support for the model by demonstrating that CD and proprioception are randomly mixed in spinal mossy fibers and that properties of granule cells are consistent with a nonlinear recoding of these signals.

Materials and Methods

Experimental preparation.

All experiments performed in this study adhere to the American Physiological Society Guiding Principles in the Care and Use of Animals and were approved by the Institutional Animal Care and Use Committee of Columbia University. Mormyrid fish (7–14 cm in length) of either sex of the species Gnathonemus petersii were used in these experiments. Surgical procedures to expose eminentia granularis posterior (EGp) for recording were similar to those described previously (Sawtell, 2010). An additional anterior portion of the skull was removed to expose the optic tectum. The anesthetic (MS-222; 1:25,000) was then removed. To evoke tail movements, we targeted microelectrodes (tungsten, 0.005-inch-diameter, 5 MΩ, 12° beveled tip; A-M Systems) to a site in the anterior portion of the optic tectum that evoked ipsilateral movements, consistent with previous reports in goldfish (Herrero et al., 1998). Brief, high-frequency (10–15 pulses at 500 Hz) microstimulation evoked rapid, isolated tail movements. A laser displacement sensor (LK-503; Keyence) measured tail displacement from the midline (spatial precision, 50 μm; measurement delay, 2 ms). After tail movements were measured, gallamine triethiodide (Flaxedil) was given (∼20 μg/cm body length) to paralyze the fish. Paralysis blocks the effect of motor neurons on all muscles, including the electric organ, which prevents the EOD. The motor command signal that would normally elicit an EOD continues to be generated by the fish at a variable rate of 2–5 Hz. The EOD motor command can be measured precisely (see below). This preparation allows us to observe the central effects of movement-related CD in isolation from the electrosensory input that would normally result in an EOD and in isolation from the proprioceptive input that would normally occur as a result of movements.

To engage proprioceptive feedback, tectal microstimulation-evoked tail displacement was measured by a laser and then that signal was fed back into the servomotor to deliver passive tail movements that mimicked the microstimulation-evoked movement before paralysis. The fish's tail was lightly held between two glass rods positioned posterior to the electric organ. The rods were held by a manipulator mounted to a computer-controlled servomotor (Pacific Laser Equipment). A partition was placed between the tail and the rest of the fish to prevent water waves from activating lateral line receptors. Movements were ∼20° from the midline at velocities up to 200°/s.

Electrophysiology.

The EOD motor command signal was recorded with an electrode placed over the electric organ in the tail. Extracellular recordings from the medial zone (MZ) of ELL were made with glass microelectrodes filled with 2 m NaCl (8–10 MΩ). ELL contains three zones, each of which contains a somatotopic map of the body surface and is innervated by a distinct class of electroreceptor afferent. MZ afferents are sensitive to changes in the amplitude of the fish's own EOD, dorsolateral zone (DLZ) afferents to the amplitude and shape of the EOD, and ventrolateral zone afferents to low-frequency electrical fields, e.g., those emitted by other animals in the water. Responses of both MZ and DLZ afferents are affected strongly by tail movements. This study focuses on the MZ because negative images based on proprioception and skeletomotor CD have been characterized previously in this zone (Sawtell and Williams, 2008; Requarth and Sawtell, 2014). Previous observations that plasticity and negative images based on electric organ CD are similar in all three zones of ELL (Bell, 1982; Bell and Grant, 1992; Kennedy et al., 2014) suggest that the present results from the MZ may generalize to the other zones of ELL. Identification of ELL cell types was aided by previous intracellular recording and labeling studies in which characteristic electric organ CD (EOCD) and electrosensory responses were linked with cell morphology (Bell and Grant, 1992; Bell et al., 1997a; Mohr et al., 2003). Because ELL is a laminar structure, with different cell types located in different layers, recording location is also useful in identifying cell types. The laminar location of the recording electrode within ELL can be judged accurately based on characteristics of prominent EOCD-evoked and electrosensory stimulus (ES)-evoked field potentials (Bell and Grant, 1992; Bell et al., 1992). ELL cells can be classified broadly as E- or I-cells: E-cells are excited by an increase in local EOD amplitude in the center of their receptive fields, and I-cells are inhibited by such a stimulus. We recorded from I-cells located in or just above the ganglion layer, which likely included both interneurons (medium ganglion MG1 cells) and efferent neurons known as large ganglion cells. We also recorded from E-cells located below the ganglion layer, which were probably efferent neurons known as large fusiform cells.

Extracellular recordings from mossy fibers were made with glass microelectrodes filled with 2 m NaCl (40–100 MΩ). Criteria for distinguishing mossy fiber recordings from other EGp units were the same as those described previously (Sawtell, 2010).

In vivo whole-cell recordings from granule cells in EGp were made using methods described previously (Sawtell, 2010). Electrodes (9–12 MΩ) were filled with an internal solution containing K-gluconate (122 mm), KCl (7 mm), HEPES (10 mm), Na₂ATP (0.5 mm), MgATP (2 mm), EGTA (0.5 mm), and 0.5% biocytin, pH 7.2, 280–290 mOsm). No correction was made for liquid junction potentials. Only cells with stable membrane potentials more hyperpolarized than −50 mV and access resistance <100 MΩ were analyzed. All experiments were performed without holding current, unless noted otherwise. Membrane potentials were filtered at 3–10 kHz and digitized at 20 kHz (CED Power1401 hardware and Spike2 software; Cambridge Electronics Design).

ES pairing experiments.

ES pairing experiments were conducted using extracellular recordings from ELL principal cells. Cells that did not show plasticity (∼15% of all recorded cells) under any condition were excluded from the analysis. This is not unexpected, because there are known nonplastic cell types in ELL (Mohr et al., 2003).

Electrosensory responses were evoked by simultaneous global stimulation of the entire fish and local stimulation restricted to small area of the skin. Global stimuli were delivered by passing current between a small chloride silver ball inserted through the mouth into the stomach of the fish and a second electrode placed in the water near the tail of the fish in an outside-positive configuration. The ES referred to here is the modulation of the local field. Local stimuli were delivered with a bipolar stimulating electrode consisting of two small Ag–AgCl balls 5 mm apart. The electrode was held perpendicular to the skin at a distance of ∼2 mm. For both global and local stimuli, brief pulses of current were delivered 4.5 ms after EOD command through the electrodes to activate electroreceptors. Absolute current strength for local stimuli ranged from ±5 to 10 μA, whereas current strength for global stimuli ranged from 200 to 400 mA. These values were chosen such that the amplitude of electrosensory-evoked field potentials evoked by global stimulation approximately matched those evoked by the EOD, as measured in a previous study in which the natural EOD was left intact (Sawtell and Williams, 2008). The strength and polarity of the local stimulus was adjusted to approximately mimic the increases and decreases in electrosensory-evoked field potentials observed previously in response to ipsilateral and contralateral tail bends (Sawtell and Williams, 2008). Small adjustments to the local amplitude were made on a cell-by-cell basis to strongly inhibit the cell with minimal current. The spatial profile of the local stimulus used here is unlike changes in the amplitude of the fish's electrical field generated by actual tail movements, which are probably more spatially diffuse. Modulations of the local ES amplitude were used here (instead of modulation of the global stimulus amplitude) because they result in stronger modulations of ELL neuron firing and more rapid formation of negative images. We controlled EOD motor command rate by lowering a concentric bipolar stimulating electrode (FHC) into the brain along the midline in or near the axons of the pre-command nucleus, which course close to the midline along the ventral surface of the brainstem to the command nucleus (∼5 mm depth). Brief, single pulses of 0.2 ms reliably evoked an EOD motor command at low current strengths (10–20 μA), allowing experimental control over discharge frequency. We typically microstimulated the EOD command at ∼13 Hz.

In ES pairing experiments, we varied the amplitude of the local ES in the center of the receptive field of the recorded cell to deliver a time-varying pattern of electrosensory stimulation based on the waveform of the tail movement recorded before paralysis. Because change in local EOD amplitude is proportional to tail displacement for small angles, such a protocol approximates the electrosensory consequences induced by real tail movements. Tectal microstimulation was always separated by at least 1.25 s. Pairing was conducted for 10–15 min. The neural response to tectal microstimulation and/or tail displacement was compared immediately before and after the pairing period.

Computational model and analytical results.

Our simulated network consisted of an intermediate layer of n = 2000 units with a sigmoid nonlinear input–output function f_s,θ(x) = $1/\left(1+\exp \left(\frac{\theta -x}{s}\right)\right)$, with threshold (i.e., half-maximum point) θ = 0 and scale s = 0.2. Each unit received “paired” and “unpaired” inputs, x_i^p(t) and x_i^u(t), which were determined as follows. For each intermediate layer unit, we selected two functions randomly, independently, and uniformly from the set {cos2πkt, sin2πkt; k = 1, 2,…, 50}. Each selected function was then independently designated as paired or unpaired with equal probability. The input x_i^p(t) was then set as the sum of the (up to two) paired functions, and the input x_i^u(t) was then set as the sum of the (up to two) unpaired functions. Throughout, the weights were trained under the conditions that only the paired inputs x_i^p were active and the unpaired inputs x_i^u set to 0, such that the network output, defined as the sum of the nonlinear units with weights w_i, was given by the following:

Under these conditions, plasticity was simulated by setting the weights w_i to minimize the expected least-squared error between the network output V(t) and the target function h(t), with t ranging over the interval [0, 1] to represent time after movement motor command. Assuming the individual units to be noisy, the expected least-squares error is obtained by setting the weights w as follows:

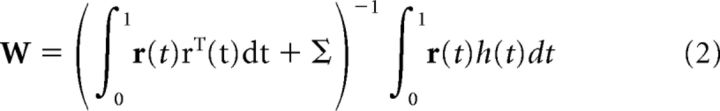where r(t) is a vector containing the outputs of the nonlinear units at time t, and Σ is a diagonal matrix with entries equal to the trial-to-trial variance of the output of each nonlinear unit. In our simulations, we set the diagonals of the noise matrix as Σ_ii = 10.

Once the weights were determined, we calculated the network output under three probe conditions: (1) with just the paired input present, given by Equation 1; (2) with just the unpaired inputs $V\left(t\right)={\displaystyle {\sum }_{i=1}^N{w}_i{f}_{s,\theta }\left(x_i^u\left(t\right)\right)}$; and (3) with the two inputs combined $V\left(t\right)={\displaystyle {\sum }_{i=1}^N{w}_i{f}_{s,\theta }\left(x_i^p\left(t\right)x_i^u\left(t\right)\right)}$. The plotted results were averages of 15 repeated simulations with different randomly chosen input functions and labels provided to each nonlinear unit.

To analyze the parameter dependence of the observed suppression effect (see Fig. 4E), we considered learning rules in which the magnitude of the weight change is proportional to the presynaptic firing rate during learning. For simplicity, we considered learning a single time point (i.e., no t dependence) with the input values x^p and x^u independently distributed as Gaussian variables with 0 mean and unit variance. In this case, the output enhancement/suppression, given as the product of the weight change magnitude |Δw|∼f_s,θ(x^p) and the difference in firing rates f_s,θ(x^p + x^u) − f_s,θ(x^p) has the following expectation value:

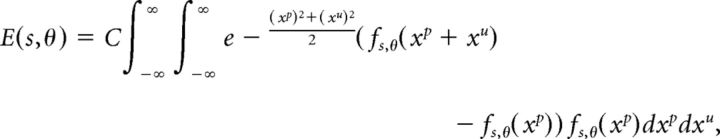with the proportionality constant C depending on the learning rate and duration of pairing. We plotted the above expression with C set to normalize the maximum magnitude of the above expression to unity.

Figure 4.

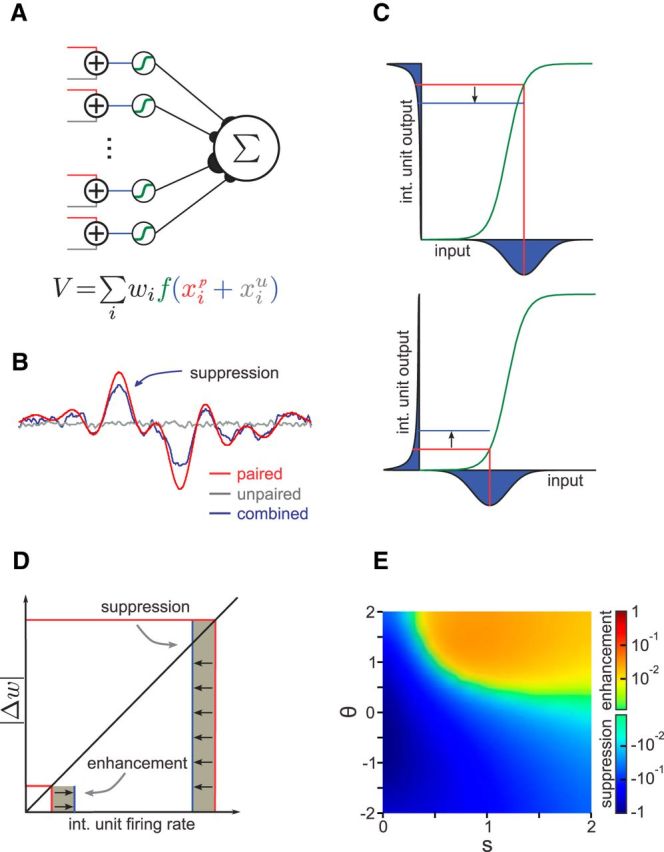
Network model with randomly combined inputs and nonlinear processing. A, Model schematic. The paired (red) and unpaired (gray) inputs are added and passed through an intermediate layer containing a sigmoid nonlinearity (green). The network output is the weighted sum of the outputs of the intermediate layer units. B, Simulation results when the network fits an arbitrary function with only the paired inputs active but is tested in three cases: (1) paired inputs only (red); (2) unpaired inputs only (gray); and (3) both inputs combined (blue). The unpaired input suppresses the learned response of the network to the paired input. C, Interaction between the paired and unpaired inputs to an intermediate layer unit, with a sigmoid nonlinearity (green). The paired input value and resulting output are indicated by vertical and horizontal red lines, respectively. For the given paired input value (vertical red lines), the distributions (over values of the unpaired input) for the combined input (x-axis) and resulting combined output (y-axis) are shown in blue. The blue line indicates the mean output in the combined case. Top, When the paired input falls within the concave region of the nonlinearity (above the threshold), the output distribution is skewed such that the mean combined output is below the response to the paired input alone. Bottom, When the paired input falls within the convex region of the nonlinearity (below the threshold), the output distribution is skewed such that the mean combined output is above the response to the paired input alone. int., Intermediate layer. D, Contributions of the intermediate layer interactions shown in C to network output. The contribution to the change in network output (shaded area) is given by the product of the change in weight and the firing rate. Because the magnitude of the learned weight change is proportional to the firing rate, the suppression of high firing rates by the unpaired input has a larger effect on the learned response of the network than the enhancement of low firing rates. E, Parameter dependence of suppression/enhancement effects. The effect of suppression is stronger and favored for either low thresholds (θ) and/or narrow nonlinearity widths (s). The threshold and width are in units of the paired input SD, with a threshold value of 0 corresponding to the mean of the training input distribution. Values are plotted relative to the maximum effect magnitude on a logarithmic scale (see Materials and Methods).

Data analysis and statistics.

Data analysis was performed offline in MATLAB (MathWorks) and Spike2 (Cambridge Electronic Design). Data are expressed as mean ± SD, unless otherwise noted.

We constructed granule cell input–output curves as follows. After obtaining a stable whole-cell configuration, small amounts of current were injected into cells in 5 s steps. Spikes were counted from 0 to 60 ms after the EOD motor command. Spikes were rarely observed outside of this window except at the highest currents. Data were used to fit to a sigmoid input–output function defined by the following equation:

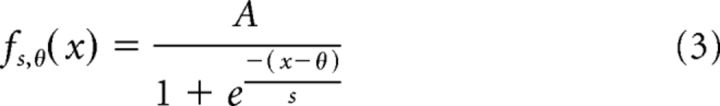where f(x) equals either spike count per command or instantaneous firing rate as a function of current injection amplitude, x equals current step value, θ is half-maximum point in picoamperes, and s reflects the inverse of the steepness of the sigmoid. All fit parameters are collated into Table 1.

Table 1.

Fit parameters for granule cell input–output functions

Parameters	Granule cell
	1	2	3	4	5	6
Spikes/cmd
A (spikes/cmd)	1.86	3.55	2.01	6.19	3.94	2.49
θ (pA)	35.2	13.8	9.42	10.9	15.1	11.9
s (pA)	7.78	1.46	0.497	1.31	3.61	1.85
V50 (mV)	16.0	13.6	16.0	14.8	9.66	7.54
Peak instantaneous firing rate
A (Hz)	165.7	136.2	90.6	192.9	204.9	121.4
θ (pA)	35.2	11.2	9.37	11.0	11.2	11.9
s (pA)	7.78	1.46	0.497	1.31	3.61	1.85
V50 (mV)	16.0	13.6	16.0	14.8	9.66	7.54

Input–output responses (Fig. 6A) for six granule cells were fit to a sigmoid nonlinearity (see Eq. 3 in Materials and Methods). Spikes/cmd refers to the number of action potentials observed up to 60 ms after the EOD motor command. The bottom half lists parameters when peak instantaneous firing rate was calculated rather than spikes/cmd.

We constructed a current versus voltage curve by measuring the mean change in membrane potential attributable to current injection. V₅₀ is the membrane depolarization corresponding to the fitted half-maximum point current injection. EOCD amplitude was defined as the peak depolarization relative to the resting potential calculated from the average response to the EOD command in the absence of holding current. Tail depolarization was defined as the peak depolarization caused by temporal summation of proprioceptive EPSPs during passive tail bending measured relative to the resting membrane potential. EOCD + tail is the arithmetic sum of those two calculated values.

Integrated modulations of ELL principal cells or mossy fibers were computed by summing over a small window (200 ms) after tectal microstimulation or onset of passive tail movement. Values are expressed in percentage change from baseline firing rate.

Tests for statistical significance are noted in the text. Differences were judged to be significant at p < 0.05.

Results

Nonlinear interactions between negative images based on CD and proprioception

Although roles for CD and proprioception in the generation of negative images in the mormyrid ELL have been described previously (Sawtell and Williams, 2008; Requarth and Sawtell, 2014), it is not known how such signals interact under conditions resembling self-generated movements, i.e., when both streams of information are available. We explored such interactions by performing a series of experiments in which we compared responses of ELL neurons before and after pairing an ES with different movement-related signals, i.e., CD, proprioception, or both. These experiments took advantage of a previously developed “fictive” movement preparation (Sawtell and Williams, 2008; Requarth and Sawtell, 2014). Before neuromuscular paralysis, microstimulation of the optic tectum is used to evoke a rapid tail movement that moves the electric organ closer to the receptive field of the recorded cell. After paralysis, microstimulation evokes movement motor commands in the absence of movement, allowing us to monitor the effect of CD signals on neural responses in the absence of proprioceptive feedback. In addition, we can move the tail passively with a computer-controlled stage in a way that mimics the tail movement evoked by tectal microstimulation before paralysis. This setup allows us to engage CD and proprioceptive inputs either separately or together and, as described next, to control their relationship to an ES. It is likely that proprioceptive responses induced by passive movements in paralyzed fish are similar to those attributable to natural movements. Proprioception in fish is simpler than in higher vertebrates, being mediated by free endings in muscle tissue and tendons rather than by a more elaborate muscle spindle (Barker et al., 1974; Srivastava, 1977; Bone, 1979; Srivastava, 1979). The lack of muscle spindles implies that fish do not possess any functional or anatomical equivalent of the independent efferent control over proprioceptors exerted by the gamma motoneurons, as described in mammals (Boyd, 1980; Hulliger, 1984). Finally, it is important to note that the movement-related CD signals that are a focus of this study are completely distinct from EOCD signals that have been the focus of numerous previous studies of mormyrid fish.

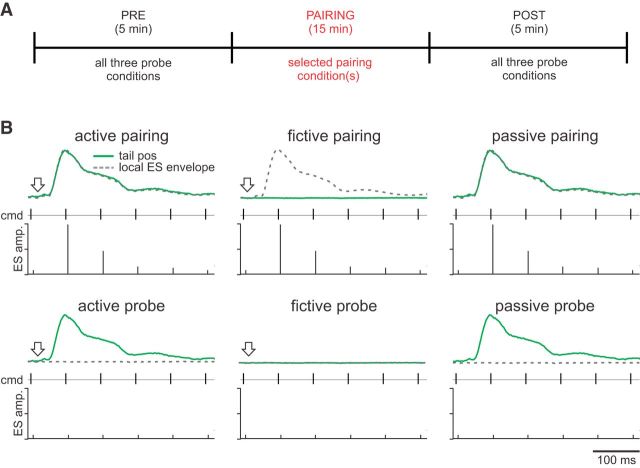
We studied negative images in well isolated single units recorded in the MZ of ELL (see Materials and Methods). Based on recording depth, EOCD, and electrosensory responses, these units likely included both MG cells and E- and I-type efferent cells (see Materials and Methods). Units were tested under three conditions before and after pairing with a local ES. During the pairing, we modulated the ES amplitude in a pattern that matched the temporal profile of the tail movement (mimicking the electrosensory effects of moving the electric organ closer to electroreceptors on the skin) and paired with one or more conditions (Fig. 1A). We refer to conditions in which the ES was unmodulated as “probes.” The pairing and probe conditions are schematized in Figure 1B. The conditions are as follows: (1) active, in which we microstimulated the optic tectum (arrow) in a paralyzed fish while delivering a rapid tail movement that matched the temporal profile of the microstimulation-evoked movement measured before paralysis (green trace), thereby engaging both CD and proprioceptive feedback; (2) fictive, in which tectal microstimulation was delivered in the absence of a tail movement, thereby engaging CD without proprioceptive feedback; and (3) passive, in which a rapid tail movement was delivered without microstimulation, thereby engaging proprioceptive feedback without CD. Hence, this preparation allowed us to engage movement-related signals—CD and proprioception—either separately or together and to monitor their effects on neural responses before and after manipulating their electrosensory consequences.

Figure 1.

Schematic of pairing experiment protocols. A, In all experiments, ELL neuron responses were recorded extracellularly in the MZ under three conditions (active, fictive, and passive; described below) before and after a 15 min pairing period with an ES under one or more of these conditions. B, The three conditions are as follows: (1) active (left column), in which we microstimulated the optic tectum while delivering a rapid tail movement; (2) fictive (middle column), in which tectal microstimulation was delivered in the absence of a tail movement; and (3) passive (right column), in which a rapid tail movement was delivered without microstimulation. For each condition, during pairing, the ES was modulated in a pattern that matched the temporal profile of the tail movement before paralysis (top row, dotted gray line). Before and after pairing, the ES was unmodulated (bottom row). In each panel, the top green trace represents passive tail movements. The dotted gray trace is the waveform envelope used to determine the amplitude of the local ES. The middle row shows the timing of the EOD motor commands. The bottom row schematizes the local ES. The local ES amplitude was set to the value of the envelope at the time of the command. A constant-value global ES was delivered in conjunction with the local one. The arrow, when present, represents the time of microstimulation. amp, Amplitude; cmd, command; tail pos, tail position.

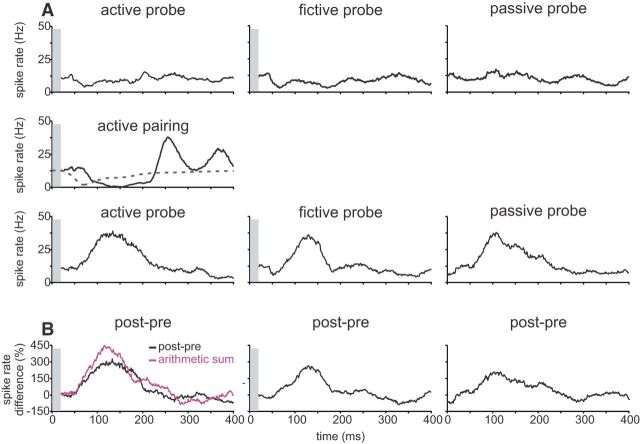
Data from one neuron in which an ES was paired under the active condition is shown in Figure 2. Before pairing, the neuron exhibited little response under active, fictive, or passive probe conditions (Fig. 2A, top row). After pairing, the neuron exhibited a strong response during the active probe that was opposite in polarity and approximately matched in time to the response evoked by the ES during pairing, i.e., the change in the response (Fig. 2B, post-pre) resembled a negative image of the effect of the ES during pairing. Because later components of the electrosensory response during pairing (>200 ms) were not always reflected in negative images, we focused our analysis on the initial component of the negative image. Note that previous studies have shown that negative images are bidirectional, i.e., pairing with an excitatory ES results in a reduction in the neural response after pairing, whereas pairing with an inhibitory ES results in an increase (Bell, 1982; Requarth and Sawtell, 2014). To facilitate a quantitative comparison of negative images across different neurons, we always paired with an inhibitory ES, i.e., a decrease in local EOD amplitude for E-cells and an increase in local EOD amplitude for I-cells.

Figure 2.

ELL neurons exhibit negative images when paired under the active condition. A, Representative ELL neuron recorded extracellularly while being paired under the active condition. Before pairing, the neuron exhibited little response to the active, fictive, and passive probe conditions (top row). During pairing, the neuron was inhibited by an ES that was modulated in a pattern that matched the temporal profile of the tail movement before paralysis (middle row). After pairing, the neuron exhibited strong responses under all three probe conditions that were opposite in polarity and approximately matched the temporal profile of the response evoked by the ES during pairing (bottom row). B, Difference traces reveal negative images under all three conditions. Note that the arithmetic sum of the fictive and the passive (purple) is less than the response observed under the active condition. In all panels, gray bars obscure microstimulation artifacts.

Interestingly, after pairing under the active condition (tectal stimulation plus passive tail displacement), negative images were also observed under fictive (tectal stimulation alone) and passive (tail displacement alone) probe conditions (Fig. 2B). These results suggest that both CD and proprioceptive feedback are used to generate negative images if both signals are available. Moreover, negative images based on CD and proprioceptive feedback appeared similar in their magnitude and timing. As will be discussed further below, negative images observed under active conditions, i.e., based on CD and proprioception, were smaller than would be expected based on a linear summation of negative images observed under fictive and passive conditions, i.e., based on CD and proprioception alone (Fig. 2B). Results for all active pairings (n = 9), along with those for additional experiments in which negative images were induced by pairing an ES with only one class of movement-related signal (fictive and passive pairings), are summarized in Figure 3. Pairing under fictive or passive conditions revealed negative images for the paired condition but not for the unpaired condition (fictive, n = 9; passive, n = 8; Fig. 3B,C). Hence, negative images can be formed using either CD or proprioceptive feedback alone and do not “transfer” across modalities.

Figure 3.

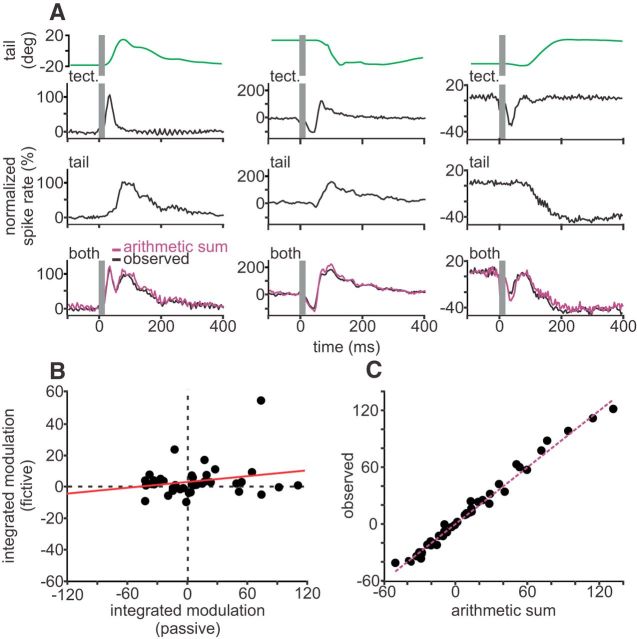
Negative images reveal nonlinear interactions between CD and proprioception. A, Active pairing. Average of difference traces across ELL neurons showing effects of pairing under active conditions, during which an ES was paired with simultaneous tectal microstimulation and a rapid tail movement. Left, Difference trace measured under the paired (active) condition. Middle, Difference trace measured when probing under the fictive condition. Right, Difference trace measured when probing under the passive condition. Note that the passive and fictive contributions do not sum linearly (purple line is arithmetic sum of fictive and passive traces). B, Fictive pairing. Average of difference traces across ELL neurons showing effects of pairing under fictive conditions, during which an ES was paired with tectal microstimulation alone. Note that probing under active conditions reveals a reduced negative image relative to the arithmetic sum (purple). C, Passive pairing. Average of difference traces across ELL neurons showing effects of pairing under passive conditions, during which an ES was paired with a rapid tail movement alone. Note that probing under active conditions reveals a reduced negative image. D, Pairing alternately under active and passive conditions. Average of difference traces across ELL neurons showing effects of pairing under active and passive conditions, during which an ES was alternately paired with rapid tail movements alone, followed by simultaneous rapid tail movements and microstimulation. Note that similar negative images were formed in both trained conditions (left and right panels) despite a robust contribution from CD signals (middle panel). E, Scatter plot of all recorded ELL neurons, plotting the observed response under the active condition versus the arithmetic sum of the fictive and passive conditions. Note that nearly all dots lie below the unity line (dotted purple). In all panels, gray outlines indicate SEM across cells and gray bars obscure microstimulation artifacts.

Fictive and passive pairings also revealed unexpected interactions between CD and proprioception. Namely, we found that, when both the paired and unpaired signals were engaged (Fig. 3B,C, active probes), negative images induced by fictive or passive pairings were reduced, i.e., negative images observed under the active condition were less than the arithmetic sum of the responses observed under the passive and fictive conditions (fictive: arithmetic, 199 ± 113% change in integrated modulation; observed, 117 ± 58% change in integrated modulation, n = 9, p = 0.027; passive: arithmetic, 168 ± 106% change in integrated modulation; observed, 85 ± 55% in integrated modulation, n = 8, p = 0.0035, paired t test; Fig. 3B,C, left column). Hence, the presence of the unpaired signal suppresses the negative images based on the paired signal. Although sublinear summation of synaptic inputs onto the principal cells themselves, attributable to reduction in driving force, could explain the sublinear combination of inputs observed under conditions of active pairing (Figs. 2B, 3A), the suppressive effects observed under conditions of fictive or passive pairing (Fig. 3B,C) seem to require additional explanation.

A final set of pairing experiments provided additional evidence for nonlinear interactions between CD and proprioception and also suggested a functional interpretation for such interactions. In these experiments, we probed all three conditions, as above, but then paired the ES alternately under active and passive conditions. ELL neurons exhibited a capacity to form similar negative images based on CD and proprioception (Fig. 3D, active probe) or on proprioception alone (Fig. 3D, passive probe). Moreover, as expected for a nonlinear system but not a linear one, probing under fictive conditions revealed a contribution from CD signals (Fig. 3D, middle column). The capacity to form similar negative images based on different but overlapping sets of signals, e.g., CD and proprioception under active conditions and proprioception alone under passive conditions, could be ethologically relevant. A given change in the position of the electric organ relative to electroreceptors will have the same electrosensory consequence regardless of whether it is self-generated (engaging both CD and proprioception) or attributable to external forces (engaging proprioception alone). Cancellation of movement-related electrosensory input under such conditions would require the capacity to generate equivalent negative images based on CD and proprioception or proprioception alone.

Finally, consistent with a nonlinear system, the scatter plot of all recorded cells shows that the observed response during the active probe condition is consistently less than the arithmetic sum of the fictive and passive probe conditions (Fig. 3E; arithmetic, 277 ± 214% change in integrated modulation; observed, 178 ± 149% change in integrated modulation, n = 34, p < 0.0001, paired t test).

Explanation of nonlinear interactions by a simple network model

We used the properties of negative images described above—suppression of the paired response by the unpaired input, lack of transference, and sublinear combination of inputs—to constrain a simple network model of negative image formation (Fig. 4A). The model includes both paired (red) and unpaired (gray) inputs, which are combined in an intermediate layer. Fifty percent of the intermediate layer units received both paired and unpaired input, and 50% received only paired or unpaired input. The firing rate of each intermediate layer unit is determined by applying an input–output function to the sum of its inputs. The output of the network is then given by the weighted sum of the firing rates of the intermediate layer units. Considered in relation to ELL circuitry, the two sets of input signals represent proprioceptive and CD information carried by the mossy fibers, the intermediate layer units correspond to granule cells, and the output layer represents an ELL principal cell. Because the mossy fibers carrying proprioceptive and CD signals are tonically active (Bell et al., 1992; Sawtell, 2010), the input values used in the mathematical model correspond to modulations around this tonic rate. These modulations can be positive or negative, corresponding to increases or decreases in the input drive to granule cells.

To simulate the experimental pairing protocol, we trained the network output (i.e., the ELL principal cell response) to fit an arbitrary function by least mean-squared learning of the weights (Fig. 4B; see Materials and Methods). To mimic the different conditions during training and probing, we trained the network using only one set of inputs (i.e., proprioceptive or CD) and then testing in three cases: (1) paired inputs only, (2) unpaired inputs only, and (3) both inputs combined. These conditions mimic the experiments in Figure 3, B or C, allowing us to investigate the conditions under which the network exhibited the experimentally observed properties of (1) lack of transference across input modalities, and (2) sublinear combination of inputs, and (3) suppression of the negative image by the unpaired response.

For the network to exhibit a lack of transference, as observed in the negative images, the signals provided by the two sets of inputs to a given intermediate layer unit (i.e., a granule cell) must be on average uncorrelated with each other. That is, an intermediate layer unit cannot preferentially receive similarly tuned paired and unpaired inputs. For the network to exhibit the observed sublinear addition of the responses to the paired and unpaired inputs, the network must contain a nonlinearity after the paired and unpaired inputs are combined in the intermediate layer; otherwise, the response to the combined inputs would simply be the sum of the responses to the individual inputs. Note that the model does not distinguish between the cases in which the mixing occurs within the granule cells or upstream within the mossy fibers. Therefore, we simulated the pairing and probing procedures as follows: the paired and unpaired inputs were uncorrelated, and a sigmoid input–output function was applied at the intermediate layer units (Fig. 4B). This network clearly recapitulates both the lack of transference from paired response to unpaired response (Fig. 4B, gray line) and the sublinear combination of inputs (Fig. 4B, blue line).

To explore the origin of the observed suppressive effects, we examined the interaction among the paired input value, the unpaired input distribution, and the parameters of the nonlinearity (Fig. 4C). We first considered the relationship between the responses to the paired and combined (i.e., paired plus unpaired) inputs at the level of an individual granule cell. For a given paired input, if the unpaired input is positive (i.e., increases the input drive of the granule cell above the tonic level), then the firing rate of the intermediate layer unit increases. If the unpaired input is negative (i.e., decreases the input drive of the granule cell below the tonic level), then the firing rate of the intermediate layer unit decreases. By considering the probability distribution of all possible unpaired inputs (Fig. 4C, distributions below the horizontal axes), an expected value of the combined response can be calculated (Fig. 4C, horizontal red lines). For the symmetric unpaired input distribution modeled here, the expected input strength (Fig. 4C, vertical red lines) for the combined case is equal to that of the paired input. However, because of the nonlinearity of the input–output function in the intermediate layer unit, the expected output firing rate for the combined case does not necessarily equal the output response to the paired input alone (Fig. 4C, horizontal blue lines). For example, because of saturation effects near the concave region of the input–output function of the intermediate layer unit, increases in input can have less effect on the output response than decreases in input. Thus, when the paired input falls in the concave region of the nonlinearity, the firing rate distribution during the combined case is skewed such that the mean of the distribution is less than the response to the paired input alone (Fig. 4C, top), consistent with Jensen's inequality. Therefore, when the paired input is combined with the unpaired input distribution, there will be on average a reduction in the firing rate of the intermediate layer unit, which contributes to suppression of the learned response. The opposite case, in which the nonlinearity threshold is high relative to the value of the paired input, results on average in an increase in the firing rate of the intermediate layer unit (Fig. 4C, bottom), which would, hypothetically, contribute to enhancement of the learned response. Because the output unit receives a large number of inputs from the intermediate layer—MG cells are estimated to receive on the order of 20,000 granule cell inputs (Meek et al., 1996)—we are justified in focusing on the average change of the output in an intermediate layer unit attributable to the addition of the untrained input.

For a given input pattern to the network, some intermediate layer units receive strong input above the threshold, and others receive weak input below the threshold. Whether there is net suppression or net enhancement depends on the distribution of paired inputs relative to the distribution of thresholds. However, if the magnitude of the synaptic weight change is proportional to the input firing rate, as suggested by previous experimental and theoretical studies (Roberts and Bell, 2000; Harvey-Girard et al., 2010), the reduction of high firing rates by the unpaired input will have a larger effect on the output of the network than the enhancement of low firing rates (Fig. 4D). As a result, suppression rather than enhancement occurs in a large region of the parameter space for the width and threshold of the nonlinearity (Fig. 4E; see Materials and Methods). Furthermore, even for parameters that favor enhancement, the effect of this enhancement is substantially less than that of suppression in other parameter regions. This last point is important because granule cell populations exhibit a distribution of thresholds (Kennedy et al., 2014) and nonlinearity widths (See Table 1).

Overall, this theoretical account suggests that all of the observed properties of negative images observed experimentally can be explained by a simple network architecture, inspired by ELL circuitry, in which CD and proprioceptive inputs are coded as random nonlinear mixtures before the strength of these inputs is adjusted at the level of the principal cells.

Mixtures of proprioceptive and CD signals conveyed by a spinal mossy fiber pathway

The model described above suggests that random, nonlinear mixtures of CD and proprioception can explain properties of negative images. We next asked how these signals are actually represented, beginning at the level of the mossy fiber inputs to granule cells. Previous anatomical, physiological, and inactivation studies suggest that CD and proprioceptive information used for negative images is conveyed via spinocerebellar mossy fiber pathways that terminate on granule cells located in the EGp (Bell et al., 1981, 1992; Requarth and Sawtell, 2014). Two such pathways exist, sharing numerous similarities with dorsal and ventral spinocerebellar pathways in mammals. The first is a dorsal column pathway consisting of the axons of primary sensory neurons that project to the lateral funicular nucleus (FL2), which in turn provides mossy fiber input to the ipsilateral EGp (Szabo et al., 1979). The second originates from a lateral cell column extending over all spinal segments and sends mossy fibers directly to the contralateral EGp (Szabo et al., 1990). Although previous studies have shown that mossy fibers originating from the spinal cord respond to passive body movements (engaging proprioception) and to tectal microstimulation of brain centers that evoke movement (engaging CD; Sawtell, 2010; Requarth and Sawtell, 2014), it is not known whether individual mossy fibers respond to both classes of input. Furthermore, nothing is known about the specific nature of responses in FL2 neurons.

First, we recorded from putative FL2 neurons deep in the brainstem. Although putative FL2 neurons could be strongly modulated by passive displacement of the tail, trunk, or fins, none responded to tectal microstimulation, suggesting that this pathway is predominantly or entirely sensory (n = 10; data not shown). Next, we used high-resistance microelectrodes to record extracellularly from putative mossy fiber axons in EGp itself, as described previously (Bell et al., 1992; Sawtell, 2010). These recordings likely represent axons originating both from FL2 and directly from the spinal cord. We found numerous mossy fibers within EGp that exhibited responses to both tectal microstimulation and passive tail displacements (n = 42). The fraction of fibers exhibiting such mixed responses was approximately one-third in our experiments, although this is likely to be an underestimate. Because we only moved the caudal portion of the tail of the fish, we would have missed proprioceptive responses related to other body parts, such as the trunk and fin, which have been observed in other studies (Bell et al., 1992; Sawtell, 2010). Likewise, we microstimulated at just one site in the tectum using just one set of stimulation parameters. Additional microstimulation sites or parameters or more natural patterns of motor commands could have revealed additional CD responses.

Mossy fibers that exhibited such mixed responses were studied under conditions similar to the active, fictive, and passive conditions used to study negative images. The three examples in Figure 5A are typical of the responses we observed. The same mossy fibers showed short-latency bursts or pauses under fictive conditions (Fig. 5A, first row) along with either excitatory or inhibitory responses that tracked tail position under passive conditions (Fig. 5A, second row). Hence, CD and proprioceptive information are clearly mixed in individual mossy fibers. Furthermore, we found that bursts or pauses caused by tectal stimulation could be mixed with excitatory or inhibitory proprioceptive responses. The lack of correlation (R² = 0.054, n = 42; Fig. 5B) between integrated firing rate modulations under fictive versus passive conditions is consistent with random mixing of CD and proprioceptive signals in mossy fibers, as suggested by our modeling. Additional mixing of CD and proprioceptive signals is likely to occur because of convergence of different mossy fibers onto granule cells. We also observed that the combination of CD and proprioceptive signals in mossy fibers is strikingly linear (R² = 0.99, n = 42; Fig. 5C), with no significant difference between the arithmetic sum and the observed response under active conditions (arithmetic, 11.3 ± 41.9% change in integrated modulation; observed, 12.4 ± 42.7% change in integrated modulation; p = 0.28, sign test). These results suggest that an additional stage of nonlinear processing is required to account for the observed properties of negative images.

Figure 5.

Linear mixing of proprioceptive and CD information in mossy fibers. A, Normalized firing rate modulations from extracellular recordings of three representative mossy fibers recorded in EGp under fictive (top row), passive (middle row), and active (bottom row) conditions. Tail position is shown above recordings in green. The arithmetic sum of the integrated spike rate modulations under passive and fictive conditions is plotted in purple. tect, Optic tectum. B, Scatter plot of integrated modulations under passive conditions plotted against integrated modulations under fictive conditions. C, Integrated modulations of mossy fibers under active conditions plotted against the arithmetic sum of the integrated modulations during passive and fictive conditions. Note that the modulations appear to sum linearly, falling near the unity line (purple).

Evidence for nonlinear recoding of mossy fiber inputs in granule cells

Signals conveyed by mossy fibers are recoded in granule cells before they reach ELL principal cells. Although nonlinear recoding could occur in granule cells, as suggested by theories of mammalian cerebellar function (Marr, 1969; Albus, 1971), whether this is actually the case for EGp granule cells is unknown. One way to fulfill the specific requirements suggested by our modeling would be for mossy fiber inputs to drive granule cells into a saturating region of their input–output curves. Although we attempted to address this possibility directly by recording responses of granule cells under fictive, passive, and active conditions similar to those used to induce negative images, granule cells that exhibited responses under both fictive and passive conditions were encountered too rarely for this approach to be feasible. This is not unexpected given the extremely large numbers of EGp granule cells and the numerous sources of mossy fiber input they receive in addition to movement-related signals from the spinal cord.

As an alternative approach, we measured granule cell input–output functions in response to current injection in vivo to estimate the amount of depolarization required to saturate firing. We then reanalyzed a large set of granule cells recorded in a previous study (Sawtell, 2010; Kennedy et al., 2014) to estimate the amount of depolarization attributable to mossy fiber inputs that would be expected under conditions of negative image formation. Input–output functions for two example granule cells are shown in Figure 6A. Like most granule cells in EGp, both of these cells exhibited a prominent depolarization related to the EOD motor command (Bell et al., 1992; Kennedy et al., 2014). Under paralyzed conditions, the fish emits the EOD command spontaneously at a rate of 2–5 Hz. For all but the largest current injections, action potentials were caused by the temporal summation of depolarizations attributable to intracellular current injection and those attributable to the EOD command input (Fig. 6A, top traces). For this reason and because input from mormyromast electroreceptors is also processed in relation to the EOD command, we analyzed action potential firing within a small time window after the EOD command. Relationships between injected current and granule cell spiking were well fit by sigmoid functions (n = 6; Fig. 6A; Table 1) and showed clear signs of saturation (i.e., no increase in command-locked spiking for several current steps) in response to small amounts of injected current. Results were similar when we analyzed maximum spike frequency instead of the number of spikes per command (Table 1).

Figure 6.

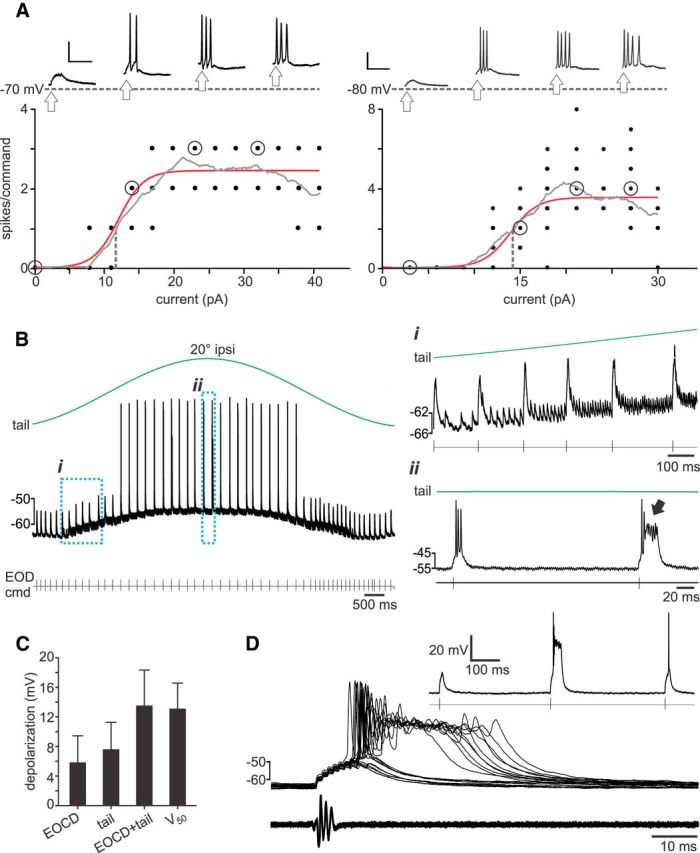
Evidence for nonlinear recoding in granule cells. A, In vivo whole-cell recording from two granule cells, illustrating typical responses to intracellular current injections. The number of spikes fired per EOD motor command is plotted as a function of current injection along with a sigmoid fit (red) and a moving boxcar average (gray). Dotted vertical line indicates half-maximum point of the fitted sigmoid curve. Above, Representative command-locked responses at varying levels of injected current (corresponding to the open circles along the fitted input–output curve) plotted above resting membrane potential (gray dotted line). The time of the command is indicated by arrows. Calibration: 20 mV, 25 ms. B, Trace from a representative granule cell in which tail movements (top trace) resulted in depolarization and action potential firing when the tail was at ipsilateral (ipsi) positions. The first expanded region (i) shows the presence of two distinct EPSP: the larger is related to the EOD command (cmd), and the smaller smoothly varies in rate of occurrence with tail position and hence is considered to be a proprioceptive input. The second expanded region (ii) shows strong action potential firing (including a burst indicated by the arrow) occurring when EOD motor commands are issued when the tail is at an ipsilateral position. C, Depolarizations attributable to EOCD and proprioceptive mossy fiber inputs compared with the depolarization (V₅₀) caused by current injection at half-maximum values. D, Overlaid traces showing responses to the EOD motor command in an example granule cell (no holding current is applied). The EOD evokes a large, stereotyped EPSP accompanied by zero to three spikes or, in some cases, an all-or-none burst consisting of several fast spikes, followed by a broad plateau potential. Inset shows responses to three consecutive EOD commands, the second of which evokes a burst.

To ask whether depolarization attributable to naturally occurring mossy fiber inputs (including those conveying both EOD motor command and movement-related signals) could drive granule cells into a saturating region of their input–output curves, we turned to a large existing dataset of 230 granule cells recorded in an awake, paralyzed preparation similar to that used in the present study (Sawtell, 2010; Kennedy et al., 2014). Although responses to tectal microstimulation were not obtained in these experiments, 45 granule cells received proprioceptive mossy fiber input, as judged by a prominent EPSP whose rate of occurrence was strongly modulated by passive tail movement (Fig. 6B). Tail movements in these studies were of similar amplitude but substantially slower (0.1–0.5 Hz) than those used in the present study. Thirty-six of these granule cells also exhibited a second, distinct EPSP waveform time-locked to the EOD motor command (Fig. 6B), consistent with a previous report of multimodal integration of proprioceptive and CD input related to the EOD motor command (also referred as EOCD) in a majority of granule cells (Sawtell, 2010). The combined depolarization attributable to proprioceptive and EOCD mossy fiber inputs are similar in magnitude (13.4 ± 4.7 mV, n = 36; Fig. 6C) to the depolarizations occurring at the half-maximum point (Fig. 6A, vertical gray dotted line) of the granule cell input–output curves (12.9 ± 3.5 mV, n = 6; Fig. 6C). Although not definitive, these observations are consistent with the idea that some granule cells are likely to be operating in a saturating region of their input–output curves during the passive, fictive, and active pairing conditions used to induce negative images in the present study.

Finally, we note that distinctive all-or-none bursts were observed in a subset of granule cells. Bursts consisted of two to seven action potentials (peak frequency of ∼400 Hz) of decreasing amplitude riding on top of a large depolarizing wave (amplitude, 26.4 ± 6.0 mV; width at half-height, 25.6 ± 9.7 ms; n = 40 EOD command-evoked bursts from 14 cells; Fig. 6D). In some granule cells, natural patterns of mossy fiber input, e.g., EOD command input and proprioceptive, were sufficient to evoke such bursts (Fig. 6B,D). Bursts in response to small current injections (10–30 pA), EOD command mossy fiber input, or proprioceptive mossy fiber input were observed in 54 of 230 examined granule cells. Burst firing was not the object of these studies, and we suspect that bursts could have been revealed in a larger fraction of cells using larger currents or a wider range of stimuli to engage mossy fiber inputs. The presence of bursts in a subset of granule cells provides an additional mechanism that could fulfill the requirement for nonlinear coding of CD and proprioceptive signals suggested by our model.

Discussion

Predicting the sensory consequences of an animal's own movements is important for a variety of functions, from cancelling self-generated sensory inputs (Sperry, 1950; von Holst, 1950) to online control of movements under conditions of delayed and/or noisy sensory feedback (Wolpert and Miall, 1996), yet relatively little is known about how such predictions are generated in neural circuits. Previous studies of electrosensory systems of several distinct groups of fish have identified neural correlates for the generation and subtraction of predictions of electrosensory consequences of movements (Bastian, 1996; Bodznick et al., 1999; Bol et al., 2011), termed negative images. The accessibility of electrosensory systems to circuit-level analysis provides an opportunity to address the general issue of how sensory and motor signals related to movements are transformed into specific predictions about movement consequences. The present study provides an analysis of the respective roles of motor CD versus proprioceptive feedback in generating negative images of the predictable electrosensory consequences of the fish's own movements.

A central finding of this study is that approximately equivalent negative images are formed using either CD or proprioception and that, under conditions approximating self-generated movements, both are used. The equivalence of negative images based on CD or proprioception is remarkable given the very different nature of the signals—motor versus sensory—and suggests that proprioception is not always too delayed to perform real-time function, such as cancellation (Wang et al., 2007; Wurtz, 2008). Sensory cancellation based on either CD or proprioception, as suggested here, contrasts with results from the primate vestibular system, which suggest that cancellation of vestibular reafference depends on a comparison between motor signals related to head movements and the resulting proprioceptive feedback (i.e., the proprioceptive input must match that which is expected based on the motor command; Roy and Cullen, 2004). From a functional standpoint, negative images based on CD or proprioception makes sense for electric fish, because electrosensory consequences of movements should be cancelled whether movements are self-generated or attributable to external forces. Finally, although passive movements used in this study were as rapid as possible given our apparatus (200°/s), it is important to note that we cannot rule out the possibility that even faster movements might have revealed delays in proprioceptive feedback and a requirement for CD.

In addition to demonstrating that both CD and proprioception are used for generating negative images, our experiments revealed unexpected interactions between the two signals. Most notably, we found that, after pairing under fictive or passive conditions, i.e., with CD or proprioception alone, negative images were actively suppressed by the additional presence of the unpaired signal. A simple network model provided insight into these interactions, suggesting that all of the observed properties of negative images, including suppression by the unpaired signal, can be explained if CD and proprioceptive signals are coded as random, nonlinear mixtures before the generation of negative images.

Therefore, an additional goal of this study was to characterize the actual encoding of CD and proprioceptive information at the level of mossy fibers and granule cell inputs to ELL. Although such encoding has been studied previously, it was not known whether CD and proprioceptive signals are mixed at either the level of mossy fibers or granule cells. Our results clearly demonstrate that such mixing occurs already at the level of mossy fibers and appears to be random, in that no systematic relationship was observed between sensory and motor responses within the same fibers. The population of mixed mossy fibers recorded here likely corresponds to a lateral column system in the mormyrid spinal cord that shares a number of anatomical similarities with the mammalian ventral spinocerebellar tract (Szabo et al., 1990). Mixed spinocerebellar pathways have been studied extensively in mammals (Oscarsson, 1965; Arshavsky et al., 1978; Hantman and Jessell, 2010; Jankowska et al., 2011; Fedirchuk et al., 2013; Spanne and Jörntell, 2013). Most accounts of the function of such mixing in mammalian systems have posited some specific logic underlying interactions between sensory and motor signals (Lundberg, 1971; Spanne and Jörntell, 2013). Our results suggest a simpler view in which such mixtures are components of a random basis that could allow for flexible predictions based on either sensory or motor signals. Although the linear interactions observed between sensory and motor responses in mossy fibers is consistent with linear properties of mossy fiber neurons described in mammals (Kolkman et al., 2011), such linear mixing alone clearly does not fulfill the requirement suggested by our network model. Finally, we expect that additional mixing of proprioceptive and CD signals occurs in EGp granule cells. This possibility is consistent with past reports in mormyrid fish providing electrophysiological evidence for multimodal integration in EGp granule cells (Sawtell, 2010) and with an anatomical study showing convergence of pontine (likely motor signals) and cuneate (likely proprioceptive signals) mossy fibers onto the same granule cells in some regions of the mouse cerebellum (Huang et al., 2013).

Nonlinear recoding of mossy fiber inputs in granule cells is a key feature of theoretical accounts of cerebellar cortex (Marr, 1969; Albus, 1971) and has received some experimental support from studies of mammalian cerebellar granule cells (D'Angelo et al., 2001; Chadderton et al., 2004; Barmack and Yakhnitsa, 2008; Ruigrok et al., 2011). There are numerous possible mechanisms that could contribute to such nonlinear recoding. Although we focused on the straightforward possibility that depolarization attributable to excitatory mossy fiber inputs is sufficiently strong to push granule cells into a saturating region of their input–output functions, our results do not rule out additional mechanisms, such as normalization via Golgi cell inhibition (Marr, 1969; Albus, 1971; Crowley et al., 2009; Rothman et al., 2009). Indeed, Golgi cells have been shown to be present in EGp and respond to both proprioceptive and EOCD input (Campbell et al., 2007; Sawtell, 2010; Kennedy et al., 2014).

Strong depolarization observed in EGp granule cells is attributable in part to previously described multimodal integration of separate spinal and EOD command mossy fiber inputs (Sawtell, 2010). Because the timing of the EOD command is independent of the fish's movements (Toerring and Moller, 1984), EOD command input simply acts as an additional source of depolarization that will summate with depolarization from movement-related mossy fibers. Our analysis suggests that such depolarization is likely to be strong enough to drive some, but not all, granule cells toward saturation. A previous study has shown that granule cells exhibit substantial diversity in the distance between their resting potentials and spike threshold (Kennedy et al., 2014). Similar diversity has been observed in mammalian cerebellar granule cells, perhaps because of heterogeneous Golgi cell inhibition (Chadderton et al., 2004; Crowley et al., 2009; Schwartz et al., 2012).

The observation that interactions between proprioceptive and CD signals are sublinear could be explained if strongly activated granule cells (those operating near saturation) contribute most to negative images. Our network model offers an explanation for why this may be. Nonlinear interactions between CD and proprioceptive signals observed in the context of negative images are believed to reflect granule cell inputs that have undergone synaptic plasticity. If such plasticity is proportional to granule cell firing rate, the most active granule cells will, indeed, provide the greatest contribution to learned changes in the network output (Fig. 4E). In vitro studies of weakly electric gymnotiform fish have shown that burst firing is required to induce long-term synaptic depression (LTD) in ELL neurons and that the magnitude of LTD is greater for larger bursts (Harvey-Girard et al., 2010). Bursts have also been shown to be potent triggers for LTD at parallel synapses onto Purkinje cells (Wang et al., 2000). Such a nonlinear plasticity rule would exaggerate the suppressive effects predicted by our model. The dramatic burst firing observed here in some granule cells is intriguing in this context. Our model makes the testable prediction that manipulations that render granule cells less excitable should favor enhancement of negative images by the unpaired input instead of the suppression observed in the present study.

What is the functional advantage of the scheme suggested here, i.e., negative images based on random, nonlinear mixtures of CD and proprioception? Although the capacity to generate negative images based on two separate streams of information may reduce uncertainty and allow for more accurate or robust sensory cancellation, it also poses a problem. The same change in body position may result from motor commands, external forces, or combinations of both. Although a linear system, in which CD and proprioceptive inputs are simply added, could not effectively use both streams under these conditions, a system in which the two streams of information are combined nonlinearly could. Experimental support for this idea is provided by our observation that similar negative images could be generated and stored simultaneously based on CD and proprioception and on proprioception alone (Fig. 3D). Finally, it is interesting to note that mixed nonlinear coding schemes are likely to be widely useful. Theories of cerebellar function posit a random, nonlinear recoding of mossy fiber inputs in granule cells (Marr, 1969; Albus, 1971). Experimental evidence and theoretical arguments for mixed nonlinear coding schemes have also been provided for the cerebral cortex in the context of a variety of functions from sensorimotor transformations to complex cognitive tasks (Zipser and Andersen, 1988; Pouget and Sejnowski, 1997; Mante et al., 2013; Rigotti et al., 2013).