Frequency domain optoacoustic tomography using amplitude and phase

Abstract

We introduce optoacoustic tomographic imaging using intensity modulated light sources and collecting amplitude and phase information in the frequency domain. Imaging is performed at multiple modulation frequencies. The forward modeling uses the Green's function solution to the pressure wave equation in frequency domain and the resulting inverse problem is solved using regularized least squares minimization. We study the effect of the number of frequencies and of the bandwidth employed on the image quality achieved. The possibility of employing an all-frequency domain optoacoustic imaging for experimental measurements is studied as a function of noise. We conclude that frequency domain optoacoustic tomography may evolve to a practical experimental method using light intensity modulated sources, with advantages over time-domain optoacoustics.

1. Introduction

Optoacoustic imaging has been conventionally implemented in the time domain (TD) due to several reasons. TD optoacoustic imaging offers efficient ultrasonic signal generation with high signal-to-noise ratio (SNR) due to the ultra-short high-energy excitation of tissue [1]. Additionally, wavelength tunable laser sources enable multispectral optoacoustic imaging [2,3]. Based on time of flight measurements, image reconstruction can be performed using closed-form methods including backprojection algorithms [4] and time reverse methods [5] which solve the inverse problem by projecting the measured signal back in time. Model-based approaches have been further proposed to improve the reconstruction accuracy compared to backprojection methods [6].

Frequency domain (FD) optoacoustic imaging has been already considered by sweeping the frequency of an intensity modulated optical source (chirp) instead of pulsed excitation [7,8]. Operation in the frequency domain offers several advantages over imaging in the time domain. FD sources may be more cost effective than TD systems and come with smaller form factors than TD systems, since stable and practical continuous wave (CW) laser sources can be employed. Furthermore, narrowband signal detection combined with high duty cycles can enable strong rejection of incoherent noise to offer measurements with sufficient signal to noise ratio (SNR).

The chirp technique encodes the time delay of sound propagation into frequency in order to determine distance. Therefore time is an essential component of this method, since the distance is calculated as the time that it takes a certain frequency to appear on the transducer. This calculation is done on an indirect basis based on a cross-correlation function [7,9,10], mixing the detected sound waveform with a reference measurement representative of the signal illuminating the tissue under investigation.

Single frequency sources have been applied in raster scan mode to localizing the underlying absorbers [11,12]. These methods enable spatial tracking in conjunction with acoustic focusing approaches, due to the phase ambiguity problem [11]. In addition, tomographic imaging using chirp sources has been introduced, demonstrating the possibility of using projections in combination with intensity modulated sources [7].

We present for the first time to our knowledge, frequency domain optoacoustic tomography using amplitude and phase information, i.e. using complex acoustic measurements. The data obtained do not require time varying frequency components and cross-correlation detection as in chirp mode detection. Instead we show that tomographic images are formed from information obtained using amplitude and phase sources operating in multiple discrete frequencies, which can be arbitrarily placed over a band of several MHz. Correspondingly image reconstruction is achieved by inverting the frequency domain optoacoustic pressure equation. We demonstrate the tomographic capacity of the method at the absence of any acoustic focusing, even though it would be possible to also use this approach in the context of focused, raster scan image formation settings. We show herein that formulation of the problem as a frequency-domain Helmholtz equation delivers a linear system of equations based on the Green's function solutions. Inversion can be then achieved using a regularized least-squares formulation to achieve localization using measurements at multiple frequencies simultaneously.

To showcase the performance of frequency domain optoacoustic imaging as a function of discrete frequencies, we utilized synthetic data within a frequency-domain image reconstruction scheme. Of primary importance herein was to explore the possibility of the experimental application of the method proposed. For this reason we considered different noise conditions to generate data that could correspond to experimental systems implemented in the frequency domain. We discuss the possible advantages of the proposed method and predict the development of practical systems.

2. Theory and methods

2.1. Theoretical background

Under conditions of thermal and stress confinement, the three-dimensional frequency domain optoacoustic pressure in acoustically homogenous infinite medium can be described by the time independent Helmholtz equation as

$$({\nabla }^2+k^2)p(r,\omega )=\frac{-j\omega \beta }{C_p}H(r,\omega )\text{,}$$ (1)

where k is the acoustic wave number given as k = ω/c_a (c_a denotes the acoustic speed of sound in water), β is the thermal expansion coefficient and C_p is the specific heat capacity. Variables p(r, ω) and H(r, ω) represent the acoustic pressure wave and source term at position r and angular frequency ω, respectively. Throughout this work $j=\sqrt{-1}$. The absorbed energy density function H(r, ω) can be further described as

$$H(r,\omega )=\vartheta {\mu }_a(r)I_0(r,\omega )\text{,}$$ (2)

where ϑ is the dimensionless energy conversion coefficient and μ_a(r) is the local optical absorption coefficient. I₀(r, ω) is the diffuse photon density wave (DPDW) denoting the fluence at location r.

The Green's function solution Eq. (1) for a source located at origin of an infinite medium (i.e. H(r, ω) = δ(r)) in the three dimensional space is denoted by g(r, ω) and given as

$$g(r,\omega )=\frac{-jA\omega }{4\pi \left|r\right|}{e}^{j((\omega /c)\left|r\right|+{\varphi }_a)}\text{,}$$ (3)

where ϕ_a is a phase constant due to the thermoelastic conversion of tissue [8]. The constant A is further given in terms of the tissue physical properties used in Eq. (1) as

$$A=\frac{\beta }{C_p}\text{.}$$ (4)

2.2. Forward modeling and inversion

The forward model for FD optoacoustic tomography is schematically depicted in Fig. 1. The transducer placed on the perimeter of the sample located at r_d is assumed to be a point detector, with equal sensitivity to all points within the circular sample. The transducer scans N equispaced detection positions spanning 360° around the sample. This particular measurement geometry and detector configuration is used for demonstration purposes herein. Nevertheless, the proposed formulations are readily generalizable to arbitrary geometries and configurations. The sample area is discretized with a rectilinear grid with V nodes and an edge size d. Assuming the conditions of infinite medium, realizable in practice by immersing the sample in water, the pressure wave generated by a hypothetical absorber located at position r₀ is then given by the Green's function solution of Eq. (3). Accordingly, the pressure p(θ_n, ω) at position θ_n and modulation frequency ω is given by a summation of pressure signals emanating from all voxels within the imaging space. Hence,

$$\text{p}(\omega )=\text{W}(\omega )X\text{,}$$ (5)

where p(ω) is a complex column vector denoting the measured complex signals (amplitude and phase of the pressure wave) at N detector positions. X is a real non-negative column vector denoting the unknown absorption multiplied by the local absorbed energy density (μ_a(r)I₀(r, ω)) of the V mesh nodes. W(ω) denotes the N × V complex weight matrix and is given as

$$\text{W}(\omega )=-jA{e}^{j{\varphi }_a}\left(\begin{array}{ccc}\hfill w_{11}\hfill & \hfill \dots \hfill & \hfill w_{1V}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill w_{N1}\hfill & \hfill \cdots \hfill & \hfill w_{NV}\hfill \end{array}\right),w_{nv}=\omega \frac{e^{j((\omega /c)\left|r(v)-r_d(n)\right|)}}{\left|r(v)-r_d(n)\right|}\text{,}$$ (6)

where r_d(n) denotes the nth detector position, r(v) is the position of the voxel v and A is the constant given in Eq. (4). The fluence I₀(r, ω) is independent of the location of the transducer and can be found by modeling the light propagation in the sample volume. Light propagation modeling can be achieved, for instance, via finite element method (FEM)-based discretization of the diffusion equation in the frequency domain [13,14].

Fig. 1.

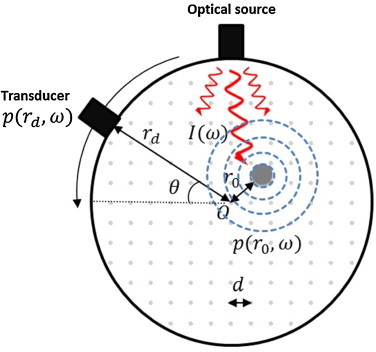
Schematic diagram of the proposed FD optoacoustic tomography technique; the tissue is illuminated at one or several locations simultaneously, using an amplitude-modulated CW laser with a group of distinct frequencies ω. The absorbing object located at r₀ emits acoustic waves which are detected by the transducer at r_d. The detected acoustic signal is then converted to phase and amplitude information using narrowband detection/homodyne detection. The gray dots denote the voxel points used to discretize the sample for the forward modeling.

To enable high spatial localization, the optical light is intensity modulated at F different excitation frequencies ω₁, …, ω_F and the amplitude and phase of the generated acoustic waves are measured at all F frequencies for each projection angle. Moreover, the modulation frequency ω creates a complex wave number of k_ω = μ_a − (jω/c) in the FD diffusion equation (which governs the propagation of modulated light in turbid tissue), where c is the speed of light. For typical values of μ_a and ω (such as ω < 2π × 100 MHz and μ_a < 0.5 cm⁻¹), the real part of k_ω is much larger than its imaginary part. For example, for μ_a = 0.1 cm⁻¹ and ω = 2π × 100 MHz, we have the optical complex wave number given as k_ω ≈ (100 − 2j)/m). As a result for frequencies less than 100 MHz – typical in optoacoustic tomography – the effect of ω on the fluence I₀(r, ω) can be ignored. Therefore, the full forward model can be written as

$$\overline{\text{p}}=\overline{\text{W}}X,\text{where}\overline{\text{p}}=\left(\begin{array}{c}\hfill \text{p}({\omega }_1)\hfill \\ \hfill ⋮\hfill \\ \hfill \text{p}({\omega }_F)\hfill \end{array}\right),\overline{\text{W}}=\left(\begin{array}{c}\hfill \text{W}({\omega }_1)\hfill \\ \hfill ⋮\hfill \\ \hfill \text{W}({\omega }_F)\hfill \end{array}\right)\text{.}$$ (7)

Finally, the inversion of Eq. (7) can be achieved using Tikhonov regularization as

$$X_0=\text{arg}\text{min}\left({∥\text{Re}\left\{\overline{\text{W}}\right\}X-\text{Re}\left\{\overline{\text{p}}\right\}∥}_2^2+{∥\text{Im}\left\{\overline{\text{W}}\right\}X-\text{Im}\left\{\overline{\text{p}}\right\}∥}_2^2+\lambda {∥X∥}_2^2\right),\text{sub. to}X\ge 0\text{,}$$ (8)

where Re and Im denote the real and imaginary parts of the corresponding arrays, respectively.λ is the regularization parameter and was set to the point of maximum curvature in the corresponding L-curve [15]. The optimization problem of Eq. (8) was solved using the least squares method (LSQR) with 100 iterations.

Each entry of the vector X contains multiplicative terms from the local absorption and the local fluence, i.e. I₀(r). Accurate knowledge about the fluence can be then used to reconstruct the absorption μ_a(r) from the reconstructed vector X₀. However, the problem of fluence estimation is outside of the scope of this work. Therefore for the sake of simplicity, in the rest of this work we assume a fluence value of 1 in the entire sample. The vector X is then equal to the local optical absorption of tissue on the respective mesh nodes. As such, the vector X has an SI unit of one over unit length. We further describe the vector X as

$$X=x{\mu }_0\text{,}$$ (9)

where μ₀ was to a typical tissue absorption value of 0.03 cm⁻¹. In this fashion, the entries of x are unit-less and have an average value of 1 for general tissue.

2.3. Generation of synthetic data and inversion

Acoustic signals in the frequency domain are simulated as follows. For a given tissue geometry, the tissue volume is first discretized using a rectilinear mesh with V nodes and the weight matrix $\overline{\text{W}}$ is built accordingly, as described above in Eq. (7). The simulated measurement vector is then given as $\overline{\text{p}}=\overline{\text{W}}X$, where X is a V × 1 vector, whose entries denote the absorption of the simulated object. For the simulation purposes, we assumed A = 1 and ϕ_a = 0 in Eq. (6).

Data simulations assumed a circular geometry containing different absorbing objects. The circular geometry was a two-dimensional section of a three-dimensional cylinder with a diameter of 12 mm and was selected as an upper limit of mesoscopic implementations of optoacoustic imaging. The selected geometry was discretized using a rectilinear mesh with a resolution of 50 μm. Acoustic detection was assumed over 90 locations equally spaced around 360°.

Two sets of absorbing objects were numerically simulated in the circular geometry. The first set consisted of three small circular objects as shown in Fig. 2(a). The objects 1, 2, 3 had absorptions of 1, 2 and 1.5 μ₀, as defined in Eq. (9), and diameters of 1.1, 0.5 and 0.9 mm, respectively. For convenience, the term μ₀ is not further shown in the ensuing graphs in Section 2. This set of objects was employed to validate the performance of the proposed method in differentiating properties of small, localized objects and reconstructing their relatively intensities. The second set of absorbing objects employed herein consisted of a more complex geometrical pattern by assuming a cross shape with a thickness of 0.6 mm and length of 4 mm, as shown in Fig. 2(a).

Fig. 2.

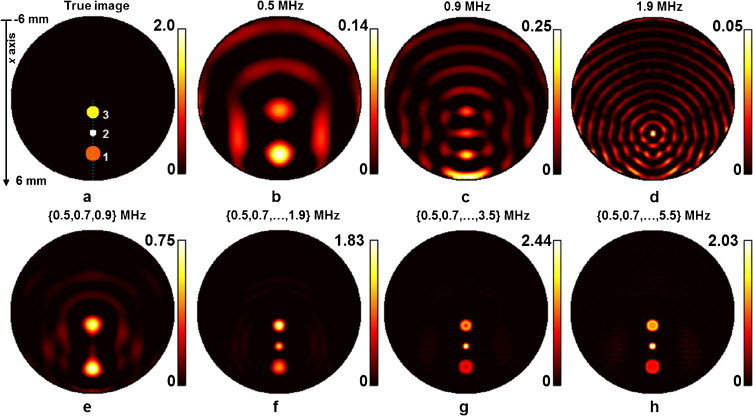
Reconstruction results for the 3 small absorbers at a resolution of 50 μm; (a) true absorption image for the circular phantom (diameter 12 mm), containing 3 objects (absorption of 1, 2 and 1.5 μ₀ and diameters of 1.1, 0.5 and 0.9 mm for objects 1, 2 and 3, respectively). Reconstructions using single frequencies are shown for f = 0.5 MHz in (b), f = 0.9 MHz in (c) and for f = 1.9 MHz in (d). Panels (e–h) show image reconstructions for designated frequency groups consisting of 3, 8, 16 and 26 frequencies, respectively. No noise was added to the synthetic measurements for these reconstructions.

Simulations were performed for discrete frequencies between 900 kHz and 5.5 MHz with steps of 200 kHz. Reconstruction results were presented then for single frequencies as well as groups of frequencies, with the largest group consisting of 28 frequencies, i.e. [0.5,0.7,…,5.3,5.5] MHz.

The effect of measurement noise was simulated by adding white Gaussian noise with zero mean to the simulated measurements. Specifically, the noisy measurement $\overline{\text{q}}$ was synthetized as

$$\begin{array}{c}\hfill \text{Re}\left\{\overline{\text{q}}\right\}=\text{Re}\left\{\overline{\text{p}}\right\}+{\eta }_r\hfill \\ \hfill \text{Im}\left\{\overline{\text{q}}\right\}=\text{Im}\left\{\overline{\text{p}}\right\}+{\eta }_i\hfill \end{array}\text{,}$$ (10)

where η_r and η_i are both independent Gaussian random processes with zero mean and variance ${\sigma }_n/\sqrt{2}$. Accordingly, the random variable η_r + jη_i has a variance of σ_n. Note that this additive noise represents the measurement noise after homodyne detection and not the noise at the output of the transducer. The SNR is then defined as

$$\text{SNR}=20{\text{\hspace{0.17em}log}}_{10}\left(\frac{{\sigma }_p}{{\sigma }_n}\right)\text{,}$$ (11)

where σ_p denotes the variance of $\overline{\text{p}}$, the synthetic signal. The resulting SNR is described in decibel (dB) units. As such, positive (negative) values of SNR in dB imply a signal power stronger (weaker) than the noise power. Reconstructions were performed without and with synthetic noise. The noisy signals had SNRs ranging from 3.4 dB to −20.2 dB (as defined in Eq. (11)).

3. Results

3.1. Simulation results using single and multiple frequencies

Fig. 2 presents the reconstruction results for the first set of objects consisting of 3 small absorbing objects, as described in Section 2.3. Fig. 2(a) shows the true intensities of the three objects. Fig. 2(b) shows the reconstructed absorption image when a single frequency of 0.5 MHz is used for illumination. Reconstruction results using single frequencies of 0.9 and 0.9 MHz are presented in Fig. 2(c) and (d), respectively. Fig. 2(e)–(f) shows reconstruction results when combining measurements at frequencies of [0.5,0.7,0.9] MHz, [0.5,0.7,…,1.9] MHz, [0.5,0.7,…,3.3,3.5] MHz and [0.5,0.7,…,5.3,5.5] MHz, respectively. To clearly observe the effect of the frequency selection on the reconstructions, the simulated data used in Fig. 2 assumed no added noise.

A clear pattern emerges after observations of the results of Fig. 2. Whereas reconstructions at single frequencies reveal features of the original image, they do not manage to offer an accurate representation of the underlying absorption distribution shown in Fig. 2(a). Interestingly, it appears that different size objects appear better at different frequencies, i.e. a resonance effect of illumination frequency to spatial frequency is observed. However the overall appearance of artifacts and the challenges in capturing the small absorbers points to the challenges of performing frequency-domain optoacoustics at a single frequency. The accuracy of the method significantly improves when frequencies over a range are employed. As expected the use of a larger number of frequencies spanning a larger frequency band gives the most accurate representation of the distribution simulated. The use of only low frequencies fails to reconstruct the small object #2 in Fig. 2(e). Moreover, the accuracy in object definition improves when high-frequency components are added in the inversion, in a progressive manner, as can be observed by inspecting Fig. 2(f)–(h).

Fig. 3 shows the profiles of the reconstructed signal across the vertical radius shown in Fig. 2(a). Specifically, the dash-dotted, dashed, dotted and solid black curves in Fig. 3 show the signal profile for the frequency sets [0.5,0.7,0.9] MHz, [0.5,0.7,…,1.9] MHz, [0.5,0.7,…,3.3,3.5] MHz and [0.5,0.7,…,5.3,5.5] MHz (consisting respectively of 3, 8, 16 and 26 distinct frequencies), respectively, corresponding to Fig. 2(e)–(f). As observed, the reconstructions for frequency bandwidths of less than 3 MHz show significant overshoot or undershoot effects (with respect to the true values). The reconstructions for the 5 MHz bandwidth (frequency set [0.5,0.7,…,5.3,5.5] MHz) have the least fluctuations but show Gibbs-like ripples.

Fig. 3.

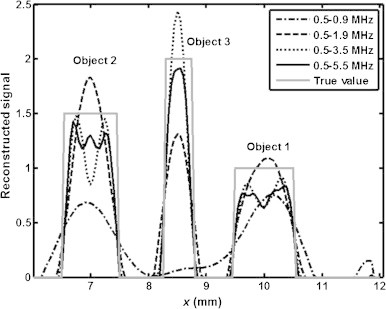
Reconstructed signal profiles for the denoted frequency sets as well as the true value (gray solid curve) for the 3 objects across the dotted line segment shown in Fig. 2(a).

Fig. 4 corroborates these findings by reconstructing a more elaborate shape compared to the one demonstrated in Fig. 2. Similar to Fig. 2, the simulated data herein assumed no added noise. Reconstructions using single frequencies of 0.5, 1 and 2 MHz are shown in Fig. 4(b)–(d), respectively. Fig. 2(e)–(f) present reconstruction results for frequency sets [0.5,0.7,0.9] MHz, [0.5,0.7,…,1.9] MHz, [0.5,0.7,…,3.3,3.5] MHz and [0.5,0.7,…,5.3,5.5] MHz, respectively. A similar behavior to the one seen in Fig. 2 is observed. Images using single frequency reconstructions cannot accurately represent the simulated absorption pattern. However, in contrast to Fig. 2 no obvious features of the cross are seen in Fig. 4(b), (c) or (d). Instead, the appearance of artifacts is clearly evident. Conversely, reconstructions using multiple frequencies dramatically change the appearance of the images. A more reliable reconstruction is achieved as the frequency range and the number of frequencies increases. Nevertheless the more elaborate pattern also showcases some quantification limitations. The reconstructed cross pattern shows differences to the initial absorption pattern simulated since there is a variation of reconstructed absorption along the cross. A smaller absorption value is reconstructed at the middle of the cross compared to the edges of the cross.

Fig. 4.

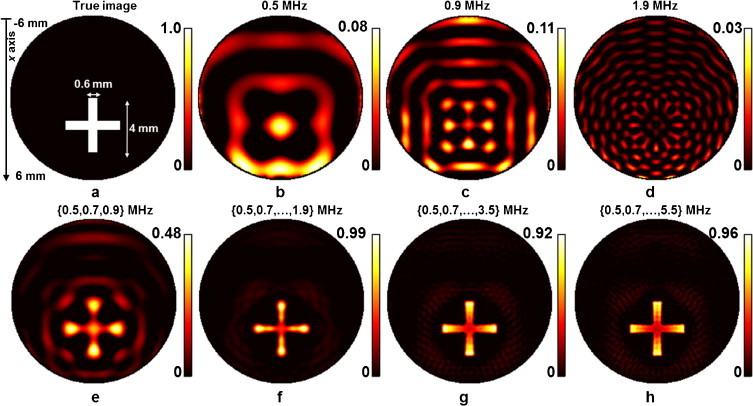
Reconstruction results for the cross-shaped object shown in (a). Reconstructions using single frequencies are shown for f = 0.5 MHz in (b), f = 0.9 MHz in (c) and for f = 1.9 MHz in (d). Panels (e–h) show reconstructions for designated frequency groups consisting of 3, 8, 16 and 26 frequencies, respectively. No noise was added to the synthetic measurements for these reconstructions.

3.2. The impact of noise on the reconstruction accuracy

Fig. 5 demonstrates the impact of noise on the reconstructed images as a function of the noise power in the simulated measurements. The absorption distribution is the same as shown in Fig. 2 (a). Fig. 5(a) is repeated from Fig. 2(h) and contains no noise. Subsequently Fig. 5(b)–(h) shows the reconstructed results at diminishing SNR values of 3.5 dB, −2.9 dB, −6.5 dB, −10.6 dB, −14.7 dB, −17.6 dB and −20.2 dB, respectively (noise was synthetized and added as described in Section 2.3). As can be observed in Fig. 5(b)–(h), the three objects are readily recognizable for SNR's as low as −15 dB. For SNR = −14.7 dB, the 3 objects can be still recognized in Fig. 5(f). For SNR values of −17.6 and −20.2 dB, no features can be reliably recognizable in the reconstructed image of Fig. 5(g) and (h). The speckle-like pattern of the reconstructed noise signal can be attributed to statistical independence of the noise random vectors η_i and η_r in Eq. (10). Moreover, it can be seen across Fig. 5(b)–(h) that the intensity of the reconstructed artifacts increases with increasing noise power. However, the intensities of the reconstructed signals remain relatively unchanged.

Fig. 5.

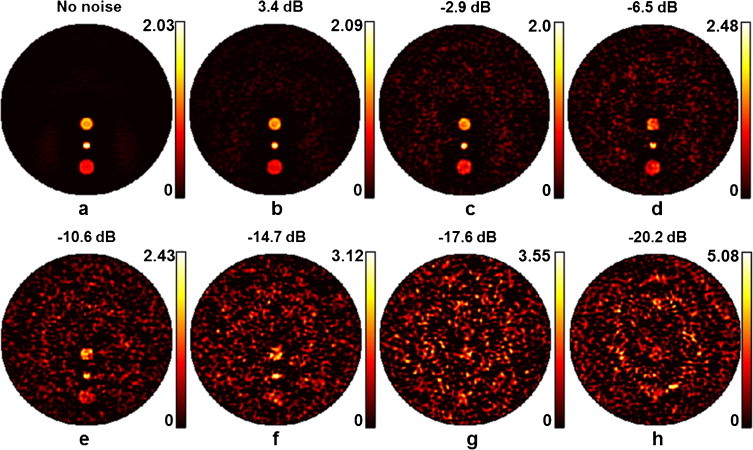
Simulation results at different noise levels for the phantom and objects shown in Fig. 2(a); (a) reconstruction when no noise is added to the synthetic measurements, (b)–(f) reconstruction results for noisy measurements with SNR values of 3.4, −2.6, −6.5, −10.6, −14.7, −17.6 and −20.2 dB, respectively. The frequency range was f = [0.5,0.7,…,5.3,5.5] MHz in all cases.

Fig. 6 presents a graphical analysis of the signals reconstructed in Fig. 5. Fig. 6(a) shows the average values of the reconstructed signal intensities in the positions of the three objects, as a function of noise intensity. These averages were obtained by averaging the reconstructed signal intensities within the span of each object. Fig. 6(b) depicts the reconstructed signal profiles along the dotted line segment of Fig. 2(a) for SNR values of −2.9, −10.6 and −14.7 dB. As observed, the reconstructed signal for SNR = −14.7 dB (dotted curve) has large over- and under-shoots in within the regions of objects 1 and 3. However, the reconstructed absorption profiles of Fig. 6(b) all have significantly larger values within the object regions (where the gray curve has a positive value) than outside (where the gray curve is 0). Fig. 6(a) shows that the reconstruction accuracy is almost unaffected by noise for SNR > −14 dB. Also for SNR > −14 dB, all reconstructions demonstrated a drop in the absolute intensity with respected to their true values. For instance, the object 2 with a true absorption value of 2 μ₀, had a reconstructed value of approximately 1.5 μ₀ for SNR > −10 dB. This drop is due to the low-pass filtered nature of the reconstructions. In other words, tissue illumination with a given bandwidth can only partially recover the sharp object edges. This intensity drop is also obvious from the profiles seen in Fig. 6(b). Fig. 6(a) further shows that for SNR values as low as −14.7 dB, the 3 objects are still reconstructed according to their order of intensity. The signal intensity of Fig. 6(a) at the SNR value of −14.7 dB seems to best match the true value. However, this is an accidental result and is due to noise fluctuations. For SNR < −17 dB no object is recognizable and the reconstructions consist almost entirely of noise artifacts.

Fig. 6.

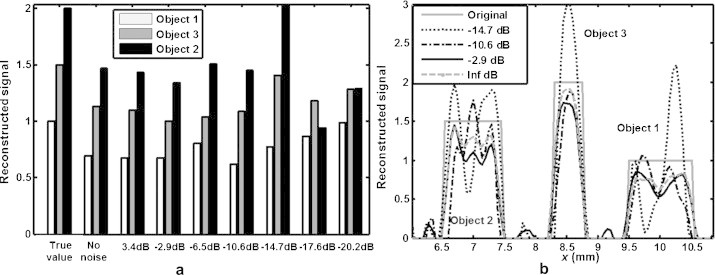
Profiles of the reconstruction signal using noisy measurements; (a) bar plot showing average signal values for the 3 objects at different noise levels (shown on x-axis), (b) reconstructed signal profiles for SNR values −2.9, −10.6 and −14.7 dB, as well as the true value (gray solid curve) for the 3 objects across the dotted line segment shown in Fig. 2(a). The frequency set was f = [0.5,0.7,…,5.3,5.5] MHz in all cases.

4. Discussion

The study herein examined the possibility of using amplitude and phase measurements for optoacoustic imaging. For this reason data were simulated assuming different absorption patterns illuminated at multiple frequencies and at different SNR levels. An array of 90 detectors was used for all the reconstructions shown herein. The detectors were placed over 360° around the object in an equidistant arrangement. The simulations clearly demonstrated the possibility of recovering the absorption distribution using frequency domain measurements obtained over multiple frequencies.

A distinct difference between previous implementations in the frequency domain using chirp illumination is that the method presented is a “true” frequency domain implementation, which is independent of time. Instead the amplitude and phase information of the propagating sound waves were measured without assumptions on any time dependencies. The premise herein is that the illumination is always on and there is no time-variance of any aspect of the illumination. In that respect averaging over time only improves the signal to noise ratio of the data acquired but is not otherwise essential in the particulars of image formation. Instead the selection of frequencies is an important factor that affects image quality. Different ultrasonic frequencies essentially relate to different spatial frequencies in the image. Correspondingly, an image that contains multiple spatial frequencies cannot be accurately captured by a single frequency. The results showcase that it is not possible to resolve different sizes unless different corresponding frequencies are utilized. In addition, reconstructions using measurements in single frequencies result in images that contain artifacts. This is because while all objects contribute in the ultrasonic signals detected, the information available to the inversion algorithm is not sufficient to accurately resolve the origin of these signals. In other words, the inversion problem constructed in a single frequency is ill-posed, i.e. multiple solutions satisfy it.

The inversion performed was overall ill-posed, especially in the presence of noise, even when multiple frequencies were employed. For this reason, image generation was based on model-based forward model and an inversion approach that employed regularization. The method yielded satisfactory reconstruction even at increasing noise levels, confirming that all-frequency domain measurements can be employed for optoacoustic imaging.

The proposed method achieved reasonable object localization for SNR values as low as −14 dB as seen in Figs. 5 and 6. The SNR value of −14 dB corresponds to noise energy of ∼25 times larger than the signal energy. The SNR values reported herein denote “in-band” SNR values. The term “in-band” refers to a signal or noise ratio calculated for the particular bandwidth employed for detection. In other words, only the noise power at the excitation frequencies affects the SNR, as calculated in Eq. (11). This is because the noise at other frequencies is rejected by the homodyne detection. Any acquisition hardware developed for frequency domain optoacoustics would be designed to maximize the SNR by minimizing the in-band noise, consistent with the observations.

The simulation results were presented in this work for point detectors placed uniformly over 90 angular locations on a circle around the sample. More generally, the method can be expanded to arbitrary geometries and detector configurations in limited or full views operating in 2D or 3D modes, for uniformly or non-uniformly sampled frequencies. The transducer shape and acoustic heterogeneities can be further taken into account in the proposed model-based inversion, in a fashion similar to the model-based time-domain inversion proposed in [16]. The specific impacts of various system parameters on the reconstructions are yet to be established and are the subject of ongoing work. Herein we employed a total of 90 detectors, which was shown adequate to reconstruct the information present in the images. While the objects employed herein were rather simple in nature, in vivo imaging would contain more complex shapes. In vivo imaging may require a larger number of detectors and frequencies in order to reconstruct more complex shapes and account for noise.

An advantage of the proposed frequency-domain method over time-domain (TD) approach is that it can lead to cost effective implementations. TD systems employ complex high-peak-energy pulsed lasers, which come at a high cost. An important feature of frequency domain methods is that they operate at much larger duty cycle than TD methods. Therefore they can achieve the same SNR as TD methods but using lasers of lower peak energy, for example inexpensive CW lasers.

FD optoacoustic tomography offers versatility in terms of frequency selection. This characteristic can lead to the design of multiple-frequency FD systems in comparison to chirp-based FD systems, which operate only at one frequency at any given time. The simultaneous use of multiple frequencies can accelerate the operation of FD methods, by collecting all necessary frequencies in real-time and continuously. Therefore there is no need for considering data-acquisition delays as in TD systems or chirp-systems. The ability to utilize multiple frequencies leads to another compelling feature. Multiple wavelengths can be carried by different frequencies and also acquired in parallel. Therefore, FD methods can lead to the implementation of real-time multispectral imaging.

The reconstruction accuracy of the proposed technique is nevertheless limited by the number and bandwidth of the frequencies used. As observed in Figs. 2 and 3, meaningful object reconstruction was possible only when an adequate number of frequencies are used (at least 8 frequencies for the simulation results herein). Reconstructions with single frequencies generally lead to the appearance of strong artifacts. A low single frequency (such as <1 MHz) results in reconstruction of slow-varying artifacts. Correspondingly, a single high frequency results in an image containing strong high spatial frequency artifacts. Analogous results are observed when using multi-frequency measurements over narrow frequency bands. As evinced in the results herein, high-fidelity imaging is achieved when measurements over a broad span of frequencies is considered. A maximum total number of 28 frequencies were used in this work for demonstration purposes. Increasing the number of frequencies is expected to consistently improve the performance. However, the maximum achievable number of frequencies should be eventually determined by optimizing a trade-off between signal power per frequency and transducer bandwidth. Optimal frequency selection and spacing given such system parameters is an interesting technical design problem and is a subject of ongoing research.

In conclusion, we proposed herein frequency-domain optoacoustic tomography, using CW illumination modulated at multiple frequencies. A model-based formulation based on the Green's function solution to the wave equation in frequency domain was proposed. This formulation enabled accurate object localization and characterization through regularized iterative inversion. The simulations results were presented for synthetic data obtained from numerical phantoms. The results demonstrated reconstruction of optical absorbers of complex shapes using measured phase and amplitude data in presence of strong measurement noise. Optimal system design based on development of specific trade-off schemes between various system parameters is the next logical step of future work.

Conflict of interest

VN has financial interests in iThera Medical GmbH; a company that commercializes optoacoustic technology. The other authors declare that there are no conflicts of interest.

Biographies

Pouyan Mohajerani studied electrical engineering at Sharif University of Technology and later received his M.Sc. in electrical engineering from Georgia Institute of Technology in 2004. He is currently a Ph.D. student in the Institute for Biological and Medical Imaging (IBMI) at Technische Universität München and Helmholtz Zentrum München, Munich, Germany. His current research interests are in fluorescence tomography, inverse problems as well as optoacoustic imaging and tomography.

Stephan Kellnberger received his diploma in electrical engineering from the Friedrich-Alexander-Universität Erlangen-Nürnberg in 2007, and his Ph.D. degree from the Technische Universität München in 2013. He is currently a postdoctoral fellow at the Institute for Biological and Medical Imaging (IBMI) at the Helmholtz Zentrum München and Technische Universität München (TUM). His research interests include the development of novel opto- and thermoacoustic imaging systems in time and frequency domain, new acoustic sensing methods and the application of magnetic nanoparticles in thermoacoustic imaging.

Vasilis Ntziachristos studied electrical engineering at Aristotle University in Thessaloniki, Greece and received his Master's and Doctorate degrees from the Bioengineering Department of the University of Pennsylvania. He served as assistant professor and director of the Laboratory for Bio-Optics and Molecular Imaging at Harvard University and Massachusetts General Hospital. He is currently a Professor of Medicine, Professor of Electrical Engineering and Chair for Biological Imaging (CBI) at the Technische Universität München (TUM) and the Director of the Institute for Biological and Medical Imaging (IBMI) at the Helmholtz Zentrum München. His research concentrates on basic research and translation of novel optical and optoacoustic in vivo imaging for addressing unmet biological and clinical needs. He has received several awards including the 2013 Gottfried Leibniz Prize, the 2011 Schrödinger Award and the 2011 Basic Science Award from the World Molecular Imaging Society. He is an author of more than 230 peer reviewed publications, the editor of the Photoacoustics Journal and serves on many international editorial and scientific boards in the fields of optics and photoacoustics.