Commentary on "Mediation analysis without sequential ignorability: Using baseline covariates interacted with random assignment as instrumental variables" by Dylan Small

Abstract

I applaud Dr. Small for advancing causal mediation analysis and thank the editors for the opportunity to comment on this valuable article. Small’s project was to relax and test the assumptions on which a previously proposed model relies; in the second half of this discussion I will assess those assumptions and others on which the model hinges. But first I will review the various schools of mediation analysis and situate the estimand considered by Small within the somewhat esoteric domain of mediation estimands.

Taxonomy of mediation effects

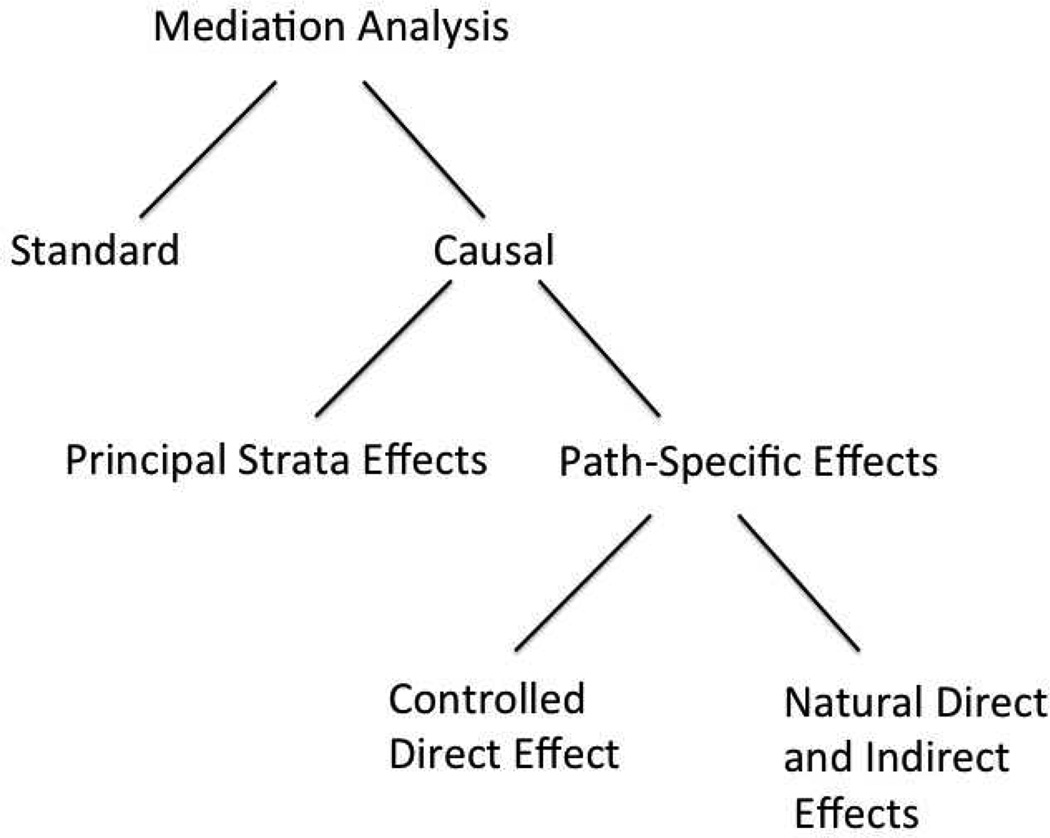
Mediation analysis is concerned with the way in which a treatment or exposure effects an outcome. If the treatment affects a mediator which in turn affects the outcome, we say that the treatment has an indirect effect on the outcome through the mediator. If the treatment affects the outcome without operating through the mediator, it has a direct effect on the outcome with respect to the mediator. (Direct and indirect effects are always defined with respect to a particular mediator; to claim that a treatment has a direct effect on an outcome is not to claim that there are no intervening variables on the causal pathway from the treatment to the outcome but only that the specified mediator is not on the pathway.) There are a variety of different approaches to mediation analysis. Historically mediation analysis was firmly routed in linear structural equation models, with mediated effects defined in terms of the parameters of those models. This is sometimes called “standard” analysis, to differentiate it from the more recent development of causal mediation analysis, which defines mediated effects in terms of potential outcomes. Causal mediation analysis comprises two types of mediation effects: principle strata effects and path-specific effects. I will briefly describe the former, for completeness, but focus on the latter, as did Small. The relations among different types of mediated effects are depicted in Figure 1.

Figure 1.

Classification Tree for Mediation Analysis

Standard Mediation Analysis

Standard mediation analysis defines direct and indirect effects in terms of the coefficients of linear structural equation models (Baron and Kenny, 1986; Judd and Kenny, 1981). For example the product method estimates the parameters of the models

$$Y_i={\beta }_0+{\beta }_1{R}_i+{\beta }_2{M}_i+{\beta }_3^{\prime }{\mathbf{X}}_i+{\epsilon }_i$$ (1)

$$M_i={\alpha }_0+{\alpha }_1{R}_i+{\alpha }_2^{\prime }{\mathbf{X}}_i+{\delta }_i$$ (2)

(Y is the outcome, M is the mediator, R is the treatment, X is a vector of covariates, and ε_i and δ_i are mean-zero error terms) and defines the direct effect to be β₁ and the indirect effect to be α₁β₂ (Baron and Kenny, 1986). When the regression models are derived from structural equation models these definitions have intuitive appeal and seem to correspond to the definitions of direct and indirect effects I gave above. However, effects so defined often do not formally correspond to the causal interpretations they are given (Sobel, 1990). These definitions require that all baseline confounders of the treatment-outcome and mediator-outcome relationships be included in X (Small, 2012). They also require that the two linear models given above are correctly specified, in other words that the relationships among the variables are truly linear, and in particular that there is no treatment-mediator interaction (Pearl, 2011).

Causal Mediation Analysis

Causal mediation analysis defines the direct and indirect effects of interest in terms of potential or counterfactual outcomes (Pearl, 2000; Rubin, 1974, 2005). In contrast to standard mediation analysis, in causal mediation analysis the causal effects are primary and the models secondary.

Path-specific effects

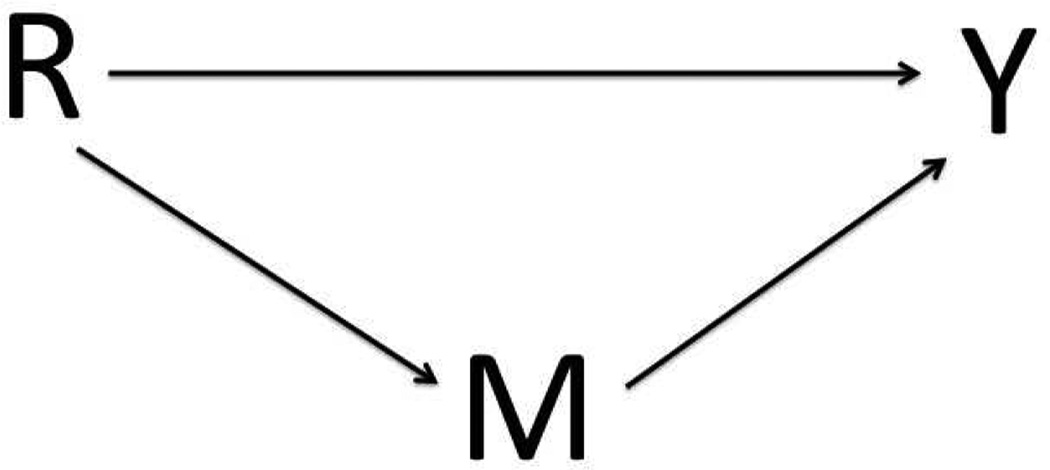
The term path-specific effects was introduced by Pearl (2001) to describe effects that travel along specific causal pathways represented on causal diagrams like that in Figure 2. If each of the arrows in Figure 2 represents a causal effect, then, roughly, the direct effect of R on Y with mediator M is the effect along the path R → Y. There are two different ways to formalize the notion of a direct effect. The controlled direct effect captures the effect of R on Y if one were to intervene on M and set it to a prescribed baseline value m. Intervening on M in this way blocks R from affecting M. The natural direct effect captures the effect of R on Y if M is allowed to be affected by R but its effect on Y is blocked.

Figure 2.

Causal diagram of the relations among a treatment R, a mediator M, and an outcome Y

Using Small’s notation, $Y_i^{(r,m)}$ is the potential outcome for subject i under an intervention that sets R_i to r and M_i to m. Suppose R is binary with reference value 0. The controlled direct effect (CDE) of R on Y with respect to M is $CDE(m)\equiv Y_i^{(1,m)}-Y_i^{(0,m)}$. This is the difference in average counterfactual outcomes under two different values of R when M is set to a specified value m in both terms of the contrast. It may be different for different values of m. The parameter θ_Mi in Small’s article is defined as a controlled direct effect. In the PROSPECT study analyzed by Small, the CDE is the effect of treatment on depression holding use of prescription drugs constant either at m = 0 (no prescription drug use) or m = 1 (some prescription drug use). This effect can be used to answer the following question: If we intervened to set prescription drug use to m for everyone in the population, would being assigned to a depression specialist still have an effect on depression after four months, or would the depression specialist be obviated by the intervention we’d already performed on prescription drug use?

The natural direct effect (NDE) of R on Y with respect to M is $Y_i^{(1,M_i^{(0)})}-Y_i^{(0,M_i^{(0)})}$ where $M_i^{(0)}$ is the counterfactual value that M_i would have obtained if we had intervened to set R_i to 0. Like the CDE this effect fixes M at the same value in both terms of the contrast in order to block the effect of R on Y along the R → M → Y path; the difference is that it is fixed not at a specified value but rather at the value that it would naturally have obtained if R had been 0. In the PROSPECT study the NDE is the effect of treatment on depression holding use of prescription drugs at the value it would have taken under no treatment. If subject i would have used prescription drugs to treat his depression if he were randomized to the control group, then $M_i^{(0)}=1$ and the NDE for subject i is $Y_i^{(1,1)}-Y_i^{(0,1)}$, which is CDE(1), that is, the CDE evaluated at m = 1. The population average NDE is an average of CDE(m) for different values m, weighted by the distribution of M⁽⁰⁾ in the population. The NDE can answer the question, what effect does being assigned to a depression specialist have on depression after four months, if being assigned to the specialist is not allowed to influence prescription drug use? Pearl (2001) calls the CDE a prescriptive measure and the NDE a descriptive measure. The CDE can inform policy; the NDE describes causal mechanisms.

The indirect effect of R on Y through M is the effect of R on Y along the path R → M → Y in Figure 2. The total effect (TE) of R on Y is $Y_i^{(1)}-Y_i^{(0)}$, where $Y_i^{(r)}$ is the outcome that individual i would display if randomized to group r. A desirable property of mediation effects is that the total effect be a sum of the direct and indirect effects. Subtracting the NDE from the TE gives the natural indirect effect $Y_i^{(1,M_i^{(1)})}-Y_i^{(1,M_i^{(0)})}$, which blocks the causal pathway R → Y. Subtracting the CDE from the TE, on the other hand, does not have a counterfactual interpretation. Indeed, there is no notion of a controlled indirect effect, because no contrast of potential outcomes $Y_i^{(r,m)}$ allows R to affect M.

Natural mediated effects have been criticized for being non-experimental quantities. That is, there is no experimental design that can identify these effects without additional assumptions (Robins and Richardson, 2010). The controlled direct effect, on the other hand, can be identified by an experiment in which the mediator, in addition to the treatment, is randomized.

Principal strata effects

Principal strata are latent groups defined by the pair of counterfactuals (M⁽⁰⁾,M⁽¹⁾). The principal strata direct effect is the effect of R on Y in the subgroup of subjects belonging to the principal strata in which M⁽⁰⁾ = M⁽¹⁾. Because M⁽⁰⁾ = M⁽¹⁾ for the individuals in this subgroup, R does not have an effect on M and therefore any effect of R on Y is not through M. There is no analogous notion of a principal strata indirect effect, because in general the effect of R on Y in each of the strata in which M⁽⁰⁾ ≠ M⁽¹⁾ may include effects that are through M and effects that are not through M.

Connections among the different direct effects

The NDE and NIE can be defined as meaningful mediated effects in any context, though in some they may not be identifiable. The CDE is equal to the NDE when there is no treatment-mediator interaction for the CDE, that is, when CDE(m) is constant in m. In this case the difference between the TE and the CDE can be interpreted as an indirect effect, because it must be equal to the NIE. When the outcome and mediator models are linear and there is no treatment-mediator interaction in the outcome model, i.e. when the models given in 1 and 2 are correctly specified, then the standard method identifies the NDE, which is equal to the CDE.

Assumptions and sensitivity analyses

The contribution of Small’s article is to weaken and test the identifying assumptions of a previously proposed model for the direct effect in the presence of unmeasured mediator-outcome confounding. Prying models loose from reliance on implausible identifying assumptions, and testing the sensitivity of model-based conclusions to untestable or implausible assumptions, are arguably two of the most important tasks for statisticians concerned with causal inference.

Small considers the context in which the model in 1 is correctly specified. This implies that the coefficient on R in that model is equal to the CDE which is equal to the NDE. However, some of the required covariates X are unmeasured, namely some confounders of the mediator-outcome relationship. Previous work proposed an instrumental variables estimator of the direct effect in the presence of unmeasured mediator-outcome confounding, but it relied on the strong and generally implausible assumption of rank preservation (RP) (Ten Have et al., 2007). Rank preservation is the assumption that if subject i would have a lower depression measure than subject j when both subjects are in the control condition, then subject i must also have a lower depression measure than subject j when both subjects are in the treatment condition. This assumption is satisfied if the treatment effect is the same for all subjects; although the assumption of uniform treatment effects is stronger than RP they are often used interchangeably (Robins 1992). Ten Have et al. (2007) made the RP assumptions that the direct effect of randomization and the effect of the mediator on the outcome are uniform across all subjects. RP is a biologically implausible assumption, as the effect of treatment will almost certainly depend on individuals’ behaviors and characteristics. It plays a critical role in the history of g-estimation and structural nested models (e.g. Robins 1998), having been used as a heuristic tool to motivate and explain g-estimation in many different contexts. In some contexts, notably when instrumental variables are used to compensate for unmeasured confounding, RP serves as a crucial identifying assumption. Because of its implausibility, finding ways to weaken this assumption should be a priority whenever model-based conclusions depend on it. (Note that in some of the settings for which RP serves an heuristic purpose, models with and without RP give rise to identical estimation and testing procedures Robins 1998.)

Small did just that in his article, replacing the RP assumption with two less restrictive assumptions: that the direct effect of randomization and the effect of the mediator on the outcome are mean-independent of measured baseline covariates, and that the observed value of the mediator is independent of its effect on the outcome conditional on randomization and baseline covariates. Both of these assumptions are entailed by the assumption of uniform direct and mediated effects, but their implications are much weaker (and therefore more plausible) than uniform effects. Furthermore, Small provided an easy-to-implement sensitivity analysis for the assumption that the direct effect of randomization and the effect of the mediator on the outcome are mean-independent of measured baseline covariates.

While eliminating the assumption of uniform treatment effects goes a long way towards making Small’s model more realistic, the model still requires that the outcome be linear in the treatment, mediator, and covariates, and in particular that there be no treatment-mediator interaction. In the context of the PROSPECT study that Small considers, this means that there is no interaction between assignment to a depression specialist and prescription drug use in predicting four-month depression. Particularly because the mediator is an indicator of any prescription drug use rather than a continuous measure of prescription drug use, I think it is possible that the no-interaction assumption is violated in this data. This would likely be the case if subjects with prescription drug use in the control group were less compliant their prescriptions than those in the treatment group, for example failing to take their drugs regularly or to refill their prescriptions. In this case subjects in the treatment group might benefit more from prescription drug use than those in the control group. Several authors have proposed sensitivity analyses for natural direct and indirect effects in the presence of unmeasured mediator-outcome confounding (Hafeman, 2011; Imai et al., 2010; VanderWeele, 2010); it would be interesting to compare Small’s analysis to an analysis of the PROSPECT data using these models, which do not presume linear relationships or the absence of interactions.

Conclusion

Small took on the important challenge of relaxing the rank preservation assumption for instrumental variable estimators of the direct effect in the presence of unmeasured mediator-outcome confounding. The result is an estimator that relies on far more reasonable assumptions than previous proposals. Some of the assumptions on which it relies are likely to fail to hold in some settings; Small proposed a sensitivity analysis for one of them. However, the task of relaxing and testing identifying assumptions remains unfinished.