Modeling Pathological Speech Perception From Data With Similarity Labels

Abstract

The current state of the art in judging pathological speech intelligibility is subjective assessment performed by trained speech pathologists (SLP). These tests, however, are inconsistent, costly and, oftentimes suffer from poor intra- and inter-judge reliability. As such, consistent, reliable, and perceptually-relevant objective evaluations of pathological speech are critical. Here, we propose a data-driven approach to this problem. We propose new cost functions for examining data from a series of experiments, whereby we ask certified SLPs to rate pathological speech along the perceptual dimensions that contribute to decreased intelligibility. We consider qualitative feedback from SLPs in the form of comparisons similar to statements “Is Speaker A's rhythm more similar to Speaker B or Speaker C?” Data of this form is common in behavioral research, but is different from the traditional data structures expected in supervised (data matrix + class labels) or unsupervised (data matrix) machine learning. The proposed method identifies relevant acoustic features that correlate with the ordinal data collected during the experiment. Using these features, we show that we are able to develop objective measures of the speech signal degradation that correlate well with SLP responses.

1. Introduction

The assessment of speech intelligibility is the cornerstone of clinical practice in speech-language pathology, as it indexes a patient's communicative handicap. However, clinical assessments are predominantly conducted through subjective tests performed by trained speech-language pathologists (e.g. making subjective estimations of the amount of speech that can be understood, number of words correctly understood in a standard test battery, etc.). Subjective tests, however, can be inconsistent, costly and, oftentimes, not repeatable. In particular, repeated exposure to the same subject over time can influence the ratings [1, 2, 3, 4]. As such, there is an inherent ambiguity about whether the patient's intelligibility is improving or whether the listener has adapted their listening strategy so that it better matches the patient's speaking style.

To overcome these problems, there has been an expressed desire to develop efficient, objective, and reliable measures that can be added to the clinical repertoire. Here, we propose a data-driven approach to this problem. We propose a framework to process collected data from SLPs in order to identify specific features that are strong correlates to the SLPs ratings. We consider qualitative feedback from SLPs in the form of comparisons similar to statements like: ”Speaker A sounds more like speaker B than speaker C.” An alternative to this paradigm is to ask listeners to rate the speakers along a scale (e.g. typical to abnormal). Research suggests that quantitative feedback of this form can be unreliable; as a result, comparative input that doesn't require ratings along an absolute scale is oftentimes preferred [5] [6] [7] [8]. Mathematically, these statements can be expressed as ordinal constraints. If we represent each speech signal from speakers A, B, and C by the vectors x_A, x_B, and x_C (by extracting a set of features) , then feedback from these experiments can be modeled as inequalities of the form d(x_A, x_B) < d(x_A, x_C), where d(*, *) denotes some distance measure. Data of this form are common in behavioral research, but are different from the traditional data structures expected in supervised (data matrix + class labels) or unsupervised (data matrix) machine learning. Here, we propose an algorithm for learning from data of this form. The results show that the algorithm is able to identify relevant dimensions of the speech signal that preserve the direction of the dissimilarities. Using these features, we successfully design algorithms for predicting the rating of certified speech language pathologists along different perceptual dimensions.

2. Relation to Prior Work

Existing work on analyzing pathological speech has been limited to automated assessment of the intelligibility of the signal. A number of approaches rely on estimating subjective intelligibility through the use of pre-trained automatic speech recognition (ASR) algorithms [9]. These algorithms are trained on healthy speech and the error rate on pathological speech serves as a proxy for estimating the intelligibility decrement. Research in blind algorithms for intelligibility assessment has been more limited. In telecommunications, the ITU-P.563 standard has been shown to correlate well with speech quality, however this is not optimized for pathological speech and, in fact, it aims to measure speech quality, not intelligibility [10]. In [11], [12] and [13], the authors attempt to estimate dysarthric speech intelligibility using a set of selected acoustic features. Although the algorithms have shown some success in a narrow context, the feature sets used in these papers do not make use of long-term rhythm disturbances in the signal, common in the dysarthrias.

In contrast to these methods, here the goal is not to automate intelligibility/quality assessment. Rather, using a newly developed feature selection method, we aim to isolate specific acoustic cues that correlate with the way that SLPs judge pathological speech similarity. Using these features, we aim to develop listening models capable of evaluating speech along different perceptual dimensions.

In the machine learning literature, significant work has been done on ranking algorithms - an overview of the existing ranking literature can be found in [14]. Although related to ranking, the tools proposed here deal with relative distances between points in the set (e.g. d(x_A, x_B) < d(x_A, x_C) not x_A < x_B). Often the goal in the ranking literature is to learn a mapping from a vector (features) into a real number that represents the rank of that object from among a set. Here, the goal is to perform feature selection using relative dissimilarities between points.

3. Learning With Similarity Labels

The goal of our research here is to identify acoustic features that correlate well to the responses collected from certified speech language pathologists asked to identify perceptual similarity between pathological speech signals. In this section, we describe a set of candidate features extracted from each speech signal, we develop the cost function, identify an appropriate distance measure, and develop a framework for solving the cost function.

3.1. Feature Description

EMS

The envelope modulation spectrum (EMS) is a representation of the slow amplitude modulations in a signal and the distribution of energy in the amplitude fluctuations across designated frequencies, collapsed over time [15]. It has been shown to be a useful indicator of atypical rhythm patterns in pathological speech [15]. The speech segment, x(t), is first filtered into 7 octave bands with center frequencies of 125, 250, 500, 1000, 2000, 4000, and 8000 Hz. Let h_i(t) denote the filter associated with the ith octave. The filtered signal x_i(t) is then denoted by,

$$x_i(t)=h_i(t)\ast x(t).$$ (1)

The envelope in the ith octave, denoted by env_i(t), is extracted by:

$${\mathit{\text{env}}}_i(t)=h_{\text{LPF}}(t)\ast \mathcal{H}\{x(t)\}$$ (2)

where, (ℋ {·} denotes the Hilbert transform and h_LPF(t) is the impulse response of a 20 Hz low-pass filter. Once the amplitude envelope of the signal is obtained, the low-frequency variation in the amplitude levels of the signal can be examined. Fourier analysis is used to quantify the temporal regularities of the signal. With this, six EMS metrics are computed from the resulting envelope spectrum for each of the 7 octave bands, x_i(t), and the full signal, x(t): 1) peak frequency; 2) peak amplitude; 3) energy in the spectrum from 3-6 Hz; 4) energy in spectrum from 0-4 Hz; 5) energy in spectrum from 4-10 Hz; and 6) energy ratio between 0-4 Hz band and 4-10 Hz band. This results in a 48-dimensional feature vector.

LTAS

The long-term average spectrum (LTAS) features capture atypical average spectral information in the signal [16]. Nasality, breathiness, and atypical loudness variation, all of which are common causes of intelligibility deficits in pathological speech, present themselves as atypical distributions of energy across the spectrum; LTAS attempts to measure these cues in each octave. For each of the 7 octave bands, x_i(t), and the original signal, x(t), the LTAS features set consists of the: 1) average normalized RMS energy; 2) RMS energy standard deviation; 3) RMS energy range; and 4) pairwise variability of RMS energy between ensuing 20 ms frames. This results in a 28-dimensional feature vector.

P.563

The ITU-T P.563 standard for blind speech quality assessment [10] is designed to measure speech quality using a parameter set that measures atypical and unnatural voice and articulatory quality. There are five major classes of features deemed appropriate for our purposes: 1) basic speech descriptors, such as pitch and loudness information; 2) vocal tract analysis, including statistics derived from estimates of vocal tract area based on the cascaded tube model; 3) speech statistics, which calculate the skewness and kurtosis of the cepstral and linear prediction coefficients (LPC); 4) static SNR, measurements of signal-to-noise ratio, estimates of background noise, and estimates of spectral clarity based on a harmonic-to-noise ratio; and 5) segmental SNR, or dynamic noise, where the SNR is calculated on a frame-by-frame basis. In the standard, a subjective rating (MOS, or Mean Opinion Score), is obtained through a non-linear combination of the above features. Here, we make use of the same feature set for our analysis, by combining all feature sets into one vector. For a detailed description of each feature, including the mathematical derivation, please refer to [10, 17].

After extraction of each feature set, we concatenate the features into a single feature vector, x. This is extracted for each sentence spoken by each individual in our data set. The data is described in detail in section 4.

3.2. Cost Function Derivation

Let us consider a set of collected similarity responses from a single SLP organized in a set S. For feature selection, we define a selector vector w that identifies the set of features that are the strongest correlates to the SLP's choices. In (3) we define a notional optimization problem that embeds the SLP responses in the constraints, with slack variables, s_ijk to account for inconsistent responses, and element-wise multiplication between the selector variable and the features (w_t ○ x_i).

$$\begin{array}{ll}\underset{\mathbf{w},s_{\mathit{\text{ijk}}}}{\text{minimize}}\hfill & \sum _{(i,j,k)\in \mathit{S}}{s}_{\mathit{\text{ijk}}}+\mathrm{\lambda }g(\mathbf{w})\hfill \\ \text{subject to}\hfill & d_{\mathit{\text{ij}}}^2(\mathbf{w})-d_{\mathit{\text{ik}}}^2(\mathbf{w})-s_{\mathit{\text{ijk}}}\le 0,\forall (i,j,k)\in \mathit{S}\hfill \\ \hfill & s_{\mathit{\text{ijk}}}>0,\forall (i,j,k)\in \mathit{S}\hfill \end{array}$$ (3)

where d_ij(w) = d(w ○ x_i, w ○ x_j) and x ○ y denotes element-wise multiplication. The regularizer in (3), g(w), gives us flexibility in how we perform feature selection under this framework. Possibilities include Tikhonov regularization, the sparsity-inducing L₁ norm, the L_2,1 norm popular in multi-task learning.

3.3. Defining the Distance Metric

We use the weighted Euclidean distance to measure similarity between points:

$$d_{\mathit{\text{ij}}}(\mathbf{W})=\sqrt{{({\mathrm{x}}_i-{\mathrm{x}}_j)}^{\mathrm{T}}\mathbf{W}({\mathrm{x}}_i-{\mathrm{x}}_j)}$$ (4)

$$=\sqrt{\sum _z\mathbf{W}(z,z){({\mathrm{x}}_i(z)-{\mathrm{x}}_j(z))}^2}$$ (5)

$$=\sqrt{\sum _z\mathbf{W}(z,z){\mathbf{y}}_{\mathit{\text{ij}}}(z)},$$ (6)

where y_ij = (x_i − x_j)². If we define the selector vector,w, in (3) as the diagonal of our weight matrix, W, then we can write the euclidean distance constraint in vector form as:

$$d_{\mathit{\text{ij}}}(\mathbf{w})=\sqrt{{\mathbf{w}}^T{\mathbf{y}}_{\mathit{\text{ij}}}}$$ (7)

Although here we derive a distance constraint based on Euclidean distance, other distance measures can be considered. Examples include the Mahalanobis distance, or perhaps even Kernel methods.

3.4. Solving the Cost Function

Combining the distance metric in (7) with the cost function formulation in (3) and using the sparsity-inducing L1 norm, we obtain the following complete optimization problem:

$$\begin{array}{ll}\underset{\mathbf{w},s_{\mathit{\text{ijk}}}}{\text{minimize}}\hfill & \sum _{(i,j,k)\in \mathit{S}}{s}_{\mathit{\text{ijk}}}+\mathrm{\lambda }{\Vert \mathbf{w}\Vert }_1\hfill \\ \text{subject to}\hfill & {\mathbf{w}}^T{\mathbf{y}}_{\mathit{\text{ij}}}-{\mathbf{w}}^T{\mathbf{y}}_{\mathit{\text{ik}}}-s_{\mathit{\text{ijk}}}\le 0,\forall (i,j,k)\in \mathit{S}\hfill \\ \hfill & s_{\mathit{\text{ijk}}}>0,\forall (i,j,k)\in \mathit{S}\hfill \end{array}$$ (8)

The cost function consists of two terms: the L1 constraint and term that depends on the slack variables. The L1 constraint ensures that the optimal selector vector, w, is sparse; the slack variable term serves to penalizes the use of slack variables and ensures that the constraints are preserved. The constraint set aims to preserve the order of the similarities and enforces a positivity constraint on s_ijk. The optimization problem in (8) is convex. In fact, by replacing the L1 constraint with a set of linear constraints, it can be cast as a linear program [18]. Here, we make use of the CVX package to solve for the optimal selector vector and slack variables [19], [20].

4. Results

We evaluate the algorithm on the following two examples.

An Academic Example

In Fig. 1 (a), we generate a set of exemplars neatly organized in a two-dimensional square grid. Next, we embed the 2-D data into 5 dimensions by appending 3 random features to each exemplars. The value of each feature is drawn from (0, 1). This 5-D data set is embedded in two dimensions using multi-dimensional scaling (MDS). This is shown in Fig. 1 (b). In this example, the goal is to identify which of the five features preserve the correct ordering of the exemplars on the grid. We generate a set of 200 random dissimilarities from Fig. 1 (a) to use in the proposed algorithm. We solve the L1-constrained optimization problem in (xxx) and we identify the feature selector vector w that best preserves those dissimilarities. The algorithm correctly identifies 2 non-zero elements in w that correspond to the first 2 dimensions of the 5-dimensional feature vector. Using only the non-zero values of w, we generate a 2-D MDS embedding based on a weighted Euclidean distance measure. This is shown in Fig. 1 (c). As is obvious from the figure, the algorithm correctly identifies the structure of the original embedding using only the similarities. As expected, there is a difference in embedding scale since only similarities are used and not absolute distances.

Fig. 1.

An academic example for evaluating the feature selection algorithm. In (a), we show a 2-dimensional data set with the points arranged on a grid. In (b), we append 3 random dimensions to the data in (a) and plot a 2-dimensions embedding using MDS. In (c), we identify the two features that preserve the similarities from the data (a).

Pathological Speech Evaluation

For this evaluation we use data collected at the Motor Speech Disorders Lab at ASU. This data consists of speech samples, split at the sentence level, from over 100 patients (5 - 10 minutes of speech per individual), presenting with diverse speech degradation patterns of varying severity. We select a representative sample of 33 individuals from this database. Six certified SLPs blinded to speakers' medical and dysarthria subtype diagnoses participated. The task was to evaluate the 33 dysarthric speakers along 5 perceptual dimensions: Severity, Nasality, Vocal Quality, Articulatory Precision, and Prosody. In particular, the listeners were instructed to place a marker along a scale (ranging from normal to severely abnormal) that corresponded to their assessment of the speaker. In order to evaluate the developed algorithm, we convert the scaled responses to similarities by converting distances between responses to similarity labels (similar to what was done in the academic example). The purpose of doing this was to evaluate the ability of the proposed algorithm to reliably select relevant features using only similarity input.

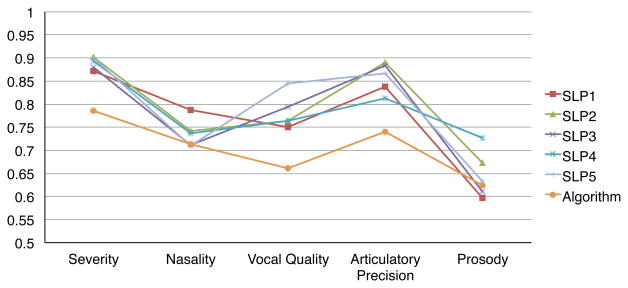
We consider a single SLP from the set of six. For this individual, we identify a subset of features from the candidate set described in section 3.1 that best preserves the similarities along each perceptual dimension. Using this selected feature set, we learn a regression model that predicts one rating for each of the five perceptual dimensions - this can be thought of as a computational listening model for the SLP we analyzed. The algorithms are trained using part of the collected data and evaluated on the remaining set. In Fig. 2, we show the correlation of the remaining five SLP ratings and the algorithm ratings to each other on the test set. The results suggest that the algorithm predicts reasonable ratings for the listeners with an average correlation coefficient of 0.7 to the other SLPs (compared to an average correlation coefficient of 0.8 for the SLP ratings compared to each other). This is a confirmation that the correct features were selected using the proposed approach.

Fig. 2.

A comparison of the correlation in responses from SLPs with those generated by the algorithm.

5. Conclusion

In this work we propose a new method for learning from data with similarity labels of the form “A is more like B than C.” The algorithm is assessed on a problem of identifying relevant acoustic features that correspond to ratings made by certified speech language pathologists on pathological speech. We show that, using the features selected by this algorithm, we are able to develop predictive models that reliably evaluate pathological speech. An obvious next step in this analysis is to extend this beyond models of single SLP to models for aggregate SLP responses - this can be done by solving the cost function in (8) with new group sparsity regularizes (e.g. the L₂₁ norm). In addition, considering different distance functions (perhaps weighted by a denoising vector) in the analysis could yield new optimization algorithms that may be more robust for noisy speech.