ADVANTAGES OF MCNPX-BASED LATTICE TALLY OVER MESH TALLY IN HIGH-SPEED MONTE CARLO DOSE RECONSTRUCTION FOR PROTON RADIOTHERAPY

Abstract

Monte Carlo simulations are increasingly used to reconstruct dose distributions in radiotherapy research studies. Many studies have used the MCNPX Monte Carlo code with a mesh tally for dose reconstructions. However, when the number of voxels in the simulated patient anatomy is large, the computation time for a mesh tally can become prohibitively long. The purpose of this work was to test the feasibility of using lattice tally instead of mesh tally for whole-body dose reconstructions. We did this by comparing the dosimetric accuracy and computation time of lattice tallies with those of mesh tallies for craniospinal proton irradiation. The two tally methods generated nearly identical dosimetric results, within 1% in dose and within 1 mm distance-to-agreement for 99% of the voxels. For a typical craniospinal proton treatment field, simulation speed was 4 to 17 times faster using the lattice tally than using the mesh tally, depending on the numbers of proton histories and voxels. We conclude that the lattice tally is an acceptable substitute for the mesh tally in dose reconstruction, making it a suitable potential candidate for clinical treatment planning.

I. INTRODUCTION

Monte Carlo simulations are increasingly used to reconstruct whole-body dose distributions in patients who received radiotherapy because they provide detailed and accurate out-of-field dosimetric results.^1–12 The Monte Carlo N-Particle eXtended (MCNPX) code, which is a general-purpose radiation transport code developed by Los Alamos National Laboratory,¹³ has been widely used in radiotherapy research applications for simulating primary and secondary doses in proton therapy.^1,3,4,7–12 However, whole-body dose reconstructions remain challenging because of complexity and long simulation times.

The most commonly used approach in MCNPX to record dose distributions is the mesh tally, a method of scoring a quantity of interest on an artificial grid overlaid on the problem geometry. Our group has previously reported on the use of MCNPX to simulate both therapeutic doses and stray radiation doses for patients receiving proton therapy.^4,7,9–12 The mesh tally, used in all previous studies from our group, provided good accuracy and functionality. However, the long simulation times associated with this method were problematic. An alternative approach is the lattice tally, which is based on the repeated structures feature in MCNPX.^14,15 However, relatively few published studies have reported using the lattice tally for proton radiotherapy applications. We therefore sought to investigate using the lattice tally to reduce Monte Carlo simulation times for whole-body dose reconstruction in proton therapy. In addition, we sought to quantify the level of dosimetric agreement between the lattice and mesh tallies. To accomplish these goals, both the mesh tally and the lattice tally were implemented in dose reconstructions for a patient who had received craniospinal irradiation (CSI) with proton beams.

II. MATERIALS AND METHODS

II.A. Proton Therapy Treatment Technique

In the present study, we obtained dosimetric results from simulations of a proton CSI treatment that involved two cranial fields (beams 1 and 2), three spinal fields (beams 3, 4, and 5), and a boost field to the resection bed. The plan was for a 13-year-old girl with medulloblastoma who had been treated in our clinic with proton CSI of 23.4 Gy at 1.8 Gy/fraction to each of the cranial and spinal fields, and a boost of 30.6 Gy to the posterior cranial fossa. For simplicity, we omitted the boost field in this report; it contributed little to the total computation time, regardless of the tally method. Computed tomography (CT) images of 2.5-mm-thick slices were obtained from the top of the patient’s head to the top of the thighs. The planning target volume was defined in each CT slice.

II.B. Geometry Setup of the Voxelized Patient Phantom

MCNPX code version 2.6b was used to model the proton beam delivery system and the patient (Fig. 1). An in-house code, the Monte Carlo Proton Radiotherapy Treatment Planning code,¹⁶ was used to generate all necessary Monte Carlo input files and to run the simulations in parallel on a 1072-CPU cluster with 2.6-GHz, 64-bit AMD processors. Nuclear interaction cross-section libraries were used for particle energy <150 MeV (Ref. 17); for higher energy, Bertini intranuclear-cascade model was used. MCNPX has many physics model options such as CEM and INCL, but the default Bertini model was used for consistency with past calculations and because it matches relevant benchmark results. Additional information on the physics models used can be found elsewhere.^11,12 The source proton energy is treatment site dependent.¹⁰ The patient was represented as a lattice of voxels, which was created based on the three-dimensional CT images of the patient using the methods described by Taddei et al.¹⁰ The voxel size was increased from ~2 × 2 × 2.5 mm to ~4 × 4 × 5 mm to reduce memory requirements in the Monte Carlo system. The matrix of Hounsfield Unit values in these voxels was then converted into corresponding matrices of material compositions and mass density values. The elemental material compositions of organs and tissues were taken from Woodard and White.¹⁸

Fig. 1.

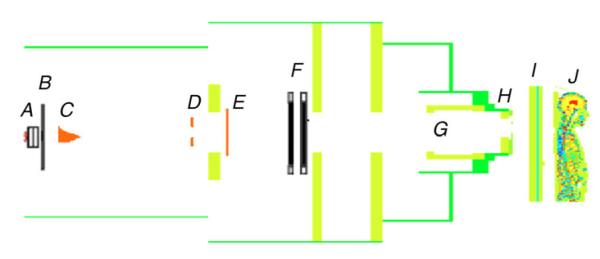
Geometric model of proton therapy unit and the voxelized phantom oriented for the superior spinal proton field. The beam delivery system includes a vacuum window (A), a beam profile monitor (B), a range modulator wheel (C), a second scatterer (D), a range shifter assembly (E), backup and primary monitors (F), the snout (G), the range compensator (H), the treatment couch (I), and the patient (J).

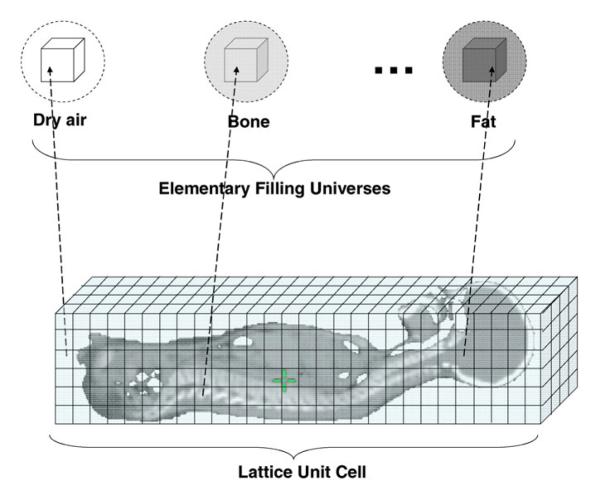
In defining the patient lattice, we took advantage of MCNPX’s repeated-structure capability, which makes it possible to use a relatively small number of predefined cells to represent a much larger object.¹³ The creation of a voxelized phantom has been described previously¹⁹ and is briefly introduced here.

First, in the cell block of the input file, we defined 217 “elementary filling universes” (i.e., predefined cells). These elementary filling universes were subsequently used to fill the lattices, which are defined below. The concept of universe is defined in MCNPX as either a single cell or a collection of cells that can be used to fill other cells.¹³ An example of a card defining an elementary filling universe in MCNPX is

     1  5102 −0.00187  −21  u=1

In this card, the first three numbers show that cell number 1 was assigned to material index 5102 (dry air) with a mass density of 0.00187 g cm⁻³. Cell 1 is also the elementary filling universe number 1 (u = 1) and is inside (as indicated by the minus sign) surface 21, which is the sphere that contains this filling universe. For simplicity, all the elementary filling universes were defined using this same sphere. The other elementary filling universes (217 in all) were defined in a similar way, each with a unique combination of material composition and mass density.

Second, we defined the “lattice unit cell,” which is the complete three-dimensional lattice representing the object of interest (e.g., the patient, surrounding air, and treatment couch):

   205 0 −2 1 −4 3 −6 5  u=205  lat=1  fill=0:127
   0:93 0:196 &
        1 19r 2 2 1 2r 2 1 2 1 2 2 1 …

This card shows that cell 205 is the lattice unit cell and was filled with a “void” with material denoted by the index 0. Void was used here because the whole lattice unit cell was subsequently completely filled by elementary filling universes; i.e., the material of the lattice unit cell itself was not specified here. Cell 205 was also a universe (u = 205) and will be later used to fill the “cell containing lattice” (defined below). The starting voxel of lattice filling was a cubic box defined by six planes (−2 1 −4 3 −6 5). The rectangular type of lattice (lat = 1) was used in this case, consisting of 128 × 94 × 197 voxels along the x, y, and z axes, respectively, and each voxel corresponded to a voxel in the patient data set. After the continuation symbol “&,” an array of 2 370 304 elementary filling universes (described above) were defined; only the first 32 universes are listed here. One elementary filling universe filled each voxel. We conserved computer memory by creating only 217 elementary filling universes and using the repetition record keyword “r” to define the voxels with the same material composition (as opposed to defining each voxel with a unique elementary filling universe).

Finally, we defined one “cell containing lattice,” a rectangular box that enclosed the lattice unit cell, and this box has the same size as the lattice unit cell. For instance, cell containing lattice 206 in this work was defined as follows:

   206  0  11 −12 13 −14 15 −16 fill=205

Here, cell 206, the cell containing lattice defined by six planes (11 −12 13 −14 15 −16), was assigned to a void material (0) and filled with universe 205, which was the lattice unit cell defined above. Figure 2 schematically illustrates the setup of the voxelized patient phantom.

Fig. 2.

Schematic illustration of setup of the voxelized patient phantom.

II.C. Mesh Tally

The mesh tally method was described in a previous study¹⁰ and is briefly reviewed here. In the mesh tally procedure used to score therapeutic proton absorbed dose, a grid of cubic voxels was superimposed on the patient lattice unit cell (defined in Sec II.B). For simplicity, we chose the size and location of the mesh grid to exactly coincide with those of the lattice unit cell; that is, each voxel of the mesh corresponded to one voxel of the lattice unit cell. The cards that defined the mesh tally in the input file for the energy deposition of protons were

   TMESH
   RMESH11: h pedep
    CORA11 −25.049 127i 24.951
    CORB11 −18.799 93i 17.920
    CORC11 −48.125 196i 50.375
   ENDMD

where the keywords TMESH and ENDMD begin and end the mesh definition, RMESH11 specifies a type 1 mesh tally, h specifies that protons were scored, and pedep specifies that the tally recorded average energy deposition per unit volume (MeV/cm³ per source particle). The card “CORA11 −25.049 127i 24.951” defined the rectangular mesh in the x direction, with 128 mesh grids between x coordinates −25.049 and 24.951. Similarly, the y and z axes of the mesh were defined with the CORB and CORC cards, respectively.

The energy deposition in each voxel in this mesh tally was recorded to a binary MDATA file. The program GRIDCONV, included with MCNPX, was used to convert the binary data files to ASCII files. The mass densities of all voxels were recorded separately, and an in-house code was used to calculate absorbed dose (by dividing energy deposition by the corresponding mass density value), as well as to perform further postprocessing.

II.D. Lattice Tally

The lattice tally approach utilized the lattice unit cells defined in Sec. II.B directly, obviating the need to define a mesh. The lattice tally was defined as

    F6: h (205 < 205[0:127 0:93 0:196] < 206)
    SD6  0.0763  2370303r

The keyword F6 specifies that the quantity to tally is energy deposition. The cells inside the parentheses include all the voxels in the lattice unit cell. The SD (segment divisor) card was used because MCNPX could not accurately calculate the required voxel volumes for tallies involving repeated structures.¹³ The volume of each voxel (0.0763 cm³) was instead specified explicitly using the repetition keyword “r”. The results of the lattice tally were written to an MCTAL file in ASCII format using the card PRDMP 2j 1.

II.E. Computation Time and Dose Comparison

We characterized the Monte Carlo computation times (in CPU minutes) for lattice and mesh tallies as functions of the number of proton histories and phantom voxels. For simplicity, only the simulations of the upper spinal field (beam 3) were used.

To compare the three-dimensional dose distributions of lattice and mesh tallies in a quantitative manner, we conducted a gamma analysis.²⁰ The dosimetric results were considered to be sufficiently close if at least 99% of the voxels had γ values <1. The γ criteria we used were a 1% difference in absorbed dose and a 1-mm distance-to-agreement.

III. RESULTS AND DISCUSSION

The mesh and lattice tallies predicted almost identical dose distributions in the patient (Fig. 3). For the plan’s two cranial and three spinal beams, only ~1 in 5000 voxels had a γ value above 1. The dosimetric differences, which were clinically insignificant, are most likely attributable to minor differences in the particle tracking and to related rounding and truncation errors.

Fig. 3.

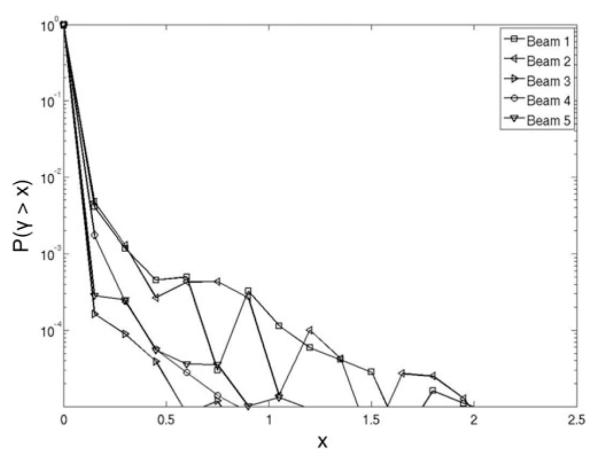
Probability P(γ > x), where x is a certain calculated γ value, that a voxel’s γ value will exceed the γ criteria (1% of dose and 1-mm distance-to-agreement) as a function of the x value, using the dose distribution from the mesh tally dosimetric results as the reference. Probability curves are plotted separately for two cranial fields (beams 1 and 2) and three spinal fields (beams 3, 4, and 5).

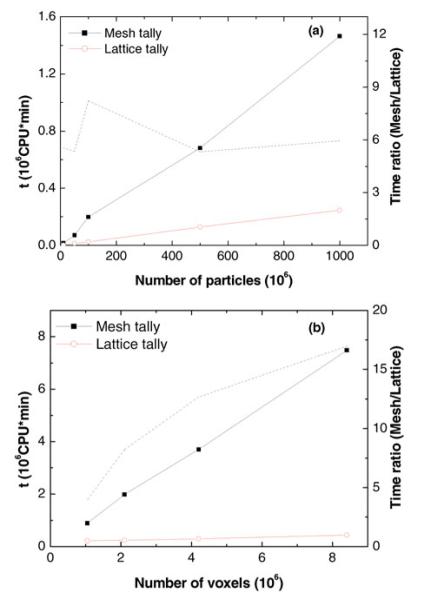
Figure 4 shows the Monte Carlo simulation times for the lattice and mesh tallies of the upper spinal field. The lattice tally was faster than the mesh tally for simulations involving 10 million to 1 billion particle histories (2 million voxels), and 1.1 million to 8.4 million voxels (100 million particles). The lattice tally required from 4 to 17 times less computation time than the mesh tally, where the increase in calculation speed increased with the number of voxels. The increase in calculation speed remained nearly constant (a factor of ~6) as the number of simulation histories was varied between 10 million and 1 billion.

Fig. 4.

Computation time (t) of different tallies for a spinal field in CSI proton therapy as a function of (a) the number of particles simulated and (b) the number of voxels in the lattice unit cell. The ratio of computation time is shown as dashed lines.

The mesh tally was slower than the lattice tally because it duplicated some calculations already performed by the particle-tracking algorithm in the lattice representation of the CT image data. Specifically, the transport algorithm of the mesh tally calculates the location (voxel) of a particle in the lattice unit cell at each condensed history step. Thus, in our simulations using the mesh tally, even though the mesh exactly coincided with the size and locations of the lattice unit cell, the transport algorithm additionally had to determine in which voxel in the mesh a particle was, essentially duplicating the calculation of determining which voxel of the lattice the same particle was in. This determination is not efficient because the mesh tally does not assume congruence with the lattice mesh and must account for the general case of locating the mesh tally cell and determining if multiple mesh tally cells have been traversed in the course of transport through a lattice cell.

The mesh tally is useful for visualization of results. In particular, the MCNPX graphics capability enables plotting the mesh tally results superimposed over the problem geometry, whereas tallies in the geometric lattice cannot be plotted superimposed over the geometry.¹³ However, the mesh tally is computationally slow because at each step in the particle transport the location in the superimposed mesh tally must be located. In the general case, in which the lattice and mesh do not coincide, the dual calculation of particle location is necessary. However, for the special case of coincident voxel definitions, duplicate tracking makes the mesh tally slower.

Besides improved speed and simplicity, a major advantage of the lattice tally is that it provides statistical tests for convergence of dosimetric results²¹ and other statistical information. Convergence of dosimetric results is important because it qualitatively increases confidence in the predicted doses.¹³ All Monte Carlo calculations will give an answer, but that answer can be falsely converged: It may appear to be correct even though important regions of geometry, energy, physics processes, or other regions of phase space are insufficiently sampled. The MCNPX statistical checks are very powerful and nearly always can identify false convergence due to undersampling.¹³

These results have several implications. The higher computational efficiency of the lattice tally will facilitate routine dose simulations while preserving the proven dosimetric accuracy of the mesh tally. Currently, long computation time is one of the major remaining barriers to the routine use of the Monte Carlo method in proton radiotherapy. The lattice tally will also allow for better reporting of the remaining uncertainty and on statistical tests for convergence. Minimizing and characterizing uncertainties are important for dose reconstruction and risk assessments,²² e.g., comparative risk analysis between different treatment methods.

IV. CONCLUSION

This study demonstrated that the lattice tally is an advantageous alternative to the mesh tally for patient dose reconstructions in proton therapy. The lattice tally was typically one order of magnitude faster than the mesh tally, with an increasing speed advantage for dose reconstructions involving larger numbers of voxels. Furthermore, the dose distributions predicted by the mesh and the lattice tallies were virtually identical, as assessed using the gamma index technique.

The tally methods described in this study are neither MCNPX-specific nor version-specific. They are also available in such codes as MCNP5 and MCNP6. Although this study focused on proton therapy, the lattice tally may also be applicable to other radiotherapy modalities, e.g., external-beam photon therapy and brachytherapy. Additional investigations of the dosimetric accuracy and computational efficiency of the lattice tally for other radiotherapies are under way in our laboratory.