Estimation and Testing of Gene Expression Heterosis

Abstract

Heterosis, also known as the hybrid vigor, occurs when the mean phenotype of hybrid off-spring is superior to that of its two inbred parents. The heterosis phenomenon is extensively utilized in agriculture though the molecular basis is still unknown. In an effort to understand phenotypic heterosis at the molecular level, researchers have begun to compare expression levels of thousands of genes between parental inbred lines and their hybrid offspring to search for evidence of gene expression heterosis. Standard statistical approaches for separately analyzing expression data for each gene can produce biased and highly variable estimates and unreliable tests of heterosis. To address these shortcomings, we develop a hierarchical model to borrow information across genes. Using our modeling framework, we derive empirical Bayes estimators and an inference strategy to identify gene expression heterosis. Simulation results show that our proposed method outperforms the more traditional strategy used to detect gene expression heterosis. This article has supplementary material online.

1 INTRODUCTION

Heterosis, or hybrid vigor, refers to the enhanced phenotype of hybrid progeny relative to their inbred parents. Taking maize as an example, the offspring from crossing the inbred lines B73 and Mo17 are taller, mature faster, and produce greater yields than their parental lines (Hallauer and Miranda, 1981). Since heterosis was scientifically documented by Darwin (1876), it has been successfully manipulated to improve many species for food, feed, and fuel industries, such as rice (Yu et al., 1997), alfalfa (Riday and Brummer, 2002), tomatoes (Krieger et al., 2010), and fish (Wohlfarth, 1993). Despite the intensive study and successful utilization of heterosis, the basic genomic mechanisms remain unclear (Coors and Pandey, 1999; Lippman and Zamir, 2007). Researchers speculate that gene expression heterosis could be among the mechanisms responsible for the phenotypic heterosis (Swanson-Wagner et al., 2006; Springer and Stupar, 2007).

Due to advancements in high-throughput genomics technology (such as microarray and next-generation sequencing of RNA), it is now possible to simultaneously measure and compare expression levels of thousands of genes in parental lines and their hybrid offspring to search for evidence of gene expression heterosis. It is of particular interest to test if a gene exhibits any of the following three forms of gene expression heterosis: high-parent heterosis (HPH), low-parent heterosis (LPH), or mid-parent heterosis (MPH). A gene is said to exhibit HPH if the mean expression level of the offspring is greater than the maximum of the two parental means, LPH if the mean expression level of the offspring is smaller than the minimum of the two parental means, and MPH if the mean expression level of the off-spring is not equal to the average of parental means. Let i index the genotypes of the two parents (i = 1, 2) and the offspring (i = 3). Let j (j = 1, …, J) index the genes, where J denotes the total number of genes under study. We use μ_ij to denote the mean expression level of gene j of genotype i. Let h_j = μ_3j − max{μ_1j, μ_2j}, l_j = min{μ_1j, μ_2j}− μ_3j, and m_j = μ_3j − (μ_1j + μ_2j)/2. With these notations, gene j exhibits HPH, LPH, or MPH if and only if h_j > 0, l_j > 0, or m_j ≠ 0, respectively.

Past work on estimating gene expression heterosis using microarray data (Swanson-Wagner et al., 2006; Wang et al., 2006; Bassene et al., 2010) has used separate estimates for each gene obtained by replacing population means (μ_ij, i = 1, 2, 3, j = 1, ···, J) with corresponding sample averages. These sample average estimators of h_j and l_j are problematic because they are biased and tend to underestimate h_j and l_j (see Appendix A). Though the sample average estimator of m_j is unbiased, with only a few observations for each gene in a typical microarray experiment, the sample average estimators of m_j, h_j, and l_j may each be highly variable.

Because high-throughput technologies measure expression of hundreds of thousands of genes simultaneously, we can utilize information across genes to improve estimation and testing of gene expression heterosis for each individual gene. For gene j, we define two latent variables α_j = (μ_1j − μ_2j)/2 and δ_j = μ_3j − (μ_1j + μ_2j)/2. Notice that all three types of gene expression heterosis can be written as functions of |α_j| and δ_j; that is, h_j = δ_j − |α_j|, l_j = − |α_j|− δ_j, and m_j = δ_j. Thus, modeling of |α_j| and δ_j helps to develop statistical inferences for all three types of gene expression heterosis. We model α_j, the half parental difference, as a draw from a mixture of a point-mass-at-0 distribution and a normal distribution. This implies that |α_j| is equal to 0 with some probability π_α and equal to the absolute value of a draw from a normal distribution with probability 1 − π_α. The point-mass distribution in the mixture model represents the case where the parental gene expression levels are equal, while the normal component corresponds to genes whose expression levels differ between the two parental lines. Similarly, we model δ_j, the difference between the offspring mean and the average of the parental means, with another mixture model that has normal and point-mass-at-0 component distributions. We estimate the parameters for these mixture distributions based on observed data from all genes. Under an empirical Bayes framework, we derive posterior distributions of α_j and δ_j and draw inferences about gene expression heterosis from estimates of these posteriors.

We compare the empirical Bayes method with the sample average method through simulation studies where datasets were generated based on real heterosis microarray experiments or hypothetical probability models. Simulation studies show that the empirical Bayes estimators of h_j, l_j, and m_j have smaller mean square errors (MSEs) than the sample average estimators that have been used previously. Furthermore, the empirical Bayes estimators of h_j and l_j are less biased than the sample average estimators, and the inferences we draw using our empirical Bayes approach are superior to traditional approaches for detecting all forms of heterosis.

The remainder of the paper proceeds as follows. Section 2 presents the proposed hierarchical model in full detail. Section 3 derives the empirical Bayes estimators and inference strategy based on the framework constructed in section 2. Section 4 summarizes analysis results of two real experiments. Section 5 presents results of several simulation studies. Section 6 summarizes our work. R code and C code for the analysis of real experiments in section 4, the simulation studies in section 5, and the implementation of all our algorithms is available upon request.

2 HIERARCHICAL GENE EXPRESSION HETEROSIS MODEL

Let y_ijk denote the normalized log-scale gene expression measurement for genotype i, gene j, and biological replicate k, where k = 1, ···, n_i, and n_i is the total number of replicates for genotype i. As is common in microarray data analysis, we assume the dataset for gene j (y_ijk, i = 1, 2, 3, k = 1, ···, n_i) consists of independent observations, and that $y_{\mathit{ijk}}~\mathrm{N}({\mu }_{ij},{\sigma }_j^2)$. The sample average method estimates h_j, l_j, and m_j by ĥ_j = ȳ_3j· − max{ȳ_1j·, ȳ_2j·}, l̂_j = min{ȳ_1j·, ȳ_2j·} − ȳ_3j·, and m̂_j = ȳ_3j· − (ȳ_1j· + ȳ_2j·)/2, where ${\overline{y}}_{ij·}={\sum }_{k=1}^{n_i}{y}_{\mathit{ijk}}/n_i$. Furthermore, ${\sigma }_j^2$ is estimated by $S_j^2={\sum }_{i=1}^3{\sum }_{k=1}^{n_i}{(y_{\mathit{ijk}}-{\overline{y}}_{ij·})}^2/(n_1+n_2+n_3-3)$.

In the previous section, we defined α_j = (μ_1j − μ_2j)/2 and δ_j = μ_3j − (μ_1j + μ_2j)/2. In order to share information across genes to improve estimation of gene expression heterosis, we propose the following models (1) – (3) for α_j, δ_j, and the error variance ${\sigma }_j^2$. Suppose

$${\alpha }_j~{\pi }_{\alpha }{\mathbf{1}}_{[{\alpha }_j=0]}+(1-{\pi }_a){\mathbf{1}}_{[{\alpha }_j\ne 0]}\mathrm{N}({\mu }_{\alpha },{\sigma }_{\alpha }^2),$$ (1)

$${\delta }_j~{\pi }_{\delta }{\mathbf{1}}_{[{\delta }_j=0]}+(1-{\pi }_{\delta }){\mathbf{1}}_{[{\delta }_j\ne 0]}\mathrm{N}({\mu }_{\delta },{\sigma }_{\delta }^2),$$ (2)

$${\sigma }_j^2~d_0{\sigma }_0^2{\chi }_{d_0}^{-2},$$ (3)

and all α_j’s, δ_j’s, and ${\sigma }_j^2$’s, are mutually independent.

The scaled inverse χ² model for the error variances ${\sigma }_1^2,\dots ,{\sigma }_J^2$ given in (3) follows Smyth (2004). The mixture model for α_j in (1) models the cases where parental means are equal and where parental means differ, respectively. The hyperparameter π_α specifies the proportion of genes that are equally expressed between two parents. Similarly, the mixture model for δ_j in (2) describes the cases where mean gene expression in the offspring is equal or not to the average of two parental means. When necessary, the model (1)–(3) may be modified as needed to better capture the features of a given dataset. For example, the mixture model could include more than one normal distribution component for α_j or δ_j. Although all subsequent derivations are for the model specified in (1)–(3), it is straightforward to modify our proposed approach to handle more complex models.

With no loss of information about expression heterosis, the data can be summarized by the sufficient statistics α̂_j ≡ (ȳ_1j· − ȳ_2j·)/2, δ̂_j ≡ ȳ_3j· − (ȳ_1j· + ȳ_2j·)/2, and $S_j^2(j=1,\dots ,J)$. Clearly, α̂_j and δ̂_j are the natural sample average estimators of α_j and δ_j, respectively. Based on the normality assumption for y_ijk, the conditional distributions of α̂_j, δ̂_j, and $S_j^2$ – given α_j, δ_j and ${\sigma }_j^2$ – are

$$({\widehat{\alpha }}_j\mid {\alpha }_j,{\sigma }_j^2)~\mathrm{N}\left({\alpha }_j,\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right),$$ (4)

$$\left({\widehat{\delta }}_j\mid {\delta }_j,{\sigma }_j^2\right)~\mathrm{N}\left({\delta }_j,\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right),\text{and}$$ (5)

$$(S_j^2\mid {\sigma }_j^2)~\frac{{\sigma }_j^2{\chi }_{n_1+n_2+n_3-3}^2}{n_1+n_2+n_3-3}.$$ (6)

By combining (1), (3), and (4), it follows that the marginal distribution of α̂_j is a two-component mixture distribution, where each component density is itself an infinite mixture of normal distributions with common mean but varying variance. This marginal distribution is determined by the hyperparameters π_α, μ_α, ${\sigma }_{\alpha }^2$, d₀, and ${\sigma }_0^2$. Similarly, the marginal of distribution of δ̂_j has an analogous form and is determined by the hyperparameters π_δ, μ_δ, ${\sigma }_{\delta }^2$, d₀, and ${\sigma }_0^2$.

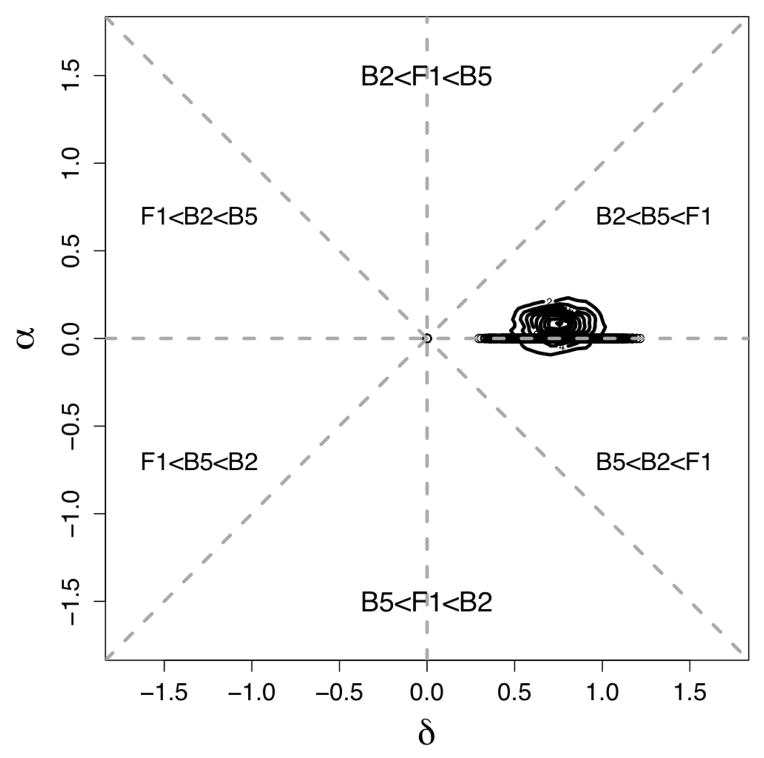
Figures 1(a) and 1(b) present histograms of empirical marginal distributions and scatter-plots for α̂_j and δ̂_j from an alfalfa experiment and a maize experiment, respectively. Each of these datasets is discussed in more detail in section 4, but we introduce the plots here to provide some empirical support for the model described in this section. Using methods discussed in Appendix C, we obtain estimates of our model hyperparameters, and the hyperparameter estimates determine fitted marginal densities which are plotted on top of the histograms as red lines. The fitted marginal distributions adequately capture the shape of the empirical distributions. Furthermore, the lack of correlation between α̂_j and δ̂_j in the scatterplots supports our model assumption of independence between α_j and δ_j. Thus, for both datasets, the model presented in section 2 appears to be consistent with the main features of the data illustrated in these plots.

Figure 1.

Scatterplots of α̂_j vs. δ̂_j and histograms of empirical marginal distributions of α̂_j and δ̂_j (j = 1, ···, J) based on two real heterosis experiments. The relative sizes of α_j’s and δ_j’s partition the two-dimensional space virtually into subsets based on the mean expression levels of two inbred parents and their hybrid offspring as shown by dashed lines. Fitted curves represent estimated marginal densities based on the assumed model described in section 2. (a) Alfalfa dataset. B2, B5 and F1 denote the genotypes of the two parental inbred lines and the hybrid offspring, respectively. (b) Maize dataset. B73, Mo17 and F1 denote the genotypes of the two parental inbred lines and the hybrid offspring, respectively.

3 EMPIRICAL BAYES ESTIMATION AND TESTING OF GENE EXPRESSION HETEROSIS

Obtaining estimates of our model hyperparameters is the first step in our empirical Bayes approach. We use the method of Smyth (2004) to estimate d₀ and ${\sigma }_0^2$. We estimate other hyperparameters by a combined approach of the moment method and the marginal maximum likelihood method using data from all genes. The details of our proposed approach are provided in Appendix C. Because thousands of genes in one experiment are used to obtain the estimates of the hyperparameters, we claim that adopting the usual empirical Bayes strategy (i.e., treating these unknown hyperparameters as known and equal to their estimates) does not seriously affect the performance of the inferential procedures we describe in this section. This claim is supported by simulation studies presented in sections 4 and 5.

Once estimates of the hyperparameters have been obtained, our goal is to draw inferences regarding expression heterosis for individual genes. Based on (1) – (6), an expression for the joint posterior distribution of (α_j, δ_j) given α̂_j, δ̂_j, and $S_j^2$ is derived and illustrated in Appendix B. Sampling from the joint posterior distribution of (α_j, δ_j) allows us to approximate the posterior distributions of h_j, l_j, and m_j via the relationships h_j = δ_j − |α_j|, l_j = −|α_j|− δ_j, and m_j = δ_j. Based on the form of the posterior of (α_j, δ_j), one common method for sampling α_j and δ_j is through a Markov chain Monte Carlo (MCMC) method, such as using the Metropolis-Hastings algorithm. We have developed and implemented such a Metropolis-Hastings algorithm as illustrated in the online supplement. A good approximation of the posterior distributions of h_j, l_j, and m_j requires a large number of draws from the joint posterior distribution of (α_j, δ_j) for each gene j. By using the Metropolis-Hastings algorithm, an analysis of simulated data for only 1,000 genes took around 5 hours to complete (see more details in the online supplement). Although parallelism and/or more sophisticated sampling algorithms could help to reduce the computing time, the large number of genes in a typical transcript profiling experiment motivates us to find a faster alternative.

To substantially reduce the computing requirement and maintain good approximations of the posterior distributions of h_j, l_j, and m_j, we derive in Appendix B an approximation to the joint posterior distribution of (α_j, δ_j) given by

$$p({\alpha }_j,{\delta }_j\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)\approx P_{1j}{\mathbf{1}}_{[{\alpha }_j=0,{\delta }_j=0]}+$$ (7a)

$$P_{2j}{\mathbf{1}}_{[{\alpha }_j\ne 0,{\delta }_j=0]}\varphi \left({\alpha }_j|{\stackrel{\sim }{\mu }}_{{\alpha }_j},{\stackrel{\sim }{\sigma }}_{{\alpha }_j}^2\right)+$$ (7b)

$$P_{3j}{\mathbf{1}}_{[{\alpha }_j=0,{\delta }_j\ne 0]}\varphi \left({\delta }_j|{\stackrel{\sim }{\mu }}_{{\delta }_j},{\stackrel{\sim }{\sigma }}_{{\delta }_j}^2\right)+$$ (7c)

$$P_{4j}{\mathbf{1}}_{[{\alpha }_j\ne 0,{\delta }_j\ne 0]}\varphi \left({\alpha }_j|{\stackrel{\sim }{\mu }}_{{\alpha }_j},{\stackrel{\sim }{\sigma }}_{{\alpha }_j}^2\right)\varphi \left({\delta }_j|{\stackrel{\sim }{\mu }}_{{\delta }_j},{\stackrel{\sim }{\sigma }}_{{\delta }_j}^2\right),$$ (7d)

where ϕ(x|μ, σ²) denotes the normal density with mean μ and variance σ² evaluated at x,

$${\stackrel{\sim }{\sigma }}_j^2={\mathrm{E}}^{-1}(1/{\sigma }_j^2/S_j^2)=\frac{(n_1+n_2+n_3-3)S_j^2+d_0{\sigma }_0^2}{(n_1+n_2+n_3-3)+d_0},$$ (8a)

$${\stackrel{\sim }{\mu }}_{{\alpha }_j}=\frac{{\sigma }_{\alpha }^2{\widehat{\alpha }}_j+(1/(4n_1)+1/(4n_2)){\stackrel{\sim }{\sigma }}_j^2{\mu }_{\alpha }}{{\sigma }_{\alpha }^2+(1/(4n_1)+1/(4n_2)){\stackrel{\sim }{\sigma }}_j^2},$$ (8b)

$${\stackrel{\sim }{\sigma }}_{{\alpha }_j}^2=\frac{{\sigma }_{\alpha }^2(1/(4n_1)+1/(4n_2)){\stackrel{\sim }{\sigma }}_j^2}{{\sigma }_{\alpha }^2+(1/(4n_1)+1/(4n_2)){\stackrel{\sim }{\sigma }}_j^2},$$ (8c)

$${\stackrel{\sim }{\mu }}_{{\delta }_j}=\frac{{\sigma }_{\delta }^2{\widehat{\delta }}_j+(1/(4n_1)+1/(4n_2)+1/n_3){\stackrel{\sim }{\sigma }}_2^2{\mu }_{\delta }}{{\sigma }_{\delta }^2+(1/(4n_1)+1/(4n_2)+1/n_3){\stackrel{\sim }{\sigma }}_j^2},$$ (8d)

$${\stackrel{\sim }{\sigma }}_{{\delta }_j}^2=\frac{{\sigma }_{\delta }^2(1/(4n_1)+1/(4n_2)+1/n_3){\stackrel{\sim }{\sigma }}_j^2}{{\sigma }_{\delta }^2+(1/(4n_1)+1/(4n_2)+1/n_3){\stackrel{\sim }{\sigma }}_j^2},$$ (8e)

and the probabilities P_1j, P_2j, P_3j, and P_4j sum to 1 and are defined in Appendix B. The approximation to the joint posterior distribution of α_j and δ_j in (7) is a mixture of four joint distributions, where both α_j and δ_j are from point-mass-at-0 as in (7a); δ_j is from point-mass-at-0 and α_j is from a normal distribution as in (7b); α_j is from point-mass-at-0 and δ_j is from a normal distribution as in (7c); and both α_j and δ_j are from normal distributions as in (7d). The approximate posterior mixture distribution combines information from prior models and empirical observations. For example, μ̃_αj can be expressed as a weighted average of μ_α (the prior mean of α_j given α_j ≠ 0) and α̂_j (an estimate of α_j based on sample means), where the weight on μ_α is proportional to the prior precision of α_j given ${\alpha }_j\ne 0(1/{\sigma }_{\alpha }^2)$, and the weight on α̂_j is proportional to an estimate of the conditional precision of α̂_j given ${\alpha }_j(1/\widehat{\text{Var}}({\widehat{\alpha }}_j\mid {\alpha }_j))$. Similarly, ${\stackrel{\sim }{\sigma }}_{{\alpha }_j}^2$ is the inverse of the average of the precisions $1/{\sigma }_{\alpha }^2$ and $1/\widehat{\text{Var}}({\widehat{\alpha }}_j\mid {\alpha }_j)$.

The approximation of the joint posterior distribution in (7) allows us to substantially reduce the computing requirement because we no longer need to go through a large number of MCMC iterations, but can instead directly sample from either a point-mass-at-0 distribution or a normal distribution. In addition, this leads to accurate approximations of the posterior distributions of h_j, l_j, and m_j, as demonstrated by simulation studies in section 5 and in the online supplement.

Given the fully specified approximate posteriors of α_j and δ_j and plugging in estimated hyperparameters, it is straightforward to approximate posterior distributions of h_j, l_j, and m_j by simulation. We propose to use the estimated posterior expectations ${\stackrel{\sim }{h}}_j=\widehat{\mathrm{E}}(h_j\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2),{\stackrel{\sim }{l}}_j=\widehat{\mathrm{E}}(l_j\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)$, and ${\stackrel{\sim }{m}}_j=\widehat{\mathrm{E}}(m_j\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)$ as point estimators for h_j, l_j, and m_j, respectively. Tests of HPH, LPH, and MPH, respectively, for each gene j are based on the estimated posterior probabilities ${\stackrel{\sim }{p}}_{h_j}=\widehat{P}(h_j>0\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)=\widehat{P}({\delta }_j>\mid {\alpha }_j\mid \mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2),{\stackrel{\sim }{p}}_{l_j}=\widehat{P}(l_j>0\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)=\widehat{P}({\delta }_j<-\mid {\alpha }_j\mid \mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)$, and ${\stackrel{\sim }{p}}_{m_j}=\widehat{P}(m_j\ne 0\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)=\widehat{P}({\delta }_j\ne 0\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)$. For any cutoff c ∈ (0, 1), we declare that gene j exhibits HPH, LPH, or MPH if and only if p̃_hj ≥c, p̃_lj ≥ c, or p̃_mj ≥ c, respectively.

We also use the estimated posterior probabilities to estimate false discovery rates (FDRs) for any family of tests that involves one test per gene. The number of positives, R(c), is the number of genes declared to exhibit a type of gene expression heterosis given the cutoff c. Taking HPH as an example, $R(c)={\sum }_{j=1}^J{\mathbf{1}}_{[{\stackrel{\sim }{p}}_{h_j}\ge c]}$. The number of false positives, V (c), is estimated as $\widehat{V}(c)={\sum }_{j=1}^J{\mathbf{1}}_{[{\stackrel{\sim }{p}}_{h_j}\ge c]}(1-{\stackrel{\sim }{p}}_{h_j})$, and the estimated FDR for HPH based on estimated posterior probabilities is $\widehat{\text{FDR}}(c)=\widehat{V}(c)/R(c)$ given cutoff c. Calculations of estimated FDRs for testing LPH and MPH are similar.

4 EXAMPLE DATA ANALYSIS

4.1 Analysis of an Alfalfa Dataset

We used our method to analyze an alfalfa dataset on gene expression in parental lines B2 and B5 and the hybrid genotype (B2×B5). The data are available in the Gene Expression Omnibus (GEO) database (Barrett et al., 2011) with series number GSE25034. Each genotype had 3 biological replicates measured with Affymetrix Medicago Genome Array (Platform GPL4652). The robust multi-array average (RMA) method (Irizarry et al., 2003) was used to obtain normalized expression measures for each probeset on the array. Non-alfalfa probesets associated with the bacterial genome Sinorhizobium meliloti, along with all other probesets called absent by Affymetrix microarray suite version 5 software in all samples were filtered from the dataset (McClintick and Edenberg, 2006) to leave 31,865 probesets for analysis. The hyperparameters estimated from our proposed method are summarized in row 1 of Table 1.

Table 1.

Estimated hyperparameters (obtained by using the methods described in Appendix C) and empirical estimates of bias and MSE of our hyperparameter estimators based on analysis of 1,000 datasets simulated with hyperparameters estimated from the alfalfa and maize datasets as the true hyperparameter values.

Parameters	πα	μα	${\sigma }_{\alpha }^2$	πδ	μδ	${\sigma }_{\delta }^2$	d0	${\sigma }_0^2$
Alfalfa Exp	0.870	0.011	0.087	0.405	−0.020	0.232	2.52	0.035
Bias	−5.33e-2	−2.92e-3	−1.12e-2	−2.72e-2	6.77e-4	−3.53e-3	1.60e-3	9.36e-6
MSE	2.85e-3	2.54e-5	1.31e-4	7.64e-4	1.34e-5	2.38e-5	6.11e-4	6.34e-8
Maize Exp	0.331	0.002	0.022	0.647	−0.008	0.046	2.34	0.030
Bias	2.85e-3	−1.31e-5	1.19e-4	1.48e-3	6.10e-5	4.50e-4	-1.20e-3	4.14e-7
MSE	6.45e-5	2.90e-6	1.99e-7	5.73e-5	1.31e-5	2.12e-6	9.20e-4	7.67e-8

A simulation study was conducted to assess the estimation of hyperparameters. We used the estimated hyperparameter values in Table 1 as the true parameter values to simulate data for 31,865 genes based on the hierarchical model described in sections 2 and 3. Then, we re-estimated the hyperparameters using the simulated data. We repeated this procedure 1,000 times. The estimated bias and MSE in Table 1 for each hyperparameter estimator based on these 1,000 replications show that our hyperparameter estimators are reasonably accurate and precise.

For any gene j, we sample h_j, l_j, and m_j by simulating α_j and δ_j from the approximate joint posterior distribution (7). As an example, the contour plot of 10,000 random draws of α₂₀ and δ₂₀ from the approximate joint posterior distribution of gene “AFFX-Msa-ubq11-3_at” (gene number 20) is plotted in Figure 2. This gene has been reported to be one of the polyubiquitin genes involved in directing protein recycling and related functions (Geer et al., 2010). Based on these draws, ${\stackrel{\sim }{p}}_{h_{20}}=\widehat{P}({\delta }_{20}>\mid {\alpha }_{20}\mid \mid {\widehat{\alpha }}_{20},{\widehat{\delta }}_{20},S_{20}^2)\approx 0.998$, which gives strong evidence of HPH for this gene. As described in section 3, we can also use the estimated posterior distributions of α_j and δ_j to test for any given type of heterosis while controlling FDR at a specified level. For example, we color-coded points in Figure 2(a) of the online supplement to highlight genes significant at approximate FDR level 0.05 when testing for HPH (red), LPH (blue), or MPH (red, blue, or green), respectively.

Figure 2.

Example estimated posterior distribution for a gene exhibiting significant evidence of HPH (gene “AFFX-Msa-ubq11-3_at” in the alfalfa dataset).

We also used a traditional approach based on a separate analysis for each gene to analyze the alfalfa dataset. Sample average estimates and ordinary t-tests were used to identify significant evidence of heterosis. Taking HPH as an example, if ȳ_1j· ≥ ȳ_2j·, then ĥ_j = ȳ_3j· − ȳ_1j·, and the t statistic for the one-sided ordinary t-test is ${\widehat{h}}_j/\sqrt{(1/n_3+1/n_1)S_j^2}$. Similarly, we tested for LPH using a one-sided ordinary t-test, and we tested for MPH using a two-sided ordinary t-test of m_j = 0. Given the p-values from the ordinary t-tests, we controlled FDR for the sample average method using the q-value method described by Storey and Tibshirani (2003).

The numbers of genes exhibiting significant evidence of the three types of gene expression heterosis when controlling FDR at approximately 0.05 by the sample average method and the empirical Bayes method, respectively, are in Table 2. Our empirical Bayes method identifies far more significant genes than the sample average approach.

Table 2.

Number of genes declared to exhibit gene expression heterosis by the sample average method and the empirical Bayes method.

Datasets	Heterosis	Sample Average	Empirical Bayes
Alfalfa Dataset	HPH	2475	3529
	LPH	2121	4077
	MPH	4813	8046
Maize Dataset	HPH	55	390
	LPH	197	595
	MPH	1181	1447

4.2 Analysis of a Maize Dataset

Swanson-Wagner et al. (2009) compared gene expression of maize inbred lines B73 and Mo17 and their hybrid offspring. They studied a total of 13,999 genes in their microarray experiment with 10 biological replicates for each of the three genotypes. The dataset is downloadable in GEO with series number GSE16136.

Log-scale expression measurements were lowess normalized within each slide and median centered. The normalized data were analyzed with our empirical Bayes method, and the estimated hyperparameters are summarized in Table 1 row 4. The simulation described in section 4.1 was repeated for the maize results to estimate the bias and MSE of the hyperparameter estimators. The results are summarized in the last two rows of Table 1.

Based on posterior distributions of α_j and δ_j, we color-coded points in Figure 2(b) of the online supplement to highlight genes significant at approximate FDR level 0.05 when testing for HPH (red), LPH (blue), or MPH (red, blue, or green), respectively. The reported numbers of genes exhibiting each of the three types of gene expression heterosis identified by the sample average method and the empirical Bayes method, respectively, are listed in Table 2 where FDR was controlled at the 0.05 level. Once again, the empirical Bayes method reported more significant genes for all three types of gene expression heterosis than the sample average method.

5 ADDITIONAL SIMULATION STUDIES

5.1 Simulation Study Based on the Alfalfa Experiment

We simulated 100 datasets based on the hierarchical model defined by (1) – (6) using hyper-parameters equal to the estimated values from the alfalfa experiment in Table 1. For each dataset, we simulated 31,865 genes (the same number of genes in the alfalfa experiment) and 3 biological replicates for each genotype.

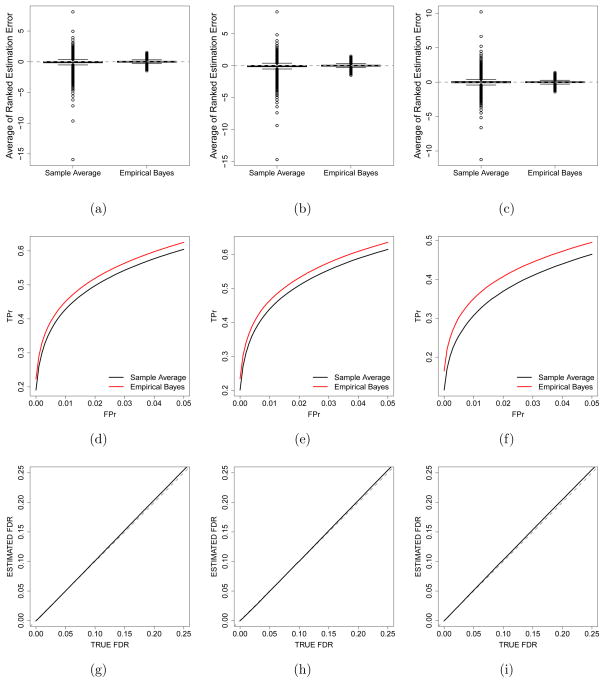
We used the empirical Bayes method to estimate h_j, l_j, and m_j for all j. For each dataset and each type of heterosis, we ranked the estimation errors from most negative to most positive, then we averaged the estimation errors of the same rank across the 100 datasets. We used the same approach for the sample average method. The box plots of averages of ranked estimation errors are plotted in Figure 3(a) for h_j’s, Figure 3(b) for l_j’s, and Figure 3(c) for m_j’s. These box plots suggest that the empirical Bayes method on average has smaller ranked estimation errors than the sample average method. The box plots also show that the averages of ranked estimation errors by the empirical Bayes method have narrower interquartile ranges than the sample average method for estimating each type of heterosis. Table 3 summarizes the averaged estimation biases and MSEs across all genes in all datasets. The empirical Bayes estimators have smaller biases and MSEs than the sample average estimators for all types of heterosis. Both the plots and statistics show substantial improvement of the empirical Bayes method over the sample average method.

Figure 3.

Plots for the simulation study 5.1 based on the alfalfa data. Top row: box plots of ranked estimation errors averaged over 100 simulated datasets. Middle row: ROC curves averaged over 100 simulated datasets. Bottom row: estimated FDRs based on posterior probabilities versus true FDRs. Left column: HPH. Middle column: LPH. Right column: MPH.

Table 3.

Comparison of the average bias and MSE of the sample average estimators and the empirical Bayes estimators.

Simulations	Variables	Bias ×104		MSE ×103
		Sample Average	Empirical Bayes	Sample Average	Empirical Bayes
Alfalfa Dataset	hj	−830	−2.76	111	31.6
	lj	−827	1.18	109	31.7
	mj	−2.02	−1.97	83.1	28.1
Maize Dataset	hj	−252	1.44	39.5	7.10
	lj	−254	0.212	38.8	7.10
	mj	0.697	0.616	30.9	4.89
Probability Models	hj	−596	47.2	55.0	20.8
	lj	−598	44.5	55.6	20.8
	mj	0.945	1.36	41.5	15.8

For each dataset, we computed the true positive rate (TPr) given a set of fixed levels of false positive rate (FPr) for testing each type of gene expression heterosis by the sample average method and the empirical Bayes method, respectively. Then, we averaged the TPrs across 100 datasets for each given level of FPr for each of the two methods. The resulting average receiver operating characteristic (ROC) curves are plotted in Figures 3(d)–3(f) for testing HPH, LPH, and MPH, respectively. We only plotted over the range of FPr between 0 and 0.05 because FPr>0.05 is rarely of interest in practice. The ROC curves demonstrate that our proposed tests identify more true positives than the sample average method given any fixed level of FPr for testing each type of gene expression heterosis.

By the empirical Bayes method, we estimated the FDRs for testing each type of gene expression heterosis as described in section 3. Then, for each level of estimated FDR, the true FDRs were calculated by averaging the proportions of false positives among the declared heterosis genes across 100 datasets for each type of gene expression heterosis. We plotted the estimated FDRs against the true FDRs in Figures 3(g)–3(i) for testing HPH, LPH, and MPH, respectively. The plots show results for the range of estimated FDR from 0 to 0.25 because only the region of small FDRs is relevant in practice. All three curves show that the estimated FDRs based on posterior probabilities are very close to the true levels, which demonstrates that the proposed method controls FDR as desired.

All results presented above and throughout the paper are based on the approximate joint posterior density in (7). We compared this proposed fast and approximate method with sampling from posterior distribution via the Metropolis-Hastings algorithm. Comparison results are discussed in the online supplement. In summary, we found that while the estimated posterior probabilities of exhibiting HPH, LPH, and MPH are very similar for both methods, our approximate method is more than 1,000 times faster than the Metropolis-Hastings approach.

5.2 Simulation Study Based on the Maize Experiment

The estimated hyperparameters of the maize experiment were used as the true parameter values to simulate 100 microarray datasets, each with 13,999 genes (the number of genes in the maize experiment) and 10 biological replicates for each gene of each genotype.

We analyzed these 100 datasets by the empirical Bayes method and the sample average method. The estimated bias and MSE of h_j, l_j, and m_j estimators averaged across all genes in all datasets are summarized in Table 3. Table 3 shows that the empirical Bayes estimators are more accurate and more precise than the sample average method in estimating all types of heterosis. Figure 3 of the online supplement provides box plots, ROC curves, and FDR plots for the maize simulation results that are very similar to those displayed in Figure 3 for the alfalfa simulation in section 5.1.

5.3 Simulation Study Based on Probability Models

To further assess the performance of the proposed empirical Bayes method, we simulated data using distributions different from those proposed in (1) and (2). Specifically, we simulated α_j’s from a mixture distribution with a point-mass-at-0 and a t distribution with a small number of degrees of freedom (2) and a non-centrality parameter (ncp) 0.01. Independently from α_j’s, we simulated δ_j’s from a mixture model with a point-mass-at-0 and two normal distributions N(−0.05, 0.2) and N(0, 0.2). We simulated data for 100 microarray datasets, where each dataset contains 5,000 genes with 3 biological replicates for each of three genotypes. Based on the estimated hyperparameters for the alfalfa experiment and the maize experiment, we set π_α=0.8, π_δ=0.6, and simulated ${\sigma }_j^2$ from a scaled inverse χ² distribution with parameters d₀=2.8 and ${\sigma }_0^2=0.025$.

Though the data were not simulated from the proposed model, our empirical Bayes estimators, compared to the sample average estimators, have substantially smaller average bias and MSE for h_j and l_j as shown in Table 3. Although the averaged estimated bias for m_j is slightly bigger than that of the sample average method, the averaged estimated MSE is reduced by the empirical Bayes method. Figure 4 of the online supplement provides box plots, ROC curves, and FDR plots (analogous to those in Figure 3 of section 5.1) that show the empirical Bayes method improves upon the sample average method even though the data-generating model differs from the assumptions in (1) and (2).

6 DISCUSSION

Gene expression heterosis is speculated to be one possible explanation for phenotypic heterosis of traits like plant height or grain yield. One natural strategy for estimation (called the sample average method in this paper) is to simply use the sample means to replace the population means when estimating the three types of gene expression heterosis. Because there are often few observations for each gene in a microarray experiment, such estimates have high standard errors. In addition, the sample average estimators for high-parent heterosis and low-parent heterosis are also biased estimators. Furthermore, the natural t-based testing strategies that accompany the sample average method yield low detection power for all forms of gene expression heterosis.

A shrinkage method based on the sample average estimators can improve inferences on gene expression heterosis by sharing information across genes. We developed hierarchical models by placing a mixture prior model on each of two latent variables. Using an empirical Bayes method, the sample average estimates of gene expression heterosis were adjusted and shrunk towards prior means estimated from the data. The extent of shrinkage was also estimated empirically based on data. Through simulation studies based on real datasets and different probability models, we demonstrated that our empirical Bayes estimators have substantially smaller bias and MSE than the sample average estimators, and the inferences for all three types of gene expression heterosis based on the posterior probabilities also yield higher TPrs given any level of FPr than the ordinary t-tests based on the sample average estimates. We also showed that using posterior probabilities of exhibiting any type of gene expression heterosis to estimate FDR yields accurate estimates of the actual FDR. Thus, the methods we have developed provide researchers with substantially improved statistical tools for studying gene expression heterosis.

The results presented in section 4 focus on identifying individual genes that show significant evidence of expression heterosis of various types. Rather than attempting to identify individual genes, our approach can also be used to estimate global values like the proportion of all genes that exhibit a given type of heterosis. For example, the proportion of maize genes exhibiting HPH is estimated by the average posterior probability of HPH, ${\sum }_{j=1}^J{\stackrel{\sim }{p}}_{h_j}/J=0.122$. This estimated proportion includes genes where expression in the hybrid is only slightly higher than the maximum parental expression. In some cases, scientists prefer to concentrate on large changes in expression. With our empirical Bayes approach, it is straightforward to estimate the posterior probability of h_j > k for any constant k. For example, with k = log(1.5), the average posterior probability of h_j > k in the maize data is 0.0006. This indicates that genes with hybrid expression (on the original scale) more than 1.5 times that of the high parent are relatively rare.

Our work has focused on the use of gene expression measurements that can be modeled, at least approximately, by linear models with normally distributed errors. This is a standard modeling approach for microarray data. While there are thousands of existing microarray datasets and more generated nearly every day, next-generation sequencing of RNA (RNA-Seq) is an increasingly popular technology for obtaining gene expression measurements. At the present state of the technology, RNA-Seq data are perhaps best treated as counts and modeled with generalized linear models involving overdispersed Poisson or negative binomial distributions (see, for example, Anders and Huber, 2010; Robinson et al., 2010; Lund et al., 2012; McCarthy et al., 2012). We believe the hierarchical modeling ideas we have proposed in the linear model framework are also likely to be very useful in a generalized linear model framework for the study of gene expression heterosis using RNA-Seq data. Developing the details of such an extension is the subject of some of our ongoing and future research.

APPENDIX A: BIAS OF THE SAMPLE AVERAGE ESTIMATORS OF HIGH AND LOW PARENT HETEROSIS

Based on the definitions in section 2, we can rewrite the sample average estimator of h_j = δ_j − |α_j| as δ̂_j − |α̂_j|. Although α̂_j and δ̂_j are both unbiased estimators of α_j and δ_j, respectively,

$$\begin{array}{l}E(\mid {\widehat{\alpha }}_j\mid )=E(-{\widehat{\alpha }}_j{1}_{[{\widehat{\alpha }}_j<0]})+E({\widehat{\alpha }}_j{1}_{[{\widehat{\alpha }}_j\ge 0]})\\ =\mid E(-{\widehat{\alpha }}_j{1}_{[{\widehat{\alpha }}_j<0]})+E({\widehat{\alpha }}_j{1}_{[{\widehat{\alpha }}_j\ge 0]})\mid \\ >\mid E({\widehat{\alpha }}_j{1}_{[{\widehat{\alpha }}_j<0]})+E({\widehat{\alpha }}_j{1}_{[{\widehat{\alpha }}_j\ge 0]})\mid =\mid E({\widehat{\alpha }}_j)\mid =\mid {\alpha }_j\mid .\end{array}$$

Thus, E(ĥ_j) = E(δ̂_j −|α̂_j|) < δ_j −|α_j| = h_j. Likewise, E(l̂_j) = E(−|α̂_j| − δ̂_j) < −|α_j| −δ_j = l_j. Thus, the sample average estimators of h_j and l_j are both biased estimators that, on average, underestimate high-parent and low-parent heterosis, respectively.

APPENDIX B: DERIVATION AND APPROXIMATION OF THE JOINT POSTERIOR DISTRIBUTION OF α_j AND δ_j

Let p(·) denote a generic probability density function. We have

$$\begin{array}{l}p\left({\alpha }_j,{\delta }_j|{\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2\right)\propto p({\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2\mid {\alpha }_j,{\delta }_j)p({\alpha }_j,{\delta }_j)\\ ={\int }_0^{\infty }p({\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2,{\sigma }_j^2\mid {\alpha }_j,{\delta }_j)d{\sigma }_j^{2}p({\alpha }_j,{\delta }_j)\\ ={\int }_0^{\infty }p({\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2\mid {\sigma }_j^2,{\alpha }_j,{\delta }_j)p({\sigma }_j^2\mid {\alpha }_j,{\delta }_j)d{\sigma }_j^{2}p({\alpha }_j,{\delta }_j)\\ ={\int }_0^{\infty }p({\widehat{\alpha }}_j\mid {\alpha }_j,{\sigma }_j^2)p({\alpha }_j)p({\widehat{\delta }}_j\mid {\delta }_j,{\sigma }_j^2)p({\delta }_j)p(S_j^2\mid {\sigma }_j^2)p({\sigma }_j^2)d{\sigma }_j^2\end{array}$$ (9)

by the conditional independence of α̂_j, δ̂_j, and $S_j^2$ given α_j, δ_j, ${\sigma }_j^2$; the independence of α_j, δ_j, and ${\sigma }_j^2$; the independence of α̂_j and δ_j; the independence of δ̂_j and α_j; and the independence of $S_j^2$ from α_j and δ_j.

It can be shown that

$$\begin{array}{l}p({\widehat{\alpha }}_j\mid {\alpha }_j,{\sigma }_j^2)p({\alpha }_j)={\mathbf{1}}_{[{\alpha }_j=0]}{\pi }_{\alpha }\varphi \left({\widehat{\alpha }}_j|0,\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\\ +{\mathbf{1}}_{[{\alpha }_j\ne 0]}(1-{\pi }_{\alpha })\varphi \left({\widehat{\alpha }}_j|{\mu }_{\alpha },{\sigma }_{\alpha }^2+\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\varphi ({\alpha }_j\mid {\stackrel{\sim }{\mu }}_{{\alpha }_j}^{\ast },{\stackrel{\sim }{\sigma }}_{{\alpha }_j}^{\ast 2}),\end{array}$$ (10)

where

$${\stackrel{\sim }{\mu }}_{{\alpha }_j}^{\ast }=\frac{{\sigma }_{\alpha }^2{\widehat{\alpha }}_j+(1/(4n_1)+1/(4n_2)){\sigma }_j^2{\mu }_{\alpha }}{{\sigma }_{\alpha }^2+(1/(4n_1)+1/(4n_2)){\sigma }_j^2}\text{and}{\stackrel{\sim }{\sigma }}_{{\alpha }_j}^{\ast 2}=\frac{{\sigma }_{\alpha }^2(1/(4n_1)+1/(4n_2)){\sigma }_j^2}{{\sigma }_{\alpha }^2+(1/(4n_1)+1/(4n_2)){\sigma }_j^2}.$$

Similarly,

$$\begin{array}{l}p({\widehat{\delta }}_j\mid {\delta }_j,{\sigma }_j^2)p({\delta }_j)={\mathbf{1}}_{[{\delta }_j=0]}{\pi }_{\delta }\varphi \left({\widehat{\delta }}_j|0,\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)\\ +{\mathbf{1}}_{[{\delta }_j\ne 0]}(1-{\pi }_{\delta })\varphi \left({\widehat{\delta }}_j|{\mu }_{\delta },{\sigma }_{\delta }^2+\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)\varphi ({\delta }_j\mid {\stackrel{\sim }{\mu }}_{{\delta }_j}^{\ast },{\stackrel{\sim }{\sigma }}_{{\delta }_j}^{\ast 2}),\end{array}$$ (11)

where

$$\begin{array}{c}{\stackrel{\sim }{\mu }}_{{\delta }_j}^{\ast }=\frac{{\sigma }_{\delta }^2{\widehat{\delta }}_j+(1/(4n_1)+1/(4n_2)+1/n_3){\sigma }_j^2{\mu }_{\delta }}{{\sigma }_{\delta }^2+(1/(4n_1)+1/(4n_2)+1/n_3){\sigma }_j^2}\text{and}\\ {\stackrel{\sim }{\sigma }}_{{\delta }_j}^{\ast 2}=\frac{{\sigma }_{\delta }^2(1/(4n_1)+1/(4n_2)+1/n_3){\sigma }_j^2}{{\sigma }_{\delta }^2+(1/(4n_1)+1/(4n_2)+1/n_3){\sigma }_j^2}.\end{array}$$

Substituting (10) and (11) into (9) and noting that $p(S_j^2\mid {\sigma }_j^2)p({\sigma }_j^2)\propto p({\sigma }_j^2\mid S_j^2)$ yields

$$\begin{array}{l}p({\alpha }_j,{\delta }_j\mid {\widehat{\alpha }}_j,{\widehat{\delta }}_j,S_j^2)\\ \propto {\pi }_{\alpha }{\pi }_{\delta }{\mathbf{1}}_{[{\alpha }_j=0,{\delta }_j=0]}{\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|0,\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\varphi \left({\widehat{\delta }}_j|0,\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)\times p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2\end{array}$$ (12a)

$$\begin{array}{l}+(1-{\pi }_{\alpha }){\pi }_{\delta }{\mathbf{1}}_{[{\alpha }_j\ne 0,{\delta }_j=0]}{\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|{\mu }_{\alpha },{\sigma }_{\alpha }^2+\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\varphi \left({\alpha }_j|{\stackrel{\sim }{\mu }}_{{\alpha }_j}^{\ast },{\stackrel{\sim }{\sigma }}_{{\alpha }_j}^{\ast 2}\right)\times \\ \varphi \left({\widehat{\delta }}_j|0,\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2\end{array}$$ (12b)

$$\begin{array}{l}+{\pi }_{\alpha }(1-{\pi }_{\delta }){\mathbf{1}}_{[{\alpha }_j=0,{\delta }_j\ne 0]}{\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|0,\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\times \\ \varphi \left({\widehat{\delta }}_j|{\mu }_{\delta },{\sigma }_{\delta }^2+\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)\varphi \left({\delta }_j|{\stackrel{\sim }{\mu }}_{{\delta }_j}^{\ast },{\stackrel{\sim }{\sigma }}_{{\delta }_j}^{\ast 2}\right)p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2\end{array}$$ (12c)

$$\begin{array}{l}+(1-{\pi }_{\alpha })(1-{\pi }_{\delta }){\mathbf{1}}_{[{\alpha }_j\ne 0,{\delta }_j\ne 0]}{\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|{\mu }_{\alpha },{\sigma }_{\alpha }^2+\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\varphi \left({\alpha }_j|{\stackrel{\sim }{\mu }}_{{\alpha }_j}^{\ast },{\stackrel{\sim }{\sigma }}_{{\alpha }_j}^{\ast 2}\right)\times \\ \varphi \left({\widehat{\delta }}_j|{\mu }_{\delta },{\sigma }_{\delta }^2+\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)\varphi \left({\delta }_j|{\stackrel{\sim }{\mu }}_{{\delta }_j}^{\ast },{\stackrel{\sim }{\sigma }}_{{\delta }_j}^{\ast 2}\right)p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2.\end{array}$$ (12d)

To obtain reliable statistical inferences of α_j and δ_j, as well as inferences of h_j, l_j, and m_j, we need to draw a sufficiently large sample from the posterior distribution proportional to (12) for each gene j. One approach is to use the Metropolis-Hastings algorithm (see the online supplement). However, due to the inefficiency of the Metropolis-Hastings algorithm and the complex structure in (12), obtaining a sufficiently large sample for each of the tens of thousands of genes in a typical microarray experiment requires extensive computing power. Methods, such as parallel computing, could reduce the computing time, but the total amount of required computing power remains substantial.

Here, we propose a novel method to approximate the joint posterior density, which dramatically decreases the required computing power and, at the same time, maintains accurate estimation of the posterior distribution. Specifically, we define ${\stackrel{\sim }{\sigma }}_j^2$ as the inverse of the posterior mean of $1/{\sigma }_j^2$ given $S_j^2$ as in (8a). We use ${\stackrel{\sim }{\sigma }}_j^2$ in place of ${\sigma }_j^2$ in the conditional distributions of α_j and δ_j; that is, we replace ${\sigma }_j^2$ with ${\stackrel{\sim }{\sigma }}_j^2$ in ${\stackrel{\sim }{\mu }}_{{\alpha }_j}^{\ast },{\stackrel{\sim }{\sigma }}_{{\alpha }_j}^{\ast 2},{\stackrel{\sim }{\mu }}_{{\delta }_j}^{\ast }$, and ${\stackrel{\sim }{\sigma }}_{{\delta }_j}^{\ast 2}$ to obtain μ̃_αj, ${\stackrel{\sim }{\sigma }}_{{\alpha }_j}^2$, μ̃_δj, and ${\stackrel{\sim }{\sigma }}_{{\delta }_j}^2$ given in (8b)–(8e). This simple replacement of ${\sigma }_j^2$ by ${\stackrel{\sim }{\sigma }}_j^2$ in the above four terms leads to the form of (7). We then approximate the posterior of α_j and δ_j by (7) where P_kj = C_kj/(C_1j + C_2j + C_3j + C_4j) (k = 1, ···, 4) with

$$C_{1j}={\pi }_{\alpha }{\pi }_{\delta }{\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|0,\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\varphi \left({\widehat{\delta }}_j|0,\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2,$$ (13a)

$$C_{2j}=(1-{\pi }_{\alpha }){\pi }_{\delta }{\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|{\mu }_{\alpha },{\sigma }_{\alpha }^2+\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\times \varphi \left({\widehat{\delta }}_j|0,\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2,$$ (13b)

$$C_{3j}={\pi }_{\alpha }(1-{\pi }_{\delta }){\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|0,\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\times \varphi \left({\widehat{\delta }}_j|{\mu }_{\delta },{\sigma }_{\delta }^2+\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2,$$ (13c)

and

$$C_{4j}=(1-{\pi }_{\alpha })(1-{\pi }_{\delta }){\int }_0^{\infty }\varphi \left({\widehat{\alpha }}_j|{\mu }_{\alpha },{\sigma }_{\alpha }^2+\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)\times \varphi \left({\widehat{\delta }}_j|{\mu }_{\delta },{\sigma }_{\delta }^2+\left(\frac{1}{4n_1}+\frac{1}{4n_2}+\frac{1}{n_3}\right){\sigma }_j^2\right)p({\sigma }_j^2\mid S_j^2)d{\sigma }_j^2.$$ (13d)

After this simplification, we no longer need to draw samples from the joint posterior distribution using an iterative algorithm, such as the Metropolis-Hastings method. Instead, we can sample directly from a point-mass-at-0 distribution or a normal distribution as shown in (7). Although we still need to estimate constants C_1j, C_2j, C_3j, and C_4j by simulation, the required computations are straightforward and efficient. Thus, the required computing power is dramatically reduced. The online supplement contains a comparison of results for sampling via Metropolis-Hastings and the approximation (7).

APPENDIX C: ESTIMATION OF HYPERPARAMETERS

The hyperparameters to be estimated are π_α, μ_α, ${\sigma }_{\alpha }^2$, π_δ, μ_δ, ${\sigma }_{\delta }^2$, d₀, and ${\sigma }_0^2$. As noted in section 3, we use the method of Smyth (2004) to estimate d₀ and ${\sigma }_0^2$. In all subsequent calculations, we replace the unknown values of d₀ and ${\sigma }_0^2$ with their estimates. To estimate the remaining hyperparameters, we initially suppose that ${\sigma }_1^2,\dots ,{\sigma }_J^2$ are fixed, known constants. Then, based on the proposed model in section 2, we have

$$({\widehat{\alpha }}_j\mid {\pi }_{\alpha },{\mu }_{\alpha },{\sigma }_{\alpha }^2)~{\pi }_{\alpha }\mathrm{N}\left(0,\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right)+(1-{\pi }_{\alpha })\mathrm{N}\left({\mu }_{\alpha },\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}+{\sigma }_{\alpha }^2\right).$$ (14)

By equating the first and the second distribution moments with the corresponding sample moments of (α̂_j |π_α, μ_α, ${\sigma }_{\alpha }^2$), we have

$$\{\begin{array}{lll}\hfill \frac{1}{J}{\sum }_{j=1}^J{\widehat{\alpha }}_j& \approx \hfill & (1-{\pi }_{\alpha }){\mu }_{\alpha }\hfill \\ \hfill \frac{1}{J}{\sum }_{j=1}^J\left[{\widehat{\alpha }}_j^2-\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right]& \approx \hfill & (1-{\pi }_{\alpha })({\mu }_{\alpha }^2+{\alpha }_{\alpha }^2)\hfill \end{array}$$ (15)

Based on (15), μ_α and ${\sigma }_{\alpha }^2$ can be written as functions of π_α as follows.

$$\{\begin{array}{lll}{\mu }_{\alpha }\hfill & \approx \hfill & \frac{1}{J}{\sum }_{j=1}^J{\widehat{\alpha }}_j/(1-{\pi }_{\alpha })\hfill \\ {\sigma }_{\alpha }^2\hfill & \approx \hfill & \frac{1}{J}{\sum }_{j=1}^J\left[{\widehat{\alpha }}_j^2-\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\frac{{\sigma }_j^2}{4}\right]/(1-{\pi }_{\alpha })-\left(\frac{1}{J}{\sum }_{j=1}^J{\widehat{\alpha }}_j^2\right)/{(1-{\pi }_{\alpha })}^2\hfill \end{array}$$ (16)

Plugging (16) in (14) and replacing ${\sigma }_j^2$ with ${\stackrel{\sim }{\sigma }}_j^2={\mathrm{E}}^{-1}(1/{\sigma }_j^2\mid S_j^2)$, we can approximate the distribution of (α̂_j |π_α, μ_α, ${\sigma }_{\alpha }^2$) as a function with only one unknown parameter π_α. We then estimate π_α by maximizing the resulting approximate joint likelihood of the α̂_j’s for all genes with constraint π_α ∈ (0, 1). The estimates of μ_α and ${\sigma }_{\alpha }^2$ are computed by replacing π_α with its estimate and replacing ${\sigma }_j^2$ with ${\stackrel{\sim }{\sigma }}_j^2$ in (16). A completely analogous procedure is used to estimate μ_δ, ${\sigma }_{\delta }^2$, and π_δ.