Predicting Tick Presence by Environmental Risk Mapping

Abstract

Public health statistics recorded an increasing trend in the incidence of tick bites and erythema migrans (EM) in the Netherlands. We investigated whether the disease incidence could be predicted by a spatially explicit categorization model, based on environmental factors and a training set of tick absence–presence data. Presence and absence of Ixodes ricinus were determined by the blanket-dragging method at numerous sites spread over the Netherlands. The probability of tick presence on a 1 km by 1 km square grid was estimated from the field data using a satellite-based methodology. Expert elicitation was conducted to provide a Bayesian prior per landscape type. We applied a linear model to test for a linear relationship between incidence of EM consultations by general practitioners in the Netherlands and the estimated probability of tick presence. Ticks were present at 252 distinct sampling coordinates and absent at 425. Tick presence was estimated for 54% of the total land cover. Our model has predictive power for tick presence in the Netherlands, tick-bite incidence per municipality correlated significantly with the average probability of tick presence per grid. The estimated intercept of the linear model was positive and significant. This indicates that a significant fraction of the tick-bite consultations could be attributed to the I. ricinus population outside the resident municipality.

Introduction

Borrelia burgdorferi s.l. is the bacteria that causes Lyme disease in humans. In Europe, the main vector is the tick Ixodes ricinus. In the Netherlands, Lyme disease is on the rise; there has been a threefold increase in consultations of general practitioners (GP) for tick bites and Lyme disease since 1994 (1). This rise can be partially explained by spatiotemporal increases in the abundance and activity of questing ticks, as the total area suitable for tick persistence including forest areas expanded in the Netherlands (2). The concomitant increase in these time series data sets indicates that tick activity might be explained based on environmental factors.

Risk mapping was used to predict the spatial distribution of tsetse flies in Africa based on environmental factors (3). The methodology also accurately delineated the areas of mosquito presence, both regionally and globally (4). It was the modeling tool of choice for identifying the distribution of malaria (5), tick-borne encephalitis (6), blue tongue epidemic in Europe (7), and Lyme disease in Belgium (8). While all surveillance targets a specific microorganism involved in a specific infectious disease, the algorithms, and the satellite images in the risk mapping methodology are generally applicable in a broad range of infectious disease contexts, including Lyme disease in the Netherlands. A complex interplay of vegetation, climatic conditions, and vertebrate hosts determine where the disease-transmitting vector, I. ricinus, can maintain its lifecycle. Nymphal and adult ticks for example, start questing after the winter season once the daily maximum temperatures during a week exceeds 7°C on average (9). Vegetation provides different degrees of shelter for ticks. Satellite images of vegetation and climatic variables are expected to provide necessary information to identify tick suitable areas.

I. ricinus requires three blood meals (choosing from a plethora of warm and cold blooded vertebrates) to complete their life cycle. Larvae feed primarily on small animals while nymphs and adults preferably feed on larger vertebrates such as hare and deer (10). The abundance of ticks greatly depends on the abundance of feeding and propagation hosts (11, 12). Here, regional roe deer population densities are utilized to identify the presence of I. ricinus, in addition to the satellite images.

Experts on ticks are able to estimate the tick density and activity for a particular land type. It is possible to quantify this prior knowledge. The methodology, expert elicitation, has been applied to a food-risk-assessment study (13). We applied the method to estimate the tick densities and activities for heterogeneous Dutch land surfaces, and used the estimates as Bayesian priors in our analyses of the field data.

Standard blanket dragging (14, 15) is the method to collect ticks searching for a blood meal. Although the blanket fails to catch molting, resting, and feeding ticks, it is currently the best method for measuring public health risk. Here, we predicted the presence of I. ricinus based on the field surveillance, satellite images, and host population densities. The number of tick-bite consultations by GP in the Netherlands (16) is a measure of tick presence, independent of field surveillance. The tick-bite consultation statistics are an empirical input into the analysis to validate the predicted tick presence.

Materials and Methods

Data collection

Sampling of I. ricinus

Ticks were collected by blanket dragging (blanket 1 m × 1 m) at 677 distinct coordinates in the Netherlands between April 2000 and September 2013 (the full list of coordinates is available on request). The dataset in this analysis includes data described in three publications. First, the study conducted each month from April to October in the period 2000–2004 at forest, dune, heather, and City Park (17). Second, the study conducted each month from April to September in the period 2000–2008 at vegetation-rich dune, City Park, heather, and forest areas (18). Third, the study conducted each month from July 2006 to December 2007 at forest areas (19). The rest of the dataset consists of three additional tick collections. Firstly, a study conducted each month from April to July in the 3-year period 2011–2013 at randomly generated sampling coordinates over the whole nation. Only incomplete and scarce information is available about the flora and fauna present at these areas. Secondly, the studies conducted in June, July, and August in the 2-year period 2012–2013 at City Parks, forest, and the ground adjacent to a walking path. Thirdly, the studies conducted in June 2012 and in May, June, July, and September 2013 at dune, heath, and forest areas. Ticks were dragged over 200 m² after which an average per 100 m² was calculated. The sum of nymphal and adult ticks, the two active life stages of I. ricinus, was recorded into the database. A sampling coordinate is assigned a state “tick is absent” if the sum is below or equal to a set threshold (default zero), and “present” otherwise.

Satellite images

We downloaded the satellite imageries from the MODIS ftp site (20). Tile h18v3 covers the Netherlands. Satellite images from the period January 2005 to June 2012 were downloaded and used for subsequent analysis in this study. Table 1 summarizes the images used.

Table 1.

Summary of the MODIS products used.

Name	Data	Short name	HDF layer	Resolution	Time granularity
EVI	Enhanced vegetation index	MOD13Q1	2	250 m2	16 days
DLST	Daytime land surface temperature	MOD11A1	1	1 km2	1 day
NLST	Nighttime land surface temperature	MOD11A1	5	1 km2	1 day
MIR	Middle infra red	MCD43A4	7	250 m2	16 days

See also the online resource https://lpdaac.usgs.gov/products/modis_products_table. Briefly, EVI is a measure of vegetation density, DLST and NLST measure temperature, and MIR is a measure of vegetation regrowth rate.

To all satellite images and all following spatial maps, a water mask and a mask removing neighboring countries has been applied.

Roe deer population densities

Estimates on the regional roe deer population density per square kilometer (2008) was extracted from the roe deer database (Royal Dutch Hunting Association).

Soil moisture

Soil moisture maps were calculated by the hydrological bureau FutureWater by means of the hydrological SPHY-model on a spatial resolution of 250 m × 250 m (21). The soil moisture fraction is the result of the hydrological budget equation, with precipitation and upward seepage as incoming fluxes. Output fluxes are evaporation, run-off, drainage from root zone and sub-zone, and downward seepage. Furthermore, percolation and capillary rise are taken into account.

Mathematical analysis

Our aim is to classify pixels as either suitable for ticks (an event denoted C⁺) or not suitable for ticks (C⁻). This classification is made using the data collected in the form of maps. The absence–presence data of the ticks, with the values of the maps at their locations, constitute the training set. For the satellite images, we have many images per year. In order to obtain a manageable data set that retains some of the seasonality, we employ a Fourier analysis. The classification is based on a quadratic discriminant analysis (QDA), aided by a Bayesian inclusion of expert opinion data.

Fourier analysis

A Fourier analysis is a technique for decomposing a signal into oscillating components; we follow the exposition as detailed in Ref. (22), chapter 7.7, and also Ref. (4). In the current context, the signal is the time series of the satellite image at a pixel. Each of these components represents a cosine with a certain frequency, and has phase and amplitude coefficients. An efficient method for performing a Fourier analysis is the “fast Fourier transform” (FFT). It applies only to equidistant data points, and thus we linearly interpolate the signal to daily values. We excluded time series with more than 20% missing values (e.g., due to cloud cover), and set the pixel to the symbolic value “NA,” this pixel does not contribute to the model any more.

For all other pixels, we extract the phase and amplitude of the yearly oscillation (emulating seasonal effects), the half-yearly oscillation, and the bi-yearly oscillation. Finally, we include the average, which has no phase, only amplitude. In total, the 8-year signal is now represented by seven components.

Quadratic discriminant analysis

Since the method of QDA is not widely used, we will outline the method briefly. The derivation is based on Ref. (23).

After the Fourier transform procedure, we evaluate the k Fourier components at each pixel of each satellite image, at the n presence points and at the m absence points. This yields vectors $x_1^{+},\dots ,x_n^{+}$, each $x_j^{+}\in R^{\mathrm{\kappa }}$ containing all Fourier coefficients taken at presence location j. Analogously for the absence points, we have vectors $x_1^{-},\dots ,x_m^{-}$. We assume that each vector is a realization of a multivariate Gaussian distribution, one distribution for the presence points, and one for the absence points. Let X denote a vector of Fourier coefficients, then,

$$\begin{array}{llll}\hfill X|C^{+}& \sim N\left({\mathrm{\mu }}^{+},{\sum }^{+}\right)& \hfill & \\ \hfill X|C^{-}& \sim N\left({\mathrm{\mu }}^{-},{\sum }^{-}\right)& \hfill & \end{array}$$

We construct the matrix $X^{+}\in R^{k\times n}$ by column wise concatenation of the vectors $x_1^{+},\dots ,x_n^{+}$. Similarly, we define for the absence points a matrix $X^{-}\in R^{k\times m}$. We use these matrices for calculation of the estimators ${\widehat{\mathrm{\mu }}}^{+}$, ${\widehat{\Sigma }}^{+}$, and ${\widehat{\mathrm{\mu }}}^{-}$, ${\widehat{\Sigma }}^{-}$ of the means and covariance matrices.

Let f⁺ and f⁻ denote the corresponding probability density functions. Now at a new point x ∈R^k, corresponding to a location where no tick presence or absence observation is available, we wish to determine the probability of tick presence. Using Bayes’ theorem, and the symbolic notation P(C⁺) for the probability of belonging to the positive group, we may write

$$P\left(C^{+}|X=x\right)=\frac{f^{+}\left(x\right)P\left(C^{+}\right)}{f^{+}\left(x\right)P\left(C^{+}\right)+f^{-}\left(x\right)P\left(C^{-}\right)}$$ (1)

Under the assumption of common covariance matrices between groups, Σ⁺ = Σ⁻ ≡Σ, and uninformed priors P(C⁺) = P(C⁻) = 1/2, we arrive at linear discriminant analysis by checking if

$$\begin{array}{llll}\hfill \log \left(\frac{P\left(C^{+}|X=x\right)}{P\left(C^{-}|X=x\right)}\right)& ={\left({\mathrm{\mu }}^{+}-{\mathrm{\mu }}^{-}\right)}^T{\sum }^{-1}x& \hfill & \\ \hfill & +\frac{1}{2}{\left({\mathrm{\mu }}^{+}+{\mathrm{\mu }}^{-}\right)}^T{\sum }^{-1}\left({\mathrm{\mu }}^{+}-{\mathrm{\mu }}^{-}\right)& \hfill & \end{array}$$

is below or above zero. Thus, the decision boundary is a hyperplane, and the classifier is linear in x. We do not make these assumptions, and work with separate covariance matrices for absence and presence. Furthermore, we use expert opinions for the prior probabilities. Instead of a classifier based on probability ratios, we work with the QDA probability of presence, given by

$$\begin{array}{llll}\hfill & P\left(C^{+}|x\right)=& \hfill & \\ \hfill & \frac{P\left(C^{+}\right)|{\sum }^{+}{|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}{D}^2(x,C^{+})}}{P\left(C^{+}\right)|{\sum }^{+}{|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}{D}^2(x,C^{+})}+P\left(C^{-}\right)|{\sum }^{-}{|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}{D}^2(x,C^{-})}}& \hfill & \end{array}$$

with the Mahalanobis distance defined by

$$D^2\left(x,C^{+}\right)={\left(x-{\mathrm{\mu }}^{+}\right)}^T{\left({\sum }^{+}\right)}^{-1}\left(x-{\mathrm{\mu }}^{+}\right)$$

We estimate the mean and covariance matrices by the sample mean and covariance as stated above. A straightforward implementation of the algorithm would be computationally expensive, as the number of covariates and the number of pixels are both large. However, by diagonalizing the covariance matrices, and some further time saving application of linear algebra [detailed in Ref. (23)], the calculations simplify tremendously. Next, observe that

$$D^2\left(X,C^{+}\right)={\left(X-{\mathrm{\mu }}^{+}\right)}^T{\left({\sum }^{+}\right)}^{-1∕2}{\left({\sum }^{+}\right)}^{-1∕2}\left(X-{\mathrm{\mu }}^{+}\right)$$

Thus, since conditional on C⁺, X is normally distributed, observe that Z = (X − μ⁺)^T(Σ⁺)^−1/2 ~ N(0, 1) and $D^2\left(Z,C^{+}\right)=Z^{T}Z={\sum }_{i=1}^n{Z}_i^2$. Since the sum of n standard normal random variables is distributed as ${\mathrm{\chi }}_n^2$, we have a criterium for prediction uncertainty by comparing D² to a set percentile of the chi-squared distribution with n degrees of freedom. We exclude pixels below this percentile, and set them to a symbolic “no-prediction” value. Those pixels will be colored as white in the figures. We use a default of 90%, but evaluate other settings in the supplementary material.

Expert elicitation

Thirteen individuals were selected based either on their affinity to tick research or on their affiliation to landscapes where ticks are expected to be found (e.g., experts from forest services). We asked the experts a probable range of questing nymphal plus adult tick densities per 100 m² for a number of specific landscape types. The Netherlands is partitioned into 39 land types (24). The experts were asked to provide a range between 0 and 200 ticks per 100 m². At the start of the elicitation, we instructed an expert that the questionnaires contain one or more questions in order to calibrate the participant’s expertise.

We represent the answer of expert i to question q by the vector, ν_i,q = (p₀, …, p₂₀₀) where p_j is the probability that the questing nymphal and adult tick density equals j. We set

$$P_{i,q,j}=\left\{\begin{array}{cc}\hfill {\left(b_{i,q}-a_{i,q}+1\right)}^{-1}\hfill & \hfill j\in \left[a_{i,q},b_{i,q}\right]\hfill \\ \hfill 0\hfill & \hfill \mathrm{otherwise}\hfill \\ \hfill \hfill \end{array}\right.$$

where [a_i,q, b_i,q] is the response of expert i to question q.

First, we determine a weight for each expert by calibration using their answers $p_{i,q}^{\prime }$ to control questions. Control questions are the measurements on the densities of nymphal plus adult ticks (H. Sprong, personal communication) in the following land types: salt water (0 ticks per 100 m²), corn ( <2 per 100 m²), heather (2–20 per 100 m²), and deciduous forest (20–200 per m²). We represented a control question by the vectors c₁ to c₄. We determine a weight for each expert by,

$$W_i={\displaystyle \prod _{q=1}^4}{p}_{i,q}^{\prime }.c_q$$

then normalizing the weight over all experts $w_i=\frac{W_i}{{\sum }_{j=1}^n{W}_j}$ (we use the lower case letter for the normalized weights). This is a strict weighting, which invalidates an expert who gave an answer disjoint to one of the control questions. Responses from the experts to the actual questions were weighted by the w_i and combined to obtain an empirical probability density function for the number of ticks,

$$P\left(\mathrm{tick}\mathrm{density}=j|q\right)={\displaystyle \sum _{i=1}^n}{w}_i{p}_{i,q,j}$$

Finally, from this probability we construct the Bayesian prior, by setting a threshold t to distinguish absence and presence (very low numbers may be accidental, non-endemic, presence),

$$P\left(C^{+}|q\right)=1-{\displaystyle \sum _{j=1}^{t-1}}P\left(\mathrm{tick}\mathrm{density}=j|q\right)$$

Our default threshold is t  = 1 but we evaluate other scenarios in the supplementary material. For each pixel, we determine the land-use type, and use the corresponding P(C⁺ | q) as a prior.

Independent support using EM consultation statistics

Estimation of the number of tick-bite consultations in the Netherlands was as described elsewhere (1). In short, we use Dutch GP consultation data over 2009, regarding erythema migrans (EM), an expanding skin lesion occurring after several days or weeks at the site of the tick bite. This dataset was aggregated on a municipality level, and we used it to validate our predicted presence of ticks. For this purpose, we changed the spatial unit in our prediction to a municipality by averaging the probability of tick presence over all 1 km by 1 km grids enclosed by the municipality boundary. We only include pixels that were significant at the 90% level. We applied a linear model and calculated the P-value for the slope being significantly different from zero.

Results

Observed absence and presence of I. ricinus

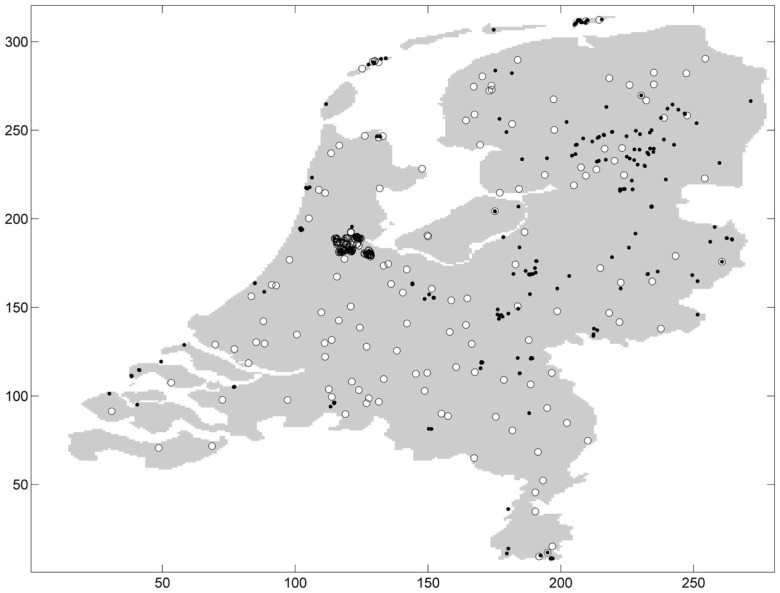
Ticks were sampled at 677 distinct geographic coordinates (Figure 1). Sampling was conducted only once at the majority of sampling coordinates and up to three repeated samplings at few sampling coordinates. Ticks were present at 252 distinct sampling coordinates: one tick (either nymphal or adult stage) or more were found on the blanket at these sampling coordinates. Ticks were absent at 425 distinct sampling coordinates. Some distinct sampling coordinates fell into the same pixel, and aggregating the sampling coordinates by pixel resulted in 177 presence pixels and 163 absence pixels. In one absence pixel, I. ricinus was absent at all sampling coordinates within the pixel.

Figure 1.

Absence (white circle) and presence (black dot) of ticks in the Netherlands.

Prior tick presence probabilities per land-use type

We applied expert elicitation to estimate a Bayesian prior for the probability of presence of nymphal plus adult ticks per unit area of a specific land type. The prior probability of tick presence was less than 0.5 at 12 land types, mainly cultivated areas and vegetation-poor grounds. Prior probability of tick presence was greater than 0.5 at 25 land types of a wider variety (Figure 2).

Figure 2.

Summary of the expert elicitation, showing the probability of tick presence for several land-use types.

Estimates on tick suitable grids

The blanket dragging, covering 100 m² each, at 677 distinct coordinates during our multi-year surveillance for I. ricinus is approximately equal to 7 ha of the investigated area in total. For the remaining land surface (99.98% of the total land surface), the presence of I. ricinus needs to be extrapolated from the outcomes of the sampling coordinates. Classifying all the sampling coordinates into either presence or absence, we estimated the probability that I. ricinus is present, for each 1 km by 1 km square grids enclosed by the nation border (Figure 3). Summing all the 1 km by 1 km grids by the weighs of the presence probabilities, we estimated that total tick suitable area is 20,698 km². By counting pixels, we estimate the total land surface of the Netherlands as 35,001 km². Hence, an estimated 54% of the land surface meets the conditions for maintaining the tick life cycle.

Figure 3.

Estimated map of tick presence based on the sampling coordinates (Figure 1), roe deer densities, soil moisture, and the satellite images: EVI, NLST, DLST, and MIR. The risk is indicated by colors ranging from 0 (green, no risk) to 1 (red, maximum risk). White pixels indicate “no prediction.” Pixels not within Dutch land surface (e.g., water bodies) are indicated in blue. The leftmost (A) has the “no-prediction” pixels censored; the rightmost (B) shows all predictions.

Independent support using EM consultation statistics

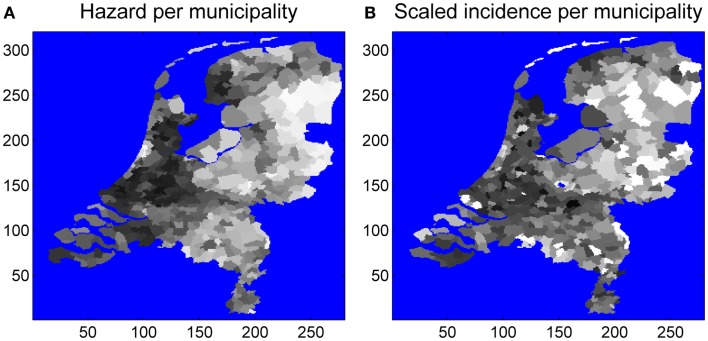
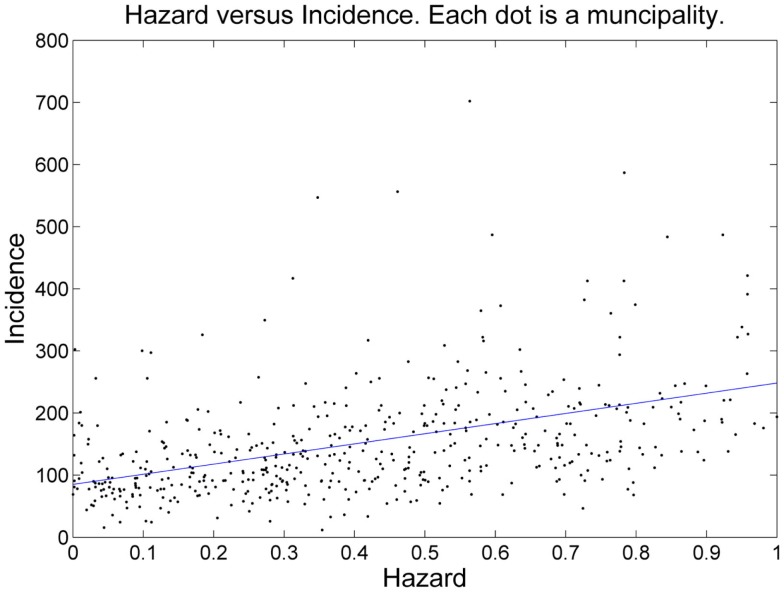
The number of tick-bite consultations by GPs in the Netherlands (16) is an alternative measure of tick presence, independent of field surveillance by the blanket-dragging method. Hence, the estimated probability of tick presence is expected to correlate positively with the consultation statistics. Figure 4 shows the aggregation of EM incidence and predicted risk to the municipality level. To assess linear correlation we also performed a linear regression at this municipality level (Figure 5). The linear relationship between our prediction and the consultation statistics was positive (slope 137) and significant (P-value <0.001). The estimated intercept of the linear model was also positive (95) and significant (P-value <0.001).

Figure 4.

EM consultations (A) and tick presence per municipality (B). Averages were taken over all pixels in a municipality, and numbers were scaled between zero and one.

Figure 5.

Scatterplot of risk (x-axis) versus incidence (y-axis). The blue line is the linear regression line.

Alternative scenarios

In order to assess the impact of modeling choices, we ran the model with other parameter settings, and an alternative corroborating scenario. Firstly, we varied the number of ticks below which a sampling occasion is marked as negative. The rationale for this is that a very low number of ticks may indicate ticks that are not from an established population, but rather ticks that accidentally ended up in a tick-free area. Secondly, we varied the cutoff for the value for “no prediction.” Table S1 of the supplementary material gives the results in terms of the P-value of the comparison with EM-cases. The tick presence threshold of zero is clearly superior. For the no-prediction cutoff, it seems that even very low cutoff values still yield good results. This is probably since the validation is at the municipality level, while inclusion or exclusion due to “no-prediction” is at the pixel level. Misclassifications may cancel out by this procedure. A second alternative scenario set consisted of replacement of the EM notifications by tick-bite notifications (with, or without EM). This yields the results as given in Table S1 of the supplementary material. We observe P-values much lower than for tick-bite consultation, indicating that tick presence correlates better with EM consultations than with tick bites in general. Figures associated to these tables may also be found in the supplementary material.

Discussion

We applied a quadratic discriminant model (QDA) for predicting suitability for ticks, based on environmental covariates. The model was trained using a set a tick absence/presence points. Probabilities of tick presence were averaged over each municipality of the Netherlands, with the aim to validate the prediction with an independent measure of tick presence: estimated numbers of consultations of EM per municipality. The estimate for the intercept of the linear model was positive and significant. We observe that even in the municipalities where the mean probability of tick presence is near zero, tick bites were recorded, with an average of 95 consultations per 100,000 residents (the intercept of the linear model, Figure 5). In municipalities where the mean probability of tick presence is close to one, tick-bite consultations reached 232 consultations per 100,000 residents, almost a tripling compared to the municipalities where the mean probability of tick presence is predicted to be almost zero. We interpret the intercept as cases that obtained their tick-bite outside of the municipality of residence; hence this part of the risk of a tick-bite might not be explained by local risk factors. The increase over the entire range of the risk of a tick bite, 137 per 100,000 residents can be explained by the local risk factors. Roughly speaking, our model explains 2/3rd of the risk of a tick bite.

This study is a first attempt to map tick presence in the Netherlands using environmental and biological factors. The tick-bite incidence independently supports our predictions. Nonetheless, a high variability in incidence of tick bites per municipality remains un-accounted for by the presence of ticks only. To reduce the high variability, the methodology implemented in this study could be extended by considering additional biological and social factors that are missing in our current approach.

First, a potentially better proxy for the Lyme-disease incidence than the tick-presence would be the density of infected ticks. The density of infected ticks is equal to the sum of densities of larval, nymphal, and adult ticks weighted by instar-specific prevalence estimates of Borrelia burgdorferi. We leave tick abundance as an option to investigate at a later stage. The analysis will be more involved, since tick abundance will vary greatly over the year.

Next, as small mammals are important for the Borrelia life cycle their population density is a potential biological factor that might reduce the variability. However, nationwide estimates on local population densities for any specific rodent species in the Netherlands are currently unavailable. Lastly, an inclusion of social factors in our methodology (e.g., human activities) might help to reduce the high variability in predicted disease incidence. An example is an exposure map indicating where people are likely to receive a tick bite. A source of information regarding human activities is an on-going study in the Netherlands in which any person can report the location where they received a tick bite in a past day by visiting a website (www.tekenradar.nl).

Note that in the current study, we do not attempt any model selection. In principle, using for example cross-validation, we could compare the explanatory power of models with different sets of satellite data. Also, techniques exist that assess the importance of individual variables within fixed models. However, this falls out of the scope of our current paper, which was simply to demonstrate that a riskmap may be constructed, which has good correspondence to independent incidence data. In the future, we hope to further pursue model selection methods.

It is common to set up surveillance solely for catching and identifying the disease-transmitting vector species. Due to this common practice, a statistical methodology to estimate the vector distribution necessarily assumes pseudo-absence, a set of geographic coordinates at which the vector is assumed absent. For us, it was straightforward to eliminate the pseudo-absence; we requested our trained volunteers to report absence when no I. ricinus tick attached to the blanket. Absence of I. ricinus on a blanket was recorded more than 400 times in our field surveillance database.

Empirical observations of absence have limitations. An absence record indicates that either: (1) the tick I. ricinus was absent at the sampling coordinates, or (2) by chance the blanket-dragging failed to catch any I. ricinus. An estimate on the fraction of false absence records in our database is lacking, but the most sensible interpretation of the hundreds of absence records in our database is the former explanation. We expect furthermore that the statistical algorithm is robust to a small fraction of false absent signals in our surveillance database. A positive and significant correlation with the independent indicator of tick presence, i.e., tick-bite consultations, further corroborates that this potential artifact in the data collection procedure is a marginal limitation in this study.

Bayesian prior probabilities of the tick presence were estimated from expert knowledge on all major land types in the Netherlands. Effects on the predicted I. ricinus distribution, however, were not visibly present. We might infer from this observation that our model contains at least as much information as the prior distribution. To test this hypothesis, we ran the riskmapping model with only the expert elicitation data, and used this as the only input. We find that the significance of the correlation with human cases is strongly reduced, but still highly significant (P-value <0.0001). Also, the risk is highly clustered around one, and the number of no-prediction points has grown to high numbers.

Concerning the modeling approach, we opted for QDA, a robust and proven algorithm for unsupervised classification. Alternatives are certainly possible. For example, logistic regression may be used to predict binary outcomes. However, since in logistic regression the logit of the probability of presence is modeled by a linear function, we expect the QDA algorithm to outperform logistic regression. Also, for future work, state-of-the art techniques like boosted regression trees, or random forests are promising candidates for classification.

In summary, we identified large-scale areas in the Netherlands where environmental conditions are likely to be suitable for maintaining the I. ricinus life cycle. An independent proxy for the tick presence, estimates on the number of tick bites on humans (1), is consistent with our identification based on satellite images and the host population densities. In conclusion, we presented a validated statistical approach to identifying areas where the human’s exposure to the Lyme-disease transmitting vector I. ricinus is expected to be high.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at http://www.frontiersin.org/Journal/10.3389/fpubh.2014.00238/abstract