Validity of Bioelectrical Impedance Measurement in Predicting Fat-Free Mass of Chinese Children and Adolescents

Abstract

Background

The current study aimed to examine the validity of various published bioelectrical impedance analysis (BIA) equations in estimating FFM among Chinese children and adolescents and to develop BIA equations for the estimation of fat-free mass (FFM) appropriate for Chinese children and adolescents.

Material/Methods

A total of 255 healthy Chinese children and adolescents aged 9 to 19 years old (127 males and 128 females) from Tianjin, China, participated in the BIA measurement at 50 kHz between the hand and the foot. The criterion measure of FFM was also employed using dual-energy X-ray absorptiometry (DEXA). FFM estimated from 24 published BIA equations was cross-validated against the criterion measure from DEXA. Multiple linear regression was conducted to examine alternative BIA equation for the studied population.

Results

FFM estimated from the 24 published BIA equations yielded high correlations with the directly measured FFM from DEXA. However, none of the 24 equations was statistically equivalent with the DEXA-measured FFM. Using multiple linear regression and cross-validation against DEXA measurement, an alternative prediction equation was determined as follows: FFM (kg)=1.613+0.742×height (cm)2/impedance (Ω)+0.151×body weight (kg); R²=0.95; SEE=2.45kg; CV=6.5, 93.7% of the residuals of all the participants fell within the 95% limits of agreement.

Conclusions

BIA was highly correlated with FFM in Chinese children and adolescents. When the new developed BIA equations are applied, BIA can provide a practical and valid measurement of body composition in Chinese children and adolescents.

Background

The World Health Organization has classified childhood obesity as one of the most serious public health challenges of the 21^st century [1]. Besides causing social and emotional impairments, this condition has significant adverse effects on health and has been associated with increased risk of cardiovascular disease, type II diabetes, hypertension, stroke, and certain types of cancer [2,3]. The International Obesity Task Force (IOTF) has reported that among the world’s children between the ages of 5 to 17 years, 10% are overweight, with estimates of overall childhood obesity ranging between 30 to 45 million [4]. In China, in particular, the progressive increasing trend in prevalence of childhood obesity is alarming [5]. Between 1991 and 2000, the prevalence of childhood obesity in large, coastal Chinese metropolitan cities increased from 1.8% to 9.1% for boys and from 1.4% to 4.8% for girls. The prevalence of childhood obesity in older Children in China is higher than in younger children [6].

Obesity is generally defined as abnormal or excessive fat accumulation accompanied by increased risks to general health [7]. Classical 2-component models describe the human body as the sum of fat and fat-free body compartments. Fat mass can be estimated as total body weight minus fat-free mass. Therefore, the ability to accurately assess body composition in children, including fat mass and fat-free mass, is necessary to develop effective prevention and treatment strategies for childhood obesity [8].

Many laboratory methods have been developed to measure body composition in adults and children, and these include the underwater weighing method, air-displacement plethysmography (ADP), and dual-energy X-ray absorptiometry (DEXA). The basic principle underlying DEXA is that the attenuation of X-rays with high- and low-photon energies is measureable and is dependent on the thickness, density, and chemical composition of the underlying tissue. DEXA in particular has been reported to provide acceptable accuracy and reliability in measuring body compositions of children [9], as justified by its successful validation against the multi-component model in children [10].

Although the method has emerged as a practical measure to validate other measures of body composition [11], the method requires costly equipment, complicated methodology, and experienced technicians. Therefore, transportable equipment and convenient field methods have been developed to measure body fat in a more efficient and economically practical manner. The most popular of these methods are skinfold thickness (SFT) measurement and bioelectric impedance analysis (BIA). Skinfold thickness measurement is easily administered and practical for large studies. However, it requires trained testers, compressibility of skinfold thickness may be affected by age, and accurately measuring the thickness of persons who are obese or heavily muscled is difficult [11].

BIA, on the other hand, is a relatively simple, quick, and non-invasive method that gives reliable measurements of body composition regardless of body composition, with small intra- and inter-observer variability [12]. With the BIA method, low-level electrical current is passed through a human body, and the impedance (Z), or opposition to the flow of current, is measured with a BIA analyzer. In the human body, lean tissue is good electrical conductor because it contains large amounts of water and electrolyte, and the fact that fat is anhydrous and is a poor conductor. When the volume of total body water is large, the current flows more easily through the body with less resistance. Since BIA does not require exposure to radioactivity or submersion in water, it has gained particular popularity as a practical measure of body composition in field studies involving children. Accordingly, some empirical equations have been developed for the estimation of total body water (TBW), fat-free mass (FFM), and percent body fat (%BF) among children [11]. The BIA method, however, has been shown to be less accurate when a generalized equation is applied for different ethnic groups [11,13,14]; thus, the related predictive equations are generally population-specific [15,16].

Most of the published BIA equations for children and adolescents were developed based upon white populations. To date, only 1 BIA equation in the public literature was developed specifically for Chinese children, but the criterion measurement used in that study was SFT [17] and the previously mentioned SFT limitations call into question its appropriateness for use in this manner. A study of the ethnicity-related appropriateness of the 19 published BIA equations indicated that none were ideally suited for use among the sub-populations of Chinese and Indian children, aged 5 to 15 years, in the overall study population of New Zealand residents [18]. Thus, there is a need for focused studies to test the validity of the BIA method for estimating body composition in ethnic-specific populations, such as Chinese children and adolescents. In addition, no study to date has attempted to cross-validate the accuracy of published BIA equations in predicting FFM in Chinese children and adolescents.

Therefore, the purposes of the current study were: 1) to examine the validity of various published BIA equations in estimating FFM in Chinese children and adolescents using DEXA as the reference measurement of body composition, and 2) to develop BIA equations for the estimation of FFM appropriate to Chinese children and adolescents.

Material and Methods

Participants

A total of 255 healthy Chinese children and adolescents, aged 9 to 19 years old, were recruited from schools in Tianjin, China. Older children are better able to cooperate during tests; therefore, children aged 9 years to 19 years were included in the target group in the current study. A stratified sampling method was used to recruit a heterogeneous sample that covers a wide range of ages and body compositions according to age and sex-specific BMI distributions among Chinese children [19,20]. Participants were recruited from local primary and primary and secondary schools according to the following categories: BMI lower than the 30^th percentile for age- and sex-specific BMI distribution; BMI between the 30^th and 70^th percentile for age- and sex-specific BMI distribution; and BMI higher than the 70^th percentile for age- and sex-specific BMI distribution [19]. There were total 33 categories. Each category included at least 8 participants [20]. Generally, large samples (N=100–400 subjects) are needed to ensure that the data are representative of the population for whom the equation was developed [11]. In our study, 255 healthy Chinese children and adolescents aged 9 to 19 years old were recruited. This ensures that the statistical conclusions are valid. Written informed consent was obtained from all participants or the parent/guardians upon study enrolment. The study was conducted with pre-approval provided by the Ethics Committee of the Chinese University of Hong Kong.

Measurements

Anthropometric measurements

Body weight and height were measured with each study participant in minimal clothing and on bare feet. Body height was measured to the nearest 0.5 cm using a fixed stadiometer (Holtain Ltd., Crymych, Dyfed, UK). Body weight was measured to the nearest 0.1 kg using a standard scale (TBF model 543; Tanita, Tokyo, Japan). The participant’s stage of sexual maturation was estimated through a self-assessment method using Tanner’s pictures representing the 5 stages of the development of secondary sexual characteristics [21].

DEXA measurement

DEXA was measured using the GE Lunar Prodigy instrument and accompanying software, version 10.51.006 (GE Healthcare, Madison, WI, USA). A trained investigator performed all DEXA measurements according to instructions from the DEXA manufacturers. The resultant DEXA measurement was then applied as the criterion measurement for body composition in terms of fat mass (FM), lean tissue mass (LTM), and bone mineral content (BMC). Individual FFM values from DEXA were calculated as the sum of LTM and BMC.

BIA measurement

Resistance (R) and reactance (X) were measured at 50 kHz using a Biodynamics BIA 310e Analyzer (Biodynamics Corp., Seattle, WA, USA) with a tetrapolar arrangement of standard electrodes (Red Dot 2330; 3M Healthcare, St. Paul, MN, USA) according to a standard protocol [22]. The average of the repeated measurements of R or X, agreeing to within 2 ohm of each other, was used in the subsequent analysis [22]. Impedance (Z) was calculated using following equation [11]:

$$Z=\sqrt{R^2+X^2}$$

The resistance index [(RI=height²/R) (cm²/Ω)] and impedance index [(ZI=height²/Z) (cm²/Ω)] were calculated.

Data reduction and statistical analyses

A literature search was conducted to identify published BIA equations for calculating children’s FFM, using the following 2 inclusion criteria: 1) developed for calculating FFM in healthy children and adolescents in the 9- to19-years-old age range; and 2) requiring inputted values of only basic anthropometric variables (weight, height, and sex) and either resistance or impedance values at a traditional single frequency (50 kHz). Ultimately, 24 published BIA equations were selected [13,17,18,22–39]. Table 1 below shows the information of the BIA equation.

Table 1.

Published BIA equations for the prediction of FFM in children and adolescents.

Equation number	Citation	Participants characteristics	Equation for FFM	R2	SEE (kg)
1	Bedogni et al. [23]	8–12 y (C); n=52 M/F	(0.7 × H2/Z)+4.8	0.95	1.5
2	Boileau [24]	8–16 y (C); n (NR)	(0.657 × H2/R) + (0.16 × W) − (0.131 × sex) + 4.138 (sex: M=−1, F=1)	0.97	1.8
3	Cordain et al. [25]	9–14 y (NR); n=14 M, 16 F	(0.81 × H2/R) + 6.86	0.69	4.08
4	de Lorenzo et al. [26]	7.7–13.0 (NR); n=20 M, 15 F	(0.588 × H2/Z) + (0.211 × W) + 2.33	0.92	1.0
5	Deurenberg et al. [27]	7–25 y (C); n=130 M, 116 F	(0.438 × H2/R) + (0.308 × W) + (1.6 × sex) + (0.07 × H) − 8.5 (sex: M=1, F=0)	0.99	2.39
6	Deurenberg et al. [28]	7–15 y (NR); n=166 M/F	(0.406 × H2/R) + (0.36 × W) + (0.56 × sex) + (0.056 × H) − 6.48 (sex: M=1, F=0)	0.97	1.68
7		≥16 y (NR); n=661 M/F	(0.340 × H2/R) + (15.34 × H) + (0.273 × W) − (0.127 × age) + (4.56 × sex) − 12.44 (sex: M=1, F=0)	0.93	2.63
8	Duncan et al. [18]	5–14 (As); n=39 M, 40 F	(0.533 × H2/R) + (0.329 × W) + 0.04	0.98	1.49
9	Eston et al. [17]	11–17 y (As); n=48 M, 46 F	(0.52 × H2/R) + (0.28 × W) + 3.25	0.93	2.20
10	Horlick et al. [29]	4–18 y (C,AA,Af,As); n=645 M, 602 F	[(0.459 × H2/R) + (0.064 × W) + 3.474]/[(0.769 − (0.009 × age) − (0.016 × sex)] (sex: M=1, F=0)	0.997	0.93
11	Houtkooper et al. [30]	10–14 y (C); n=53 M, 41 F	(0.58 × H2/R) + (0.24 × W) + 2.69	0.93	2.0
12	Houtkooper et al. [31]	10–19 y (C); n=225 M/F	(0.61 × H2/R) + (0.25 × W) + 1.31	0.95	2.10
13	Kim et al. [32]	9–14 y (As); n=141 M	(0.56 × H2/Z) + (0.20 × W) + 1.66	0.97	1.59
14	Lewy et al. [33]	M 11.4±1.4 y; F 10.2±0.4 y; n=19 M, 17 F (AA)	(0.84 × H2/R) + 1.10	0.97	1.47
15	Morrison et al. [34]	6–17 y (AA); n=61 F	(0.78 × H2/R) + (0.1 × X)+ (0.18 × W) − 8.78	0.99	1.95
16		6–17 y (C); n=65 F	(0.56 × H2/R) + (0.06 × X) + (0.34 × W) − 6.41	0.99	NR
17	Nielsen et al. [35]	9–11 y (C); n=52 M, 49 F	(0.54 × H2/R) + (0.05 × X) + (0.06 × H) + (0.09 × W) + (0.97 × sex) − 5.11 (sex: M=1, F=0)	0.95	NR
18	Pietrobelli et al. [36]	7–14 y (C); n=50 M, 25 F	(0.694 × H2/Z) − (1.097 × sex) + 5.344 (sex: M=0, F=1)	0.90	5.12
19	Rush et al. [22]	5–14 y (C,P); n=83 M, 89 F	(0.622 × H2/R) + (0.234 × W) + 1.166	0.96	2.44
20	Schaefer et al. [37]	3.9–19.3 y (C); n=59 M, 53 F	(0.65 × H2/R) + (0.68 × age) + 0.15	0.975	1.98
21	Sun et al. [13]	12–94 y (C,As); n=669 M, 944 F	(0.65 × H2/R) + (0.26 × W) + (0.02 × R) − 10.68 (sex: M)	0.90	3.9
22			(0.69 × H2/R) + (0.17 × W) + (0.02 × R) − 9.53 (sex: F)	0.83	2.9
23	Suprasongsin et al. [38]	10–22 y (C); n=21 M, 21 F	(0.524 × H2/R) + (0.415 × W) − 0.32	0.96	2.8
24	Tyrrell et al. [39]	5–10.9 y (C,P); n=82 M/F	(0.31 × H2/Z) + (0.17 × H) + (0.11 × W) + (0.942 × sex) − 14.96 (sex: M=2, F=1)	0.97	NR

C – Caucasian; As – Asian; AA – American African; Af – African; P – Polynesian; NR – no report; H – body height in cm; W – body weight in kg; M – male; F – female; R – resistance in Ω; Z – impedance in Ω; X – reactance in Ω. R² – regression coefficients; SEE – standard error of estimate.

All data are reported as mean ± standard deviation (SD). Data were tested for normal distribution using the Kolmogorov-Smirnov test. If data were not normally distributed, data were transformed into normalized data using log transformation. The independent t-test was used to determine the difference in physical characteristics of the participants, body compartments, and BIA variables between males and females. The 5% level was chosen as the threshold for statistical significance.

Cross-validation of published BIA equations

Individual FFM values from different BIA equations were calculated. To examine the validity of each BIA equation in predicting FFM, cross-validations were conducted using samples of a specific age range suggested by each BIA equation (Step I) and for all participants (9–19 years old) involved in the current study (Step II).

The paired t-test was used to determine the mean difference in FFM between each BIA equation and the direct measurement made by DEXA. Pearson’s correlation coefficient was used to investigate the relationship of FFM for each BIA equation and the direct DEXA measurement, as well as the relationship between bias and the FFM of DEXA. Bias and the 95% limits of agreement (mean of the difference ±1.96 SD) were calculated to indicate the overall precision of the measurements [40]. The 5% level was chosen as the threshold for statistical significance. The pure error in FFM between each BIA equation with DEXA measurement was assessed using the total error [11] as follows:

$$\text{TE}=\sqrt{\sum {(\text{Y}-{\text{Y}}^{\prime })}^2/\text{N}}$$

where Y – observed values, Y′ – predicted values, and N – the number of participants in the sample.

Development of alternative BIA equations

The DEXA-derived FFM was applied as the criterion for the development of prediction equations through multiple regression analysis based on the following potentially influencing variables: body weight, age, body height, BMI, RI, ZI, R, Z, X, sex (coded as female=0 and male=1), and Tanner’s stages. These predictive variables were chosen a priori based upon evidenced biological relations to FFM (body weight and body height), theoretical relations to body water (RI, ZI, R, Z, and X), recognized sex differences in growth, maturation and body composition, and evidenced improvements in the prediction of FFM reported in published equations, as well as ease of assessment of each variable [35].

A double cross-validation approach was used to determine the predicative accuracy of the prediction equations. To this end, the total sample was split randomly into 2 groups through a simple random sampling [11], and the data corresponding to each group were used to derive a prediction equation. Each equation was then applied to the other group to test its predictive accuracy. If the equations proved similar, with comparable cross-validation performance, a single equation was developed for the entire sample. To evaluate the potential improvement in the prediction equations with the addition of new variables, covariance analysis was used to compare the multiple regression models performance with the 2 randomized groups [41]. Model selection was carried out using the stepwise variable selection and the best subsets regression procedure. As a prerequisite, potential predictive variables were first screened for a linear relationship with the observed FFM. Mallow’s Cp statistic [42] and Bayesian information criterion (BIC) [43] were applied to determine the appropriate number of predictors. High R² values, small standard error of the estimate (SEE), small Cp values, and small BIC values were considered indicators of an optimal model.

The equations were then examined for the significance of the regression coefficients. A variance inflation factor (VIF) was actuated to assess the influence of each coefficient on the prediction equations [44]. Finally, the calculation of pure error (the root mean square of the mean of the differences between the measured and predicted FFM) was used to assess the accuracy of the predictive equations in cross-validation. Differences between measured and predicted FFMs were calculated using the Bland-Altman method [40], whereby Bland-Altman plots were also used to illustrate the residual errors. Again, a 5% level was chosen as the threshold for statistical significance.

Results

Descriptive statistics

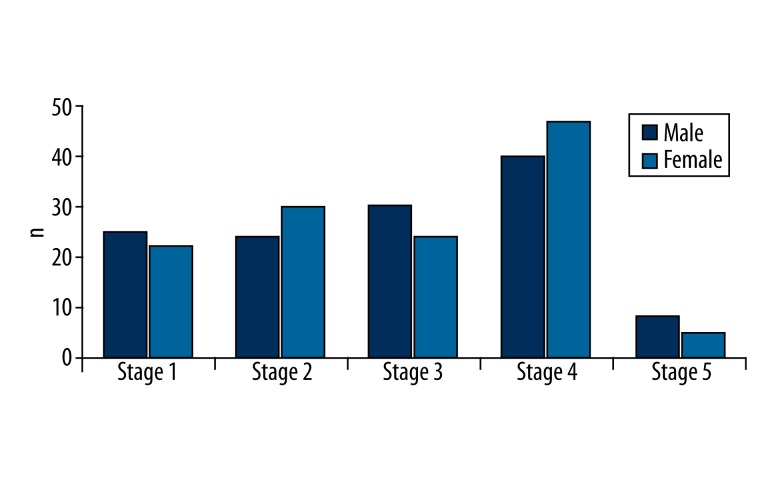
The physical characteristics, body compartment factors, and BIA variables of study participants are presented in Table 2. There was no significant difference in the mean age of the sexes, but the mean body weight, height, and BMI were higher in the male group than in the female group. In addition, the mean values of the individual body compartments and BIA variables were significantly different between the sexes, possibly reflecting the differences in sexual maturation (80.3% of males and 82.8% of females had entered puberty, as indicated by the Tanner scale pubertal stage ≥2 classification for appearance of pubic hair or breasts in females) (Figure 1).

Table 2.

Descriptive statistics of physical characteristics, body compartments and BIA variables of study participants.

	Male (n=127)	Female (n=128)	Total (n=255)
	Mean (SD)	Mean (SD)	Mean (SD)
Age in years	13.8 (2.9)	13.7 (2.8)	13.7 (2.8)
Height in cm	161.8 (14.0)	154.3 (9.8)	158.0 (12.6)
Weight in kg	55.9 (17.0)	47.4 (11.3)	51.7 (15.0)
BMI in kg2/m	21.0 (4.2)	19.7 (3.2)	20.3 (3.8)
LTM in kg	41.0 (11.2)	31.0 (5.5)	36.0 (10.1)
BMC in kg	2.0 (0.7)	1.7 (0.5)	1.9 (0.6)
FM in kg	12.7 (9.5)	14.3 (6.8)	13.5 (8.3)
FFM in kg	43.0 (11.8)	32.8 (5.9)	37.8 (10.6)
%BF	20.8 (9.9)	27.9 (7.7)	24.3 (9.5)
X in Ω	47.4 (9.8)	52.1 (7.9)	49.7 (9.1)
R in Ω	620.8 (97.7)	742.8 (80.2)	682.0 (108.1)
Z in Ω	622.7 (97.8)	744.7 (80.3)	683.9 (108.2)
RI in cm2/Ω	44.2 (12.6)	32.6 (5.8)	38.4 (11.3)
ZI in cm2/Ω	44.1 (12.5)	32.5 (5.8)	38.3 (11.3)

BMI – body mass index; LTM – lean tissue mass measured by dual-energy X-ray absorptiometry (DEXA); BMC – bone mineral content measured by DEXA; FM – fat mass measured by DEXA; %BF – body fat percentage measured by DEXA; FFM – fat-free mass calculated as the sum of LTM and BMC; X – reactance measured by bioelectrical impedance analysis (BIA); R – resistance measured by BIA; $\text{Z}-\text{impedance}=\sqrt{R^2+X^2}$; RI – resistance index = height²/R; ZI – impedance index = height²/Z.

Figure 1.

Stages of sexual maturation among study population.

Cross-validation of published BIA equations

Most of the 24 published BIA equations for predicting FFM showed an acceptable level of correlation between predicted and observed FFM upon evaluation with the current study sample, with the SEE ranging from 0.87 to 5.12 kg.

Cross-validation of published BIA equations: Step I

In the first step of the cross-validation evaluation, only the estimated FFM values of the samples from the current study (falling within the specified age range prescribed by each of the previously published BIA equations) were evaluated. One equation (Equation 14) was excluded from this analysis because the original publication had not provided a specified age range. The evaluation of the remaining 23 BIA equations showed that the predicted FFM values from each were highly correlated with the observed FFM values (Table 3). However, paired t-test analysis showed that only 3 of the BIA equations were not significantly different from the DEXA-measured FFM (Equations 2, 7, and 8), 5 were overestimated (Equations 3, 10, 21, 22, and 23) and the remaining 16 were underestimated. Two of the 3 BIA equations with similarity to the DEXA-measured FFM values (Equations 2 and 8) had a significant negative correlation between the bias and the observed FFM, indicating that the FFM was underestimated at high values and overestimated at low values in the present sample. The third equation (Equation 7), developed by Deurenberg et al., was only applicable in populations older than 16 years old in the present sample.

Table 3.

Cross-validation of published BIA equations for the prediction of FFM in Chinese children and adolescents: Step I (using samples of a specific age range suggested by each BIA equation).

Equation number	Citation	n, Sex, Age**	DEXA-FFM in kg, mean (SD)	Predicted FFM in kg, mean (SD)	p by t-test	Bias*	TE*	ry-y′	ry-y′,y, p	95% limits of agreement*
1	Bedogni et al. [23]	98, M/F, 8–12	29.47 (5.65)	26.30 (4.55)	0.000	−3.17	3.71	0.951	−0.683, 0.000	−6.95, 0.61
2	Boileau [24]	217, M/F, 6–16	36.45 (10.00)	36.30 (8.83)	0.421	−0.15	2.68	0.967	−0.547, 0.000	−5.40, 5.10
3	Cordain et al. [25]	170, M/F, 9–14	34.37 (9.02)	35.14 (7.42)	0.001	0.78	3.21	0.946	−0.639, 0.000	−5.34, 6.89
4	de Lorenzo et al. [26]	133, M/F, 7.7–13	32.09 (7.69)	31.01 (6.84)	0.000	−1.09	2.34	0.966	−0.522, 0.000	−5.16, 2.99
5	Deurenberg et al. [27]	255, M/F, 7–25	37.88 (10.61)	36.14 (10.30)	0.000	−1.73	3.15	0.969	−0.240, 0.000	−6.90, 3.44
6	Deurenberg et al. [28]	198, M/F, 7–15	35.26 (9.14)	34.24 (8.68)	0.000	−1.02	2.84	0.957	−0.314, 0.000	−6.23, 4.20
7		57, M/F, >16	46.98 (10.41)	47.48 (10.88)	0.177	0.50	2.79	0.967	0.041, 0.760	−4.93, 5.94
8	Duncan et al. [18]	170, M/F, 5–14	34.37 (9.02)	34.03 (8.71)	0.087	−0.34	2.57	0.959	−0.260, 0.001	−5.35, 4.68
9	Eston et al. [17]	182, M/F, 11–17	40.45 (9.77)	39.77 (8.98)	0.003	−0.69	3.15	0.949	−0.403, 0.000	−6.74, 5.36
10	Horlick et al. [29	245, M/F, 4–18	37.51 (10.55)	38.07 (10.58)	0.001	0.55	2.56	0.972	−0.107, 0.096	−4.35, 5.46
11	Houtkooper et al. [30]	141, M/F, 10–14	36.01 (8.88)	35.52 (7.92)	0.024	−0.50	2.62	0.959	−0.500, 0.000	−5.55, 4.56
12	Houtkooper et al. [31]	226, M/F, 10–19	39.35 (10.29)	38.96 (10.01)	0.036	−0.39	2.82	0.962	−0.235, 0.000	−5.89, 5.10
13	Kim et al. [33]	85, M, 9–14	37.71 (10.21)	33.19 (8.18)	0.000	−4.53	5.51	0.962	−0.721, 0.000	−11.12, 1.74
15	Morrison et al. [34]	121, F, 6–17	32.48 (5.85)	29.96 (5.88)	0.000	−2.51	3.18	0.944	−0.150, 0.101	−6.35, 1.32
16		121, F, 6–17	32.48 (5.85)	30.38 (7.25)	0.000	−2.09	3.39	0.938	−0.114, 0.201	−7.35, 3.17
17	Nielsen et al. [35]	78, M/F, 9–11	28.41 (5.34)	26.17 (4.43)	0.000	−2.24	2.70	0.969	−0.691, 0.000	−5.23, 0.75
18	Pietrobelli et al. [36]	170, M/F, 7–14	34.37 (9.02)	28.96 (6.59)	0.000	−5.41	6.48	0.942	−0.786, 0000	−12.43, 1.62
19	Rush et al. [22]	170, M/F, 5–14	34.37 (9.02)	33.82 (8.34)	0.004	−0.55	2.47	0.964	−0.402, 0.000	−5.28, 4.19
20	Schaefer et al. [37]	250, M/F, 4–19.3	37.67 (10.57)	34.19 (8.54)	0.000	−3.49	4.77	0.962	−0.689, 0.000	−9.89, 2.91
21	Sun et al. [12]	128, F, 12–94	32.78 (5.88)	35.90 (4.81)	0.000	3.12	3.62	0.961	−0.693, 0.000	−0.49, 6.73
22		127, M, 12–94	43.02 (11.78)	45.01 (10.53)	0.000	1.99	3.77	0.965	−0.508, 0.000	−4.23, 8.30
23	Suprasongsin et al. [38]	226, M/F, 10–22	39.35 (10.29)	42.72 (11.36)	0.000	3.37	4.91	0.950	0.141 0.034	−3.65, 10.39
24	Tyrrell et al. [39]	58, M/F, 5–10.9	27.34 (4.04)	23.61 (3.25)	0.000	−3.73	3.96	0.956	−0.701, 0.000	−6.34, −1.11

FFM – fat-free mass; Bias – BIA-predicated; FFM – DEXA-measured FFM; TE – total error; r_y-y′ – correlation coefficient between DEXA-measured FFM and BIA-predicted FFM; r_y-y′,y – correlation coefficient between the bias and the DEXA-measured FFM.

^*data presented in kg;

^**data presented in years.

Cross-validation of published BIA equations: Step II

In the second step of the cross-validation evaluation, the estimated FFM values of all 24 BIA equations were calculated using all the samples in the current study, without regard to the age range specified in the published equations, and were compared with the DEXA-measured FFM values. As shown in Table 4, paired t-test analysis showed significant differences in FFM among most of the BIA equations; only 4 of the BIA equations were not significantly different from the DEXA-measured FFM (Equations 2, 3, 9, and 12) with DEXA measurements, 5 BIA equations provided overestimates of DEXA-measured FFM (Equations 7, 10, 21, 22, and 23), and the remaining 15 provided underestimates. However, Bland-Altman analysis found significant negative correlations between the bias and the observed FFM for those 4 BIA equations that had showed no differences from the DEXA-measured FFM, indicating that FFM was underestimated at high values and overestimated at low values in the present sample. In summary, all of the published BIA equations failed to predict the FFM in the present sample.

Table 4.

Cross-validation of published BIA equations for the prediction of FFM in Chinese children and adolescents: Step II (all participants in current study).

Equation number	Publication	n, Sex	DEXA-FFM in kg, mean (SD)	Predicted FFM in kg, mean (SD)	p by t-test	Bias*	TE*	ry-y′	ry-y′,y, p	95% limits of agreement
1	Bedogni et al.[ 23]	255, M/F	37.88 (10.61)	31.60 (7.90)	0.000	−6.28	7.32	0.959	−0.805, 0.000	−13.67, 1.11
2	Boileau [24]	255, M/F	37.88 (10.61)	37.63 (9.60)	0.140	−0.25	2.72	0.969	−0.483, 0.000	−5.57, 5.06
3	Cordain et al. [25]	255, M/F	37.88 (10.61)	37.96 (9.17)	0.683	0.08	3.16	0.959	−0.570, 0.000	−6.13, 6.29
4	de Lorenzo et al. [26]	255, M/F	37.88 (10.61)	35.74 (9.43)	0.000	−2.14	3.53	0.968	−0.529, 0.000	−7.65, 3.37
5	Deurenberg et al. [27]	255, M/F	37.88 (10.61)	36.14 (10.30)	0.000	−1.73	3.15	0.969	−0.240, 0.000	−6.90, 3.44
6	Deurenberg et al. [28]	255, M/F	37.88 (10.61)	36.80 (10.30)	0.000	−1.08	3.13	0.961	−0.244, 0.000	−6.85, 4.70
7		255, M/F	37.88 (10.61)	39.48 (10.22)	0.000	1.60	3.17	0.966	−0.271, 0.000	−3.76, 6.98
8	Duncan et al. [18]	255, M/F	37.88 (10.61)	37.50 (10.51)	0.040	−0.38	2.97	0.961	−0.172, 0.004	−6.16, 5.40
9	Eston et al. [17]	255, M/F	37.88 (10.61)	37.68 (9.68)	0.270	−0.20	2.90	0.963	−0.445, 0.000	−5.88, 5.48
10	Horlick et al. [29]	255, M/F	37.88 (10.61)	38.65 (10.91)	0.000	0.77	2.82	0.969	−0.015, 0.811	−4.55, 6.10
11	Houtkooper et al. [30]	255, M/F	37.88 (10.61)	37.35 (9.78)	0.003	−0.52	2.81	0.966	−0.420, 0.000	−5.95, 4.90
12	Houtkooper et al. [31]	255, M/F	37.88 (10.61)	37.64 (10.25)	0.169	−0.23	2.73	0.967	−0.259, 0.000	−5.57, 5.10
13	Kim et al. [32]	127, M	43.02 (11.78)	37.52 (10.05)	0.000	−5.50	6.45	0.964	−0.617, 0.000	−12.14, 1.14
14	Lewy et al. [33]	255, M/F	37.88 (10.61)	33.35 (9.53)	0.000	−4.52	5.47	0.959	−0.480, 0.000	−10.56, 1.51
15	Morrison et al. [34]	128, F	32.78 (5.90)	30.41 (6.14)	0.000	−2.36	3.11	0.944	−0.048, 0.587	−6.35, 1.61
16		128, F	32.78 (5.90)	30.83 (7.39)	0.000	−1.94	3.33	0.942	0.393, 0.000	−7.26, 3.37
17	Nielsen et al. [35]	255, M/F	37.88 (10.61)	32.72 (8.03)	0.000	−5.15	6.12	0.975	−0.842, 0.000	−11.63, 1.32
18	Pietrobelli et al. [36]	255, M/F	37.88 (10.61)	31.36 (8.13)	0.000	−6.52	7.48	0.957	−0.737, 0.000	13.74, 0.72
19	Rush et al. [22]	255, M/F	37.88 (10.61)	37.13 (10.16)	0.000	−0.74	2.79	0.967	−0.291, 0.000	−6.03, 4.54
20		255, M/F	37.88 (10.61)	34.45 (8.68)	0.000	−3.43	4.74	0.962	−0.689, 0.000	−9.86, 3.00
21	Schaefer et al. [37]	128, F	32.78 (5.90)	35.90 (4.81)	0.000	3.12	3.62	0.961	−0.693, 0.000	−0.49, 6.73
22	Sun et al.[14]	127, M	43.02 (11.78)	45.01 (10.53)	0.000	1.99	3.77	0.965	−0.503, 0.000	−4.32, 8.30
23		255, M/F	37.88 (10.61)	41.23 (11.65)	0.000	3.36	4.82	0.956	0.150, 0.017	−3.44, 10.15
24	Suprasongsin et al. [38]	255, M/F	37.88 (10.61)	30.87 (7.10)	0.000	−7.01	8.04	0.978	−0.929, 0.000	−14.75, 0.73

FFM – fat-free mass; Bias – BIA-predicated FFM and DEXA-measured FFM; TE – total error; r_y-y′ – correlation coefficient between DEXA-measured FFM and BIA-predicted FFM; r_y-y′,y – correlation coefficient between the bias and the DEXA-measured FFM.

^*data presented in kg.

Alternative BIA equations for Chinese children and adolescents

Analysis of the 2 predictive equations, based on the randomly divided Groups A and B of the study population, showed that age, BMI, X, R, and Z were not significant predictors in either equation (Table 5). The parameters of Tanner’s stages, height, and sex were excluded from the regression model, owing to the high Cp and BIC values. Subsequently, an equation was developed for each randomized group using all possible subset regressions that included ZI and weight for predicting FFM. The VIF for these 2 predicting variables was <10, indicating that collinearity was not observed between the 2 independent variables.

Table 5.

Descriptive statistics of physical characteristics, FFM and BIA variables of Group A and Group B.

	Group A (n=127, M=63, F=64)	Group B (n=128, M=64 F=64)
	Mean (SD)	Mean (SD)
Age in years	13.7 (3.0)	13.8 (2.7)
Height in cm	157.4 (12.8)	158.5 (12.7)
Weight in kg	50.5 (14.2)	51.7 (15.9)
BMI in kg2/m	20.0 (3.5)	20.6 (4.0)
FFM in kg	37.5 (10.4)	38.2 (10.7)
X in Ω	49.7 (10.3)	49.7 (7.8)
R in Ω	681.0 (112.0)	682.8 (104.0)
Z in Ω	682.9 (112.0)	684.6 (104.2)
RI in cm2/Ω	38.1 (11.4)	38.4 (11.2)
ZI in cm2/Ω	38.2 (11.5)	38.5 (11.3)

When the regression model developed with Group A was used to predict the FFM in Group B, the results were not significantly different from the BIA-predicted FFM (37.99±10.24 kg) or the DEXA-measured FFM (38.17±10.87 kg; p=0.46) of Group B. Similarly, when the regression model developed with Group B was used to predict the FFM in Group A, no significant difference was found between either the BIA-predicted FFM (37.58±10.25 kg) or the DEXA-measured FFM (37.50±0.39 kg; p=0.72) of Group A. As shown in Table 6, similar R², SEE, and PE values were found between the 2 groups. Regression analyses of the BIA-predicted FFM in relation to the measured FFM developed for each group showed similar deviations from the line of identity, with the slopes of both groups being 0.94.

Table 6.

Prediction equations for fat-free mass validated and cross-validated using a random split-group sampling.

Group A (n=128)
DEXA-measured FFM in kg	37.50±10.39
FFM prediction equation	2.275 + 0.728 × ZI + 0.148 × body weight R2=0.94, SEE=2.60, CV=7.4%, VIF=5.7
BIA-predicted FFM in kg	37.50±10.07
Cross-validation using group B samples FFM	37.58±10.25, RSME=2.60, CV=6.9%
Group B (n=127)
DEXA-measured FFM in kg	38.17±10.87
FFM prediction equation	1.351 + 0.696 × ZI + 0.192 × body weight R2=0.94, SEE=2.69, CV=7.1%, VIF=7.6
BIA-predicted FFM in kg	38.16±10.53
Cross-validation using group A samples FFM	37.99±10.24, RSME=2.70, CV=7.1%

FFM – fat-free mass; ZI – impedance index = height²/Z; SEE – standard error of estimate; CV – coefficient of variation; VIF – variance inflation factor; RSME – root mean square error.

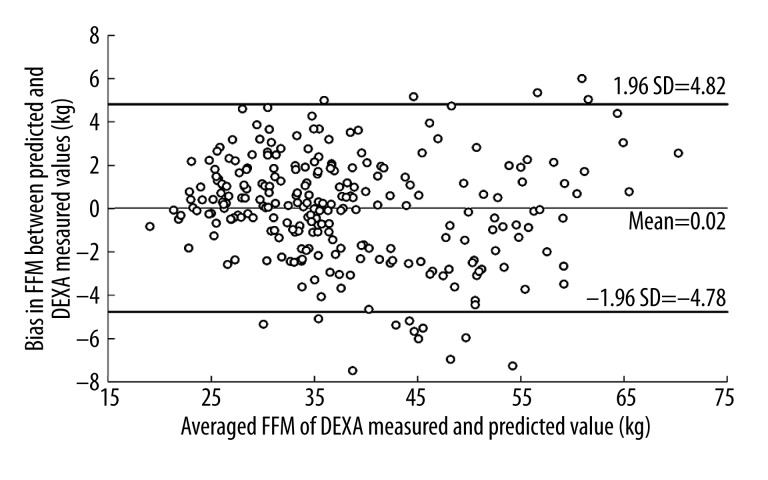
Therefore, a single BIA equation using all 255 participants was developed for the BIA prediction of FFM: (1.613+0.742×ZI+0.151× body weight), yielding R²=0.95, SEE=2.45, CV=6.5%, and VIF=6.5. The DEXA-measured FFM value was set as a dependent variable, and the ZI and body weight values were set as the independent variables in the combined groups, which were then applied as a dummy variable in the regression analysis. No group effect was detected by the regression analysis (p=0.60). ZI alone accounted for 93.3% of the variability (SEE=2.75 kg), and body weight alone accounted for 75.7% of the variability (SEE=5.24 kg). The mean difference between DEXA-measured and BIA-predicted FFM was 0.02±2.45, and the 95% limits of agreement (mean difference between DEXA-measured and BIA-predicted FFM ±1.96 SD) ranged from −4.78 to 4.82 kg FFM (Figure 2). Paired t-test analysis showed that there was no significant difference in FFM between the DEXA-measured and BIA-predicted values (37.79±10.61 kg vs. 37.77±10.35 kg, p=0.89). Bland-Altman analysis showed that for the predicting model, 93.7% of the residuals of all the participants fell within the 95% limits of agreement. Bias in FFM between the DEXA-measured and BIA-predicted values was correlated with the FFM (r=0.14, p=0.10).

Figure 2.

Bland-Altman analysis between the BIA-predicted fat-free mass and DEXA-measured fat-free mass for Chinese children and adolescents.

Discussion

The results of the current study reveal that BIA measurement is a reasonable estimate for FFM in Chinese children and adolescents. Since the study results also reaffirmed the questionable validity of previously published BIA equations for estimating FFM in Chinese children and adolescents, we developed and validated an alternative BIA-based prediction equation for FFM that is relevant for use in this particular population. In this new equation, weight-height relationships, such as those involving BMI, are used as proxy for body fat. While obtaining the direct measures of weight and height remains the simplest and most commonly used method for defining obesity among children and adolescents, if researchers intend to measure body composition in large-scale population surveys, then BIA measurement can provide an efficient alternative to laboratory measurement of body composition when accurate instruments are unavailable.

Cross-validation of published BIA equations

Twenty-four published BIA equations for predicting FFM were cross-validated using the relevant data of the present study population. As stated previously, the accuracy of BIA estimation is questionable when a generalized equation is applied to different ethnic groups [11,13]. This fact was illustrated by a study involving Swedish children, 9 to 11 years old, that used the previously published BIA equations to assess body composition; significant differences in FFM were found between the BIA predictions and the DEXA measurements for most of the BIA equations analyzed [35]. The study of Chinese and Indian children by Duncan et al. (described in the Introduction) provided similar results, demonstrating that 19 of the published BIA equations failed to accurately assess FFM in this population, as well as showing failure of the 2 BIA equations developed specifically for other children of Asian ethnicity [17, 32, 45], particularly Japanese [32,45].

In the current study, all previous BIA prediction equations (including the 3 BIA equations developed specifically for Asian children) failed to provide a valid FFM estimation for the Chinese children and adolescents assessed. These results support the recommendation of previous studies that BIA predictive equations are generally population-specific [15,16]. Ethnic differences in body compositions may explain the differences in FFM between the published BIA and the DEXA measurement and data from previous studies have indicated that Asian children and adolescents may have higher body fat content than either African-descent or white children and adolescents within the same BMI level [46–48]. Moreover, the body composition of Asian children and adolescents residing in different countries has been shown to vary significantly within the same BMI level. Indigenous Asian children and adolescents have been reported to have lower body fat than Asian children and adolescents living in regions that practice the Western lifestyle [46,49]. Thus, the different relationships between BMI and body fat among different ethnic populations may be explained by differences in dietary patterns and physical activity [50]. A similar influence may underlie the variations observed among various ethnicities in the relative subcutaneous fat distribution and relative proportions of the trunk and lower extremities to height; in particular, Asians have relatively shorter legs and more slender body builds, and are likely to have less muscle mass than their white counterparts [51].

In the current study, the 3 BIA equations developed for Asian children and adolescents did not perform well with the Chinese study population [17,18,32]. In these BIA equations, 2 studies were not cross-validated against the predictive equations [17,32]. In the study by Duncan et al., the subjects were Chinese and Indian children living in New Zealand [18]. To account for the demonstrated variations in body composition of Asian children and adolescents within the same BMI level that reside in different countries [46,49], Duncan et al. [18] suggested that the applicability of the equation to indigenous Chinese and Indian populations was uncertain (as opposed to those living in other regions, such as New Zealand) and recommended cross-validation of the FFM equation using independent samples of indigenous populations [18]. Indeed, in the current study, we found that the FFM values of indigenous Chinese children and adolescents were incorrectly estimated by the previously published BIA equations, highlighting the need for alternative BIA equations to be developed that is applicable to indigenous Chinese children and adolescents.

Development of alternative BIA equations

In the current study, a stratified sampling method was used to recruit a heterogeneous sample covering a wide range of ages and body compositions to adequately represent the various age and sex-specific BMI distributions that exist among Chinese children. The ethnic homogeneity of the study sample helped to provide better predictive estimates for the specific population of Chinese children and adolescents. Alternative BIA equations, with focused study population relevance, were developed in this study by using FFM, rather than FM, as the criterion variable to address the known biological relations between bioelectric impedance and hydrated lean tissue of the human body [11]. All of the 24 BIA equations previously validated in children and adolescents featured either RI or ZI as the major predictive variable upon cross-validation with the current study population. This result was expected, however, given that these variables provide an index of the conductive volume of the body, which is strongly associated with FFM and TBW.

Given the age range of the participants in the current study (encompassing childhood to late adolescence), it was necessary to consider potential effects of normal physical (including sexual) maturation on BIA predictions of body composition. At puberty, secretion of growth hormones leads to the increased growth and size of FFM [52]. While some previous studies have included variables describing the maturation stage, with the assumption that they may improve the BIA prediction of body composition in children and adolescents [18,35], the current study found that inclusion of the Tanner stages in the regression model was not useful because of high Cp and BIC values. Thus, maturation stage appears to not influence the accuracy of BIA equations for predicting FFM in Chinese children and adolescents. Using the 2 predictors that were found to independently account for FFM variability among the current study population (ZI and body weight), the simplest model with excellent goodness of fit was developed for predicting FFM in Chinese children and adolescents.

When the predictive ability of the BIA equations using similar predictive variables (Equations 4, 8, 9, 11, 12, 13, 19, and 23) was compared using the present study population, the adjusted R² was similar to that reported for the previous BIA equations (0.95 vs. 0.92–0.97). In contrast, the SEE of the newly developed equation (2.45 kg) was higher than those reported for several of the previous equations (Equations 4, 8, 9, 11, 12, and 13). Yet, this latter result is not surprising, since the participants in our study covered a wide range of ages and body compositions (as established by the stratified sampling method).

Unlike the few studies in the literature that have previously used a cross-validation approach to generate prediction equations for FFM based on BIA measurement in Asian children, the current study included a double cross-validation. The statistical analysis showed that the final equation developed from the entire sample performed well. The Bland-Altman 95% limits of agreement (−4.78 to 4.82 kg FFM) indicated that when the between-participant difference in FFM was <9.6 kg, the results could not be interpreted confidently as true differences. This finding is consistent with the view that BIA is better suited for a population survey than for the evaluation of FFM in individuals [18,25,28,29,37].

In population studies, the limit of agreement can decrease with larger sample size [29]. The degree of bias at the extremes of the FFM distribution is another important application of prediction equations in population studies. In the current study, when all participants were considered, 4 of the BIA equations showed acceptable levels of bias (Equations 2, 3, 9, and 12). However, all 4 of these BIA equations showed a significant negative correlation between the bias and observed FFM, indicating that they may not be ideally suited for use among Chinese children and adolescents.

In the current study, the bias between the DEXA-measured and the BIA-predicted values correlated well with the FFM, suggesting that the degree of bias does not increase or decrease significantly at the extremes of the FFM distributions. The newly-developed alternative equation is appropriate for predicting the FFM of Chinese children and adolescents, and provides researchers with an accurate and convenient method by which to assess body composition among Chinese children and adolescents in larger-scale surveys. However, the findings of the present study may have been impacted by limitations inherent to the overall study design. Specifically, the equation developed in this study may only be valid for Chinese children and adolescents between the ages of 9 to 19 years old (the age range of the study population). It is recommended that a cross-validation of this new BIA equation should be performed in a cohort of Chinese children and adolescents of a wider age range. Use of a larger sample size will also address the current study’s limitation of having relied on a relatively small study population. Cross-validation of the new BIA prediction model using more precise criterion methods, such as a 3- or 4-compartment model of human body composition, should also be considered to further determine its precise applicability. Moreover, growth factors, such as age and puberty stages, should be considered in future studies, because these factors may improve validity of BIA equations in predicting fat-free mass among Chinese children and adolescents. The socio-economic status of the population was not evaluated, which is another weakness of the study.

Conclusions

The present study demonstrates that the BIA equations developed from previous studies cannot be cross-validated in Chinese children aged 9 to 19 years. From the data collected in the present study, a new alternative BIA equation for predicting the FFM of Chinese children and adolescents has been developed. The equation is applicable over a larger range of body sizes and ages, and is more suitable than the weight-height relationship for assessing body composition in a field survey. With the use of the newly-developed BIA equations to predict FFM, BIA can provide a practical and valid measurement of body composition among Chinese children and adolescents.