Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Dec 1.
Published in final edited form as: J Cardiovasc Transl Res. 2014 Oct 30;7(9):788–796. doi: 10.1007/s12265-014-9596-y

Numerical Model of Full Cardiac Cycle Hemodynamics in a Total Artificial Heart and the Effect of Its Size on Platelet Activation

Gil Marom 1, Wei-Che Chiu 1, Jessica R Crosby 2, Katrina J DeCook 2, Saurabh Prabhakar 3, Marc Horner 4, Marvin J Slepian 1,5, Danny Bluestein 1
PMCID: PMC4245394  NIHMSID: NIHMS639115  PMID: 25354999

Abstract

The SynCardia total artificial heart (TAH) is the only FDA approved device for replacing hearts in patients with congestive heart failure. It pumps blood via pneumatically driven diaphragms and controls the flow with mechanical valves. While it has been successfully implanted in more than 1,300 patients, its size precludes implantation in smaller patients. This study’s aim was to evaluate the viability of scaled-down TAHs by quantifying thrombogenic potentials from flow patterns. Simulations of systole were first conducted with stationary valves, followed by an advanced full-cardiac-cycle model with moving valves. All the models included deforming diaphragms and platelet suspension in the blood flow. Flow stress-accumulations were computed for the platelet trajectories and thrombogenic potentials were assessed. The simulations successfully captured complex flow patterns during various phases of the cardiac-cycle. Increased stress-accumulations, but within the safety margin of acceptable thrombogenicity, were found in smaller TAHs, indicating that they are clinically viable.

Keywords: Total artificial heart, computational fluid dynamics, fluid-structure interaction, thrombogenic potential, mechanical circulatory support devices

Introduction

Though heart transplantation is the definitive therapy for patients with end-stage congestive heart failure (CHF), the chronic shortage of donor organs requires a viable solution. The SynCardia total artificial heart (TAH; SynCardia Systems, Tucson, AZ) is a complete bi-ventricular cardiac replacement system for treating bi-ventricular failure [1]. Since 2004 the TAH has been approved for use by the Food and Drug Administration (FDA) in the United States as a bridge-to-transplant device for patients at imminent risk of death from bi-ventricular heart failure [2]. Recently (2012) the TAH also received the FDA designation as a humanitarian use device (HUD), paving the way for its clinical use as a long-term implant as an alternative to transplantation, i.e. for destination therapy. The original TAH has a maximum stroke volume of 70 cc. However, smaller adults and pediatric patients are often unable to receive this TAH due to anatomical constraints [3]. In order to accommodate these patients, a 50 cc TAH considered for smaller patients and possible pediatric use has been designed [4]. A smaller 35 cc TAH is also being considered for pediatric patients, including infants.

All three TAHs have similar design that can replace the two ventricles. Each chamber pumps blood via pneumatic displacement of a polymer diaphragm [5]. Since the TAH emulates the pulsatile blood flow of native hearts, valves are required for regulating and directing the flow into and out of the chambers. The TAH employs mechanical tilting disk heart valves, initially Medtronic Hall (Medtronic Inc., Minneapolis, MN) and presently Syn-Hall™ (SynCardia Systems, Tucson, AZ), that are mounted at the inlet and outlet of each chamber [5]. Similar to most currently available mechanical circulatory support (MCS) devices, the TAH induces non-physiologic blood flow patterns and high flow shear stresses [6,7]. While these elevated stress levels may lead to platelet activation [8], to date the TAH has had a clinically acceptable thrombosis rate, being significantly lower than that observed with bi ventricular assist devices (Bi-VADs), typically continuous flow blood pumps [9,10].

In order to estimate the thrombogenic potential of a blood pumping device, numerical methods can be employed to calculate the shear stress field, as well as other hemodynamic aspects that may contribute to it, and provide detailed insights that experiments cannot capture. Computational Fluid Dynamics (CFD) and Fluid Structure Interaction (FSI) models were previously utilized in simulations of various mechanical valves [11–17] and MCS devices [18,19]. Sonntag et al. [20] employed FSI model to simulate the flow in the ReinHeart TAH device, where the diaphragm motion is controlled by a piston rather than an air pump. This study however neglected the valves by imposing simple open or closed boundary conditions. Penrose and Staples [21] suggested a FSI technique for cardiovascular devices and used it for modeling the Berlin Heart venticular assist device (VAD). The motion of the diaphragm was modeled, yet the valves were not included. Avrahami et al. [22] also modeled the flow through Berlin Heart. Although the valves in their model were fixed in the opened position, they prevent regurgitation during the closing phases by virtually change the dynamic viscosity. This method for modeling the valves was later used by Medvitz et al. [23] and Topper et al. [24] for different types of Penn State VAD. Current literature describing flow through bileaflet mechanical heart valves (MHVs) on the other hand, do employ FSI models that also simulate the leaflets motion [15,17,13,14,21]. In bileaflet MHV the leaflets can only rotate around their hinges and their motion is defined by one degree of freedom. Monoleaflets valves, like the Björk–Shiley valve and the Medtronic Hall heart valve, can simultaneously rotate and translate. Still, some two-dimensional (2-D) studies simplified the motion of Björk–Shiley by assuming it can only rotate around its pivot point [25]. Hose et al. [16] employed a 3-D FSI model to study Björk–Shiley valve where the closure motion was simplified by separating it into translation and rotation phases, a method that cannot be used to represent the complex motion of the Medtronic Hall or Syn-Hall leaflet. Pelliccioni et al. [26] presented FSI model of the Medtronic Hall valve, including both displacement and rotation, but this model was 2-D.

Although the influence of mechanical heart valves and MCS devices on platelet activation is well known, no previous study has investigated their influence on the hemodynamics in the SynCardia TAH using numerical models. The aim of the current study was to evaluate the flow regime in SynCardia TAHs and to estimate the risk of platelet damage in TAHs of varying sizes. Initially, a simpler model of a 50 cc TAH is compared to larger and smaller TAHs. These models include the deforming diaphragm, the flow driven motion of the valves’ leaflets, and the blood flow through the left chamber, but the valves are fixed in their systolic position and the boundary conditions (BCs) are only based on the pressure gradient. A multiphase model with injection of platelet particles is employed to calculate their trajectories and stress accumulation (SA) distribution. These results from the three TAH models are then compared. In the second part, a more advanced and extensive FSI model of the 70 cc TAH is presented. In addition to the features of the simpler systolic model, this model includes the coupled FSI motion of the two valves, more realistic BCs, and turbulence modeling.

Methods

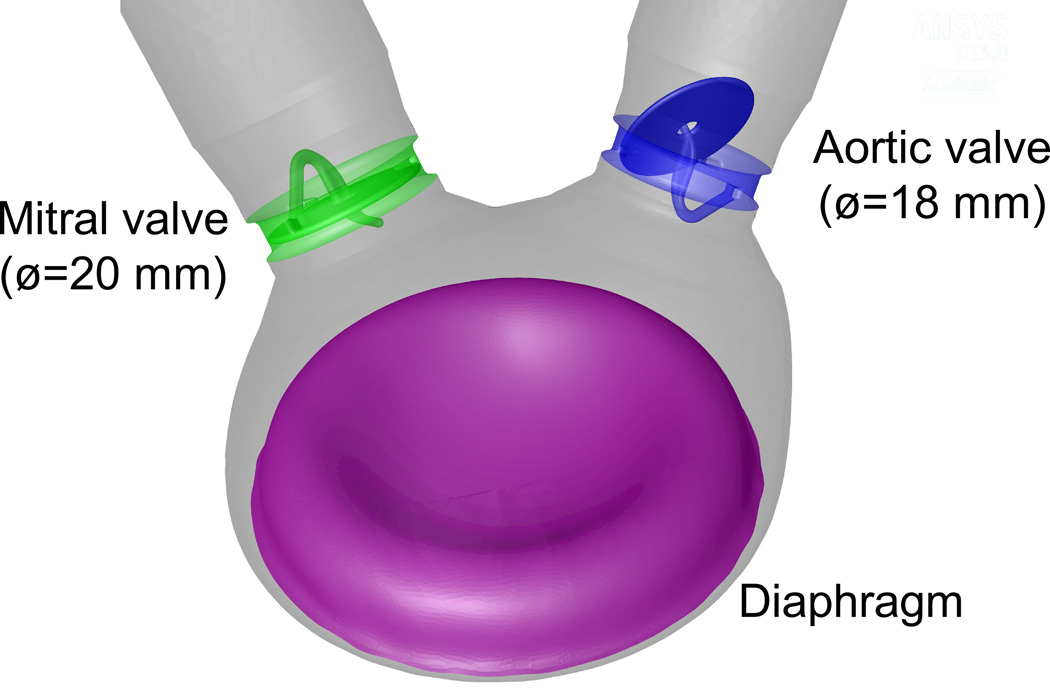
The present models focus on the flow in the left ventricular chamber of TAHs. The geometry of 50 cc TAH was reconstructed from the original TAH design (provided by the manufacturer) with Medtronic Hall mechanical valves in the mitral and aortic positions. The valves were oriented with 55° between them based on previous optimization we have performed for reduced thrombogenicity [4]. Larger and smaller models, with length scaling of 1.1 and 0.91, or maximum stroke volumes of 70 and 35 cc, respectively, are also modeled for comparison of the thrombogenic potential of platelets by flow induced stresses. These dimensions were chosen to comply with available valve sizes with nominal diameters between 16 to 22 mm. The fluid domain included the geometry of the left ventricle chamber with extended straight tubes that were connected to the two valves. Tetrahedral mesh with varying number of cells was generated for the flow domain. The number of cells varies according to the remeshing algorithm (ranging between 5 to 8 million). The mesh density was chosen based on mesh independence studies for stationary mesh because the remeshing is part of the solution itself that inevitably alter the results [27]. The mesh includes boundary layer cells in the vicinity of the diaphragm and mesh refinement near the valves. Varying time step of 5·10−5s to 1·10−3 s guaranteed convergence under all simulation conditions.

Since the 50 cc and the 35 cc TAHs are still in the design phase, there is a lack of sufficient data about the operating conditions of these devices. Hence, the models of the systolic phase only were used to compare the three device designs. During the systolic phase the valvular motions are relatively limited, thus, the mitral and aortic valves were positioned in their fully closed and fully open configurations, respectively (Fig. 1). In the more advanced model of the full cardiac cycle, the motions of the disks in the Medtronic Hall valves were also calculated utilizing user defined functions (UDFs). The coupling of the rigid body motions and the flow solution is based on the axial velocity of the disk’s center of mass. The center of mass’ axial velocity is assumed to be equal to the average velocity of the surrounding flow. The path of the center of mass and the proper rotation angle for every position on this path are based on initial “dry” finite elements analysis of the valve with constant loading. In this calculation, a small gap of 0.35 mm was kept between the contact surfaces of the disk, hinges and shaft to prevent full contact in the CFD code. This pre-defined calculated path was used to define the lateral and angular velocities at every position. The motion of all the nodes on the outer surface of the disks was calculated based on rigid body motion relative to the center of mass. Since this model focuses on hemodynamics rather than the structural mechanics, the disk’s rotation around the shaft was neglected. The motion of the fluid mesh is calculated by diffusion and remeshing algorithms.

Fig. 1.

Fig. 1

Open in a new tab

Schematic description of the 50 cc TAH with the initial configuration of the diaphragm and the valves

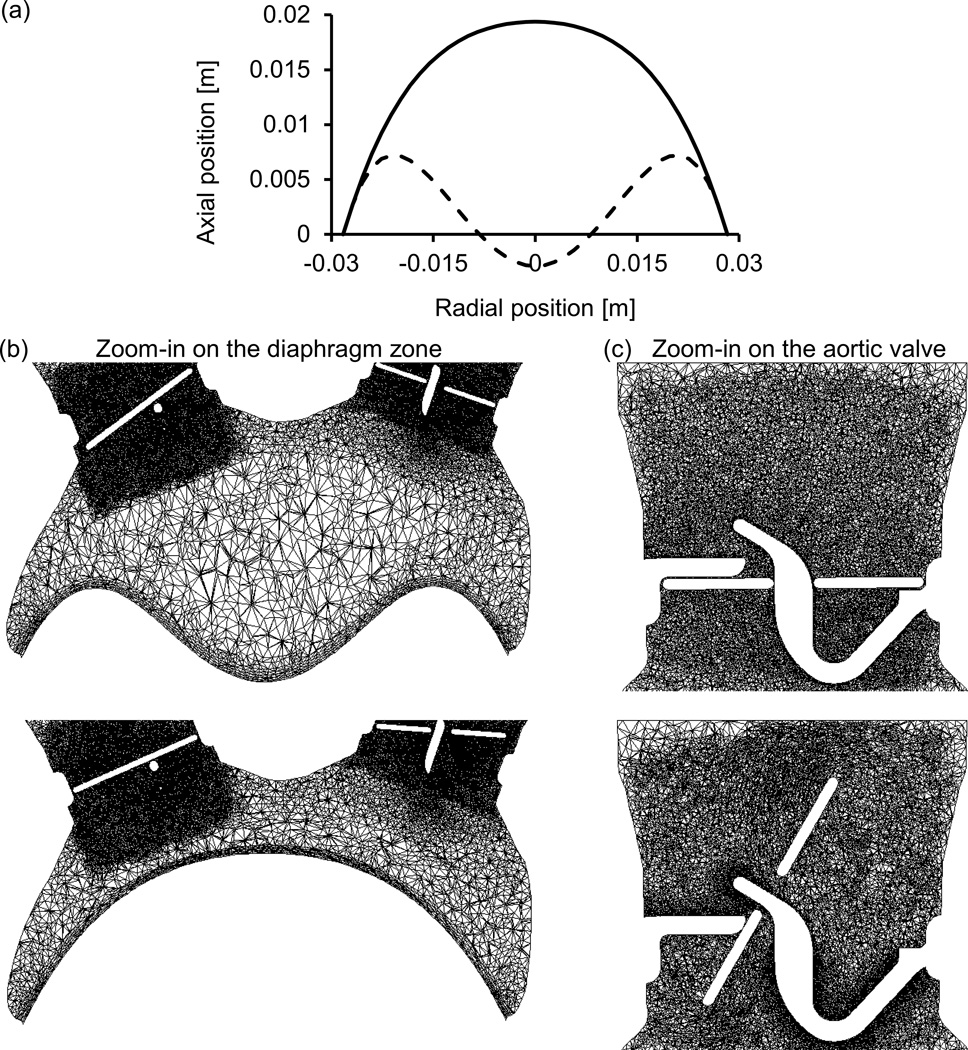
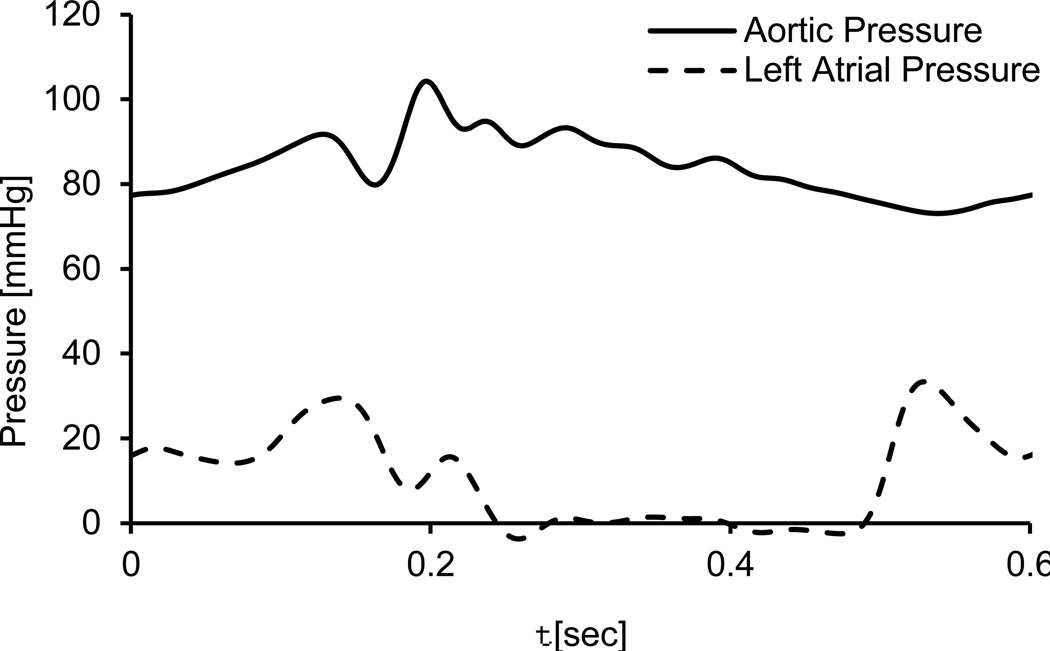
The position of the diaphragm at each time step is represented by radial biquadratic function. The systolic position of the diaphragm was based on the design drawings while the diastolic position was calculated by a contact with a pushing ball, using the finite element ANSYS Mechanical 15 (ANSYS Inc., Canonsburg, PA). The polynomial coefficients were calculated for these systolic and diastolic extremities, as shown in Fig. 2a. The motion of the diaphragm is calculated by assuming the polynomial coefficients are varying between these two extremities and that the temporal function has a sinusoidal form. This motion of the diaphragm is implemented by UDFs, and similar to the valve motions, the flow mesh in the diaphragm’s region can be remeshed. The frequency of the sinusoidal function is based on the heart rate of each device, namely 120, 140 and 164 bpm for the 70, 50 and 35 cc TAHs, respectively, in the systolic models. A frequency of 100 bpm is defined in the more advanced -of-concept FSI model, based on the experimental setup. Although these predefined sinusoidal waveforms do not fully replicate the physiologic flow conditions, they were chosen as they correspond to the TAH measured pressure waveforms, thus they can be used to demonstrate the calculation of the valves’ motion. Representative cross sections of the mesh in the regions of the diaphragm and the aortic valve, at different instances during the cycle, are presented in Figures .2b and .2c. In the simplified systolic models, the BCs are defined based on the pressure gradient relative to the aorta and the fact that the mitral valve is closed. Therefore, the outlet of the tube in the aortic side is defined as a zero pressure, and the closed mitral valve is represented with a closed tube. In the more advanced FSI model the pressure BCs at these two outlets are based on averaged and smoothed experimental data (Fig. 3). These measurements were taken using Millar SPR-524 catheters (Millar Instruments, Inc., Houston TX) from a 70 cc TAH that was connected to a Donovan Mock Circulatory System [28] (SynCardia Systems, Inc., Tucson, AZ). In order to stabilize the effects of the initial conditions, more than two cardiac cycles were simulated and only the results of the last cycle were analyzed.

Fig. 2.

Fig. 2

Open in a new tab

(a) The radial position of the diaphragm during peak systole (continuous line) and diastole (dashed line), and (b–c) representative cross sections of the dynamic mesh at different instances of the cardiac cycle. Zoom-in on the diaphragm region (b) and zoom-in on the symmetry section of the aortic valve (c)

Fig. 3.

Fig. 3

Open in a new tab

The pressure boundary conditions of the advanced FSI model as function of time

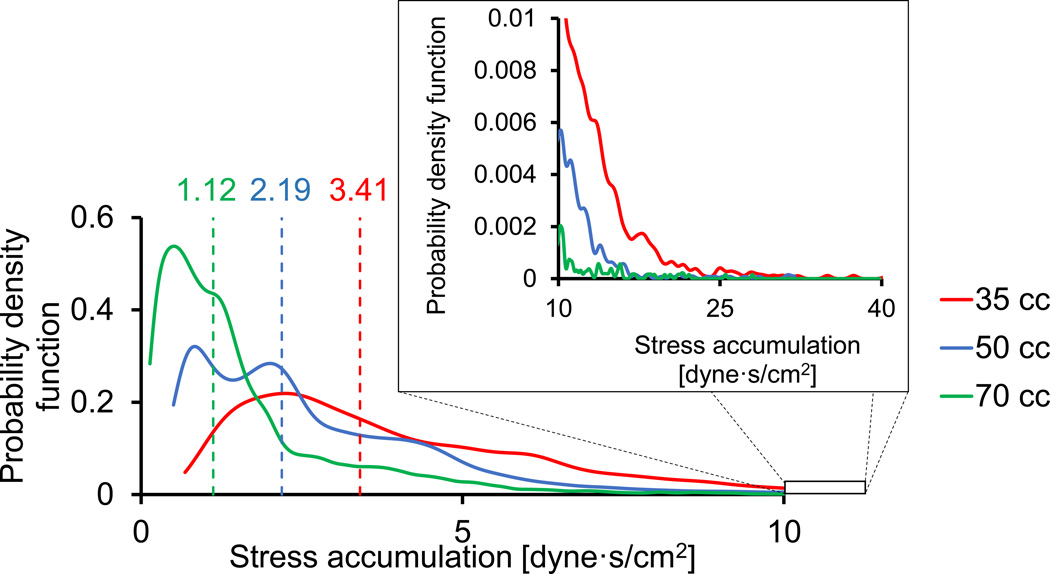
Platelet trajectories are calculated by employing a multiphase model with particle injection. Approximately 20 thousand spherical particles, with constant diameter of 3 µm and the density of the surrounding fluid, are released from a surface within the chamber. The stress history of these platelet particles are collected and rendered to calculate the SAs for each platelet trajectory. The SA is defined herein as the linear product of the stress magnitude and the exposure time [12]. In order to efficiently represent the SA of thousands of trajectories, the Probability Density Function (PDF) method is employed to statistically represent the SA distribution, or the thrombogenic footprint of the device [12]. Briefly, the PDF is the statistical distribution of all the SA values reached by each individual platelet along its corresponding flow trajectory through the device. The three TAHs are compared by the median values of SA and their distribution.

The model is solved by ANSYS Fluent 15 (ANSYS Inc., Canonsburg, PA) assuming the blood is Newtonian [23] and isothermal at temperature of 37°C. The flow is assumed laminar in the systolic flow models [29]. In the more advanced FSI model turbulence is taken into account by employing a shear stress transport (SST) k−ω model with low Reynolds number correction. This turbulence model was chosen due to its ability to resolve transitional characteristics of flows in circulatory devices, coupled with its ability to accurately predict pressure and velocity fields in these devices [30]. To improve the convergence of the dynamic mesh model, the blood is modeled as a slightly compressible liquid with a bulk modulus of 2.7·109 Pa [27]. A finite volume method was employed for solving the unsteady 3-D Navier-Stokes and mass conservation equations using Arbitrary Lagrangian Eulerian (ALE) approach for the dynamic mesh. The implicit flow solver uses second order spatial scheme and temporal discretization.

Results

In this section, the results of the three TAH size systolic models are compared and results of the advanced FSI model are presented for the 70 cc TAH. First, detailed results of the systolic 50 cc model are described, including the flow velocity field and the particles trajectories. Then, the PDF distributions of the three systolic models are compared in terms of the effect of the TAH sizing on its corresponding thrombogenic potential. Lastly, results of the advanced FSI model of the full cardiac cycle with the valves free to move are introduced.

Base case of the systolic model: SynCardia 50 cc TAH

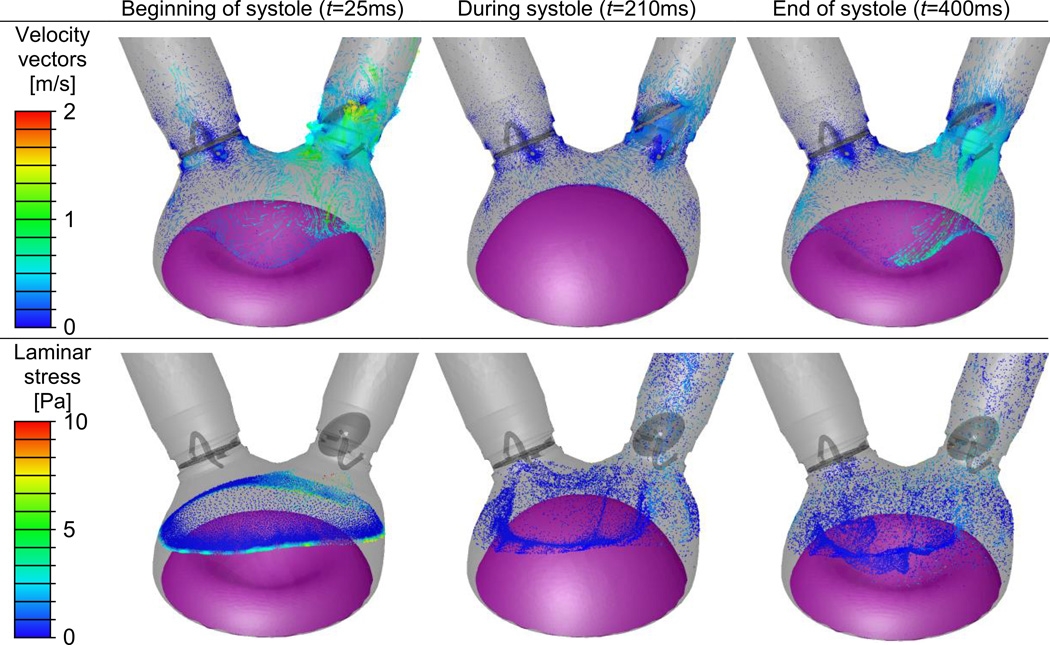
The first row of Fig. 4 shows the velocity vectors at three different instances in the 50 cc TAH. At the beginning of the systolic phase (t=25 ms), a strong flow through the aortic valve is depicted. This strong aortic flow, with maximum velocity of 1.8 m/s inside the center hole of the disk, opens the aortic valve after diastole. A regurgitant flow through the mitral valve is depicted with velocity magnitude of 0.6 m/s. This regurgitant flow was stronger earlier in the cardiac cycle when it reached velocity of 1.4 m/s. Vortices are found on the chamber side of the mitral valve at the initial systolic phase (t=25 ms). Later at systole, when the diaphragm reaches its fully inflated position (t=210 ms), the velocity of the flow through the aortic valve decreased to 0.5 m/s, following the diaphragm deceleration before starting the reverse motion. At the end of systole (t=400 ms), the strong backflow in the aortic valve should close this valve before reaching the diastole (the valves were assumed stationary at these systole only simulations). Dispersion patterns of platelets are depicted at the three instances in the second row of Fig. 4. The particles are colored by the instantaneous local laminar stress magnitude that is induced by the surrounding flow. The location of the particle releasing surface can be seen at the beginning of the systole (t=25 ms), when particle movement is still relatively small. As expected, the locations with the highest stress magnitudes are mostly near the aortic valve and the moving diaphragm.

Fig. 4.

Fig. 4

Open in a new tab

The simplified 50 cc TAH model at three instances during the systole. Velocity vectors on representative cross sections and particles location with their local laminar stress magnitudes are shown in the first and second rows, respectively

Comparison with 70 and 35 cc devices

The flow fields of the three TAH models were compared during peak systole just before the deceleration when the flow velocities and the ensuing shear stresses are the highest (at a time point of 30% of the cardiac cycle). At this time instant, the maximum velocity magnitudes increase with the decrease of the TAH dimensions (1.24, 1.16 and 0.98 m/s for the 35, 50 and 70 cc TAHs, respectively). The SA distribution of the three models are represented by their PDFs in Fig. 5. As might be expected, there is an increasing probability that platelets in the smaller devices will be subjected to higher SA values. This is apparent from the median SAs of 3.41, 2.19 and 1.12 dyne·s/cm2, for the 35, 50 and 70 cc TAHs, respectively (marked as vertical dashed lines in Fig. 5). The probability for SA of more than 10 dyne·s/cm2 is lower than 1% for all the three models. This probability may be considered negligible, with the SA values well within the safety range, i.e. well below the Hellums criterion of 35 dyne·s/cm2 threshold for platelet activation14, though the trend of a higher probability for elevated stresses in smaller TAHs is clear.

Fig. 5.

Fig. 5

Open in a new tab

Probability Density Function (PDF) of the stress accumulation of the three TAH sizes (their 'thrombogenic footprint'). The vertical dashed lines mark the median values

Advanced FSI model of the 70 cc TAH

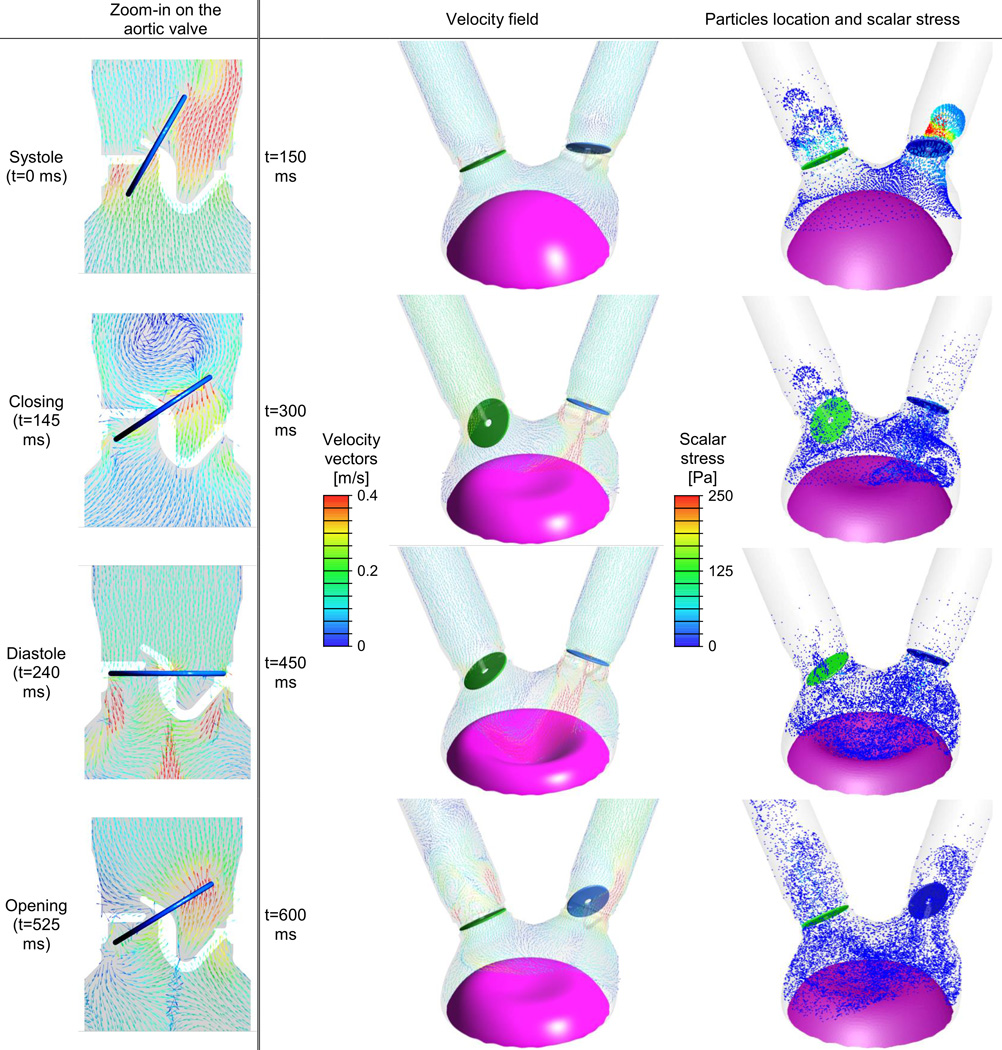
In this FSI model the motion of the two valves is calculated based on their interaction with the flow field. The left column of Fig. 6 compares the flow field on the symmetry plane of the aortic valve at four instances. The gray background marks the fluid domain, thereby showing the location of the struts. During systole (t=0 ms in Fig. 6), most of the blood flows through the larger opening on the right. The flow direction at this time is controlled mainly by the opening angle of the valve's leaflet. It should be noticed that although the velocity magnitudes in this more advanced and extensive model are relatively small (as mentioned before), the flow through the valve at this stage reaches a velocity of 0.5 m/s. The color scale of the velocity in Fig. 6 was chosen to emphasize the locations of high and low velocity magnitudes. The valve is stationary at its fully opened position for approximately one third of the cycle (191 ms), presenting an obstruction to the flow (with no-slip zero velocity on its surface). During the closing and opening phases (t=145 and 525 ms) however, the disc moves with the same velocity as the flow. In this model, the opening and closing of both valves, takes approximately 35 ms. At t=145 ms, although the aortic valve has already completed half of its excursion toward complete closure, the vortex that alters the direction of the flow is still visible at the top of the figure. Since this vortex is shown during the change in the flow direction, the velocity in its center is almost zero. During diastole there is a regurgitant flow through the central hole of the disc and through the gap between the disc and the base ring. As a result of the much smaller opening area, the flow reached a velocity magnitude of more than 1.5 m/s. During the opening (t=525 ms), after the flow changed its direction once again, most of the flow pushes the disc and is not directed mostly towards the openings (as found during the systole only few milliseconds afterwards). Obviously similar patterns can also be found in the region of the mitral valve. However, the velocity magnitudes in this region are smaller, with velocities of 0.44 and 0.49 m/s during diastole and regurgitation through the closed valve, respectively.

Fig. 6.

Fig. 6

Open in a new tab

The 70 cc SynCardia TAH FSI model at four instances during the full cardiac cycle. Velocity vectors on two representative cross sections and platelet dispersion patterns with their local scalar (laminar and turbulent) stress magnitudes are shown in the first and second columns, respectively (Animation appears in the online version of this article)

Fig. 6 compares the velocity vectors and platelet particle locations at four different instances during the cardiac cycle. The first row (t=150 ms) shows the closing of the aortic valve at the end of the systolic phase while the mitral valve is completely closed. At this instance there is regurgitant flow through the mitral valve while the flow from the aorta closes the aortic valve. The highest scalar stress, that include both laminar and turbulent stresses, are found near the aortic valve at this instance. These flow stresses are applied on the platelet particles that flowed through the valve during systole and in this instance are flowing back in the ventricle direction. Later, during the diastolic phase, the diaphragm is moving in the direction of the air chamber (t=300 ms) until it reaches its extreme position and starts to move in the opposite direction (t=450 ms). During these times, the ventricle is filed through the open mitral valve and there is a relatively strong regurgitant flow through the aortic valve, as discussed above. The highest stress levels are found in these regurgitation sites, in the central jet and in the gap between the disc and the ring. During systole (t=600 ms), blood is ejected through the aortic valve but there is also regurgitation through the closed mitral valve. Even though there is a strong flow through the open aortic valve and the regurgitation has a slightly smaller velocity magnitude, the highest scalar stress levels in this instant are still found in the regurgitation regions. At this time the particles are dispersed throughout the ventricle and the tubes, with relatively large amount of particles in the mitral tube that have arrived there with the regurgitant flow.

Discussion

This study presents numerical models of SynCardia TAHs, including three models of the systolic phase in TAHs of differing sizes and a more advanced FSI model of the 70 cc TAH full cardiac cycle. All of these models include, for the first time, motion of the diaphragm and a multiphase model of platelet particle transport. In the systolic models the valves were fixed in their systolic fully open (aortic) and fully closed (mitral) positions, with predefined BCs, as there is no available data on the physical pressures in the scaled-down devices. These models were used for comparing their thrombogenic potential. This is achieved by computing the SA of large populations of platelets along their corresponding flow trajectories, and plotting the statistical distribution of these SAs (the PDF) for each of the three TAH sizes. The PDF represents the 'thrombogenic footprint' of the device, and is an effective means of comparing the effects of the sizing on its thrombogenic potential. For this comparative study, the distributions were calculated by applying identical conditions in the three devices rather than estimating the interindividual variability. The more advanced FSI model of 70 cc TAH demonstrated the ability to model the valves motion, to impose boundary conditions that are based on actual measured data, and to additionally calculate the applied turbulent stresses acting on the platelet under these conditions. This model also introduces for the first time several new capabilities, including TAH simulation with FSI modeling of valves motion and the first 3-D FSI models of Medtronic Hall valves moving with all degrees of freedom.

While this is an FSI simulation, the lack of accurate description of the diaphragm motion prevented the flow from reaching physiologic flow rates. We are currently working on improving the pre-defined motion applied in the current simulation by gathering more accurate data on the diaphragm motion from dedicated experiments. If this data, i.e. measurement of both the pressure and the non-uniform diaphragm motion, will be available for the smaller TAHs, it will facilitate comparing the thrombogenic potential of the three devices during the entire cardiac cycle. Moreover, it will enable validation of these future models with other measured data, such as flow rates. Other possible improvements of the numerical model might include more advanced turbulence models, better spatial or temporal discretization, and FSI model of the diaphragm motion based on the pneumatic pressure that drives it.

The results of the current models depict several complex flow dynamics and flow patterns that were present both in the base case of the systolic models and in the case of the full cardiac cycle FSI model. Of particular interest is the regurgitant flow through the closed valves. Jets of blood flow through the central hole of the closed valves were present in both types of models. In the systolic 50 cc model, at the beginning of the systole (t=10 ms) there is a regurgitant jet with a velocity of 1.4 m/s through the mitral disc. This strong jet creates a vortex ring that decays rather quickly and can hardly be seen at t=25 ms (Fig. 4). Although the duration of the mitral regurgitation is very short, a low velocity flow field is found in this model leeward of the mitral valve until the end of the systole (t=400 ms in Fig. 4). Similar jets through the closed aortic and mitral valves were also found in the FSI model of the 70 cc TAH. The aortic jet was directed towards the moving diaphragm, and therefore it is hard to tell whether the complex flow field in the ventricle is a result of the diaphragm motion or the vortex ring. In this model, the leakage around the discs of the closed valves can also be clearly seen (t=240 ms for the aortic valve, as well as t=300 and 450 ms in Fig. 6). It is interesting to mention that leakage flow patterns are found even though the sizes of the discs was not altered, unlike in previous simulations that reduced the discs sizes, and therefore increased the gaps width [15,31]. This strong leakage may also be an artifact of the non-physiologic combination of the boundary conditions and diaphragm motion. There are several numerical methods to prevent this leakage, however as this paper focuses on the thrombogenic potential, and these sites are regions of elevated flow stresses, such simplification cannot be applied here. Another interesting flow pattern are the vortices on the chamber side of the closed mitral valve, that can clearly be seen in the systolic models (e.g., 25 ms in Fig. 4). These vortices are a result of the back step effect of the smaller tube diameter near the closed valve.

The calculation of the particle trajectories predicts the platelets exposure to flow stresses, taking into account the combined effect of the dynamic stress levels, platelet experiences, and the duration they are exposed to it, which is the correct way to estimate their activation potential. In the systolic models, as well as in the advanced FSI model, the highest stresses are found in the vicinity of the valves, especially within the regurgitant flow through the closed valves. The additional turbulent stresses in the more advanced model increased the stress levels relative to the systolic cases (right column of Fig. 6 and bottom row of Fig. 4, respectively). In the systolic model, almost none of the particles seems to flow through the closed mitral valve (t=400 ms in Fig. 4). This fact might indicate that although the regurgitating flow in this case was quite fast locally, its average flow rate is almost negligible. However, in the FSI of the full cardiac cycle simulation there are quite a few particles that left the ventricle and can still be found on the atrial or aortic sides of the mitral and aortic valves, respectively (Fig. 6). The main reason for this appears to be the regurgitant flow during the valves’ closure, that has shorter duration but it is much stronger than the leakage around the disc and through the central hole of the closed valves. In both models, the back and forth motion of the diaphragm disperse the particles in the chamber almost evenly until the end of the simulation.

The thrombogenic potential of the three types of TAH were compared based on their SA distribution. As mentioned before, these distributions were calculated in the systolic models only for comparative purposes, where similar assumptions were applied. Although the SA distribution can easily be calculated from the scalar flow stresses that the platelets in the advanced FSI model were subjected to, this information is not presented here as it is not comparable to the other models. In the systolic models, an increased probability for platelets in the smaller devices to be subjected to higher SA levels was found. This is attributed to both the reduced size and the higher pumping frequencies, or heart rates, that accelerate the blood flow through them. Although these findings might indicate that platelets in smaller TAHs are more prone to activation, it should be noted that the bulk of the PDF distributions of all TAH sizes are overlapping. Therefore, it is reasonable to assume that their thrombogenic potential is close. Utilizing our device thrombogenicity emulation (DTE) methodology, that we have previously employed for optimizing the thromboresistance of MCS devices, in the future minor design changes may mitigate this potential increase in stress activation [6]. Necessarily, the ultimate thrombogenicity determination may require clinical studies in human subjects (the FDA exempts SynCardia from animal experiments in TAHs, under the HUD designation), though from the above numerical simulations the thrombogenicity of scaled down devices appears safe and well below the stress threshold associated with significant platelet activation. These clinical studies could also investigate the effect of antiplatelet and anticoagulant medication or the variability of platelet reactivity.

In conclusion, numerical models of the TAH of three sizes with deforming diaphragms and particle injection, have been developed. These models were utilized for comparing the effect of scaling down the TAHs size on the thrombogenic potential, as well as to show a proof-of-concept for advanced full cardiac cycle model. The resulting flow patterns captured the mitral and aortic regurgitation, the opening and closing of the valve as a result of the blood flow, and the ensuing intricate flow dynamics generated as a result of the interaction of the valve dynamics and the flow field. There is a mild trend of increased probability that platelets in smaller devices will be exposed to elevated stresses as a result of the combined effect of higher pumping frequency and the smaller dimensions that may translate into a mild increase in platelet activation. The latter nevertheless appear to be within the safety margin of acceptable thrombogenicity levels, indicating that scaled down versions of the TAH are clinically viable for smaller and pediatric patients.

Supplementary Material

12265_2014_9596_MOESM1_ESM
Download video file (188.6MB, mpg)

Acknowledgment

We thank Matthew Pollack from Boston University for his help in reconstructing the geometry. We also thank Doug Nutter and Richard Smith for information on TAH engineering drawings and operating conditions. The software was provided by an ANSYS Academic Partnership with Stony Brook University.

Sources of Funding

This study was funded by grants from the National Institute of Health: National Institute of Biomedical Imaging and Bioengineering Quantum Award: Implementation Phase II - U01 EB012487-0 (D.B.).

Footnotes

Disclosures

Dr. Slepian declare participation in review activities for SynCardia Inc. All the other authors declare no conflict of interest. No human or animal studies were carried out by the authors for this article.

References

  • 1.Copeland JG, Smith RG, Arabia FA, Nolan PE, Sethi GK, Tsau PH, McClellan D, Slepian MJ. Cardiac replacement with a total artificial heart as a bridge to transplantation. The New England journal of medicine. 2004;351(9):859–867. doi: 10.1056/NEJMoa040186. [DOI] [PubMed] [Google Scholar]
  • 2.Slepian MJ, Smith RG, Copeland JC. The SynCardia CardioWest Total Artificial Heart. In: Baughman KL, Baumgartner WA, editors. Treatment of Advanced Heart Disease. Vol. 56. New York, NY: Fundamental and Clinical Cardiology Series. Taylor & Francis Group; 2006. pp. 473–490. [Google Scholar]
  • 3.Frazier OH, Cohn WE. Continuous-flow total heart replacement device implanted in a 55-year-old man with end-stage heart failure and severe amyloidosis. Texas Heart Institute journal / from the Texas Heart Institute of St Luke's Episcopal Hospital, Texas Children's Hospital. 2012;39(4):542–546. [PMC free article] [PubMed] [Google Scholar]
  • 4.Slepian MJ, Alemu Y, Girdhar G, Soares JS, Smith RG, Einav S, Bluestein D. The Syncardia total artificial heart: in vivo, in vitro, and computational modeling studies. J Biomech. 2013;46(2):266–275. doi: 10.1016/j.jbiomech.2012.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Platis A, Larson DF. CardioWest temporary total artificial heart. Perfusion. 2009;24(5):341–346. doi: 10.1177/0267659109351330. [DOI] [PubMed] [Google Scholar]
  • 6.Girdhar G, Xenos M, Alemu Y, Chiu WC, Lynch BE, Jesty J, Einav S, Slepian MJ, Bluestein D. Device thrombogenicity emulation: a novel method for optimizing mechanical circulatory support device thromboresistance. PLoS One. 2012;7(3):e32463. doi: 10.1371/journal.pone.0032463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Xenos M, Girdhar G, Alemu Y, Jesty J, Slepian M, Einav S, Bluestein D. Device Thrombogenicity Emulator (DTE) - design optimization methodology for cardiovascular devices: a study in two bileaflet MHV designs. Journal of biomechanics. 2010;43(12):2400–2409. doi: 10.1016/j.jbiomech.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Kroll MH, Hellums JD, McIntire LV, Schafer AI, Moake JL. Platelets and shear stress. Blood. 1996;88(5):1525–1541. [PubMed] [Google Scholar]
  • 9.Leshnower BG, Smith RG, Ohara ML, Woo J, Pochettino A, Morris RJ, Gardner TJ, Slepian MJ, Copeland JG, Acker MA. Is the total artificial heart superior to BIVAD therapy as a method of bridging patients to heart transplantation?. Paper presented at the 43rd Annual meeting of the Society of Thoracic Surgeons; January 29–31; San Diego, CA. 2007. [Google Scholar]
  • 10.Copeland JG, Copeland H, Gustafson M, Mineburg N, Covington D, Smith RG, Friedman M. Experience with more than 100 total artificial heart implants. The Journal of thoracic and cardiovascular surgery. 2012;143(3):727–734. doi: 10.1016/j.jtcvs.2011.12.002. [DOI] [PubMed] [Google Scholar]
  • 11.Richards KE, Deserranno D, Donal E, Greenberg NL, Thomas JD, Garcia MJ. Influence of structural geometry on the severity of bicuspid aortic stenosis. American journal of physiology Heart and circulatory physiology. 2004;287(3):H1410–H1416. doi: 10.1152/ajpheart.00264.2003. [DOI] [PubMed] [Google Scholar]
  • 12.Alemu Y, Bluestein D. Flow-induced platelet activation and damage accumulation in a mechanical heart valve: numerical studies. Artificial organs. 2007;31(9):677–688. doi: 10.1111/j.1525-1594.2007.00446.x. [DOI] [PubMed] [Google Scholar]
  • 13.Borazjani I, Ge L, Sotiropoulos F. High-resolution fluid-structure interaction simulations of flow through a bi-leaflet mechanical heart valve in an anatomic aorta. Ann Biomed Eng. 2010;38(2):326–344. doi: 10.1007/s10439-009-9807-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Hong T, Kim CN. A Numerical Analysis of the Blood Flow around the Bileaflet Mechanical Heart Valves with Different Rotational Implantation Angles. J Hydrodyn. 2011;23(5):607–614. [Google Scholar]
  • 15.Dumont K, Vierendeels J, Kaminsky R, van Nooten G, Verdonck P, Bluestein D. Comparison of the hemodynamic and thrombogenic performance of two bileaflet mechanical heart valves using a CFD/FSI model. Journal of biomechanical engineering. 2007;129(4):558–565. doi: 10.1115/1.2746378. [DOI] [PubMed] [Google Scholar]
  • 16.Hose DR, Narracott AJ, Penrose JM, Baguley D, Jones IP, Lawford PV. Fundamental mechanics of aortic heart valve closure. Journal of biomechanics. 2006;39(5):958–967. doi: 10.1016/j.jbiomech.2005.01.029. [DOI] [PubMed] [Google Scholar]
  • 17.Dasi LP, Ge L, Simon HA, Sotiropoulos F, Yoganathan AP. Vorticity dynamics of a bileaflet mechanical heart valve in an axisymmetric aorta. Phys Fluids. 2007;19(6):067105. [Google Scholar]
  • 18.Chiu WC, Slepian MJ, Bluestein D. Thrombus formation patterns in the HeartMate II ventricular assist device: clinical observations can be predicted by numerical simulations. ASAIO journal. 2014;60(2):237–240. doi: 10.1097/MAT.0000000000000034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Zhang J, Zhang P, Fraser KH, Griffith BP, Wu ZJ. Comparison and experimental validation of fluid dynamic numerical models for a clinical ventricular assist device. Artificial organs. 2013;37(4):380–389. doi: 10.1111/j.1525-1594.2012.01576.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Sonntag SJ, Kaufmann TAS, Busen MR, Laumen M, Linde T, Schmitz-Rode T, Steinseifer U. Simulation of a pulsatile total artificial heart: Development of a partitioned Fluid Structure Interaction model. J Fluid Struct. 2013;38:187–204. [Google Scholar]
  • 21.Penrose JMT, Staples CJ. Implicit fluid-structure coupling for simulation of cardiovascular problems. Int J Numer Meth Fl. 2002;40(3–4):467–478. [Google Scholar]
  • 22.Avrahami I, Rosenfeld M, Raz S, Einav S. Numerical model of flow in a sac-type ventricular assist device. Artificial organs. 2006;30(7):529–538. doi: 10.1111/j.1525-1594.2006.00255.x. [DOI] [PubMed] [Google Scholar]
  • 23.Medvitz RB, Reddy V, Deutsch S, Manning KB, Paterson EG. Validation of a CFD methodology for positive displacement LVAD analysis using PIV data. Journal of biomechanical engineering. 2009;131(11):111009. doi: 10.1115/1.4000116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Topper SR, Navitsky MA, Medvitz RB, Paterson EG, Siedlecki CA, Slattery MJ, Deutsch S, Rosenberg G, Manning KB. The Use of Fluid Mechanics to Predict Regions of Microscopic Thrombus Formation in Pulsatile VADs. Cardiovasc Eng Technol. 2014;5(1):54–69. doi: 10.1007/s13239-014-0174-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Govindarajan V, Udaykumar HS, Herbertson LH, Deutsch S, Manning KB, Chandran KB. Two-Dimensional FSI Simulation of Closing Dynamics of a Tilting Disk Mechanical Heart Valve. J Med Devices. 2010;4(1):011001–011001. doi: 10.1115/1.4000876. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Pelliccioni O, Cerrolaza M, Herrera M. Lattice Boltzmann dynamic simulation of a mechanical heart valve device. Math Comput Simulat. 2007;75(1–2):1–14. [Google Scholar]
  • 27.Marom G. Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves. Arch Computat Methods Eng. 2014:1–26. [Google Scholar]
  • 28.Donovan FM. Design of a hydraulic analog of the circulatory system for evaluating artificial hearts. Biomaterials, medical devices, and artificial organs. 1975;3(4):439–449. doi: 10.3109/10731197509118635. [DOI] [PubMed] [Google Scholar]
  • 29.Yoganathan AP, Chandran KB, Sotiropoulos F. Flow in prosthetic heart valves: state-of-the-art and future directions. Ann Biomed Eng. 2005;33(12):1689–1694. doi: 10.1007/s10439-005-8759-z. [DOI] [PubMed] [Google Scholar]
  • 30.Fraser KH, Zhang T, Taskin ME, Griffith BP, Wu ZJ. A quantitative comparison of mechanical blood damage parameters in rotary ventricular assist devices: shear stress, exposure time and hemolysis index. Journal of biomechanical engineering. 2012;134(8):081002. doi: 10.1115/1.4007092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Nobili M, Morbiducci U, Ponzini R, Gaudio CD, Balducci A, Grigioni M, Montevecchi FM, Redaelli A. Numerical simulation of the dynamics of a bileaflet prosthetic heart valve using a fluid–structure interaction approach. J Biomech. 2008;41:2539–2550. doi: 10.1016/j.jbiomech.2008.05.004. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

12265_2014_9596_MOESM1_ESM
Download video file (188.6MB, mpg)

RESOURCES