A 3D approximate maximum likelihood solver for localization of fish implanted with acoustic transmitters

Abstract

Better understanding of fish behavior is vital for recovery of many endangered species including salmon. The Juvenile Salmon Acoustic Telemetry System (JSATS) was developed to observe the out-migratory behavior of juvenile salmonids tagged by surgical implantation of acoustic micro-transmitters and to estimate the survival when passing through dams on the Snake and Columbia Rivers. A robust three-dimensional solver was needed to accurately and efficiently estimate the time sequence of locations of fish tagged with JSATS acoustic transmitters, to describe in sufficient detail the information needed to assess the function of dam-passage design alternatives. An approximate maximum likelihood solver was developed using measurements of time difference of arrival from all hydrophones in receiving arrays on which a transmission was detected. Field experiments demonstrated that the developed solver performed significantly better in tracking efficiency and accuracy than other solvers described in the literature.

Restoration of endangered salmonid species is the focus of considerable research and a primary focus for many fisheries scientists¹,²,³,⁴. Better understanding of the behavior of salmonids, particularly the out-migration of juveniles through impounded river systems, is critical to the design and operation of dam-passage facilities that optimize the survival of migrants⁵,⁶. Acoustic telemetry has been increasingly used over the last two decades to observe the behavior and assess the survival of fish populations⁷,⁸,⁹,¹⁰. Metrics such as time of arrival (TOA), time difference of arrival (TDOA), angle of arrival, and received signal strength are commonly used to estimate the location of fish bearing acoustic transmitters¹¹. From 2006 through the present¹²,¹³, the Juvenile Salmon Acoustic Telemetry System (JSATS) has been used to estimate the survival and observe the out-migration behavior of juvenile salmonids passing through eight large hydroelectric facilities operated by the U.S. Army Corps of Engineers (USACE) within the Federal Columbia River Power System en route to the Pacific Ocean¹⁴. JSATS consists of acoustic micro-transmitters; large, fixed-location, time-synchronized hydrophone arrays or autonomous receivers; and data management, processing and analysis software utilities¹⁴.

The time required for an acoustic signal to travel from a micro-transmitter to a hydrophone is usually not known, so the TDOAs between hydrophones in a receiving array are the measurements used to estimate a transmitter's location. For three-dimensional (3D) source location estimation, an array of at least four hydrophones and an estimate of the speed of sound between the source and the receiving hydrophones is required so that four unknown variables—a reference TOA and the three coordinates of the source location—can be solved deterministically using four quadratic (nonlinear) distance equations. These equations provide a fully determined (FD) system. When one component, such as depth, which can be estimated using a pressure sensor¹⁵, is encoded in the transmitters signal, the minimum number of hydrophones required to provide an FD system is reduced to three. When there are more hydrophones that receive a transmitter's signal than the minimum required to provide an FD system, the location estimation problem becomes an overdetermined (OD) system¹⁶.

Exact solvers¹⁷,¹⁸ using TOA estimates from four optimally selected hydrophones within a large receiving array were used to estimate the 3D positions of fish surgically implanted with JSATS acoustic micro-transmitters¹³. The efficiencies of the exact solvers could be over 90% because of the high accuracy of synchronized Global Positioning System (GPS)-based time-of-arrival estimates within the hydrophone array, the accuracy of hydrophone location surveys and estimates of sound speed, and improved performance of JSATS components. It is well known that estimates of a transmitter's location by exact solvers are sensitive to noise in the TOA/TDOA measurements, the accuracy of sound-speed and hydrophone-location estimates. Therefore, it is necessary to consider sound source localization as an optimization problem that requires error minimization.

Numerous algorithms have been developed for sound-source localization. These location estimation algorithms can be grouped into two categories¹⁹. These two categories are nonlinear methods, such as nonlinear least squares and maximum likelihood (ML) estimators, and linear methods, such as linear least squares (LLS) and weighted linear least squares, which translate the nonlinear equations into a linear system. The linear approaches are suboptimal location estimation techniques²⁰, which have low computational complexity and are easily applied. However, the accuracy of location estimates obtained using them may be poor, especially for LLS, when TOA or sound-speed measurement noise is large. To pursue an approach with high accuracy, the advantages and disadvantages of both linear and nonlinear methods need to be considered.

Foy²¹ expanded the nonlinear equations into Taylor series with an initial sound-source location guess, and then iteratively refined the location estimate. This method requires a good initial estimate of sound-source location to achieve acceptably accurate results and is computationally intensive. Chan and Ho²² proposed a two-stage maximum likelihood (TSML) method for use when TDOA estimation errors are small. In their solver, an intermediate variable was introduced to linearize nonlinear distance equations. A non-iterative and explicit solution was obtained by approximation of the ML estimator. The TSML method was shown to perform significantly better than a spherical interpolation method²³ and Taylor-series methods. Chan et al.²⁴ developed a two-dimensional (2D) closed-form algorithm, termed approximate maximum likelihood (AML), that is an approximate solution to the ML equations for solvers using TOA and TDOA estimates. This solver used LLS estimates to initialize location estimates, which significantly decreases solver computational complexity. Location estimation performance of AML solvers in the case of stationary sound sources can attain the Cramér-Rao lower bound (the lowest possible mean squared error among unbiased estimators) for certain 2D geometries and signal-to-noise ratios (SNRs), in contrast to results obtained for the same input data using TSML and other linear estimator solvers²⁵. Compared with other 3D localization algorithms, AML can achieve accurate location estimates given reasonable noise levels and provide a much better tradeoff between average location estimate errors and failure rates with an OD sensor system²⁶.

We extended the Chan et al. AML method²⁴ to a 3D solver to continuously track the movement of juvenile salmon bearing implanted acoustic micro-transmitters approaching and passing downstream through large main-stem Columbia and Snake River dams. The transmissions of implanted acoustic transmitters were received by large hydrophone arrays with GPS time-synchronized receivers positioned on the faces of the dams. Time sequences of transmitter position estimates obtained using our 3D AML solver were compared to results obtained using exact solvers. This paper presents step-by-step application of a 3D AML algorithm for sound-source localization using TDOA estimates. Field experiments were conducted in a Snake River dam forebay to assess the accuracy and efficiency of our 3D AML solver to provide sequences of location estimates for moving and stationary JSATS transmitters. The TDOA estimates needed as input for the solver were obtained with a large hydrophone array and receiver system typical of that used during projects to assess the success of dam passage by downstream migrating juvenile salmonids. Results from this new tracking solver are presented and the results compared to location estimates obtained using previously reported exact solvers.

Results

Study site

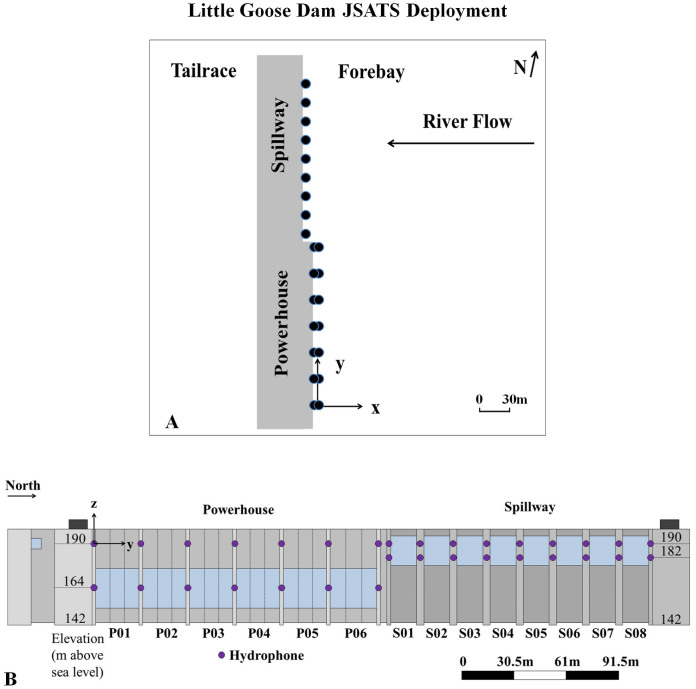
Little Goose Dam is a concrete hydroelectric gravity dam located on the Snake River in Columbia and Whitman counties in Washington State. It is part of the Federal Columbia River Power System that is operated by the USACE. The dam is located 14 km northeast of the town of Starbuck and 40 km north of Dayton. The dam consists of a powerhouse, a spillway, and a navigation lock, with adult (upstream migrant) fish ladders at either end of the dam. The dam's spillway has eight gates and is 156 m long (Figure 1a). The powerhouse is 200 m long and consists of six turbines. A temporary spillway weir was installed in 2009 at Spill Bay 1 to facilitate passage of juvenile salmonids. At each main pier nose along the dam, two hydrophones were installed at two elevations (Figure 1b); all hydrophones had the same functional specifications and geometric designs¹².

Figure 1. Deployment of Little Goose Dam JSATS hydrophones.

A) Plan view of JSATS hydrophones at Little Goose Dam on the Snake River. The black solid circles indicate the locations of dam-face hydrophones. B) Forebay view of locations of hydrophones deployed at two different elevations at each pier nose. The origin is set at the normal pool surface level near the south end of the powerhouse. The x direction is perpendicular to the dam face, while the y direction is parallel to the dam face.

The coordinates of the easting and northing system used to survey with hydrophones and to position dam structures were rotated clockwise to form a local dam-face sound-source tracking coordinate system (Figure 1). The tracking coordinate system x-axis is perpendicular to the dam and looks straight into the forebay; the y-axis runs along the dam face from south to north; and the z-axis is vertical, pointing upward from the bottom of the forebay to the water surface. The origin is set at normal pool surface elevation near the south end of the powerhouse.

Field experiments' design

The performance of various sound-source localization solvers was evaluated using equipment and protocols that permitted the location of moving and stationary acoustic transmitters to be known with high accuracy within a dam's forebay¹²,¹³. Four acoustic transmitters, referred to as tags, were suspended on monofilament fishing line at four depths below a remotely controlled boat. Tags 1 through 4 were located at depths of 2 m, 1.5 m, 1.0 m, and 0.5 m, respectively. The boat was equipped with a GPS receiver with an antenna located about 1 m above the water surface. The real-time kinematic-GPS system (Trimble GeoExplorer, Trimble Navigation Ltd., Sunnyvale, California) was used to provide benchmark measurements for comparison with the 3-D tracked locations. The GPS solution frequency was 1 Hz. The transmitters each had a unique pulse repetition interval (PRI) value. Tag 1, which was at a depth of 2 m, was operated at a 1 s PRI and was the source of the signals used for accuracy assessments¹³. The PRI of the other three tags is 2 s—one transmission every 2 seconds.

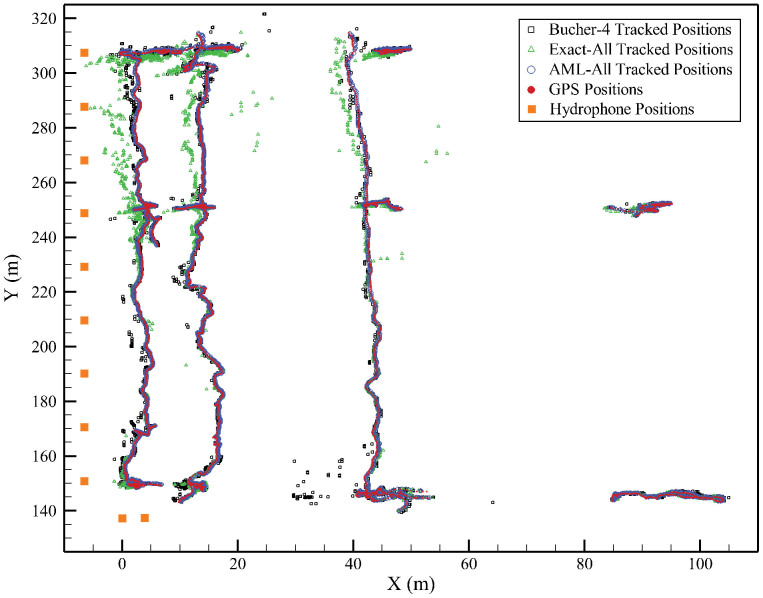
The data used to compare the tracking performance of the various solvers was acquired on March 26, 2012 prior to spillway operation season. The transmitters located below the remotely operated boat were moved in various transect patterns, similar to those observed for migrating juvenile fish, through a section of the dam's forebay in front of the dam's spillway. The area covered was large, extending from the face of the dam to a distance of 100 m upstream of the dam (Figure 2). In Figure 2, the red dots show the known location (GPS coordinates) of the remotely controlled vessel and acoustic transmitters. The GPS data was post-processed with estimated horizontal precision of 0.15 m and vertical precision of 0.17 m during the tests. Averaged PDOP value is 1.37 with a standard deviation of 0.17, while mean HDOP value is 0.73 during the testing. Water temperature, which was used to estimate sound speed, was measured as a function of time using a sensor located at the dam. Temperature stratification along the water column was not observed during the testing period. The root selection routine (RSR) for the 3D AML solver was bounded at the right side (upstream) of the dam-face hydrophones, eliminating solutions for transmitter location estimates downstream of the dam.

Figure 2. Comparison of GPS-measured positions and 3D-tracked positions of Tag 1 at Little Goose Dam spillway by Bucher-4, Exact-All and AML-All in all error analysis tests.

Dam-face hydrophones are displayed separately using orange solid squares.

The remotely operated boat was used to acquire both stationary position (SP) and moving transmitter data sets. The acquired data was used to evaluate the performance of the solvers (i.e., the error structure of transmitter location estimates) when a transmitter was stationary sufficiently long for several transmissions, or when moving when only one transmission was made at each of a sequence of locations along the trajectory of the boat. Three moving-boat tests were conducted as the boat was carried by spill flow in a south to north (y) direction at 10 m, 20 m and 50 m distances from the hydrophone array located on spillway piers. The remote boat moved at an active speed of 0.2–0.4 m/s, while the average flow velocity across the river was estimated to be smaller than 0.2 m/s during the tests. For SP tests, the boat was held as stationary as possible for at least 3 min to make sure that a sufficient number of transmissions would occur to provide adequate data sets for statistical analyses. Nine locations were initially selected, three spaced along the spill section of the dam at horizontal distances (x direction) of 10 m, 20 m and 50 m. Later, two SP tests were added at a distance of 100 m from the dam at two locations: the middle and south end of the dam's spillway.

Tested tracking solvers

The performance of the exact solvers of Bucher and Misra²⁷ and LLS¹⁸, and the developed AML solver in this study were evaluated using the stationary-position and moving-boat data sets. The solvers differ in their ability to use data from more than four hydrophones. Because of this difference, five different solution groups were computed. The Bucher solver only works with TDOAs from four hydrophones while the LLS and AML solvers work with overdetermined systems. The evaluated methods were:

1. Bucher-4: Bucher and Misra²⁷ + four hydrophones

2. Exact-4: LLS¹⁸ + four hydrophones

3. AML-4: AML²⁴ + four hydrophones

4. Exact-All: LLS¹⁸ + all possible hydrophones

5. AML-All: AML (proposed in this study) + all possible hydrophones

Above, “four hydrophones” means that, out of all hydrophones that detected a specific transmitter signal, the TDOA estimates from four hydrophones with optimum geometric configuration to estimate the 3D location of the transmitter were selected as input to the solvers. The four hydrophones were selected using developed criteria¹⁸,²⁸. This selection routine is not required by solvers with “all possible hydrophones”. For solvers that can use the TDOA estimates from all receiving hydrophones in the cable array that detect a transmitter signal, the test environment provides an OD system for 3D tracking.

Solver performance metrics

The following parameters were defined to evaluate the performance of the five solver-hydrophone combinations:

1. Transmitter location estimation efficiency

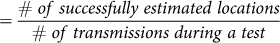
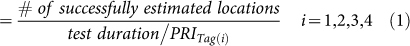
2. Transmitter location estimation errors

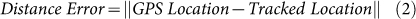
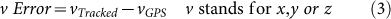
Transmitter location estimation errors are presented in four terms: distance error, x error, y error and z error. The distance error is the difference in distance between the transmitter location estimated from the GPS position coordinates from the remotely controlled boat and the transmitter location estimated using a solver. The v errors are calculated respectively in x, y, and z coordinates as differences between solver-tracked and GPS-measured values.

Another performance metric, solver efficiency, was defined as the number of successful 3D-tracked locations divided by the number of TOAs. When the detection rate is close to 100%, solver efficiency will be approximately the same as position location estimation efficiency, hereafter called “tracking efficiency.” Therefore, only tracking efficiency is used to report results in this study. For each transmission received by the hydrophone array, because of number of receiving hydrophones and measurement errors, solution with physical meaning is not guaranteed by the localization algorithm of a solver. Thus, the number of successfully estimated locations varies by estimator. Tracking efficiency can also be affected by the transmitter signals reflected (multipath) from the water surface that collide with direct path signals and prevent the receivers from detecting a transmitter signal. Lower efficiency may also be due to the uncontrolled directivity of the transmitters during the test that could have resulted in an unfavorable SNR for some transmissions that prevented their detections. Location estimation errors are the best metrics to evaluate the location estimation performance of solvers.

Comparison results of efficiency and accuracy

The x-y plane position estimates of transmitters obtained using the GPS measurements and different solver groups were compared (Figure 2), which included all transmitter location estimates used for solver performance analysis. The forebay area of interest was from y = 140 m to y = 310 m, which covered the extent of the hydrophone array at the spillway. Transmitter location estimates from AML-All were closer to GPS-based transmitter location estimates than those obtained using Bucher-4 and Exact-All. The observed differences between the performances of the solvers were more obvious toward the northern end of the spillway area. From theoretical analysis²⁸, the accuracy of the transmitter location estimates depends on the relative locations of receiving hydrophones and the sound source. The geometries of the locations of receiving hydrophones and transmitters were generally better in the southern portion of the spillway forebay area because in this area hydrophones located along the dam powerhouse that received a transmitter signal were included in the subset of hydrophones to be used for transmitter position estimation.

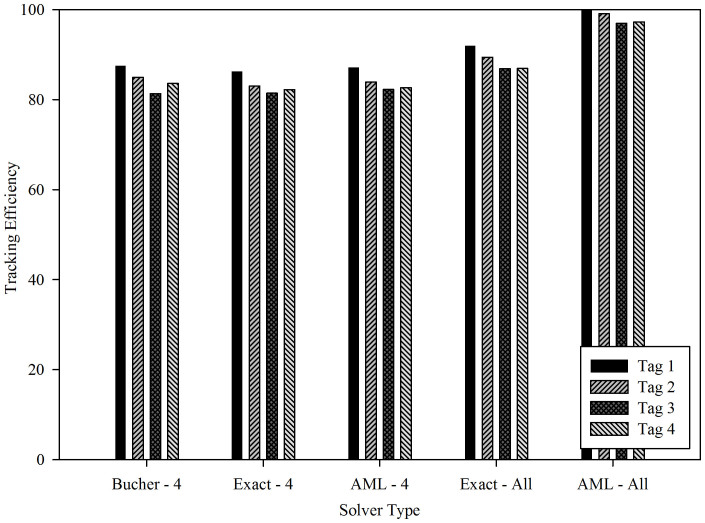
For the three FD system solvers, tracking efficiencies were similar at 82%–87% for all test scenarios (Figure 3). Of the four transmitters that were deployed, Tag 1 had the largest number of transmissions, with a 1 s PRI. Tag 1 was located deeper and probably had less direct path signal interference from multipath. The signal strength of Tag 1 was approximately 15 dB higher than others. Less multipath and stronger signal strength (higher SNR) leaded to a larger number of receiving hydrophones with accurate TOAs, which increases the probability of higher number of successfully tracked positions and as a result, higher tracking efficiency. The tracking efficiency for each tag using the Exact-All (OD solver) was 3%–6% higher than that for the same tag using any of the FD solvers. The integrated TDOA filter in AML-All can reduce errors from TOA measurements by better selection of hydrophones, which results in a greater number of successfully solved locations. AML-All had the highest efficiencies and was 8%–10% higher than Exact-All. The efficiencies of the AML-All solver were 12%–15% higher than those of the AML-4 solver. AML-All was also the only solver group where tracking efficiency for all four tags was over 95% and approaching 100%, which demonstrated significant efficiency advantages over all the other solver groups. The high tracking efficiencies of AML-All suggest that it is the best solver group to use for continuously tracking a swimming fish bearing an acoustic transmitter to avoid breaks in tracking sequences and loss of important fish-behavior information.

Figure 3. Tracking efficiency (%) of the four acoustic tags from five solver groups in all error analysis tests.

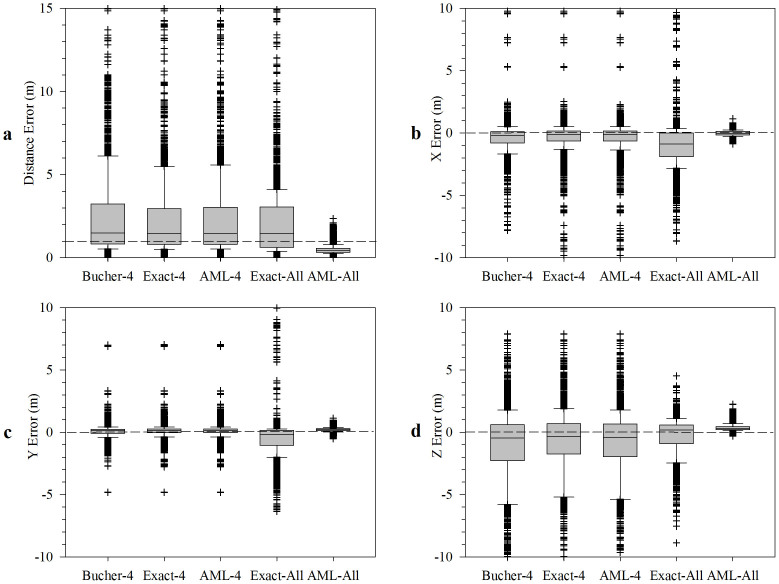
The details of transmitter location estimation errors were best shown using box plots (Figure 4). The hydrophone array was almost totally contained in the y-z plane; thus, it affected the performance of the solvers in a way that made the errors along the x direction relatively large. The AML-All solver largely decreased location estimation errors in the x (Figure 4b) and z (Figure 4d) directions, which markedly improved the tracking results. In the x direction, the standard deviation (SD) of location estimation errors decreased from 1.70 m for the Bucher-4 solver and 2.54 m for Exact-All solver to 0.21 m for the AML-All solver. In the z direction, the SD of location estimation error decreased from 4.67 m for the Bucher-4 solver and 2.59 m for the Exact-All solver to 0.27 m for the AML-All solver. The median distance error decreased from 1.49 m for Bucher-4 and 1.46 m for the Exact-All solver to 0.43 m for the AML-All solver. Meanwhile, the SD of distance errors decreased greatly from 4.47 m for the Bucher-4 solver and 4.59 m for the Exact-All solver to 0.26 m for the AML-All solver. Consequently, 99% of the total tracked location estimates obtained using the AML-All solver showed distance errors ≤ 1 m (indicated by dashed line in Figure 4a). The percentage of distance errors ≤ 1 m was 40% for the Exact-All solver. For the three FD solver groups, only one-third of all tag location estimates had distance errors less than 1 m.

Figure 4. Distributions of position errors of distance, x, y and z of Tag 1 from five solver groups in all error analysis tests.

The line in each box indicates the median value, the edges of the box are the 25th and 75th percentiles, and the whiskers extend to the most extreme values corresponding to approximately 99.3% coverage without outliers, which are displayed individually by crosses.

The results of the eleven SPs conducted were presented in four groups, 10 m, 20 m, 50 m and 100 m, based on the horizontal (x) distance of the remotely controlled boat from the dam. For the four groups, tag location estimation accuracy was summarized in terms of the root mean square errors (RMSEs) of position estimates and tracking efficiency (Table 1). Except for the AML-All solver, whose tracking efficiency was nearly 100%, the other four solver groups produced lower tracking efficiencies at 10 m than at 20 m and 50 m. This was probably caused by tag signal echoes from the dam, another source of multipath interference, and lower SNR conditions that occur in the region close to the dam caused by machinery operating within the dam, flow noise, and other sources of noise. At the maximum test range of 100 m, lower SNRs caused by propagation loss of tag signals and increased opportunity for multipath may have reduced tag signal detection rates at receiving hydrophones. The data suggest that tracking efficiency is highest at intermediate distances (i.e., 20 m and 50 m) from the dam, where SNR is optimized and factors such as multipath are minimized.

Table 1. Comparison of tracking efficiencies and position RMSEs of Tag 1 among five solver groups in stationary point tests in the forebay at 10 m, 20 m, 50 m and 100 m away from the dam face.

Distance to Dam	Bucher - 4	Exact - 4	AML - 4	Exact - All	AML - All
			Tracking Efficiency (%)
10 m	76.40	81.34	81.48	92.04	99.99
20 m	94.98	90.22	90.55	94.66	100.00
50 m	93.10	88.39	90.16	98.41	100.00
100 m	86.62	80.14	81.71	98.80	99.58
			Distance RMS Error (Unit: m)
10 m	4.08	4.65	4.74	3.44	0.42
20 m	5.42	3.99	4.25	4.57	0.48
50 m	7.83	4.94	3.92	1.98	0.82
100 m	4.27	1.39	1.40	1.14	0.65
			X RMS Error (Unit: m)
10 m	1.19	1.64	1.67	2.30	0.13
20 m	1.42	1.01	1.06	1.83	0.18
50 m	2.84	1.57	1.13	1.50	0.21
100 m	1.72	0.64	0.63	0.97	0.34
			Y RMS Error (Unit: m)
10 m	1.42	1.40	1.39	1.54	0.29
20 m	1.09	1.15	1.15	3.14	0.26
50 m	0.45	0.36	0.34	0.86	0.31
100 m	0.36	0.33	0.33	0.26	0.25
			Z RMS Error (Unit: m)
10 m	3.63	4.12	4.21	2.04	0.27
20 m	5.12	3.69	3.95	2.77	0.36
50 m	7.29	4.67	3.74	0.96	0.73
100 m	3.89	1.19	1.21	0.55	0.49

Compared to AML-All, the three FD solver groups had much higher RMSEs in all four distance groups, especially in the z (depth) coordinate. The distance RMSEs and z RMSEs approached 4 m for distances ≤ 50 m. Exact-All achieved better results, but still showed large RMSEs when distance was less than 20 m. As a result, the RMSEs for the AML-All solver for all four distance classes were never above 1 m. When the three drifting tests were included, the AML-All had an overall distance RMSE of 0.56 m, while the RMSEs along the x, y, and z directions were only 0.21 m, 0.25 m, and 0.45 m, respectively. These smaller RMSE values demonstrate the better location estimation performance of the AML-All solver over all of the other solver groups considered.

Discussion

The AML solver uses a weighted least-squares solution as the initial guess of the position of a sound source and iteratively updates the solution to an approximated ML estimate. This approach requires an initial sound-source location guess close to the actual value in order to guarantee convergence. The algorithm used in the Bucher or LLS methods is much simpler and computationally efficient, and a global solution is always guaranteed. However, in an actual operating environment, measurement noise is present from numerous sources and can reach relatively high levels affecting signal detection and TOA accuracy. Unless TDOA measurement noise is sufficiently small, these two methods result in large location estimation errors and are not useful solvers in many field environments.

Compared with selecting four hydrophones based on optimal geometries, tracking efficiency was increasing by using all receiving hydrophones from the same dimensioned hydrophone array. This is shown by the results obtained with Exact-4 and Exact-All in Table 1, although location estimation accuracy was still not significantly improved when the location was closer to the dam, (where noise is higher and multipath collisions with direct path signals from surface and dam-face reflections are more common). When TDOA outliers are frequently observed, a larger numbers of hydrophones in a receiving array may increase the probability of introducing multiple TDOA outliers into the localization algorithm, which can degrade accuracy.

To detect and exclude potential TDOA outliers presented with a larger number of hydrophones in an OD system, a timing filter was incorporated into the developed AML solver to select TDOAs that would optimize localization accuracy. This timing filter was not included in the solver groups with FD systems and Bucher or LLS methods. Selection of such “trusted” TDOAs in preference to all of the TDOAs available in an OD system has been found to be an effective strategy to lower localization error. The timing filter enables the developed solver to perform better across a range of noisy environments. Although the computational costs of the proposed AML solver with additional filtering steps are relatively higher, parallel computing guaranteed its increased performance to rapidly solve for fish positions in real-time environments. In addition, to alleviate errors when strong temperature stratification along water column (especially in midsummer) is observed, the proposed AML solver has been designed to take the temperature stratification into account. It can select the corresponding water temperature based on the estimated depth at which the fish swims.

Evaluation of the forebay solver performance showed that the AML solver had lower error in the x and z directions than other solvers. Higher localization accuracy is particularly important to correctly identify the route of passage of tagged fish. For example, correctly identifying the spill bay or turbine inlet that a fish selects depends on its position accuracy on the order of half the width of the nose pier (on the order of < 1m) that separates spill bay and turbine intakes. Equally critical are the accuracy of fish depth (z direction). The depth of entry of fish into a spill- or turbine- passage route is a factor that determines the magnitude of potentially injurious forces, such as a pressure nadir, that fish will experience during dam passage²⁹.

The forebay performance evaluation of the solver groups tested clearly showed the superior performance of the 3D AML solver that incorporated the described RSR and TDOA filters. The better localization performance of the 3D AML solver is needed to satisfy fish-behavior observation requirements of dam-passage studies, where details of the passage-search patterns of migrating fish and the details of their entry into a selected passage route are of considerable importance to designers and operators of dam fish passage facilities. The improved performance of the 3D AML solver compared to other developed solvers at ranges up to 100 m also permits consideration of fish behavior in response to water quality and flow conditions at ranges from the dam that may still be influenced by dam operations such as the balance of spill and turbine discharge from the dam. Due to the complexity of the field environment, improvements to the proposed 3D AML solver, such as reducing tracking uncertainty with the help of Kalman Filter methods, are part of our ongoing research.

Methods

Algorithm of 3D AML solver

The three-dimensional algorithm for TDOA localization applied in this study was derived from the algorithm developed by Chan et al.²⁴, where an AML estimator was presented in two dimensions for TOA and TDOA cases. In particular, the relative insensitivity of this solver to transmitter-hydrophone geometry is an improvement over the popular TSML algorithm.

The distance r_i between the source and hydrophones in an array, H_i (i = 1, …, N), is

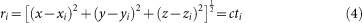where the sound-source position is s = [x,y,z]^T, superscript T stands for the transpose. The position of hydrophone H_i is (x_i,y_i,z_i), c is sound velocity estimated using water temperature measurements³⁰, t_i is the TOA from source to hydrophone H_i, and N is the number of hydrophones.

TDOAs (T_d) are determined as the difference between the other hydrophones in a receiving array and a reference hydrophone, H₁. In this study, H₁ is the hydrophone within the hydrophone array on which a transmitter signal was first detected.

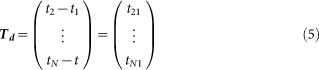Each TOA has an associated measurement noise term, which is assumed to be a zero-mean Gaussian random variable with variance 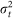. The TDOAs all include t₁ and are correlated. The covariance matrix of the TDOA estimates is¹⁸

Hence

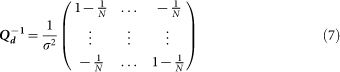Let

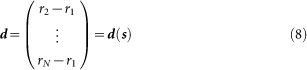Thus the expected value of T_d

The ML estimate is the s that minimizes the cost function j_d.

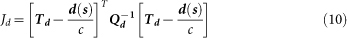Setting the gradient of j_d with respect to s equal to zero

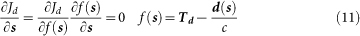gives a weighting matrix

where

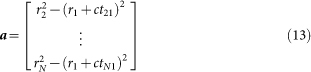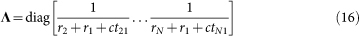Equation (12) can be written as

where

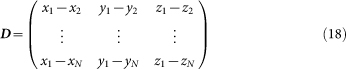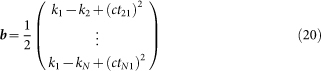The ML equations (17) are exact. Although this is a linear equation in s, the weighting matrix Φ contains elements of unknown s. Thus, the AML approach is necessary to iteratively update the values of Φ. The first step is to get the initial s by setting Φ as an identity matrix. The weighted least square of s is

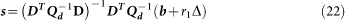Substituting Equation (22) into Equation (4) produces a quadratic in r₁; then the RSR chooses the best root to calculate the initial value of s. When there are two real nonnegative solutions, then both provide possible locations for the source. The general RSR selects the solution with smaller J_d. In field application, however, it is necessary to first identify which solution is physically possible. For this study, all hydrophones were installed at the dam face oriented into the dam forebay; thus all physically possible transmitter location solutions would be upstream of the dam. In the case of our study, this was an additional condition added to RSR before values of J_d were compared.

AML uses s from Equation (12) to calculate Φ, where

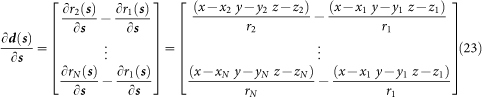Then from (17), we have

The same steps for calculating and selecting r₁ are repeated to obtain updated values of s. Iterating through Equation (24) with new s values five times produces five values of J_d. The AML solver selects the solution with the minimum J_d.

The LLS solver is applied to the same study to compare it to the AML solver. The LLS solution for s is

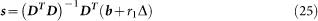The LLS solutions are called exact solutions when noise is sufficiently low. However, the LLS solver does not consider errors introduced by TDOA measurement noise.

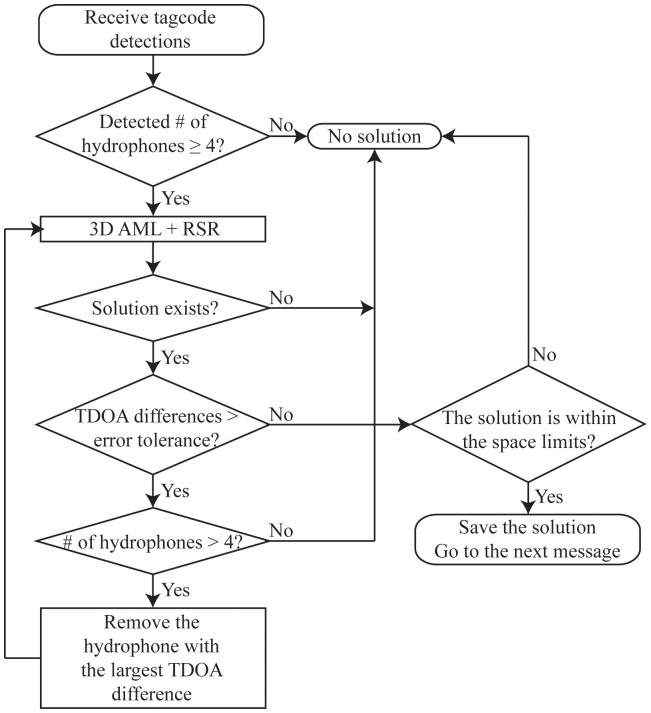
In the AML algorithm, the weighting matrix uses the covariance matrix of TOA/TDOA measurements. The distances between array hydrophones and the tag are also considered to improve weighting terms, because SNR is related to the hydrophone-tag distances. Longer distances between a shallow sound source and a receiving hydrophone increase the probability of multipath interference; therefore, hydrophones closer to a transmitter are assigned higher weights. Also, when water temperature data with better temporal and spatial characteristics are available, the AML solver will incorporate this data to improve estimates of sound speed. In practice (as opposed to theory), when TOAs are being measured for a large number of hydrophones receiving a transmitter signal, it is possible that not all TOAs are accurately estimated. The AML algorithm considers this potential source of error by adding a processing step to filter out potentially inaccurate TDOAs. Using the initial solution for transmitter location, the TOA for each detecting hydrophone is calculated. Then computed and measured TDOAs are compared, and if the difference between the calculated TDOA and the measured TDOA is larger than specified criteria (e.g., the difference should be less than an error tolerance = 1 m/sound-speed), the tracking algorithm will not use hydrophones with TDOAs that exceed the filter criterion. The transmitter location will be estimated using the other hydrophones in the array. This step is repeated until TDOA acceptance criteria are satisfied or the location of the transmitter is determined to be unsolvable. This step greatly increases the location estimation accuracy of the AML algorithm. In addition to the TDOA filter, a space (volume) filter is also applied in field applications of the solver. An estimated transmitter location within a closely spaced sequence of estimated positions (a “track”) is compared to recent location estimates. If the new location is not within what are considered to be physically realizable movement criteria for a juvenile fish, given previous behavior observations, the location estimate is not included in the track. The data processing flow used in the 3D AML solver to estimate the location of a transmitter detected by a hydrophone array is shown in Figure 5.

Figure 5. Flowchart of the proposed 3D AML solver.

While the field evaluation study conducted was specific to the JSATS acoustic telemetry system used in USACE projects, the 3D AML solver is generic in nature and not specific to any particular sound source or receiving hydrophone array geometry. All of the solver functions are independently compiled and connected by software interfaces that can be easily modified to meet the needs of other 3D tracking projects.

Author Contributions

Z.D. designed the study; X.L. and Y.S. developed the solver algorithm; J.M., G.M., T.C., and Z.D. collected the data; X.L. and T.F. performed the data analysis. X.L., Z.D. and T.C. wrote the manuscript. All authors reviewed the manuscript.