X-ray Structure of a Hg²⁺ Complex of Mercuric Reductase (MerA) and Quantum Mechanical/Molecular Mechanical Study of Hg²⁺ Transfer between the C-Terminal and Buried Catalytic Site Cysteine Pairs

Abstract

Mercuric reductase, MerA, is a key enzyme in bacterial mercury resistance. This homodimeric enzyme captures and reduces toxic Hg²⁺ to Hg⁰, which is relatively unreactive and can exit the cell passively. Prior to reduction, the Hg²⁺ is transferred from a pair of cysteines (C558′ and C559′ using Tn501 numbering) at the C-terminus of one monomer to another pair of cysteines (C136 and C141) in the catalytic site of the other monomer. Here, we present the X-ray structure of the C-terminal Hg²⁺ complex of the C136A/C141A double mutant of the Tn501 MerA catalytic core and explore the molecular mechanism of this Hg transfer with quantum mechanical/molecular mechanical (QM/MM) calculations. The transfer is found to be nearly thermoneutral and to pass through a stable tricoordinated intermediate that is marginally less stable than the two end states. For the overall process, Hg²⁺ is always paired with at least two thiolates and thus is present at both the C-terminal and catalytic binding sites as a neutral complex. Prior to Hg²⁺ transfer, C141 is negatively charged. As Hg²⁺ is transferred into the catalytic site, a proton is transferred from C136 to C559′ while C558′ becomes negatively charged, resulting in the net transfer of a negative charge over a distance of ∼7.5 Å. Thus, the transport of this soft divalent cation is made energetically feasible by pairing a competition between multiple Cys thiols and/or thiolates for Hg²⁺ with a competition between the Hg²⁺ and protons for the thiolates.

Metal ions play important functional roles in biological systems but can also be significant environmental pollutants. A detailed understanding of the mechanisms of speciation and transfer of heavy metals in biological and environmental systems is thus of both fundamental and practical interest. Among those chemical mechanisms involving heavy metals, of particular biological importance are ion transfers in proteins.¹

Some microorganisms are able to overcome high concentrations of toxic heavy metals and can directly biotransform contaminants to innocuous or immobile forms.^2,3 A key example is mercury resistance in bacteria conferred by the mer operon, which encodes a suite of proteins that carry out the transport and reduction of Hg²⁺ to transform this toxic ion into less toxic, elemental Hg⁰.^2,4Mer loci have been discovered in many different species, underscoring the ubiquitous nature of this mode of mercury detoxification among bacterial communities.^2,5

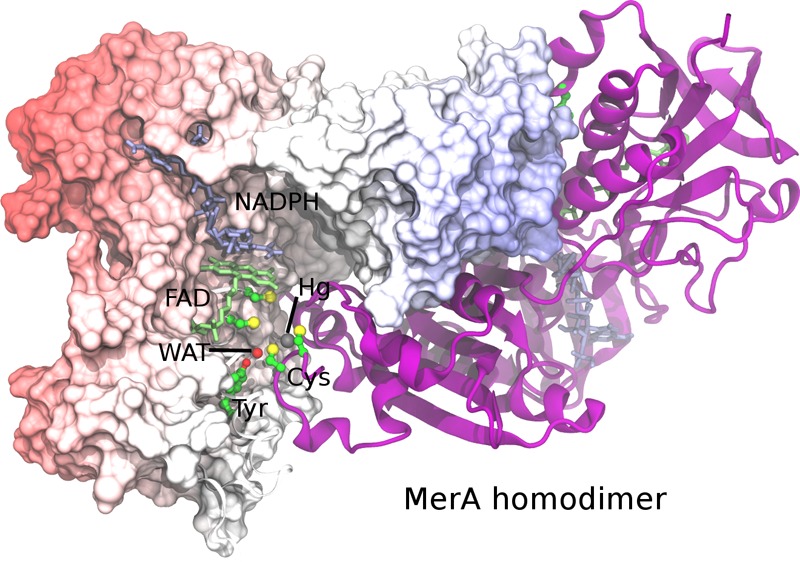
One of the key enzymes in the mer system is mercuric reductase, MerA, which catalyzes the reduction of Hg²⁺ to Hg⁰ within the bacterial cytoplasm.^2,6 The active form of MerA is a homodimer in which the two active sites within the catalytic core domain are found at the dimer interface and comprise residues from both monomers (Figure 1). To compete with other cellular thiols for its Hg²⁺ substrate, each chain of the MerA dimer contains three pairs of strictly conserved cysteines that serve as binding sites for Hg²⁺ transfer and provide a platform for Hg²⁺ reduction. One cysteine pair (C11/C14, numbering hereafter adapted from Tn501 MerA^4,7 from Pseudomonas aeruginosa) is located in the small, N-terminal metallochaperone-like domains of MerA (NmerA, not shown in Figure 1) in a GMXCXXC motif that is present in many metalloproteins, including the homologous periplasmic Hg²⁺ transporter, MerP.⁸⁻¹⁰ NmerA binds and delivers Hg²⁺ to the C-terminal cysteine pair, C558′ and C559′, of the other monomer near the surface of the MerA dimer interface.^7,11,12 After Hg²⁺ binds to the C558′/C559′ cysteine pair, the flexible C-terminal tail must change conformations to move the complex from the surface to the protein interior where Hg²⁺ is transferred to the active site cysteine pair, C136 and C141,¹³⁻¹⁵ located adjacent to the isoalloxazine ring of the flavin adenine dinucleotide (FAD) cofactor (Figure 1).¹⁶ From the opposite face of FAD, the other substrate, dihydronicotinamide adenine dinucleotide phosphate (NADPH), transfers hydride to FAD, yielding the two-electron reduced FADH^– and oxidized NADP⁺. Subsequently, FADH^– reduces the C141–S-Hg(II)–S-C136 complex to yield Hg⁰ in a reaction that proceeds to completion; i.e., with stoichiometric quantities of NADPH and Hg(SR)₂ substrate, all of the NADPH is consumed.^13,14 As expected, mutation of either C136 or C141 or both results in a total loss of Hg²⁺ reductase activity.¹⁷ The overall Hg²⁺ transfer and reduction processes are shown in Scheme 1.

Figure 1.

Stereo (walleye) image of the interfacial active site of the MerA homodimer with monomer chains in cyan and magenta. FAD, NADP⁺, and residues with cyan carbons are from the left monomer. Amino acid residues with magenta carbons are from the right monomer. Several ordered water molecules are shown as red spheres. Other atoms are colored red for oxygen, blue for nitrogen, and yellow for sulfur. The structure was constructed from an overlay of the AACC Hg²⁺/NADP⁺ complex (PDB 4K7Z, magenta) and the oxidized wild type (CCCC) enzyme (PDB 1ZK7, cyan) with only one chain from each shown for clarity. FAD molecules from the left monomer in both structures are shown to highlight the close alignment of the two structures. Abbreviations: CCCC, wild type MerA; CCAA, Cys136 Cys141 Ala558 Ala559 Tn501 MerA; AACC, Ala136 Ala141 Cys558 Cys559 Tn501 MerA; NADPH, dihydronicotinamide adenine dinucleotide phosphate; FAD, flavin adenine dinucleotide.

Scheme 1. Hg²⁺ Transfer and Reduction in the MerA Core Domain.

The reduced and oxidized cofactors are shown in blue and red, respectively. The two chains of the MerA homodimer are shown in orange and green. The dashed line represents the charge transfer interactions between the C141 thiolate and FAD. K_h is the equilibrium constant between the NADPH/FAD and NADP⁺/FADH^– redox states. The red arrow shows the Hg²⁺ transfer studied in this work.

A critical role for the C558′/C559′ pair in Hg²⁺ transfer and/or reduction was initially suggested by the observation that the CCAA mutant retains only 0.09% of the steady-state catalytic activity of the wild type (CCCC) enzyme with typical Hg(SR)₂ substrates.¹⁸ Pre-steady-state kinetic studies with alternative substrates subsequently showed that the C-terminal cysteines are essential for efficient acquisition of Hg²⁺ from the incoming Hg(SR)₂ substrate and transfer into the active site, but they are not directly involved in the catalytic reduction step.^13,14 Thus, with HgBr₂ as substrate, from which the bromide ligands dissociate as stable anions (Br^–) with no need for protonation, the CCAA enzyme can acquire Hg²⁺ through an alternative channel and reduce Hg²⁺ as rapidly as the CCCC enzyme.¹³ In contrast, with physiologically relevant Hg(SR)₂ substrates in which the thiol ligands are more basic and require protonation, successive Hg²⁺ transfers from substrate at the protein surface all the way into the catalytic site of the CCCC enzyme occur at an overall rate exceeding that of turnover (≥224 s^–1 vs 12–15 s^–1 for k_cat), while the single Hg²⁺ transfer from the Hg(SR)₂ substrate to the active site of the CCAA mutant occurs at least 10³-fold more slowly and results in a complex that is inhibited toward reduction due to an apparent increase in negative charge in the active site.¹⁴ Thus, the C558′/C559′ cysteine pair is critical both for displacing the high-affinity ligands of physiological Hg(SR)₂ substrates and for presenting Hg²⁺ for efficient transfer into the active site to yield a neutral, readily reducible complex.

How the enzyme catalyzes these efficient transfers is one of the fundamental questions of interest in understanding the overall catalytic mechanism of MerA. Previous studies have shown that exchange of thiol ligands in Hg(SR)₂ complexes in aqueous solution occurs through the formation of transient or semistable tricoordinate [Hg(SR)₃]⁻ complexes, with faster rates of formation of the tricoordinate species at high pH where the thiolate anion predominates, and rates for loss of a ligand from the tricoordinate complex favored by protonation of the leaving thiol ligand.¹⁹ Thus, we anticipate a similar mechanism likely occurs in the enzyme with a need for acid/base catalysis.

To gain additional insight into intramolecular Hg²⁺ transfer in MerA, we determined the X-ray structure of the C-terminal Hg²⁺ complex of a double active-site mutant of the Tn501 MerA core and performed DFT-based QM/MM simulations to explore Hg²⁺ transfer pathways from the C-terminal cysteine pair to the active site. Based on the mechanistic principles noted above and the X-ray structure (Figure 1), we propose a potential pathway for Hg²⁺ transfer in the MerA core and determine the corresponding potential energy profile. The results from the calculations provide a detailed picture of Hg²⁺ transfer likely to be of general applicability in biological systems.

Methods

AACC MerA Protein and Complex Preparation

Mutation of codons for cysteines 136 and 141 to alanines in the merA gene for the Tn501 catalytic core construct (pET3d:cmerA⁷) was performed following the QuikChange (Stratagene) protocols with appropriate primers to generate pET3d:AACCcmerA for expression of the AACC double mutant of the MerA catalytic core. The protein was expressed in Escherichia coli BL21(DE3) pLysS cells, purified, and stored as previously described.⁷ Prior to complex formation, the purified protein was first incubated with 5 mM dithiothreitol (DTT) for 30 min at 4 °C, separated from DTT by gravity gel filtration through Sephadex G-25, and the reduced thiol content assayed using dithionitrobenzoic acid as previously described.⁷ The Hg²⁺ complex of the C-terminal cysteines was generated by stoichiometric titration with Hg-bis-thionitrobenzoate [Hg(TNB)₂],⁷ separated from TNB by gel filtration, and concentrated to ∼25 mg/mL in 50 mM potassium phosphate buffer (KPi), pH 7.3. Glycerol was added to 5% (v/v) for storage at −80 °C for shipping to the University of Toronto.

Crystallization, Data Collection, and Structure Determination

Co-crystals of the NADP⁺/Hg²⁺ complex of AACC Tn501 MerA catalytic core were grown using the hanging drop vapor diffusion technique. Glycerol was removed from the 2:1 (Hg/dimer) Hg²⁺-AACC protein complex by repeated washing in centricon-30 concentrators with 50 mM KPi, pH 7.3, after which 2 μL of 25 mg/mL protein solution were mixed with 2 μL of 0.1 M Tris, pH 9.4, 20 mM NADP⁺, 2.0 M (NH₄)₂SO₄ and the drop then equilibrated against 0.5 mL of this solution at room temperature. After growth, crystals were harvested, transferred to the reservoir solution with 16% (w/v) glycerol added for cryo-protection.

Diffraction data sets were collected at APS, BIOCARS beamline 14BM-C at a wavelength of 0.90 Å equipped with an ADSC Q4 CCD detector. All data sets were processed with the help of the program packages DENZO and SCALEPACK.²⁰ The CNS v. 1.0 program suite²¹ was used to solve the structure by molecular replacement. REFMAC v. 5.7.0032²² and Coot 0.6.2 were used for structure refinement. The atomic models were generated in the graphics program O.²³ Parameters for data collection and refinement are summarized in Table S1, Supporting Information.

Model Preparation for Simulations

Coordinates for the MerA core domain were obtained from the 1.5 Å X-ray crystal structure of the AACC homodimer presented herein (PDB 4K7Z). In this structure, each monomer contains an NADP⁺ and FAD cofactor in positions analogous to the structure of MerA from Bacillus sp. strain RC607¹⁶ and a Hg²⁺ ion bound to the C-terminal cysteine pair (C558/C559 and C558′/C559′) (Figure 1). The C136 and C141 side chains were modeled from corresponding Ala mutations in AACC, NADPH was modeled from NADP⁺, and this structure was taken as the initial configuration for Hg²⁺ transfer. The low experimentally observed pK_a (∼5.0) of C141^24,25 renders it a thiolate at physiological pH (7.0), forming a charge-transfer complex with FAD.²⁶ For the other residues, protonation states were assigned on the basis of manual inspection of the environment of each polar residue, and on pK_a values predicted by PROPKA²⁷⁻²⁹ at pH 7.0. All crystal waters were retained and the orientations of the hydrogen atoms were optimized before further operations on this model were performed.

The CHARMM27 force field³⁰ with CMAP corrections³¹ and the TIP3P water model³² were used to describe the protein, NADPH and FAD, and the solvent. Stochastic boundary conditions³³ were applied in the QM/MM simulations. The sulfur atom of C558′ was chosen as the reference center for partitioning the system into a reaction zone and a reservoir zone, and the former was further divided into a reaction region and a buffer region. The reaction region was a sphere of radius (R) 23 Å, and the buffer region with R between 23 and 25 Å. The Adopted Basis Newton–Raphson (ABNR) method was used for all energy minimizations. Before proceeding to the reaction coordinate driving (RCD) calculations, the system was heated with MD from 50 to 100 K over 60 ps and then the energy was minimized until convergence with an average gradient tolerance of 10^–4 kcal mol^–1 Å^–1 to relax unfavorable interactions. Atoms in the QM region were fixed during heating but were fully relaxed during the energy minimization.

QM/MM Method and Reaction Coordinate Driving Calculations

GAMESS-US³⁴ and CHARMM^35,36 were used for the QM/MM calculations. The QM region included the Hg²⁺ ion, the side chains of C136, C141, C558′, and C559′, and the crystal water molecule (WAT) hydrogen bonded to C136 and C558′, with the rest of the system comprising the MM subsystem. Hydrogen link atoms³⁷ between the Cβ and Cα atoms of the QM residues were added to separate the QM and MM regions. The QM region was described by density functional theory (DFT) with the B3PW91 functional,^38,39 which has been applied successfully to studies of group 12 dihalides⁴⁰ and solvation,⁴¹ Hg–C bond cleavage by organomercurial lyase,⁴² and Hg(II) ligand binding.⁴³ The 6-31+G(d) basis set⁴⁴⁻⁴⁶ was used for all nonmetal atoms (H, C, N, O, S), and the SBKJC effective core potential (ECP) and basis set⁴⁷⁻⁴⁹ were used for Hg.

The reaction coordinate driving (RCD) method with a harmonic restraint potential of 900 kcal mol^–1 Å^–2 was used to calculate a minimum energy path (MEP) for the Hg²⁺ transfer from the C-terminal cysteine pair to the active site cysteine pair. The reaction coordinates for each elementary step in the reaction are shown in Figure S1 of the Supporting Information (SI). Forward and backward scans were performed to obtain a smooth reaction path for each step. An iterative QM/MM optimization strategy⁵⁰ was used in each step of the reaction coordinate driving calculations.

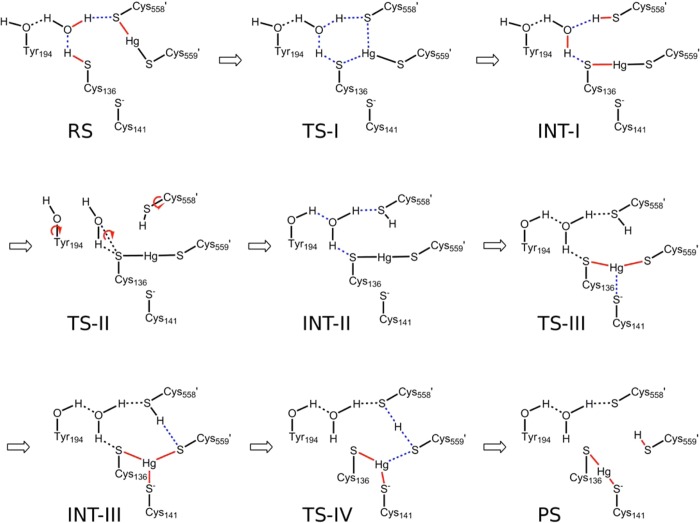
To explore potential intermediate states during the Hg²⁺ transfer, the Hg²⁺ ion was driven systematically between C136, C558′, and C559′, which form a plane. The energies of structures on each path were minimized without restraints to identify stable intermediate states. Two configurations, labeled INT-I and INT-II, in which Hg²⁺ is bound between one active-site cysteine and one C-terminal cysteine, i.e., C136–Hg-C559′, were found. These stable states were connected by both forward- and backward-scanning RCD runs. After the scans reached convergence with total energy differences of two rounds of scans less than 1 kcal mol^–1, the reaction was driven toward the product state from INT-II and back to the reaction state from INT-I with a series of forward-and-backward RCD scans. As each step of the transfer is reversible, the minimum energy pathway of Steps I to IV were assembled to create the complete reaction path (Scheme 2, Figure 2).

Scheme 2. Proposed Hg(II) Transfer Pathway in the Catalytic Core of MerA.

Figure 2.

QM/MM minimum energy pathway for Hg²⁺ transfer and charge distributions at the stationary points. At each step, the electrostatic potential is mapped onto the electron density isosurface. Energies (relative to RS) are shown in parentheses. Note that, compared with Figure 1, the active site here is viewed from the bottom looking up through Y535′ at the C-terminal cysteines.

Gas-phase and continuum calculations for the QM region at the stationary points along the MEP were performed to estimate the energetic contribution from the rest of the enzyme. The B3PW91/6-31+G(d)/SBKJC level of theory and the IEF-PCM continuum solvent model⁵¹ with Bondi radii⁵² and a dielectric constant of 78.4 were used for all calculations. To investigate whether this representation is adequate for the present purposes, larger basis sets were employed with Gaussian09⁵³ to calculate single-point energies of the isolated QM region of the reactant state (RS), product state (PS), intermediate state (INT) and the transition state (TS) obtained with 6-31+G)(d)/SBKJC. The following basis sets and ECPs were used: 6-31+G(d)/SBKJC, 6-31+G(d)/SDD,⁵⁴ 6-31G(d)/SDD, and aug-cc-pVTZ (aTZ)⁵⁵ with the corresponding aTZ-pp pseudopotential. We also assessed the effects of dispersion on the aTZ/aTZ-pp energies by including DFT-D3 empirical dispersion corrections.^56,57 The energy profile obtained with SBKJC agrees well with that from the widely used SDD method and aTZ/aTZ-pp with DFT-D3 empirical dispersion corrections (Figure S2, Supporting Information).

Results and Discussion

Structure of the AACC Hg²⁺/NADP⁺ Complex

Although structures of the catalytic core of MerA from both the Bacillus sp. RC607¹⁶ and the Tn501⁷ operons are available, neither has Hg²⁺ bound. Thus, as an initial step to investigate the Hg²⁺ transfer pathway, we generated the C136A/C141A double alanine mutant (AACC) in the truncated Tn501 catalytic core construct.⁷ This construct lacks the NmerA domains and previously yielded much higher resolution structural data than the full-length Bacillus enzyme. Crystals of the AACC/NADP⁺ complex with Hg²⁺ bound to C558′/C559′ were obtained under similar conditions and in the same space group as those of the wild type CCCC enzyme (PDB 1ZK7) and diffracted to 1.5 Å resolution (cf. Table S1; PDB 4K7Z). Figure S3 shows a structural alignment of the full CCCC and AACC dimers (RMSD = 0.16 Å for backbone atoms), and Figure 1 shows a composite figure with one chain from CCCC (cyan) and one chain from AACC (magenta) to demonstrate the relative positioning of both pairs of cysteines to each other and to the cofactors and other active site residues.

As indicated above, we anticipate Hg²⁺ transfer in MerA will occur in a similar fashion as in aqueous solution, which has been shown to occur primarily through formation of transient tricoordinate [Hg(SR)₃]⁻ complexes facilitated by acid/base catalysis.¹⁹ As shown in the structural overlay in Figure 1, the C136 thiol lies close to the C558′–Hg-C559′ complex in the dimer cleft while the C141 thiolate lies deeper in the active site cavity behind V421, strongly suggesting C136 will make the initial attack. For acid/base catalysis, the only obvious polar residues near both C558′/C559′ and C136/C141 cysteine pairs are two conserved tyrosines (Y194 and Y535′) and a few ordered water molecules, while a conserved glutamate (E540′) lies somewhat more removed and near only C559′. Previous mutations of either tyrosine to phenylalanine in MerA from Bacillus sp. RC607 decreased the catalytic activity, but that corresponding to Y194 was most dramatic,⁵⁸ making it a likely candidate for an acid/base catalyst. In the structure, the Y194 phenol interacts with an ordered water molecule (WAT) that lies within hydrogen bonding distance to both C136 and C558′ (Figure 1, dashed lines) suggesting WAT participates as the actual acid/base catalyst for proton transfer between the cysteines, while Y194 may assist in its positioning without transferring a proton. On the basis of these observations, we propose that only WAT, the four cysteine side-chains, and Hg²⁺ are directly involved in the bond-making and breaking reactions and have included these in the QM region for the simulations, but have left Y194 in the MM region.

QM/MM Simulation

The overall QM/MM MEP is shown in Figure 2, and the geometries and energetics of each step of the path are described in detail below. We then analyze the energetics in terms of the overall contributions from the enzyme with comparisons with gas-phase and polarizable continuum calculations.

The Hg²⁺ transfer is modeled with a QM/MM MEP calculated using four distinct steps that capture representative configurations of the system during the Hg²⁺ transfer (Scheme 2). The net result of the pathway is that, as the Hg²⁺ is transferred from the C-terminal cysteine pair (C558′:C559′) to the active site cysteine pair (C136:C141), a proton is transferred in the opposite direction and a negative charge is transferred over a distance of ∼7.5 Å, from the interior cysteine C141 to C558′. The presence of a C558′ thiolate anion in the PS complex is consistent with the observation of an apparent pK_a of ∼6.5 for C558′ in the oxidized enzyme in which C141 and C136 form a neutral disulfide similar to the neutral C141–Hg–C136 complex.¹²

In this reaction path, as the Hg²⁺ is transferred inward the proton is shuttled outward from the active site through the ordered water molecule (WAT) observed in X-ray crystal structures of the wild type (PDB 1ZK7) and the AACC mutant (PDB 4K7Z) used for the simulation. Specifically, the proton is transferred from C136 to C558′ (through WAT) and then from C558′ to C559′, each proton transfer being used to drive the transfer of Hg²⁺ toward the active site by destabilizing the interactions between the targeted thiolate and Hg²⁺.

Proposed Hg²⁺ Transfer Pathway in the MerA Core

Scheme 2 shows the proposed Hg(II) transfer pathway in the catalytic core of MerA.

Step I: Hg²⁺ Transfer from C558′ to C136

The first step of the reaction exchanges H⁺ and Hg²⁺ between C136 and C558′ to form an intermediate (INT-1) that is 9.0 kcal mol^–1 less stable than the reactant state (RS) (Figure 2). The H⁺ is shuttled via a Grotthuss-like mechanism⁵⁹ (Scheme 2) through a hydrogen bond network that links C136, WAT, and C558′ and is anchored by a hydrogen bond donated from WAT to the Y194 phenol (Figure 3A). As the proton is transferred, the bond between Hg²⁺ and C558′ is broken, and a bond between Hg²⁺ and C136 is formed. The transition state, TS-I, consists of a distorted H₃O⁺ species and Hg²⁺ in a tricoordinated complex with the thiolates of C136, C558′, and C559′ (Figure 3B). The excess H⁺ on WAT interacts strongly with C136 and C558′, which in turn weakens their interactions with Hg²⁺ (Hg–S distances of 2.60 and 2.84 Å, respectively) compared to C559′ (2.48 Å). The network of interactions in TS-I spreads the charge density over the distorted hydronium and the tricoordinated Hg²⁺ complex, rather than exhibiting zwitterionic character (Figure 2). This spreading of charge provides some stabilization to TS-I, but the potential energy barrier remains high (20.4 kcal mol^–1), which we discuss further below. Collapse of TS-I leads to INT-I, characterized by a neutral C558′ thiol and Hg²⁺ bis-coordinated to the C559′ and C136 thiolates (Figure 4A). All of the corresponding hydrogen bonds between WAT and the side chains of T194, C136, and C558′ are longer and therefore weaker in INT-I than in RS (Figures 3A and 4A). The weakened hydrogen bonds are consistent with the relative instability of INT-I, which facilitates the hydrogen bond rearrangement in the next step.

Figure 3.

Optimized geometries of (A) RS and (B) TS-I. H-bond distances are shown in blue and covalent bond lengths in black. Relative to Figure 1, Figures 3–6 are rotated backward by ∼135° about a horizontal axis. Heteroatoms are shown in standard CPK colors with red for oxygen, yellow for sulfur, white for hydrogen, dark gray for mercury, and light gray for carbon atoms. Nonpolar hydrogen atoms are omitted for clarity.

Figure 4.

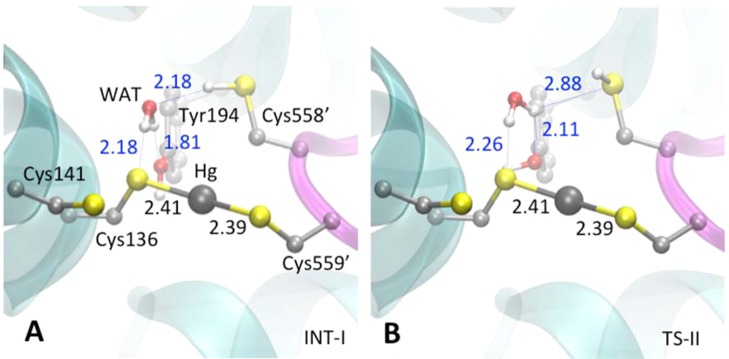
Optimized geometries of (A) INT-I and (B) TS-II. Coloring scheme can be found in Figure 3 caption.

Step II: Hydrogen Bond Network Rearrangement

The second step involves a reorganization of the hydrogen bonding network of the C136 thiolate, WAT, Y194, and the C558′ thiol (Scheme 2) in INT-I to form INT-II (Figure 4A). The WAT, Y194 phenol, and C558′ thiol rotate more or less synchronously to form INT-II (Figure 5A). The negative charge density on C558′ decreases significantly in TS-II relative to INT-I (Figure 2) as its hydrogen bond to WAT is broken (Figure 4B). Furthermore, the negative charge density on C558′ is again reduced (i.e., becomes more positive) as TS-II relaxes to INT-II and the C558′ thiol sulfur accepts an electron-withdrawing hydrogen bond from WAT. The energy barrier (relative to INT-I) for Step II is 9.2 kcal mol^–1 (Figure 2). In INT-II, WAT accepts a hydrogen bond from Y194 and donates two hydrogen bonds to C558′ and C136 (Scheme 2 and Figure 5A). INT-II is only slightly less stable (0.8 kcal mol^–1) than INT-I (Figure 2) even though the hydrogen bond networks in the two states are different. Comparing INT-I and INT-II, the type of hydrogen bond changes, from S–H···O in INT-I to O–H···S in INT-II. Consideration of CCSD(T) hydrogen bond energies computed at the estimated complete basis set (CBS) limit suggests that the contribution to the overall energy difference from hydrogen bonding between the two states is small.⁶⁰

Figure 5.

Optimized geometries of (A) INT-II and (B) TS-III. Coloring scheme can be found in Figure 3 caption.

Step III: Formation of a Tri-Coordinated Intermediate State, INT-III

In the third step of the Hg²⁺ transfer pathway, the C141 thiolate attacks Hg²⁺ (Figure 5B) to form a tricoordinated intermediate (INT-III) that also includes C136 and C559′ (Figure 6A). A hydrogen bond between C559′ and the phenol of Y535′ (cf. Figure 1) is formed at TS-III but is subsequently broken when a hydrogen bond is formed with C558′ in INT-III. The hydrogen bond network in INT-III increases the extent of charge delocalization and thereby stabilizes the tricoordinated complex (see below). The potential energy barrier of Step III (relative to INT-II) is 10.8 kcal mol^–1, and INT-III is a relatively stable intermediate that is only 1.1 kcal mol^–1 higher in energy than the RS (Figure 2). The enhanced stability of INT-III is accompanied by a significant delocalization of negative charge across the tricoordinated complex and hydrogen-bonded active site residues.

Figure 6.

Optimized geometries of (A) INT-III, (B) TS-IV, and (C) PS. Coloring scheme can be found in Figure 3 caption.

The trigonal planar complex INT-III possesses significant configurational differences from TS-I. First, the three Hg–S bond lengths in this complex are nearly equal to each other, with the Hg–S(C136) bond slightly longer (2.56 Å). An S–H···S hydrogen bond is formed between C558′ and C559′, but the interaction appears too weak to affect the Hg–S(C559′) bond length. As described above, the anionic tricoordinated complex of TS-I has longer bonds due to strong interactions with the excess proton bound to WAT, the energetics of which largely destabilize TS-I compared to INT-III.

Step IV: Hg²⁺ Binding to the Active-Site Cysteine Pair

In the final step of the path, the tricoordinated Hg²⁺ intermediate relaxes to the bis-coordinated complex with C136 and C141 as the proton is transferred from C558′ to C559′. The final product state (PS) consists of a C558′ thiolate, C559′ thiol, and the (C136)S–Hg–S(C141) complex, which is poised for Hg²⁺ reduction by way of the NADPH and FAD cofactors (Scheme 1). Upon formation of the neutral complex between Hg²⁺ and the thiolates of C136 and C141, WAT moves away from C136 to interact more closely with the negatively charged C558′ thiolate (Figure 6C). The potential energy barrier for Step IV (relative to INT-III) is 7.2 kcal mol^–1, and the PS is 2 kcal mol^–1 lower in energy than RS, which we discuss in more detail below.

Comparisons between QM/MM and Gas-Phase/Continuum Calculations

In the protein, the overall energetics favors the PS by around 2 kcal mol^–1 compared to the RS. Assuming the bis-coordinated Hg²⁺ is equally stable when bound to either cysteine pair, the relative pK_a’s of the two pairs of cysteines might be expected to lead to the reaction being slightly exothermic because energy would be gained from transferring H⁺ from the inner C136:C141 pair to the outer C558′:C559′ pair as the Hg²⁺ is transferred. The calculated MEP agrees well with these expectations. However, two contributions are neglected in this study that likely cancel. First, if dynamic sampling were carried out, the thiolate that is semiexposed to solvent in the PS might be further stabilized (relative to the RS), yielding a more exothermic transfer of Hg²⁺. This would have the effect that the PS would be destabilized relative to the RS in the present pathway. At the same time, however, the RS is also destabilized. In the setup of the QM region, C141 is treated as a thiolate, based on its experimentally determined pK_a of ∼5.^24,25 The deprotonated, anionic state of C141 is stabilized by electronic interactions with the FAD, which reduce its pK_a.²⁴ These interactions are not fully accounted for in the present QM/MM calculations because the FAD was included in the MM region to make the calculations computationally feasible. Most importantly, neither error is expected to be that large, as the pK_a shift of C141 is only 4 units, and only a small number of water molecules interact with the semiexposed thiolate in the PS. However, correcting for these effects might be expected to stabilize both the RS and PS relative to INT-III. To test these ideas and evaluate the role that the enzyme plays in Hg²⁺ transfer, DFT calculations were applied to the isolated QM region in the absence of the rest of the enzyme using the geometries of the minima (RS, INT-I, INT-II, INT-III, and PS) and transition states (TS-I to TS-IV) from the optimized QM/MM MEP (Figure 7).

Figure 7.

Energy profiles for Hg²⁺ transfer in the gas phase, aqueous phase, and in MerA. All energies were calculated with the same QM region geometries and are displayed relative to RS. The enzyme and continuum solvent contributions (open circles, dashed lines) were calculated by subtracting the gas-phase energies from the respective paths.

Gas-Phase Energetics

In the absence of the enzyme, the exposed and isolated C141 thiolate (Figure 3A) destabilizes the RS significantly. INT-III and the PS are significantly more stable than the RS, with the tricoordinated complex (INT-III) being the most stable point on the path in the gas phase, −45.5 kcal mol^–1 lower in energy than the RS (Figure 7). This increased stabilization stems from spreading the negative charge of the system across the tricoordinated Hg²⁺ complex. TS-I, the other configuration with a nominally tricoordinated Hg²⁺, is only 7.3 kcal mol^–1 higher in energy than RS, but 52.7 kcal mol^–1 higher in energy than INT-III. The relative instability of TS-I stems from its neutral components; the negative charge largely remains on the C141 thiolate. INT-I, TS-II, INT-II, and TS-III all have similar energies and are more stable than the RS (Figure 7). Comparing the PS to the RS, the gas-phase reaction is exothermic by ∼20 kcal mol^–1. This energy difference can be understood in terms of the C141 and C558′ thiolates in the RS and PS, respectively. Compared to the isolated C141 thiolate in the RS (Figure 3A), the C558′ thiolate in the PS forms hydrogen bonds with WAT and C559′ (Figure 6C).

Comparison between Enzyme and Continuum Solvent

When contributions from continuum solvent are included, the exposed and isolated C141 thiolate (Figure 3A) is significantly stabilized relative to the gas phase. INT-III is still the most stable point on the path but is only −4.9 kcal mol^–1 lower in energy than the RS (a change of around +40 kcal mol^–1, see Figure 7). The difference between INT-III and TS-I is reduced from 52.7 kcal mol^–1 to 18.6 kcal mol^–1. TS-I is 13.8 kcal mol^–1 higher in energy than the RS, an increase of 6.5 kcal mol^–1 compared to the corresponding gas-phase energy difference. The energy difference between the RS and PS is very similar to that in the full enzyme (Figure 7). In other words, continuum solvation stabilizes the exposed C141 thiolate in the RS by ∼18 kcal mol^–1 relative to the more buried C558′ thiolate in the PS.

When the full enzyme and explicit solvent from the QM/MM MEP are included, the RS is similarly stabilized relative to INT-III and the PS by ∼46.5 and 18 kcal mol^–1, respectively. The C141 thiolate is located ∼3.5 Å from the plane of the neutral isoalloxazine group of FAD (cf. Figure 1B), and ∼5.5 Å from the K145 ammonium group, which is in a salt bridge with the E284 carboxylate. C141 is located at the base of an α-helix, which may also provide helix dipole charge stabilization for the anion.⁶¹ In the PS, the semiexposed C558′ thiolate gains one additional hydrogen bond from an MM water molecule in the MEP. It may also interact electrostatically with the ammonium group of K193, which is located ∼6 Å away in an interaction with the backbone carbonyl of V553. It is unlikely that the enzyme provides as much electrostatic stabilization as the continuum solvent, but the energetic effects are qualitatively similar. While the contributions from the enzyme MM electrostatic environment stabilize the RS relative to the gas phase as noted above, they also clearly destabilize the latter portion of the reaction path relative to the initial step(s) (dashed lines in Figure 7). In this way, the electrostatic environment around the C558′ thiolate in the PS may further drive a conformational change of the C-terminal loop such that the C558′/C559′ cysteine pair becomes more solvent-exposed, a step that is essential for acquisition of the next Hg²⁺ from NmerA or other Hg(SR)₂ substrates during enzyme turnover.

Relationship of MEP to Experimental Observations

A final consideration in this analysis is how the energetic and mechanistic characteristics of the MEP determined here relate to the rates and intermediates observed in kinetic and titration studies of the wild type (CCCC) and C-terminal (CCAC and CCCA) mutant MerA proteins. Energetically, the near thermoneutrality of the overall transfer from RS to PS and the relative stability of the three-coordinate intermediate INT-III are consistent with the accumulation of ≥50% of species with Hg²⁺ bound at the active site that has been observed both in titrations¹⁵ and kinetic studies of wild type MerA with Hg(SR)₂ substrates.¹⁴ Thus, these elements of the simulated pathway are likely to be robust independent of the pathway itself. In addition, with the exception of the first step, the barriers for all other steps (7.2–10.8 kcal mol^–1) are lower than the maximal free energy of ∼13.5 kcal mol^–1 (estimated with transition state theory) for any step in the pathway from the observed rate constant (224 s^–1) for Hg²⁺ transfer through the entire pathway from initial exchange with Hg(Cys)₂ all the way into the active site of the wild type (CCCC) enzyme,¹⁴ suggesting the general mechanistic characteristics of these steps are also relatively robust.

On the other hand, the energetic cost of the first step in the computed pathway, at 20.4 kcal mol^–1, is much higher than the maximal free energy estimated (∼13.5 kcal mol^–1) from the observed rate constant (224 s^–1) for the overall Hg²⁺ transfer pathway¹⁴ and is also inconsistent with the rate for overall turnover of the enzyme (12–15 s^–1).^6,7,18 While configurational sampling along reaction coordinates may expose other pathways, reduce the free-energy barrier, and bring the computed values into better agreement with experiment, the reason for the discrepancy remains an open question. Such potential of mean force calculations are still computationally intensive at the DFT level, and semiempirical methods, while computationally more feasible, await a set of reliable parameters for systems containing Hg and S.^62,63 A closer analysis of the characteristics of TS-I and RS, however, suggests the likely cause of the high barrier is the presence of a neutral water molecule rather than a stronger base to initiate the reaction. In aqueous solution, [Hg(SR)₃]⁻ complexes form rapidly at pH values ≥9 where thiolates predominate (thiol pK_a ∼ 9) and rapidly dissociate to Hg(SR)₂ and RSH below an apparent pK_a of ∼7 for the thiol in the [(RSH)Hg(SR)₂] complex.^19,64 Hg(SR)₂ complexes are stable down to at least pH 2, indicating a pK_a < 2 for the (RSH)Hg(SR) complex.⁶⁴ These observations suggest that substantial deprotonation of C136 to a thiolate would be needed for rapid formation of a three-coordinate TS or INT, which is consistent with the much lower barrier (10.8 kcal mol^–1) determined for attack of the C141 thiolate on the C136–Hg–C559′ complex in the conversion of INT-II to INT-III in the MEP. In the current RS QM model, however, the neutral water is not basic enough (hydronium pK_a = −1.7) to deprotonate a thiol (pK_a ≈ 9) to a significant extent nor acidic enough (pK_a = 15.7) to protonate a thiolate in a Hg(SR)₂ complex (pK_a < 2).⁶⁴ Thus, Step 1 in this model proceeds with the weakly nucleophilic C136 thiol initiating attack on the neutral C558′–Hg-C559′ complex, i.e., without activation of either the nucleophile or the electrophile. The result is a significant energetic cost as TS-I can only be reached when sufficient C136–S-Hg bond formation and C558′–S-Hg bond weakening occur to shift their respective pK_a’s toward each other until they are essentially the same, as suggested by the nearly identical hydrogen bond lengths between the distorted hydronium ion and the two cysteine sulfurs in TS-I (Figure 3B).

The above considerations notwithstanding, the arrangement of residues in the active site as observed in the X-ray structure strongly suggests the core elements (four Cys side chains, Hg²⁺, and WAT) of the current model are correct. However, to increase negative charge character on the C136 sulfur, additional components would be needed in the QM region of the model that allow full or partial Grotthuss proton transfer from WAT and/or the C136 thiol to a negatively charged residue in an initial step. One potential pathway would involve a proton transfer from WAT to the E540′ carboxylate via the Y194 phenol, several additional water molecules, and possibly the Y535′ phenol. In a second potential pathway, the C141 thiolate could accept the proton from C136 in the first step, but would then need to be deprotonated in a later step to form the C136–S-Hg²⁺–S-C141 complex. From its deeply buried position in the active site, the most likely pathway for that proton transfer would involve the 2′- and 4′-OH groups of the FAD ribityl side chain, 1–2 additional water molecules, and the Y194 phenol group. A third potential pathway would involve transfer from the C136 thiol to a phosphate oxygen in the FAD cofactor via WAT, the Y194 phenol, and two very well ordered water molecules observed in the X-ray structure (Figure 1). Of the three pathways, the last two are more appealing as catalytic pathways because the components of both are well ordered in the enzyme structure. All of these alternative pathways involve the migration of a “proton hole” to the active site cysteine residues, which may both facilitate the mobility of the Hg²⁺ and be more favorable at physiological pH (∼7.4).⁶⁵ Unfortunately, to explore any of these pathways for activation would require significant expansion of the QM region at a prohibitive computational cost. Regardless, the combined insights gained from the current simulation and the detailed analysis of the X-ray structure provide testable predictions for roles of these other active site residues in the catalytic pathway.

Besides the energetic considerations, the MEP determined here also identifies C558′ as the first of the C-terminal thiols to dissociate leaving C559′ in the 2- and 3-coordinate complexes with the active site thiolates. This result is in contrast to previous postulates predicting C559′ as first to dissociate,^2,14 which were based primarily on the observation of Cd²⁺ complexed to the equivalent of C136, Y194, Y535′, and C558′ in the Bacillus MerA X-ray structure.¹⁶ However, the orientation of that distorted tetrahedral complex would place the Hg²⁺ in a position that would be largely inaccessible by the C141 thiolate, which is inconsistent with the observation that Hg²⁺ does become fully bound to the C136/C141 pair for reduction. The reverse order identified here for dissociation of C558′ first is much more consistent with that observation and also provides a clearer rationale for the relative reactivities observed in vitro for the two C-terminal single alanine MerA mutants (CCAC and CCCA) with Hg(SR)₂ substrates.⁶⁶ As both mutants retain only one of the C-terminal cysteines, they can only displace one free thiol from the incoming Hg(SR)₂ substrate, and then must drag the other bound ligand as far into the dimer cleft as possible for C136 to initiate attack on the mixed enzyme–Cys-Hg-SR complex. With relatively small mercaptoethanol (S-ME) as the external ligand, the CCCA enzyme, which retains only C558′, was found to catalyze several cycles of reduction as fast as the wild type enzyme.⁶⁶ Initially this finding was thought to support the postulate that the C136–Hg–Cys558′ complex was a key intermediate in the binding pathway. However, in light of the structure and simulation results, a simpler explanation is that the C558′–Hg-S-ME complex can be positioned well into the cleft for optimal attack by C136 and dissociation of C558′ as in the wild type enzyme. In contrast, catalytic turnover of the same substrate by the CCAC enzyme, which retains only C559′, is ∼20-fold slower,⁶⁶ which makes sense in the context of the structure, as the positioning of the C559′–Hg-S-ME complex for attack by C136 would be less optimal and would likely require the C-terminal tail to adopt an energetically less favorable position for the reaction to occur.

Concluding Remarks

Building on our previous studies detailing the modes of transfer of Hg²⁺ between the N-terminal domain (NmerA) and the C-terminal cysteine pair (C588′ and C589′) of MerA,¹¹ the X-ray structure and QM/MM calculations presented here provide molecular-scale insight into how Hg²⁺ is transferred from the C-terminal cysteines into the MerA core for reduction to Hg⁰. To accomplish these transfers, Hg²⁺ is always paired with at least two thiolates and thus binds to the N-terminal, C-terminal, and core domains as a neutral complex. MerA orchestrates the transport of this soft divalent cation by pairing a competition between Cys thiolates and Hg²⁺ with a corresponding competition between Hg²⁺ and protons for the Cys thiolates. We have previously discussed this competition in more general terms relevant to Hg speciation.⁴³ Considering the similar energies of the reactant and product states, the present MEP and the pK_a values of the cysteines involved,⁶⁷ we expect that the interaction enthalpies between the pairs of cysteines in MerA and Hg²⁺ should be similar to that with two glutathione molecules in the cytoplasm. Thus, we propose an entropic driving force for each sequential Hg²⁺ transfer, i.e., the transfer from two free thiols in the cytoplasm to the dynamic metallochaperone-like NmerA, followed by the transfer from NmerA to the extended C-terminal loop of the MerA, followed by the transfer from the C-terminal loop to the reactive core of the enzyme. From our analysis of the underlying quantum mechanical energetics of computed reaction pathways, we find that MerA makes the Hg²⁺ transfers feasible by electrostatic stabilization of the reactant and product states relative to the intermediates, preventing the system from being trapped in deep potential wells. These findings are of general relevance for understanding the mechanisms of heavy metal trafficking in biological systems.

Supporting Information Available

Table S1, additional Figures S1–S3, the coordinates of the QM atoms in the RS, INT(I–III), TS(I–IV), and PS. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^¶ Center for Molecular Modeling and Design, Department of Medicinal Chemistry, School of Pharmacy, Fudan University, Shanghai 201203, China.

Author Present Address

^◆ Department of Chemistry, Earlham College, Richmond, IN.

Author Present Address

^○ Structural Genomics Consortium, Toronto, ON, M5G 1L7, Canada.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States