Azimuthal Polarization Filtering for Accurate, Precise, and Robust Single-Molecule Localization Microscopy

Abstract

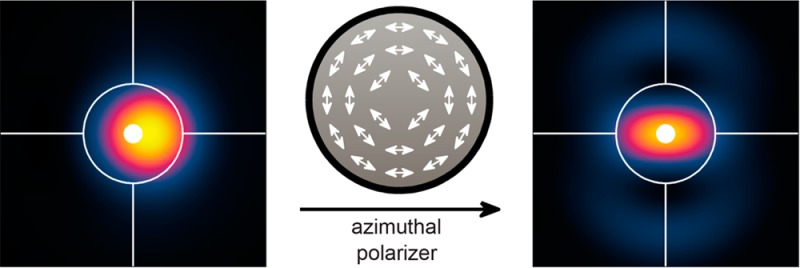
Many single nanoemitters such as fluorescent molecules produce dipole radiation that leads to systematic position errors in both particle tracking and super-resolution microscopy. Via vectorial diffraction equations and simulations, we show that imaging only azimuthally polarized light in the microscope naturally avoids emission from the z-component of the transition dipole moment, resulting in negligible localization errors for all emitter orientations and degrees of objective lens misfocus. Furthermore, localization accuracy is maintained even in the presence of aberrations resulting from imaging in mismatched media.

Single-molecule localization microscopy has made possible the nanoscale imaging of biological and material specimens with visible light, elucidating previously unobserved cellular structures¹⁻⁷ and polymer structural detail^8,9 with resolution beyond the diffraction limit (∼λ/2 ≈ 250 nm). While many different mechanisms have been utilized since 2006 to achieve super-resolution, such as (F)PALM,^10,11 STORM,¹² and PAINT,¹³ this family of methods relies upon the active control of single molecules in order to stochastically switch molecular labels between active states (molecules fluoresce in response to excitation light) and dark states (molecules do not fluoresce). Once the concentration of active molecules has been lowered such that each molecule is resolvable by a diffraction-limited microscope, the location of each molecule is estimated via image fitting or other statistical methods.^14,15 Then, another stochastic collection of molecules can be activated and their positions measured. This cycle continues until the structure of interest has been sampled with sufficient density, and finally, a reconstructed image of the specimen can be computed with resolution beyond the diffraction limit. A related optical measurement technique, two-dimensional (2D) and three-dimensional (3D) single particle tracking, images an individual emitter or scatterer and follows its position with nanometric precision as a function of time, providing scientists with unprecedented ability to directly observe molecular behaviors and interactions in living cells.^7,16 These methods can use fluorescent objects such as a single molecule, a nitrogen-vacancy (NV) center in diamond, or a semiconductor nanocrystal (e.g., quantum dots and rods), or can rely on scattering from a nanoscale metal particle such as a gold nanorod, etc. For simplicity, we refer to these single emitters or scatterers as molecules below.

The statistical precision with which a molecule’s position can be estimated from an image is termed the localization precision and scales primarily as the inverse square root of the number of photons N detected from the molecule.¹⁷⁻¹⁹ It is commonly measured by computing the standard deviation σ_x of repeated measurements x_i of the location of a molecule, given in one dimension by

1

where x̅ is the mean of the measurements. For the brightest of emitters, localization precisions of 1 nm are possible.²⁰⁻²² However, a key performance metric that is often overlooked in single-molecule imaging is that of localization accuracy, defined as the difference between the mean x̅ of repeated localizations and the molecule’s true position. In particular, accurate estimation of a molecule’s position from its image requires an accurate model of image formation by the microscope. Many super-resolution analysis methods assume that the image of a molecule generated by an optical system, called its point spread function (PSF), is equivalent to that of a point source and thus circularly symmetric, and images are often fit to an Airy disk or 2D Gaussian function.²³ However, the emission pattern of an orientationally fixed single molecule resembles that of an oscillating electric dipole in the far field.^24,25 Thus, the PSF of a rotationally fixed or moderately constrained single molecule is asymmetric, and the center of mass of its image shifts position as a function of molecular orientation and microscope defocus, leading to ∼100 nm localization errors when a microscope is misfocused by 200 nm.^23,26−28 Such errors affect both imaging applications designed to elucidate a structure below the diffraction limit, as well as tracking of spatially separated emitters in space and time. These errors also affect other orientationally constrained single-particle labels that emit or scatter light in a dipole-like radiation pattern, such as gold nanorods,^29,30 NV centers in diamond,^31,32 and semiconductor quantum rods.^33,34

Fortunately, several solutions to these systematic errors exist for single-molecule localization microscopy. The first is to simply ensure that the fluorescent probe is rotationally mobile, such that its transition dipole moment explores a large range of angles during a camera’s acquisition time; thus, the molecule effectively looks like an isotropic point source. For example, if the molecule’s transition dipole moment explores a cone of half angle α > 60° in rotational space, the localization error is bounded to ≤10 nm.²⁸ A second solution is to incorporate molecular dipole emission effects into a sophisticated model that is used for single-molecule image analysis; some of these methods specifically engineer the microscope PSF for additional orientation information. The molecular PSF is no longer assumed to be circularly symmetric, and the image fitting algorithm can now extract accurate molecular positions even if the image’s center of mass is shifted away from the molecule’s true position. Such approaches have been proposed and demonstrated for both 2D^18,35,36 and 3D^37,38 single-molecule imaging.

In this Letter, we propose a third solution to the dipole shift problem, namely, the use of an azimuthal polarization filter or azimuthal polarizer. This all-optical approach for correcting dipole mislocalization errors is compatible with any widefield epifluorescence microscope capable of imaging single molecules; can work with any nanoscale dipole emitter or scatterer regardless of wavelength, label attachment chemistry, sample geometry, or label rotational mobility; and does not require modeling of the exact imaging system in order to localize single emitters with nanoscale accuracy. We demonstrate, via vectorial diffraction equations and simulations, how the azimuthal polarizer enforces symmetry in the back focal and image planes of the microscope, thereby leading to images whose centers of mass always reflect the true position of the molecules in the sample of interest. We also characterize how reduced collection efficiency due to polarization filtering affects localization precision. Finally, we show that this scheme is robust against aberrations arising from refractive index mismatch of the sample, an aberration common while imaging biological specimens.

A fully vectorial electromagnetic model for the image formation of a single-molecule dipole by a high numerical aperture microscope (Figure 1A) gives key insight into the source of localization errors and how to mitigate them. In particular, it allows us to predict how an oscillating electric dipole’s angular emission spectrum is projected by the microscope into its back focal plane, also referred to as the pupil or Fourier plane. The specific patterns of illumination within this plane give rise to localization errors in super-resolution microscopy, and the symmetry of the polarized electric fields here too provides an elegant solution for eliminating these errors.

Figure 1.

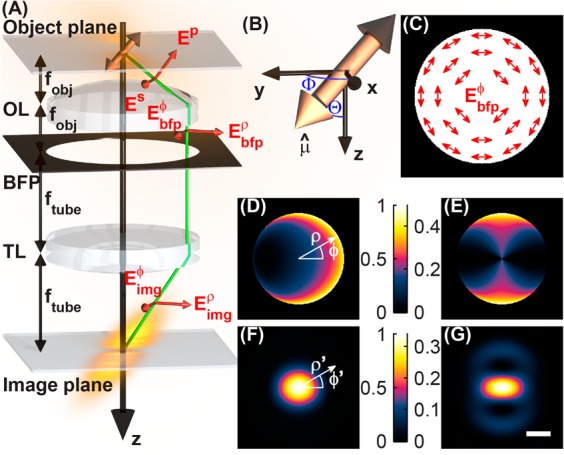
Simulation of image formation of a single dipole emitter by a high numerical aperture microscope. (A) Schematic of the optical imaging system (focal lengths not to scale), where OL denotes the objective lens with focal length f_obj, BFP denotes the back focal plane or pupil plane, and TL denotes the tube lens with focal length f_tube. The green line illustrates how rays are refracted in the microscope, and red vectors show how electric field polarization vectors propagate through the imaging system. With f_obj ≪ f_tube, the electric field emerging from the tube lens has a negligible z component. (B) Coordinate system for expressing the orientation of a molecule’s transition dipole moment in terms of a unit vector μ̂ or a pair of polar and azimuthal angles {Θ,Φ}. (C) Schematic of the azimuthally polarized electric field in back focal plane of the imaging system. The proposed azimuthal polarization filter has a spatially varying output polarization axis; it perfectly transmits electric fields parallel to the illustrated vectors and attenuates perpendicular ones. (D) A conventional clear-aperture microscope and (E) a microscope with an azimuthal polarization filter project different intensity distributions in their back focal planes from a molecular dipole emitter ({Θ = 45°,Φ = 0°} depicted here) embedded in matched media. In-focus intensity images of a molecular dipole emitter for (F) a clear-aperture microscope and (G) a microscope with the azimuthal polarizer. Azimuthal polarization filtering enforces a C₂ symmetry in both the pupil and the image plane intensity distributions but reduces the light transmission through the microscope; the intensities of these images are plotted relative to those of the clear-aperture microscope. Scale bar = 200 nm.

To consider the emission pattern of a single fluorescent molecule, first the orientation of the molecule’s transition dipole moment μ̂ can be parametrized in terms of its projection onto Cartesian unit vectors or in terms of a polar angle Θ and an azimuthal angle Φ in spherical coordinates (Figure 1B). The two descriptions are related by

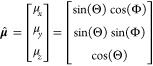2

In the far field, that is for distances r away from the dipole such that |r| ≫ λ, the intensity distribution resembles a torus given by

3

where λ is the emission wavelength and η is the angle between the vectors r and μ̂. The objective lens of a microscope collects the radiation from the dipole and collimates it to project its angular emission spectrum onto the back focal plane. We specify the lens to have a focal length f_obj and a numerical aperture NA = n₁ sin (θ_max), where n₁ is the refractive index of the immersion medium (n₁ = 1.518 for an oil-immersion lens) and θ_max is the maximum collection angle for the objective lens. Rays with inclination θ ≤ θ_max relative to the optical axis, collected from a dipole located at the focal point of the lens, are refracted such that they are parallel to the optical axis. The S-polarized component with respect to the face of the objective lens remains unchanged, but the P-polarized component is rotated so that it is perpendicular to the optical axis (Figure 1A). The field in the back focal plane is thus succinctly written as^39,40

4

where ρ is the normalized position in the back focal plane (with |ρ| = 1 corresponding to a distance of f_obj from the optical axis) and ρ̂ and ϕ̂ are the radial and azimuthal unit vectors, respectively, in cylindrical coordinates. Therefore, the radius of the circle that illuminates the back focal plane is given by ρ_max = sin(θ_max) = NA/n₁. Transforming eq 4 into Green’s tensor notation,²⁵ we obtain

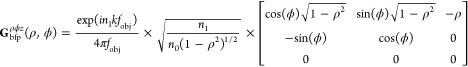5

and

6

where the ρϕz superscript explicitly denotes that the rows of the Green’s tensor G_bfp^ρϕz and electric field E_bfp are expressed in terms of the cylindrical unit vectors ρ̂, ϕ̂, and ẑ; n₀ is the refractive index at the back focal plane (typically air, n₀ = 1); we have assumed that the molecule resides in the ideal immersion media for the objective lens; the wavevector is given by k = 2π/λ; z is the distance between the molecule and the focal plane of the objective lens; and A is the amplitude of the molecule’s dipole moment. Note that these expressions are mathematically equivalent to the more conventional form of the Green’s tensor in Cartesian unit vectors, given by⁴¹

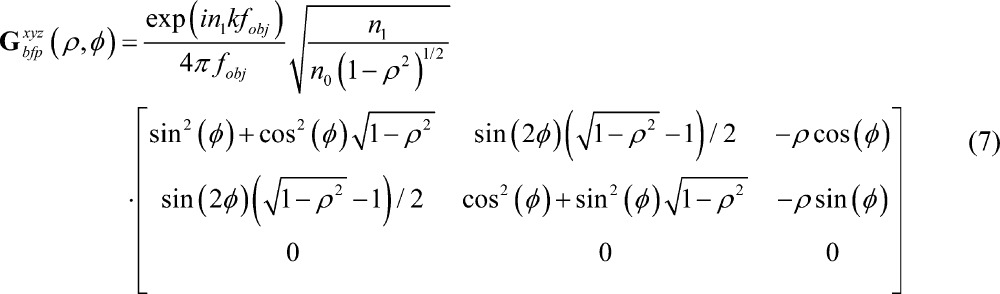7

and eq 6 with the cylindrical superscript ρϕz replaced by the Cartesian superscript xyz. Conversion between the two unit vector bases can be accomplished via the multiplication of a spatially varying rotation matrix R(ϕ), such that

8

and

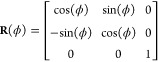9

The electric field in the back focal plane is then projected into the microscope image plane by the tube lens with focal length f_tube. Since high numerical aperture objectives typically have small focal lengths such that f_obj ≪ f_tube, light rays emerging from the tube lens travel mostly parallel to the optical axis, and we can use scalar diffraction theory to model light propagation through the tube lens. Thus, the electric field distribution in the image plane is the scaled Fourier transform of the electric field in the back focal plane, written as

10

where (ρ′,ϕ′) are cylindrical coordinates in the image plane and C is a complex constant. When displaying intensity images of the back focal plane or the image plane, we plot the field intensity ∥E_bfp^xyz∥² or ∥E_img∥².

Single-molecule dipoles that are oriented perpendicular to the optical axis (Θ = 90°) exhibit negligible localization error.^23,26,27 This property arises from the fact that the intensity distribution in the back focal plane exhibits C₂ symmetry that is preserved in the molecule’s image when the objective lens is defocused. When the molecule is tilted out of the sample plane (0° < Θ < 90°), the intensity distribution in the back focal plane no longer exhibits this symmetry (Figure 1D), leading to asymmetry in the molecule’s image and localization errors when the objective is defocused and symmetric estimators are used. Examining eq 5, we observe the special property that the z component of any single-molecule dipole does not couple into the azimuthally polarized electric field in the back focal plane (note the zero in row 2, column 3). In other words, the azimuthally polarized light arises from the in-plane projection of the dipole moment (μ_xx̂ + μ_yŷ), transforming the effective orientation of the single molecule to be perpendicular to the optical axis (Θ = 90°). Thus, if an azimuthal polarization filter (a spatially varying polarizer whose polarization axis at each position is oriented along ϕ̂, Figure 1C) is inserted into the optical detection path at the back focal plane, the resulting back focal plane intensity (Figure 1E) and image (Figure 1G) regain their C₂ symmetry regardless of defocus. If the centroid of this image is used for measuring the transverse (xy) position of a single emitter, this measurement will not contain any localization error resulting from the dipole orientation effect. This filtering scheme is compatible with any optical excitation geometry since it only needs to be inserted into the fluorescence detection optics at the pupil plane, and it provides the proper filtering for all molecules in the sample volume simultaneously.

Imaging simulations using the above equations were implemented by a custom MATLAB (MathWorks, Natick, MA) script (see Supporting Information for details). We model a single-molecule dipole emitting at λ = 600 nm embedded in a medium matching the refractive index of immersion oil (n₁ = 1.518). This light is collected by a high numerical aperture objective lens (NA = 1.4). The 3D PSFs for a dipole oriented at {Θ = 45°,Φ = 0°} are computed for a conventional clear-aperture microscope (Figure 2A) and a microscope with an azimuthal polarizer (Figure 2B). (The azimuthal PSFs for other molecular orientations are provided in Supporting Figure S1.) The apparent shift in the PSF’s center is clearly visible for the normal microscope, while the azimuthally polarized PSF remains centered regardless of objective defocus. Nonlinear least-squares fitting of xy cross sections of these PSFs to a 2D elliptical Gaussian function quantifies the localization error Δr for both imaging systems (Figure 2); similar localization errors would occur for any other estimator ignoring the exact dipole radiation pattern. The localization error for unpolarized imaging increases for both increasing defocus (z) and increasing molecular tilt away from the sample plane (smaller Θ, Figure 2C); for Θ = 60°, Δr = 13 nm at z = 100 nm, and Δr = 28 nm at z = 200 nm, while for Θ = 45°, Δr = 46 nm at z = 200 nm. Remarkably, the imaging system with an azimuthal polarization filter exhibits zero localization error for any molecular orientation and any misfocus amount (Figure 2D). Furthermore, the azimuthal filter restores localization accuracy when any dipole-like emitter’s position is measured.

Figure 2.

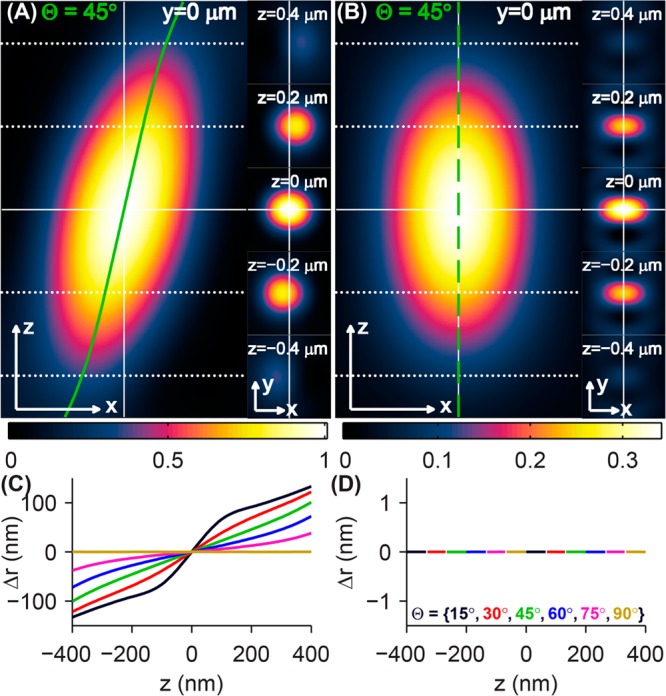
Simulated 3D PSFs and localization errors of rotationally fixed single dipole emitters. PSFs of a molecule oriented at {Θ = 45°,Φ = 0°} produced by (A) a microscope with a clear back focal plane and (B) a microscope with an azimuthal polarization filter. Cross sections of the 3D PSF in the xz (left) and xy (right) planes show the apparent shift of the dipole’s position as a function of defocus in the conventional microscope (solid green line in A), while the apparent lateral position of the molecule in the azimuthally polarized microscope remains fixed for all z positions (dashed green line in B). The intensity of the azimuthally polarized images is plotted relative to that of the clear-aperture microscope images. The apparent lateral position of an oriented molecule (black: Θ = 15°, red: Θ = 30°, green: Θ = 45°, blue: Θ = 60°, magenta: Θ = 75°, and gold: Θ = 90°) is computed as a function of defocus z for (C) the conventional microscope and (D) the azimuthally polarized microscope by fitting images to a 2D elliptical Gaussian function. The localization error Δr can be as large as ±100 nm for a defocus of 200 nm for conventional imaging. The imaging system with an azimuthal polarizer exhibits no localization error for any molecular orientation and any amount of objective lens defocus. Scale/axes arrows = 200 nm.

Azimuthal polarization filtering naturally leads to reduced light collection efficiency for the imaging system. This collection efficiency is a function of molecular orientation (Figure 3A), since an anisotropic emission pattern will be collected differently by the imaging system for different orientations of a dipole emitter. For Θ = 90°, the azimuthally polarized imaging system collects 65% of the light captured by the conventional microscope. For an inclined molecule (Θ = 45°), the clear-aperture microscope collection efficiency drops to 81%, while with an azimuthal polarizer, the light collection efficiency is reduced to 33% compared to the unpolarized microscope with Θ = 90°. Since the azimuthally polarized light in the back focal plane only contains contributions from the in-plane component of the dipole, the collection efficiency for the azimuthally polarized microscope drops to zero for molecules oriented along the optical axis (Θ = 0°). While these optical losses could be regarded as a disadvantage, the lost photons are precisely those that lead to unwanted localization errors, so the loss in photons is a small price to pay for greatly improved accuracy.

Figure 3.

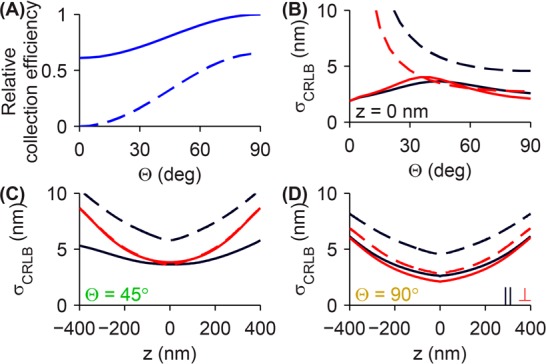
Effect of light collection efficiency on localization precision. (A) The clear aperture microscope is able to capture more light from a molecule oriented in the sample plane (Θ = 90°) than a dipole oriented along the optical axis (Θ = 0°) (solid line). With azimuthal polarization filtering, the light collection efficiency is reduced to 65% for in-plane dipoles (dashed line). Collection efficiencies are plotted relative to the total light captured by the clear-aperture microscope for Θ = 90°. (B) The limit of 2D localization precision, as computed by the Cramér–Rao lower bound (CRLB), as a function of dipole orientation for the clear aperture microscope (solid lines) and a microscope with an azimuthal polarizer (dashed lines) along the direction parallel to the in-plane transition dipole moment (μ_xx̂ + μ_yŷ, black lines) and the perpendicular direction (red lines). The CRLB for molecules whose polar orientation angle is less than 15° (<3.4% of all possible molecular orientations) is omitted for readability. The limit of localization precision is also shown as a function of lens defocus z for an emitter oriented at (C) Θ = 45° and (D) Θ = 90°. All calculations assume 1000 photons are captured in the clear aperture microscope images for all molecular orientations and defocus positions, while the azimuthally polarized images have correspondingly fewer numbers of detected photons due to a reduced light collection efficiency (A).

The effect of this reduced collection efficiency on localization precision can be quantified by calculating the Fisher information matrix I, used previously to characterize the limit of localization precision obtainable via super-resolution microscopy.⁴²⁻⁴⁴ Fisher information provides a convenient, quantitative metric for comparing the performance of estimation algorithms in the presence of statistical noise regardless of their implementation details. The inverse of the Fisher information matrix, called the Cramér-Rao lower bound (CRLB), provides a lower limit for the variance var (ξ̂) of any unbiased estimator ξ̂; that is

11

Since we are interested in the limit of 2D localization precision σ_CRLB, we calculate the square root of the inverse of the Fisher information matrix to compare the localization performance of conventional single-molecule microscopy against azimuthally polarized microscopy. The equations that express Fisher information as a function of PSF shape, number of detected photons, camera pixelation, and fluorescence background noise are described in the Supporting Information.

The limit of localization precision for the conventional and the azimuthally polarized microscopes are plotted in Figure 3B as a function of molecular polar orientation Θ for an in-focus molecule, with 1000 photons detected by the conventional microscope. (Camera pixelation and fluorescence background noise are not included here. However, they are incorporated into our computations of the limit of localization precision in Supporting Figure S2.) Instead of computing σ_CRLB along the Cartesian axes, we plot it along axes relative to the molecule’s orientation: the direction parallel to the in-plane projection of the dipole μ_xx̂ + μ_yŷ and the perpendicular direction, thereby exploiting the symmetry of the image. Due to the reduced number of photons in the azimuthally polarized image, its limit of localization precision is 4.6 nm versus 2.6 nm for the unpolarized image along the direction parallel to the dipole for an in-plane molecule. However, since the azimuthal image is narrower than the conventional image along the perpendicular direction, its limit of localization precision compares better against the conventional image: 2.8 nm versus 2.1 nm. As the molecule becomes more inclined relative to the sample plane (smaller Θ), the limit of localization precision for both imaging methods worsens gradually due to reduced collection efficiency. Therefore, one can expect a localization precision degradation of 50–75% along the parallel direction and <30% along the perpendicular direction when using an azimuthal polarizer across a range of molecular orientations that are pumped reasonably efficiently by widefield excitation (Θ ≥ 30°). Nevertheless, this loss in localization precision is more than offset by the substantial improvement in accuracy of azimuthal imaging.

We also compare the limit of localization precision for the two methods as a function of defocus (z) for two dipole orientations, Θ = 45° and Θ = 90°. We observe that both imaging methods have worse localization precision as defocus increases as expected from gradual blurring of the molecular PSFs. For an in-focus molecule inclined at Θ = 45° (Figure 3C), the azimuthally polarized image has modestly worse localization precision (5.8 nm along the parallel and 3.5 nm along the perpendicular directions) compared to the conventional image (3.6 nm along the parallel and 3.8 nm along the perpendicular). Defocus makes the localization precision penalty worse along the parallel direction (7.4 nm for azimuthal vs 4.2 nm for conventional at z = 200 nm), but the localization precision along the perpendicular direction is nearly identical for the two microscopes for all z. For Θ = 90°, the localization precision curves for the azimuthally polarized and conventional microscopes are nearly parallel as a function of defocus. Thus, we can expect the localization precision of an azimuthally polarized microscope to be 1.3–1.75 times larger than that of a conventional microscope, depending on the molecular orientation and localization axis. (The precision of using a least-squares algorithm to fit pixelated azimuthally polarized images with a 2D elliptical Gaussian function is comparable to the limit predicted by the CRLB. See Supporting Figures S2 and S3 for details.) Again, this decrease in localization precision is tolerable for most experimental applications because of the dramatic improvement in localization accuracy.

A key difficulty encountered while calibrating and removing dipole position error in localization microscopy is the optical aberrations that can perturb the single-molecule images. Since detailed modeling of the dipole emission is needed to predict the exact molecular PSFs projected by an imaging system, aberrations like astigmatism, spherical aberration, and coma too need to be modeled in order for these methods^18,35−38 to remain accurate. Here, we demonstrate that azimuthal polarization filtering is robust against the spherical aberration associated with imaging dipole-like emitters in mismatched media (e.g., focusing an oil-immersion objective into water) frequently encountered when imaging biological specimens (see the Supporting Information for formulas that modify G_bfp^ρϕz for the presence of index mismatch).

Images of a molecular dipole emitter (Θ = 45°) immersed in water at several depths (z_d = {200, 400, 600, 800} nm) above the coverglass are shown for the conventional (Figure 4A–D) and azimuthally polarized (Figure 4E–H) microscopes when the objective is defocused z = 200 nm above the position of best focus. Note the increasing circular symmetry apparent in both microscopes as the emitter moves further from the coverglass; this circular character is a result of increasing spherical aberration. Remarkably, spherical aberration slightly increases the accuracy of the conventional microscope with increasing depth (Δr = 58 nm for a depth of 200 nm compared to Δr = 41 nm for an emitter depth of 800 nm). However, these errors are still orders of magnitude greater than those of the microscope with the azimuthal polarizer. Since spherical aberration is itself a circularly symmetric aberration when modeled in the back focal plane of the microscope, adding spherical aberration does not change the C₂ symmetry of the azimuthally polarized single-molecule images. The center of the bright central spot in the azimuthally polarized dipole images remains an accurate indicator of the true lateral position of the molecule, regardless of how far the molecule is embedded in mismatched media or the amount of defocus of the objective lens.

Figure 4.

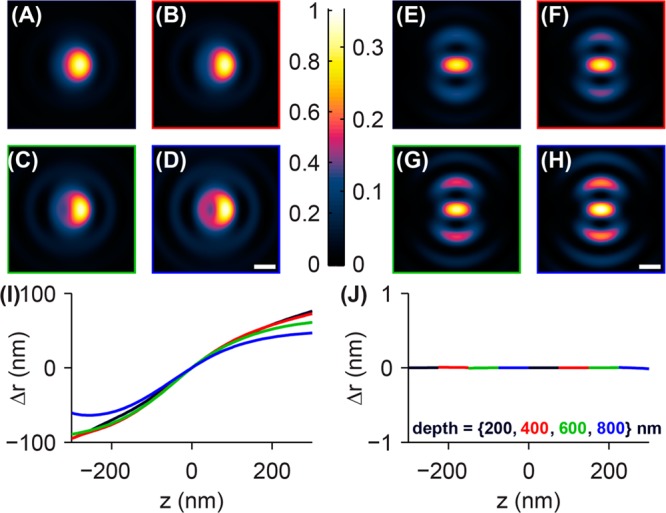
Effect of refractive index mismatch on images and localization error of single-molecule dipole emitters at various depths. Images of a fixed single molecule (Θ = 45°) immersed in water (n₂ = 1.333) at depths of (A) 200 nm, (B) 400 nm, (C) 600 nm, and (D) 800 nm from the coverglass–water interface are shown for the clear aperture microscope with an oil-immersion objective lens (n₁ = 1.518); the objective lens position is 200 nm above the position of best focus. Images of emitters at corresponding depths are shown for the azimuthally polarized microscope in E–H. The azimuthally polarized images are plotted in intensity units relative to those of the clear-aperture images. Scale bars = 200 nm. (I) Fitting the images to a 2D elliptical Gaussian function yields measurements of the localization error in the clear-aperture microscope as a function of emitter depth (black = 200 nm, red = 400 nm, green = 600 nm, and blue = 800 nm) and objective lens defocus z. The localization error worsens for increasing defocus z and decreasing emitter depth. (J) The microscope with an azimuthal polarizer exhibits no localization error for a large range of depths and defocus amounts, demonstrating that it is robust to index mismatch aberrations common during biological imaging.

In summary, we propose an azimuthal polarization filter that counteracts the localization error arising from the asymmetry inherent in the emission pattern of a molecular dipole. In particular, we show that the filtered image only contains light from the in-plane projection of the molecule’s transition dipole moment, ensuring that no localization error is incurred as a function of misfocus. As a consequence of rejecting the radially polarized light emitted by the dipole, this filter reduces the collection efficiency of the microscope, thereby worsening its localization precision by 30–75% depending upon molecular orientation, a small price to pay for the dramatic increase in accuracy. In principle, light split into radial and azimuthal polarization channels (as opposed to linear polarization channels common today) in a microscope can be used to measure molecular orientation and position simultaneously within a sample; this strategy recaptures the light thrown away by the azimuthal polarization filter while providing additional physical information about the dipole-like emitters. We reserve this demonstration as the subject of a future study.

An important advantage of the proposed azimuthal polarization filter is its all-optical nature of canceling localization error and, thus, its simplicity of implementation. This filter can be inserted into the back focal plane of a conventional epifluorescence microscope with minimal modifications to its detection optics. A detailed model of the imaging system is not necessary in order to implement an accurate fluorophore localization algorithm; in fact, a simple 2D elliptical Gaussian model of the molecular PSF is sufficient for subnanometer localization accuracy. Furthermore, this localization accuracy is robust against the spherical aberration associated with imaging molecules embedded in mismatched media relative to microscope coverglass, again using a simple elliptical Gaussian model for the microscope PSF. While such polarization optics are not currently commercially available, we believe that certain geometrical transformation strategies^45,46 or metal grating structures⁴⁷ could be adapted to implement an azimuthal polarization filter for super-resolution fluorescence microscopy and single-particle tracking. In the future with these optics readily available, the dipole emission effect will no longer be a source of systematic errors in single-molecule localization microscopy.

Supporting Information Available

Includes mathematical framework for modeling the image formation of single molecules embedded in mismatched media, details for simulating back focal plane and image plane intensity distributions, Fisher information matrices for estimation of emitter positions in 2D, images of azimuthally polarized PSFs for various molecular orientations, plots of the limit of localization precision for typical detector pixelation and fluorescence background noise present in single-molecule experiments, and simulated measurement of localization precision via fitting of pixelated azimuthally polarized PSFs. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States