Abstract
Allosteric regulation is an essential function of many proteins that control a variety of different processes such as catalysis, signal transduction, and gene regulation. Structural rearrangements have historically been considered the main means of communication between different parts of a protein. Recent studies have highlighted the importance, however, of changes in protein flexibility as an effective way to mediate allosteric communication across a protein. Scapharca dimeric hemoglobin (HbI) is the simplest possible allosteric system, with cooperative ligand binding between two identical subunits. Thermodynamic equilibrium studies of the binding of oxygen to HbI have shown that cooperativity is an entropically driven effect. The change in entropy of the system observed upon ligand binding may arise from changes in the protein, the ligand, or the water of the system. The goal of this study is to determine the contribution of the change in entropy of the protein backbone to HbI cooperative binding. Molecular dynamics simulations and nuclear magnetic resonance relaxation techniques have revealed that the fast internal motions of HbI contribute to the cooperative binding to carbon monoxide in two ways: (1) by contributing favorably to the free energy of the system and (2) by participating in the cooperative mechanism at the HbI subunit interface. The internal dynamics of the weakly cooperative HbI mutant, F97Y, were also investigated with the same methods. The changes in backbone NH dynamics observed for F97Y HbI upon ligand binding are not as large as for the wild type, in agreement with the reduced cooperativity observed for this mutant. The results of this study indicate that interface flexibility and backbone conformational entropy of HbI participate in and are important for the cooperative mechanism of carbon monoxide binding.
Allosteric regulation is an essential function of many proteins that control a variety of different processes such as catalysis, signal transduction, and gene regulation.1−3 Structural rearrangements have historically been considered the main means of communication between different parts of a protein. Recent studies have highlighted the importance, however, of changes in protein flexibility as an effective way to mediate allosteric communication across a protein.4−7
The dimeric hemoglobin from Scapharca inaequivalvis (a blood clam) (HbI) is the simplest possible allosteric system, with cooperative ligand binding between two identical subunits. HbI is unusual in this regard, as other known allosteric hemoglobins invariably incorporate unlike subunits. Because of its simplicity, HbI is an excellent system for directly exploring key issues of allostery. Equilibrium and kinetic experiments definitively establish that both O2 and CO bind cooperatively with no modulation of ligand affinity by non-heme ligands.8,9 Cooperativity in CO binding is evident in the increase in combination velocity as binding proceeds.9 Analyses of kinetic and equilibrium data for both oxygen and CO within the framework of the MWC allosteric model for wild-type HbI and its mutants10,11 provide remarkably good agreement for binding both ligands, strongly suggesting a very similar cooperative mechanism is operative for CO and O2. Consistent with these results are the crystallographic findings of very similar structures for HbI-CO and HbI-O2.12,13 The dimer is formed by apposition of helices E and F,12,13 bringing the heme groups into close proximity and permitting more direct communication in HbI than in mammalian hemoglobins. This assembly, which we term an “EF dimer”, has now been found in hemoglobins from echinoderms14 and megadalton annelid hemoglobin complexes.15
Ligand binding in HbI is associated with localized structural transitions (Figure 1) characterized by only a slight change in quaternary structure (3.3° subunit rotation) but with striking tertiary changes at the dimeric interface, including the movement of Phe 97 from the heme pocket into the interface.13 This side chain motion disrupts a cluster of well-ordered water molecules. As a result, the observed water molecules in the crystal structures are more abundant and more ordered in the unliganded interface than in the liganded form.10,13 The limited quaternary structural transitions of HbI permit the full expression of cooperative oxygen binding within the crystal lattice,16 a rare phenomenon not even observed with the related tetrameric S. ineaquivalvis hemoglobin.17 This property has permitted the use of time-resolved crystallographic analysis with nanosecond time resolution to follow the key kinetic structural transitions, triggered by photodissociation of CO, that underlie cooperative ligand binding.18 These crystallographic results have been supplemented with time-resolved X-ray solution scattering results that reveal overall kinetic pathways that follow ligand release.19 The kinetic structural transitions revealed by these studies rely on conformational flexibility whose thermodynamic contribution to cooperative ligand binding is the subject of this study.
Figure 1.
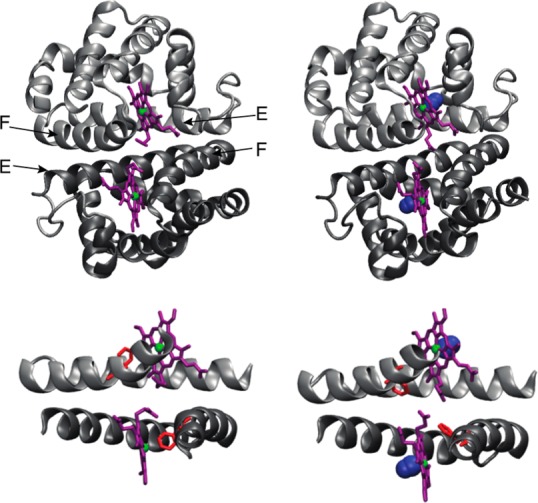
Crystal structures of the unliganded and CO-bound HbI. The HbI homodimer subunits are colored dark and light gray. Purple sticks represent the prosthetic heme group. Iron is colored green. CO is colored blue. The structures of unliganded HbI (left) and CO-HbI (right) are generated from the PDB entries 4SDH and 3SDH, respectively. Interfacial helices E and F are shown at the bottom, to highlight the conformational transition undergone by Phe 97 (red) upon CO binding. The structural representation was drawn using VMD.26
Thermodynamic equilibrium studies of binding of oxygen to HbI have shown that cooperativity in HbI is an entropically driven effect.20 In particular, the differences in free energy (ΔΔG) and entropy [T(ΔΔS)] between the first and second oxygen binding event are −1.3 and −5.3 kcal/mol at 298 K, respectively. Hence, in HbI, binding of the second oxygen molecule is made thermodynamically more favorable by a less negative ΔS. This effect could result from a ligand-linked change in the conformational entropy of HbI, that of the water surrounding HbI, or a combination of both. The idea that cooperativity could arise from changes in protein conformational dynamics upon ligand binding was originally introduced in 1984 by Dryden and Cooper.21 In this entropically driven allosteric mechanism, small changes in the protein conformational fluctuations add up to a significant difference in free energy (ΔΔG) and become the origin of the allosteric response. The importance of changes to protein dynamics in ligand binding processes has recently been highlighted in nuclear magnetic resonance (NMR) relaxation studies.22−24
All of this evidence implies a central role of the structure and dynamics of HbI and of the interfacial water in allosteric communication between the two binding sites. In this study, we investigated how changes in HbI flexibility contribute to cooperativity using molecular dynamics simulations and NMR spectroscopy.
To analyze how changes in protein dynamics are coupled to and correlated with structural changes upon ligand binding, we compared the internal dynamics of wild-type (WT) HbI with those of the F97Y HbI mutant. In this mutant protein, the side chain at position 97 is locked in the dimeric interface, mimicking the high-affinity conformation.25 In F97Y HbI, the structural transition associated with ligand binding, from the low-affinity state to the high-affinity state, is completely restricted. Relative to WT HbI, F97Y HbI has reduced cooperativity, characterized by a Hill coefficient of 1.1. Therefore, this mutant protein allowed us to examine the role played by changes in protein flexibility in allostery when structural changes associated with ligand binding are severely reduced and the protein is trapped in a high-affinity state. We found that CO binding has a weaker effect on the backbone NH dynamics of F97Y HbI than on those of WT HbI, implying that the internal dynamics contribute to the cooperative binding of carbon monoxide. This work demonstrates the importance of the modulation of flexibility in cooperative ligand binding.
Materials and Methods
Simulation Methods
The coordinates for the set of four HbI systems, namely, wild type bound and free and F97Y HbI bound and free, were obtained from PDB entries 3SDH, 4SDH, 2AUO, and 2AUP, respectively. The structure files for the homodimer systems were generated using the corresponding plugin within VMD version 1.9.1.26 The protein and the water molecules that were resolved in the original PDB files were placed in a 100 Å3 simulation box, which was then filled with additional TIP3 water molecules. The net charge of the system was neutralized with Cl– ions.
All simulations were implemented with NAMD27 version 2.9 along with the CHARMM27 force-field parameterization.28 The long-range electrostatic interactions were computed with the particle mesh Ewald (PME) method. A smooth cutoff for the vdW interactions was set to 12 Å with a switching distance of 10 Å. The distances for all hydrogen bonds in the homodimers were constrained using the SHAKE algorithm,29 while those for the water molecules were kept rigid using the SETTLE algorithm.30
The simulation protocol goes as follows. First, the systems were energy-minimized using a conjugate gradient method coupled to a line-search algorithm for 50000 steps, which was more than sufficient to reach convergence. The energy minimization was followed by a series of thermalization, equilibration, and production runs under periodic boundary conditions performed in the NPT ensemble. The thermalization schedule was conducted using a time step of 0.5 fs under constant-pressure (1 atm) conditions using a Langevin barostat by bringing the system from a temperature of 10 K to the target temperature of 298 K in 10 K increments via temperature reassignments every 1.0 ps. Once the target temperature was reached, the simulation proceeded for a total of 300 ps. The systems were further equilibrated at a constant temperature (298 K) and pressure (1 atm) for a total of 500 ps with 1 fs time steps under the action of Langevin temperature control. The Langevin pressure control values for the oscillation period and damping coefficient were set to 200 and 100 fs, respectively, and the damping coefficient in the Langevin thermostat was set to 0.1 ps–1. The time step was then increased to 2 fs, and the systems were allowed to equilibrate for 1 ns in the final preparation for production runs. For each system, three 20 ns production runs and one 200 ns production run were collected. The results from the 200 ns runs did not differ significantly from those from the 20 ns runs; as a consequence, the 200 ns production runs were divided into 20 ns blocks and combined with the 20 ns production runs for data analysis.
Additional simulations of CO-bound and free WT HbI were performed in the NVE ensemble. The systems were first minimized using a conjugate gradient algorithm and then equilibrated in the isothermal–isobaric ensemble using Langevin dynamics and the Nosé–Hoover Langevin piston method. Subsequently, equilibration was performed in the NVE ensemble with velocity reassignment to generate three trajectories with independent velocities and to ensure the stability of the temperature. The systems were then simulated in the NVE ensemble for 8 ns. The first 2 ns were sufficient for the final equilibration, as judged by the backbone and all-atom rmsd. An additional 6 ns were collected and used to confirm the results of the longer NPT ensemble simulations. The Lipari–Szabo order parameters of the simulations in the NVE and NPT ensembles agree within the error. In addition, the transitional behavior of the Phe 97 χ1 dihedral angle was observed in these shorter trajectories, as well.
To characterize the structural and dynamical changes between the free and bound state of HbI, we calculated the radius of gyration, the secondary structure, the rms fluctuations, the dihedral angle χ1 defined by the C, Cα, Cβ, and Cγ atoms of residue Phe 97 in the WT and Tyr 97 in F97Y mutant HbI, and Lipari–Szabo order parameters31,32 using VMD26 along with bespoke programs previously described elsewhere.33
Protein Expression and Purification
HbI was expressed in Escherichia coli Q-cells34 under the control of a T7 promoter, in M9 minimal medium supplemented with a standard vitamin mix and a solution with traces of metals.35 To label HbI, the glucose and ammonium chloride of M9 was substituted with 13C- and 15N-labeled compounds, respectively. HbI was induced for 6 h with 1 mM isopropyl β-d-1-thiogalactopyranoside (IPTG) and supplemented with 84 μM aminolevulinic acid (ALA).
HbI and F97Y HbI were purified as previously described.35 Cell pellets were resuspended in 0.5 M Tris (pH 8.0), 100 mM NaCl, 10 mM ethylenediaminetetraacetic acid (EDTA), 1 mM phenylmethylsulfonyl fluoride (PMSF), and 5% (w/v) glycerol. Cells were lysed by sonication, duty cycle 7, for 30 s every minute for 5 min. The lysed cell solution was treated with DNase1, RNaseA, and 6 mM MgCl2 for 30 min. Cellular debris was pelleted by centrifugation at 15000 rpm. Contaminates salt out of solution at 45% saturation with ammonium sulfate; HbI salts out at 95% saturation with ammonium sulfate. HbI was isolated using a DEAE column in 40 mM 2-(cyclohexylamino)ethanesulfonic acid (CHES) (pH 9.0) and a CM Sepharose column in 40 mM 2-[4-(2-hydroxyethyl)piperazin-1-yl]ethanesulfonic acid (HEPES) (pH 7.0).
Sample Preparation
CO-liganded samples were prepared by flushing the tubes with CO before adding CO-saturated hemoglobin and sealing. Unliganded HbI samples were prepared from CO-HbI; to remove CO, samples were first agitated and flashed with white light in the presence of oxygen. Then to produce unliganded samples, O2-HbI was exposed to flashes with white light in a N2 environment overnight. A trace amount of sodium dithionite was added to deoxy-HbI samples before being sealed with epoxy within the anaerobic chamber. Absorbance at 534, 416, or 422 nm light indicates the presence of deoxy-HbI, O2-HbI, or CO-HbI, respectively. Similar procedures have been successfully used on other hemoglobins for many years.36−38
NMR Spectroscopy
The backbone resonance assignments of HbI in the liganded and unliganded states were obtained39 and are available from the BioMagResBank as entries 25285 and 25286, respectively. Three-dimensional (3D) sensitivity-enhanced gradient-selected 1H–15N TROSY (transverse relaxation-optimized spectroscopy) triple-resonance experiments [HNCA, HN(CO)CA, HNCACB, CBCA(CO)NH, HNCO, and HN(CA)CO]40,41 were conducted at 14.1 T and 298 K using uniformly 2H-, 13C-, and 15N-labeled 0.6 mM F97Y HbI [50 mM HEPES (pH 7.0), 150 mM NaCl, and 95% H2O/5% D2O]. Additional 3D 15N-edited 1H–1H NOESY and HMQC-NOESY-HSQC experiments were conducted at 14.1 T and 298 K and used to aid in the backbone resonance assignment of F97Y HbI in both the free and bound states. All NMR 15N relaxation experiments were performed at 298 K on uniformly 15N-labeled samples of HbI and F97Y HbI [50 mM HEPES (pH 7.0), 150 mM NaCl, and 95% H2O/5% D2O] at the following concentrations: 0.8 mM CO-HbI, 0.8 mM unliganded HbI, 0.7 mM CO-F97Y, and 1.0 mM unliganded F97Y. All NMR triple-resonance and 15N spin relaxation data were collected on a Varian Inova spectrometer operating at 600 MHz equipped with a triple-resonance cold probe. The temperature was calibrated using a sample of 100% methanol. 15N R1 and R2 values and {1H}–15N NOEs were measured using standard methods.42 Nine relaxation delays, two of which were duplicates, were used to measure R1 and R2. Relaxation delays ranged between 0 and 0.666 s for R1 and between 0 and 0.090 s for R2. The interval between 180° pulses in the CMPG experiment used to measure R2 was 1.5 ms. Three sets of NOE data (proton-saturated and nonsaturated spectra) were collected in an interleaved manner. Data were acquired with 128 (t1) × 2048 (t2) complex points and spectral widths of 2200 × 8000 Hz. Data processing was performed using NMRPipe,43 Sparky,44 and Curvefit (www.palmer.hs.columbia.edu), along with programs written in house. Intensities of cross-peaks were used to quantify relaxation, and uncertainties were estimated from duplicate (R1 and R2) or triplicate (NOE) experiments.
Model-Free Analysis
The dominant source of an amide 15N spin relaxation is the dipolar interaction with the attached proton spin and the chemical shift anisotropy (CSA) mechanism. The experimentally measured relaxation rates R1 and R2 and the NOE are dependent on linear combinations of the spectral density function at specific frequencies45
| 1 |
| 2 |
| 3 |
where c = ωNΔσ/√3, d = (μ0hγHγN/8π2)⟨rNH⟩–3, μ0 is the permeability of free space, h is Planck’s constant, γH and γN are the gyromagnetic ratios of the H and N nuclei, respectively, rHN is 1.04 Å, and Δσ = −162 ppm is the 15N CSA.
Relaxation rates were analyzed using the Lipari–Szabo model-free formalism.31,32 The Lipari–Szabo model-free formalism assumes that the internal motion of the N–H vector is uncorrelated with the overall rotational motion of the protein and is characterized by two parameters: a generalized order parameter, S2, which defines the amplitude of the motion, and an effective internal correlation time, τe, which measures the time scale. In the Lipari–Szabo formalism extended by Clore et al.,46 the spectral density function can be described as
| 4 |
where S2 = Sf2Ss2, 1/τf′ = 1/τf + 1/τm, and 1/τs = 1/τs + 1/τm. S2 is the generalized order parameter, and Sf2 and Ss2 are the generalized order parameters of the fast and slow components, respectively, of internal motion. The order parameter is a measure of the degree of freedom of the motion of the intermolecular amide bond vector; S2 is equal to 1 if the motion is completely restricted and is equal to 0 for isotropic motion. τm is the isotropic rotational correlation time, and τf and τs are the effective correlation times of the fast and slow internal motions, respectively. Both τf and τs are much faster than τm.
Values of the R2/R1 ratio were used to estimate the rotational diffusion tensor using the program r2r1_diffusion (www.palmer.hs.columbia.edu). Residues that have a value of the R2 rate constant more than one standard deviation from the mean and/or have NOE values of <0.65 were excluded from this analysis.47
The relaxation data were analyzed using the program FAST Modelfree48 (http://xbeams.chem.yale.edu/∼loria) and Modelfree 4.20 (www.palmer.hs.columbia.edu). Five different motional models were used to facilitate the analysis of the relaxation data.49 For models 1–4, S2 = Sf2. Model 1 optimizes Sf2 assuming that internal motions are very fast (τf ≈ 0) and slow internal motions are negligible (Ss2 = 1, and τs = 0). Model 2 optimizes Sf2 and τf = τe assuming slow internal motions are negligible (Ss2 = 1, and τs = 0). Models 3 and 4 are the same as models 1 and 2, respectively, but include the chemical exchange term Rex. Model 5 optimizes Sf2, Ss2, and τs = τe and assumes that internal motions on the fast time scale are very fast (τf ≈ 0).
Order parameters have been used to estimate an upper bound for the change in entropy, ΔS, resulting from conformational restriction:50
| 5 |
where N is the total number of affected nuclei, Sa,i and Sb,i are the order parameters of the ith spin in states a and b, respectively, and kb is Boltzmann’s constant. This equation accounts for only the entropic effect of the part of the conformational ensemble characterized by the set of S2 values and neglects any correlation between spins.
Results
Characterization of the Structure and Dynamics of HbI in Solution Using MD Simulations
HbI Structure in Solution
Analysis of the solution structures of WT HbI and the F97Y mutant from the MD trajectories in the free and CO-bound states shows only minor differences from the X-ray structures of these proteins. HbI is a symmetric dimer in solution; the small difference observed between the X-ray structures of the two subunits is lost, and the system relaxes to a symmetric structure during the equilibration period of the trajectories (Table 1). Our results are in agreement with those of a previous Raman spectral study of unliganded HbI, where the observation of only a single set of lines had indicated that the protein is symmetric in solution.51 These results indicate that the small asymmetry observed between the two subunits in the liganded and unliganded HbI crystal structures results from lattice interactions and is not fundamental to the function of HbI.
Table 1. Means and Errors of the Radii of Gyration Calculated from the MD Simulations.
| protein | rgyr of dimer (Å) | rgyr of subunit A (Å) | rgyr of subunit B (Å) |
|---|---|---|---|
| unliganded WT | 19.21 ± 0.09 | 15.03 ± 0.09 | 15.01 ± 0.07 |
| CO-bound WT | 19.23 ± 0.07 | 14.96 ± 0.06 | 14.96 ± 0.06 |
| unliganded F97Y | 19.23 ± 0.07 | 15.03 ± 0.10 | 15.04 ± 0.08 |
| CO-bound F97Y | 19.15 ± 0.07 | 14.95 ± 0.05 | 14.96 ± 0.06 |
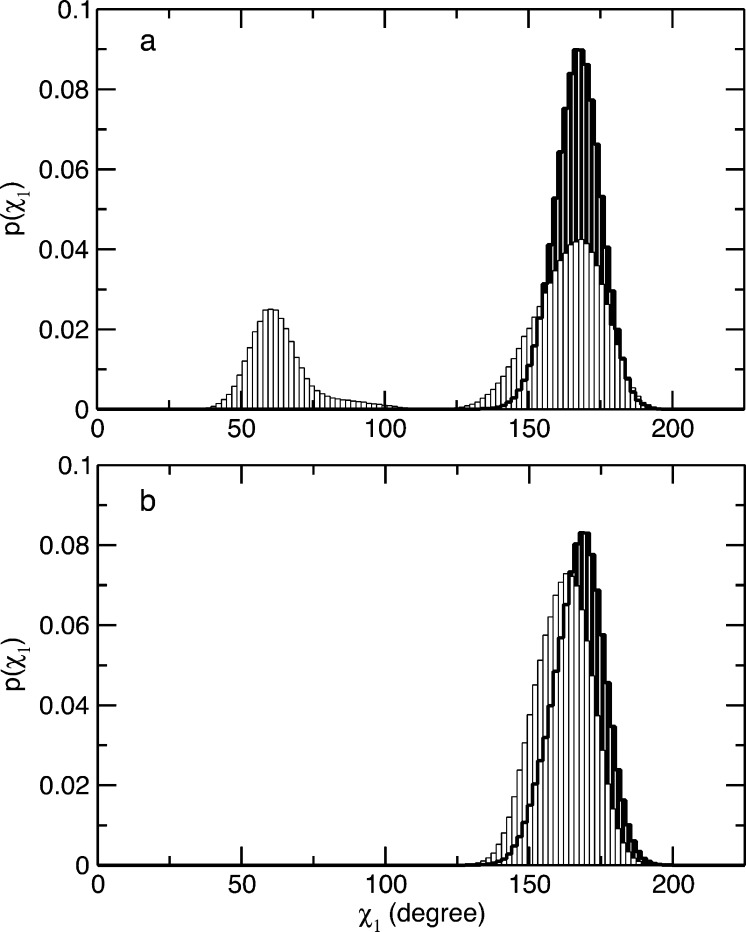
One of the main differences observed in the X-ray structures of the free and bound states of HbI is the movement of the side chain of Phe 97 from the heme pocket into the interface,13 as indicated by the change in the χ1 angle [from ≈60° to ≈160° upon binding CO (Figure 1)]. These conformations of the side chain of Phe 97 are termed as T- and R-state conformations, characterized by χ1 values of ≈60° and ≈160°, respectively. Analysis of the MD trajectories showed that while the side chain of Phe 97 always maintains the R-state conformation when bound to CO, the side chain of Phe 97 fluctuates between the T- and R-state conformations in the absence of CO, as shown in Figure 2a. This result is remarkably different from the X-ray structures and from what was observed in a previous MD study of HbI.13,52 The observed discrepancy can be explained considering that in this study WT HbI and the F97Y mutant were simulated for a much longer time. The MD trajectories previously collected by Zhou and co-workers of WT HbI in the free and bound states are 1 ns long. We collected longer trajectories, three 20 ns long and one 200 ns long trajectories for each protein in each state. Each protein was equilibrated for a period of 6 ns. The transition of the side chain of Phe 97 from the T to R state occurs in the absence of CO during the equilibration period, after which the side chain fluctuates between the two states.
Figure 2.
Population distribution of dihedral angle χ1 of residue 97. Shown are the distributions of the populations of dihedral angle χ1, defined by the C, Cα, Cβ, and Cγ atoms of residue 97, calculated from the MD simulations of WT HbI (a) and F97Y HbI (b). The histograms calculated from the MD trajectories of the unliganded and liganded proteins are colored white and black, respectively.
For the entire lengths of the simulations of F97Y mutant HbI, the side chain for Tyr 97 is always in the bound-state conformation in the presence and absence of CO, as observed in the X-ray structures (Figure 2b).
Dynamics of HbI in Solution
The dynamics of HbI in solution were analyzed to fully understand the dynamic changes undergone by this protein upon ligand binding and particularly to investigate the important role of the interfacial residues. In addition, to test the hypothesis that the internal dynamics of HbI is coupled to its allosteric regulation, the fast internal motions of the weakly cooperative R-state mimetic, F97Y HbI, were simulated and compared with the dynamics of WT HbI.
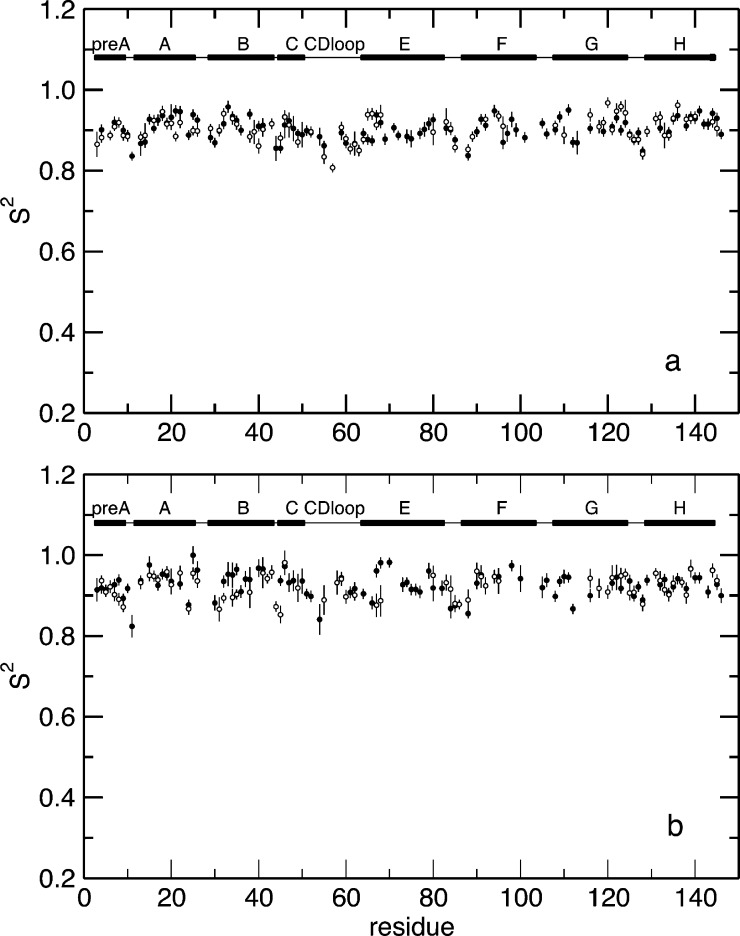
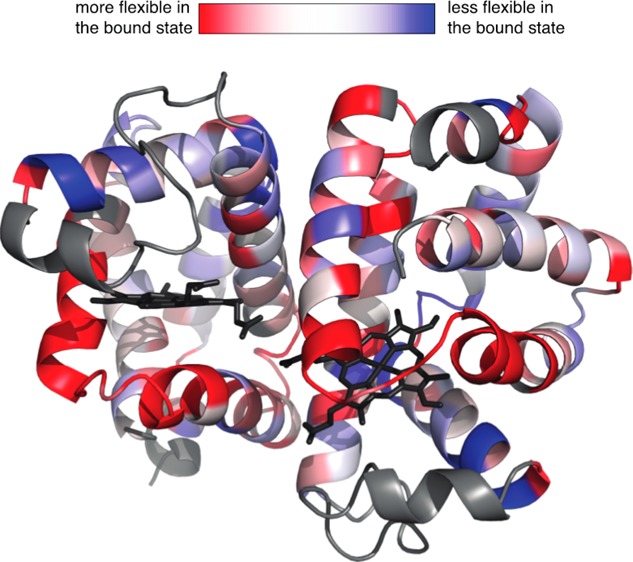
To characterize the internal dynamics, the Lipari–Szabo order parameters, S2, were calculated from the MD simulation of WT HbI and the F97Y mutant in the liganded and unliganded states (Figure S1 of the Supporting Information). To be able to validate our findings against experimental data, we focused our analysis on the dynamics of the backbone amide groups. The computed S2 values are in good agreement with the experimentally determined values (described below), as shown in Figure 3, with the exception of helix C and the CD loop (highlighted with a red box in Figure 3), where the large errors in the order parameters indicate that the MD simulations have not converged in these regions of the protein. For this reason, residues from helix C and the CD loop were excluded from the following analysis. The order parameter difference between the free and bound states represents the change in backbone NH dynamics that occurs upon ligand binding. The calculated difference of the order parameters between the free and bound states shows that there are small differences in the internal dynamics of the protein in these two states (Figure S1 of the Supporting Information and Figure 4). In the WT protein, the largest differences are observed in the pre-A, B, F, and G helices (Figure 4), while the F97Y internal dynamics are most affected by binding in helices E and F. From Figure 4, one can make the qualitative observation that the residues surrounding the heme group become more flexible upon ligand binding. This tendency is more evident in the WT where, for example, the backbone amide groups of helices E and F that become more flexible upon CO binding are located on the heme-facing side of the helix. The backbone amide groups of both WT and F97Y HbI become globally more flexible upon binding CO, but this effect is more pronounced in the WT protein than in the F97Y mutant (Table 2). Comparison of the difference of the backbone NH S2 values with the computed rms fluctuations of each helix (Figure 5) shows a good correlation of the data: a decreased average order parameter of a helix associated with binding corresponds to an increased rms fluctuation from the average structure of the helix, and vice versa. Helix G of WT HbI shows the largest rms fluctuation difference between the free and bound states. This is a result of the fraying of the N-terminus of helix G that is observed with a much higher probability in the CO-bound state (Figure 6). In addition, the C-terminus of helix F is less stable in the CO-bound state of WT HbI than in the unliganded state.
Figure 3.
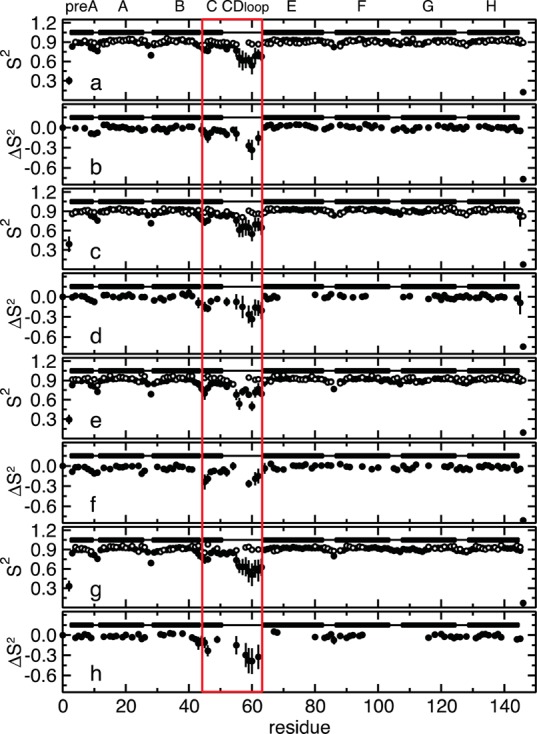
Comparison of the experimentally determined order parameters, S2, with those calculated from the MD simulations. The S2 values are shown as a function of the protein sequence for WT CO-bound HbI (a), unliganded WT HbI (c), CO-bound F97Y HbI (e), and unliganded F97Y HbI (g). Experimentally determined S2 values are shown as empty circles, and S2 values calculated from the MD simulations are shown as filled circles. The difference between the simulated and experimental S2 (ΔS2 = SMD2 – Sexp2) is shown as a function of residue number for WT CO-bound HbI (b), unliganded WT HbI (d), CO-bound F97Y HbI (f), and unliganded F97Y HbI (h). Secondary structural elements are shown at the top of each plot. Solid bars represent α-helices, and lines represent loops. Helix C and the CD loop are highlighted with a red box.
Figure 4.
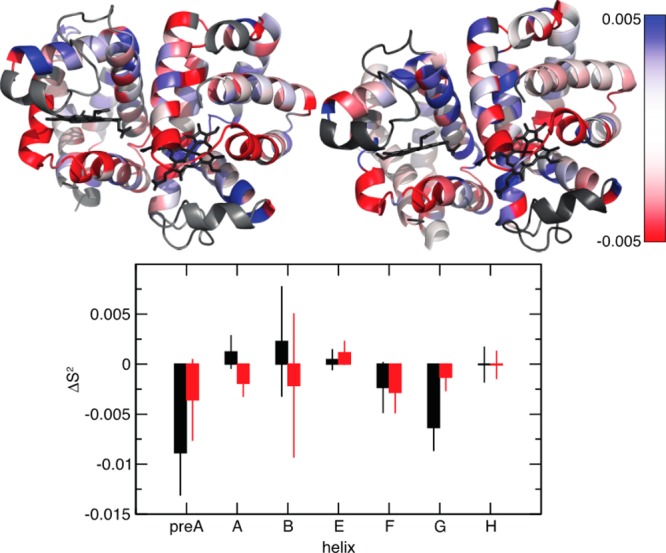
Difference in the order parameter between the free and bound states calculated from the MD simulations. The top panel shows ΔS2 = SCO2 – Sfree2 calculated for each residue of WT and F97Y HbI mapped onto the respective structure. The structure of WT HbI is shown on the left and that of F97Y HbI on the right. The color scale goes from red (ΔS2 = −0.005) to white (ΔS2 = 0) to blue (ΔS2 = 0.005). Residues characterized by a ΔS2 value of ≤−0.005 are colored red, and residues characterized by a ΔS2 value of ≥0.005 are colored blue. Proline residues and residues located on helix C and on the CD loop are colored gray. The structural representation was drawn using PyMOL.57 The bottom panel shows the difference in the order parameter between the liganded and unliganded states, averaged for each secondary structural element (ΔS2 = ⟨SCO2 – Sfree2⟩) between CO-bound and free WT HbI (black) and F97Y HbI (red).
Table 2. Average Order Parameters Calculated from the MD Trajectories for Each Secondary Structural Element of HbI and F97Y HbI in the Liganded and Unliganded States.
| structural element | 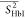 |
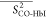 |
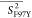 |
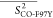 |
|---|---|---|---|---|
| pre-A | 0.880 ± 0.004 | 0.875 ± 0.004 | 0.878 ± 0.004 | 0.877 ± 0.005 |
| A | 0.913 ± 0.002 | 0.916 ± 0.001 | 0.916 ± 0.001 | 0.913 ± 0.002 |
| B | 0.899 ± 0.003 | 0.898 ± 0.003 | 0.905 ± 0.003 | 0.900 ± 0.003 |
| C | 0.82 ± 0.02 | 0.81 ± 0.03 | 0.83 ± 0.02 | 0.81 ± 0.03 |
| CD loop | 0.69 ± 0.05 | 0.73 ± 0.04 | 0.72 ± 0.04 | 0.71 ± 0.03 |
| E | 0.921 ± 0.001 | 0.922 ± 0.001 | 0.920 ± 0.002 | 0.923 ± 0.001 |
| F | 0.918 ± 0.002 | 0.914 ± 0.003 | 0.918 ± 0.002 | 0.916 ± 0.002 |
| G | 0.910 ± 0.001 | 0.897 ± 0.004 | 0.908 ± 0.001 | 0.907 ± 0.001 |
| H | 0.918 ± 0.001 | 0.917 ± 0.001 | 0.918 ± 0.001 | 0.916 ± 0.001 |
Figure 5.

Root-mean-square (rms) fluctuations calculated for the α-helices of HbI from the MD simulations. The rms fluctuations of each α-helix of the protein are colored black for WT HbI and red for F97Y-HbI; opaque and transparent bars are used for the liganded and unliganded states, respectively. The backbone N, C, and O atoms were used to calculate the rms fluctuations. The error bars were calculated from the standard deviation among the trajectories.
Figure 6.
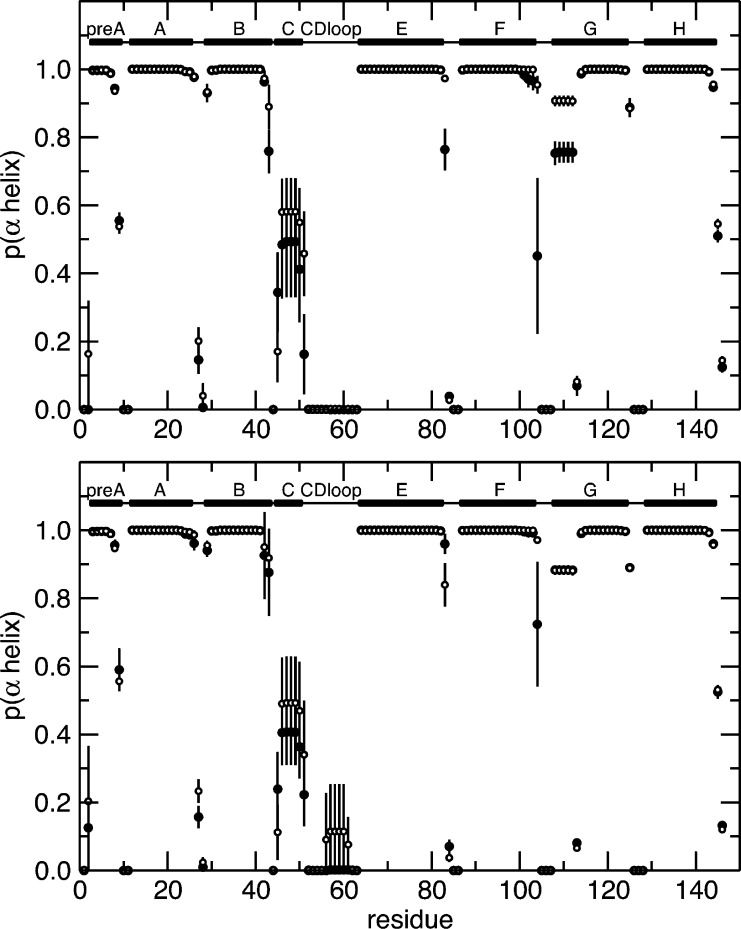
Secondary structure probability. The probability of being in an α-helix is shown for each residue of HbI as a function of the protein sequence. The probabilities calculated for each residue from the MD trajectories of the unliganded and liganded protein are shown with empty and filled circles, respectively. The top plot shows the results calculated from the MD simulation of WT HbI and the bottom plot those of F97Y HbI. Secondary structural elements are shown at the top of each plot. Solid bars represent α-helices, and lines represent loops.
Thermodynamic equilibrium studies of binding of oxygen to HbI have shown that binding of the second oxygen molecule is made more favorable by a less negative entropic term, ΔS.20 The computed S2 values for the backbone amide groups were used to estimate the change in backbone conformational entropy associated with binding.50 The protein conformational entropic contribution to the binding free energy of carbon monoxide (TΔS) was estimated to be 1.8 ± 0.6 kcal/mol for WT and 1.3 ± 0.6 kcal/mol for F97Y. The results of the MD simulations show that as in the WT protein, F97Y HbI also becomes more flexible upon binding CO but to a smaller degree than the WT protein. The reduced effect that CO binding has on the internal dynamics of the protein can explain the reduced cooperativity observed in this mutant protein relative to that of WT HbI. Figure 7 shows the contribution made by each helix to the conformational entropy. Helices pre-A, F, and G make the largest contribution to the conformational entropy. In the WT protein, the contribution from helix pre-A and helix G is larger than in the mutant protein. The backbone amide dynamics in the interfacial helices E and F are affected differently by binding the ligand and consequently have opposite effects on the entropic change associated with binding. Helix C and the CD loop were excluded from this analysis because these regions of the protein need longer trajectories to converge (Figure 3).
Figure 7.
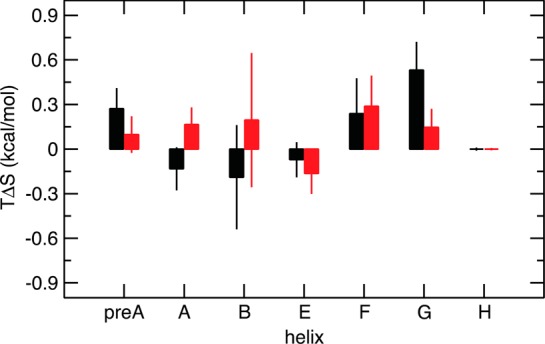
Change in conformational entropy associated with CO binding calculated for each α-helix of HbI from the MD simulations. Conformational entropic contribution to the binding free energy of carbon monoxide, TΔS, estimated for each helix for WT HbI (black) and F97Y HbI (red).
NMR Studies of HbI and F97Y HbI
HbI Is a Symmetric Dimer in Solution
In agreement with what was observed in the MD simulations, HbI is a symmetric dimer in solution in both the liganded and unliganded states, as confirmed by the observation of only one set of signals corresponding to a monomeric subunit in two-dimensional (2D) 1H–15N correlation spectra (Figure S2 of the Supporting Information).
Because of autoxidation of the heme iron in oxygenated hemoglobins, carbon monoxide (CO) is often used as an O2 mimic in studies that require long incubation with a ligand, as in the studies reported here. There is strong evidence that this is appropriate for HbI. As described above, crystallographic, kinetic, and equilibrium studies combined with allosteric analysis strongly imply a fundamental thermodynamic similarity in the cooperative binding of both ligands to HbI.9,11−13
Figure S2 of the Supporting Information shows the different spectra acquired for CO-bound and unbound HbI. The chemical shift differences between these two spectra are due to the presence of the paramagnetic Fe2+ in the unliganded state but also reflect the structural changes undergone by the protein upon CO binding. Even the subtle ligand-linked structural changes in HbI detected by X-ray crystallography (between 0.5 and 1 Å) result in significant differences in chemical shift values. In HbI, the structural change, although relatively localized, affects the chemical environment of the entire dimeric interface because ligand binding is coupled with a change in quaternary structure (3.3° subunit rotation)13 in addition to striking tertiary changes at the core of the interface.
Resonance Assignments
The backbone assignments of unliganded and CO-liganded HbI were determined (BioMagResBank entries 25286 and 25285, respectively).39 The backbone assignment of unliganded F97Y HbI was determined using three-dimensional triple-resonance 1H–15N TROSY experiments, including HNCO, HN(CA)CO, HNCA, HN(CO)CA, HNCACB, and CBCA(CO)NH40 collected at 14.1 T and at 298 K using uniformly 2H-, 13C-, and 15N-labeled samples. Assignments of the CO-bound F97Y mutant HbI were obtained by comparison with the spectrum of CO-bound WT HbI supplemented by the use of 1H–1H NOESY and HMQC-NOESY-HSQC experiments.40 Each subunit of HbI consists of 146 residues. In addition to the three proline residues that do not give rise to a signal in a 2D 1H–15N correlation spectrum, the residues that could not be assigned due to overlap or the lack of a signal are listed in row a of Table S1 of the Supporting Information.
Effect of the Paramagnetic Fe2+ in the Unliganded State on the Relaxation Rates
The presence of a paramagnetic center in the unliganded state of HbI dramatically affects the relaxation properties of the nearby nuclei. Because of the increased transverse relaxation rates, the signal of many of the residues on helix E and helix F is too weak to be detected in the unliganded state. The paramagnetic contribution, caused by interaction with the metal ion, to the transverse and longitudinal relaxation rates is a function of the distance from the Fe2+ ion with 1/r6 dependence. As a consequence, the paramagnetic effect is the dominant contribution to R1, R2, and NOE for nuclei proximal to the Fe center but will be negligible for nuclei that are >11.5 Å from the paramagnetic center as shown in Figure S3 of the Supporting Information. Residues with a non-negligible paramagnetic contribution to the relaxation rates can be easily identified from a plot of the relaxation times as a function of 1/rN–Fe6, where rN–Fe is the distance between the amide N and the Fe2+ ion.53 The residues with a detectable signal that were used in the model-free analysis were found not to be susceptible to the paramagnetic interaction with the Fe2+ ion, as shown by the independence of their transverse, T2, and longitudinal, T1, relaxation times from rN–Fe (Figure S3 of the Supporting Information).
Internal Dynamics of HbI
NMR 15N longitudinal, R1, and transverse, R2, relaxation rate constants and {1H}–15N nuclear Overhauser enhancement (NOE)11 were measured for all the spectrally resolved amide backbone groups in WT and F97Y HbI in both the liganded and unliganded states at 14.1 T and 298 K (Figure S4 of the Supporting Information). Residues for which relaxation parameters could not be accurately determined, because of severe spectral overlap or low signal intensities, were excluded from the model-free analysis and are listed in rows b and c, respectively, of Table S1 of the Supporting Information.
Laboratory-frame relaxation data were analyzed using the Lipari–Szabo model-free formalism.32 Knowledge of the rotational diffusion properties of HbI is necessary for model-free analysis. Analysis of the R1/R2 ratio was used to estimate the overall rotational correlation time47 and determine the axially symmetric diffusion model to be the best representation for the rotational diffusion of WT HbI and F97Y HbI in both the liganded and unliganded states. The F test was used to determine that the axially symmetric diffusion tensor was an improvement over the isotropic diffusion model for both WT and F97Y HbI in both the bound and free states. The resulting axially symmetric diffusion tensor is described by Diso = (9.41 ± 0.01) × 106 s–1 and D∥/D⊥ = 1.05 ± 0.01 for WT HbI in the liganded state and Diso = (9.88 ± 0.01) × 106 s–1 and D∥/D⊥ = 1.11 ± 0.01 for WT HbI in the unliganded state. The axially symmetric diffusion tensor that was found to describe the F97Y HbI mutant was characterized by Diso = (1.03 ± 0.01) × 107 s–1 and D∥/D⊥ = 1.07 ± 0.01 in the liganded state and Diso = (9.86 ± 0.02) × 106 s–1 and D∥/D⊥ = 1.17 ± 0.02 in the unliganded state. The values of Diso and D∥/D⊥ obtained from the analysis of R1/R2 were used as initial input in the first round of model selection in the model-free analysis.
The order parameters, S2, describing the amplitude of the backbone motion on the picosecond to nanosecond time scale, were calculated for WT HbI and F97Y HbI in the free and CO-bound states (Figure 8 and Figure S5 of the Supporting Information). These experimentally determined S2 values were used for the validation of the computational model, through direct comparison of the simulated and experimental S2 values (Figure 3). The NMR study of the internal dynamics of WT HbI and F97Y HbI confirms that the dynamics are affected by CO binding (Figure 8). A residue-by-residue comparison between the free and bound states is difficult because S2 values are not available for the same residues in both states. For this reason, the S2 values were averaged for each secondary structural element to draw some general conclusions about the effect of ligand binding on the dynamics of these proteins (Table 3), although caution should be used particularly when the number of observations is quite low and uneven.
Figure 8.
Backbone order parameters (S2) of HbI and F97Y HbI. Order parameters, S2, are shown as a function of residue number for WT HbI (a) and F97Y HbI (b). S2 values calculated for CO-bound HbI are shown as filled circles, and S2 values for unliganded HbI are shown as empty circles. Secondary structural elements are shown at the top of each plot. Solid bars represent α-helices, and lines represent loops.
Table 3. Averages of the Experimentally Derived Order Parameters for Each Secondary Structural Element of HbI and F97Y HbI in the Liganded and Unliganded Statesa.
| structural element | 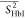 |
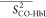 |
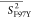 |
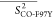 |
|---|---|---|---|---|
| pre-A | 0.892 ± 0.007 (6/7) | 0.907 ± 0.008 (3/7) | 0.906 ± 0.006 (6/7) | 0.918 ± 0.007 (6/7) |
| A | 0.908 ± 0.005 (9/14) | 0.917 ± 0.005 (12/14) | 0.937 ± 0.005 (9/14) | 0.942 ± 0.006 (9/14) |
| B | 0.905 ± 0.005 (10/15) | 0.913 ± 0.004 (11/15) | 0.915 ± 0.009 (8/15) | 0.941 ± 0.007 (10/15) |
| C | 0.90 ± 0.01 (4/6) | 0.90 ± 0.01 (6/6) | 0.92 ± 0.02 (3/6) | 0.94 ± 0.01 (5/6) |
| CD loop | 0.862 ± 0.005 (8/13) | 0.881 ± 0.007 (7/13) | 0.91 ± 0.01 (5/13) | 0.902 ± 0.008 (6/13) |
| E | 0.917 ± 0.008 (6/19) | 0.910 ± 0.005 (16/19) | 0.90 ± 0.02 (3/19) | 0.931 ± 0.005 (13/19) |
| F | 0.902 ± 0.007 (5/16) | 0.903 ± 0.005 (11/16) | 0.93 ± 0.01 (6/16) | 0.933 ± 0.008 (6/16) |
| G | 0.928 ± 0.006 (10/16) | 0.908 ± 0.005 (11/16) | 0.936 ± 0.009 (6/16) | 0.921 ± 0.006 (9/16) |
| H | 0.921 ± 0.005 (11/16) | 0.923 ± 0.004 (11/16) | 0.933 ± 0.006 (9/16) | 0.935 ± 0.004 (12/16) |
The number of residues whose relaxation data could be used to calculate the order parameters is shown in parentheses.
When averaged S2 values are compared, F97Y HbI is generally more rigid than WT HbI, in the free and bound state. When the backbone NH order parameters calculated in the liganded and unliganded states of each protein are compared, the most obvious difference between the internal dynamics is observed at helix B, which upon CO binding becomes more rigid in F97Y HbI than in WT HbI, where the observed changes are more heterogeneous. The opposite is true in helix G, which is more flexible in the bound state than in the unliganded state for both proteins, but more so in WT HbI than in F97Y HbI.
Most residues of HbI in the free state fit to simpler models than in the CO-bound state, indicating a reduced flexibility of the protein in the unbound state. Figure 9 shows the residues that required a chemical exchange contribution, Rex, to the relaxation model in the fitting. In the CO-bound state, 10 residues, mostly located on interfacial helices E and F, were fit to a motional model that used an Rex term, while only two residues required a non-zero chemical exchange contribution to relaxation. The presence of a chemical exchange contribution, Rex, to R2 for residues located on interfacial helices E and F indicates the presence of conformational fluctuations occurring on the microsecond to millisecond time scale. These fluctuations might be important in the ligand release mechanism.
Figure 9.
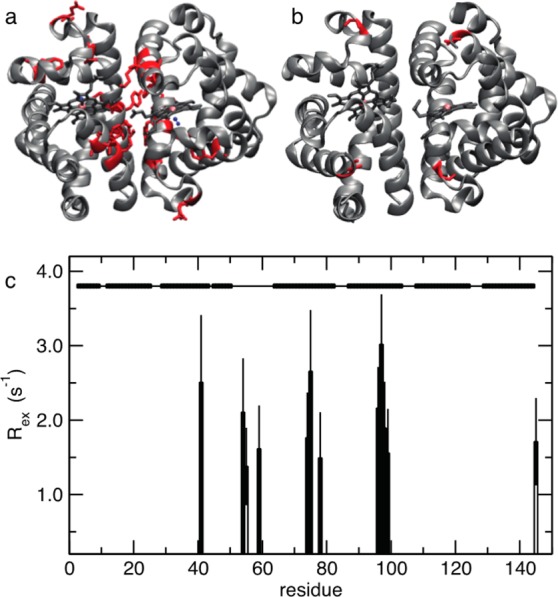
Chemical exchange contributions determined from the Lipari–Szabo model-free analysis of the 15N spin relaxation measurement parameters of HbI. Residues with non-zero chemical exchange contributions, Rex, determined from 15N spin relaxation data, are mapped in red on the structure of the protein for CO-bound HbI (a) and unliganded HbI (b). The structural representation was drawn using VMD.26Rex is shown as a function of protein sequence with filled bars and empty bars for CO-bound HbI and unliganded HbI, respectively (c). Secondary structural elements are shown at the top of the plot. Solid bars represent α-helices, and lines represent loops.
Fewer residues in F97Y HbI required the inclusion of a chemical exchange contribution to the transverse relaxation rate constant compared to the number in the wild type, only four in the liganded state and one in the free state, as shown in Figure S6 of the Supporting Information, confirming that this protein has reduced flexibility relative to that of the wild type.
From the backbone NH order parameters, the protein conformational entropic contribution to the binding free energy of carbon monoxide (TΔS) was estimated to be 1 kcal/mol. Because of the increased transverse relaxation rates, the signal of many of the residues on interfacial helices E and F is too weak to be detected in the unliganded state. Thus, because of the presence of a paramagnetic center in the unliganded state of HbI, we cannot collect NMR data for many of the residues of helices E and F. The conformational entropy change that we estimated from the order parameters accounts only for the changes in conformational fluctuations of the residues with an experimentally derived order parameter; furthermore, it neglects any correlation between spins. When estimating the change in conformational entropy from the experimentally derived order parameters, we are using a small subset of residues for which we have data from both the bound and free states, 61 residues for the WT and 42 for the F97Y mutant. This number of residues is smaller than the total number of available experimentally derived order parameters for the bound and free states. In addition, using molecular dynamics simulations described above, we estimated that the largest contribution to the conformational entropy of binding comes from the backbone NH groups for which we do not have experimental data. For these reasons, the value of TΔS estimated from the NMR order parameters needs to be taken with caution but may represent a lower limit; nevertheless, it supports the hypothesis that the increased protein backbone flexibility associated with ligand binding contributes to cooperativity in HbI.
On average, F97Y HbI is more rigid in the CO-bound state than in the free state. The estimated contribution to the free energy of binding arising from the conformational restriction associated with CO binding is −4 kcal/mol. Unfortunately, accurate thermodynamic parameters for the two steps of ligand binding to F97Y are not available. Again, this result is likely to be inaccurate as it suffers from the same limitations mentioned above, particularly because even more than for WT HbI, we were not able to calculate the order parameters, S2, of many residues in the unliganded state.
The differences between the values of TΔS obtained from the experimentally determined S2 values and those obtained from the MD simulations result from the lack of experimental relaxation data for many backbone NH groups in the unliganded state for the wild type and particularly for the F97Y mutant protein, and from the exclusion of the residues of helix C and the CD loop in the evaluation of TΔS from the MD simulation (see above). Nevertheless, the overall trend from both computational analysis and NMR experiments is similar, thus supporting a contribution of conformational entropy to HbI cooperativity.
Discussion
Structural studies of HbI have been powerful in demonstrating the important role of local structural rearrangements in cooperative ligand binding. In this study, using computer simulation and NMR relaxation methods, we tested the hypothesis that the dynamics of HbI are also involved in HbI cooperativity. We demonstrate that the backbone flexibility of HbI contributes to cooperativity in two ways: (1) by contributing favorably to the free energy of binding and (2) by participating in the cooperative mechanism at the HbI subunit interface.
To determine if the changes in backbone NH dynamics observed for HbI upon ligand binding were connected to its allosteric behavior, we compared the results obtained for WT HbI with those of the high-affinity-state mimic mutant protein F97Y HbI. This mutant protein of HbI explores the mutation of the phenylalanine on helix F whose side chain conformational transition, from the heme pocket to the dimeric interface, plays a central role in the allosteric mechanism of HbI and is characterized by a greatly reduced cooperativity. If the increased flexibility observed upon binding drives cooperativity, we expected this mutant to show a different change in dynamics upon ligand binding. Indeed, we found that the change in backbone NH flexibility of F97Y HbI associated with CO binding is diminished throughout this mutant protein relative to the wild-type protein. The change in conformational entropy associated with ligand binding is not as favorable in F97Y HbI as it is in WT HbI. These results demonstrate that changes in conformational entropy contribute together with structural changes to the cooperative mechanism of HbI.
X-ray crystallography has shown that HbI undergoes a quaternary structural rearrangement upon ligand binding; the HbI subunits rotate by 3.3°.13 In addition, helix F of HbI undergoes the largest conformational change upon ligand binding. This conformational rearrangement by helix F, including Phe 97, is critical, as is evident by the loss of cooperativity in the F97Y mutant of HbI. F97Y HbI undergoes a similar change in quaternary structure characterized by a 3.0° subunit rotation.25 However, for both the unliganded and CO-bound states of F97Y HbI, the tyrosine side chain at position 97 remains in the hydrophilic interface; this prevents helix F from undergoing a conformational transition that brings its backbone closer to the heme.13
In this study, we coupled molecular dynamics simulations with NMR relaxation measurements to investigate the role played by protein dynamics in cooperativity. Because of the presence of a paramagnetic center in the unliganded state of HbI, we were not able to collect NMR data for many of the residues of interfacial helices E and F. This dramatically impacted our ability to experimentally estimate the effect of ligand binding on the internal dynamics of the protein, and its role in cooperativity. Integration of the NMR data with the results of the MD simulations of HbI and F97Y HbI in the unliganded state has been essential to fully understand the dynamic changes of the interfacial residues. MD simulations are not subject to the experimental limitations of the NMR studies and allow us to collect data on all the residues of the protein, including the interfacial residues that may be particularly important to allostery. One important focus of this study was the validation of the computational model through direct comparison of the simulation results with experimental observations of the structure and dynamics of HbI obtained using NMR spectroscopy. The good agreement observed between the experimentally determined order parameters and those calculated from the MD simulations (Figure 3) ensures that MD simulations of HbI and F97Y HbI are able to capture the dynamics of these proteins and their changes between the free and bound states. Our studies have shown that ligand binding promotes a change in the backbone NH dynamics of helix F of both HbI and F97Y HbI but does not affect the backbone NH dynamics of the second interfacial helix (E) (Figure 4). Thus, both the structure and dynamics of helix F of wild-type HbI are sensitive to ligand binding. The C-termini of helices F and G are the regions of the protein whose backbone NH dynamics are affected the most by ligand binding in both WT and F97Y, but the increased flexibility observed for helix G upon binding in the WT protein is not as large in F97Y HbI. In general, we observed that the backbone NH groups of residues surrounding the heme group become more flexible upon ligand binding (Figure 4), particularly in the WT where, for example, the largest increase in flexibility is observed for the residues of helices E and F that face the heme group.
The changes in backbone NH dynamics observed upon CO binding in WT HbI and F97Y HbI have magnitudes similar to the magnitudes of those previously observed in human HbA.36 Although the subunits of HbI and HbA have the same myoglobin fold, their assembly is very different; thus, HbI and HbA have completely different subunit interfaces. For this reason, a direct comparison of the dynamics of the proteins is difficult. The changes in dynamics of the backbone amide groups observed in HbA upon CO binding exhibit a trend that is much less uniform than what we observed for HbI and are instead more randomly distributed along the sequence of the protein. In addition, several residues on helices G and H were found to be dynamic on a slow time scale (microsecond to millisecond) as indicated by the need for a non-zero Rex term in the model-free analysis.36 In HbA, helices G and H are located along the intradimer interfaces: α1β1 and α2β2. In HbI, we found that residues with a non-zero chemical exchange contribution, Rex, to R2 were mostly located on helices E and F, which are also interfacial helices. These results suggest that conformational fluctuations occurring on the microsecond to millisecond time scale at subunit interfaces might be important in the function of the protein.
Equilibrium thermodynamic studies of oxygen binding show that HbI cooperativity is driven by favorable changes in entropy. In this study, we have probed the backbone dynamics of HbI to investigate the role of conformational entropy in the cooperative mechanism of carbon monoxide binding. Several studies have shown that the dynamics of the side chain are rich and heterogeneous and are often more dramatically affected by ligand binding than those of the backbone.54 In addition, it has been shown that the side chain dynamics are uncoupled from those of the backbone.55,56 For these reasons, it will be important to study the side chain dynamics of a HbI as well as the backbone to fully characterize the dynamical changes undergone upon CO binding and to obtain a more accurate estimate of the changes in protein conformational entropy occurring upon ligand binding. Nonetheless, although we observed subtle changes in backbone NH dynamics upon CO binding, from these we obtain an estimate for the difference in conformational entropy between bound and unbound states of HbI that indicates a significant contribution to HbI cooperativity (from the MD simulations, TΔS = 1.8 ± 0.6 kcal/mol). The change in conformational entropy that we estimate from the MD simulations of F97Y mutant is not as large as for the WT (TΔS = 1.3 ± 0.6 kcal/mol), which is consistent with the reduced cooperativity observed for this mutant. This work provides the first direct evidence, based on both experimental and computational approaches, that changes in backbone conformational entropy favor HbI cooperativity.
The favorable entropic changes observed in cooperative oxygen binding in HbI will have contributions from both protein conformational entropy and solvent entropy. Previous studies of HbI have highlighted the importance of the interfacial water molecules in the cooperative mechanism of HbI.13,52 We are currently investigating the coupling between the change in structure and dynamics of the interfacial helices (E and F) and of the interfacial water and its role in cooperativity. These studies will build on our findings presented here that establish a contribution by protein conformational entropy to HbI ligand binding cooperativity.
Acknowledgments
We thank Troy W. Whitfield for helpful discussion.
Glossary
Abbreviations
- HbI
dimeric hemoglobin from S. inaequivalvis
- MD
molecular dynamics
- MWC
Monod–Wyman–Changeux allosteric model
- HMQC
heteronuclear multiple-quantum coherence
- HSQC
heteronuclear single-quantum coherence
- NOESY
nuclear Overhauser effect spectroscopy
- NMR
nuclear magnetic resonance
- PDB
Protein Data Bank
- rmsd
root-mean-square deviation
- TROSY
transverse relaxation-optimized spectroscopy
- WT
wild type.
Supporting Information Available
A table containing the missing residues from the NMR relaxation studies of HbI and F97Y HbI in the free and bound states, a figure illustrating the backbone order parameters (S2) of HbI and F97Y HbI calculated from the MD simulations, a figure illustrating the difference between the free and CO-bound NMR spectra of HbI, a figure of the longitudinal and transverse relaxation times as a function of the distance from the metal ions, a figure of the relaxation rates of WT and F97Y HbI, a figure of the model-free parameters of WT and F97Y HbI, and a figure illustrating the chemical exchange contribution determined from the Lipari–Szabo model-free analysis of the 15N spin relaxation measurement parameters of F97Y HbI. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Contributions
J.M.L. and M.A. contributed equally to this work.
This work was supported by National Institutes of Health Grant GM098763.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Pardee A. B.; Reddy G. P. (2003) Beginnings of feedback inhibition, allostery, and multi-protein complexes. Gene 321, 17–23. [DOI] [PubMed] [Google Scholar]
- Kantrowitz E. R. (2012) Allostery and cooperativity in Escherichia coli aspartate transcarbamoylase. Arch. Biochem. Biophys. 519, 81–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuxe K.; Borroto-Escuela D. O.; Marcellino D.; Romero-Fernandez W.; Frankowska M.; Guidolin D.; Filip M.; Ferraro L.; Woods A. S.; Tarakanov A.; Ciruela F.; Agnati L. F.; Tanganelli S. (2012) GPCR heteromers and their allosteric receptor-receptor interactions. Curr. Med. Chem. 19, 356–363. [DOI] [PubMed] [Google Scholar]
- Popovych N.; Sun S.; Ebright R. H.; Kalodimos C. G. (2006) Dynamically driven protein allostery. Nat. Struct. Mol. Biol. 13, 831–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalodimos C. G. (2012) Protein function and allostery: A dynamic relationship. Ann. N.Y. Acad. Sci. 1260, 81–86. [DOI] [PubMed] [Google Scholar]
- Tzeng S. R.; Kalodimos C. G. (2009) Dynamic activation of an allosteric regulatory protein. Nature 462, 368–372. [DOI] [PubMed] [Google Scholar]
- Petit C. M.; Zhang J.; Sapienza P. J.; Fuentes E. J.; Lee A. L. (2009) Hidden dynamic allostery in a PDZ domain. Proc. Natl. Acad. Sci. U.S.A. 106, 18249–18254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiancone E.; Vecchini P.; Verzili D.; Ascoli F.; Antonini E. (1981) Dimeric and tetrameric hemoglobins from the mollusc Scapharca inaequivalvis. Structural and functional properties. J. Mol. Biol. 152, 577–592. [DOI] [PubMed] [Google Scholar]
- Antonini E.; Ascoli F.; Brunori M.; Chiancone E.; Verzili D.; Morris R. J.; Gibson Q. H. (1984) Kinetics of ligand binding and quaternary conformational change in the homodimeric hemoglobin from Scapharca inaequivalvis. J. Biol. Chem. 259, 6730–6738. [PubMed] [Google Scholar]
- Royer W. E. Jr.; Pardanani A.; Gibson Q. H.; Peterson E. S.; Friedman J. M. (1996) Ordered water molecules as key allosteric mediators in a cooperative dimeric hemoglobin. Proc. Natl. Acad. Sci. U.S.A. 93, 14526–14531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols J. C.; Royer W. E. Jr.; Gibson Q. H. (2006) An optical signal correlated with the allosteric transition in Scapharca inaequivalvis HbI. Biochemistry 45, 15748–15755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Condon P. J.; Royer W. E. Jr. (1994) Crystal structure of oxygenated Scapharca dimeric hemoglobin at 1.7-Å resolution. J. Biol. Chem. 269, 25259–25267. [DOI] [PubMed] [Google Scholar]
- Royer W. E. (1994) High-resolution crystallographic analysis of a co-operative dimeric hemoglobin. J. Mol. Biol. 235, 657–681. [DOI] [PubMed] [Google Scholar]
- Mitchell D. T.; Kitto G. B.; Hackert M. L. (1995) Structural analysis of monomeric hemichrome and dimeric cyanomet hemoglobins from Caudina arenicola. J. Mol. Biol. 251, 421–431. [DOI] [PubMed] [Google Scholar]
- Royer W. E.; Sharma H.; Strand K.; Knapp J. E.; Bhyravbhatla B. (2006) Lumbricus erythrocruorin at 3.5 Å resolution: Architecture of a megadalton respiratory complex. Structure 14, 1167–1177. [DOI] [PubMed] [Google Scholar]
- Mozzarelli A.; Bettati S.; Rivetti C.; Rossi G. L.; Colotti G.; Chiancone E. (1996) Cooperative oxygen binding to Scapharca inaequivalvis hemoglobin in the crystal. J. Biol. Chem. 271, 3627–3632. [DOI] [PubMed] [Google Scholar]
- Ronda L.; Bettati S.; Henry E. R.; Kashav T.; Sanders J. M.; Royer W. E.; Mozzarelli A. (2013) Tertiary and quaternary allostery in tetrameric hemoglobin from Scapharca inaequivalvis. Biochemistry 52, 2108–2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp J. E.; Pahl R.; Srajer V.; Royer W. E. Jr. (2006) Allosteric action in real time: Time-resolved crystallographic studies of a cooperative dimeric hemoglobin. Proc. Natl. Acad. Sci. U.S.A. 103, 7649–7654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim K. H.; Muniyappan S.; Oang K. Y.; Kim J. G.; Nozawa S.; Sato T.; Koshihara S. Y.; Henning R.; Kosheleva I.; Ki H.; Kim Y.; Kim T. W.; Kim J.; Adachi S.; Ihee H. (2012) Direct observation of cooperative protein structural dynamics of homodimeric hemoglobin from 100 ps to 10 ms with pump-probe X-ray solution scattering. J. Am. Chem. Soc. 134, 7001–7008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikeda-Saito M.; Yonetani T.; Chiancone E.; Ascoli F.; Verzili D.; Antonini E. (1983) Thermodynamic properties of oxygen equilibria of dimeric and tetrameric hemoglobins from Scapharca inaequivalvis. J. Mol. Biol. 170, 1009–1018. [DOI] [PubMed] [Google Scholar]
- Cooper A.; Dryden D. T. (1984) Allostery without conformational change. A plausible model. Eur. Biophys. J. 11, 103–109. [DOI] [PubMed] [Google Scholar]
- Wand A. J. (2001) Dynamic activation of protein function: A view emerging from NMR spectroscopy. Nat. Struct. Biol. 8, 926–931. [DOI] [PubMed] [Google Scholar]
- Frederick K. K.; Kranz J. K.; Wand A. J. (2006) Characterization of the backbone and side chain dynamics of the CaM-CaMKIp complex reveals microscopic contributions to protein conformational entropy. Biochemistry 45, 9841–9848. [DOI] [PubMed] [Google Scholar]
- Wand A. J. (2013) The dark energy of proteins comes to light: Conformational entropy and its role in protein function revealed by NMR relaxation. Curr. Opin. Struct. Biol. 23, 75–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp J. E.; Bonham M. A.; Gibson Q. H.; Nichols J. C.; Royer W. E. Jr. (2005) Residue F4 plays a key role in modulating oxygen affinity and cooperativity in Scapharca dimeric hemoglobin. Biochemistry 44, 14419–14430. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. (1996) VMD: Visual molecular dynamics. J. Mol. Graphics 14, 33–38. [DOI] [PubMed] [Google Scholar]
- Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. (2005) Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F. T. K.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher W. E.; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiorkiewicz-Kuczera J.; Yin D.; Karplus M. (1998) All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- Ryckaert J. P.; Ciccotti G.; Berendsen H. J. C. (1997) Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 23, 327–341. [Google Scholar]
- Miyamoto S.; Kollman P. (1992) Settle: An analytical version of the shake and rattle algorithm for rigid water models. J. Comput. Chem. 13, 952–962. [Google Scholar]
- Lipari G.; Szabo A. (1982) Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules: 1. Analysis of experimental results. J. Am. Chem. Soc. 104, 4559–4570. [Google Scholar]
- Lipari G.; Szabo A. (1982) Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 104, 4546–4559. [Google Scholar]
- Morgan B. R.; Massi F. (2010) A computational study of RNA binding and specificity in the tandem zinc finger domain of TIS11d. Protein Sci. 19, 1222–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mergulhao F. J.; Summers D. K.; Monteiro G. A. (2005) Recombinant protein secretion in Escherichia coli. Biotechnol. Adv. 23, 177–202. [DOI] [PubMed] [Google Scholar]
- Summerford C. M.; Pardanani A.; Betts A. H.; Poteete A. R.; Colotti G.; Royer W. E. Jr. (1995) Bacterial expression of Scapharca dimeric hemoglobin: A simple model system for investigating protein cooperatively. Protein Eng. 8, 593–599. [DOI] [PubMed] [Google Scholar]
- Song X. J.; Yuan Y.; Simplaceanu V.; Sahu S. C.; Ho N. T.; Ho C. (2007) A comparative NMR study of the polypeptide backbone dynamics of hemoglobin in the deoxy and carbonmonoxy forms. Biochemistry 46, 6795–6803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho C. (1992) Proton nuclear magnetic resonance studies on hemoglobin: Cooperative interactions and partially ligated intermediates. Adv. Protein Chem. 43, 153–312. [DOI] [PubMed] [Google Scholar]
- Volkman B. F.; Alam S. L.; Satterlee J. D.; Markley J. L. (1998) Solution structure and backbone dynamics of component IV Glycera dibranchiata monomeric hemoglobin-CO. Biochemistry 37, 10906–10919. [DOI] [PubMed] [Google Scholar]
- Laine J. M., and Massi F.. Backbone 1H, 13C and 15N resonance assignments of the unliganded and CO-bound states of Scapharca dimeric hemoglobin (manuscript in preparation).
- Cavanagh J., Fairbrother W. J., Palmer A. G. III, and Skelton N. J. (1996) Protein NMR Spectroscopy: Principles and Practice, Academic Press, San Diego. [Google Scholar]
- Loria J. P.; Rance M.; Palmer A. G. (1999) Transverse-relaxation-optimized (TROSY) gradient-enhanced triple-resonance NMR spectroscopy. J. Magn. Reson. 141, 180–184. [DOI] [PubMed] [Google Scholar]
- Farrow N. A.; Muhandiram R.; Singer A. U.; Pascal S. M.; Kay C. M.; Gish G.; Shoelson S. E.; Pawson T.; Formankay J. D.; Kay L. E. (1994) Backbone dynamics of a free and a phosphopeptide-complexed src homology-2 domain studied by N-15 NMR relaxation. Biochemistry 33, 5984–6003. [DOI] [PubMed] [Google Scholar]
- Delaglio F.; Grzesiek S.; Vuister G. W.; Zhu G.; Pfeifer J.; Bax A. (1995) NMRPipe: A multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR 6, 277–293. [DOI] [PubMed] [Google Scholar]
- Goddard T. D., and Kneller D. G. (2003) SPARKY 3, University of California, San Francisco. [Google Scholar]
- Abragam A. (1961) Principles of Nuclear Magnetism, Oxford University Press, Oxford, U.K. [Google Scholar]
- Clore G. M.; Szabo A.; Bax A.; Kay L. E.; Driscoll P. C.; Gronenborn A. M. (1990) Deviations from the simple 2-parameter model-free approach to the interpretation of N-15 nuclear magnetic-relaxation of proteins. J. Am. Chem. Soc. 112, 4989–4991. [Google Scholar]
- Tjandra N.; Feller S.; Pastor R.; Bax A. (1995) Rotational diffusion anisotropy of human ubiquitin from N-15 NMR relaxation. J. Am. Chem. Soc. 117, 12562–12566. [Google Scholar]
- Cole R.; Loria J. P. (2003) FAST-modelfree: A program for rapid automated analysis of solution NMR spin-relaxation data. J. Biomol. NMR 26, 203–213. [DOI] [PubMed] [Google Scholar]
- Mandel A. M.; Akke M.; Palmer A. G. (1995) Backbone dynamics of Escherichia coli ribonuclease-H1: Correlations with structure and function in an active enzyme. J. Cell. Biochem. 29. [DOI] [PubMed] [Google Scholar]
- Yang D. W.; Kay L. E. (1996) Contributions to conformational entropy arising from bond vector fluctuations measured from NMR-derived order parameters: Application to protein folding. J. Mol. Biol. 263, 369–382. [DOI] [PubMed] [Google Scholar]
- Guarrera L.; Colotti G.; Boffi A.; Chiancone E.; Das T. K.; Rousseau D. L.; Gibson Q. H. (1998) The apolar distal histidine mutant (His69→Val) of the homodimeric Scapharca hemoglobin is in an R-like conformation. Biochemistry 37, 5608–5615. [DOI] [PubMed] [Google Scholar]
- Zhou Y.; Zhou H.; Karplus M. (2003) Cooperativity in Scapharca dimeric hemoglobin: Simulation of binding intermediates and elucidation of the role of interfacial water. J. Mol. Biol. 326, 593–606. [DOI] [PubMed] [Google Scholar]
- Bertini I.; Luchinat C.; Piccioli M. (2001) Paramagnetic probes in metalloproteins. Methods Enzymol. 339, 314–340. [DOI] [PubMed] [Google Scholar]
- Wand A. J.; Moorman V. R.; Harpole K. W. (2013) A surprising role for conformational entropy in protein function. Top. Curr. Chem. 337, 69–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frederick K. K.; Marlow M. S.; Valentine K. G.; Wand A. J. (2007) Conformational entropy in molecular recognition by proteins. Nature 448, 325–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Igumenova T. I.; Frederick K. K.; Wand A. J. (2006) Characterization of the fast dynamics of protein amino acid side chains using NMR relaxation in solution. Chem. Rev. 106, 1672–1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLano W. L. (2002) The PyMOL molecular graphics system, DeLano Scientific, San Carlos, CA. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.