Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Nov 28;4:7193. doi: 10.1038/srep07193

Elastic Moduli of Permanently Densified Silica Glasses

T Deschamps 1,a, J Margueritat 1, C Martinet 1, A Mermet 1, B Champagnon 1
PMCID: PMC4246209  PMID: 25431218

Abstract

Modelling the mechanical response of silica glass is still challenging, due to the lack of knowledge concerning the elastic properties of intermediate states of densification. An extensive Brillouin Light Scattering study on permanently densified silica glasses after cold compression in diamond anvil cell has been carried out, in order to deduce the elastic properties of such glasses and to provide new insights concerning the densification process. From sound velocity measurements, we derive phenomenological laws linking the elastic moduli of silica glass as a function of its densification ratio. The found elastic moduli are in excellent agreement with the sparse data extracted from literature, and we show that they do not depend on the thermodynamic path taken during densification (room temperature or heating). We also demonstrate that the longitudinal sound velocity exhibits an anomalous behavior, displaying a minimum for a densification ratio of 5%, and highlight the fact that this anomaly has to be distinguished from the compressibility anomaly of a-SiO2 in the elastic domain.

It is well known that glassy materials, despite their strong brittleness character, can undergo plastic deformation under high stresses, such as high hydrostatic pressure or indentation1,2. Two different mechanisms are involved during plastic deformation: a volume-conservative one, i.e shear flow, and a permanent densification3,4. Such densification can vary drastically depending on the atomic packing density, i.e on the free volume of the starting material5,6. Greaves et al. have demonstrated in numerous types of glasses, that the Poisson's ratio of an amorphous material (which is related to its atomic packing density), is an excellent criterion to identify its ability to permanently densify6. Unlike metallic glasses or soda-lime silicate glasses, strong oxide glasses such as a-GeO2 or a-SiO2 can densify up to 15% and 21% respectively, due to their open, tetrahedrally-connected network. For fused silica, the elastic yield under hydrostatic pressure at ambient temperature is around 9 GPa7. Below the elastic yield, the deformation is purely reversible. Above 9 GPa, permanent structural changes occur and the retrieved sample is densified. The densification is gradual up to 25 GPa (known as the saturation pressure), a pressure marking the end of the densification process (saturating at 21%). The elastic yield and the saturation pressure can be reduced if the sample is simultaneously heated during compression or if shear stresses occur8. Between these two pressures (determining the onset of the densification and its saturation), the densification ratio increases continuously7. However, despite extensive experimental and simulation studies on SiO2 under high pressure9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30, the structural modifications and the elastic properties of such mildly densified glasses are not well understood. This lack of knowledge restricts the modelling of plastic deformation31,32,33,34,35.

The aim of this study is to characterize by Brillouin spectroscopy a large set of densified samples after cold compression in order to deduce a relation linking elastic moduli of silica glasses with the densification ratio. From longitudinal sound velocities measurements, we first deduce the longitudinal modulus as a function of the density. Thanks to the Cauchy relation, all the elastic moduli are then calculated, providing phenomenological laws which link a-SiO2 density with the elastic moduli. These laws display excellent agreement with the sparse data extracted from literature, whatever the thermodynamic path taken during the densification process (room temperature or heating), revealing that the elastic properties only depend on the glass density. Finally, the observed anormal behavior of the longitudinal sound velocity, which shows a minimum at 5% of densification ratio, is interpreted at the structural scale. The fundamental differences between this anomaly and the well-known compressibility anomaly observed in the elastic regime36 are highlighted.

Results

The diamond anvil cell (DAC) was used to densify Suprasil 300 vitreous SiO2 from Heraeus ([OH < 1 ppm] at ambient temperature, applying hydrostatic pressures37 (details can be found in the Methods). Seven SiO2 samples were compressed in the DAC at different permanent densification ratios Δρ/ρ, depending on the pressure reached. The densification ratios of the compressed samples, which have been already determined in a previous study7, are displayed Table 1.

Table 1. Maximum pressure reached in the DAC and densification ratio of the recovered samples. Compression was carried out at Tamb with a holding time of 24 h at Pmax. The values of the elastic moduli of the compressed samples are also displayed.

Pmax (GPa) 0 9.8 12.0 13.6 14.6 15.5 18.1 26.2
Δρ/ρ (%) 0 1.4 4.4 8.6 11.7 14.3 19.1 21.0
Elastic Moduli                
L (GPa) 77.3 77.3 78.4 85.6 92.2 102.8 123.2 132.2
G (GPa) 30.4 30.4 30.7 32.8 34.8 38.0 44.0 46.7
K (GPa) 36.8 36.8 37.5 41.8 45.8 52.1 64.5 69.9
E (GPa) 71.5 71.5 72.4 78.1 83.3 91.7 107.6 114.6
ν 0.176 0.176 0.178 0.188 0.197 0.207 0.222 0.227
Open in a new tab

All the recovered samples were then put on a crystalline silicon plate in order to record ex situ the back-scattered Brillouin signal displayed in Fig. 1 (see Methods). In such a configuration, the longitudinal Brillouin shift allows measuring the longitudinal sound velocity using the relation Eq. 1, resulting from the conservation law:

graphic file with name srep07193-m1.jpg

where cl is the longitudinal sound wave velocity, νl the Brillouin frequency, λ the laser wavelength, and n the refractive index.

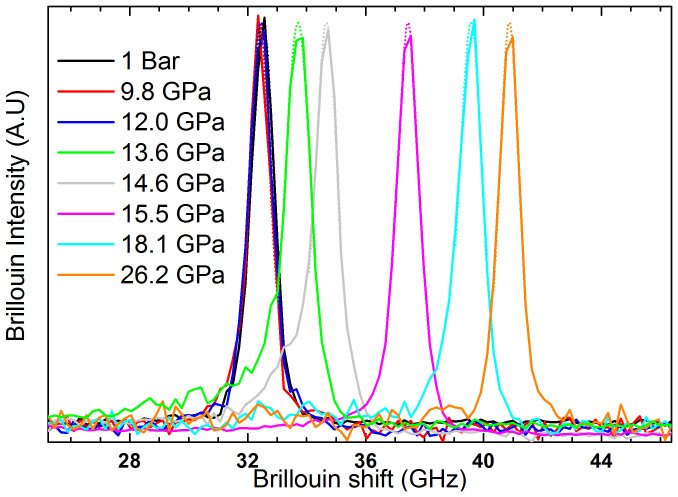
Figure 1. Brillouin spectra of the pristine silica sample (black line) and of the permanently densified a-SiO2 samples after hydrostatic compression in DAC (the spectra are recorded ex situ).

Figure 1

Open in a new tab

The first three Brillouin lines (1 Bar, 9.8 and 12.0 GPa) are almost indistinguishable. Dotted lines represent the Lorentzian fits.

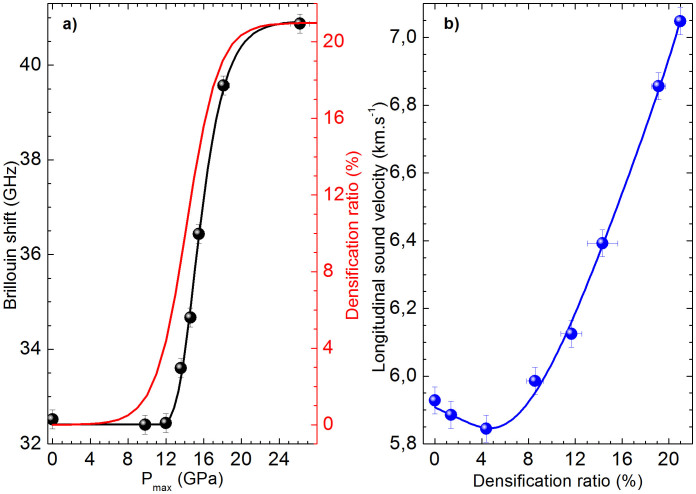
Fig. 2a displays the evolution of the longitudinal Brillouin frequency shift as well as the permanent densification ratio as a function of the pressure reached.

Figure 2.

Figure 2

Open in a new tab

(a) Longitudinal Brillouin line shift versus pressure reached Pmax, recorded at atmospheric pressure, i.e after densification. The experimental points (black circles) are fitted using a Gompertz function (black line). The red line represents the evolution of the permanent densification ratio (right scale) as a function of Pmax5,6,7. (b) Longitudinal wave velocity cl as a function of permanent densification ratio, calculated by combining Eq. 1, 2, 3 and 4. cl displays a minimum at Δρ/ρ = 5%.

Although permanent densification starts from 9 GPa, the shift of the Brillouin line, corresponding to the longitudinal acoustic mode, is roughly invariant for Pmax ≤ 12 GPa, with a frequency of 32.4 GHz. Above Pmax = 12 GPa, the Brillouin line shifts monotonously toward higher frequencies and saturates at 40.8 GHz for Pmax ≥ 25 GPa. Such variation of the Brillouin shift νl with Pmax, with an abrupt increase at 12 GPa, can be fitted using a Gompertz function rather than a simpler sigmoidal function:

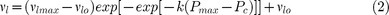graphic file with name srep07193-m2.jpg

where νl0 = 32.4 GHz and νlmax = 40.9 GHz are respectively the Brillouin shift of the non-densified and the fully densified silica, Pc = 15.0 GPa and k = 0.546 are two fitting parameters.

While no variation of the shift of the Brillouin line is observed below Pmax = 12 GPa, the elastic yield of silica around 9 GPa has been exceeded, resulting in a permanent densification. The offset between these two pressure values is not an uncertainty as previously shown from Raman measurements on the same samples7.

The evolution of the densification ratio Δρ/ρ of a pure silica glass with Pmax is today well established in the case of a hydrostatic compression at ambient temperature5,7. This evolution is well described by the following sigmoidal relation:

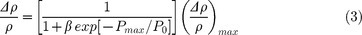graphic file with name srep07193-m3.jpg

where (Δρ/ρ)max = 21% is the maximum densification ratio, β = 5000 and P0 = 1.67 GPa are two fitting parameters.

According to Eq. 1, the evolution of the longitudinal sound velocity cl as a function of the densification ratio Δρ/ρ can be deduced from the Brillouin shift νl and the refractive index n, which both depend on Pmax, i.e on the densification ratio (see Eq. 3). The dependence of νl is given by Eq. 2 and the variation of the refractive index n has been deduced from the data of Tan et al.38, which have highlighted the linear relation linking n and Δρ/ρ in permanently densified silica:

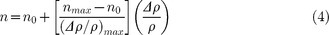graphic file with name srep07193-m4.jpg

where n0 = 1.459 and nmax = 1.543 are respectively the refractive index of non-densified and fully-densified (21%) silica glass. Hence, combining the four previous equations, the evolution of the longitudinal sound velocity as a function of the densification ratio has been calculated and is displayed in Fig. 2b.

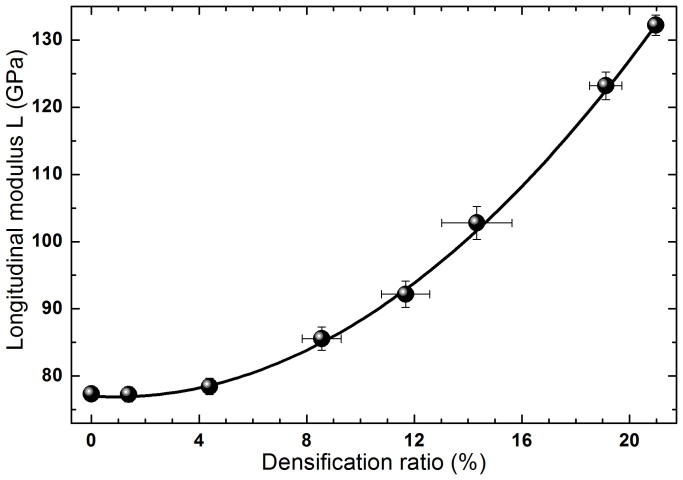
The longitudinal sound velocity cl decreases from 5930 m.s−1 to 5840 m.s−1 when increasing Δρ/ρ from 0 to 5%. Above 5%, cl increases monotonously with the densification up to 7050 m.s−1. Thus, the longitudinal sound velocity exhibits a minimum as a function of the densification ratio. Such behaviour recalls the well-known compressibility anomaly observed in silica glass under pressure, between Patmo and 3 GPa39,40,41,42,43,44,45,46,47,48. Nevertheless, these two anomalies need to be clearly distinguished: one appears after plastic deformation while the other takes place in the elastic regime of silica glass. This aspect will be discussed later. To go further, we have evaluated the elastic moduli of permanently densified silica glasses. The longitudinal (or P-waves) modulus L, function of the density and longitudinal sound velocity cl, can be directly deduced from our Brillouin scattering measurements and is reported in Fig. 3. The analytical relation linking L to Δρ/ρ can be deduced from the four previous equations.

Figure 3. Longitudinal modulus L of silica glass as a function of the densification ratio.

Figure 3

Open in a new tab

Full black circles are the data calculated from Brillouin scattering results. The black line represents the polynomial fit from Eq. 5.

In the range Δρ/ρ = [0–0.21], this relation between L and Δρ/ρ is accurately fitted by a second order polynomial function:

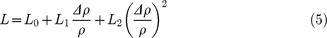graphic file with name srep07193-m5.jpg

where L0 = 77 GPa is the longitudinal modulus of pristine silica glass, L1 = −24 GPa and L2 = 1370 GPa.

On the other hand, the transverse sound velocity, which would provide all the other elastic moduli, is lacking. However, for isotropic solids such as glasses, the generalized Cauchy relation49, linking the longitudinal modulus L to the shear modulus G, can be applied:

graphic file with name srep07193-m6.jpg

This relation was shown to hold with constant values a = −24.8 and b = 3.36 for differently densified silica glass samples18.

Knowing L and G as a function of the permanent densification ratio, all the elastic moduli can be then determined, applying the well-known relations for homogeneous isotropic materials recalled in Table 2.

Table 2. Relations between elastic moduli: K, ν, and E as a function of L and G.

K ν E
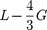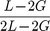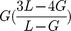Inline graphic Inline graphic Inline graphic
Open in a new tab

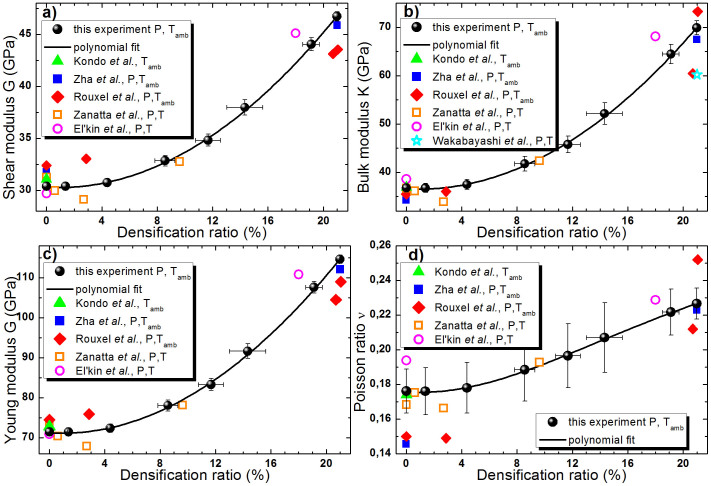
The evolution of the shear, bulk, and Young moduli (as well as the Poisson ratio) with densification ratio are displayed in Fig. 4.

Figure 4.

Figure 4

Open in a new tab

(a) Shear modulus G, (b) Bulk modulus K, (c) Young modulus E and (d) Poisson ratio ν as a function of the densification ratio. Full black circles are deduced from our Brillouin scattering measurements, applying the Cauchy relation Eq.6. The lines represents the fits deduced from Eq. 5,6 and Table 2. The results are compared with previous measurements after densification at Tamb by Kondo et al.50 (full green triangles), Zha et al.41 (full blue squares) and Rouxel et al.3 (full red diamonds), and after densification at high temperature by Zanatta et al.18 (empty orange squares), El'kin et al.51 (empty purple circles) and Wakabayashi et al.19 (empty cyan star).

The L, G, K and E moduli exhibit similar behaviours with densification: a monotonous enhancement is observed from 0 to 21% densification ratio, but the rate of this enhancement is extremely low, up to Δρ/ρ = 5%, due to the softening of the sound velocity in this densification range. The bulk modulus shows the greater enhancement, from 37 GPa for a non-densified SiO2 glass to 70 GPa for a fully densified one. Although the existing data concerning elastic moduli after cold densification of silica glass are sparse in the literature, some comparisons with previous experiments can be made. From the longitudinal and transverse sound velocities measurements of Polian et al.40 and Zha et al.41 for pristine and fully densified silica glass in a DAC, the deduced elastic moduli L ≈ 77 GPa, G ≈ 32 GPa, K ≈ 34 GPa, E ≈ 73 GPa and L ≈ 129 GPa, G ≈ 46 GPa, K ≈67 GPa, E ≈ 112 GPa respectively are in excellent agreement with our results. As shown in Fig. 4d, the evolution of the Poisson ratio is roughly constant up to 5% densification (ν ≈ 0.18), and then increases almost linearly to ν ≈ 0.23 up to a densification ratio of 21%. These data are also in good agreement with previous measurements on permanently densified samples at Tamb3,35,41, thereby further validating the use of the Cauchy relation.

Let us now compare our results with elastic moduli of densified a-SiO2 at high temperature, determined by Brillouin scattering18, ultrasonic measurements51 and by fitting the Birch-Murnaghan equation of states to the volume data recorded during compression19. For cold and hot compressions, the P-T routes to plastically deform SiO2 glass are extremely different. Such differences in thermodynamic paths provide glasses with same density but different structures52. Despite this, the elastic moduli are similar (Fig. 4). This result supports the conclusion that the values of the elastic moduli only depend on the densification ratio of the glass, and not on the thermodynamical way to reach the permanent densification. This means that the relations given previously linking elastic moduli with Δρ/ρ are valuable for all densified a-SiO2, whatever the thermodynamic paths taken to compress them.

Discussion

In order to discuss the permanent structural changes responsible for such evolution of the elastic moduli, first let us recall some general aspects concerning the densification process. At ambient pressure, silica glass has an open three-dimensional network structure, consisting of corner-shared SiO4 tetrahedra which forms wide Si–O–Si bond-angles and ring size distributions. Several kinds of structural transformations occur during the compaction under high pressure. Between Patmo and 3 GPa, reversible structural transitions similar to those which underlie the β→α transition in cristobalite, first suggested by Vukcevich36, were recently observed in molecular-dynamic simulations44,45. This change in the six-fold ring conformation is responsible for the softening of the elastic moduli under pressure, i.e the well-known “compressibility anomaly”39,40,41,42,43. Indeed, the β-like rings, which are more symmetric than α-like rings, have higher elastic moduli. Upon compression, the β-like rings collapse into α-like rings by an abrupt rotation of Si–O–Si bridges, and the elastic moduli of silica glass decrease gradually from Patmo up to 3 GPa. A gradual reduction of the Si–O–Si bond angle is also observed under compaction and is reversible below 9 GPa. The rate of the Si–O–Si angle reduction is maximal at 3 GPa, i.e at the pressure where the compressibility is maximal42. Below 9 GPa, the structural transformation occurs without breaking any bonds.

Above 9 GPa which marks the elastic-plastic transition, the glass deformation results in an irreversible change of the network topology implying permanent densification. The appearance of intermediate fivefold Si–O coordination defects explains the network reorganization23,28,46. These local plastic events are gradual between 9 and 25 GPa, as can be seen on previous Raman scattering experiments7. The intermediate range order is highly affected by the densification process. Notably the ring statistics change drastically, with the formation of smaller average ring size55, and the Si–O–Si angles gradually decrease with permanent densification7,26. These structural transformations are responsible for the permanent densification, which saturates for a compression-decompression cycle up to 25 GPa, and were previously interpreted in terms of a growing proportion of high density amorphous (HDA) local structure48 in the frame of the LDA-HDA amorphous-amorphous transition15,53,54. When Pmax ≥ 25 GPa, the maximum densification ratio of 21% is reached, indicating the inability of silica to accommodate further irreversible structural changes. Further compression of silica glass above 20–25 GPa leads to an increase in the Si–O coordination number, from a tetrahedral to an octahedral amorphous network55,56. This reversible transformation ends around 40 GPa57,58.

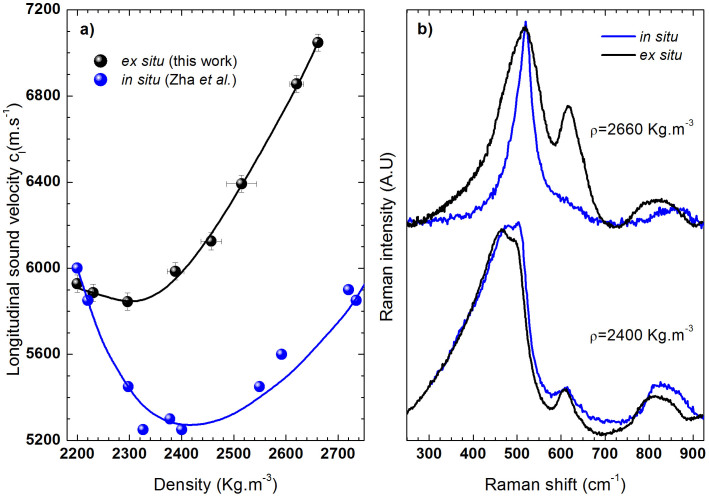
Using Brillouin spectroscopy, we have shown herein that after cold compression the longitudinal wave velocity decreases with the densification ratio at the beginning of the permanent densification. Such behaviour was also reported recently on SiO2 samples heated and quenched at high pressure in a multi-anvil apparatus18. In this later article, the authors explain that the resulting sound velocities are consistent with previous measurements of Zha et al.41. However, the measurements of Zha et al. concern the elastic deformation of silica glass followed in situ by Brillouin scattering. We argue that such comparison between plastic and elastic deformations appears to be incorrect. To illustrate this point, we plot Fig. 5a the longitudinal sound velocity as a function of silica glass density from in situ experiments41 and ex situ experiments (our data and the one of Zanatta et al.18). It is worth noting that the article of Zha et al. displays sound velocity as a function of pressure, but also provides the relation between the applied hydrostatic pressure and the in situ glass density.

Figure 5.

Figure 5

Open in a new tab

(a) Longitudinal sound velocity cl as a function of density on permanently densified silica glass (black circles) and during in situ experiments (blue circles from Zha et al.41). (b) Comparison of Raman spectra recorded in situ (blue lines) and ex situ (black lines) on glasses of same density, at two different densities ρ = 2400 Kg.m−3 and ρ = 2660 Kg.m−3. The ex situ spectra are extracted from Deschamps et al.7 and in situ spectra have been recorded at 3.0 GPa and 6.7 GPa, corresponding respectively to a density of ρ = 2400 Kg.m−3 and ρ = 2660 Kg.m−3 during elastic deformation.

For both ex situ and in situ experiments, the longitudinal sound velocity cl displays a non-monotonous behaviour, with a minimum as a function of the density. However, the two behaviours must be distinguished. For in situ measurements, cl decreases strongly from 6000 m.s−1 at Patmo (ρ = 2200 Kg.m−3) down to 5300 m.s−1 at 3 GPa (ρ = 2400 Kg.m−3), and then increases monotonously. We note that cl = 5600 m.s−1 at 6.7 GPa (ρ = 2660 Kg.m−3). The large amplitude of the anomalous decrease of cl observed in situ at the beginning of the compression makes the anomaly visible on the elastic moduli.

This behaviour is at variance with ex situ experiments, where cl first decreases slightly from 6000 m.s−1 to 5850 m.s−1 at ρ = 2300 Kg.m−3 and then increases drastically up to 7050 m.s−1 at the density maximum of a permanently compressed silica glass (ρ = 2660 Kg.m−3). The longitudinal sound velocity experiences a much less pronounced minimum than the one observed in situ, and the elastic moduli display a monotonous behaviour with densification. At ρ = 2660 Kg.m−3, cl is largely above the initial value, implying the hardening of the glass with densification (Fig. 3), while at this density, in situ data show that cl < 6000 m.s−1.

In order to compare the structure of silica glass at similar densities during in situ experiments and after permanent densification, Fig. 5b displays simultaneously in situ and ex situ Raman spectra at ρ = 2400 Kg.m−3 and ρ = 2660 Kg.m−3. The ex situ spectra have been recorded on the samples recovered after compression in the DAC up to Pmax = 13.6 GPa and 26.2 GPa, i.e densified at ρ = 2400 Kg.m−3 and ρ = 2660 Kg.m−3 respectively. The in situ spectra have been recorded in the DAC at P = 3 GPa and P = 6.7 GPa, corresponding to those same densities41. These spectra clearly confirm the fundamental differences between in situ and ex situ experiments. At equivalent density, strong discrepancies appear in the a-SiO2 structure. In particular, the main band is sharper and the D2 band (breathing modes of 3-membered rings) located at 600 cm−1 is weaker in situ, revealing strong differences in the Si–O–Si angles distribution and ring statistics. The planar geometry and the high symmetry of small rings conferring a lower compressibility to a-SiO2 network, the formation of smaller rings during plastic deformation is probably responsible for the glass hardening. Such permanent structural transformations have also been revealed by Raman spectroscopy on pure silica glass after indentation59,60. Indeed, indentation causes an increase of the D1 and D2 defect lines and a shift of the main band to higher frequencies. The similarities observed when comparing the SiO2 Raman spectra after hydrostatic compression and indentation clearly shows that the plastic deformation through indentation is driven by compaction rather than shear-flow. More details concerning ex situ Raman characterization and its relevance to characterize indented glasses can be found in a previous study (see Deschamps et al.7).

In spite of the fundamental differences between in situ and ex situ transformations, the decrease of the sound velocity as a function of the density observed at the beginning of the permanent densification can be still explained by the β→α cristobalite-like transition which gradually softens the structure. Up to the elastic yield around 9 GPa, this transition is fully reversible. Above 9 GPa, the plastic deformation probably involves a gradual and permanent conformation change from β-like to α-like 6-fold rings: a certain part (depending on Pmax) of the β rings population is permanently transformed into α rings type. Such phenomenon perfectly describe the gradual weakening and loss of the compressibility anomaly with the densification ratio47,48. The minimum of the sound velocity versus permanent densification can be well explained by the competition between two different irreversible mechanisms: the β→α transition which softens the structure, and the formation of smaller rings making the network elastically stronger.

In the recent article of Keryvin et al.35 which proposes a mechanical model of silica glass under hydrostatic pressure, the authors use a linear function to describe the evolution of the elastic moduli versus densification ratio. It is also specified by the authors that the lack of information between 4% and 20% prevents a more accurate law. Our results clearly reveal that the evolution of elastic moduli is far from linear (see Fig. 3 and 4). Taking into account the polynomial laws proposed previously would considerably improve such modelling, whether for hydrostatic compression or indentation31,35.

Methods

A diamond anvil cell (DAC) was used to densify Suprasil 300 vitreous SiO2 from Heraeus ([OH < 1 ppm] at ambient temperature. The pressures reached in the DAC were determined in situ by the ruby-fluorescence method. The hole of the metal gasket, 200 μm in diameter, was filled with a glass splinter (typically 50 μm in size), several ruby spheres, and a liquid pressure medium (a 20:4:1 mixture of methanol-ethanol-water). This pressure medium has been reported to remain perfectly hydrostatic up to 12 GPa and quasi-hydrostatic above37. All the recovered samples were in one piece, suggesting low shear stresses during the compression-decompression cycle.

The Brillouin scattering signal was recorded using a Sandercock tandem Fabry Perot coupled with a microscope in back-scattering geometry. The excitation source used was a Nd3+-YAG laser operating at λ = 532 nm.

Author Contributions

B.C. designed the research. T.D. and C.M. carried out high pressure experiments. J.M., T.D. and A.M. carried out Brillouin measurements. T.D. performed data analysis and wrote the paper. All the authors reviewed the manuscript.

References

  1. Taylor E. W. Plastic deformation of optical glass. Nature 163, 323–323 (1949). [Google Scholar]
  2. Bridgman P. W. & Simon I. Effects of very high pressures on glass. J. Appl. Phys. 24, 405–413 (1953). [Google Scholar]
  3. Rouxel T., Ji H., Guin J. P., Augereau F. & Rufflé B. Indentation deformation mechanism in glass: Densification versus shear flow. J. Appl. Phys. 107, 094903 (2010). [Google Scholar]
  4. Deschamps T., Martinet C., Bruneel J. L. & Champagnon. Soda-lime silicate glass under hydrostatic pressure and indentation: A micro-Raman study. B. J. Phys.: Condens. Matter 23, 035402 (2011). [DOI] [PubMed] [Google Scholar]
  5. Rouxel T., Ji H., Hammouda T. & Moréac A. Poisson's ratio and the densification of glass under high pressure. Phys. Rev. Lett. 100, 225501 (2008). [DOI] [PubMed] [Google Scholar]
  6. Greaves G. N., Greer A. L., Lakes R. S. & Rouxel T. Poisson's ratio and modern materials. Nat. Mater. 10, 823–837 (2011). [DOI] [PubMed] [Google Scholar]
  7. Deschamps T. et al. Permanent densification of compressed silica glass: a Raman-density calibration curve. J. Phys.: Condens. Matter 25, 025402 (2013). [DOI] [PubMed] [Google Scholar]
  8. Mackenzie J. D. & Laforce R. P. High-pressure densification of glass and the effects of shear. Nature 197, 480–481 (1963). [Google Scholar]
  9. McMillan P., Piriou B. & Couty R. A Raman study of pressure-densified vitreous silica. J. Chem. Phys. 81, 4234–4236 (1984). [Google Scholar]
  10. Polian A. & Grimsditch M. Room temperature densification of a-SiO2 versus pressure. Phys. Rev. B 41, 6086–6087 (1990). [DOI] [PubMed] [Google Scholar]
  11. Grimsditch M. Polymorphism in amorphous SiO2. Phys. Rev. Lett. 52, 2379–2381 (1984). [Google Scholar]
  12. Sugai S. & Onodera A. Medium-range order in permanently densified SiO2 and GeO2 glass. Phys. Rev. Lett. 77, 4210–4213 (1996). [DOI] [PubMed] [Google Scholar]
  13. Polsky C., Smith K. H. & Wolf G. H. Effect of pressure on the absolute Raman scattering cross section of SiO2 and GeO2 glasses. J. Non-Cryst. Solids 248, 159–168 (1999). [Google Scholar]
  14. Schroeder J. et al. Raman scattering and Boson peaks in glasses: Temperature and pressure effects. J. Non-Cryst. Solids 349, 88–97 (2004). [Google Scholar]
  15. Champagnon B. et al. High pressure elastic and plastic deformations: in situ diamond anvil cell Raman experiments. J. Non-Cryst. Solids 354, 569–573 (2008). [Google Scholar]
  16. Vandembroucq D. et al. Density hardening plasticity and mechanical ageing of silica glass under pressure: a Raman spectroscopic study. J. Phys.: Condens. Matter 20, 485221 (2008). [Google Scholar]
  17. Poe B. T., Romano C. & Henderson G. Raman and XANES spectrocopy of permanently densified vitreous silica. J. Non-Cryst. Solids 341, 162–169 (2004). [Google Scholar]
  18. Zanatta M. et al. Elastic properties of permanently densified silica glass: a Raman, Brillouin light, and x-ray scattering study. Phys. Rev. B 81, 212201 (2010). [Google Scholar]
  19. Wakabayashi D., Funamori N., Sato T. & Taniguchi T. Compression behaviour of densified SiO2 glass. Phys. Rev. B 84, 144103 (2011). [Google Scholar]
  20. Wu M., Liang Y., Jiang J. Z. & John S. T. Structure and properties of dense silica glass. Sci. Rep. 2, 398 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Yuan F. & Huang L. Brittle to ductile transition in densified silica glass. Sci. Rep. 4, 5035 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jin W., Kalia R. K., Vashishta P. & Rino J. P. Structural transformation in densified silica glass: a molecular-dynamics study. Phys. Rev. B 50, 118 (1994). [DOI] [PubMed] [Google Scholar]
  23. Della Valle R. G. & Venuti E. High-pressure densification of silica glass: a molecular-dynamics simulation. Phys. Rev. B 54, 3809 (1996). [DOI] [PubMed] [Google Scholar]
  24. Lacks D. J. First order amorphous-amorphous transformation in silica. Phys. Rev. Lett. 84, 4629–4632 (2000). [DOI] [PubMed] [Google Scholar]
  25. Trachenko K. & Dove M. T. Intermediate states in pressurized silica glass: Reversibility window analogue. Phys. Rev. B 67, 212203 (2003). [Google Scholar]
  26. Huang L. & Kieffer J. Amorphous-amorphous transitions in silica glass. II. Irreversible transitions and densification limit. Phys. Rev. B 69, 224204 (2004). [Google Scholar]
  27. Léonforte F., Tanguy A., Wittmer J. P. & Barrat J. L. Inhomogeneous elastic response of silica glass. Phys. Rev. Lett. 97, 055501 (2006). [DOI] [PubMed] [Google Scholar]
  28. Liang Y., Miranda C. R. & Scandolo S. Mechanical strength and coordination defects in compressed silica glass: Molecular-dynamics simulations. Phys. Rev. B 75, 024205 (2007). [Google Scholar]
  29. Izvekov S. & Rice B. M. Mechanism of densification in silica glass under pressure as revealed by a bottom-up pairwise effective interaction model. J. Chem. Phys. 136, 134508 (2012). [DOI] [PubMed] [Google Scholar]
  30. Li N., Sakidja R., Aryal S. & Ching W. Y. Densification of a continuous random network model of amorphous SiO2 glass. Phys. Chem. Chem. Phys. 16, 1500–1514 (2014). [DOI] [PubMed] [Google Scholar]
  31. Kermouche G., Barthel E., Vandembroucq D. & Dubujet P. Mechanical modelling of indentation-induced densification in amorphous silica. Acta Mater. 56, 3222–3228 (2008). [Google Scholar]
  32. Gadelrab K. R., Bonilla F. A. & Chiesa M. Densification modelling of fused silica under nanoindentation. J. Non-Cryst. Solids 358, 392–398 (2012). [Google Scholar]
  33. Lacroix L., Teisseire J., Kermouche G. & Barthel E. Plastic deformation and residual stresses in amorphous silica pillars under uniaxial loading. Acta Mater. 20, 5555–5566 (2012). [Google Scholar]
  34. Kylimis D. A. & Delaye J. M. Nanoindentation of pristine and disordered silica: Molecular-dynamics simulation. J. Non-Cryst. Solids 382, 87–94 (2013). [Google Scholar]
  35. Keryvin V. et al. Constitutive modeling of the densification process in silica glass under hydrostatic pressure. Acta Mater. 62, 250 (2014). [Google Scholar]
  36. Vukcevich M. R. A new interpretation of the anomalous properties of vitreous silica. J. Non-Cryst. Solids 11, 25–63 (1972). [Google Scholar]
  37. Klotz S., Chervin J. C., Munsch P. & Le Marchand G. J. Hydrostatic limits of 11 pressure transmitting media. Phys. D: Appl. Phys. 42, 075413 (2009). [Google Scholar]
  38. Tan C., Arndt J. & Xie H. Optical properties of densified silica glass. Physica B 252, 28–33 (1998). [Google Scholar]
  39. Meade C. & Jeanloz R. Frequency-dependent equation of state of fused silica to 10 GPa. Phys. Rev. B 35, 236–244 (1987). [DOI] [PubMed] [Google Scholar]
  40. Polian A. & Grimsditch M. Sound velocities and refractive index of densified a-SiO2 to 25 GPa. Phys. Rev. B 47, 13979–13982 (1993). [DOI] [PubMed] [Google Scholar]
  41. Zha C. S., Hemley R. J., Mao H. K., Duffy T. S. & Meade C. Sound velocities and refractive index of SiO2 glass to 57.5 GPa by Brillouin scattering. Phys. Rev. B 50, 13105–13112 (1994). [DOI] [PubMed] [Google Scholar]
  42. Deschamps T., Martinet C., de Ligny D. & Champagnon B. Elastic anomalous behaviour of silica glass under high-pressure: In situ Raman study. J. Non-Cryst. Solids 355, 1095–1098 (2009). [Google Scholar]
  43. Deschamps T., Martinet C., Bruneel J. L., de Ligny D. & Champagnon B. Low-frequency Raman scattering under high pressure in diamond anvil cell: Experimental protocol and application to GeO2 and SiO2 boson peaks. J. Non-Cryst. Solids 358, 3156–3160 (2012). [Google Scholar]
  44. Huang L. & Kieffer J. Amorphous-amorphous transitions in silica glass. I. Reversible transitions and thermomechanical anomalies. Phys. Rev. B 69, 224203 (2004). [Google Scholar]
  45. Huang L., Duranduru M. & Kieffer J. Transformation pathways of silica under high pressure. Nat. Mater. 5, 977–981 (2006). [DOI] [PubMed] [Google Scholar]
  46. Mantisi B., Tanguy A., Kermouche G. & Barthel E. Atomistic response of a model silica glass under shear and pressure. Eur. Phys. J. B 85, 304 (2012). [Google Scholar]
  47. Huang L. & Kieffer J. Anomalous thermomechanical properties and laser induced densification of vitreous silica. Appl. Phys. Lett. 89, 141915 (2006). [Google Scholar]
  48. Sonneville S. et al. Progressive transformations of silica glass upon densification. J. Chem. Phys. 137, 124505 (2012). [DOI] [PubMed] [Google Scholar]
  49. Wang W. H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 57, 487–656 (2012). [Google Scholar]
  50. Kondo K., Ito S. & Sawaoka A. Nonlinear pressure dependence of the elastic moduli fused quartz up to 3 GPa. J. Appl. Phys. 52, 2826–2831 (1981). [Google Scholar]
  51. El'kin F. S., Brazhkin V. V., Khvostantsev L. G., Tsiok O. B. & Lyapin A. G. In situ study of the mechanism of formation of pressure-densified SiO2 glasses. JETP Lett. 75, 342–347 (2002). [Google Scholar]
  52. Liang Y., Miranda C. R. & Scandolo S. Temperature-induced densification of compressed SiO2 glass: A molecular dynamics study. High Press. Res. 28, 35–44 (2008). [Google Scholar]
  53. Brazhkin V. V. & Lyapin A. G. High-pressure phase transformations in liquids and amorphous solids. J. Phys.: Condens. Matter 15, 6059–6084 (2003). [Google Scholar]
  54. Furhmann S., Deschamps T., Champagnon B. & Wondraczek L. A reconstructive polyamorphous transition in borosilicate glass induced by irreversible compaction. J. Chem. Phys. 140, 054501 (2014). [DOI] [PubMed] [Google Scholar]
  55. Meade C., Hemley R. J. & Mao H. K. High-pressure X-ray-diffraction of SiO2 glass. Phys. Rev. Lett. 69, 1387–1390 (1992). [DOI] [PubMed] [Google Scholar]
  56. Sato T. & Funamori N. Sixfold-coordinated amorphous polymorph of SiO2 under high pressure. Phys. Rev. Lett. 101, 25502 (2008). [DOI] [PubMed] [Google Scholar]
  57. Benmore C. J. et al. Structural and topological changes in silica glass at pressure. Phys. Rev. B 81, 054105 (2010). [Google Scholar]
  58. Sato T. & Funamori N. High-pressure structural transformation of SiO2 glass up to 100 GPa. Phys. Rev. B 82, 184102 (2010). [Google Scholar]
  59. Perriot A. et al. Raman microspectroscopic characterization of amorphous silica plastic behaviour. J. Am. Ceram. Soc. 89, 596–601 (2006). [Google Scholar]
  60. Winterstein-Beckmann A., Mönke D., Palles D., Kamitsos E. I. & Wondraczek L. Raman spectroscopic study of structural changes induced by micro-indentation in low alkali borosilicate glasses. J. Non-Cryst. Solids 401, 110–114 (2014). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES