Field-induced superconducting phase of FeSe in the BCS-BEC cross-over

Significance

The BCS-BEC (Bardeen–Cooper–Schrieffer––Bose–Einstein-condensate) cross-over bridges the two important theories of bound particles in a unified picture with the ratio of the attractive interaction to the Fermi energy as a tuning parameter. A key issue is to understand the intermediate regime, where new states of matter may emerge. Here, we show that the Fermi energy of FeSe is extremely small, resulting in that this system can be regarded as an extraordinary “high-temperature” superconductor located at the verge of a BCS-BEC cross-over. Most importantly, we discover the emergence of an unexpected superconducting phase in strong magnetic fields, demonstrating that the Zeeman splitting comparable to the Fermi energy leads to a strong modification of the properties of fermionic systems in such a regime.

Abstract

Fermi systems in the cross-over regime between weakly coupled Bardeen–Cooper–Schrieffer (BCS) and strongly coupled Bose–Einstein-condensate (BEC) limits are among the most fascinating objects to study the behavior of an assembly of strongly interacting particles. The physics of this cross-over has been of considerable interest both in the fields of condensed matter and ultracold atoms. One of the most challenging issues in this regime is the effect of large spin imbalance on a Fermi system under magnetic fields. Although several exotic physical properties have been predicted theoretically, the experimental realization of such an unusual superconducting state has not been achieved so far. Here we show that pure single crystals of superconducting FeSe offer the possibility to enter the previously unexplored realm where the three energies, Fermi energy ${\epsilon }_{\text{F}}$, superconducting gap Δ, and Zeeman energy, become comparable. Through the superfluid response, transport, thermoelectric response, and spectroscopic-imaging scanning tunneling microscopy, we demonstrate that ${\epsilon }_{\text{F}}$ of FeSe is extremely small, with the ratio $\mathrm{\Delta }/{\epsilon }_{\text{F}}\sim 1\left(\sim 0.3\right)$ in the electron (hole) band. Moreover, thermal-conductivity measurements give evidence of a distinct phase line below the upper critical field, where the Zeeman energy becomes comparable to ${\epsilon }_{\text{F}}$ and Δ. The observation of this field-induced phase provides insights into previously poorly understood aspects of the highly spin-polarized Fermi liquid in the BCS-BEC cross-over regime.

Superconductivity in most metals is well explained by the weak-coupling Bardeen–Cooper–Schrieffer (BCS) theory, where the pairing instability arises from weak attractive interactions in a degenerate fermionic system. In the opposite limit of Bose–Einstein condensate (BEC), composite bosons consisting of strongly coupled fermions condense into a coherent quantum state (1, 2). In BCS superconductors, the superconducting transition temperature is usually several orders of magnitude smaller than the Fermi temperature, $T_{\text{c}}/T_{\text{F}}={10}^{-5}$–${10}^{-4}$, whereas in the BEC limit $T_{\text{c}}/T_{\text{F}}$ is of the order of ${10}^{-1}$. Even in the high-$T_{\text{c}}$ cuprates, $T_{\text{c}}/T_{\text{F}}$ is merely of the order of ${10}^{-2}$ at optimal doping. Of particular interest is the BCS-BEC cross-over regime with intermediate coupling strength. In this regime the size of interacting pairs ($\sim \xi$), which is known as the coherence length, becomes comparable to the average distance between particles ($\sim 1/k_{\text{F}}$), i.e., $k_{\text{F}}\xi \sim 1$ (3–5), where $k_{\text{F}}$ is the Fermi momentum. This regime is expected to have the highest values of $T_{\text{c}}/T_{\text{F}}=0.1-0.2$ and $\mathrm{\Delta }/{\epsilon }_{\text{F}}\sim 0.5$ ever observed in any fermionic superfluid.

One intriguing issue concerns the role of spin imbalance: whether it will lead to a strong modification of the properties of the Fermi system in the cross-over regime. This problem has been of considerable interest not only in the context of superconductivity but also in ultracold-atom physics (6–8). However, such Fermi systems have been extremely hard to access. In superconductors, the spin imbalance can be introduced through the Zeeman effect by applying a strong magnetic field. Again, in the high-$T_{\text{c}}$ cuprates, the Zeeman energy at the upper critical field at $T\ll T_{\text{c}}$ is of the order of only ${10}^{-2}{\epsilon }_{\text{F}}$. In ultracold atoms, although several exotic superfluid states have been proposed (9, 10), cooling the systems down to sufficiently low temperature ($T\ll T_{\text{c}}$) is not easily attained.

FeSe provides an ideal platform for studying a highly spin-polarized Fermi system in the cross-over regime. FeSe is the simplest iron-based layered superconductor (Fig. 1A, Inset) with $T_{\text{c}}$ of $\sim$9 K (11). The structural transition from tetragonal to orthorhombic crystal symmetry occurs at $T_{\text{s}}\approx$ 90 K and a large electronic in-plane anisotropy appears. In contrast with the other iron-based compounds, no magnetic order occurs below $T_{\text{s}}$. A prominent feature of the pseudobinary “11” family (FeSe_1−x Te_x) is the presence of very shallow pockets, as reported by angle-resolved photoemission spectroscopy (ARPES). Although a possible BCS-BEC cross-over has been suggested in the bands around the $\mathrm{\Gamma }$-point (12, 13), it is still an open question whether all bands are in such a cross-over regime. Moreover, it should be noted that high-quality single crystals are highly requisite for the study of the cross-over regime, as exotic superconductivity often is extremely sensitive to impurities. Previous FeSe_x single crystals are strongly disordered, as indicated by large residual resistivity ${\rho }_0$ and small residual resistivity ratio $RRR$, typically 0.1 mΩ cm and $\sim$5, respectively (14).

Fig. 1.

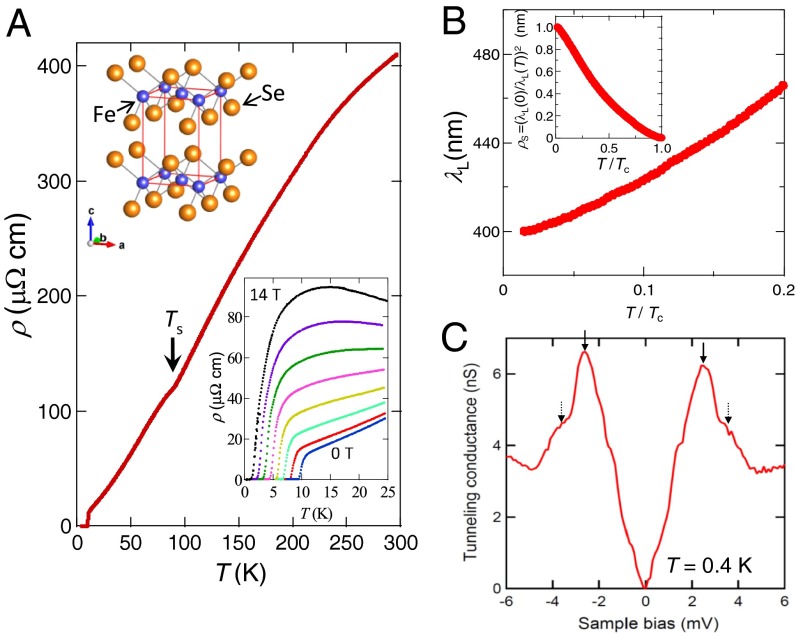
Normal and superconducting properties of high-quality single crystals of FeSe. (A) Temperature dependence of the in-plane resistivity ρ of FeSe. The structural transition occurs at $T_{\text{s}}\approx$ 90 K. (Upper Inset) Crystal structure. (Lower Inset) $\rho \left(T\right)$ in magnetic field ($\mathit{H}\Vert c$). From bottom to top, ${\mu }_{0}H=$ 0, 2, 4, 6, 8, 10, 12, and 14 T is applied. (B) Temperature dependence of the London penetration depth. (Inset) Superfluid density normalized by the zero temperature value ${\rho }_{\text{s}}\equiv {\lambda }_{\text{L}}^2\left(0\right)/{\lambda }_{\text{L}}^2\left(T\right)$. (C) Tunneling conductance spectrum at $T=0.4$ K. The peaks at $\pm 2.5$ meV (arrows) and shoulder structures at $\pm 3.5$ meV (dashed arrows) indicate the multiple superconducting gaps.

Results and Discussion

BCS-BEC Cross-Over.

By using high-quality single crystals of FeSe (SI Text, section 1 and Figs. S1 and S2) which have become available recently, we have measured the transport properties (Fig. 1A). In zero field, the temperature dependence of the resistivity ρ can be described by $\rho ={\rho }_0+A{T}^{\alpha }$ with $\alpha =1.05-1.2$ below 25 K. Taking $\rho \left(T_{\text{c}}^{+}\right)\approx 10\hspace{0.17em}\mu \mathrm{\Omega }\hspace{0.5em}\mathrm{cm}$ as the upper limit of ${\rho }_0$ leads to $RRR>40$, i.e., a factor of 10 higher than previous samples. In the present crystals $T_c$ defined by the zero resistivity is 9.5 K, which is higher than $T_c\sim 8$ K of the low $RRR$ samples (14). A remarkably large magnetoresistance (Fig. 1A, Inset) not observed in previously studied low-$RRR$ crystals (14) supports that the crystal is very clean (SI Text, section 2 and Fig. S3A). The strongly T-dependent Hall coefficient $R_{\text{H}}$ below $\sim$60 K indicates that the electron and hole mobilities are of the same order (SI Text, section 2 and Fig. S3B). The London penetration depth ${\lambda }_{\text{L}}$ shows a quasi–T-linear dependence, ${\lambda }_{\text{L}}\left(T\right)\propto T^{1.4}$, for $T/T_{\text{c}}<0.2$, suggesting the presence of line nodes in the superconducting gap (Fig. 1B). Fig. 1C shows the tunneling conductance, which is proportional to the density of states, measured with a scanning tunneling microscope at 0.4 K. The V-shaped spectrum at low bias voltages likewise indicates the presence of line nodes, which is consistent with previously reported observations (15). We note that the line nodes are accidental, not symmetry protected, i.e., the gap function is extended s wave, because the nodes are absent in samples with low $RRR$ (16). Distinct peaks and shoulder structures in the spectra indicate the presence of (at least) two superconducting gaps ($\mathrm{\Delta }\approx$2.5 and 3.5 meV), reflecting the multiband nature.

The high quality of the single crystals enables us to estimate the Fermi energies ${\epsilon }_{\text{F}}^{\text{e}}$ and ${\epsilon }_{\text{F}}^{\text{h}}$ from the band edges of electron and hole sheets, respectively, by using several techniques; all of them consistently point to extremely small Fermi energies. In 2D systems ${\epsilon }_{\text{F}}$ is related to ${\lambda }_{\text{L}}\left(0\right)$ as ${\epsilon }_{\text{F}}=\left(\pi {\hslash }^{2}d/{\mu }_0{e}^2\right){\lambda }_{\text{L}}^{-2}\left(0\right)$, where d is the interlayer distance and ${\mu }_0$ is the vacuum permeability. From the T dependence of ${\lambda }_{\text{L}}\left(T\right)$, we obtain ${\lambda }_{\text{L}}\left(0\right)\approx 400$ nm (Fig. 1B and SI Text, section 3 and Fig. S4) (17). Very recent quantum oscillation measurements on the present FeSe crystals revealed that the Fermi surface consists of one hole sheet and one (compensating) electron sheet (Fig. 2A) (18). Then ${\lambda }_{\text{L}}$ can be written as $1/{\lambda }_{\text{L}}^2=1/{\left({\lambda }_{\text{L}}^{\text{e}}\right)}^2+1/{\left({\lambda }_{\text{L}}^{\text{h}}\right)}^2$, where ${\lambda }_{\text{L}}^{\text{e}}$ and ${\lambda }_{\text{L}}^{\text{h}}$ represent the contribution from the electron and hole sheets, respectively. Assuming that two sheets have similar effective masses as indicated by the Hall effect (see below and SI Text, section 2), we estimate ${\epsilon }_{\text{F}}^{\text{e}}\sim {\epsilon }_{\text{F}}^{\text{h}}\sim 7-8$ meV. The magnitude of the Fermi energy can also be inferred from the thermoelectric response in the normal state (SI Text, section 2). From the Seebeck coefficient S, the upper limit of ${\epsilon }_{\text{F}}^{\text{e}}$ is deduced to be ∼10 meV (SI Text, section 2 and Fig. S3C). Moreover, the sign change of $R_{\text{H}}\left(T\right)$ at 60 K (SI Text, section 2 and Fig. S3B) indicates that the Fermi energies ${\epsilon }_{\text{F}}^{\text{e}}$ and ${\epsilon }_{\text{F}}^{\text{h}}$ are of similar size, a feature also observed in underdoped cuprate superconductors with small electron and hole pockets (19). In contrast with the cuprate case, however, $R_{\text{H}}$ in FeSe almost vanishes at high temperatures, which sheds light on the unique feature of FeSe with extremely small Fermi energy.

Fig. 2.

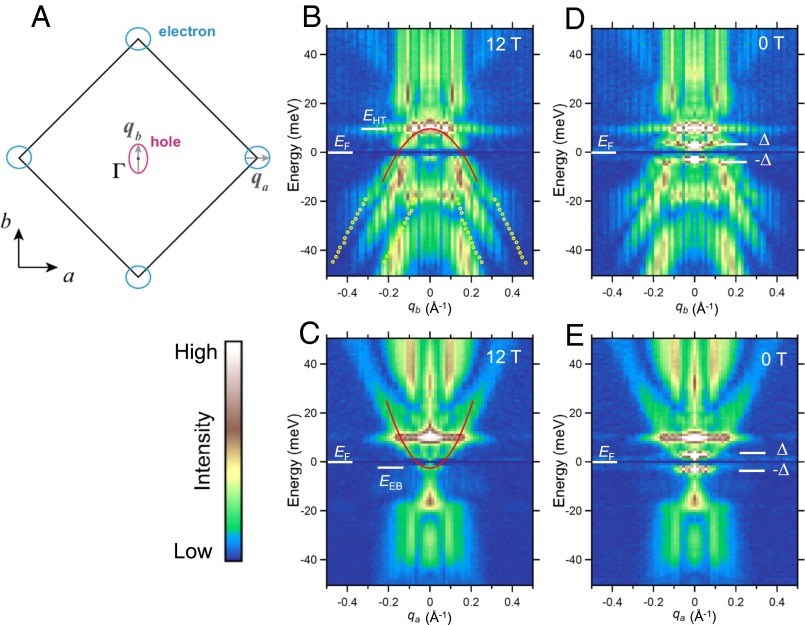
Band dispersions obtained from the QPI pattern. (A) Schematic figure of the Fermi surface of FeSe inferred from QPI. (B and C) QPI dispersions at 12 T obtained by taking linecuts from the energy-dependent Fourier-transformed normalized conductance images (SI Text, section 4 and Fig. S5) along $q_a$ and $q_b$, respectively. A q-independent feature at ∼+10 meV is associated with defect states (SI Text, section 4 and Fig. S6). Peak positions of the representative branches are fitted with parabolic function to obtain Fermi energies and effective masses (solid lines). The top (bottom) of the hole (electron) band $E_{\text{HT}}$ ($E_{\text{EB}}$) is indicated by white bars. Expected intraband scattering vectors associated with the α-band detected by ARPES (22) are plotted in B by yellow circles. (D and E) QPI dispersions at $H=0$. A pair of sharp intensity peaks ($\pm \mathrm{\Delta }$) appears at $E\approx \pm 2$ meV due to the opening of the superconducting gap. Superconducting gap defined by the positions of the coherence peaks (white bars) are comparable to the Fermi energies. Note that the feature attributed to defect states is independent of field.

We can determine the electron and hole Fermi energies directly by measuring the electronic dispersion curves in momentum space yielding ${\epsilon }_{\text{F}}^{\text{h}}=E_{\text{HT}}-E_{\text{F}}$ (${\epsilon }_{\text{F}}^{\text{e}}=E_{\text{F}}-E_{\text{EB}}$) for the hole (electron) band. Here $E_{\text{HT}}$ ($E_{\text{EB}}$) is the energy of the top (bottom) of the hole (electron) band and $E_{\text{F}}$ is the electrochemical potential. For this assignment, we exploit spectroscopic-imaging scanning tunneling microscopy to observe the quasiparticle interference (QPI) patterns (20, 21) associated with electron waves scattered off by defects. By taking the Fourier transform of energy-dependent normalized conductance images, characteristic wave vectors of electrons at different energies reflecting the band dispersion can be determined (SI Text, section 4). The observed QPI patterns of FeSe at 1.5 K (SI Text, section 4 and Fig. S5) consist of hole- and electron-like branches that disperse along the crystallographic b and $a\left(<b\right)$ directions, respectively. These branches can naturally be ascribed to the hole and electron sheets illustrated in Fig. 2A. The QPI signals exhibit a strong in-plane anisotropy. Such an anisotropy is consistent with the largely elongated vortex core structure (15). The origin of the strong in-plane anisotropy of the QPI signals is unclear, but a possible cause may be the orbital ordering in the orthorhombic phase.

As shown in Fig. 2 B and C, full dispersion curves of hole- and electron-like branches are clearly identified by taking linecuts from the series of Fourier-transformed conductance images (SI Text, section 4 and Fig. S5). Here, a magnetic field ${\mu }_{0}H=12$ T is applied parallel to the c axis ($\mathit{H}\Vert c$) to mostly suppress superconductivity. Multiple hole-like branches are identified in Fig. 2B. Because QPI signals include both intra- and interband scattering processes, it is difficult to disentangle all of the QPI branches to resolve the bare band structure. Nevertheless, the top of the hole band can be faithfully determined to yield ${\epsilon }_{\text{F}}^{\text{h}}\sim$ 10 meV from the highest energy of the topmost branch. This branch is quantitatively consistent with the intraband scattering associated with the α-band detected by ARPES (22). In the case of the electron-like branch, an even smaller band bottom of ${\epsilon }_{\text{F}}^{\text{e}}\sim$ 2–3 meV is estimated (Fig. 2C). These small values are consistent with the ones estimated from the superfluid and thermoelectric responses. The effective mass of electron (hole) determined by QPI assuming parabolic dispersion is 2.5 $m_0$ (3.5 $m_0$), where $m_0$ is the free-electron mass. The observation of comparable effective masses of electrons and holes is consistent with the Hall-effect data (SI Text, section 2). We stress that the electronic structure obtained from QPI, including masses of electron and hole, the size and the number of each pocket, and the magnitude of the Fermi energies, is consistent with the values recently reported by the quantum oscillations in the quantitative level (18). Remarkably, the superconducting gaps are of the same order as the Fermi energy of each band, $\mathrm{\Delta }/{\epsilon }_F^e\sim 1$ (Fig. 2D) and $\mathrm{\Delta }/{\epsilon }_F^h\sim 0.3$ (Fig. 2E), implying the BCS-BEC cross-over regime. Additional strong support of the cross-over is provided by extremely small $k_F\xi \sim$1–4. Here, $k_F$ of the electron (hole) sheet obtained from Fig. 2C (Fig. 2B) is roughly 0.3 (0.75) nm⁻¹, and ξ determined from the upper critical field ($\sim 17$ T) is roughly 5 nm.

Field-Induced Superconducting Phase.

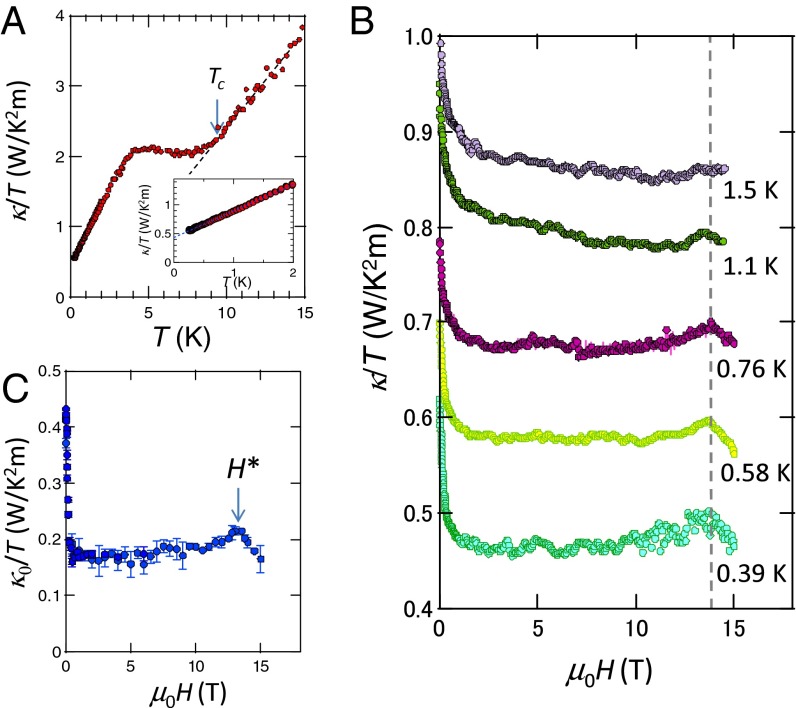
So far we discussed the relation between ${\epsilon }_{\text{F}}$ and Δ. How does the Zeeman energy scale ${\mu }_{\text{B}}H$, where ${\mu }_{\text{B}}$ is the Bohr magneton, enter the game? The thermal conductivity κ is well suited to address the issue of how the magnetic field affects the extraordinary pairing state by probing quasiparticle excitations out of the superconducting condensate, as the Cooper pair condensate does not contribute to heat transport. Figure 3A shows the T dependence of $\kappa /T$ in zero field. Below $T_{\text{c}}$, κ is enhanced due to the suppression of quasiparticle scattering rates owing to the gap formation. As shown in Fig. 3A (Inset), $\kappa /T$ at low temperatures is well fitted as $\kappa /T={\kappa }_0/T+\beta T$, similar to Tl₂Ba₂CuO_6+δ (23). The presence of the residual ${\kappa }_0/T$ at $T\to 0$ is consistent with line nodes in the gap.

Fig. 3.

Field-induced transition revealed by the thermal conductivity. (A) Temperature dependence of the in-plane thermal conductivity divided by temperature, $\kappa /T$. Arrow marked $T_{\text{c}}$ indicates the onset temperature of the superconductivity determined by zero resistivity (Fig. 1A) and zero thermoelectric power (SI Text, section 2 and Fig. S3C). (Inset) $\kappa /T$ at low temperatures. (B) Magnetic-field dependence of $\kappa /T$ at low temperatures ($\mathit{H}\Vert c$). No hysteresis with respect to the field-sweep direction is observed. $\kappa /T$ shows a plateau-like behavior in a wide field range. At $H^{\mathrm{\ast }}$, $\kappa /T$ shows a cusp-like peak, suggestive of a nearly temperature-independent transition (dashed line). At 1.5 K, the cusp disappears and a weak structure (within the accuracy of the measurement) is observed at lower field. (C) Magnetic-field dependence of $\kappa /T$ in the zero-temperature limit, ${\kappa }_0/T$, obtained by linear extrapolation of $\kappa /T$ versus T at low temperatures.

Fig. 3B shows the H dependence of $\kappa /T$ for $\mathit{H}\Vert c$ well below $T_{\text{c}}$ obtained after averaging over many field sweeps at constant temperatures. Beyond the initial steep drop at low fields, likely caused by the suppression of the quasiparticle mean-free path ${\ell }_{\text{e}}$ through the introduction of vortices, $\kappa \left(H\right)/T$ becomes nearly H-independent. Similar behavior has been reported for Bi₂Sr₂CaCu₂O₈ (24) and CeCoIn₅ (25). It has been suggested that the nearly H-independent κ reflects a compensation between the enhancement of the density of states by magnetic field in nodal superconductors (Doppler shift) and the concomitant reduction in ${\ell }_{\text{e}}$ due to increased scattering from vortices (26). At high fields, above the smoothly varying background, $\kappa \left(H\right)/T$ exhibits a cusp-like feature at a field $H^{\mathrm{\ast }}$ that is practically independent of T. The height of the cusp-like peak decreases with increasing T. To further analyze our data, the $\kappa /T$ values at different temperatures are extrapolated to $T=0$ for each field value measured to yield ${\kappa }_0\left(H\right)/T$ as shown in Fig. 3C, corroborating the robustness of the cusp. In particular, the cusp of ${\kappa }_0/T$ is unrelated to phonon heat transport because phonons do not contribute to $\kappa /T$ for $T\to 0$. Because the thermal conductivity has no fluctuation corrections (27), the cusp of κ usually corresponds to the mean-field phase transition. We note that at $H^{\mathrm{\ast }}$ the field dependence of magnetic torque shows no discernible anomaly (SI Text, section 5 and Fig. S7). However, such a difference of the sensitivity to the transition in different measurements has been reported for the field-induced transition between two superconducting phases in CeCoIn₅, which is hardly resolved in magnetization (28), despite clear anomaly in some other bulk probes (29). Moreover, the hysteresis in the magnetization due to vortex pinning may smear out a possible torque anomaly at $H^{\mathrm{\ast }}$.

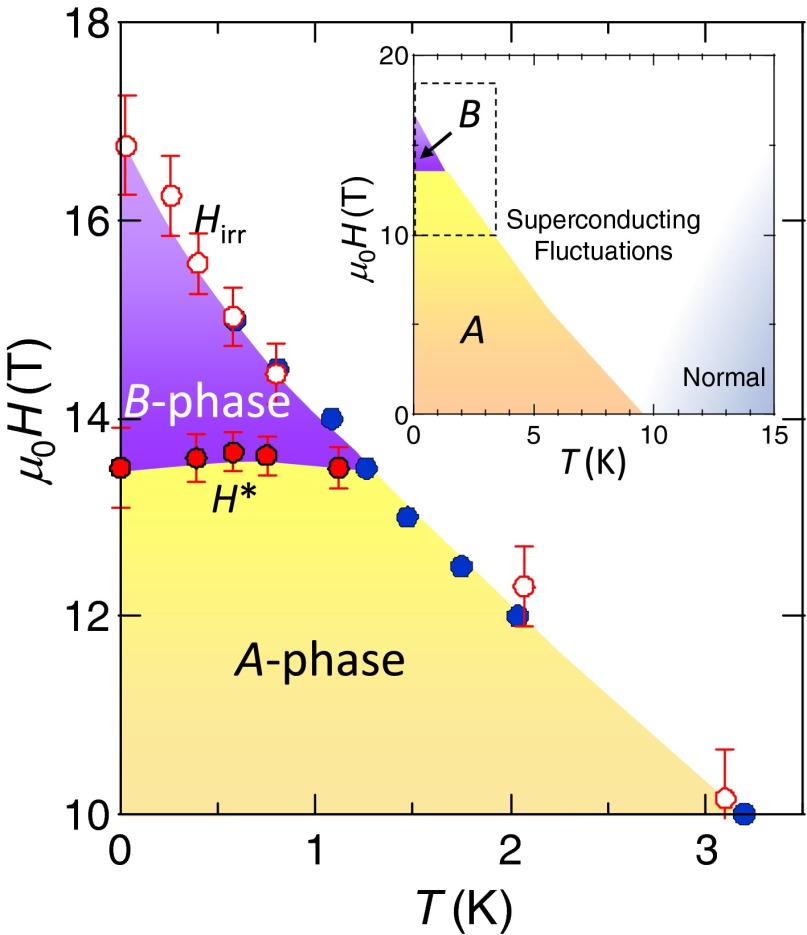
Fig. 4 displays the H-T phase diagram for $\mathit{H}\Vert c$. The irreversibility fields $H_{\text{irr}}$ at low temperatures extend to fields well above $H^{\mathrm{\ast }}$, indicating that $H^{\mathrm{\ast }}$ is located inside the superconducting state. The anomaly at $H^{\mathrm{\ast }}$ is not caused by some changes of the flux-line lattice, such as melting transition, because the peak field determined by the torque is strongly T-dependent and well below $H^{\mathrm{\ast }}$ (SI Text, section 5 and Fig. S7), indicating that the flux-line lattice is already highly disordered at $H^{\mathrm{\ast }}$.

Fig. 4.

H-T phase diagram of FeSe for $\mathit{H}\Vert c$. Solid blue and open red circles represent $H_{\text{irr}}$ determined by zero resistivity and the onset of hysteresis loops of the magnetic torque, respectively. The mean-field upper critical field is above $H_{\text{irr}}$. Solid red circles represent $H^{\mathrm{\ast }}$ determined by the cusp of $\kappa \left(H\right)/T$ shown in Fig. 3 B and C, separating a high-field superconducting phase (B phase) from the low-field phase (A phase). (Inset) Overall H-T phase diagram. Superconducting fluctuation regime is determined by the temperature at which the resistivity deviates from the behavior expected in conventional semimetallic systems.

As shown in Fig. 1A (Inset), the resistivity at ${\mu }_{0}H=14$ T increases with decreasing temperature and decreases after showing a broad maximum at around 15 K. The T dependence at high temperature is a typical behavior of the very pure compensated semimetals. However, the decrease of the resistivity at low-temperature regime is not expected in conventional semimetals. This unusual decrease may be attributed to the strong superconducting fluctuations above $H_{\text{irr}}$ (Fig. 4, Inset). In higher fields the fluctuation region expands to higher $T>T_{\text{c}}$. In fact, the Ginzburg number, which is given by $G_{\text{i}}\sim {\left(T_{\text{c}}/T_{\text{F}}\right)}^4$ within the BCS framework (30), is orders of magnitude larger than in any other superconductors. This large range of fluctuations may be related to the presence of preformed pairs predicted in the BCS-BEC cross-over regime (1, 3–5).

The appearance of the high-field phase (B phase in Fig. 4) where three characteristic energy scales are comparable, ${\mu }_{\text{B}}{H}^{\mathrm{\ast }}\sim {\epsilon }_{\text{F}}\sim \mathrm{\Delta }\left(0\right)$, suggests a phase transition of the Fermi liquid with strong spin imbalance in the BCS-BEC cross-over regime. Whether the observed distinct phase arises from strong spin imbalance and/or a BCS-BEC cross-over, however, needs to be resolved in the future with particular attention to multiband effects. We discuss two possible scenarios. (i) The phase line might signal an electronic transition akin to a Lifshitz transition, i.e., a topology change of the Fermi surface. Indeed, the phase line would be independent of T and smeared by thermal fluctuations. However, the fact that this phase line vanishes at $H_{\text{irr}}$ would be accidental. Furthermore, the absence of any discernible anomaly in torque magnetometry at $H^{\mathrm{\ast }}$ (SI Text, section 5 and Fig. S7) implies that the $\kappa \left(H\right)/T$ anomaly at $H^{\mathrm{\ast }}$ is not caused by a Lifshitz transition nor, for that matter, by a spin-density–wave type of magnetic order. (ii) Comparable Fermi and Zeeman energies may lead to an unprecedented superconducting state of highly spin-polarized electrons, such as spin-triplet pairing and an admixture of even- and odd-frequency pairing (31). Comparable gap and Zeeman energies may alternatively induce a Fulde–Ferrell–Larkin–Ovchinnikov (FFLO)-like state with Cooper pairs having finite total momentum ($\mathit{k}\uparrow$, $-\mathit{k}+\mathit{q}\downarrow$) owing to the pairing channel between the Zeeman–split Fermi surfaces (29). The FFLO state requires a large Maki parameter, i.e., a ratio of orbital and Pauli-paramagnetic limiting fields, ${\alpha }_{\text{M}}\equiv \sqrt{2}{H}_{\text{c}2}^{\text{orb}}/H_{\text{c}2}^{\text{P}}>1.5$ in the BCS limit. In this regime, ${\alpha }_{\text{M}}\approx 2m^{\mathrm{\ast }}/m_0\cdot \mathrm{\Delta }/{\epsilon }_{\text{F}}$, yielding, for FeSe, ${\alpha }_{\text{M}}$ as large as ∼5 ($\sim 2.5$) in the electron (hole) pockets. This estimate may be questionable in the regime of $\mathrm{\Delta }/{\epsilon }_{\text{F}}$ for FeSe. In any case, we stress that the high-field phase is not a simple FFLO phase because in the multiband superconductor FeSe the interaction between electron and hole bands is crucial. Even in the single-band systems, it has been suggested that the FFLO state becomes unstable in the cross-over regime (32). Our work should motivate further studies in the field of strongly interacting Fermi liquids near the BCS-BEC cross-over regime and in the presence of large spin imbalance, which remains largely unexplored and might bridge the areas of condensed-matter and ultracold-atom systems.