Putting things in order

Identifying and characterizing dependence among a set of variables (also called features, covariates, and factors) is at the core of statistics. Since the concept of “correlation” was introduced by Sir Francis Galton (1) in the late 1800s, many measures of associations have been proposed to capture the notion of nonindependence between two variables, x and y. The work of Wang et al. (2) is the latest installment to this long history of developments, with their measure motivated by identifying gene pairs with correlated expression patterns from high-throughput microarray data.

Consider yeast expression data analyzed in the paper by Wang et al. (2). With 6,000 genes, there are around 18,000,000 gene pairs, and it is a daunting task to sort through these many pairs to identify those having genuine dependencies. In a perfect world where all of the dependent relationships are linear and there are no data anomalies, we can use Pearson correlation efficient (3) coupled with statistical significance assessment to rank order all of the gene pairs. In fact, Pearson correlation efficient is still the most commonly used method to infer dependent relationships in microarray data analysis.

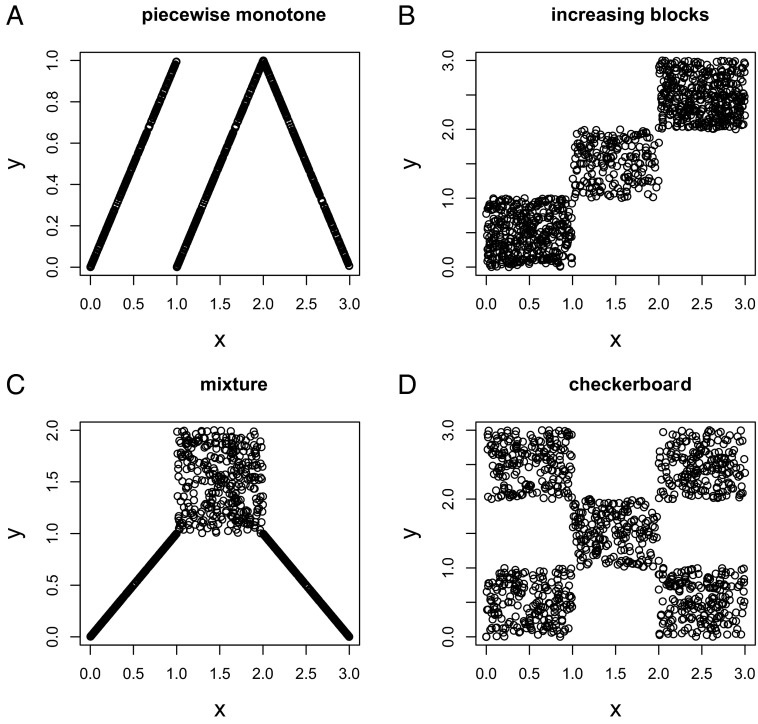
Despite its popularity, it is well known that Pearson correlation has limitations in the presence of nonlinear relationships (e.g., Fig. 1A) and outliers. When only a few pairs are of interest, individual scatterplots may be visually inspected to reduce false-positive and false-negative rates due to the inadequacies in the Pearson correlation measure. However, a more robust and powerful measure is needed when millions of correlations are investigated because even a very small proportion of false positives or negatives will translate into thousands of incorrect inferences. In fact, many alternative measures have been used in analyzing correlations among genes. Spearman rank correlation (4) uses ranks instead of raw observations and is robust against outliers, but may still fail in the face of nonmonotocinity. There are many other measures available (e.g., refs. 5–7), with a recent surge of interest (e.g., refs. 8–10) that has been in part driven by the very rich and complex data that have become available in recent years and the need to have robust and powerful methods to mine these data and to identify true associations without extensive human interventions.

Fig. 1.

(A–D) Four relationship patterns to illustrate the information source for W₂ statistic discussed in Wang et al. (2).

We note that two recently introduced measures have drawn considerable attention in the literature: distance correlation (dcor) (8) and maximal information coefficient (MIC) (9). Let (x_i, y_i) denote the ith observed pair for x and y. For dcor, it first calculates the pairwise distances among all pairs of x, d_x(i, j) = |x_i – x_j| and those among all pairs of y, d_y(i, j) = |y_i – y_j|. Then dcor is calculated as the correlation between the two sets of doubly centered distances derived from the pairwise distances. It was shown in (8) that dcor is 0 only if x and y are independent, a desired statistical property. MIC (9) was developed based on the mutual information idea where the uncertainty of y (defined through entropy) conditional on x is evaluated. The 2D space for (x, y) is first partitioned into r rows and c columns. The MIC algorithm then finds the r × c grid that has the highest induced mutual information for x and y. It looks through many (r, c) combinations to identify the one with the largest normalized score. Therefore, MIC may be interpreted as the variance/uncertainty of y explained by x. The pros and cons of these two relatively new measures and their comparisons with existing ones have been of much debate lately through theoretical investigations (e.g., equitability), simulation studies, and empirical data analyses (11–15).

The approach developed in ref. 2 departs from the existing methods with the reasoning that the rank (order) patterns across a subset of observations may offer very useful information on nonindependence. For a given set of observations (x_i, y_i), i = 1,…,n, instead of casting the problem as measuring uncertainty about y given x, Wang et al. (2) look for consistency of rank orders across a subset of observations. For example, if two variables are perfectly correlated via a monotone functional relationship, for any subset of observations, the orders among the y_i can be totally inferred from the orders among the x_i, whether the association is positive or negative. It is easy to see that if we allow for either positive or negative association, looking at a pair of observations will not be informative. Now consider three observations: (x₁, y₁), (x₂, y₂), and (x₃, y₃). If there is perfect monotone (either increasing or decreasing) relationship between x and y, we would be able to infer the orders of (y₁, y₂, y₃) completely from those of (x₁, x₂, x₃), either with the same orders or reverse orders. However, when x and y are independent, the orders are only aligned between x and y with a probability of 2/3! = 1/3. When the data are collected from time course data, only consecutive triplets will be considered, the test is called W₁. When no natural ordering of the observations exists, Wang et al. (2) propose to consider all possible combinations. With a total of n observations, we will have n(n − 1)(n − 2)/6 possible combinations, and the corresponding test is called W₂. The test proposed by Wang et al. is to evaluate the total number of successes, where a success is defined as either perfect matching or reverse matching, across all three observation combinations. In the case of perfect monotone dependence, the success probability is 1 (the alternative hypothesis); and the success probability is 1/3, when there is no dependence between the two variables (null hypothesis). Therefore, when there is no temporal relationship among the observations, we will have the testing problem involving n(n − 1)(n − 2)/6 Bernoulli trials, where the null hypothesis has success probability of 1/3, and any statistical evidence against the null would indicate some level of dependence between x and y. The mathematical challenge for statistical inference is that the outcomes from these n(n − 1)(n − 2)/6 combinations are not independent as they are all derived from a set of n observations. Wang et al. (2) provide elegant results that incorporate dependencies in statistical inference, both for the null hypothesis of independence, and under two specific alternative hypotheses, leading to insights on the power of their methods.

The measures in ref. 2 are designed to capture local dependencies, with the statistic W₁ specific to model time course expression data, whereas W₂ does not favor local dependencies as all of the combinations are considered. The authors describe an algorithm that counts W₁ with a running time of O(kn log k) and counts W₂ with a running time of O(kn log n), where a subset of k from a total of n observations are considered. The great computational efficiency achieved by this algorithm makes it very attractive. The simulation results demonstrate that for time course data where the correlation patterns are local, the proposed W₁ and W₂ have much better performance than the competing methods. In the other cases, the W₂ measure still enjoys good performance and is ranked as one of the best methods considered. Here we focus on W₂ to see from where it draws information on nonindependence. There are four relationship patterns shown in Fig. 1. Fig. 1A is the piecewise monotone case which is rigorously studied by Wang et al. (2). In this case, the association information is mostly drawn from each of the three segments, and with limited information offered from observations across the segments. Fig. 1B does not have local association patterns, and the dependency information is drawn from points across segments. So W₂ is effective even in the absence of local associations. Fig. 1C is the case where both local and global associations are present, and the statistic W₂ is capable of incorporating both types of information. Of the most interest is the checkerboard pattern shown in Fig. 1D. With some elementary analysis, it can be shown that if the observations are randomly drawn from the five blocks in the checkerboard, the success probability for three observations is 137/375 versus 125/375 when there is no association. So W₂ is able to extract some dependency information even in this scenario, although the power is limited with a small sample size.

As discussed by Wang et al. (2), their proposed measures can be extended to increase power against other, less simple alternatives. For example, different weights can be assigned to the n(n − 1)( n − 2)/6 combinations when three observations are analyzed, as some triplets likely carry more information than others. The time course set-up is at the extreme of this scheme, where only consecutive observations are considered. The interactions can also take on various forms to accommodate similar ranks as suggested by the authors.

Although the idea of looking for local association signals in genomics data is not new, e.g., biclustering methods to identify rows and columns in a microarray data that show consistent patterns (16), the objective is different here in that the goal is to identify gene pairs showing signals for nonindependency. When millions of pairs are considered, it is natural to use the statistics to order pairs, where the measures may have some interpretations. Despites its lack of robustness and low power against nonlinear alternatives, one good property of the Pearson correlation is that r² can be interpreted as the proportion of variance for one variable explained by the other variable. Spearman correlation, distance correlation, and mutual information are also interpretable to some extent. It seems to be nontrivial to translate the statistics proposed in ref. 2 to an easily interpretable measure. It would also be desirable to develop some methods to locate the specific dependency in the data, after the null hypothesis is rejected. For example, the concept of local correlation has been advocated to characterize varying correlations in the data (17). Moreover, the proposed approach may also be extended to consider the inference of conditional independence.

As for any measure, there are certain limitations, and interpretations should be made with caution. For example, when a statistically significant result is found, it may be due to the nonindependence between the two variables, or it could be due to some artifacts. It is well known that data normalization is a key step in microarray analysis, and spurious associations may be found if data are not properly normalized. Different association measures may be more or less robust to potentially systematic biases, and their relative merits need to be carefully studied in this context. Now with a new and computationally efficient approach to capturing nonindependent gene pairs from microarray data, and more generally, nonindependency of pairs of random variables in any data, more will be learned through the collection and analysis of big data by putting things in order.