Significance
Pathogens, invasive species, rumors, or innovations spread much more quickly around the world nowadays than in previous centuries. The speedup is caused by more frequent long-range dispersal, for example via air traffic. These jumps are crucial because they can generate satellite “outbreaks” at many distant locations, thus rapidly increasing the total rate of spread. We present a simple intuitive argument that captures the resulting spreading patterns. We show that even rare long-range jumps can transform the spread of simple epidemics from wave-like to a very fast type of “metastatic” growth. More generally, our approach can be used to describe how new evolutionary variants spread and thus improves our predictive understanding of the speed of Darwinian adaptation.
Keywords: long-range dispersal, selective sweeps, epidemics, range expansions, species invasions
Abstract
The spreading of evolutionary novelties across populations is the central element of adaptation. Unless populations are well mixed (like bacteria in a shaken test tube), the spreading dynamics depend not only on fitness differences but also on the dispersal behavior of the species. Spreading at a constant speed is generally predicted when dispersal is sufficiently short ranged, specifically when the dispersal kernel falls off exponentially or faster. However, the case of long-range dispersal is unresolved: Although it is clear that even rare long-range jumps can lead to a drastic speedup—as air-traffic–mediated epidemics show—it has been difficult to quantify the ensuing stochastic dynamical process. However, such knowledge is indispensable for a predictive understanding of many spreading processes in natural populations. We present a simple iterative scaling approximation supported by simulations and rigorous bounds that accurately predicts evolutionary spread, which is determined by a trade-off between frequency and potential effectiveness of long-distance jumps. In contrast to the exponential laws predicted by deterministic “mean-field” approximations, we show that the asymptotic spatial growth is according to either a power law or a stretched exponential, depending on the tails of the dispersal kernel. More importantly, we provide a full time-dependent description of the convergence to the asymptotic behavior, which can be anomalously slow and is relevant even for long times. Our results also apply to spreading dynamics on networks with a spectrum of long-range links under certain conditions on the probabilities of long-distance travel: These are relevant for the spread of epidemics.
Humans have developed convenient transport mechanisms for nearly any spatial scale relevant to the globe. We walk to the grocery store, bike to school, drive between cities, or take an airplane to cross continents. Such efficient transport across many scales has changed the way we and organisms traveling with us are distributed across the globe (1–5). This has severe consequences for the spread of epidemics: Nowadays, human infectious diseases rarely remain confined to small spatial regions, but instead spread rapidly across countries and continents by travel of infected individuals (6).
Besides hitchhiking with humans or other animals, small living things such as seeds, microbes, or algae are easily caught by wind or sea currents, resulting in passive transport over large spatial scales (7–16). Effective long-distance dispersal is also widespread in the animal kingdom, occurring when individuals primarily disperse locally but occasionally move over long distances. And such animals, too, can transport smaller organisms.
These active and passive mechanisms of long-range dispersal are generally expected to accelerate the growth of fitter mutants in spatially extended populations. However, how can one estimate the resulting speedup and the associated spatiotemporal patterns of growth? When dispersal is only short range, the competition between mutants and nonmutated (“wild-type”) individuals is local, confined to small regions in which they are both present at the same time. As a consequence, a compact mutant population emerges that spreads at a constant speed, as first predicted by Fisher (17) and Kolmogorov et al. (18): Such selective sweeps are slow and dispersal is limited. In the extreme opposite limit in which the dispersal is so rapid that it does not limit the growth of the mutant population, the competition is global and the behavior the same as for a fully mixed (panmictic) population: Mutant numbers grow exponentially fast. It is relevant for our purposes to note that in both the short-range and extreme long-range cases, the dynamics after the establishment of the initial mutant population are essentially deterministic.
When there is a broad spectrum of distances over which dispersal occurs, the behavior is far more subtle than that of either of the well-studied limits. When a mutant individual undergoes a long-distance dispersal event—a jump—from the primary mutant population into a pristine population lacking the beneficial mutation, this mutant can found a new satellite subpopulation, which can then expand and be the source of further jumps, as shown in Fig. 1 B and C. Consequently, long-range jumps can dramatically increase the rate of growth of the mutant population. Potentially, even very rare jumps over exceptionally large distances could be important (14). If this is the case, then the stochastic nature of the jumps that drive the dynamics will be essential.
Fig. 1.
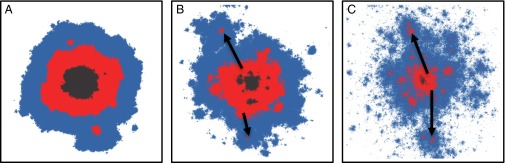
Evolutionary spread sensitively depends on the dispersal behavior of individuals. For a broad class of models with “short-range migration,” the mutant subpopulation expands at a constant speed that characterizes the advance of the mutant–nonmutant boundary. With long-range dispersal the spread is much faster. Shown are 2D simulations for the simple case of a jump distribution that has a broad tail characterized by a power-law exponent . A–C show the distribution of the mutant population at the time when half of the habitat is occupied by mutants. The color of a site indicates whether a site was filled in the first (black), second (red), or last (blue) third of the total run time. (A) When the jump distribution decays sufficiently rapidly, , the asymptotic growth resembles, in two dimensions, a disk growing at a μ–dependent constant speed. (B) For , satellite seeds become clearly visible and these drive superlinear power-law growth. These seeds were generated by long-range jumps, as indicated by arrows. (C) The dynamics are changed drastically for , becoming controlled by very long-distance jumps, which seed new expanding satellite clusters. As a result of this “metastatic” growth, the spreading is faster than any power law, although markedly slower than exponential. A–C were created by the simulations described in the main text, with parameters in A, in B, and in C. (To avoid any boundary effects, the lattice size was chosen to be much larger than depicted regions.)
Although evolutionary spread with long-range jumps has been simulated stochastically in a number of biological contexts (6, 8, 19–23), few analytic results have been obtained on the ensuing stochastic dynamics (19, 24–26). Most analyses have resorted to deterministic approximations (27–35), which are successful for describing both the local and global dispersal limits. However, in between these extreme limits, stochasticity drastically changes the spreading dynamics of the mutant population. This is particularly striking when the probability of jumps decays as a power law of the distance. Just such a distance spectrum of dispersal is characteristic of various biological systems (36–41), including humans (3). We will show that the behavior is controlled by a trade-off between frequency and potential effectiveness of long-distance jumps and the whole spectrum of jump distances can matter. The goal of this paper is to develop the theory of stochastic spreading dynamics when the dispersal is neither short range nor global.
Long-distance dispersal can occur either on a fixed network or more homogeneously in space. For simplicity, we focus on the completely homogeneous case and then show that many of the results also apply for an inhomogeneous transportation network with hubs between which the long-distance jumps occur. For definiteness, we consider for most of the paper the evolutionary scenario of the spread of a single beneficial mutation, but, by analogy, the results can be applied to other contexts, such as the spread of infectious disease or of invasive species.
Basic Model
The underlying model of spatial spread of a beneficial mutant is a population in a d-dimensional space with local competition that keeps the population density constant at and equipped with a probability that any individual jumps to any particular point a distance r away of per time per area, per length, or per volume. At a very low rate, mutants can appear that have a selective advantage, s, over the original population. A lattice version of this model is more convenient for simulations (and for aspects of the analysis): Each lattice site represents a “deme” with fixed population size, with the competition only within a deme and the jump migration between demes. Initially, a single mutant occurs and if, as occurs with probability proportional to s, it survives stochastic drift to establish, it will take over the local population. When the total rate of migration between demes is much slower than this local sweep time, the spatial spread is essentially from demes that are all mutants to demes that are all of the original type.
Short jumps result in a mutant population that spreads spatially at a roughly constant rate. However, with long-range jumps, new mutant populations are occasionally seeded far away from the place from which they came, and these also grow. The consequences of such long jumps are the key issues that we need to understand. As we shall see, the interesting behaviors can be conveniently classified when the jump rate has a power-law tail at long distances, specifically, with (with positive μ needed for the total jump rate to be finite). Crudely, the behavior can be divided into two types: linear growth of the radius of the region that the mutants have taken over and faster than linear growth. In Fig. 1, these two behaviors are illustrated via simulations on 2D lattices. In addition to the mutant-occupied region at several times, shown are some of the longest jumps that occur and the clusters of occupied regions that grow from these. In Fig. 1A, there are no jumps that are of comparable length to the size of the mutant region at the time at which they occur, and the rate of growth of the characteristic linear size of the mutant region—loosely its radius—is roughly constant in time; i.e., . In Fig. 1 B and C, is longer range and very long jumps are observed. These result in faster-than-linear growth of the radius of the mutant region, as shown. Before developing analytic predictions for the patterns of evolutionary spread, we report our simulation results in detail.
Results
Simulated Spreading Dynamics.
We have carried out extensive simulations of a simple lattice model, in which the sites form either a one-dimensional, of length L, or two-dimensional square array. Boundary conditions are chosen to be periodic, but typically do not matter unless the filling fraction becomes of order one. As it is the spreading dynamics at long times that we are interested in, we assume that the local sweeps in a deme are fast compared with migration. We can then ignore the logistic growth process within demes, so that when jumps occur and establish a new mutant population, it is saturated in the new deme by the next time step. Therefore, it is convenient to lump together the probability of an individual to jump, the density of the population from which the jumps occur, and the probability (proportional to s) that the mutant establishes a new population: We define so that is the rate at which a saturated mutant population near x nucleates a mutant population near y. In each computational time step, we pick a source and target site randomly such that their distance r is sampled from the (discretized) jump distribution —with the a lattice site. If the source site is a mutant and the target site a wild type, the identity of the target site is updated to mutant. We measure time in units of time steps. The lattice sizes are chosen large enough (up to ) so that we can observe the growth dynamics over several orders of magnitude undisturbed by boundary effects. See SI Text, section SI1 for more details on the simulation algorithm.
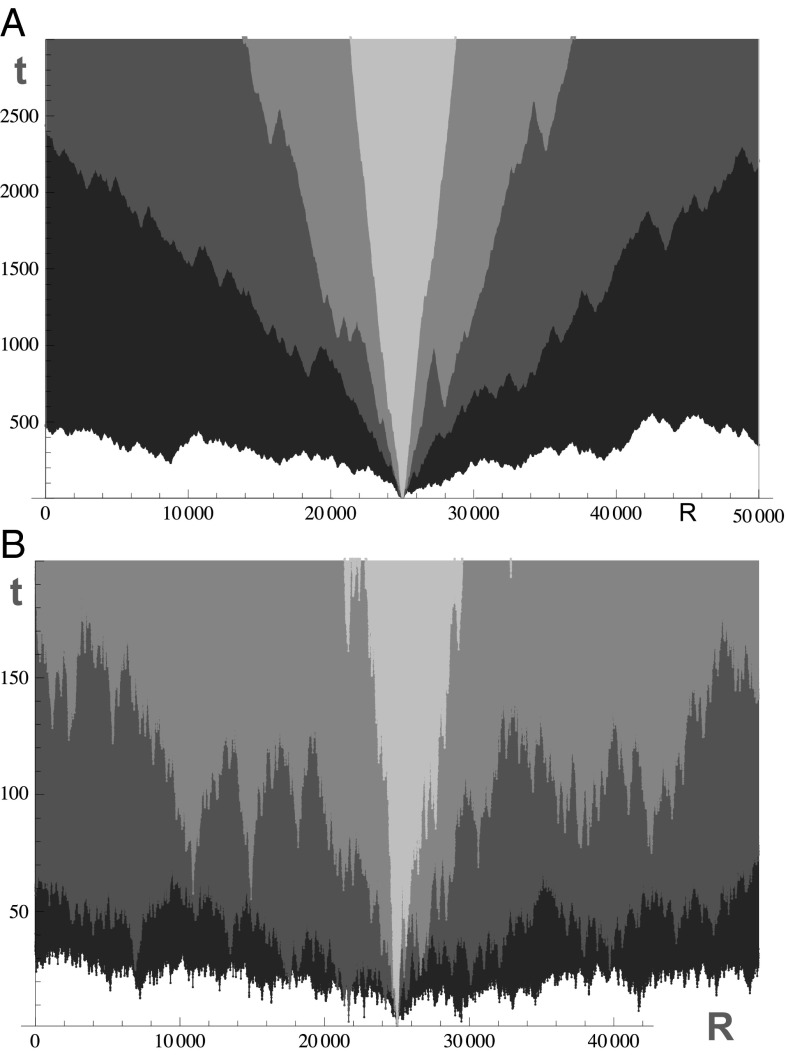
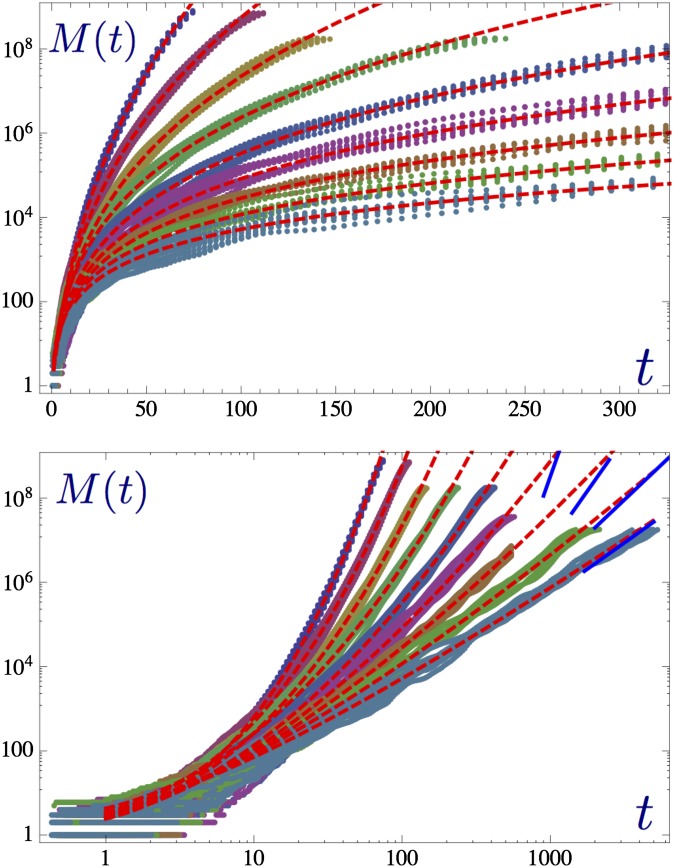
The growth of mutant populations generated by our simulations is best visualized in a space–time portrait. Fig. 2 A and B shows the overlaid space–time plots of multiple runs in the regimes and , respectively. Fig. 3 shows the growth dynamics of the mutant population over large timescales and length scales for various values of μ. For , the dynamics clearly approach a power law. For , the simulations are consistent with stretched exponentials. The intermediate regime is elusive, as we cannot extract a clear asymptotic behavior on the timescales feasible in simulations. The behavior in two dimensions is qualitatively similar, as shown in Fig. S1. Lowering the rate of long-range jumps compared to short-range jumps between neighboring sites leads to a delayed cross-over to the super-linear regimes, as shown in Fig. S2.
Fig. 2.
Stochastic growth of a mutant population over time in one dimension. Each level of shading represents a single simulation run. (A) Regime of power-law growth. The values of μ are in order of increasing darkness. Note that, in two dimensions, corresponds to the marginal case separating linear growth from superlinear growth . (B) Regime of very fast growth with μ near , which is the marginal case separating power-law growth from stretched exponential growth . The values of μ are in order of increasing darkness.
Fig. 3.
Summary of the quantitative spreading dynamics in one spatial dimension. The total number, , of mutant sites is plotted as a function of time t, for various long-range jump kernels. Each colored cloud represents data obtained from 10 runs for a given jump kernel. The data are for from top to bottom. Red dashed lines represent predictions obtained from Eq. 8 with fitted magnitude scales for M and t. In the double-logarithmic plot at the bottom of each plot, short blue lines indicate the predicted asymptotic power-law behavior for . For and , the dynamics are still far away from the asymptotic power law, which is indicative of the very slow crossover.
To explain these dynamics in detail, we develop an analytical theory that is able to predict not only the asymptotic growth dynamics but also the crucial transients.
Breakdown of Deterministic Approximation.
Traditionally, analyses of spreading dynamics start with a deterministic approximation of the selective and dispersal dynamics—ignoring both stochasticity and the discreteness of individuals. To set up consideration of the actual stochastic dynamics, we first give results in this deterministic approximation and show that these exhibit hints of why they break down.
When the jump rate decreases exponentially or faster with distance, the spread is qualitatively similar to simple diffusive dispersal and the extent of the mutant population expands linearly in time. However, when the scale of the exponential falloff is long, the speed, v, is faster than the classic result for local dispersal (17, 18), , which depends only on the diffusion coefficient, : Specifically, consider with coefficient so that the diffusion constant D is independent of the characteristic length, b, of the jumps. A linear deterministic approximation for the mutant population density in a spatial continuum and a saddle point analysis to find the distance at which the population density becomes substantial yield, as for the conventional diffusive case, the correct asymptotic speed. The resulting expression for the speed is modified from the diffusive result by a function of the only dimensionless parameter, . For , , the diffusive predictions obtain as expected, but for , , which is much larger.
We now provide a simple argument as to why the deterministic approximation drastically overshoots the stochastic spreading dynamics for broader than exponentially decaying jump kernels . The origin of the very rapid spread is the feeding of the populations far away by direct jumps from near the origin: This immediately produces a finite population density at any location, R. After a time of order has passed, the exponential growth of the local population near R takes off, proportional to , and further jumps to that region no longer matter much. The time at which this local mutant population saturates suggests that the radius of the region taken over by the mutant population, , is given simply by . In the deterministic approximation, this is a lower bound as seeding by intermediate jumps (as occurs especially for or smaller) can only make the spread faster. For the marginal case of exponential dispersal discussed above, this simple approximation yields , correct for large b (i.e., ), implying that very long jumps directly to R indeed dominate for large distances R. (For small b, in contrast, the speed is much faster than bs because the spread is dominated by multiple small jumps: The diffusion approximation is then good.)
If has a longer-than-exponential tail (42), in particular, (43), the spread in the deterministic approximation becomes exponentially fast: yields . Thus, the total mutant population is . This grows almost as fast as in a fully mixed population, with the population growth rate slower only by a factor of . This factor approaches unity as , the point at which the spatial structure becomes irrelevant as the jumps typically span the full system.
We can now understand why the deterministic approximation fails miserably for very long-range jumps. In the time, , during which the jumps into a region from near the origin are supposed to lead to exponential growth of the local population even a large distance R, away, the expected total number of jumps to the whole region R or farther from the origin is only of order : Thus the probability that any jumps have occurred is very small for large R and the deterministic approximation must fail (19, 44).
With local dispersal, the deterministic approximation is a good starting point with only modest corrections to the expansion speed at high population density, the most significant effect of stochasticity being fluctuations in the speed of the front (45). At the opposite extreme of jump rate independent of distance, the deterministic approximation is also good with the mutant population growing as and fluctuations causing only stochastic variability and a systematic reduction in the coefficient, a: These arise from early times when the population is small. It is thus surprising that in the regimes intermediate between these two, the deterministic approximation is not even qualitatively reasonable.
Iterative Scaling Argument.
We assume that, at long times, most of the sites are filled out to some distance scale and that the density decreases sufficiently steeply for larger distances, such that the total mutant population, , is proportional to . The validity of this assumption follows from more accurate analyses given in SI Text, section SI3. We call the crossover scale the core radius or “size” of the mutant population.
In the dynamical regimes of interest, the core population grows primarily because it “absorbs” satellite clusters, which themselves were seeded by jumps from the core population. We now show that the rate of seeding of new mutant satellite clusters and the growth of the core populations by mergers with previously seeded clusters have to satisfy an iterative condition that enables us to determine the typical spreading dynamics of the mutant population.
It is convenient to illustrate our argument using a space–time diagram, Fig. 4, in which the growth of the core has the shape of a funnel. Now consider the edge of this funnel at time T (gray circle in Fig. 4). The only way that this edge can become populated is by becoming part of a population subcluster seeded by an appropriate long-range jump at an earlier time. To this end, the seed of this subcluster must have been established somewhere in the inverted blue funnel in Fig. 4. This “target” funnel has the same shape as the space–time portrait of the growing total population, but its stem is placed at and the mouth opens backward in time. Note that if grows faster than linearly, space–time plots of the growing cluster and the funnel have concave boundaries: This necessitates a jump from the source to the funnel of length much longer than , as shown.
Fig. 4.
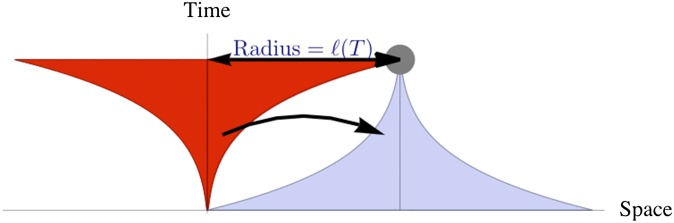
Sketch of the growth of the compact core of a cluster (red) due to long-range jumps. For the (gray) point at distance to be occupied at time t, a seed typically must become established somewhere in the blue space–time region (“target funnel”) by means of a long-range jump (black arrow) from the red “source” region. This schematic leads to the iterative scaling approximation in Eq. 1. Note that the concavity of the source-funnel geometry, leading to a gap between red and blue regions, is key to our arguments and enables neglecting effects of jumps into the gap region.
Now, we argue the consistency of growth and seeding requires that there is, on average, about one jump from the source to the target funnel: If it were unlikely that even one jump leads from the source to the target region, then the assumed shape for the source funnel would be too large and its edge (gray circle in Fig. 4) would, typically, not be occupied. Conversely, if the expected number of jumps was much larger than 1, then seeding would occur so frequently that a much larger funnel than the assumed one would typically be filled by the time T.
The condition of having, on average, about one jump from source to target region can be stated mathematically as
| [1] |
in d dimensions, where denotes a d-dimensional ball of radius centered at the origin, and we have taken the point of interest to be with e a unit vector in an arbitrary direction. The kernel represents the rate per d-dimensional volume of (established) jumps of size r. Eq. 1 mathematizes the space–time picture of Fig. 4: To calculate the expected number of jumps from the red source to the blue target funnel, we need a time integral, , and two space integrals—one for the source funnel, , and one for the target funnel, —over the probability density to jump from the source point x to the target point .
Note that the above intuitive picture is further sharpened in SI Text, section SI2 and justified by developing rigorous bounds in SI Text, section SI3.
Asymptotic Results for Power-Law Jumps.
We now show that the asymptotic growth dynamics are essentially constrained by the above iterative scaling argument. Specifically, although the argument is more general, we consider a power-law jump distribution
| [2] |
for large enough r. The prefactor ε in amalgamates all of the factors that determine the rate density of successful jumps, including population density and establishment probability.
For the intermediate-range case , Eqs. 1 and 2 exhibit the asymptotic scaling solution
| [3] |
the form of which could have been guessed by dimensional analysis. Inserting the ansatz [3] into Eq. 1 determines the prefactor in this iterative scaling approximation, up to an order-unity coefficient: Details are in SI Text, section SI2.B. Interestingly, the value depends very sensitively on μ and runs from 0 to ∞ as μ passes through the interval from d to . This can be seen in Fig. S3, where is plotted as a function of μ for : It drops very steeply, as , for , and diverges as for . As we discuss below, these singularities are a manifestation of intermediate asymptotic regimes that lead to very slow convergence to the asymptotic behavior.
We now turn to the (very) long-range case, , for which a direct solution to [1] cannot be found (and the dimensional analysis argument gives nonsense). However, much can be learned by approximating [1] using , anticipating the very rapid growth and thus likely smallness of x and y compared with :
| [4] |
(ignoring two factors from the angular integrations). With growing subexponentially, the largest contributions will come from , which reflects the approximate time reversal symmetry of the source and target funnels in Fig. 4. Once we have found the form of , the validity of the ansatz can be tested by checking whether the is much larger than . Indeed, for the solution to [4] is a rapidly growing stretched exponential,
| [5] |
which can be checked by direct insertion into Eq. 4. Note that as , and grows exponentially as for a flat distribution of long-range jumps that extends out to the size of the system: i.e., the globally mixed limit. In the opposite limit of small, and the coefficient diverges as shown below. We note that the asymptotic stretched-exponential growth for also arises in models of “chemical distance” and certain types of spatial spread for network models with a similar power-law distribution of long-distance connections: However, the prefactors in the exponent are different (24, 46). We discuss the connections between these in SI Text, section SI3.
For the marginal case, , the asymptotic behavior is similarly found to be
| [6] |
We show below that this behavior also represents an important intermediate asymptotic regime that dominates the dynamics over a wide range of times for μ close to d: This is the source of the singular behavior of the coefficients and in this regime.
Our source-funnel argument obviously neglects jumps that originate from the not fully filled regions outside the core radius . An improved version of the funnel argument is presented in SI Text, section SI2.E, which also allows us to estimate the probability of occupancy outside the core region. Further, we present in SI Text, section SI3 outlines of rigorous proofs of lower and upper bounds for the asymptotic growth laws in one dimension, including the slow crossovers near the marginal case. The linear growth for in one dimension has been proved by Mollison (19). After the present paper was essentially complete, we became aware of a recent preprint by Chatterjee and Dey (26) who obtained rigorous bounds in all dimensions for the leading asymptotic behaviors in the three superlinear regimes. Our bounds are considerably tighter than theirs, including the coefficient and leading corrections to the asymptotic behavior in the marginal case and the absence of logarithmic prefactors in the power-law regime: Comparisons are discussed in SI Text, section SI3. More importantly, our bounds are explicitly for the iterative scaling analyses, thereby justifying them (and future uses of them). Our bounds hence include the full crossovers for μ near d (in one dimension), rather than just the asymptotic results: As we next show, understanding these crossovers is essential.
Crossovers and Beyond Asymptopia.
Asymptotic laws are of limited value without some understanding of their regime of validity, especially if the approach to the asymptotic behavior is slow. And such knowledge is crucially needed to interpret and make use of results from simulations.
Assuming that long jumps are typically much rarer than short jumps, they will become important only after enough time has elapsed that there have been at least some jumps of order . This condition can be used to determine a crossover time and length scale from linear to superlinear growth (SI Text, section SI2.A). For the purpose of this section, it is convenient to measure time and length in units of these elementary crossover scales.
At times much longer than 1 (in rescaled time), we expect another slow crossover close to the boundary between the stretched-exponential and power-law regimes. Thus, we must take a closer look at the dynamics in the vicinity of the marginal case, . As , the integrand in Eq. 4 develops a sharp peak at : half-way between the bounds of the integral. Laplace’s method can then be used to approximate the integral leading to a simplified recurrence relation for the rescaled core radius ,
| [7] |
This is good only to a numerical factor of order unity that can be eliminated by rescaling t and to a larger logarithmic factor associated with the narrowness of the range of integration and its dependence on t and . The associated subdominant corrections, analyzed in SI Text, section SI2.C, are negligible if we focus on the behavior on logarithmic scales in space and time—natural given their relationships. Defining and and taking the binary logarithm, , of Eq. 7 yields a linear recurrence relation that can be solved exactly (SI Text, section SI2.B). Rescaling ℓ can be used to make , whence
| [8] |
where we introduced the variable , which measures the distance to the marginal case.
The asymptotic scaling for reproduces the earlier predicted power-law regime [3] and yields the prefactor , up to correction that is subdominant for small δ (compare Fig. S3). For , the asymptotics yields the stretched exponential in [5] and fixes the prefactor , which could not be obtained from the basic asymptotic analysis carried out above.
The singular prefactors for give warnings of breakdown of the asymptotic results except at very long times. This peculiar behavior is the consequence of an intermediate asymptotic regime that dominates the dynamics close to the marginal case. This leads to slow convergence to the eventual asymptotic behavior for μ near d. The asymptotic scaling can be observed only on times and length such that
| [9] |
On smaller times, the dynamics are similar to those of the marginal case [6]. The rapid divergence of the logarithm of the time after which the asymptotic results obtain makes it nearly impossible to clearly observe the asymptotic limits: In one-dimensional simulations this problem occurs when , as is clearly visible in Fig. 3, and it is likely even harder to observe in natural systems. This underscores the need for the much fuller analysis of the spreading dynamics as in [8].
Although the dynamics at moderate times will be dominated by the initial growth characteristic of the marginal case, we expect [8] to be a good description of the universal dynamics at large even when δ is small. The limit while is fixed is particularly interesting, as the solution [8] then reduces to a scaling form
| [10] |
with
| [11] |
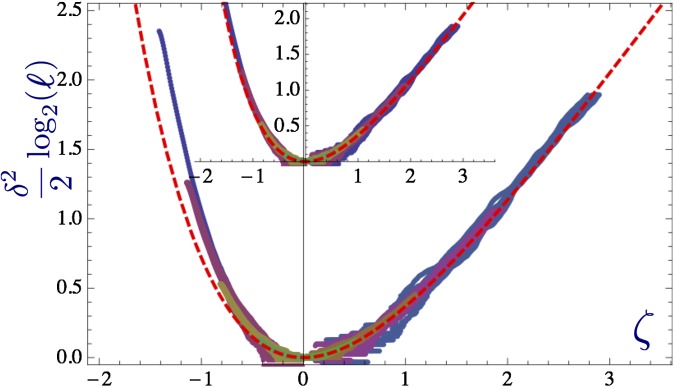
This scaling form allows us to test by simulations our analytic results across all intermediate asymptotic regimes, by plotting data obtained for different δ in one scaling plot (Fig. 5). To make the approximation uniformly valid both in the scaling regime and at asymptotically long times outside of it, we can simply replace, for , the scaling variable by (with η defined in [5]). The scaling form [10] will then be valid up to corrections that are small compared with the ones given in all regimes: We thus use this form for the scaling fits in Fig. 5, Inset, plotting data obtained for different δ in one scaling plot, thereby testing our solution across all intermediate asymptotic regimes.
Fig. 5.
Data for different are predicted to collapse on a scaling plot close to the marginal case between the stretched-exponential and power-law growth regimes, here demonstrated for the one-dimensional case . The main plot shows the rescaled sizes of the mutant population vs. rescaled log-time . The differently colored datasets correspond to 10 realizations with power-law exponents (same colors as in Fig. 3, Upper). The simulated data collapse reasonably well with the dashed red line, representing the predicted scaling function . Inset depicts the same data scaled slightly differently away from the scaling regime such that the horizontal axis for shows (with η defined in [5]), upon which the data collapse improves. Note that as so that the stretched exponential form is recovered for ζ large and negative.
Heterogeneities and Dynamics on Networks.
Thus far we have considered spatially uniform systems, in which the jump probability between two points depends only on their separation. However, long-distance transport processes may be very heterogeneous. An extreme example is airplane travel, which occurs on a network of links between airports with mixtures of short- and long-distance flights, plus local transportation to and from airports. A simple model is to consider each site to have a number of connections from it, with the probability of a connection between each pair of sites a distance r away being , independently for each pair: Note that although the network is heterogeneous, statistically the system is still homogeneous as the connection probability does not depend on position. If the rate at which jumps occur across a connection of length r is , then, averaged over all pairs of sites, the rate of jumps of distance r is . How similar is this to a homogeneous model with the same , in particular if ? If there are a large number of possible connections along which the key jumps can occur to get from a source region of size to a funnel of similar size a distance away, then the fact that these occur to and from only a small fraction of the sites should not matter for the large length-scale behavior. The number of such connections is with, making the ansatz that, as in the homogeneous case, (ignoring subdominant factors) we have . Thus, the condition for our results to be valid asymptotically is that with the inverse of the function : i.e., in the exponential, marginal, and power-law cases, respectively, that , , and .
If there are insufficient numbers of connections for the heterogeneity of the network to be effectively averaged over, the behavior changes. The extreme situation is when there is a distance-independent rate for jumps along the longest connection out of a site: i.e., . In this case, jumps along the path with the shortest number of steps, S, to get from the origin to a point R will reach that point in a time proportional to S; i.e., . The geometrical problem of obtaining the statistics of has been analyzed by Biskup (24, 46). For , and long jumps do not matter, whereas for , with the same exponent η as in the homogeneous case we have analyzed. The difference between this result and ours is only in the power-law-of-T prefactor of arising from the integral over time: This does not exist in the extreme network limit. In the marginal case, , with α dependent on the coefficient of the power-law decay of the connection probability.
If the probability of a jump along a long-distance connection decays with distance but more slowly than , the behavior is similar: For again the ubiquitous stretched exponential behavior occurs, whereas for there are too few connections only if in which case the number of steps and the time are both proportional to the distance. The marginal cases we have not analyzed further.
For natural transport processes, the probabilities of long dispersal events will depend on both the source and the destination. If the heterogeneities are weak on large length scales, our results still obtain. However, if there are sufficiently strong large-scale heterogeneities, either in a spatial continuum or in the network structure (i.e., location of nodes and links and the jump rates along these or hub-spoke structure with multiple links from a small subset of sites), then the spatial spread will be heterogeneous even on large scales: How this reflects the underlying heterogeneities of the dispersal has to be analyzed on a case-by-case basis.
Discussion
Modeling Evolutionary Spread.
We have studied the impact of long-range jumps on evolutionary spreading, using the example of mutants that carry a favorable genetic variant. To this end, we analyzed a simple model in which long-range jumps lead to the continual seeding of new clusters of mutants, which themselves grow and send out more migrant mutants. The ultimate merging of these satellite clusters limits the overall growth of the mutant population, and it is a balance of seeding and merging of subclusters that controls the spreading behavior.
To classify the phenomena emerging from this model, we focused on jump distributions that exhibit a power-law tail. We found that, with power-law jumps, four generic behaviors are possible on sufficiently long times: The effective radius of the mutant population grows at constant speed, as a superlinear power law of time, as a stretched exponential, or simply exponentially depending on the exponent, , of the power-law decay of the jump probability. These predictions are in contrast to deterministic approximations that predict exponential growth for power-law decaying jump kernels (27, 28, 30, 31). In dimensions more than one, the results also contradict the naive expectation from dynamics of neutral dispersal, that a finite diffusion coefficient is sufficient for conventional behavior (in this context, finite speed of spreading): Specifically, the variance in dispersal distances is finite for , but the spread is superlinear—indeed stretched exponential for . That superlinear dynamics can occur for is not surprising as even a migrating individual undergoes a Levy flight: More surprising is that this occurs even when the dynamics of individuals are, on large scales, like a normal random walk.
The breakdowns of both deterministic and diffusive expectations are indicative of the importance of fluctuations: The dynamics are dominated by very rare—but not too rare—jumps: roughly, the most unlikely that occur at all up to that time. One of the consequences of this control by the rare jumps is the relatively minor role played by the linear growth speed v of individual clusters due to short-range migration: In the regime of power-law growth, the asymptotic growth of the mutant population becomes (to leading order) independent of v although when individual clusters grow more slowly, the asymptotic regime is reached at a later time. In the stretched exponential regime, the growth of subclusters sets the crossover time from linear to stretched exponential and thus determines the prefactor in the power law that characterizes the logarithm of the mutant population size (Crossovers and Beyond Asymptopia).
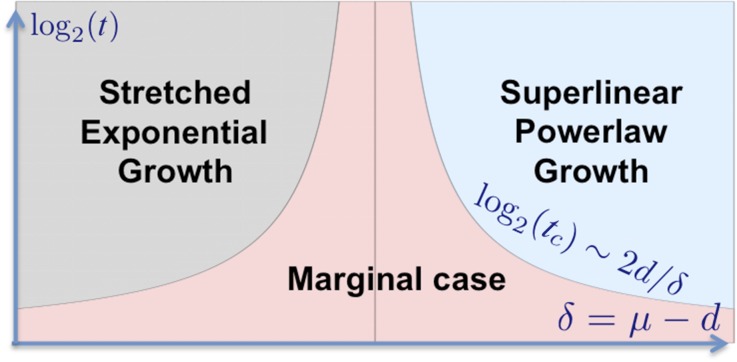
An important feature of the spreading dynamics is that the approach to the asymptotic behavior is very slow in the vicinity of the marginal cases, as illustrated in Fig. 6. Consider, for instance, the 2D case, where we have asymptotically stretched exponential growth for : For , the epidemic has to run for times to reach the asymptotic regime. By that time, the mutant population with would have certainly spread over the surface of the earth, so that the asymptotic laws alone are in fact of limited value.
Fig. 6.
Close to the marginal case, , the spreading dynamics exhibit three behaviors. On asymptotically large times, either stretched exponential growth for or superlinear power-law growth for occurs. However, the approach to the asymptotic regime is extremely slow for μ close to d. For log-times , the behavior is controlled by the dynamics of the marginal case. Note that crossover behavior also obtains near the borderline between linear and superlinear behavior at ; compare SI Text, section SI2.D and Fig. S4.
However, based on a simple geometrical argument illustrated in Fig. 4, we could show that the full crossover dynamics can be understood from a trade-off between frequency and potential effectiveness of long-distance jumps: Jumps of a given size are more abundant at late times (source funnel is large) but they are most effective at early times (blue funnel is large). As a result, the key jumps that dominate the filled regions at time T predictably occur near half that time. This led to a simple recurrence relation for the spread at time T in terms of its behavior at time (Eq. 7). Its exact solution predicts a universal crossover function for the transient dynamics near that could be reproduced by simulations for different power-law exponents collapsed onto one scaling plot; compare Fig. 5. The good agreement of the predicted scaling function and simulation results provides strong support for the iterative scaling approximation. The rigorous bounds whose proofs are outlined in SI Text, section SI3 provide further support. Understanding this crossover is essential for making sense of, and extrapolating from, simulations as asymptotic behavior is not visible until enormous system sizes even when the exponent μ is more than 0.2 from its marginal value.
Another benefit of the ability of the simple iterative scaling argument to capture well nonasymptotic behavior is that it can be used in cases in which the dispersal spectrum of jumps is not a simple power law, e.g., with a crossover from one form to another as a function of distance. And the heuristic picture that it gives rise to—an exponential hierarchy of timescales separated by roughly factors of 2—is suggestive even in more complicated situations. That such a structure should emerge without a hierarchal structure of the underlying space or dynamics is perhaps surprising.
Potential Applications and Dynamics of Epidemics.
Our primary biological aim is the qualitative and semiquantitative understanding that emerges from consideration of the simple models and analyses of these, especially demonstrating how rapid spatial spread of beneficial mutations or other biological novelties can be even with very limited long-range dispersal. As the models do not depend on any detailed information about the biology or dispersal mechanisms, they can be considered as a basic null model for spreading dynamics in physical, rather than more abstract network, space.
The empirical literature suggests that fat-tailed spectra of spatial dispersal are common in the biological world (8, 13, 36–41). Because most of these are surely neither a constant power law over a wide range of scales nor spatially homogeneous, our detailed results are not directly applicable. However, as discussed above, our iterative scaling argument is more general and can be applied with more complicated distance dependence, anisotropy, or even directional migration (47). Furthermore, some of the heterogeneities of the dispersal will be averaged out for the overall spread, while affecting when mutants are likely to arrive at particular locations.
For dispersal via hitchhiking on human transport, either of pathogens or of commensals such as fruit flies with food, the apparent heterogeneities are large because of the nature of transportation networks. Nevertheless, data from tracking dollar bills and mobile phones indicate that dispersal of humans can be reasonably approximated by a power law with (3, 4), cut off by an exponential tail for jump distances larger than 400 km (4) (as obtained from dataset in ref. 4, tracking mobile phone users). The exponent of the power-law part falls into the asymptotic regime of stretched-exponential growth with exponent . However, due to the exponential cutoff and the slow crossovers, the asymptotics are of little predictive value. Given the inferred kernel, we would then expect the growth dynamics to follow Eq. 8 until the key jumps fall into the exponential tail of the truncated power-law kernel, upon which linear growth (at a speed set by the exponential tail) would ensue.
Whether transport via a network with hubs at many scales fundamentally changes the dynamics of an expanding population of hitchhikers from that with more homogeneous jump processes depends on the nature of how the population expands. For spread of a human epidemic, there are several possible scenarios. If the human population is reasonably uniform spatially, and the chance that a person travels from, say, his or her home to another person’s home is primarily a function of the distance between these rather than the specific locations, then whether the properties of the transportation network matter depends on features of the disease. If individuals are infectious for the whole time the outbreak lasts and if transmission is primarily at end points of journeys rather than en route—for example, HIV—then the transportation network plays no role except to provide the spatial jumps. At the other extreme is whether individuals living near hubs are more likely to travel (or even whether destinations near hubs are more likely) and, more so, whether infections are likely to occur en route, in which case the structure of the transportation network—as well as of spectra of city sizes, etc.—matters a great deal. In between these limits the network (or lack of it in places) may matter for initial local spread but at longer times the network structure may effectively average out and the dynamics be more like those of the homogeneous models. The two opposite limits and behavior in between these, together with the specific network model we analyzed with jumping probabilities depending on distance even in the presence of a connection—as is true from airports—all illustrate an important point: Geometrical properties of networks alone rarely determine their properties; quantitative aspects, such as probabilities of moving along links and what exists at the nodes, are crucial.
More complicated epidemic models can be discussed within the same framework: The model discussed thus far corresponds to an SI model, the most basic epidemic model, which consists of susceptible and infected individuals only. Many important epidemics are characterized by rather short infectious periods, so that one has to take into account the transition from infected to recovered: SIR models of the interaction between susceptible (S), infected (I) and recovered (R) individuals. This changes fundamentally the geometry of the space–time analysis in Fig. 4. Whereas the target funnel remains a full funnel, the source funnel becomes hollow: The center of the population consists mostly of fully recovered individuals, whose long-range jumps are irrelevant. The relevant source population of infected individuals is primarily near the boundaries of the funnel. This leads to a break in the time symmetry of the argument. As a result, the spreading crosses over from the behavior described above to genuine SIR behavior. The SIR dynamics are closely related to the scaling of graph distance in networks with power-law distributions of link lengths (24, 46), as recently shown by 1D and 2D simulations (48, 49). In particular, the limited time of infectiousness causes wave-like spreading at a constant speed for . However, importantly, the spreading velocity is controlled by the SI dynamics we have studied until a time of order of the infectious period. Analogous crossovers from SI to SIR occur also with longer-range jumps. More generally, other complications can be discussed in our framework, and we expect new behaviors, depending on how they modify the geometry of the source to target-funnel picture.
We expect our approach to be useful also for investigating genetic consequences of range expansions and genetic hitchhiking on spatial selective sweeps with long-distance dispersal (50–53). A generalization of the analysis of the phenomenon of “allele surfing,” which has been mainly analyzed assuming short-range migration so far (54–56), could be used to clarify the conditions under which long-distance dispersal increases or decreases genetic diversity—both effects have been seen in simulations (57–59). New effects arise due to the “patchiness” (60) generated by the proliferation of satellite clusters that are seeded by long-range jumps, as, e.g., observed in many plant species (61). A needed further step is the analysis of the interaction between multiple spreading processes, for instance generated by the occurrence of multiple beneficial variants in a population, which leads to soft sweeps or clonal interference in space (62, 63). Whereas colliding clones strongly hinder each other’s spread with only short-range migration, rare long-distance jumps may overcome these constraints (62), leading to irregular global spreading as we have found for a single clone.
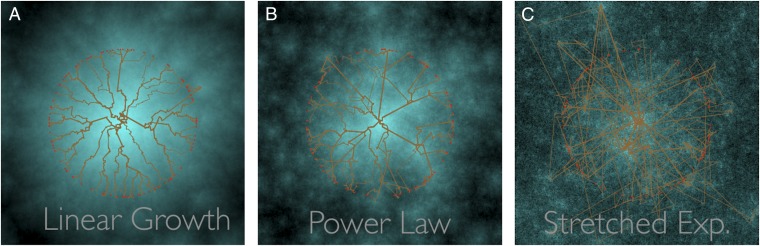
Finally, our analyses naturally provide information on the typical structure of coalescent trees backward in time. For a given site, the path of jumps by which the site was colonized can be plotted as in Fig. 7. Doing this for many sites yields coalescent trees, which can reveal the key long-range jumps shared by many lineages. In general, such genealogical information is helpful for reconstructing the demographic history of a species. In the particular context of epidemics, combining spatiotemporal sampling of rapidly evolving pathogens with whole-genome sequencing is now making it possible to construct corresponding “infection” trees, and their analysis is used to identify major infection routes (64). For such inference purposes, it would be interesting to investigate the statistical properties of coalescence trees generated by simple models such as ours and how they depend on the dispersal properties, network structure, and other features of epidemic models.
Fig. 7.
(A–C) Coalescent trees, or infection trees in epidemiology, generated by power-law dispersal. A, B, and C each represent one simulation run with parameter , , and , respectively. For each run, 100 lattice sites indicated as red points equidistant from the start point at the origin were sampled. For each labeled site the path that led to its colonization is plotted. The resulting coalescence trees are characteristic of the three different regimes and reveal the long-range jumps that drove the colonization process. The background represents the colonization process in time with the color of each site indicating its colonization time (light, early; dark, late).
Supplementary Material
Acknowledgments
We wish to thank Rava da Silveira for useful discussions. This work was partially supported by a Simons Investigator award from the Simons Foundation (O.H.), the Deutsche Forschungsgemeinschaft via Grant HA 5163/2-1 (to O.H.), and the National Science Foundation via Grants DMS-1120699 (to D.S.F.) and PHY-1305433 (to D.S.F.).
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1404663111/-/DCSupplemental.
References
- 1.Ruiz GM, et al. Global spread of microorganisms by ships. Nature. 2000;408(6808):49–50. doi: 10.1038/35040695. [DOI] [PubMed] [Google Scholar]
- 2.Suarez AV, Holway DA, Case TJ. Patterns of spread in biological invasions dominated by long-distance jump dispersal: Insights from argentine ants. Proc Natl Acad Sci USA. 2001;98:1095–1100. doi: 10.1073/pnas.98.3.1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brockmann D, Hufnagel L, Geisel T. The scaling laws of human travel. Nature. 2006;439:462–465. doi: 10.1038/nature04292. [DOI] [PubMed] [Google Scholar]
- 4.Gonzalez M, Hidalgo C, Barabási A. Understanding individual human mobility patterns. Nature. 2008;453:779–782. doi: 10.1038/nature06958. [DOI] [PubMed] [Google Scholar]
- 5.Rhee I, et al. On the levy-walk nature of human mobility. IEEE/ACM Trans Netw. 2011;19:630–643. [Google Scholar]
- 6.Brockmann D, Helbing D. The hidden geometry of complex, network-driven contagion phenomena. Science. 2013;342:1337–1342. doi: 10.1126/science.1245200. [DOI] [PubMed] [Google Scholar]
- 7.Clark JS. Why trees migrate so fast: Confronting theory with dispersal biology and the paleorecord. Am Nat. 1998;152:204–224. doi: 10.1086/286162. [DOI] [PubMed] [Google Scholar]
- 8.Clark JS, Silman M, Kern R, Macklin E, HilleRisLambers J. Seed dispersal near and far: Patterns across temperate and tropical forests. Ecology. 1999;80:1475–1494. [Google Scholar]
- 9.Brown JK, Hovmoller MS. Aerial dispersal of pathogens on the global and continental scales and its impact on plant disease. Science. 2002;297:537–541. doi: 10.1126/science.1072678. [DOI] [PubMed] [Google Scholar]
- 10.McCallum H, Harvell D, Dobson A. Rates of spread of marine pathogens. Ecol Lett. 2003;6:1062–1067. [Google Scholar]
- 11.D’Ovidio F, Fernández V, Hernández-García E, López C. Mixing structures in the Mediterranean sea from finite-size lyapunov exponents. Geophys Res Lett. 2004;31(17):1–4. [Google Scholar]
- 12.Martin A. Phytoplankton patchiness: The role of lateral stirring and mixing. Prog Oceanogr. 2003;57(2):125–174. [Google Scholar]
- 13.Levin SA, Muller-Landau HC, Nathan R, Chave J. The ecology and evolution of seed dispersal: A theoretical perspective. Annu Rev Ecol Evol Syst. 2003;34:575–604. [Google Scholar]
- 14.Nathan R. Long-distance dispersal of plants. Science. 2006;313:786–788. doi: 10.1126/science.1124975. [DOI] [PubMed] [Google Scholar]
- 15.Perlekar P, Benzi R, Nelson D, Toschi F. Population dynamics at high Reynolds number. Phys Rev Lett. 2010;105:144501. doi: 10.1103/PhysRevLett.105.144501. [DOI] [PubMed] [Google Scholar]
- 16.Gillespie RG, et al. Long-distance dispersal: A framework for hypothesis testing. Trends Ecol Evol. 2012;27(1):47–56. doi: 10.1016/j.tree.2011.08.009. [DOI] [PubMed] [Google Scholar]
- 17.Fisher RA. The wave of advance of advantageous genes. Ann Eugen. 1937;7:355–369. [Google Scholar]
- 18.Kolmogorov A, Petrovsky I, Piskunov N. Study of the diffusion equation with growth of the quantity of matter and its application to a biological problem. Bull Univ Moscow Ser Int Sec A. 1937;1:1–25. [Google Scholar]
- 19.Mollison D. 1972. The rate of spatial propagation of simple epidemics. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, eds Le Cam LM, Neyman J, Scott EL (Univ of California Press, Berkeley, CA), Vol 3, pp 579–614.
- 20.Clark JS, Lewis M, McLachlan JS, HilleRisLambers J. Estimating population spread: What can we forecast and how well? Ecology. 2003;84:1979–1988. [Google Scholar]
- 21.Filipe J, Maule M. Effects of dispersal mechanisms on spatio-temporal development of epidemics. J Theor Biol. 2004;226(2):125–141. doi: 10.1016/s0022-5193(03)00278-9. [DOI] [PubMed] [Google Scholar]
- 22.Cannas SA, Marco DE, Montemurro MA. Long range dispersal and spatial pattern formation in biological invasions. Math Biosci. 2006;203(2):155–170. doi: 10.1016/j.mbs.2006.06.005. [DOI] [PubMed] [Google Scholar]
- 23.Marco DE, Montemurro MA, Cannas SA. Comparing short and long-distance dispersal: Modelling and field case studies. Ecography. 2011;34:671–682. [Google Scholar]
- 24.Biskup M. On the scaling of the chemical distance in long-range percolation models. Ann Probab. 2004;32(4):2938–2977. [Google Scholar]
- 25.Aldous DJ. 2010. When knowing early matters: Gossip, percolation and Nash equilibria. arXiv:1005.4846.
- 26.Chatterjee S, Dey PS. 2013. Multiple phase transitions in long-range first-passage percolation on square lattices. arXiv:1309.5757.
- 27.Mollison D. Spatial contact models for ecological and epidemic spread. J R Stat Soc B. 1977;39(3):283–326. [Google Scholar]
- 28.Kot M, Lewis M, Van Den Driessche P. Dispersal data and the spread of invading organisms. Ecology. 1996;77:2027–2042. [Google Scholar]
- 29.Neubert MG, Caswell H. Demography and dispersal: Calculation and sensitivity analysis of invasion speed for structured populations. Ecology. 2000;81:1613–1628. [Google Scholar]
- 30.Mancinelli R, Vergni D, Vulpiani A. Superfast front propagation in reactive systems with non-Gaussian diffusion. Europhys Lett. 2002;60:532. [Google Scholar]
- 31.del Castillo-Negrete D, Carreras B, Lynch V. Front dynamics in reaction-diffusion systems with Levy flights: A fractional diffusion approach. Phys Rev Lett. 2003;91:18302. doi: 10.1103/PhysRevLett.91.018302. [DOI] [PubMed] [Google Scholar]
- 32.Medlock J, Kot M. Spreading disease: Integro-differential equations old and new. Math Biosci. 2003;184:201–222. doi: 10.1016/s0025-5564(03)00041-5. [DOI] [PubMed] [Google Scholar]
- 33.Brockmann D, Hufnagel L. Front propagation in reaction-superdiffusion dynamics: Taming Levy flights with fluctuations. Phys Rev Lett. 2007;98:178301. [Google Scholar]
- 34.Coville J, Dupaigne L. On a non-local equation arising in population dynamics. Proc R Soc Edinb Sec A Math. 2007;137:727–755. [Google Scholar]
- 35.del Castillo-Negrete D. Truncation effects in superdiffusive front propagation with Lévy flights. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;79:031120. doi: 10.1103/PhysRevE.79.031120. [DOI] [PubMed] [Google Scholar]
- 36.Levandowsky M, Schuster FL, White BS. Random movements of soil amebas. Acta Protozool. 1997;36:237–248. [Google Scholar]
- 37.Klafter J, White BS, Levandowsky M. Microzooplankton feeding behavior and the Levy walk. Biological Motion, Lecture Notes in Biomathematics. In: Alt W, Hoffmann G, editors. Vol 89. Springer; Berlin: 1990. pp. 281–293. [Google Scholar]
- 38.Atkinson R, Rhodes C, Macdonald D, Anderson R. Scale-free dynamics in the movement patterns of jackals. Oikos. 2002;98(1):134–140. [Google Scholar]
- 39.Fritz H, Said S, Weimerskirch H. Scale–dependent hierarchical adjustments of movement patterns in a long–range foraging seabird. Proc R Soc Lond B Biol Sci. 2003;270:1143–1148. doi: 10.1098/rspb.2003.2350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ramos-Fernandez G, et al. Lévy walk patterns in the foraging movements of spider monkeys (Ateles geoffroyi) Behav Ecol Sociobiol. 2004;55:223–230. [Google Scholar]
- 41.Dai X, Shannon G, Slotow R, Page B, Duffy K. Short-duration daytime movements of a cow herd of African elephants. J Mammal. 2007;88(1):151–157. [Google Scholar]
- 42.Garnier J. Accelerating solutions in integro-differential equations. SIAM J Math Anal. 2011;43:1955–1974. [Google Scholar]
- 43.Cabré X, Roquejoffre J-M. Propagation de fronts dans les équations de fisher–kpp avec diffusion fractionnaire [Front propagation in Fisher–KPP equations with fractional diffusion] C R Acad Sci Paris. 2009;347:1361–1366. [Google Scholar]
- 44.Marvel SA, Martin T, Doering CR, Lusseau D, Newman MEJ. The small-world effect is a modern phenomenon. arXiv:1310.2636 2013 [Google Scholar]
- 45.Van Saarloos W. Front propagation into unstable states. Phys Rep. 2003;386:29–222. [Google Scholar]
- 46.Biskup M. 2004. Graph diameter in long-range percolation. arXiv:0406379.
- 47.Armsworth PR, Roughgarden JE. The impact of directed versus random movement on population dynamics and biodiversity patterns. Am Nat. 2005;165:449–465. doi: 10.1086/428595. [DOI] [PubMed] [Google Scholar]
- 48.Grassberger P. Sir epidemics with long-range infection in one dimension. J Stat Mech. 2013;2013:P04004. [Google Scholar]
- 49.Grassberger P. Two-dimensional SIR epidemics with long range infection. J Stat Phys. 2013;153:289–311. [Google Scholar]
- 50.Excoffier L, Foll M, Petit RJ. Genetic consequences of range expansions. Annu Rev Ecol Evol Syst. 2009;40:481–501. [Google Scholar]
- 51.Novembre J, Di Rienzo A. Spatial patterns of variation due to natural selection in humans. Nat Rev Genet. 2009;10:745–755. doi: 10.1038/nrg2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Slatkin M, Wiehe T. Genetic hitch-hiking in a subdivided population. Genet Res. 1998;71(02):155–160. doi: 10.1017/s001667239800319x. [DOI] [PubMed] [Google Scholar]
- 53.Barton N, Etheridge A, Kelleher J, Veber A. Genetic hitchhiking in spatially extended populations. Theor Popul Biol. 2013;87:75–89. doi: 10.1016/j.tpb.2012.12.001. [DOI] [PubMed] [Google Scholar]
- 54.Edmonds CA, Lillie AS, Cavalli-Sforza LL. Mutations arising in the wave front of an expanding population. Proc Natl Acad Sci USA. 2004;101:975–979. doi: 10.1073/pnas.0308064100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Klopfstein S, Currat M, Excoffier L. The fate of mutations surfing on the wave of a range expansion. Mol Biol Evol. 2006;23:482–490. doi: 10.1093/molbev/msj057. [DOI] [PubMed] [Google Scholar]
- 56.Hallatschek O, Nelson DR. Gene surfing in expanding populations. Theor Popul Biol. 2008;73(1):158–170. doi: 10.1016/j.tpb.2007.08.008. [DOI] [PubMed] [Google Scholar]
- 57.Nichols RA, Hewitt GM. The genetic consequences of long distance dispersal during colonization. Heredity. 1994;72:312–317. [Google Scholar]
- 58.Bialozyt R, Ziegenhagen B, Petit R. Contrasting effects of long distance seed dispersal on genetic diversity during range expansion. J Evol Biol. 2006;19(1):12–20. doi: 10.1111/j.1420-9101.2005.00995.x. [DOI] [PubMed] [Google Scholar]
- 59.Berthouly-Salazar C, et al. Long-distance dispersal maximizes evolutionary potential during rapid geographic range expansion. Mol Ecol. 2013;22:5793–5804. doi: 10.1111/mec.12538. [DOI] [PubMed] [Google Scholar]
- 60.Lewis M, Pacala S. Modeling and analysis of stochastic invasion processes. J Math Biol. 2000;41:387–429. doi: 10.1007/s002850000050. [DOI] [PubMed] [Google Scholar]
- 61.Moody ME, Mack RN. Controlling the spread of plant invasions: The importance of nascent foci. J Appl Ecol. 1988;25:1009–1021. [Google Scholar]
- 62.Ralph P, Coop G. Parallel adaptation: One or many waves of advance of an advantageous allele? Genetics. 2010;186:647–668. doi: 10.1534/genetics.110.119594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Martens E, Hallatschek O. Interfering waves of adaptation promote spatial mixing. Genetics. 2011;189:1045–1060. doi: 10.1534/genetics.111.130112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Matthews L, Woolhouse M. New approaches to quantifying the spread of infection. Nat Rev Microbiol. 2005;3:529–536. doi: 10.1038/nrmicro1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.