Far-infrared surface emissivity and climate

Significance

We find that many of the Earth's climate variables, including surface temperature, outgoing longwave radiation, cooling rates, and frozen surface extent, are sensitive to far-IR surface emissivity, a largely unconstrained, temporally and spatially heterogeneous scaling factor for the blackbody radiation from the surface at wavelengths between 15 μm and 100 μm. We also describe a previously unidentified mechanism that amplifies high-latitude and high-altitude warming in finding significantly lower values of far-IR emissivity for ocean and desert surfaces than for sea ice and snow. This leads to a decrease in surface emission at far-IR wavelengths, reduced cooling to space, and warmer radiative surface temperatures. Far-IR emissivity can be measured from spectrally resolved observations, but such measurements have not yet been made.

Abstract

Presently, there are no global measurement constraints on the surface emissivity at wavelengths longer than 15 μm, even though this surface property in this far-IR region has a direct impact on the outgoing longwave radiation (OLR) and infrared cooling rates where the column precipitable water vapor (PWV) is less than 1 mm. Such dry conditions are common for high-altitude and high-latitude locations, with the potential for modeled climate to be impacted by uncertain surface characteristics. This paper explores the sensitivity of instantaneous OLR and cooling rates to changes in far-IR surface emissivity and how this unconstrained property impacts climate model projections. At high latitudes and altitudes, a 0.05 change in emissivity due to mineralogy and snow grain size can cause a 1.8–2.0 W m⁻² difference in the instantaneous clear-sky OLR. A variety of radiative transfer techniques have been used to model the far-IR spectral emissivities of surface types defined by the International Geosphere-Biosphere Program. Incorporating these far-IR surface emissivities into the Representative Concentration Pathway (RCP) 8.5 scenario of the Community Earth System Model leads to discernible changes in the spatial patterns of surface temperature, OLR, and frozen surface extent. The model results differ at high latitudes by as much as 2°K, 10 W m⁻², and 15%, respectively, after only 25 y of integration. Additionally, the calculated difference in far-IR emissivity between ocean and sea ice of between 0.1 and 0.2, suggests the potential for a far-IR positive feedback for polar climate change.

Terrestrial emission plays a critical role in the climate system (1), and over 99% of this radiation occurs in the wavelength range from 5 to 100 μm (2,000 cm⁻¹ to 100 cm⁻¹). However, there have been very few spectrally resolved measurements of terrestrial emission at wavelengths between 15.4 μm and 100 μm (650 cm⁻¹ to 100 cm⁻¹), often referred to as the far infrared, even though approximately half of the terrestrial radiation occurs over this subset of infrared wavelengths (2). Under moist conditions, the atmosphere is opaque to the surface in the far infrared, but the atmosphere becomes partially transparent to the surface under arid conditions. The terms that affect radiation in the far infrared, which are surface, water vapor, and cloud emission, are inferred from measurements in other spectral regions (typically midinfrared wavelengths from 5 μm to 15.4 μm) (3), and it is possible to check for consistency with outgoing longwave radiation (OLR) measurements from the Clouds and the Earth’s Radiant Energy System (CERES) instrument, which covers between 5 μm and 50 μm (2,000 cm⁻¹ to 200 cm⁻¹) (4). It has been demonstrated, however, that this approach can be problematic for water vapor and cloud energetics due to compensating errors (5, 6).

The paucity of measurements in the far infrared has frustrated efforts to characterize what may be affecting this spectral region, but the limited measurements that do exist (7−10) suggest the importance of the far infrared for radiometric accuracy in the radiative transfer codes used in climate models (11). For example, Turner et al. (12) found that changing the water vapor continuum absorption in the Community Earth System Model, which affects far-IR radiation, leads to changes in the vertical distribution of radiative cooling. This, in turn, changes the evolution of temperature, water vapor, and cloud profiles. Moreover, there is evidence that cloud optical properties in this spectral region are difficult to characterize without direct measurements (13, 14). However, the role of far-IR surface emissivity on the radiation budget, including surface emission, OLR, cooling rates, and ultimately climate variables, has not been explored as much as for clouds and water vapor.

The infrared radiative energy budget is wavelength dependent and represents the contributions of surface and atmospheric emission that are contingent on the optical depth profile. This is realized, for example, in the solution to the radiative transfer equation for broadband OLR. OLR is a function of the temperature profile, the profiles of absorbing species, the radiative surface temperature, and surface emissivity, and is given by the following equation:

$$\text{OLR}={\displaystyle {\int }_0^{\infty }d\nu \left[{\mathit{ϵ}}_{\nu }^s{B}_{\nu }\left(T_s\right){\mathcal{T}}_{\nu }^F\left(0,\infty \right)+\left(1-{\mathit{ϵ}}_{\nu }^s\right)F_{\nu }^{\mathit{atm,down}}\left(z=0\right){\mathcal{T}}_{\nu }^F\left(0,\infty \right)+F_{\nu }^{\mathit{atm,up}}\left(z=\infty \right)\right]},$$ [1]

where ${\mathit{ϵ}}_{\nu }^s$ is the spectrally dependent, angularly averaged surface emissivity at frequency $\nu$, $B_{\nu }$ is the spectrally dependent black-body flux as a function of radiative surface temperature $T_s$, $F_{\nu }^{\mathit{atm,down}}\left(z=0\right)$ is the downwelling spectrally dependent flux from atmosphere at the surface, $F_{\nu }^{\mathit{atm,up}}\left(z=\infty \right)$ is the upwelling spectrally dependent flux from the atmosphere at the top-of-atmosphere, and ${\mathcal{T}}_{\nu }^F\left(0,\infty \right)$ is the spectrally dependent flux transmittance between the surface $\left(z=0\right)$ and the top-of-atmosphere $\left(z=\infty \right)$. The three terms in the brackets of the interior integrand of the RHS of Eq. 1 are the spectrally varying contributions to the OLR originated from surface emission, from the reflection of downwelling radiation from a nonblack surface, and from atmospheric emission, respectively.

The surface emissivity term, which is necessary to perform complete column infrared radiative transfer calculations, is exactly unity for an ideal blackbody, but emissivity of real surfaces can be spectrally dependent and is generally lower than unity. Emissivity characterization of real materials is highly nontrivial because of microscopic heterogeneity, surface reflections, and surface geometry (15). It exhibits angular and spectral dependence, and its characterization outside of the laboratory requires remote sensing, as terrestrial surfaces exhibit great spectral and temporal variation in this quantity (16, 17). While there is extensive information on angularly averaged surface emissivity over bands at midinfrared wavelengths from 5 μm to 14 μm derived from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) measurements (18−20), Moderate Resolution Imaging Spectroradiometer (MODIS) (e.g., refs.21 and 22), and other thermal infrared sounders including Atmospheric Infrared Sounder (AIRS) and Infrared Atmospheric Sounding Interferometer (e.g., refs. 23 and 24), there is no comprehensive knowledge of angularly averaged terrestrial surface emissivity outside of the laboratory at far-IR wavelengths because there are no comprehensive measurements at those wavelengths. What is known about far-IR surface emissivity is derived from laboratory measurements and research on planetary environments. Surveys of the optical properties of snow found both a minimum and a maximum in the imaginary index of refraction in the far infrared leading to surface emissivities with a range of values from 0.96 to 0.99 depending on grain size (25, 26), with significant implications for the infrared radiation budget (27). In support of the Mars Global Surveyor Thermal Emission Spectrometer, Christensen et al. (28) developed a library of emissivities of pure mineral samples indicating diverse spectral structure of common surficial minerals at wavelengths from 15 μm to 25 μm with values as low as 0.8. Glotch et al. (29) and Glotch and Rossman (30) found similarly low values of far-IR emissivity for Martian surfaces. Cheng et al. (31) surveyed the published literature of surface refractive indices of common terrestrial minerals, including phyllosilicates, silicon dioxide, aluminum dioxide, iron oxide, and silicates, and found that far-IR angularly averaged surface emissivity can range from 0.81 to 0.97, while liquid water’s far-IR emissivity is 0.95. Microscopic and macroscopic spatial and temporal heterogeneity suggest that this aspect of surface remote sensing is an open scientific topic that can be, but has not been, determined with global far-IR measurements.

This paper evaluates the implications of reasonable far-IR surface spectral emissivity values, derived from radiative transfer calculations, for a variety of surface types, on instantaneous OLR, cooling rates, and other key climate variables. It also provides an estimate for how improved understanding of far-IR surface characteristics would be affect the modeling of critical climate variables, and discusses the consequences for high-latitude and high-altitude climate.

Methodology

We use several well-established radiative transfer techniques and one state-of-the-art Earth system model to evaluate the role of far-IR surface emissivity on instantaneous radiation and on long-term climate model performance.

Spectrally resolved transmission is calculated with the Line-By-Line Radiative Transfer Model (LBLRTM) version 12.0 (32). Broadband OLR, cooling rates, and transmission are produced with the Rapid Radiative Transfer Model (RRTMG) (32) as implemented in the PSrad radiation package (33). We use the Community Earth System Model (CESM) (34) version 1.0.5, which also uses RRTMG for its radiation calculations, to explore the implications of surface emissivity on climate variables.

CESM was run with the Representative Concentration Pathway (RCP) 8.5 forcing (35), which specifies a radiative forcing from greenhouse gases, aerosols, and land-use changes of 8.5 W m⁻² in the year 2100 (compset B_RCP8.5_CN; see Appendix A of the CESM User’s Guide for details: www.cesm.ucar.edu/models/cesm1.0/cesm). The spatial resolution was set to a 1-degree atmosphere/land grid with a nominal 1-degree ocean/ice grid using the gx1v6 ocean mask (0.9 × 1.25_gx1v6).

The model was first run with no modifications to ensure agreement with results archived in the Coupled Model Intercomparison Project—Phase 5 archive (36). Then, the model was modified to determine the sensitivity of the climate model to far-IR surface emissivity alone. This was accomplished by only adjusting the surface emissivity in RRTMG over the wavelength range from 1,000 μm to 15.9 μm (10–630 cm⁻¹) with scene-type emissivity values specified by ocean, land, and frozen surface (sea ice and land ice) for International Geosphere-Biosphere Program (IGBP) scene types (37) (hereafter, denoted as IGBP emissivity). Far-IR emissivity was specified over three bands: 10−250 cm⁻¹, 250−500 cm⁻¹, and 500−630 cm⁻¹. The emissivity of RRTMG bands at wavelengths shorter than 15.9 μm was held fixed at 1.0000. The far-IR angularly averaged emissivity over each band for ocean, desert, vegetation, and frozen surface scene types was established through radiative transfer calculations. The values for ocean scenes were calculated based on liquid water refractive indices (38) and a Fresnel equation calculation; the values for vegetation were extrapolated from the ASTER Spectral Library (18); the values for desert were calculated based on surficial mineral refractive indices and a Fresnel equation calculation; and the values for frozen surfaces were calculated based on ice refractive indices (26) and a Hapke model calculation (39) as done in ref. 27 (see Supporting Information for more details). In each call to the RRTMG routine, the land fraction, latitude, longitude, snow area, and sea ice fraction were used to create a weighted average of emissivity based on the fractional coverage of each scene type in the grid box. Once the experiment and control calculations were completed, the time series of surface temperature and frozen surface extent for the unperturbed model run and the experiment were compared.

Results

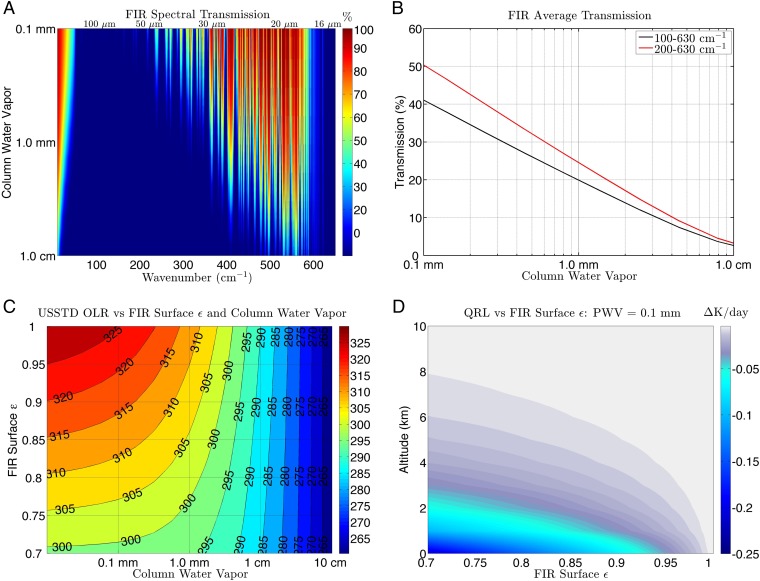
We first explored how the atmosphere becomes transparent in the far infrared and its implications for how surface emissivity impacts OLR and cooling rates. Using LBLRTM, spectral transmittance between the surface and top-of-atmosphere (TOA) was calculated for the U.S. Standard Atmosphere (40) with varying levels of water vapor from 10 cm precipitable water vapor (PWV) to 0.1 mm PWV. Fig. 1A indicates that microwindows in far-IR spectral regions become transparent, with some windows opening up at 1 cm PWV and increasing numbers of microwindows opening up below 1 mm PWV. As a point of reference, the global mean PWV is ∼2.2 cm, but is between 1.0 and 5.0 mm over Antarctica (41). Fig. 1B shows band-averaged transmission between 100 μm and 15.9 μm (100 cm⁻¹ and 630 cm⁻¹) rising to 0.41 at 0.1 mm PWV, while transmission between 200 cm⁻¹ and 630 cm⁻¹, a spectral range that covers ∼46% of total thermal emission, rises to 0.5. This is consistent with previous findings (42, 43) and has significant implications for the relationship between surface emissivity and total infrared energy budget. Fig. 1C indicates the joint relationship between PWV, surface emissivity, and OLR under clear-sky conditions. At PWV values above 1 cm, OLR is a strong function of PWV and an extremely weak function of surface emissivity. However, as the atmosphere becomes more transparent below a few millimeters PWV, far-IR surface emissivity begins to exert a significant control on OLR. At 0.1 mm PWV, the range of far-IR surface emissivities published in Cheng et al. (31) provides for a range in OLR of 7 W m⁻². Similarly, total infrared cooling rates up to 7 km in the lower atmosphere decrease with lower far-IR surface emissivity under conditions with 1 mm PWV, as shown in Fig. 1D. Total infrared cooling at the surface can be impacted by as much as 0.07 K/d under such dehydrated conditions. It should be noted that the results in Fig. 1 are illustrative and based on a single model atmosphere. There is a weak temperature dependence of water vapor absorption, and the OLR and cooling rate relationships shown in Fig. 1 will vary by ∼0.07% per °K.

Fig. 1.

(A) Spectral transmission at 1 cm⁻¹ intervals as a function of wavelength for U.S. Standard Atmosphere (40) and PWV, as calculated with LBLRTM. (B) Average transmission between 100 cm⁻¹ and 650 cm⁻¹ as a function of precipitable water vapor for the U.S. Standard Atmosphere. (C) Contour plot of the relationship between OLR and the average surface emissivity at wavelengths between 15.9 μm and 100 μm and precipitable water vapor for the U.S. Standard Atmosphere, as calculated with RRTMG (32). (D) Difference in cooling rate profiles (QRL) between the U.S. Standard Atmosphere with a water-vapor profile scaled to 0.1 mm and a far-IR surface emissivity of 1.0 and that same atmosphere with a far-IR surface emissivity noted on the abscissa.

We also performed a calculation of OLR from atmospheric conditions as measured by radiosondes in the Radiative Heating of Underexplored Bands-II campaign (43) and found that the RMS difference in OLR values associated with the range of surface emissivities in Cheng et al. (31) was 8.0 W m⁻². This is comparable to all of the radiative forcing (greenhouse gases, aerosols, and land use/land cover) in the emissions scenario with the least amount of mitigation: RCP8.5. A similar calculation based on the range of far-IR surface emissivity from 0.96 to 0.99 as published in Warren (25) produces a range of OLR values of 1.0 W m⁻².

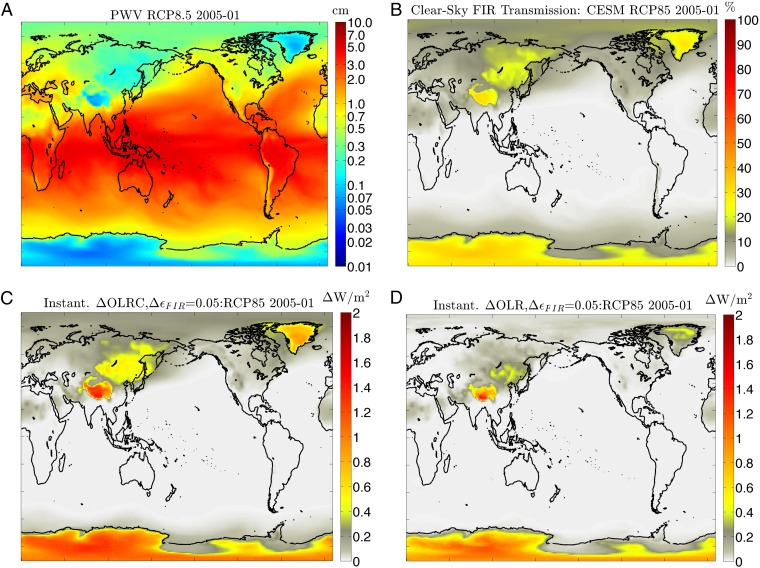
Because far-IR surface emissivity becomes influential on the atmospheric infrared radiation budget where PWV is below 1 mm, we assess the implications for climate model tendencies. First, the monthly averaged PWV values from January 2005 for the RCP8.5 integration of CESM1.0.5 shows significant portions of high-latitude and high-altitude regions with a PWV < 1 mm, as presented in Fig. 2A. The calculated far-IR transmission, as shown in Fig. 2B, is greater than 30% in Antarctica, Greenland, the Tibetan Plateau, and parts of Siberia. This has implications for the sensitivity of instantaneous clear-sky and all-sky OLR to far-IR surface emissivity. Fig. 2 C and D indicates that a spectrally gray far-IR surface emissivity perturbation of 0.05 would yield clear-sky and all-sky OLR changes of between 1.8 W m⁻² and 2 W m⁻² in the locations of low PWV, with slightly less effect under all-sky conditions, which is comparable to the change in OLR from a surface temperature change of 2 °K or a total cloud fraction change of 10% at high latitudes and altitudes.

Fig. 2.

(A) Monthly averaged PWV from CESM integration of RCP8.5 for January 2005. (B) Monthly averaged far-IR (15.9 μm and 100 μm) non-Planck-weighted transmission. (C) Instantaneous change in clear-sky OLR based on a spectrally uniform perturbation of far-IR surface emissivity of 0.05. (D) Same as C but for all-sky OLR.

Moreover, it should be noted that the column water vapor was generally overestimated in the CESM integration relative to the climatology of monthly averaged PWV retrieved from the AIRS L3 measurements (41). Therefore, the actual sensitivity of the Earth’s OLR to perturbations in far-IR emissivity may be greater than shown in Fig. 2. Nevertheless, these plots indicate that large swaths of Earth’s high-altitude and high-latitude regions exhibit nonnegligible occurrence of PWV below 1 mm.

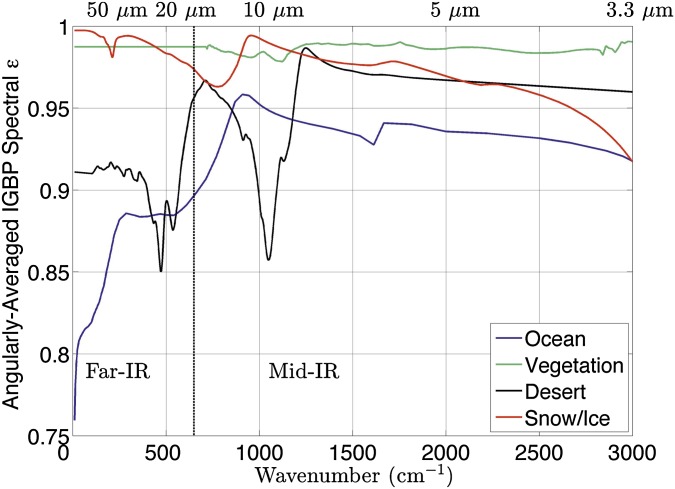
We then explored the implications of surface emissivity on global climate by running CESM under the RCP8.5 scenario with far-IR emissivity based on IGBP scene type. Fig. 3 indicates the angularly averaged, spectrally resolved surface emissivity based on radiative transfer calculations as described in Methodology. There is significant spectral structure in the far infrared, particularly for the desert surface type due to surficial minerology, and there is a substantial difference between ocean and sea ice emissivities of 0.1 around 500 cm⁻¹ to 0.2 below 100 cm⁻¹.

Fig. 3.

Angularly averaged, spectrally resolved far-IR surface emissivity for four IGBP land types (ocean, vegetation, desert, and snow) based on 3D radiative transfer calculations and published indices of refraction.

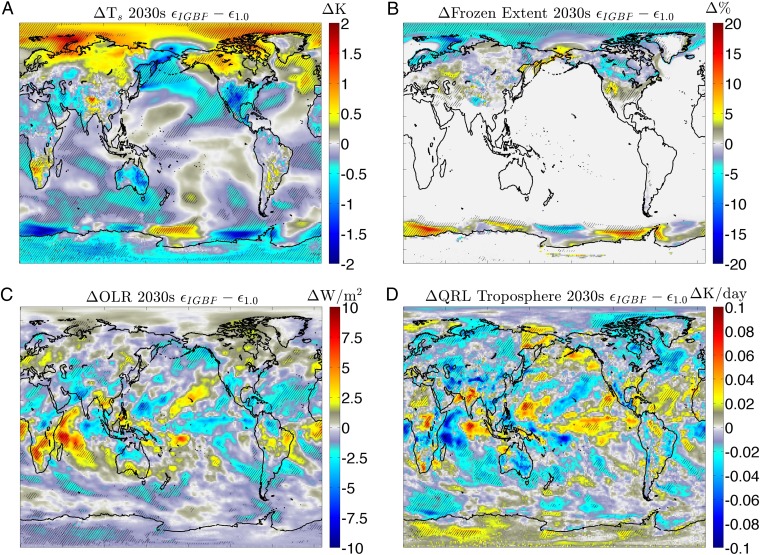
The lack of any specification for the spectral structure of this emissivity in climate models may be problematic and can be assessed. Specifically, Fig. 4 indicates that the difference between the unity assumption and an estimate of far-IR surface emissivity based on land type as shown in Fig. 3 causes CESM to produce dramatically different results in climate variables, even after only 25 y of integration. Decadally averaged surface temperatures’ change in the 2030s differs in the two integrations by up to 2 °K, with a systematic increase in temperatures with IGBP emissivity. Local differences between the two model runs in the annually averaged sea ice and snow fraction are up to 10% and 15%, respectively, with a systematic decrease in frozen surface extent at high northern latitudes in the experiment with IGBP emissivity.

Fig. 4.

Decadally averaged differences during the 2030s between an integration CESM 1.0.5 forced with RCP8.5 where far-IR emissivity is determined by IGBP land type and an integration where far-IR surface emissivity was 1.00 for all scenes for (A) radiative surface temperature, (B) frozen surface extent (sea ice and land snow fraction), (C) OLR, and (D) tropospheric cooling rates.

However, it should be noted that this extrapolation is not based on direct observations, and the unsupervised use of IGBP data has been problematic upon confrontation with data (44). We expect the results of Fig. 4 to be revised considerably when informed by direct observations.

Discussion

This work seeks to estimate the importance of understanding far-IR surface emissivity in high-altitude and high-latitude climate, despite the lack of comprehensive measurements of this quantity. It is found that far-IR surface emissivity exerts a significant amount of control under conditions where PWV is below 1 mm, which is common for high-altitude and high-latitude scenes. By changing the assumption of far-IR surface emissivity in CESM to realistic values based on published literature, it was found that a climate model produces dramatically different spatial patterns of surface temperature and frozen surface extent.

Therefore, improved spatial and temporal knowledge of far-IR surface emissivity is warranted, and can be obtained from field or remote-sensing measurements. While some atmospheric processes that affect far-IR radiation, such as water vapor and liquid clouds, can be understood through an extrapolation of information gleaned from midinfrared hyperspectral measurements, such an extrapolation could be problematic for surface processes due to (i) the almost complete lack of surface emissivity data at far-IR wavelengths, (ii) known temporal and spatial heterogeneity in midinfrared surface emissivity, and (iii) the lack of an established method for reliably extrapolating from midinfrared to far-IR surface emission.

However, the retrieval of far-IR surface emissivity from direct measurements is straightforward and has strong heritage from existing MODIS surface emissivity retrieval algorithms (e.g., ref. 21). Surface emissivity characteristics vary slowly with frequency relative to gaseous absorption, which means that errors in surface emissivity emerge as correlated signals in the far-IR microwindows that are consistent with the Planck emission based on the radiative surface temperature. The emissivity could be retrieved by analyzing microwindows between 15.4 μm and 50 μm with a focus on those between 17 μm and 30 μm, where water vapor absorbs less strongly. Given the spectrally narrow microwindows, far-IR hyperspectral measurements, informed by existing midinfrared hyperspectral surface emissivity retrieval algorithms (23, 24), are warranted. The retrieval of surface emissivity for climate studies at wavelengths longer than 50 μm is not likely to be significant given that less than 5% of terrestrial emission occurs in these wavelengths, and that water vapor exhibits strong absorption in this spectral region, even under exceptionally dry (i.e., < 0.1 mm PWV) conditions.

A far-IR spectrometer is necessary for these retrievals, and existing satellite instrumentation does not contain spectrally resolved measurements beyond 15.4 μm. There are a limited number of far-IR measurements from balloon (7), aircraft (8), and ground campaigns (9), and from measurements out to 25 μm from the Infrared Interferometer Sounder-D (IRIS-D) instrument in 1970 (45). Proposed instrumentation such as the CLimate Absolute Radiance and Refractivity Observatory (CLARREO) (46) would provide far-IR spectra that, if averaged appropriately to reduce instrumental noise and then cloud-cleared, could constrain this quantity. An alternative approach to characterizing far-IR surface emissivity could involve using a far-IR spectrometer on a long-duration, high-altitude balloon platform over Antarctica that would collect many thousands of spectra over diverse scenes with correlative measurements from extant satellite assets such as those on the Aqua, Terra, and MetOp platforms.

The sensitivity of high-latitude and high-altitude radiation to far-IR surface emission, and thus to surface emissivity, may have implications for climactic conditions at high latitudes and altitudes. In particular, on the Tibetan Plateau, where the column water vapor is often less than 1 mm, the impact of emissivity could lead to changes in the modeled Indian monsoon, through changes in the snow coverage (47). Additionally, this work’s finding of large differences in ocean and sea ice far-IR surface emissivity may lead to reduced cooling to space in polar winter over regions with recent sea ice loss, which would be another positive feedback for polar climate change. It is also warranted to explore if this reduced cooling contributes to high-latitude temperature biases exhibited by models relative to reanalyses (48).