Genetic Variation in Echinacea angustifolia Along a Climatic Gradient

Abstract

• Backgrounds and Aims Echinacea angustifolia is a widespread species distributed throughout the Great Plains region of North America. Genetic differentiation among populations was investigated along a 1500 km north–south climatic gradient in North America, a region with no major geographical barriers. The objective of the study was to determine if genetic differentiation of populations could be explained by an isolation-by-distance model or by associations with climatic parameters known to affect plant growth and survival.

• Methods Historical climatic data were used to define the nature of the climatic gradient and AFLP markers were used to establish patterns of population genetic differentiation among ten Echinacea populations collected from North Dakota to Oklahoma. A total of 1290 fragments were scored using six EcoRI/MseI and three PstI/MseI primer combinations. Assessment of the correlation between climatic, genetic and geographic distances was assessed by Mantel and partial Mantel tests.

• Key Results PstI/MseI combinations produced significantly fewer fragments, but a larger percentage was unique compared with EcoRI/MseI markers. Using estimates of F_ST, populations in Oklahoma and southern Kansas were identified as the most divergent from the other populations. Both the neighbour-joining tree and principal co-ordinate analysis clustered the populations in a north–south spatial orientation. About 60 % of the genetic variation was found within populations, 20 % among populations and the remaining 20 % was partitioned among groups that were defined by the topology of the neighbour-joining tree. Significant support was found for the isolation-by-distance model independent of the effects of annual mean precipitation, but not from annual mean temperature and freeze-free days.

• Conclusions Echinacea angustifolia populations exhibit genetic divergence along a north–south climatic gradient. The data support an isolation-by-distance restriction in gene flow that is independent of annual mean precipitation.

INTRODUCTION

The level of genetic diversity and its causes are of great interest in evolutionary biology as genetic diversity greatly affects the evolutionary potential of a species (Futuyma, 1998). Abiotic and biotic processes acting upon isolated populations are thought to be a key factor in species divergence (Grant, 1981; Loveless and Hamrick, 1984; Levin, 2003), but populations with low levels of genetic diversity may not be able to adapt to a changing environment (Ellstrand and Elam, 1993). In a widespread species, the conditions for divergence and local speciation are likely to exist in those populations at the geographical and ecological edges of the species distribution (Levin, 2003). Although geographic variation within widespread species is well reported in the literature (e.g. Holman et al., 2003), there are cases of widespread species exhibiting neither genetic nor phenotypic differences, and thus geographic distribution is not always a good predictor of genetic divergence (Gitzendanner and Soltis, 2000).

Processes of geographical divergence occur by isolating mechanisms, in part due to the restriction of gene flow between populations. Among subpopulations of a widespread species, different ecological environments and independent evolution of populations through genetic drift may lead to divergence. In the absence of a barrier that restricts gene flow, adaptation to a new environment will be limited. Geographical barriers and/or restricted gene flow coupled with differential selection pressures within the geographical range of the species should provide the opportunity for divergence. Often reports that examine the evolutionary history and distribution of a given taxa are discussed in the context of palaeoclimatic and geographic factors (e.g. Francisco-Ortega et al., 1995; Sharbel et al., 2000; Zhang et al., 2001), whereas it is clear that successful adaptation to a changing environment must exist within the context of standing genetic variation. Evidence for active speciation might be detected by varying levels of genetic divergence observed in populations of the species (Schultz and Soltis, 2001). Climatic factors are a major contributing factor in shaping the vegetation in the prairie ecosystem in North America (Weaver and Fitzpatrick, 1934). A number of environmental factors may exert selection pressure thus affecting evolutionary change, and among these are freezing events, salinity, heat and drought.

Echinacea angustifolia is a widespread species of rocky open areas in the North American plains occurring from Texas to Saskatchewan and from western Iowa to Minnesota (McGregor, 1968; Kindscher, 1989). Echinacea spp. are perennial plants and reproduce predominantly by seed but also reproduce vegetatively by crown-division (McGregor, 1968; Li, 1998). They have a long history of use in North America, and E. angustifolia was the most widely used medicinal plant of the plains Indians, and today it is a popular medicinal herb (Kindscher, 1989; Percival, 2000). The distribution of E. angustifolia along a 1500 km north–south (N–S) climatic gradient is well suited to study patterns of genetic differentiation and the underlying causes of microevolution. Within the geographic boundaries of the present study there are no major physical barriers limiting gene flow among populations. Climatic conditions that could potentially have profound effects on plant growth and reproduction vary greatly within the distribution of E. angustifolia (Table 1). Within the geographic range of our study populations, over a period of 70 years (1931–2000), average annual rainfall varied from 400 to 750 mm, and the average number of frost-free days ranged from 118 to 209. The objectives of the present study were to: (a) establish a pattern of genetic diversity among populations collected along an approx. 1500 km N–S cline from North Dakota to Oklahoma; (b) test the theory that populations at the geographic edges of its distribution exhibit the greatest genetic divergence; (c) determine if these genetic differences are correlated with a simple isolation by distance model (Wright, 1946), or alternatively; (d) determine if specific climatic attributes are correlated with the observed genetic variation among the populations thus suggesting climatic adaptation.

Table 1.

Geographic distribution and climatic parameters of Echinacea angustifolia populations and the outgroup E. sanguinea

			Collection site
Population no.	Population code	Plant no.	Latitude	Longitude	FFD	AMP (mm)	AMT (°C)
1	ND-007	1, 2, 3	47°34′51″N	103°26′12″W	118	404	5·3
2	ND-004	4, 5, 6	46°56′40″N	103°33′54″W	122	399	5·6
3	SD-002	7, 8, 9	43°54′10″N	102°26′12″W	144	427	8·3
4	NE-001	10, 11, 12	42°46′58″N	100°02′05″W	138	538	8·7
5	NE-002	13, 14, 15	41°40′37″N	99°21′56″W	131	589	9·3
6	NE-003	16, 17, 18	41°09′18″N	96°53′22″W	163	714	10·2
7	KS-CD	19, 20, 21	39°21′55″N	97°41′15″W	178	676	11·8
8	KS-HO	22, 23, 24	38°15′15″N	99°41′28″W	173	551	12·9
9	OK-WD	28, 29, 30	36°57′27″N	99°04′59″W	191	747	14·8
10	OK-CO	25, 26, 27	34°36′32″N	98°35′49″W	209	721	16·2
11	E. sanguinea*	31, 32, 33	30°58′00″N	93°13′00″W	251	1461	19·4

All data are for the period 1931–2000 for climatic divisions from which the collection sites were located. See text for additional details.

FFD, freeze-free days; AMP, annual mean precipitation; AMT, annual mean temperature.

^*USDA accession Ames 23874.

MATERIALS AND METHODS

Plant material

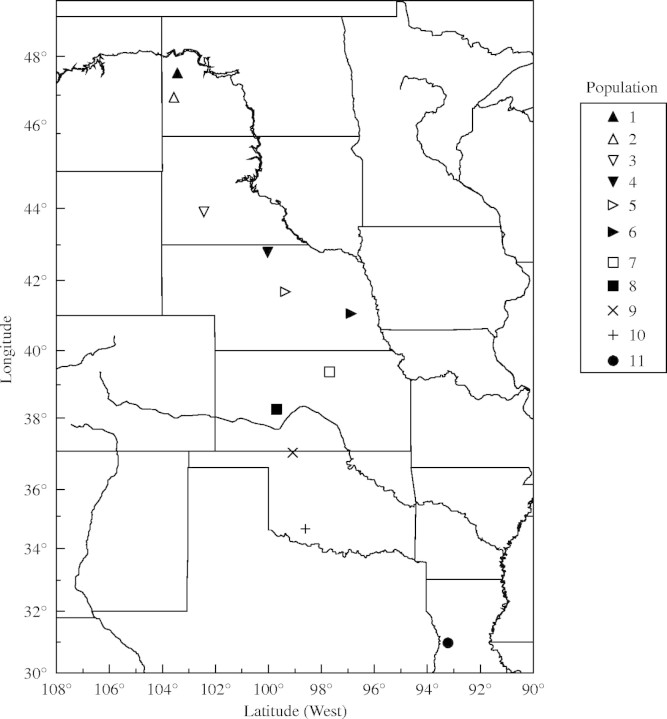
Seeds of E. angustifolia D.C. var. angustifolia sensu McGregor were collected from ten sites within the Great Plains region of the United States in September 2000 (Fig. 1 and Table 1). The distance between any two populations ranged from 71 to 1496 km. Each E. angustifolia population consisted of 200 to 300 plants with the exception of the SD-002 population, which contained 40–50 plants. At each site, 20–30 plants were chosen at random, the inflorescences collected from each plant, and kept separate to maintain the identity of each plant. The seeds were harvested and stored at 6 % moisture content at −20 °C until needed. The seeds were germinated in Petri dishes and transferred to field plots at Cal Poly Pomona where approx. 80 plants from each population were established in a common nursery. Leaves harvested from these plants served as source DNA for these experiments and no individual plant was represented more than once in the analysis. Because >90 % of the transplants survived it is likely the nursery population is genetically representative of the original populations. Voucher specimens were deposited at the University of California Herbarium, Los Angeles and their taxonomic identity confirmed by morphological keys (B. Prigge, pers. comm.). Taxon names reported herein are consistent with the USDA-ARS National Genetic Resources Information Network. Echinacea sanguinea was used as an outgroup for phylogenetic rooting purposes. Previously, E. sanguinea had been shown to be a member of the sister clade of the E. angustifolia species complex (Kim et al., 2004). McGregor (1968) reported that all species of Echinacea will readily form hybrids, suggesting a close genetic relationship and a previous report based on amplified fragment length polymorphism (AFLP) analysis concluded that each species is genetically distinct, but closely related (Kim et al., 2004). Seeds of E. sanguinea were obtained from the USDA Plant Introduction Station (Ames, IA, USA) and were originally collected in Louisiana. Accession, plant and population identification numbers, and geographic co-ordinates are given in Table 1 and the collection sites are graphically represented in Fig. 1. A matrix of geographic distances (GEO) between collection sites was calculated using the geographic co-ordinates of each site.

Fig. 1.

Collection areas of Echinacea angustifolia and the outgroup E. sanguinea.

Climatic data

Climatic data for each collection site were obtained from historical records compiled from the National Oceanic and Atmospheric Administration (NOAA, 2002). Climatic divisions, often used in agricultural and ecological modelling, are defined as regions within a state that are as climatically homogeneous as possible (NOAA, 2002). The average area encompassed by a climatic division in the present study was 26537 square km (range 18 109–48 764 square km). Thus, these data may be considered representative of a macro-environment. In four instances, collection sites (populations ND-007, NE-002, KS-HO and LA) were within 15 km of a climatic division boundary, in which case these data were averaged across those two climatic divisions.

All climatic parameters, with the exception of freeze-free days data, were recorded from 1931–2000. The statistics for freeze-free days were not calculated at each weather station for the entire 1931–2000 interval; however, data from 1951 to 1980 were available and were therefore used for this climatic parameter (NOAA, 1988). The average annual temperature for the 1931–2000 period was computed from the monthly average temperature normals which were themselves computed by averaging the monthly maximum and minimum normals (NOAA, 2002). The average annual precipitation was computed as the mean of 12 monthly normals. Freeze-free days were calculated as the median length of time between the last 0 °C temperature in spring and the first 0 °C temperature in autumn with a 90 % probability level for the 30-year period (NOAA, 1988). A climatic normal is defined as the arithmetic mean of a climatological element computed over consecutive decades (NOAA, 2002).

AFLP analysis

Genomic DNA was isolated from recently expanded leaves using a modified CTAB method (Doyle and Doyle, 1987). Freshly harvested leaves (200 mg) were homogenized in extraction buffer using a FastPrep^® System cell disrupter (Qbiogene, Inc., Carlsbad, CA, USA). The quality of the extracted DNA was estimated by measuring the 260 and 280 UV absorbance and the integrity was verified by electrophoresis on a 1·0 % agarose gel. Only samples with 260:280 ratios of 1·8–1·9 showing clear high molecular weight bands were used for AFLP analysis.

AFLP reactions were performed as described by Vos et al. (1995) with minor modifications optimized for capillary electrophoresis as previously described (Kim et al., 2004). Adapters were synthesized by Operon Technologies (Alameda, CA, USA), MseI and PstI primers were obtained from Gibco (Invitrogen Life Technologies, Baltimore, MD, USA) and phosphoramidite dye-linked EcoRI primers were synthesized by Proligo Primers and Probes (Boulder, CO, USA). All EcoRI primers were labelled with blue phosphoramidite dye (D-4 dye; Beckman-Coulter, Inc., Fullerton, CA, USA).

Preselective primer pairs with a single selective nucleotide extension of the AFLP adapter were used, whereas selective PCR primers utilized three nucleotides (Table 2). After selective amplification, 0·5 μL of the reaction products were mixed with 30 μL of sample loading solution (Beckman-Coulter, Inc., Fullerton, CA, USA) and 0·5 μL of fragment size standard was added to each sample (60–600 bp; Beckman-Coulter, Inc.). Samples were separated using capillary electrophoresis on an automated CEQ 8000 DNA fragment analysis/sequencer (Beckman-Coulter, Inc.) with running conditions as follows: denaturation at 90 °C for 120 s, injection for 30 s at 1000 V, separation at 4800 V for 60 min.

Table 2.

Oligonucleotide adapters and primers used for AFLP analysis of Echinacea angustifolia populations

Primers/adapters	Sequences
Adapters
EcoRI adapters	5′-CTCGTAGACTGCGTACC-3′
	3′-CTGACGCATGGTTAA-5′
MseI adapters	5′-GAC GATGAGTCCTGAG-3′
	3′-TACTCAGGACTCAT-5′
AFLP primers
EcoRI + 1	GACTGCGTACCAATTCA
MseI + 1	GATGAGTCCTGAGTAAC
EcoRI + 3	GACTGCGTACCAATTCACA
	GACTGCGTACCAATTCACT
	GACTGCGTACCAATTCAGG
MseI + 3	GATGAGTCCTGAGTAACAG
	GATGAGTCCTGAGTAACTG
	GATGAGTCCTGAGTAACTT
PstI + 3	GACTGCGTACATGCAGACT
	GACTGCGTACATGCAGAGG
	GACTGCGTACATGCAGACA
Selective primer combinations
EM-14	E-ACA/M-CAG
EM-15	E-AGG/M-CAG
EM-19	E-ACT/M-CTG
EM-20	E-AGG/M-CTG
EM-22	E-ACC/M-CTT
EM-25	E-AGG/M-CTT
PM-17	P-ACT/M-CTG
PM-22	P-AGG/M-CTT
PM-25	P-ACA/M-CTT

Data analysis

Fragment sizes were automatically calculated by CEQ 8000 software (ver. 4.2.0) using local Southern sizing algorithms. Each fragment was treated as a separate character and scored as either present (1) or absent (0) across all genotypes by CeqCluster fragment analysis software (Beckman-Coulter, Inc.). Inclusion or exclusion of fragments with automated fluorescent dye capillary electrophoresis systems was performed by adjusting threshold levels of signal heights and slopes. The CeqCluster software slope threshold (ST) algorithm specifies the minimum rate of signal increase on the leading edge of a given peak, while the relative peak height threshold (RPHT) specifies the minimum height (relative to the second highest peak) required before being included in the fragment list. Based on previous results a RPHT : ST of 5 : 10 was used. For each individual, the AFLP product was run in three separate capillaries, and a fragment was included only if its presence was detected in at least two of the three capillaries. Where discrepancies existed, the electropherograms were visually reviewed to reconcile ambiguities. Fragment sizes greater than 400 bp were less reproducible and were therefore omitted from the analysis.

For each pairwise comparison between individuals i and j, the 1/0 matrix was used to calculate the Dice estimate of genetic similarity [GS_D = 2a/(2a + b + c)] (equivalent to 1 – Nei and Li's genetic distance; Nei and Li, 1979), where a is the number of bands shared by i and j, b is the number of bands present in i and absent in j, and c is the number of bands present in j and absent in i for the data pooled over all primer combinations.

A genetic distance matrix (GEN), equivalent to the 1 – Dice estimate, was used to construct phenograms using the neighbour-joining (NJ) method (Saitou and Nei, 1987). Internal branch support was evaluated by bootstrap analysis (Felsenstein, 1985) of 1000 bootstrap replicate data sets with PAUP software (Beta version 10; Swofford, 2002). To visualize the dispersion of individual plants in relation to the first two principal axes of variation, principal co-ordinate analysis (Gower, 1966) was performed on the genetic similarity data (Dice estimates) matrix using the DCENTER and EIGEN modules of NTSYSpc (Rohlf, 2002).

Genetic diversity within and among populations was calculated using Arlequin (Schneider et al., 2000). The analysis of molecular variance computed by the Arlequin program generates Φ statistics, which are F-statistic analogs (Excoffier et al., 1992). Genetic variation was partitioned among groups (Φ_CT), among populations within groups (Φ_SC) and within populations Φ_ST). Group designations were based on the topology of the NJ tree. The topology-based grouping method clustered populations into four groups: Group 1, ND-004, ND-007 and SD-002; Group 2, NE-001, NE-002 and NE-003; Group 3, KS-CD and KS-HO; Group 4, OK-WD and OK-CO. It was assumed that each population was in Hardy–Weinberg equilibrium, with three randomly chosen individuals representing the population. This assumption appears to be well founded on the basis of bagging studies conducted on plants growing in a common nursery at Cal Poly Pomona. Following the bagging of 97 capitula (heads) from plants of each population, <1 % (38/16146) of the achenes produced embryos, indicating E. angustifolia is a more or less obligate out-crossing species.

To estimate the proportion of genetic differentiation between populations explained by geographical distance, the genetic (GEN) and geographic (GEO) distance dissimilarity matrices were subjected to a Mantel test of association with 1000 replications using the MXCOMP module of NTSYSpc (Rohlf, 2002). To estimate the proportion of genetic differentiation that could be associated with the climatic parameters annual mean temperature (AMT), freeze-free days (FFD) and annual mean precipitation (AMP), dissimilarity matrices were subjected to a Mantel test of association with 1000 permutations. Each matrix was constructed by subtracting the differences in values between populations. Likewise, the relationship between geographic distance and each climatic parameter was tested with a Mantel test, as described above. Because the climatic parameters and geographic distance are likely to follow a common spatial structure, the partial Mantel association test was employed to control for such spatial autocorrelation (MXCOMP module of NTSYSpc; Smouse et al., 1986; Legendre and Fortin, 1989; Roseman, 2004). A partial Mantel test is computed between matrices A and B while controlling for the effect of matrix C (Smouse et al., 1986; Legendre and Fortin, 1989). The computations are accomplished by computing an A′ matrix that contains the residuals of the linear regression values of matrix A over matrix C; computing a B′ matrix containing residual linear regression values of B over matrix C; computing the Mantel statistic between A′ and B′ (Smouse et al., 1986; Legendre and Fortin, 1989).

RESULTS

For the ten E. angustifolia populations and the outgroup E. sanguinea, 1290 fragments were scored (Table 3). Both EcoRI/MseI (EM) and PstI/MseI (PM) primer combinations were used to generate markers. There were approx. 2·3 times more fragments generated from the EM primer sets than the PM primers (Table 3). With the exception of PM25, all primer combinations generated fragments that were present in all populations. All EM and PM primer combinations generated fragments that were unique to a single population, but PM primer sets produced approx. 2·4 times more unique fragments.

Table 3.

Characteristics of fragment variation generated by nine primer combinations in the AFLP analysis of E. angustifolia (n = 30 individuals) and E. sanguinea (n = 3 individuals)

	E. angustifolia + E. sanguinea
											Total					Mean
Primer combinations	EM14	EM15	EM19	EM20	EM22	EM25	PM 17	PM22	PM25	EM	PM	Total	EM	PM
Total fragments	165	162	166	159	135	166	127	106	104	953	337	1290	159	112
Average no. of fragments per plant	69	65	65	70	64	75	34	35	26	408	95	503	68	32
No. of fragment shared by all populations	14	8	6	16	15	15	3	4	0	74	7	81	12	2
No. of fragments unique to one population	15	19	23	15	13	12	25	27	28	97	80	177	16	27
No. of fragments present in two or more populations	136	135	137	128	107	139	99	75	76	782	250	1032	130	83
Polymorphic fragments (%)	82·4	83·3	82·5	80·5	79·3	83·7	78·0	70·8	73·1	82	74	80	82	74

Fragments were scored within a range of 60–400 bp.

The average genetic distance was calculated for each population and a pairwise genetic distance matrix constructed (Table 4). Within each E. angustifolia population, the average genetic distance was 0·0272, whereas the average pairwise distance between populations was 0·0494, approx. 1·8 times the intrapopulation distance. The intrapopulation distance (located on the leading diagonal; Table 4) ranged from 0·0205 (population OK-CO) to 0·0363 (population NE-003). Excluding the outgroup, the greatest genetic distance between two populations was between OK-WD and NE-001 (0·0578), whereas the closest genetic distance observed was between OK-CO and OK-WD (0·0351). The average genetic distance between all E. angustifolia populations and the outgroup E. sanguinea, was 0·1033 (arithmetic average of the bottom row, excluding E. sanguinea values; Table 4), approximately twice the genetic distance observed among E. angustifolia populations.

Table 4.

Matrix of average genetic distance (Nei and Li, 1979) between 10 Echinacea angustifolia populations and the outgroup, E. sanguinea (n = 3 plants/population)

	ND-007	ND-004	SD-002	NE-001	NE-002	NE-003	KS-CD	KS-HO	OK-WD	OK-CO	E. sanguinea
ND-007	0·0267
ND-004	0·0371	0·0251
SD-002	0·0386	0·0424	0·0291
NE-001	0·0519	0·0487	0·0544	0·0271
NE-002	0·0509	0·0481	0·0521	0·0355	0·0263
NE-003	0·0550	0·0567	0·0532	0·0466	0·0434	0·0363
KS-CD	0·0563	0·0485	0·0557	0·0513	0·0466	0·0569	0·0271
KS-HO	0·0574	0·0548	0·0556	0·0547	0·0506	0·0566	0·0391	0·0268
OK-WD	0·0545	0·0575	0·0508	0·0578	0·0537	0·0556	0·0564	0·0546	0·0272
OK-CO	0·0555	0·0564	0·0518	0·0545	0·0508	0·0507	0·0520	0·0483	0·0351	0·0205
E. sanguinea	0·1002	0·1071	0·0986	0·1028	0·1034	0·1044	0·1000	0·0977	0·0963	0·0922	0·0360

The leading diagonal represents genetic distance within a population.

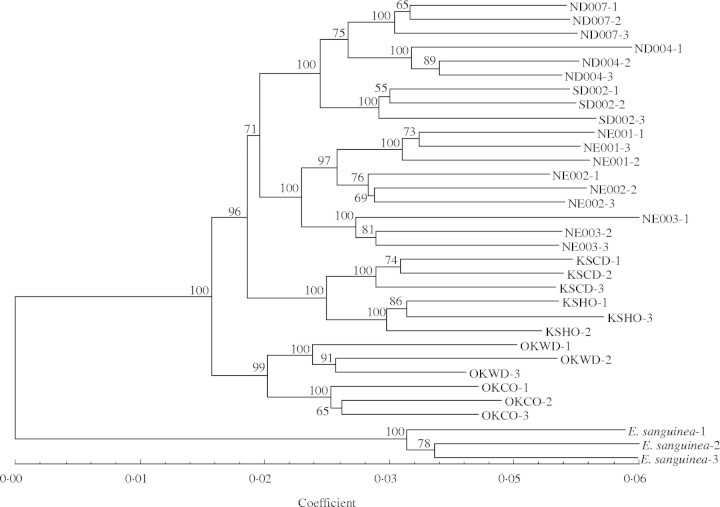
The NJ tree (Fig. 2) contained four major groups, with each node relatively well supported by high bootstrap values. The ND-004, ND-007 and SD-002 populations comprised a sister group to the NE populations, and the KS populations formed a group sister to these two clades (71 % bootstrap value). The OK populations formed a group sister to the other three groups combined.

Fig. 2.

Neighbour-joining phenogram of Echinacea angustifolia and the outgroup E. sanguinea using Nei and Li's (1979) genetic distance based on AFLP markers obtained from six EM and three PM primer combinations. Numbers shown at the node represent bootstrap values (as a percentage of 100 replicates).

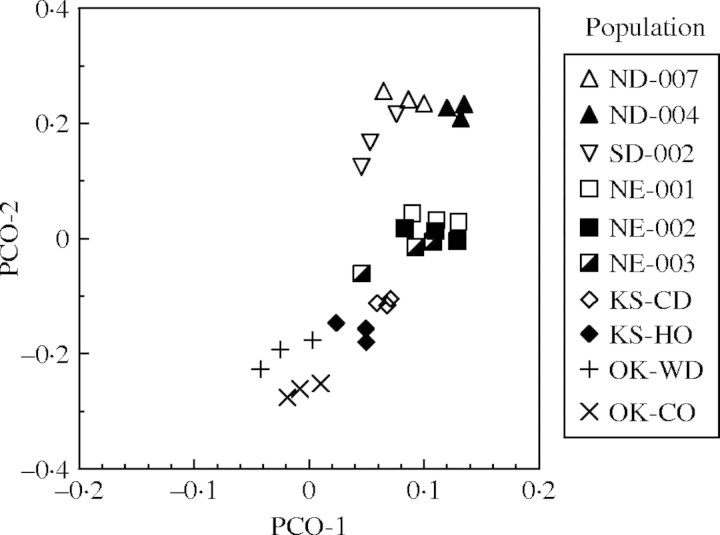
Genetic structure among the ten E. angustifolia populations was estimated by subjecting the binary fragment data to AMOVA using Arlequin. The greatest amount of variation was observed within a population (approx. 60 %), which is not unexpected in an obligate out-crossing species. The remaining variation (40 %) was equally distributed among groups and among populations within groups (Table 5). To identify genetic differentiation between pairs of populations, a matrix was constructed using Φ_ST probability values (Table 6). The southern-most populations, namely OK-WD, OK-CO and KS-HO, had the highest number of pairwise differences in the 10 × 10 matrix of Φ_ST values, suggesting a greater degree of differentiation in comparison to other populations (Table 6). With increasing geographic distance there was also a trend towards greater genetic distance as indicated by the increasing Φ_STvalues within columns (Table 6). A principal co-ordinate analysis constructed from the Dice similarity coefficient showed a pattern of population clustering consistent with the N–S origin of the populations (Figure 3). The first two co-ordinates explained approx. 24 % of the observed variation.

Table 5.

AMOVA estimates of genetic structure among 10 populations of E. angustifolia

		Observed partition
Variance	Φ statistics	Variance	% Total	P
Among groups	ΦCT = 0·197	30·0	19·9	<0·01
Among populations within groups	ΦSC = 0·242	29·6	19·4	<0·01
Within populations	ΦST = 0·392	92·6	60·8	<0·01

Each population was grouped according to the topology of the NJ tree (Fig. 2); P is the probability of having a more extreme variance component and F-statistic than the observed values by chance alone. Mantel permutations tested for significance where Φ_CT represents variation among groups; Φ_SC, variation among populations within groups; Φ_ST, variation within populations.

Group 1 = ND-004, ND-007 and SD-002; Group 2 = NE-001, NE-002 and NE-003; Group 3 = KS-CD and KS-HO; Group 4 = OK-LO and OK-WD.

Table 6.

Genetic differentiation between pairs of populations of Echinacea angustifolia expressed by Φ_ST (significance level = 0·05)

Population	ND-007	ND-004	SD-002	NE-001	NE-002	NE-003	KS-CD	KS-HO	OK-WD	OK-CO
ND-007
ND-004	0·2420
SD-002	0·2350	0·2912
NE-001	0·3944	0·3872	0·3882
NE-002	0·3527	0·3427*	0·3437	0·2058
NE-003	0·3503*	0·3727	0·3074	0·2626	0·1964
KS-CD	0·4268	0·3829*	0·3981	0·3831	0·3268	0·3602
KS-HO	0·4323	0·4199	0·3950	0·4229*	0·3601	0·3599	0·2384*
OK-WD	0·4079*	0·4317	0·3523*	0·4199*	0·3696*	0·3371	0·4155*	0·4045*
OK-CO	0·4661	0·4826	0·4215*	0·4541*	0·4083	0·3623*	0·4321	0·4018*	0·2449

Fig. 3.

Principal co-ordinates analysis among ten Echinacea angustifolia populations and the outgroup E. sanguinea. The first two dimensions accounted for approx. 24% of the variability.

A simple Mantel's association test between the climatic parameters annual mean temperature, freeze-free days and annual mean precipitation indicated significant correlations between genetic diversity and each climatic parameter (Table 7). A significant positive relationship was likewise detected between genetic and geographical distance (Table 7). However, a strong association was detected between the climatic parameters and geographic distance along the N–S cline supporting spatial autocorrelation among these variables. This would be expected as there is a N to S trend toward increasing precipitation, freeze-free days and, especially, annual mean temperature. Therefore, to separate the spatial autocorrelation and the interdependence of the climatic variables with geographic distance, a partial Mantel test was used. Once geographic distance (GEO) was controlled for, the correlation between the climatic parameters annual mean temperature and freeze-free days and genetic distance (GEN) was not significant (Table 7). The influence of geography on genetic structure was reduced from 0·54 to 0·35 when controlling for the influence of annual mean precipitation. The difference (0·1960) is attributed to the annual mean precipitation component of geographic distance. The partial Mantel test indicated a significant relationship between genetic and geographic distance when annual mean precipitation was controlled. Thus, the present data support the notion of an isolation-by-distance influence on gene flow, independent of the effects of annual mean precipitation. However, because of the strong spatial autocorrelation between geographic distances and annual mean temperature and freeze-free days, the combined effects of these parameters cannot be separated on genetic structure of the E. angustifolia populations used in these studies.

Table 7.

Simple and partial Mantel tests of association among genetic distances, geographic distance and climatic variables of Echinacea angustifolia populations

Matrix
A	B	C	R-statistic	P*
AMT	GEN		−0·5323	0·0010
AMP	GEN		−0·4296	0·0047
FFD	GEN		−0·4369	0·0010
GEO	GEN		0·5423	0·0010b
AMT	GEO		−0·9479	0·0010
AMP	GEO		−0·7022	0·0020
FFD	GEO		−0·8152	0·0001
AMT	GEN	GEO	−0·1302	0·2238
AMP	GEN	GEO	−0·1013	0·2767
FFD	GEN	GEO	−0·1991	0·1139
GEN	GEO	AMP	0·3463	0·0170†
GEN	GEO	AMT	0·0732	0·3047†
GEN	GEO	FFD	0·2056	0·0769†

The pattern of association in the dependent matrix A was compared with the predictor matrix B, while controlling for the effects of matrix C, using the partial Mantel test (Smouse et al., 1986).

Genetic distance was calculated using Nei and Li's (1979) estimate.

Climatic data are averaged values from the time period 1931–2000 with the exception of freeze-free days, which is from the time period 1951–1980.

AMT, annual mean temperature; AMP, annual mean precipitation; FFD, freeze-free days; GEN, genetic distance; GEO, geographic distance.

^*Probability that a random Z ≤ observed Z.

^†Probability that a random Z ≥ observed Z.

DISCUSSION

Genetic structure

The present data show a distinct genetic pattern among E. angustifolia populations that is consistent with a N–S spatial orientation. Most (60 %) of the observed genetic variation occurred among plants within populations, with the remaining 40 % equally distributed among groups and populations. Similar amounts of intra-population genetic variation have been reported in out-crossing species, including sunflower (approx. 70 %; Quagliaro et al., 2001) and the arctic-alpine plant Trollius europaeus (approx. 64 %; Despres et al., 2002). Using isozyme or RAPD data, Baskauf et al. (1994) and Kapteyn et al. (2002) estimated that approx. 93 % and 78 % of the variability observed among E. angustifolia populations occurred within populations. The higher amount of intra-population variability observed in their studies is most likely attributed to the different markers systems used among these studies, although sampling may also contribute to these differences. The genetic coefficient interval between each node branch of the four groups in the NJ tree is relatively short, indicating the divergence of these groups occurred within a short time period, but early in the radiation of these populations. Conversely, the branch lengths of each population within a major group are relatively long, again suggesting a relatively long period of isolation following radiation.

AFLP and population differentiation

The use of AFLP technology in phylogenetic and ecological studies is becoming increasingly popular because of its unique ability to detect polymorphisms within the genome without requiring prior sequencing information. Because AFLP faithfully generates many fragments per primer combination, differences can be detected between parental genotypes and their segregating progeny with as little as two primer combinations (E. Hayashi and D. W. Still, unpubl. res.). Results from AFLP data sets have been largely concordant with other molecular markers (Powell et al., 1996) or analyses based on gene sequencing (Spooner et al., 2005). Most, but not all, AFLP fragments of a specific size can be considered to represent the same loci (Cervera et al., 2001; Peters et al., 2001), although this likelihood apparently decreases with an increase in genetic distance between species (Mechanda et al., 2004). Large data sets can offset the assumption of orthology simply by increasing the number of independent loci sampled across a genome and establishing ‘correct’ phylogenetic relationships among species (Rokas et al., 2003). The AFLP method largely fulfills this requirement, and any non-orthologous fragments detected among populations should be overcome by the much larger number of orthologous fragments. The present data, consisting of 1290 fragments, produced an NJ tree with relatively high, to very high levels of support at most nodes (Fig. 2). The fact that each node is supported by relatively high bootstrap values, and each plant from a given population clustered to its proper population at the terminal node, supports the robustness of the AFLP technique in accurately identifying polymorphisms. Further, because the accuracy of reconstructing phenetic relationships increases with the number of independent loci assayed (Travis et al., 1996; Rokas et al., 2003) large numbers of individuals need not be genotyped for the purpose of establishing patterns of genetic differentiation among populations. Relatively little improvement in bootstrap values was found by adding four or more individuals when constructing the NJ tree. Others have demonstrated a sample size of four individuals of an out-crossing species was sufficient to assess the degree of differentiation between populations using SSR markers (Dyer and Sork, 2001).

EM/PM primers

The AFLP method was developed using AT-rich recognition sites EcoRI and MseI (EM) restriction enzymes, and it has been widely reported these markers are distributed throughout the genome (Vos et al., 1995; Jones et al., 1997; Hansen et al., 1999). However, clustering of EM markers was detected in linkage maps of A. thaliana recombinant inbred lines around centromeres (Alonso-Blanco et al., 1998). Clustering of EM-derived AFLP markers has also been reported in potato (van Eck et al., 1995), barley (Becker et al., 1995; Powell et al., 1997), soybean (Keim et al., 1997) and maize (Vuylsteke et al., 2000). Generally, low recombination rates are observed in regions surrounding centromeres (Schnable et al., 1998) which are reportedly AT-rich (Richards and Dawe, 1998) as are telomeric regions (Arabidopsis Genome Initiative, 2000). Clustering of EM markers may be a consequence of either low recombination in the heterochromatic region around the centromere (Hoopen et al., 1996) or it may simply be a result of increased restriction sites in this region. By combining experimentally derived AFLP data with in silico analyses using the sequence of Arabidopsis thaliana, Peters et al. (2001) provided convincing evidence that clustering is at least partly due to the increased frequency of AFLP restriction sites in this region, as opposed to a reduced recombination rate around the centromeric region. By replacing EM with Pst1/MseI (PM) restriction enzymes, the proportion of recognition sites occupied by GC nucleotides increases from 0·2 to 0·4, and thus GC-rich sites are targeted. The GC content of arabidopsis and rice is approx. 35 % and 44 %, respectively, with each chromosome in arabidopsis having approximately the same GC content (Arabidopsis Genome Initiative, 2000; Goff et al., 2002). In the present study, approx. 50 % fewer fragments generated by PM relative to EM primer sets were observed, perhaps indicating a lower GC content than that reported for rice or arabidopsis. Fewer PM-generated fragments have been reported in AFLP analyses in maize, tomato and yam, with reductions of 25, 15 and 64 %, respectively (Haanstra et al., 1999; Vuylsteke et al., 2000; Mignouna et al., 2002). No differences in fragment numbers were detected in cotton between PM and EM primer sets (Liu et al., 2001). In the present study, a greater percentage of PM-generated fragments was observed that were unique to a single population compared with EM primer sets. Relative levels of polymorphism appears to be species-specific as a 16 % decrease was reported for PM primer sets in tomato (Haanstra et al., 1999), whereas Liu et al. (2001) reported no differences in total fragments or polymorphisms between the EM and PM primer sets in Gossypium.

Given the preponderance of evidence that AT- and GC-rich regions are not randomly and evenly distributed throughout the genome, it is likely that assessments of population genetic differentiation based on AFLP may be affected by the choice of restriction enzymes. In the present study, the PM primer sets produced slightly different NJ topologies than the EM primer sets, and many nodes had bootstrap support values <50 % (data not shown). The topology of the NJ tree constructed from the EM data set did not change once the PM data were added, but bootstrap values did increase with the combined EM/PM dataset. These results are most likely due to the fact that, relative to PM primer sets, EM primer sets produced more fragments per primer combination and fewer polymorphisms. Because bootstrap procedures estimate the likelihood of a ‘correct’ topology by removing and replacing subsets of data from the dataset and reconstructing the tree, they will have a greater effect on the PM data than the EM data. An AFLP analysis based on combined EM/PM fragments should theoretically sample more areas of the genome than EM primer sets and therefore provide a more accurate assessment of genomic divergence among populations.

Isolation-by-distance vs. climatic selection pressures

Theoretically, the basic ingredients for genetic divergence are present within the distribution of E. angustifolia, namely a wide geographic distribution and contrasting climatic conditions. It was hypothesized that those populations at the margins of their geographic range would show the greatest amount of genetic divergence in a pairwise comparison. The NJ and principal co-ordinate analysis data of E. angustifolia exhibited clustering of each population consistent with their latitude of origin, indicating genetic divergence along their geographic distribution (Figs 2 and 3). A trend between geographic distance and increasing genetic distance (Φ_ST values) was observed (column 1, Table 6). These data show a significant isolation by distance effect and the three highest Φ_ST values were observed between ND-007 and OK-CO (0·4661), ND-004 and OK-CO (0·4826) and NE-001 and OK-CO (0·4541), thus supporting the hypothesis that the greatest divergence is at the geographic edges of the distribution of this species. The simple Mantel test also supports an isolation-by-distance model for genetic structure of these populations (GEN × GEO, R = 0·5423, P = 0·001). However, because of the strong association between climatic conditions and the N–S sampling transect, at this point it cannot be ruled out that the genetic structure is influenced by the selection pressure caused by climatic parameters. Once annual mean temperature or freeze-free days were controlled for, there was no support of an isolation-by-distance model (Table 7), although controlling for freeze-free days is marginally close to significance (GEN × GEO controlling for FFD, R = 0·2056, P = 0·0769). Controlling for the effects of annual mean precipitation resulted in support of an isolation-by-distance model, independent of the effects of precipitation.

The variation in climate along the 1500 km N–S cline suggests selection pressures among the populations could be different within the range of E. angustifolia populations sampled in this study, especially at the margins of the sampled distribution. The Mantel test of association indicated a strong support for the correlation of genetic structure with each climatic parameter (Table 7). Again, the partial Mantel test allowed the geographic influence to be removed and the relationship between genetic distance and climatic distance examined. Although climate-induced selection pressures may occur, the partial Mantel test shows that once the effect of geographic distance is removed (AMT × GEN controlling GEO) most of the correlation between each of the climatic parameters and genetic distance disappears. Neutral (AFLP) markers, by definition, are not expected to be affected by selection pressure. Instead, in a random mating population they may serve as marker alleles that can provide ways to identify regions of the genome that are associated with effects of adaptedness (Allard, 1996). Experimentally, sampling additional populations along an east–west transect would allow uncoupling of the strong N–S spatial autocorrelation with the climatic parameters. Molecular marker candidates for adaptation may alternatively be associated with quantitative trait loci which could only be identified by transplanting hybrid populations derived from parents taken from the extreme geographic distributions into two or more locations.

The genetic data represent standing genetic variation that is presented against a climatic time-frame of 70 years and, although it is not possible to project climatic conditions further than the 70-year time frame of our dataset, there is no indication that the climate of the Great Plains has changed substantially since the last ice age, roughly 10000 years ago. Genetic composition of plants has been shown to reflect climatic parameters in a relatively short time frame. Allard and coworkers (Allard, 1988; Perez de la Vega et al., 1994) have shown that within a 60-year period genetically distinct populations grown under similar environments often develop similar multi-locus allelic associations and, conversely, genetically identical material grown under different environments develops different multi-locus associations. Allelic frequencies may change within a few generations in a predominantly selfing plant, whereas in an obligate out-crossing species, such as E. angustifolia, discernible multi-locus associations would theoretically occur much more slowly. However, in either selfing or out-crossing species, a constant selection pressure must remain if the assemblages are to remain intact. Consequently, the genetic structure of a population, and assessments of divergence among populations might be more reflective of an ecological time scale rather than an evolutionary time scale. Only by resampling the same Echinacea populations over time can the potential magnitude of climatic effects on genetic diversity and allelic frequencies be evaluated. Our climatic data represent averaged events and the Mantel test statistic values indicate a strong spatial N–S association. Although the temperature–geographic autocorrelations could not be separated, it is possible that plant adaptation, and therefore a portion of the standing genetic variation, is a reflection of more extreme events such as prolonged drought or untimely freezing events, the likelihood of occurrence of which is not expected to exhibit spatial autocorrelation.

In conclusion, the present data show that populations of E. angustifolia exhibit genetic differentiation in concordance with a N–S spatial orientation. Isolation-by-distance restrictions in gene flow, independent of the influence of annual mean precipitation, appear to be the main factor for the genetic divergence observed among populations. Because directional selection is a primary force by which phenotypes (and presumably species) diverge (Rieseberg et al., 2002), the observed climatic gradient, wide geographic distribution and genetic diversity associated with the populations suggest that conditions are suitable for adaptation and divergence, especially at the margins of the distribution.