On the Factor Light in Plant Communities and its Importance for Matter Production

I. INTRODUCTION

There are two ways to investigate plant communities: the first is to study the distribution of individuals of a species in a given plant community. In this way, as Lundegårdh (1925, p. 5) criticised, we can only achieve the floristic description of a plant community according to Du Rietz (1921) and others, or the ‘formal sociology’ of Kylin (1926), without an ecological and material content. The other way is physiologically–ecologically based on the metabolism of the individuals or species that make up the community. The correct sociological relationships between individuals or species can only be explained materialistically in this way. Naturally, our scientific studies must take this ecological–sociological way.

The growth of an individual plant in a plant community, after its germination, is under the influence of macro- and micro-environmental factors, and it has to maintain its energy or carbohydrate economy under defined water, temperature and nutrient conditions. The individual itself always alters the micro-environment by its reaction to environmental factors (cf. Clements, 1916, p. 79), i.e. by its metabolism, and often just by its existence, such as by intercepting sunlight. The unit of social association is nothing else but the relationships between two individuals through their alteration of the micro-environment. These relationships are not only spatial, but also temporal; thus the succession of plant communities can be logically discussed on this basis.

The existence of a plant species in a community is sustained only by the normal growth and the vegetative and sexual reproduction of each individual belonging to the same species. The successive phenomena of germination, growth and reproduction of individuals or species should be the major concern of, as well as the key to, ecological plant sociology. According to Boysen Jensen (1932), we may call this chain of phenomena matter-production or -reproduction in the wider sense. Also, Braun-Blanquet (1951, p. 384) noted that the timing and process of germination, shoot growth, flowering, fruit and seed formation, and seed distribution are particularly important for community ecology. But we can only comprehensively understand these phenological phenomena on the basis of matter-production or -reproduction. Thus, matter-production or -reproduction is the most important and crucial factor for community ecology, or scientific sociology. At the focus of matter production is the photosynthesis by the green plant parts, as Boysen Jensen has explained in 1932. According to these considerations, the factor of light appears as the first of many different environmental factors for the ecological plant sociology of mesophytes.

In this study, the authors firstly demonstrate the productive structure of a plant community by the stratified-clipping method. Then, we will report on the light intensity in different plant communities, especially the distribution of brightness in herbosa [see Appendix for explanation of this term]. We then will, experimentally and theoretically, discuss the relationship between light extinction in a plant community and leaf quantity, exposition and distribution. The seasonal development of a plant community will be explained on the basis of productivity changes within the community. Finally, the authors will successfully calculate the productivity of the whole community indirectly on the basis of light-assimilation curves of a single leaf, the leaf quantity and the incident light intensity.

II. THE STRATIFIED-CLIPPING METHOD AND THE PRODUCTIVE STRUCTURE OF PLANT COMMUNITIES

The factor of light in plant communities has been previously studied by Wiesner (1907), Atkins and Stanbury (1932) and others, but their studies only yielded the observed light intensity and the names of the dominant species for a community. Geiger (1950) has compiled more detailed microclimatic measurements of the vertical distribution of brightness in a plant community, but also does not give a quantitative description of the examined community. It is therefore difficult to find a general law for the relationship between the factor light and plant cover. The orthodox method in plant sociology to analyse plant community structure with frequency, degree of cover or estimation methods, and even cover scores (cf. Braun-Blanquet 1951, p. 57 and 109), is qualitative and gives only a preliminary, subjective sketch of the community. Therefore, we have to quantitatively study the productive structure of a plant community with a new experimental method.

In a stand of a uniform plant formation, we measured first the vertical distribution of the relative light intensity using the Eder-Hecht grey wedge photometer. The distribution of brightness as determined by the structure of the community must generally be measured under an overcast sky, firstly because direct sunlight scatters in the community into numerous sunflecks, and secondly because direct sunlight in the open is too bright as a standard for measuring the relative light intensity in the shade of the plant community. This is very clear, as shown by Trapp (cited in Geiger, 1950, p. 305) with the determination of brightness distributions under clear and overcast skies. Therefore, we generally tried to determine brightness on overcast days (in this regard see also p. 558, and Boysen Jensen 1932, p. 42).

Following the measurement of the distribution of brightness, we analysed the productive structure of the particular plant community. We chose a plot size of 50 × 50 cm² for our herbosa. A larger plot size would be desirable, but this area was usually the largest that could be measured in a day by a few workers. Four 55-cm long sticks were placed on the ground to form a square with an exact inner area of 50 × 50 cm². We cut the plants within this square from the top in layers of 10-cm thickness, sometimes (depending on the height of the community) in layers of 5 or 20 cm (cf. also Gaird, 1945). The cut plant material was divided into species; moreover, it can be classified into two groups, namely photosynthetic and non-photosynthetic tissue, as already employed by V.H. Blackman (1919). As photosynthetic tissue, we only chose chlorophyll-rich leaf laminae (excluding the yellowed ones); the petioles were usually collected as non-photosynthetic tissue, together with stems, branches, stalks and sometimes roots. This is because only the leaf lamina can generally cater for the other tissues with its surplus assimilation (see Table 1), although according to Stålfelt (1935), the leaf sheath and the stem of oats can assimilate quite strongly. The chlorophyll content of petioles and green stems is, as can be seen in Table 1, only a fifth or less than that of laminae. The fresh weight of the sorted plant materials was measured immediately in the field with balances of the range 1 g, 2 g, 5 g, 10 g, 20 g and 100 g, sometimes 400 g or 1 kg; especially useful was a balance in the 20 g range, which used an envelope of hydrochlorinated rubber instead of a dish.

Table 1.

Chlorophyll content and CO₂ assimilation capacity of leaf laminae, petioles, and stems of some plants

Plants	Parts	Chlorophyll content (mg chlorophyll/g fresh weight)	Assimilation capacity (mg CO2/g/h)
Glycine max	Leaf lamina	2·52	8·61 (25 °C)
	Petiole	0·44	0·27 (25 °C)
Ipomoea batatas	Leaf lamina	1·39	6·20 (24 °C)
	Petiole	0·03	−0·07 (24 °C)
Brassica oleracea (young plant)	Leaf lamina	1·23	3·37 (26 °C)
	Petiole	0·14	0·02 (26 °C)
Oplismenus undulatifolius	Leaf lamina	2·50	–
	Leaf sheath	0·37	–
	Stem	0·12	–
Hordeum vulgare	Leaf lamina	2·88	–
	Leaf sheath	0·44	–
	Stem	0·21	–
Phragmites communis	Leaf lamina	2·57	–
	Leaf sheath	0·31	–
	Stem	0·36	–
Miscanthus sacchariflorus	Leaf lamina	5·70	–
	Leaf sheath	0·54	–
Helianthus tuberosus	Leaf lamina (green)	1·66	7·00 (26 °C)
	Leaf lamina (yellow)	0·47	1·70 (26 °C)
Zelkova serrata	Leaf lamina (green)	1·62	5·38 (25 °C)
	Leaf lamina (yellow)	0·57	1·55 (25 °C)

For some leaf samples, leaf area was measured (see Table 2), in order to calculate the total leaf area in m² per m² ground area, or leaf area index, from the fresh weight of leaves weighed in the field (see Table 3). The below-ground parts or the root system, especially in Phragmites or Miscanthus sacchariflorus communities, were too laborious to measure, so that we could not always make these measurements.

Table 2.

Surface development (leaf area per unit fresh weight) and water content of the leaves of some tested plants

Plants	Surface development (cm2/g fresh weight)	Water content in %
Phragmites communis	37–44	68
Miscanthus sacchariflorus	50	69
Miscanthus sinensis
Kirigamine montane meadow, 1600 m a.s.l.	49	73
near Urawa	47	–
Euphorbia adenochlora	78	75
Sanguisorba tenuifolia	64–80	68
Thalictrum simplex var. affine	72	68
Glycine soja
in the open	82	69
in the shade	131	81
Cissus japonica	45	87
Paederia chinensis	58	76
Hosta lancifolia
Tazima meadow	46	88
Kirigamine montane meadow	57	79
Sasa nipponica
in the open	74	56
in the shade	85	58

Table 3.

An example for the plant community cut into layers. Miscanthus sacchariflorus association in the Tazima meadow. On 3 June 1950. F* = Fresh weight of the photosynthetic tissue in g per 50 × 50 cm². C = fresh weight of the non-photosynthetic tissue in g per the same area. SN = stem number in 50 × 50 cm², b = fresh weight of flowers

		Miscanthus sacchariflorus					Other species					Thalictrum simplex var. affine
Height (cm)	Relative brightness (%)	F*	C	SN	F*	C	b	F*	C	b
260	100
240	–	1·3
220	78·8	11·8
200	61·0	21·6	0·6
180	42·2	31·0	5·7	1
160	39·3	22·2	27·4	4
140	26·7;33·1	12·0	49·0	7
120	31·5	15·5	64·0	8	0·3	0·5	0·3	0·3	0·5	0·3
100	31·7	11·4(0·2)	70·0	8	0·8	0·7	–	0·8	0·7	–
80	24·1	7·3(0·2)	76·0	8	2·1	1·9	1·2	2·1	1·9	1·2
60	18·2	9·0(2·4)	80·0	8	2·6	2·6	0·3	2·6	2·6	0·3
40	16·0	1·1(4·6)	82·0	8	5·6	6·0	0·2	4·0	4·0	0·2
20	13·2	–(1·2)	86·2	9	12·5(1·5)	18·3	–	2·7(0·9)	5·9	–
0	7·4;8·9	–	71·2	9	15·5(6·9)	41·9	0·3	–	6·0	–
		144·2(8·6)	612·1		39·4(8·4)	71·9	2·3	12·5(0·9)	21·6	2·0
		764·9					122·0					37·0

	Glycine soja			Galium aparine			Viola verecunda					Carex sp.	Trisetum bifidum
Height (cm)	F*	C	F*	C	F*	C	b	F*	F*	C
60
40	0·3	0·4	1·3	1·6 + b
20	0·8(0·1)	1·4	7·9(0·4)	9·5	0·7	1·0		0·3	0·1(0·1)	0·5
0	0·8(0·2)	1·8	6·0(2·8)	18·5	1·6(0·2)	6·3	0·3	0·2	0·5(0·1)	0·8
	1·9(0·3)	3·6	15·2(3·2)	29·6	2·3(0·2)	7·3	0·3	0·5	0·6(0·2)	1·3
	5·8			48·0			10·1					0·5	2·1

	Ophioglossum nipponicum			Paederia chinensis			Lapsana humilis			Trigonotis peduncularis			Equisetum arvense			Humulus japonicus
Height (cm)	F*	C	F*	C	F*	C	F*	C	F*	C	F*	C
20
0	3·7(2·9)	5·0	0·3	0·3	0·6(0·4)	1·0	0·5	0·1	1·2(0·3)	2·0	0·1	0·1
	3·7(2·9)	5·0	0·3	0·3	0·6(0·4)	1·0	0·5	0·1	1·2(0·3)	2·0	0·1	0·1
	11·6			0·6			2·0			0·6			3·5			0·2

The number of senesced stems of Euphorbia adenochlora was 62.

In Figs 1A and B, the height of the canopy is shown on the ordinate, and the fresh weight of photosynthetic tissue is shown to the left of the ordinate axis [i.e. weight = 0], while the non-photosynthetic tissue is shown to the right of the ordinate, stepwise with horizontal bars. Here, we correct for the thickness of the cut layers, so that the area of each bar represents the real weight of the tissue. The length of the bars for the non-photosynthetic tissues is half of that for the photosynthetic tissues, because the fresh weight of the former compared with the latter is too heavy to allow an orderly display, and because the area covered by stems, branches and petioles is less than that of laminae even at comparable fresh weights. The distribution of the relative light intensity is displayed on the same figure. From this figure, we can very easily view the exact productive structure of the plant community. For comparison, it is desirable to draw the original figure always at the same scale. In our experience with herbosa, it is useful to display 10 cm height as 1 cm on the ordinate, 10 g/10 cm/50 × 50 cm² of photosynthetic tissue as 1 cm on the abscissa and of non-photosynthetic tissue as 0·5 cm. The dominant species is shown with hatched bars, the subdominant with blank bars, and the accompanying and occasional species with black bars. The outer, dotted bars represent the senesced leaves of all species.

Fig. 1.

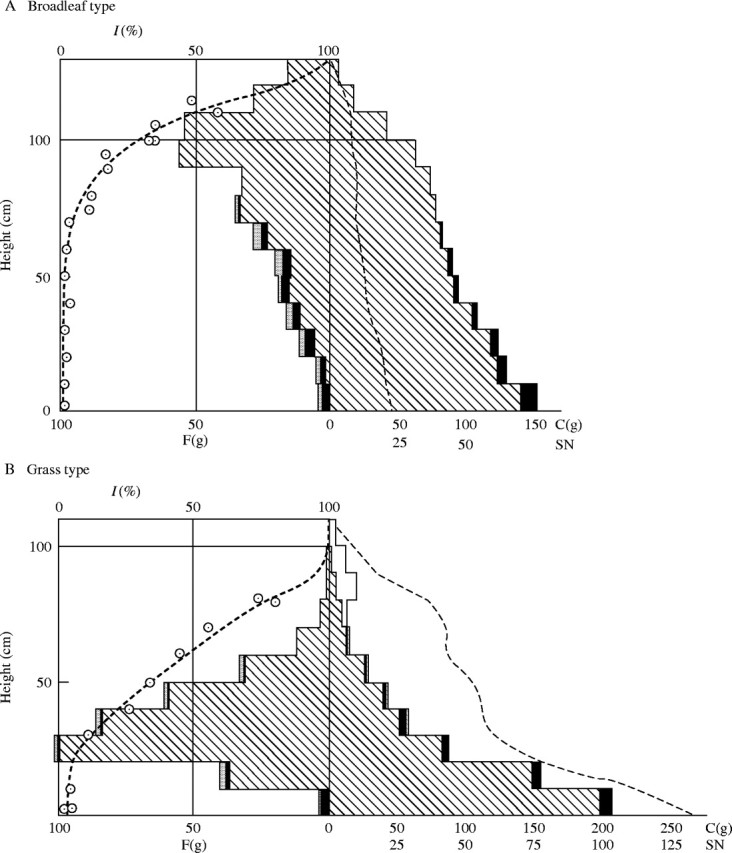
Productive structure of the plant community. The dashed thick line shows the relative light intensity. (A) Broad-leaf type: Chenopodium album var. centrorubrum-consociation. On 28 June 1949. (B) Grass type: Pennisetum japonicum-consociation (with fruits). On 28 Sept. 1949. F = Fresh weight of the photosynthetic tissue in g per 50 × 50 cm². C = fresh weight of the non-photosynthetic tissue in g per the same area. SN = stem number in 50 × 50 cm².

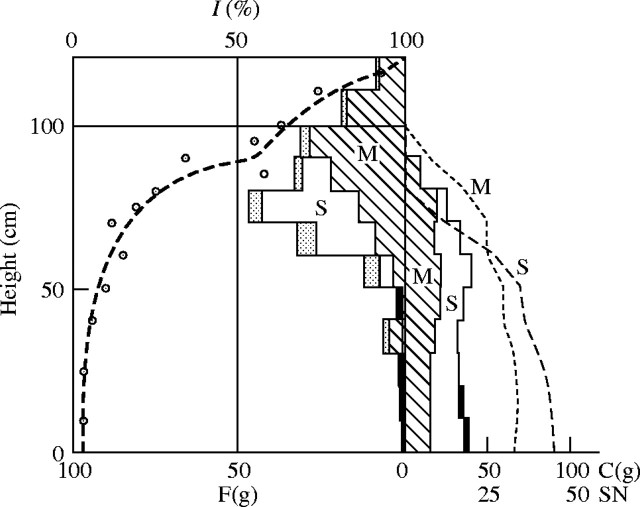
In most plant communities, the photosynthetic system is bulked in the upper layer, with the maximum of its distribution, and it decreases and tails off below this layer. For communities with horizontal leaves, or ‘broad-leaf type’, e.g. Chenopodium or Helianthus stands, the maximum at the top is more pronounced than that in communities with upright or inclined leaves, i.e. the ‘grass type’, such as in grass communities. The light intensity decreases faster in the former than in the latter. Especially in vine communities with a dense layering of leaves, the light decreases remarkably fast. When the development of the photosynthetic system in the upper layer of the plant community is weak, the light decreases slowly, and sometimes the relative light intensity below the upper synusia [see Appendix] remains 10 % or more of open daylight. In such cases, we can often see another layer of photosynthetic tissue in the lower synusia, which is, however, less developed than the upper synusia (see Fig. 9). The light intensity curve is then characterized by two connected arcs, a larger one in the upper layer, and a smaller one in the lower layer (see also Fig. 4). We will explain the cause of these phenomena when discussing the light conditions in plant communities.

Fig. 9.

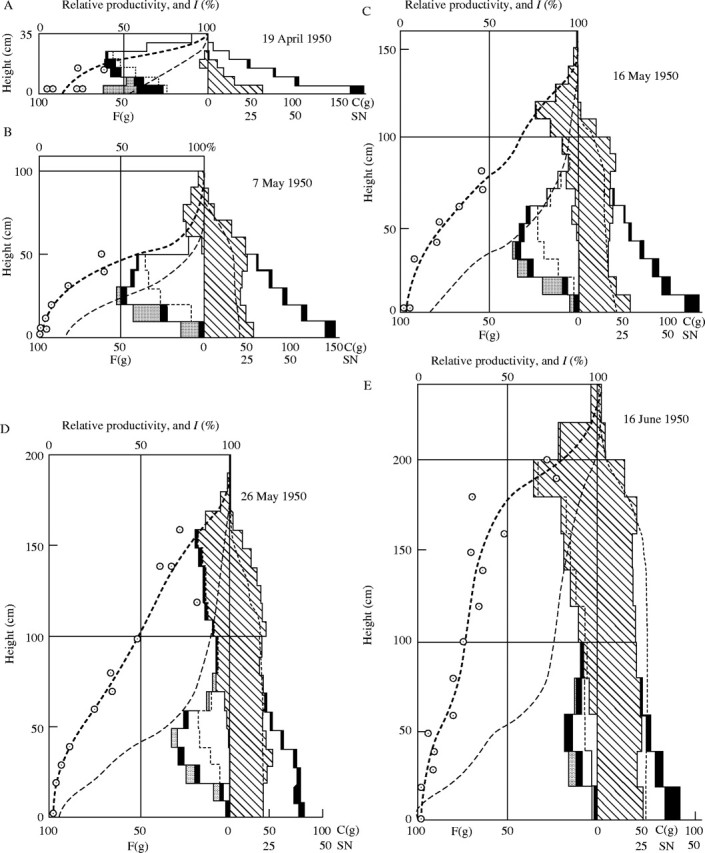
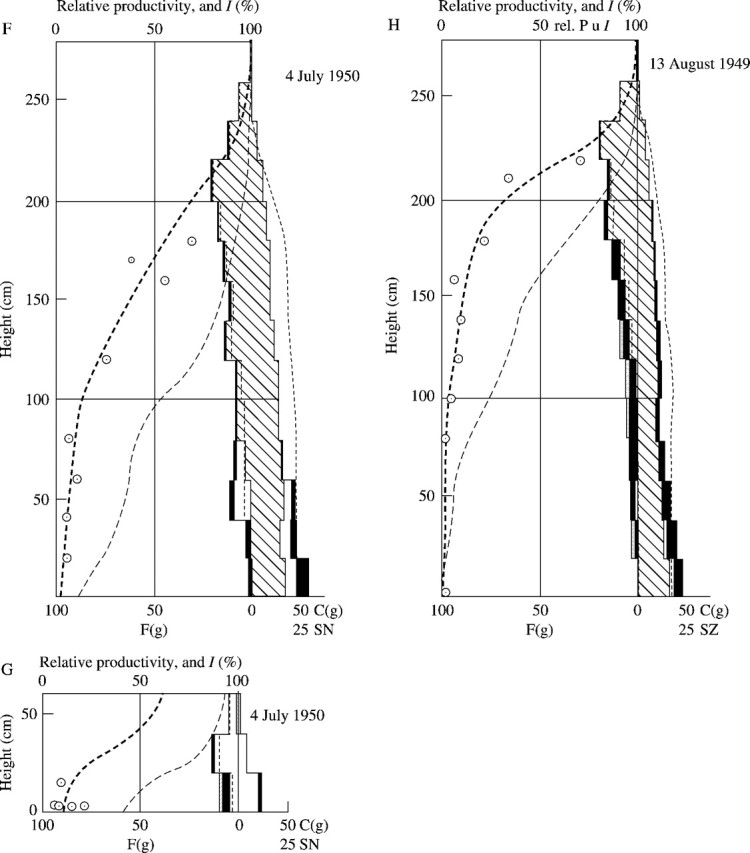
Seasonal development of the Phragmites (hatched) – Sanguisorba (blank) association (cf. the text and Tables 7–5). F = Fresh weight of the photosynthetic tissue in g per 50 × 50 cm². C = fresh weight of the non-photosynthetic tissue in g per the same area. SN = stem number in 50 × 50 cm².

Fig. 4.

Productive structure of a Miscanthus sinensis (grass type)–Sasa nipponica (broad-leaf type) association. On 14 Sept. 1949, in the Kirigamine montane meadow. F = Fresh weight of the photosynthetic tissue in g per 50 × 50 cm². C = fresh weight of the non-photosynthetic tissue in g per the same area. SN = stem number in 50 × 50 cm².

The weight of the non-photosynthetic tissue often increases in the upper layer, with its maximum usually just below the maximum of the leaf weight. At the lower end of this maximum, the portion of this tissue decreases, but closer to the ground, the stems, and often also the culms of the grasses, increase (as can easily be seen in trees), and produce a second maximum.

III. THE FACTOR LIGHT IN PLANT COMMUNITIES

A. Observed light intensity in plant communities, especially in herbosa

Because the light intensity on the forest floor can almost always strongly affect the regeneration of the forest, it has been measured by several authors in the past, as collated in the book by Geiger (1950, p. 316). The minimum relative brightness at the soil surface in forests in leaf has been reported to be between 2 % (in stands of fir or beech) and 20 % (in stands of pine or birch). According to our measurements with a photocell, or with the Eder-Hecht grey-wedge photometer, brightness values in Japanese forests were similar to those cited above (see Table 4). The darkest values were measured in a bamboo thicket of Phyllostachys nigra var. henonis, which grows almost naturally at the edge of a lowland meadow in the area of the Tone and the Arakawa rivers. In summer, we have often found several somewhat etiolated shoots, e.g. of Rosa multiflora, Cissus japonica etc., under 0·2–0·5 % brightness in this thicket.

Table 4.

Relative brightness in some forests of Japan

Plant communities	Relative brightness in %
Pinus densiflora forest	28–37
Larix leptolepis forest	13–25
Under field layer of Sasa nipponica	1·5–2
Castanea crenata forest	13–22
Quercus crispula forest	7–14
Under field layer	1·4–4·6
Fagus crenata—Quercus crispula forest	8–20
Under field layer of Sasa oseana	0·5–2·5
Chamaecyparis obtusa forest	5–15
Cryptomeria japonica forest	5–8
Shiia cuspidata forest (Laurisilvae)	2·5–5
Abies firma forest	1·7–8
Phyllostachys nigra var. Henonis thicket
In summer	0·2–0·5
In winter	2·5–4

Until today, in contrast to lignosa, there are no comprehensive systematical studies regarding the brightness in herbosa. However, its importance, e.g. for the succession in plant communities, is no less than in lignosa. Especially in Japan, grassland vegetation develops as Susono-meadow, or montane meadow, and can remain for many years as sub-climax or dis-climax vegetation. As has been pointed out by Ångstrom (1925) and Sauberer (1937, both cited in Geiger, 1950, p. 279), the brightness in the lower layers of the canopy is relatively low. The relative brightness at the soil surface of most of the herbosa observed by us is only 2–3 % (see Table 5). Thus, the darkness in herbosa can often exceed that in lignosa. This indicates that the leaf quantity of herbosa should not be less than, and in some cases even exceeds, that of forest vegetation. The leaf area index (the leaf area in m² per m² ground area) in our herbosa was generally 4–7 or higher, as shown in Table 5, and these numbers are almost the same as those previously measured in European forest vegetation (cf. Büsgen and Münch, 1927, p. 198, and Moller, 1947, p. 396). This fact is evident from the whole-sky photographs in Fig. 2. As dry matter production principally depends on leaf quantity, the productivity of herbosa might be similar to, or even more vigorous than that of lignosa. The lack of light in lushly growing herbosa may be the primary factor that determines the direction of succession, or a number of seedlings of tree species growing in herbosa must perish in the fight against herbs and grasses in the deep shade of these plants. In communities with horizontal leaves, the brightness is even less than with grasses with upright leaves (cf. Sauberer, 1937, cited in Geiger, 1950). We will elaborate on this fact below.

Table 5.

The extinction coefficient (K) and minimum light intensity (I_min) of some investigated plant communities. The plants on which the extinction coefficient was mainly determined are marked by *. F^* = fresh weight of the photosynthetic tissue in g per 50 × 50 cm², C = fresh weight of the non-photosynthetic tissue in g per the same area. F = leaf area index

Dominant species	Date	Height (m)	F*	C	F	K	Imin
1. In the Kirigamine montane meadow, 1600 m
Sasa nipponica	14. Sept. 1949	1·1	166	522	4·9	0·78	0·5
	29. Aug. 1951	0·75	123	347	3·6	0·78	0·6
Miscanthus sinensis	6. July 1949	1·3	573	990	11·1	0·31	1·3
Miscanthus sinensis–Sanguisorba officinalis	5. Aug. 1949	0·70	186	146	4·1	0·70	7·8
Miscanthus sinensis–Artemisia vulgaris	5. Aug. 1949	1·3	228	380	4·5	0·69	0·4
Sasa nipponica–Pteridium aquilinum	15. Sept. 1949	0·70	162	338	3·1	0·90	1·8
2. In the Tazima meadow
Euphorbia adenochlora	5. May 1951	0·40	130	188	4·0	0·92	0·8
Thalictrum simplex var. affine	13. April 1950	0·35	90	150	2·6	0·92	5·6
Sanguisorba tenuifolia	19. April 1950	0·35	155	227	4·0	0·52	15·0
Miscanthus sacchariflorus*–Euphorbia adenochlora	3. June 1952	2·6	184	684	3·9	0·60	7·4
Miscanthus sacchariflorus*–Thalictrum simplex var. affine	12. May 1950	1·5	248	746	5·4	0·55	2·6
Miscanthus sacchariflorus*–Sanguisorba tenuifolia	3. June 1949	1·8	183	404	4·3	0·7	1·4
Miscanthus sacchariflorus–Humulus japonicus	18. June 1949	2·0	153	522	3·6	M0·5 H1·2	0·1
Miscanthus sacchariflorus*–Glycine Soja	15. Aug. 1949	2·4	240	974	5·7	0·45	1·4
Miscanthus sacchariflorus*–Carex Royleana	22. Aug. 1949	2·5	201	598	4·1	0·28	1·2
Miscanthus sacchariflorus*–Polygonum Blumei	26. Aug. 1949	2·6	178	485	4·1	0·37	1·7
Miscanthus sacchariflorus–Phragmites communis	4. July 1949	2·4	284	954	5·6	0·45	1·4
Miscanthus sacchariflorus	28. May 1949	1·4	388	994	8·1	0·30	6·3
	15. June 1949	2·0	284	850	5·9	0·37	2·0
	17. June 1949	2·0	236	685	5·7	0·37	0·6
	2. July 1949	2·4	332	1057	7·0	0·34	1·0
	14. Aug. 1949	2·8	236	834	4·7	0·33	0·7
	8. Oct. 1949	3·0	179	1004	3·7	0·2	5·7
	4. Nov. 1949	3·0	54	1099	1·1	0·31	15·6
Phragmites communis*–Thalictrum simplex var. affine	13. May 1950	2·0	238	1335	4·8	0·45	1·8
Phragmites communis*–Sanguisorba tenuifolia	29. June 1949	2·4	259	702	5·1	0·55	0·8
Phragmites communis*–Saururus Loureiri	27. June 1949	3·0	330	823	4·7	0·35	0·4
3. Some communities in the vicinity of Tokyo
Miscanthus sinensis	5. July 1949	1·8	442	773	8·3	0·47	1·8
Heliathus tuberosus	26. May 1949	0·80	208	533	4·8	0·89	1·7
Polygonum Reynoutria	14. June 1949	1·8	335	794	6·1	0·75	0·4
Sasa paniculata	14. July 1949	1·6	156	493	5·2	0·4	6·1
Cissus japonica–Sasa paniculata	27. Sept. 1949	0·80	210	637	4·2	0·6	0·3
Pennisetum japonicum	9. Oct. 1949	0·70	298	843	6·5	0·5	2·9
Erigeron annuus	7. May 1949	0·50	187	472	4·2	0·68	5·5
Erigeron philadelphicus	7. May 1949	0·45	117	353	2·2	0·89	23·6
Arundinella hirta	14. Oct. 1949	1·3	127	304	2·5	0·55	12·8
Petasites japonicus	28. April 1950	0·45	154	268	3·1	1·4	0·8
Taxus cuspidata var. umbraculifera (scrub)	13. June 1949	1·15	599	–	4·6	0·77	1·5
Trichosanthes japonica (light intensity above 47 %)	30. Sept. 1949	1·3	82	521	1·3	1·9	5·4
Hydrangea macrophylla var. Otaksa–Trichosanthes japonica (light intensity above 44 %)	30. Sept. 1949	1·0	90	340	1·9	1·4	2·1

Fig. 2.

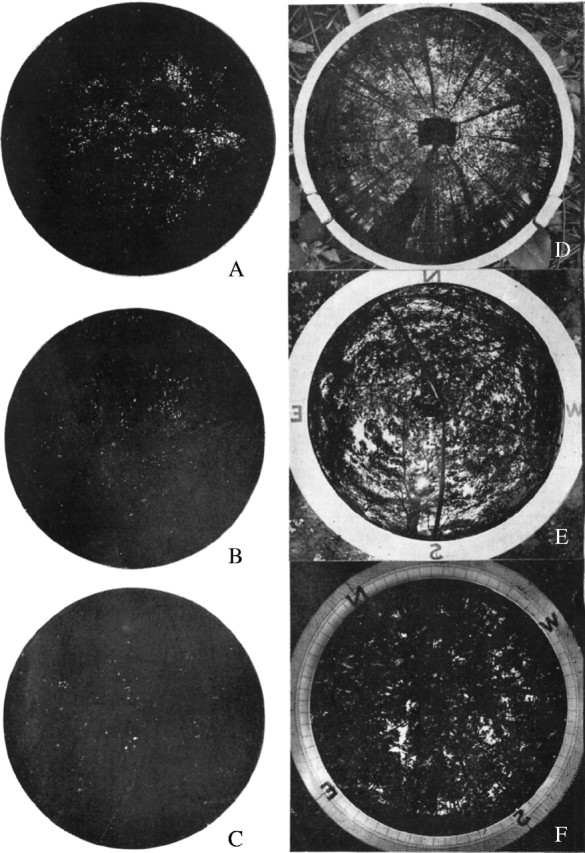
Whole-sky photograms of herbosa (A–C) and lignosa (D–F). (A) Phragmites communis, I_min = 4·5 %. (B) Miscanthus sacchariflorus, I_min = 1·2 %. (C) Helianthus tuberosus, I_min = 0·7 %. (D) Pinus densiflora, I_min = 28 %. (E) Castanea crenata, I_min = 13 %. (F) Cryptomeria japonica, I_min = 5 %.

B. Dependence of light extinction on leaf area index

The brightness in a plant community is chiefly reduced through the repeated interception of light by leaves. To demonstrate how light reduction depends on the leaf quantity in the community, in practical terms on the leaf area index, we used a graphical expression as shown in Figs 3A and B. On the abscissa we plot the leaf area index from the top down to the height in question, and on the ordinate the logarithm of the light intensity as percentage of the incoming light under an overcast sky. The figure shows an almost linear relationship between the two values, so that we can formulate this relationship following the common form of the Beer–Lambert equation of light extinction, i.e.

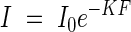where I is the shaded light intensity under the leaf area index F, I₀ is the original incoming light intensity, and K is the extinction coefficient.

Fig. 3.

Light intensity–leaf area index curves of some plant communities. (A) Upper panel. The communities of the Kirigamine montane meadow. 1, Sasa nipponica–Pteridium aquilinum (15 Sept. 1949); 2, Sasa nipponica (29 Aug. 1949); 3, the same (14 Sept. 1949); 4, The same (7 Aug. 1949); 5, Miscanthus sinensis (15 Sept. 1949); 6, the same (6 July 1949). (B) Lower Panel. The communities of the Tazima meadow and in the vicinity of Tokyo. 1, Trichosanthes japonica (30 Sept. 1949, light intensity above = 47 %); 2, Petasites japonicus (28 April 1950); 3, Chenopodium album var. centrorubrum (28 June 1949); 4, Euphorbia adenochlora (5 May 1951, in the Tazima meadow); 5, Helianthus tuberosus (26 May 1949); 6, Taxus cuspidata var. umbraculifera (13 June 1949); 7, Miscanthus sacchariflorus–Euphorbia adenochlora (30 April 1950, in the Tazima meadow); 8, Phragmites communis–Sanguisorba tenuifolia (3 June 1949, in the Tazima meadow); 9, Miscanthus sacchariflorus (15 June 1949, in the Tazima meadow); 10, Phragmites communis–Thalictrum simplex var. affine (27 July 1949, in the Tazima meadow).

From the experimental data in Table 5 and Fig. 3 we can see that the extinction coefficients K of the investigated plant communities largely fall between 0·3–1·5, and that the K-values of the majority of communities fall into two groups. The smaller values of approx. 0·3–0·5 occur almost always in grass formations, the larger ones above approx. 0·7 occur in herb or shrub formations. In other words, the light extinction by a given leaf layer is somewhat faster with broad-leaf types than with grass-types (see also Boysen Jensen, 1932, p. 54). This phenomenon can be clearly seen in communities with two layers, of which the upper one belongs to the grass-type, and the lower one to the broad-leaf type, e.g. the Miscanthus sacchariflorus–Euphorbia community, or the Phragmites–Sanguisorba community. Here, the log I/I₀–leaf area index curve appears as two lines with different slopes (see Fig. 3B, lines 7 and 8). This is also evident from the Miscanthus sinensis–Sasa community (Fig. 4). These two plants form a uniform community, but the light intensity decreases relatively more slowly in the upper Miscanthus layer (grass type) than in the lower Sasa-layer (broad-leaf type). In communities such as vines, where leaves are especially dense, or in communities with exceptionally large leaf areas, e.g. Petasites stands, the extinction coefficient is generally markedly greater than 1. These phenomena can only be generally understood after further theoretical considerations about light extinction, as this depends on the distribution and the angle of leaves.

C. Theoretical considerations on the extinction coefficients of plant communities

As mentioned above, we can divide the plant communities according to the value of the extinction coefficient into broad-leaf types and grass-types. This phenomenon appears to be primarily based on the angle of the leaf. For the broad-leaf type, the leaves are mostly horizontally positioned, but for the grass type they are inclined. For this reason, we would propose grouping the plant communities with regard to their leaf position into two types, those with horizontal leaves and those with inclined leaves. A typical example for the horizontal orientation can be seen in the leaf mosaic in the shade of a forest. Grass vegetation is a good example for inclined leaf orientation. In the upper crown layer of angiosperm trees, especially in the tropics, there are also inclined leaves.

1. Considerations of horizontal leaves. The extinction of light by horizontally positioned leaves will be discussed theoretically using a model of leaf distribution.

In a statistically uniform, ideal plant community we can consider a vertical, cylindrical unit space, which has the basal area, S. In this space, the centre of a leaf area, s, falls freely onto a horizontal plane, but is restricted within this unit space. Thus, in horizontal projection, the centres of the leaves belonging to a unit space are randomly distributed. The number of leaves in a unit space is n, and the leaves are vertically distributed as in most real plant communities in a pattern that has been demonstrated with the stratified-clipping method (see Fig. 1). However, the light extinction can be theoretically independent of the vertical leaf distribution, if the homogeneity of the community statistically holds strictly in the horizontal direction. The assemblage of such unit spaces makes up a plant community. Here, we neglect, for the time being, the stems, petioles, etc. for simplification, because their role in light extinction is relatively small compared with the leaf area. This model of a leaf community can include the mosaic-like distribution of leaves, because the leaf distribution is strictly restricted within a given unit space, and the unit space for the leaf mosaic can be chosen to be sufficiently small.

The light intensity in this ideal leaf community may be easily determined as follows: when a parallel bundle of light beams falls onto the community at an angle θ, then the projection of a leaf area s onto the ground equals s. The first leaf area shades the unit space by the ratio of s/S, i.e. the beams reaching the soil surface are [1 − (s/S)]. If S compared with s is large enough, then the leaf area distribution in a unit space that is oblique to the incoming light is statistically equal to that in a vertical unit space. If we add another leaf area s to the same unit space, then the ratio of illuminated ground area statistically becomes [1 − (s/S)]². In a unit space, there are n horizontal leaf areas distributed randomly, and the probability p for a light beam to reach the ground is shown by the following equation:

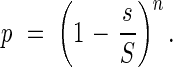This equation should hold for any chosen light angle θ. However, if S is very close to s, or θ is close to π/2, i.e. the beam comes in at very low angle, the probability p becomes almost 1, but is indefinite.

Diffuse light is nothing else but an assemblage of parallel beams from all directions, and the relationship between the light intensity I within a plant community to the incoming light intensity I₀ can be shown with this probability. The average ratio of light penetration must be identical with p. If the ratio of the incoming light from the direction of θ is ϕ(θ), then the brightness I at the horizon in the community (assuming equal sky brightness in all directions) is described by the equation

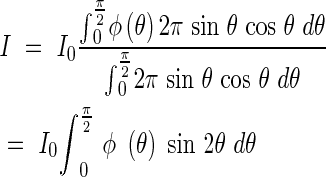For the assumed ideal community, as elaborated above, it applies that

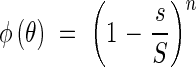so that

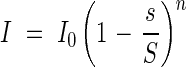This relationship holds at any position in the community, e.g. the light falling onto the nth leaf from the top:

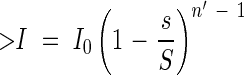with n′ < n.

Equation 2 can be transformed exponentially,

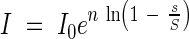This equation corresponds with the already shown equation

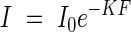The leaf area index is F = ns/S; then the extinction coefficient in the plant community may be determined according to the equation

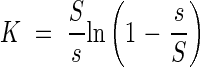The observation in real plant communities that the extinction coefficient in a particular community is almost constant, leads to the conclusion that s/S also appears to be nearly constant for a given community. This may indicate that our ideal leaf community may be very useful in explaining the brightness in real plant communities.

The more closely the ratio s/S approaches 1, the faster the light intensity decreases through the same leaf area layers, and the larger the extinction coefficient K becomes. But, the closer the ratio s/S approaches zero, in other words, the larger S becomes, the weaker is the reduction of light. At the limit, i.e. s/S ≈ 0 or S → ∞, the light in the community attenuates according to the equation

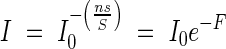That is, the extinction coefficient K equals 1, or the light extinction needs larger leaf area layers (in the horizontal position). Of course, in nature, there is no completely randomized leaf distribution. However, for example, s/S = 1/10, K is already 1·054; in other words, if the free area S is only 10 times the size of the individual leaf area s, it is sufficiently large for the extinction coefficient to decrease almost to 1. After this theoretical consideration we can understand that in most observed plant communities with horizontal broad-leaves the extinction coefficient was nearly 1. The leaves of most plants are always slightly inclined or folded, and thus the observed extinction coefficient of some plant communities of the foliage-type is somewhat smaller than the theoretical value of 1 (see below).

The natural leaf lets a part of the incoming light pass through it, and thus s and F need to be replaced with (1 − m)s and (1 − m)F, respectively, where m means the light transmittance of a leaf, and the light will be reduced by m² through double leaves. However, with light measurements using the Eder-Hecht photometer, the photographic paper shows very low sensitivity to the transmitted light; e.g., the transmittance for Petasites japonicus was 0·86–1·12 %, and for Helianthus tuberosus 0·43 %.

2. Considerations of inclined leaves. The light extinction in plant communities with inclined leaves should generally be identical to those with horizontal leaves, but the projection of the leaf area is more difficult to determine. Hence, we must first determine the mean projected area 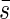for the theoretical treatment of light extinction.

To make this discussion easier, we assume the leaf area to be a rectangle s, of which two sides are positioned horizontally, and which is inclined against the horizon at an angle α. We rotate the rectangle around a vertical axis in a parallel light bundle with an incident angle θ. The shadow of the rectangle projected onto a horizontal plane can then be seen in all possible positions. We lay a co-ordinate cross onto the horizontal plane, which is centred on the rotation axis, and with one of the horizontal axes vertical to the incoming light. The space is thus divided into four quadrants I, II, III and IV. As the rectangle turns in the quadrants I, II, III and IV, the projected shadow falls as follows:

in the quadrants I and II,

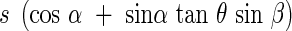in the quadrants III and IV,

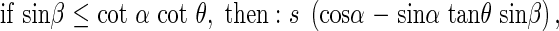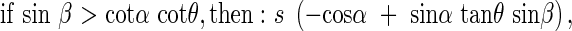where β is the angle between the horizontal axis of the co-ordinate cross and the projection of the angled side of the rectangle onto the horizontal plane. Any area can be a sum of many small rectangles, thus these relationships hold for a leaf of any given form. In natural plant communities it is very likely that for a given leaf there is another leaf in the opposite direction, or at the angle π to the first leaf. These opposing leaves belong to the opposing quadrants I and III, respectively, or II and IV, respectively, and are designated by the angle β. The average s′ of the projected area of two opposing leaves in quadrants I and II is,

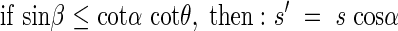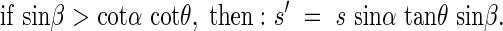With quadrants II and IV it is the same as with quadrants I and III.

The mean projected area 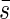of the leaf area can be estimated with s′ after the following equation by varying β from zero to π/2.

That is, if 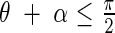then

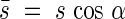if 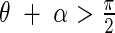then

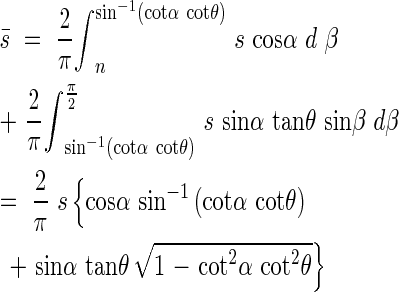With the average projected area 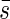we can discuss the relationships of incoming light into the plant community in the same fashion as with horizontal leaves. Again we have the equation

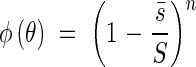This relationship should show that, generally, the total area of sunflecks in the plant community is on the whole proportional to the relative light intensity. For this reason, if the light with sunflecks was to be intercepted by movement of the leaves or the measuring instrument, the relative light intensity on clear days is almost the same as under overcast sky. The results in Fig. 5. confirm this.

Fig. 5.

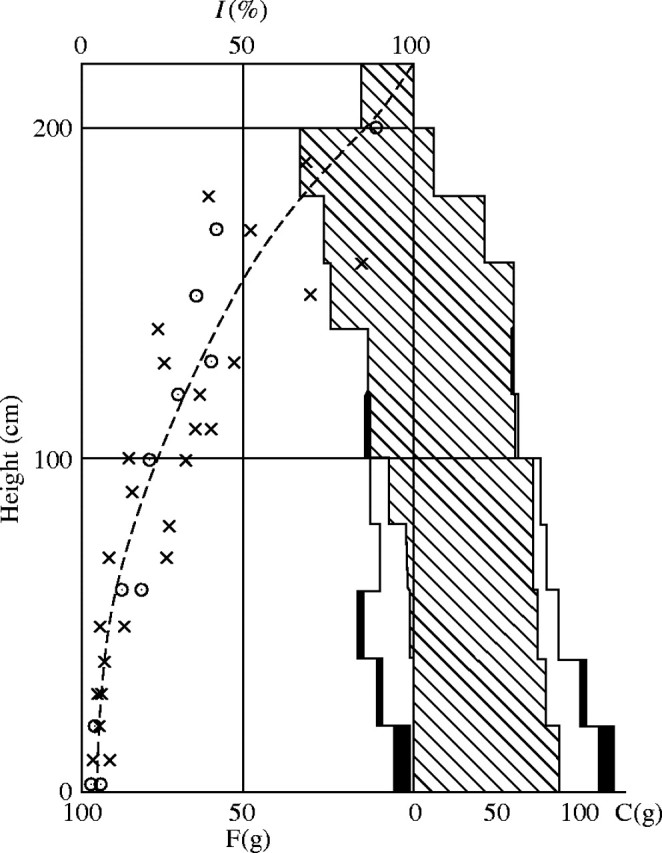
The relative brightness in a Phragmites–Thalictrum association under a clear sky (circles) and under an overcast sky (crosses). On 30 May 1949, in the Tazima meadow. F = Fresh weight of the photosynthetic tissue in g per 50 × 50 cm². C = fresh weight of the non-photosynthetic tissue in g per the same area.

With inclined leaves, there is no mosaic-like distribution of leaves, so that the condition of s/S ≈ 0 generally holds. Thus the above equation can be transformed as follows

From the equations 1, 6 and 8, we can obtain an equation for the light extinction in plant communities with angled leaves, i.e.

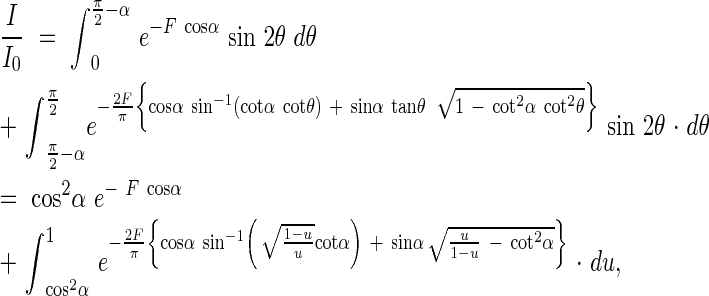where u = sin²θ.

The equation 9 is displayed in Fig. 6 with approximate values calculated for angles of inclination α of 30°, 60° and 90°. It is evident from this figure that with increasing α (leaf angle) the light extinction in the leaf community decreases. The curvature of the function of log(I/I₀) over leaf area index is slightly concave, but the curve can be replaced by straight lines in a first approximation. Here, the extinction coefficient K decreases from 1 to 0·44 with increasing leaf angle from 0° to 90° (see Fig. 7).

Fig. 6.

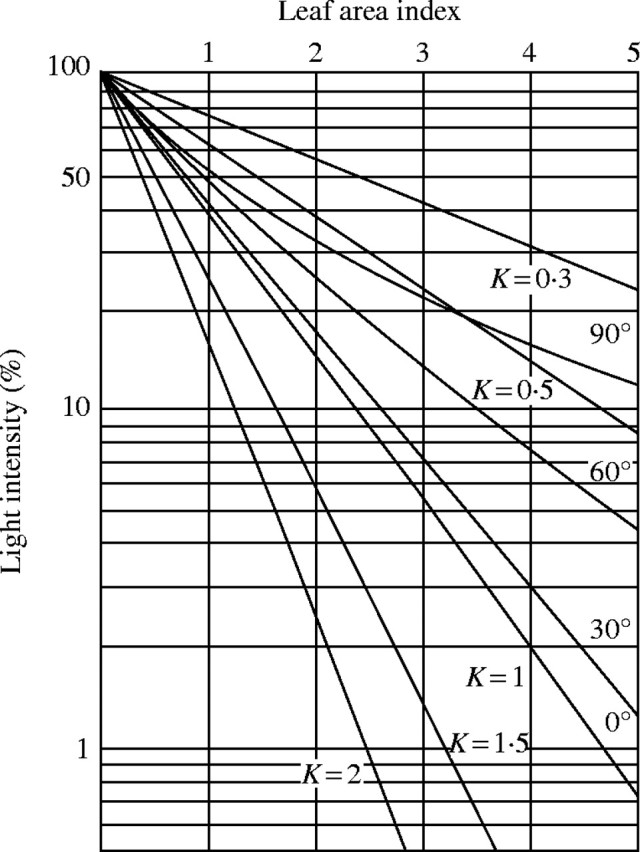
Theoretical light intensity–leaf area index curve at different leaf angles.

Fig. 7.

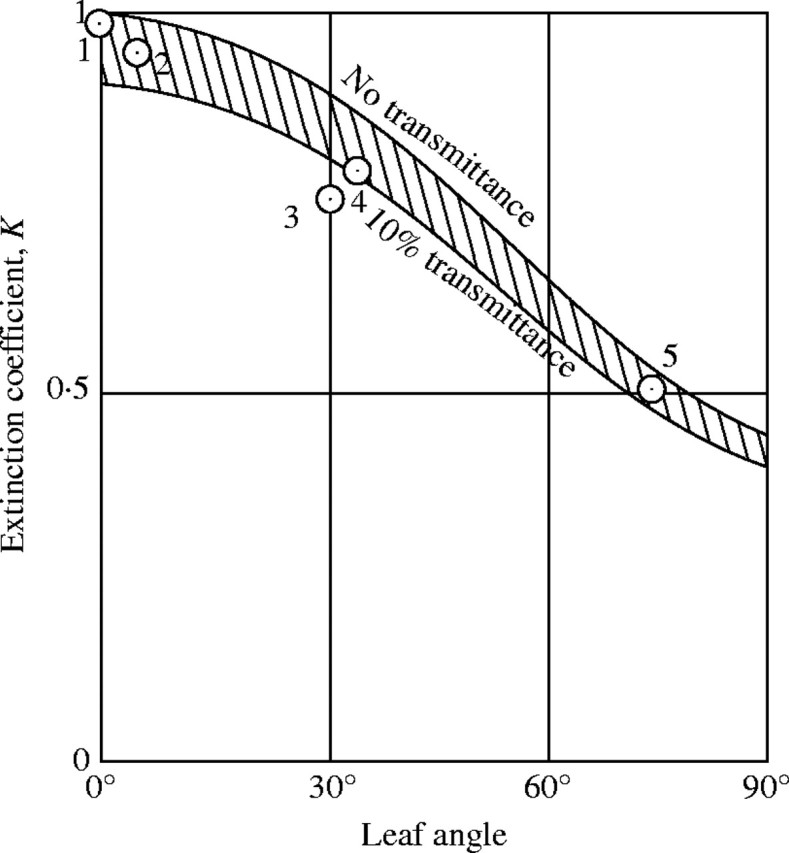
Relationship between extinction coefficient and leaf angle. 1 = Chenopodium album var. centrorubrum; 2 = Euphorbia adenochlora; 3 = Helianthus tuberosus; 4 = Sasa nipponica; 5 = Miscanthus sacchariflorus.

As to the transmittance of the leaf, the same relationships hold as previously discussed for horizontal leaves, and if we assume a transmittance of 10 % of the incoming light, then K is reduced to 0·90 for α = 0°, and to 0·40 for α = 90° (Fig. 7).

In herbosa, we have observed the relative distribution of brightness in the field, as well as leaf area and leaf angle, and we were able to show K graphically for every natural plant community. By comparing K calculated following eqn (9) with measured values, we can confirm the validity of our theoretical considerations. (Table 6, see also Fig. 7).

Table 6.

The comparison of calculated and observed extinction coefficients. F = leaf area index, K = extinction coefficient

						K
Dominant species	Date	Site	Sample area	F	Leaf angle	Observed	Calculated
Sasa nipponica	29 Aug. 1951	Kirigamine montane meadow	(1 m)2	4·4	35° (directly measured)	0·75	0·87
Miscanthus sacchariflorus	19 May 1952	Tazima meadow	(0·5 m)2 × 3	3·6	60° (photographically determined)	0·50	0·64
Euphorbia adenochlora	5 May 1951	Tazima meadow	(0·5 m)2	4·3	10° (estimated)	0·92	0·98
Helianthus tuberosus	12 Sept. 1952	Koisikawa Botanical Garden	(1 m)2	4·9	30° (photographically determined)	0·75	0·90
Osmunda cinnamomea	5 Aug. 1951	Oze moor	(1·5 m)2	2·9	60° (photographically determined)	1·24	0·64

From Table 6 it is evident that both K values can correspond well, with the exception of the Osmunda cinnamomea consociation. In this consociation, leaf areas are clustered in such a way that s/S is far from zero, and each leaflet (pinna) is more horizontal than the angle of the total leaf (frond) area.

We will discuss the ecological importance of the extinction coefficient K in the last section. The findings made in the present section will play a major role there. For the determination of K in any plant community we have to select a uniform stand. The test stand and the test area must be large enough, because with a smaller area the light beams can come in from all sides without interception by the leaves. It must also be noted that in the lower portion of the leaf crown, the light extinction can be affected through shading by stems. For example, the light–leaf area index curve in Fig. 3 bends strongly downwards towards its end. Furthermore, a decrease of K in nature may be brought about by the fact that the leaves on some plants, especially grasses, are densely positioned above each other around the stem.

IV. PRODUCTIVITY AND SEASONAL DEVELOPMENT OF PLANT COMMUNITIES

The seasonal development of a plant community depends on the change of productivity of each of the species making up that community. The productivity of plants can be calculated, albeit somewhat insufficiently, by combining the brightness, the photosynthetic activity of unit assimilating tissue, and the quantity of assimilation tissues. Brightness inside a plant community, as discussed above, generally decreases in a downward direction. Thus, also the productivity of unit tissue must decrease from top to bottom of the community. For the productivity per unit tissue of plants, we assume the average CO₂ assimilation of sun and shade leaves of Fagus, Fraxinus and Betula. The values were given by Boysen Jensen in Stoffproduktion der Pflanzen, pp. 44 and 45. We use them because we have few reliable light-assimilation curves, or have none in Japanese plants. We are currently conducting new measurements of assimilation on some native Japanese species.

We first need to transform the physiological, hourly, light-assimilation curve after Boysen Jensen into an ecological, daily, light-assimilation curve; that is, the assimilation rate will be determined for a given light intensity for each time of the day, and accumulated for the day (see also Boysen Jensen, 1932, p. 36–37). To calculate gross production or net assimilation for a whole day, one has to subtract from the gross assimilation, or cumulative assimilated quantity, the respiration during day and night, or 24 times the hourly respiration rate. We need to calculate the production under various relative brightness values. From these calculations, we can construct a daily light-assimilation curve. In this daily curve, the compensation point is slightly brighter (3·7 % in sun leaves, 1·1 % in shade leaves) than for hourly curves (670 lux or 1·3 % in sun leaves, 250 lux or 0·5 % in shade leaves) (see Fig. 8). For brightness, we assume an average value, i.e. at 0415 h and 1945 h completely dark, at 0500 h and 1900 h 0·8 klux, at 0600 h and 1800 h 8·0 klux, at 0700 h and 1700 h 26·5 klux, at 0800 h and 1600 h 37·5 klux, at 0900 h and 1500 h 44·0 klux, at 1000 h and 1400 h 47·5 klux, at 1100 h and 1300 h 49·4 klux, and at noon 50·0 klux. According to Hirayama et al. the brightness during the vegetation period in Tokyo is approx. 100 klux under a clear sky, approx. 10 klux under an overcast sky, and the fraction of sunshine hours during the same period is 0·43.

Fig. 8.

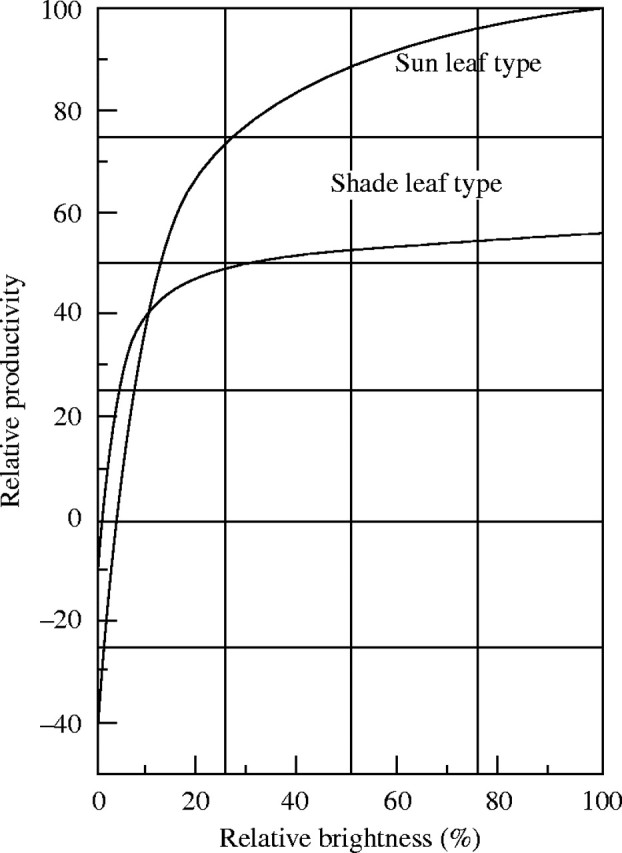
Curve of light intensity vs. daily productivity for light and shade leaf types.

The development of the lower synusia in a plant community is on the whole determined by the performance of the upper synusia in the same community. In the Tazima meadow in spring, closed communities of Euphorbia adenochlora or of Thalictrum simplex var. affine develop, and in between, the lovely pink flowers of Primula sieboldi f. spontana bloom. From the growth of the spring vegetation follows the emergence of the summer-dominant species, Miscanthus sacchariflorus and Phragmites communis. Corresponding to the rapid development of the dominant Miscanthus and Phragmites communities, the brightness above the lower layers of Euphorbia or Thalictrum constantly decreases during May and June. Finally, in summer, the brightness in stands of Miscanthus and Phragmites is only 3 % or less; this brightness represents a relative productivity of −4 % for sun leaves, and +19·5 % for shade leaves. At this point the lower synusiae decay, without new development and subsequent growth of the shade species (see Table 7). This example does not allow us to conclude beyond doubt that the poor or negative productivity in the shade of the upper synusiae brings about the decay of the lower synusiae. This is because Euphorbia, Primula and Thalictrum belong to the spring and summer species, and their above-ground parts senesce in summer or later summer (leaving underground storage organs behind), even when grown unshaded.

Table 7.

Seasonal development of the plant communities in the Tazima meadow. F^* = fresh weight of photosynthetic tissue in g per 50 × 50 cm², with the senesced tissue in parentheses. C = fresh weight of non-photosynthetic tissue in g per the same area. b = fresh weight of flowers. f = fresh weight of fruits

1. Miscanthus sacchariflorus–Euphorbia adenochlora association
	Euphorbia adenochlora					Miscanthus sacchariflorus					Other species
Date	Height (cm)	F*	C	Height (cm)	F*	C	F*	C
24 Feb. 1950	4	6	4				1	2
13 March 1950	5	20	23				3(+)	2
29 March 1950	10	52(4)	62				3	1
5 April 1950	25	93(7)	123				21	13
22 April 1950	35	106(8)	130(+b)	60	27	115	36(1)	46(+b)
30 April 1950	50	100(20)	190(+b)	100	71(+)	280	23(5)	38
3 June 1950	(Number of dead plants 62)					260	144(9)	612	39(8)	74(+b)

2. Miscanthus sacchariflorus–Thalictrum simplex var. affine association
	Thalictrum simplex var. affine					Miscanthus sacchariflorus					Other species
Date	Height (cm)	F*	C	Height (cm)	F*	C	F*	C
12 May 1950	90	34(3)	73	150	176(6)	596	23(10)	36
31 May 1949	100	22(+)	21	180	203(12)	849	6(1)	7
19 June 1950	(Number of dead plants 50)					260	275(9)	1216	6(1)	13
25 July 1949	120	2(3)	16	260	233(30)	886	8(+)	9
6 Sept. 1949	20	+	+	260	138(30)	1043	10(7)	172
8 Oct. 1949	40	1	+	300	168(32)	976(+b)	11(8)	35(+f6)
4 Nov. 1949	–	–	–	320	50(63)	1085(+f3)	4(1)	14(+f1)

3. Miscanthus sacchariflorus–Sanguisorba tenuifolia var. alba association
	Sanguisorba tenuifolia var. alba					Miscanthus sacchariflorus					Other species
Date	Height (cm)	F*	C	Height (cm)	F*	C	F*	C
3 June 1949	60	76(4)	63	180	74(5)	276	33(3)	65
9 July 1949	60	23(8)	30	260	153(15)	604	23(6)	52
26 Aug. 1949	40	(+)	+	260	130(7)	410	48(5)	75
	(Dry leaves 56 g)

4. Phragmites communis–Thalictrum simplex var. affine association
	Thalictrum simplex var. affine					Phragmites communis					Other species
Date	Height (cm)	F*	C	Height (cm)	F*	C	F*	C
13 April 1950	35	83(5)	139	5	+	3	7(+)	8
13 May 1950	110	64(5)	128	200	150(1)	1128	35(9)	79
30 May 1949	140	80(2)	151	220	263(2)	1289	15	20
26 June 1949	140	39(3)	83	300	398(10)	1168	32(1)	56
27 July 1949	180	13(9)	159	320	419(24)	1064	11(+)	23

5. Phragmites communis–Sanguisorba tenuifolia var. alba association
	Sanguisorba tenuifolia var. alba					Phragmites communis					Other species
Date	Height (cm)	F*	C	Height (cm)	F*	C	F*	C
29 March 1950	5	13	9				4	3
19 April 1950	35	135(12)	151	35	4	63	17(+)	12
7 May 1950	60	161(28)	255	110	42(+)	339	11(2)	25
16 May 1950	80	139(17)	241	160	89(1)	419	16(3)	41
26 May 1950	80	102(6)	154	200	141(5)	557	15(2)	28
3 June 1949	80	144(6)	168	200	120(+)	512	16(1)	57
16 June 1950	80	52(10)	107	220	290(3)	844	24(3)	63
	(Dry leaves 20 g)
29 June 1949	100	49(4)	77	240	175(5)	526	35(15)	99
4 July 1950	80	26(2)	62	280	216(6)	567	15(1)	48
	(Dry leaves 16 g)
*4 July 1950	60	41(4)	51	60	2	5	7	7
13 Aug. 1949	80	5(4)	18	280	157(11)	455	52(5)	100
	(Dry leaves 36 g)

^*Regenerated plants in the same quadrat, which had already been investigated on 16 May 1950 using the cutting method.

Fortunately, a very good example of the effects of productivity in the development of a plant community can be found in the Phragmites communis–Sanguisorba tenuifolia association. Sanguisorba is not a spring, but an autumn species; its leaves, when unshaded, stay green in the autumn, while the plant flowers with long white ears. Under the Phragmites community, however, the Sanguisorba synusia disappears already in summer without flowering, but the plant can develop lush foliage in the next spring before the sprouting of Phragmites.

The seasonal change of the productive structure of this association was thoroughly investigated in the years 1949 and 1950, using the stratified-clipping method. The result is displayed in Fig. 9. The leaf quantity of Sanguisorba is largely determined by the deteriorating light conditions caused by the growth of the Phragmites. Corresponding to the observed light distribution in the community, we can display the distribution curve of productivity using the relationship of light and relative productivity from Fig. 8. For the calculation of productivity we generally assume the values for the sun-leaf type, but when the light intensity decreases below 10·2 %, we use the values for shade leaves, because under these light conditions the assimilation intensity of shade leaves exceeds that of sun leaves. The productivity of each layer is the product of leaf quantity and relative productivity under a given light intensity. The calculations for each layer reveal a histogram of productivity within the community, which is represented by the thick dashed lines in Fig. 9. The real leaf distribution determined in the field changed between two measurements (within approximately 2 weeks) parallel to the previously calculated distribution of productivity. This is particularly evident in the Sanguisorba synusia. This also was evident in the year 1949. Already on 13 August 1949, there are no new leaves of Sanguisorba in the Phragmites sward, whereas there was a lush ground cover of these plants earlier in spring. When the Phragmites was cut, the leaves of Sanguisorba rapidly regenerated (see Fig. 9F). In general, the photosynthetic system in a plant community is distributed corresponding to the productivity.

Another example can be seen in the development of vine communities. Vine species such as Cissus, Paederia, Glycine or Humulus invade stands of Miscanthus sacchariflorus, or sometimes Phragmites; the growth of these vines starts later and is slower than that of the dominant grasses. In the gaps in Miscanthus or Phragmites, where the brightness is ∼10 % or more of the ambient brightness, vines can maintain their growth in spring and early summer, then wind around the dominant grasses in summer and autumn and densely cover these grasses with their leaves. Ultimately, the dominant grasses collapse due to light parasitism. We will treat this in detail in a future publication.

From these investigations we see that the seasonal development of the productive structure of a plant community mainly depends on the productivity of the plants. In natural succession, or with the regeneration of forests, the productivity of each plant species or each synusia may play an important role for the occurrence of species, the speed of succession, the determination of the climax community, etc. We thus believe that, in the near future, the determination of productivity in plants will be the focus of investigations into plant communities.

V. MATHEMATICAL BASIS FOR THE CALCULATION OF MATTER PRODUCTION IN PLANT COMMUNITIES

As matter production is, as mentioned above, the key to the solution of ecological-sociological problems in plant communities, it would be desirable if the matter production can be calculated on the basis of simple and measurable traits of a community. The direct, empirical determination of assimilation or matter production of a whole community has been carried out in the past by several authors, e.g. Boysen Jensen (1932), Moller (1947), Walter (1948), Thomas and Hill (1949), Blackman and Wilson (1950, 1951), and others. From these, we can only arrive at a description of final balance for a particular stand, at a particular time and under given conditions. With these descriptions alone, it is difficult to discover a common law of matter production of plant communities. This has to be done analytically. In the following paragraphs, we will discuss the theoretical basis for the calculation of matter production, with particular reference to the importance of the extinction coefficient.

Here, we again assume an ideal leaf community, where all leaves exhibit an identical light-assimilation curve, and where the productive conditions for each leaf, except for light, are uniform from top to bottom. In a given community, the extinction coefficient K shall also remain constant, although K may differ between communities.

The amount of assimilation as a function of the light intensity I can be described by the following equation (cf. also Tamiya, 1951, p. 168):

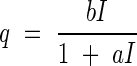where a and b are constants. The leaf always respires, so that net assimilation A has to be calculated with the equation

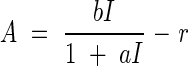where r stands for the respiration rate of the leaf.

The leaf area index from the top to a particular depth in a plant community is shown here as F′, which falls between 0 and F. The amount of light that is absorbed by the leaf area between F′ and F′ + ΔF′ is

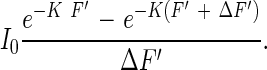According to this, the amount of light I absorbed by the unit leaf area at the same height can be shown by the equation

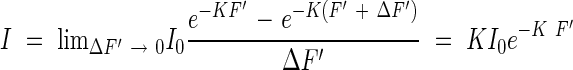Within the plant community, only small amounts of light are reflected or transmitted. Thus, we can substitute the absorbed amount of light in eqn (11) for that of the incoming light in eqn (10). The definite integral from zero to F in eqn (10) gives the productivity P of the whole leaf community over a unit ground area. That is,

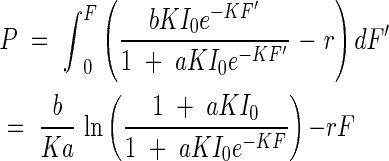From eqn (12) it is evident that the productivity can increase with the intensity of the incoming light, but that under a given light intensity, productivity has a maximum with regard to leaf area index. In other words, there is an optimum leaf quantity, for a given light intensity, for productivity in the plant community. This optimum leaf quantity also depends on the incoming light intensity. The productivity maximum in a community is caused by the fact that the leaf photosynthesis at a particular height level within the canopy is compensated by the leaf respiration. Below this height, light is lower than the compensation point, and photosynthesis is lower than respiration. For this reason, the leaves under this height usually do not participate in the positive matter production of the community, or they will be shed in time. The leaf area index from the top down to this compensation point may stand for the critical leaf area for plant productivity, because it can account for maximum production; this leaf area index shall be called here F_opt. F_opt is thus determined by the following equation:

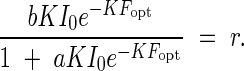The maximum production (P_max) at F_opt can be calculated by substituting F_opt in eqn (12). That is,

This equation shows that P_max at F_opt can vary considerably between communities with different extinction coefficients K, and that P_max has a maximum as a function of K. At this maximum, the differential quotient P′_max is zero, so that KI₀ is constant. With increasing incoming light intensity I₀, the extinction coefficient K at maximum P_max decreases; under low light, P_max increases with increasing K (see Fig. 10). As the net assimilation curves are generally similar among different species, this relationship will hold for different plant communities. For productivity in nature it is very important that leaves in the open and under strong light are inclined, e.g. in tropical trees or steppe grasses (i.e. K is smaller than 1), and that in contrast to this, leaves in the shadow of forests or in the lower part of a tree crown are orientated horizontally in a mosaic way (i.e. K is larger than 1).

Fig. 10.

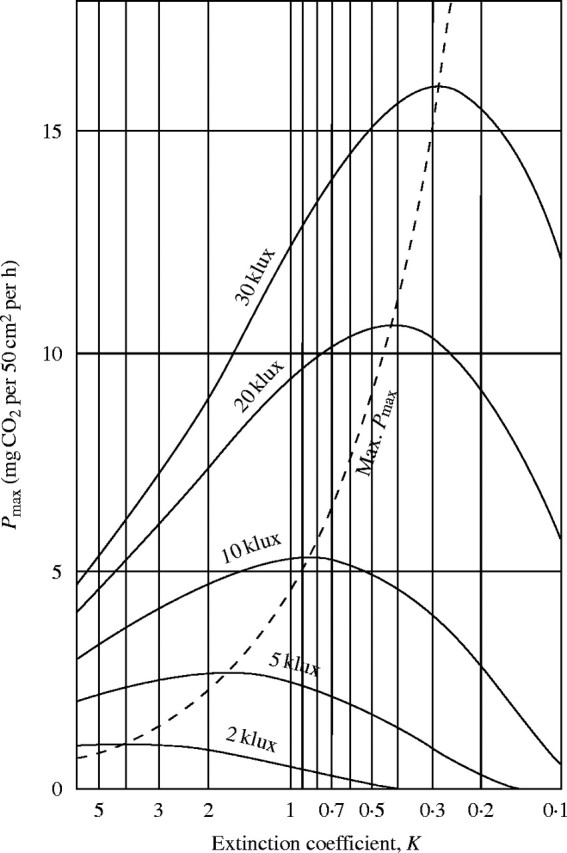
The maximum productivity (P_max) at different extinction coefficients (K) and under different light intensities.

We now have a theoretical basis for the calculation of productivity of the whole plant community on the basis of the light-assimilation curve of a single leaf. It is important however, that the production measured directly at the stand is compared with that calculated based on eqn (12). Fortunately, we have the results of Boysen Jensen's experiments with Sinapis and Avena cultures (Boysen Jensen, 1932, p. 57–64, see also 1939, p. 215).

According to Boysen Jensen, the assimilation of the unit leaf area in the stand was, on average, smaller than that of a single leaf in a horizontal position, as the leaves shaded each other. The assimilation of the stand almost linearly increased with increasing incoming light. In his study, he only reported the values for incident light, but we can estimate the light intensity in both cultures according to eqns (5) and (9) with a few assumptions, namely that the leaves of Sinapis are positioned horizontally, and that the extinction coefficient K equals 1, and that the leaves of Avena are positioned at an angle of 60°, so that K = 0·64. The assimilation of these stands can now be calculated on the basis of the observed common light-assimilation curve using our equation. The calculated values can be compared with those directly measured for the stands by Boysen Jensen.

For Sinapis we can express the assimilation curve of a single leaf in a horizontal position (Boysen Jensen, 1932, p. 57, fig. 29a) with the following equations:

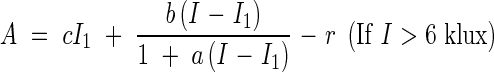or

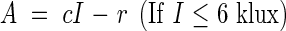where r = 0·87 (mg CO₂), I₁ = 6 (klux), a = 0·56, b = 0·64 (mg CO₂), c = 1·23 (mg CO₂). For each light intensity I we calculate the production (P) of the whole Sinapis culture by using eqn (12). The leaf area index of the Sinapis stand was 3·4, therefore the average assimilation rate per unit leaf area is given by P/F = P/3·4. These values correspond with those observed by Boysen Jensen, fig. 29b (see Table 8).

Table 8.

The theoretically calculated apparent assimilation intensity (CO₂ mg/50 cm² leaf area/hour) in the plant cultures, in comparison with the one measured experimentally by Boysen Jensen

Light intensity (klux)	Experimentally measured	Theoretically calculated
(a) For the Sinapis culture (leaf area 1180 cm2)
0	−0·87	−0·87
2·5	0	0
5·0	0·75	0·88
7·5	1·50	1·71
10·0	2·25	2·37
12·5	3·00	2·93
15·0	3·75	3·39
(b) For the Avena Culture (i. leaf area 992 and 1080 cm2)
0	−0·37	−0·37
2·5	0·55	0·56
5	1·50	1·50
7·5	2·3	2·4
10	3·0	3·2
12·5	3·6	3·8
(b) (ii. leaf area 2260 cm2)
0	−0·37	−0·37
2·5	0·35	0·13
5	1·2	0·62
7·5	1·9	1·1
10	2·3	1·6
12·5	2·7	1·9

Our calculated assimilation rate agrees quite well with that measured by Boysen Jensen. If the incoming light were to increase sufficiently, the observed linear assimilation curve would bend downwards a little, as the experiment was carried out under relatively low light.

For the Avena culture, we can test the relevance of eqn (12) in the same way. Here, r = 0·37 (mg CO₂), I₁ = 4·10 (klux), a = 0·75, b = 1·38 (mg CO₂), c = 1·31 (mg CO₂), and F = 3·0 (in fig. 30b) and 6·5 (in fig. 30c), respectively. In Table 8, the values calculated by us and measured by Boysen Jensen are compared. The calculated values correspond well with those in Boysen Jensen's fig. 30b, for the culture with less leaf area (F = 3·0), but for fig. 30c, a dense sward (F = 6·5), the calculated assimilation rates are strikingly smaller than the measured ones. In our opinion, there may be senescing and dead leaves in the lower part of the closed leaf canopy, because the calculated light intensity at depth should only be 1·02 % of the ambient brightness.

From these elaborations we can conclude that it is now possible to calculate hourly rates of production in a plant community without direct measurements (which are usually impossible in forest vegetation), and just based on simple measurable traits. However, there are further serious problems for the ecological determination of matter production. Production for days, months or a whole year is very important for ecological-sociological investigations of plant communities. For this, we need to account for, and must further study, daily or annual fluctuations in light intensity, temperature, hydration, direct sunlight versus diffuse light, sunflecks, the respiration of the non-photosynthetic plant parts, nutrients and, finally, growth of the plants. For the annual matter production, there are further complications with regard to reproduction of the photosynthetic and non-photosynthetic system, and with nutrient cycling. To ‘gain a deeper insight into the functioning of plants and plant associations’ (Boysen Jensen 1932), or to pave a way for general ecology, we need further theoretical as well as experimental investigations on the matter production and reproduction of plant communities. We are thus planning some new, exact experiments on artificial plant communities.

SUMMARY

Ecological-sociological investigations of plant communities must be based on the matter production of plants. The matter production is discussed in this study on the basis of light intensity and leaf quantity in a plant community.

1. The productive structure of a plant community is demonstrated by the stratified-clipping method. Here, we separate plant materials into photosynthetic and non-photosynthetic tissues. With diagrams of production structure, we can distinguish two main types of plant communities, the broad-leaf type and the grass-type.

2. The light intensity in forest communities is generally 2–20 % of the ambient light. The darkest community in our observations was a bamboo thicket of Phyllostachys, with a relative brightness in summer of 0·2–0·5 %. Under these conditions, some plants of the ground flora become naturally etiolated.

3. Within well-growing herbosa, it is relatively dark compared with forest shade, i.e. the relative brightness is generally only 2–3 %. The leaf area of herbosa is not less than that of lignosa. Generally, the leaf area index (in m² per m² ground area) of the observed herbosa is 4 to 7 or more.

4. The light intensity decreases by and large exponentially through the leaf layers. It thus follows the equation

   

   where I is the light intensity in the plant community, I₀ is the incoming light, K is the extinction coefficient, and F is the leaf area index. K is nearly constant for the same plant communities, but varies widely between different communities: our observations yielded values between 0·3 and 2. But, generally, K for the grass-type is approx. 0·3–0·5, and for the broad-leaf type approx. 0·7–1.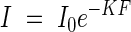

5. The light extinction in a leaf community is theoretically discussed with regard to leaf position and leaf angle. We show clearly that the extinction coefficient for ideally distributed horizontal leaves is 1, while for inclined leaves it can decrease with the leaf angle down to 0·44 (for a leaf angle of 90°). A mosaic-like leaf distribution increases K.

6. The development of the production structure of a plant community, especially of the photosynthetic system, is strongly constrained by matter production. For example, the lower layer can only develop according to the remaining productivity, which corresponds to the brightness under the leaf area of the upper layer. This phenomenon is clearly demonstrated by observations of the seasonal development of Phragmites–Sanguisorba associations and of vine communities. The lower community disappears with the growth of the upper community.

7. A theoretical equation is formulated for the calculation of matter production for a leaf community. With this equation, we can calculate total production on the basis of the light-assimilation curve for a single leaf, the leaf area index and the extinction coefficient. There is an optimal leaf area for the maximum productivity under a given incoming light intensity. A smaller extinction coefficient is advantageous for matter production under stronger light, while a larger one is more advantageous under weaker light.

8. We tested the theoretical productivity equation with Boysen Jensen's experimental data for Sinapis and Avena cultures. The calculated productivity agrees quite well with the observed one.

APPENDIX: NOTES ON THE TRANSLATION

Monsi and Saeki had a very unusual way of writing. Their German is grammatically correct, but their style is (or has become since the 1950s) unusual. This makes the German text sometimes difficult to understand, even for native speakers. I have tried to keep as much of Monsi's and Saeki's writing style as possible when translating the text into English. Monsi and Saeki often use technical terms that are no longer used, or are used today with slightly different meanings. For some of their expressions, we would use a different term today. For example, they very often use the word ‘Helligkeit’ which means brightness. Most authors these days would use the term ‘light intensity’ because it sounds more quantitative than does ‘brightness’. However, Monsi and Saeki chose ‘brightness’, and I have decided to keep it that way when translating the paper. A more liberal translation into English might be easier to read, but would do less justice to the authors' own particular style. The notes below refer to a number of words that have become largely forgotten in plant ecology, ‘herbosa’, ‘lignosa’ and ‘synusia’. These go back to the Swiss botanist Rübel, and giving his definitions actually tells us something about the background Monsi and Saeki were coming from scientifically.

Herbosa. Monsi and Saeki follow the ‘ecological-physiognomical’ classification of plant communities by Rübel (1930) into lignosa (woody communities), herbosa (herbaceous communities) and deserta (desert communities). Interestingly, the definitions of Rübel for these classes do not centre on the ‘woodiness’ of the communities. Lignosa are defined as ‘plant communities which consist of trees, shrubs, and herbs, which are closed on immobile ground in such a manner that the plants of the upper storeys create ecological conditions for the plants of the lower storeys significantly different from the conditions when these were dominant themselves’. Herbosa are ‘plant communities which consist of grasses, herbs, and non-woody cryptogams, which cover the immobile ground in such a manner that the incident light is used by the dominant species such that the soil surface is influenced’. Deserta are ‘communities which cannot cover the mobile and immobile ground in such a manner that they have a significant influence on a lower storey, i.e. they are open plant communities or cryptogam crusts’. The rationale behind this classification clearly influenced Monsi's and Saeki's thinking about the microenvironment as modified by plants. See Rübel E. 1930. Pflanzengesellschaften der Erde. Bern/Berlin: Verlag Hans Huber.

Synusia. An ecological grouping within a plant community. It often corresponds with ‘layer’, but not always, such as in epiphyte communities. See Rübel E. 1930. Pflanzengesellschaften der Erde. Bern/Berlin: Verlag Hans Huber.

Originally published as:

Über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion

Japanese Journal of Botany14: 22–52, by the Science Council of Japan, Tokyo, Japan, March 1953 (received 11 October 1952)

A new translation into English from German for the Annals of Botany with the permission of Professor Saeki, by MARCUS SCHORTEMEYER*

Ecosystem Dynamics Group, Research School of Biological Sciences, Australian National University, GPO Box 475, Canberra ACT 2601, Australia