Physical Constraints on Temperature Difference in Some Thermogenic Aroid Inflorescences

Abstract

• Backgrounds and Aims Thermogenesis in reproductive organs is known from several plant families, including the Araceae. A study was made of the relationship between temperature increase and spadix size in the subfamily Aroideae in order to determine whether the quantitative variation of heat production among species and inflorescences of different sizes follows a physical law of heat transfer.

• Methods Spadix temperature was measured in 18 species from eight genera of tropical Araceae from the basal clade of Aroideae, both in French Guiana and in the glasshouses of the Montreal Botanical Garden.

• Key Results A significant logarithmic relationship was found between the volume of the thermogenic spadix zone and the maximum temperature difference between the spadix and ambient air. Four heat transfer models were applied to the data (conductive heat transfer alone, convective heat transfer alone, radiative heat transfer alone, and convective and radiative heat transfers) to test if physical (geometric and thermic) constraints apply. Which heat transfer model was the most probable was determined by using the criterion of a classical minimization process represented by the least-squares method. Two heat transfer models appeared to fit the data well and were equivalent: conductive heat transfer alone, and convective plus radiative heat transfers.

• Conclusions The increase in the temperature difference between the spadix and ambient air appears to be physically constrained and corresponds to the value of a thermal model of heat conduction in an insulated cylinder with an internal heat source. In the models, a heat metabolic rate of 29.5 mW g⁻¹ was used, which was an acceptable value for an overall metabolic heat rate in aroid inflorescences.

INTRODUCTION

Thermogenesis in reproductive organs is known from several plant families: Araceae, Annonaceae, Arecaceae, Cycadaceae, Cyclanthaceae, Magnoliaceae, Nymphaeaceae and Zamiaceae (Prance and Arias, 1975; Tang, 1987, 1993; Gottsberger, 1990; Uemura et al., 1993; Seymour and Schultze-Motel, 1998; Azuma et al., 1999; Dieringer et al., 1999; Bernhardt, 2000; Thien et al., 2000; Lamprecht et al., 2002a, b). A few taxa are even able to control their inflorescence temperature (i.e. thermoregulate) at a given value regardless of the ambient temperature (Seymour et al., 1983; Seymour and Schultze-Motel, 1996; Seymour, 1999, 2004; Ito et al., 2003). Heat production is generally associated with the emission of fragrance and the arrival of pollinators, and it has been particularly well documented in the family Araceae (Knutson, 1974; Moodie, 1976; Seymour et al., 1983; Meeuse and Raskin, 1988; Yafuso, 1993; Seymour and Schultze-Motel, 1997, 1998, 1999; Seymour, 1999; Barabé and Gibernau, 2000; Barabé et al., 2002; Angioy et al., 2004). Although the most obvious role of the thermogenic process appears to be the dispersion into the air of scented compounds, thermogenic activities play other roles not linked with pollinator attraction, and may also be related to the unfolding of the spathe, and physiological processes such as flower development, pollen maturation, insect warming or pollen release (Seymour, 1999; Seymour and Schultze-Motel, 1999; Wada and Uemura, 2000; Barabé et al., 2002; Albre et al., 2003). Recently, it has been shown that heat may represent an energetic reward for some types of pollinators (e.g. beetles), but not for others (e.g. flies) (Seymour et al., 2003a, b).

The inflorescences of Araceae are typically composed of a spadix into which are inserted minute flowers surrounded by a modified bract, the spathe. In the subfamily Aroideae (sensu Mayo et al., 1997), the spadix bears unisexual flowers and heat is generally produced by the male flowers (fertile and sterile) or a specialized appendix (Meeuse, 1975, 1978; Skubatz et al., 1990, 1991; Bermadinger-Stabentheiner and Stabentheiner, 1995; Seymour, 1999). This increase in temperature is produced by a particular biosynthetic pathway, the cyanide-insensitive respiration that uses starch or lipids as a source of energy and results in the production of heat instead of ATP, and which is triggered by salicylic acid (James and Beevers, 1950; Lance, 1972; Nagy et al., 1972; Wedding et al., 1973; ap Rees et al., 1976, 1977; Chauveau and Lance, 1982; Walker et al., 1983; Raskin et al., 1987, 1989, 1990; Elthon et al., 1989; Skubatz et al., 1990, 1992; Lytle et al., 2000). The regulation of this biosynthetic pathway at the mitochondrial level depends on the ubiquinone, the alternative oxidase (e.g. a membrane protein) and a species-specific uncoupling protein (Wagner and Krab, 1995; Leach et al., 1996; Laloi et al., 1997; Wagner et al., 1998; Ito, 1999; Ito et al., 2003).

Numerous observations have been made on the production of heat by inflorescences of Araceae, mostly in relation to physiological processes, respiration rates and heat production involved in temperature increases, or the characterization of thermogenic patterns (Knutson, 1972, 1974; Nagy et al., 1972; Chen and Meeuse, 1975; Seymour et al., 1983; Young, 1986; Raskin et al., 1987; Skubatz et al., 1990, 1991; Bermadinger-Stabentheiner and Stabentheiner, 1995; Seymour, 1999; Gibernau and Barabé, 2000; Barabé et al., 2002). Although many analyses of thermogenesis in the Araceae have been conducted, only one study has discussed the relationship between the physical dimensions of the spadix (e.g. the mass) and the amplitude of heat production across two aroid species (Seymour et al., 1983). In fact, this aspect brings to the fore the question of the relationships between biological constraints and physical constraints during the evolution of organisms.

It is well known that during their development and evolution organisms suffer different types of constraints. In evolutionary biology, ‘constraints represents a bias or imposition of a restriction on the range of possible responses of an organism to selection’ (Hall, 1992, p.75). Maynard Smith et al. (1985) recognize two general categories of developmental constraints in evolution: universal constraints and local constraints. Universal constraints are the direct consequences of the laws of physics or mathematics and apply to all physical systems and organisms. Local constraints result from the biological properties of organisms (e.g. physiology, genetics, mode of development), and can be limited to a particular taxon. In this paper, we use the terms ‘physical’ (including mathematical laws) and ‘biological’, respectively, to designate these two types of constraints.

It has been shown that there is a possible link between the amplitude of the thermogenic peak and the size or the mass of the spadix in some non-thermoregulating Aroids (Gibernau and Barabé, 2000; Wada and Uemura, 2000), while no such relationship has been found in thermoregulating species (Seymour and Blaylock, 1999; Seymour, 2004). It is obvious that all characteristics (e.g. size, colour, form, physiological properties) of the inflorescences of a given species are derived from its genetic background. However, in this case, we can hypothesize that the size of the inflorescence would constitute a physical constraint, and the morphological and physiological properties involved in the thermogenesis represent a biological constraint.

Very few studies have dealt with the relationship of the increase of temperature according to the size of the spadix (Seymour et al., 1983; Breidenbach et al., 1997; see Tang, 1987 for cycads). By using simple thermal models it may be possible to quantify the relationship between size of the inflorescence and the maximum temperature difference with the ambient air. Four models of heat transfer (conduction, convection, radiation, and conduction plus radiation), which assumed that the inflorescence is a cylinder, were developed.

The general goals of this study were: (1) to compare the maximum temperature increase in relation to spadix size (i.e. the volume of the male zone) among 18 tropical species of Araceae with unisexual flowers belonging to the subfamily Aroideae (or the tribes Philodendreae, Homalomeneae, Anubiadeae, Culcasiae, Montrichardiae, Dieffenbachiae sensu Mayo et al., 1997); (2) to determine if the quantitative variation of heat production among species and inflorescences of different sizes follow a physical law of heat transfer; and (3) can this physical law simply represent a cylinder surface temperature caused by an internal heat source?

MATERIAL AND METHODS

All the genera studied, which belong to the subfamily Aroideae, sensu Mayo et al. (1997), are characterized by inflorescences having a male zone in the upper part and a female zone in the lower part. In the genus Philodendron there is also a sterile male zone in the middle of the inflorescence, varying in length depending on the species. For example, in Philodendron solimoesense the intermediate zone occupies 35–52 % of the total length of the inflorescence while in P. melinonii this area occupies no more than 22 %. The male zone and sterile zone are composed of morphologically similar organs, and both zones follow the same qualitative thermogenic pattern (Barabé et al., 2002). Considering that all inflorescences belong to the same morphological type, it may therefore be possible to establish a quantitative relationship between the volume of the inflorescence's male (or sterile) zone and temperature differences between the surface of the inflorescence and the ambient air in different species.

Inflorescence temperature was measured on 28 inflorescences from 18 species belonging to eight genera. Specimens were studied in French Guiana and at the Montreal Botanical Garden (MBG) in 1998 and 1999 (Gibernau et al., 1999; Barabé and Gibernau, 2000; Gibernau and Barabé, 2000, 2002; Gibernau et al., 2000, 2003).

The nine original temperature measures presented in this study were taken in 1999 between 9 August and 15 September at the MBG on the following species (the number in brackets represents the registration number at the MBG): Aglaonema crispum (24–76) (voucher at MT: Barabé & Archambault 198), Anubias barteri (3548–85) (voucher at MT: Barabé and Lavoie 138), Anubias barteri var. caladiifolia (1649–86) [voucher at Marie-Victorin Herbarium Montreal (MT): Barabé 268], Cercestis stigmaticus (4088–84) (voucher at MT: Barabé and Lavoie 139), Culcasia saxatilis (4094–840 (voucher at MT: Barabé & Chanta 91), Culcasia sp. (1072–86) (no voucher available), Culcasia sp. (1073–86) (no voucher available), Philodendron distantilobum (2601–59) (voucher at MT: Barabé 267), Philodendron cannifolium (2424–46) (voucher at MT: Barabé 266). The other data come from previously published studies of thermogenic patterns present in different species (Appendix 1). Temperatures were measured with a Digi-Sense® DualLogR® thermocouple thermometer every 10 min. To obtain the temperature of the spadix, the thermometer was inserted at approx. 5 mm depth into the spadix, in the middle of the fertile male flower. In order to correlate the inflorescence size and the heat produced, the volume of the male zone has been estimated to be a cylinder: V = πD²L/4, where D is the diameter and L the length of the male zone (see Appendix 2 for full list of abbreviations). This estimation is a simplification of the process, as in fact the axis of the spadix does not produce much heat, but only male flowers are responsible (Nagy et al., 1972; Seymour, 2001).

Previous studies have shown that the floral cycle is comparable between specimens at the Montreal Botanical Garden and in the wild (Gibernau and Barabé, 2000; Gibernau et al., 2000; M. Gibernau and D. Barabé, unpubl. res.). The environmental conditions (e.g. the ambient temperature) in the tropical greenhouses of MBG (mean ± s.d. = 22·9 ± 2·4 °C) and in the field (mean ± s.d. = 24·1 ± 0·9 °C) being comparable (t-test: t₂₆ = 1·43, P = 0·16), increases in spadix temperature can thus be integrated into a comparative analysis (Appendix 1).

RESULTS

Thermal modelling

To estimate the temperature increase resulting from metabolic heat, we considered a simple model based on a cylindrical inflorescence, insulated by a layer of air. This question, and particularly the dry heat flux, Φ_V, emanating from the inflorescence, can be examined in several ways.

1. If one supposes that the air is stagnant around the stem, then this is a case of conductive heat transfer.

2. If the air is not stagnant, then this is a case of convective heat transfer.

3. However, radiative heat transfer (heat emission by the inflorescence) can also be taken into account.

Note that there is no reason why some of these heat transfer methods cannot occur simultaneously. This is probably the case for convective and radiative heat transfers on the surface of the inflorescence. Thus if we neglect evaporation (flower transpiration), we should investigate all of these heat transfer methods. To determine which heat transfer model is the most probable, we used the criterion of a classical minimization process represented by the least-square sum method:

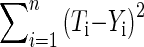Where T_i and Y_i are the theoretically calculated and experimentally measured temperatures, respectively.

The case of conductive heat transfer alone

We first consider a layer of stagnant air at a thickness of δ. Outside this boundary layer, the air is assumed to be well mixed and at a uniform temperature. We also assumed that the stem tissue produces heat at a constant rate, and the heat loss across the boundary layer can occur only through conduction. To calculate the temperature of the tissue, we employed the same equation used to measure the heating of an insulated wire by an internal heat source (Carslaw and Jaeger, 1959; Breidenbach et al., 1997; Fig. 1). Based on the results obtained from the heat conduction equation, the increase above ambient temperature is given by:

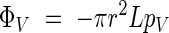Fig. 1.

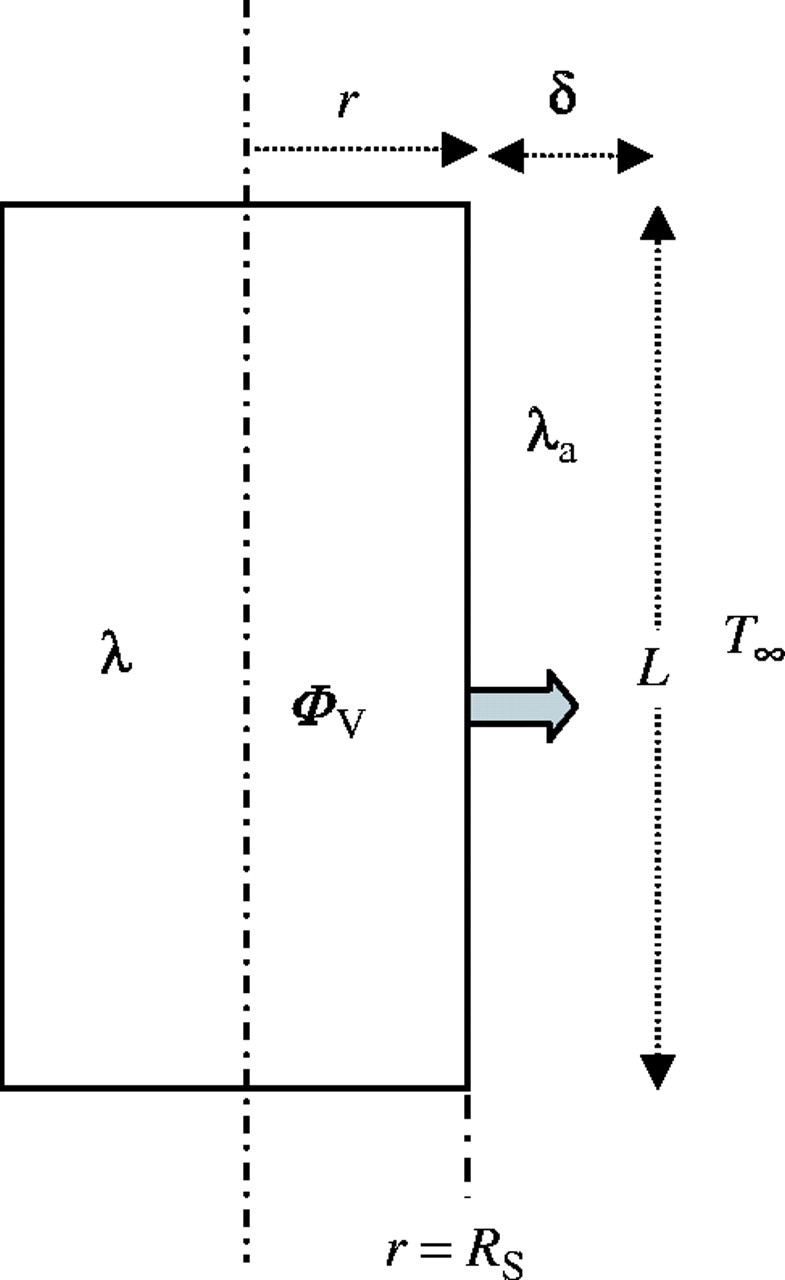
Schematic diagram of the inflorescence thermogenic zone used to study heat transfer. R_s ( = r), inflorescence radius (m); L, length of male zone inflorescence (m); T_∞, ambient air temperature (°C); Φ_V, dry heat flux leaving the male zone inflorescence (W); δ, thickness of the conductive boundary layer (m); λ, conductivity coefficient of the inflorescence (Wm⁻¹ K⁻¹); λ_a, conductivity coefficient of stagnant air (Wm⁻¹ K⁻¹).

Following Fourier's law,

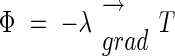we can calculate eqn (3), which represents the flux dissipated on the lateral surface of the inflorescence. Note that we have neglected the heat transfer occurring at the top and bottom surfaces of the cylinder representing the inflorescence:

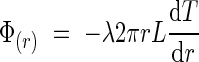where T is the surface temperature of the inflorescence. If we assume that these two equations are equal, we can easily obtain the value of the surface temperature of the inflorescence:

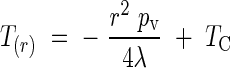where T_C is a constant to be determined. We can obtain the flux liberated by the inflorescence over the entire volume of the cylinder by calculating the mean logarithmic difference:

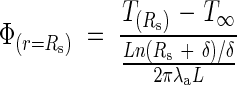By again applying Fourier's law to the radius of the cylinder, we obtain:

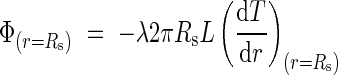The equality of eqns (5) and (6) leads finally to the value of T_C, thus:

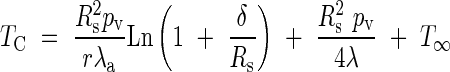Substituting the value for T_C in eqn (4) allows us to obtain the temperature distribution inside the inflorescence:

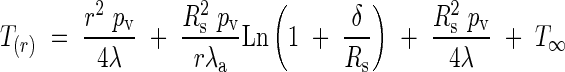By using the temperature difference ΔT_V = T_(r) − T_∞ and r = R_S we obtain a simplified expression:

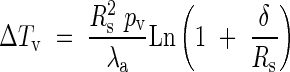This expression is analogous to the heating of an insulated wire by an internal heat source (Carslaw and Jaeger, 1959), which has also been reported in Breidenbach et al. (1997).

The case of convective heat transfer alone

In eqn (6) it was assumed that the internal energy dissipated on the lateral surface of the flower by conduction only obeys Fourier's law, but in reality this lateral heat transfer is certainly also subject to convective phenomena:

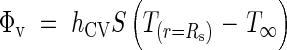where h_CV is the convective heat exchange coefficient determined by Bejan (1993) and calculated as follows:

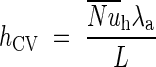With:

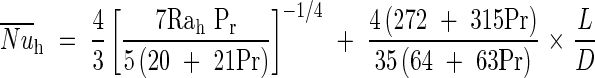and

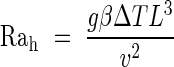Pr

By again using eqn (2) = eqn (9) we obtain a new value for ΔT_V:

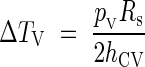The case of radiative heat transfer alone

Temperature differences in terms of radiative exchange are shown in eqn (13):

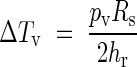To estimate the level of radiative heat exchange, we evaluated a linearized radiative heat exchange coefficient (Sacadura, 1993):

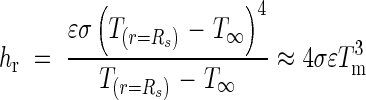Taking into account the constant values for a grey and diffusing surface (see below), for h_r we obtained an estimation of 5·1 Wm⁻² K⁻¹ for the inflorescence.

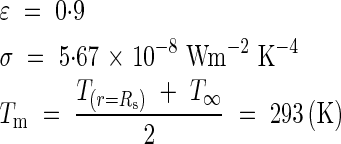The case of convective plus radiative heat transfers

Finally, eqn (15) shows temperature differences in terms of the two types of simultaneous heat transfers:

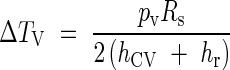Applications

Two data sets were considered: first temperature measures related only to Philodendron (eight species, 13 measurements); second, all the data (eight genera, 18 species, 28 measurements). The four thermal models were applied to the two data sets assuming that:

1. The volume-specific heat production rate of the flower is equal to 29 500 Wm⁻³. This value minimizes the different least-square sums of all the models. A value 29·8 mW g⁻¹ is mentioned for the spadix Philodendron selloum (Lamprecht et al., 2002b).

2. The thickness of the subviscous layer is equal to 0·003 m (Cuniasse-Languans, 1998).

Relationship between male zone size and temperature excess

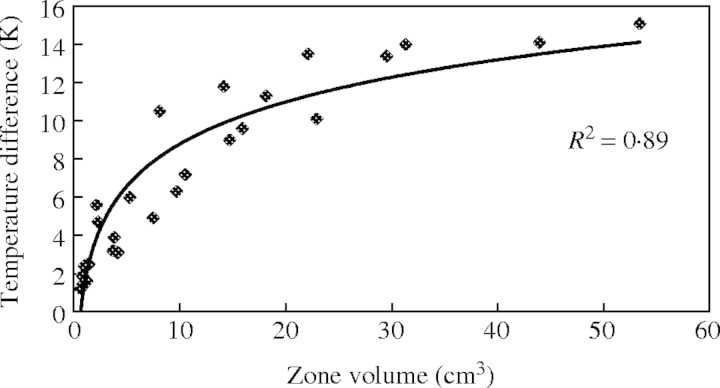
A strong logarithmic correlation exists between the volume of the male zone and the temperature difference between the inflorescence and the ambient air (Fig. 2; y = 3·1845 ln(x) + 1·4505, R² = 0·89; see data presented in Appendix 1). Hence the increase in temperature difference is steeper for small volumes (up to 10 cm³) and then flatter for larger inflorescence volumes. The maximum temperature difference between the air and the spadix increases and seems to reach a maximum around 15 K for a spadix with a male zone volume of 50–60 cm³.

Fig. 2.

Relationship between the volume of the thermogenic zone (male or male-sterile according to the aroid species) and the maximum of the temperature difference between the inflorescence and the ambient air.

Thermal modelling

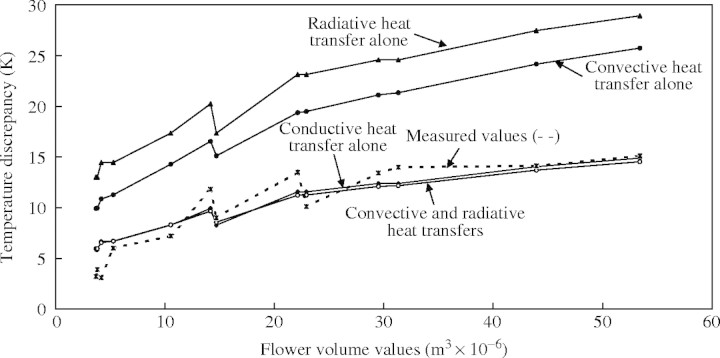
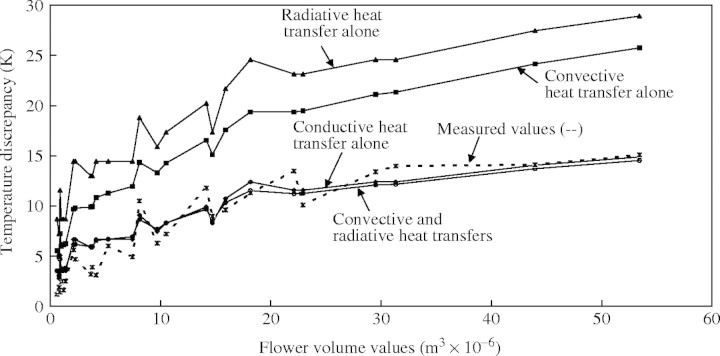
Table 1 presents the sum of the least squares for each of the four models applied to the Philodendron data set. The two most-parsimonious models of calculated heat transfer were the conductive heat transfer model and the convective plus radiative heat transfer model (Table 1, Fig. 3). In the same way, when all data were considered, the two most-parsimonious models were the conductive heat transfer model and the convective plus radiative heat transfer model (Table 1, Fig. 4).

Table 1.

Results (K²) of the minimization process (method of the least sum of squared differences) between the calculated temperature according to four heat transfer models and the measured temperatures for the eight Philodendron species and for all the species

	Conductive heat transfer alone	Convective heat transfer alone	Radiative heat transfer alone	Convective and radiative heat transfers
Eight Philodendron species	38·9	729·6	1494·0	42·2
All species	81·9	1148·9	2630·6	84·7

Fig. 3.

Relationships between the volume of the thermogenic zone and the maximum temperature difference between the inflorescence and the ambient air for the eight Philodendron species studied. Measured temperatures (dashed line) are shown together with calculated temperatures (solid lines) according to the four different heat transfer models (see text for full explanation).

Fig. 4.

Relationships between the volume of the thermogenic zone and the maximum temperature difference between the inflorescence and the ambient air for all the species studied. Measured temperatures (dashed line) are shown together with calculated temperatures (solid lines) according to the four different heat transfer models (see text for full explanation).

DISCUSSION

Our results show that the conductive heat transfer model and the convective plus radiative heat transfer model best represent the data measured. This can be explained if we consider two facts. First, there is no reason that the different kinds of heat transfer occur separately. In reality, when a temperature difference is observed at a solid–air interface (e.g. the wall of a dwelling) two types of heat transfer (convective and radiative) happen simultaneously (Trombe et al., 2004). Second, we chose for the calculations of the conductive heat transfer alone an air thickness giving an equivalent resistance to convective and radiative phenomena (Cuniasse-Languans, 1998). It should be noted that our results are in accordance with those obtained by Breidenbach et al. (1997) who also used a model of conductive heat transfer (eqn 9) to calculate temperature increases in the inflorescence of Philodendron selloum with respect to volume.

The point distribution along the curve does not follow a phylogenetic pattern. Although the point in the asymptotic part of the curve corresponds mainly to the genera Philodendron, Homalomena and Montrichardia, there is no concordance between the grouping of taxa and the empirical values in the other part of the curve. For example, if there was a correlation between phylogeny and the empirical curve, all species of Anubias and Philodendron should appear in the same part of the curve because they are close relatives. This is not the case. In the first part of the curve there are mostly genera with small inflorescences, and in the second part genera with larger inflorescences. This indicates that the grouping of taxa along the curve is not phylogenetically constrained.

The correlation between the empirical and the theoretical curves indicates two things: (1) the biological process (e.g. inflorescence surface temperature) is in close relationship with the physical law governing heat conduction at the surface of a cylinder with an internal heat source; and (2) for a given sample of inflorescences of the same type, there is a regularity in the relationship between the temperature increase and size of the male zone. This regularity is expressed by an empirical curve regardless of the species. The sample comprises species belonging to different genera in the subfamily Aroideae. It should be noted that that all the species used in this study, with the possible exception of Dieffenbachia, possess a very uniform morphology. Within the Aroideae subfamily, the relationship between temperature increase and size of the male zone follows a physical rule, indicating that the maximum temperature difference depends principally on the geometric (i.e. physical) properties of the inflorescence.

In our study, the physical model reflects the maximum temperature values as a function of the volume of the inflorescence. We were not interested in the dynamics of temperature variations during the thermogenic process. The empirical and theoretical curves are limited to peak temperature differences and do not account for a biochemical process over time. The peak of temperature increases as the volume of the inflorescence increases to reach an asymptotic level. Given that the experimental curve corresponds to a physical model, it may be hypothesized that the maximal temperature value represents a physical constraint due to the law governing the temperature on the surface of a cylinder with an internal heat source. This limiting value, which depends on the volume of the inflorescence, constitutes the physical constraint limiting the range of possible thermogenic maxima in selected genera. On the other hand, what might be the biological constraints? In Symplocarpus foetidus it is possible that spadix size affects thermoregulatory ability (Seymour, 2004). However, in this species, there is no apparent relationship between the temperature of the spadix and either the spadix's or the spathe's mass when heating is strongest (Seymour, 1999). However, in Symplocarpus renifolius there is a positive correlation between the values of cumulative temperature difference between spadix and air and the basal diameter of the spadix (Wada and Uemura, 2000). In Symplocarpus foetidus, the models developed by Seymour (2004) reveal that the dynamics of the regulation of temperature as a function of time cannot be explained by a physical model only. It involves some form of biochemical regulation, possibly by changes in a functional protein involved in thermogenesis. In that case, the biochemical process might represent a biological constraint.

The genera analysed in this study are phylogenetically related, belonging to the basal clades of Aroideae in the sense used by Mayo et al. (1997). For example, in our analysis, there are no members of the tribes Areae and Peltandreae. All members of the selected genera have a common ‘bauplan’ organization of the inflorescence. This would explain why the correlation between the size of the inflorescence and the maximum amount of heat produced corresponds to a particular theoretical curve. The heat is produced by the male and/or the sterile male zones of the inflorescence. The thermogenic process appears to be linked to the metabolic power and structure of the inflorescence (Lamprecht et al., 2002b). It may be supposed that the heat metabolic rate represents the biological constraint and the structure of the inflorescence the physical one. In our models a volume heat metabolic rate of 29 500 Wm⁻³ was used, which corresponds to the value that minimizes the different sums of squares. If we consider that the inflorescence, as a plant tissue, has a density close to 1 g cm⁻³, (1·07 in Seymour, 2001) then we can estimate a corresponding mass heat metabolic rate of 29·5 mW g⁻¹, which can be compared with mass metabolic heat rates documented for other species. Focusing on Aroids, individuals florets may have very high heat rates: 170 mW g⁻¹ in Symplocarpus foetidus (Knutson, 1974; Seymour and Blaylock, 1999), 175 mW g⁻¹ in Philodendron selloum (Seymour et al., 1983; Seymour, 1999) or 400 mW g⁻¹ in Arum maculatum (Lance, 1974). These values are much higher than overall inflorescence metabolic heat rates: 25 mW g⁻¹ in Amorphophallus paeoniifolius (Lamprecht et al., 2002a), 34·1 mW g⁻¹ in Dracunculus vulgaris (Seymour and Schultze-Motel, 1999), 40–70 mW g⁻¹ in Philodendron selloum (Seymour et al., 1983), 68–130 mW g⁻¹ in Symplocarpus foetidus (Seymour and Blaylock, 1999). Except Symplocarpus foetidus, which is a species with bisexual flowers, our estimated metabolic heat rate is a little lower than those measured, but this value is not an aberrant overall mean heat rate. The difference can be explained by the fact that temperature measurements do not take into account evaporation, which is a powerful mechanism of heat dissipation (Seymour, 2001). In fact, in Philodendron, the evaporative heat loss increased with spadix temperature in an exponential fashion such that it is multiplied by a factor of 4·3 between 30 and 45 °C (Seymour et al., 1983). If in Philodendron selloum less than 8 % of the metabolic heat production is lost by evaporative heat loss, in Dracunculus vulgaris the appendix can evaporate more heat than it generates (Seymour et al., 1983; Seymour and Schultze-Motel, 1999; Seymour, 2001).

In order to know if the obtained empirical curve is valuable for the entire family, one may test if the same relationship exists in clades with a different types of inflorescence and thermogenic patterns. For example, is this relationship also true in the tribe Areae where the spadix has a specialized appendix to produce heat that can be empty inside, or in the subfamily Pothoideae where the flowers are bisexual and the thermogenic pattern is about three weeks long?

In conclusion, the maximum temperature difference produced by an aroid inflorescence (from the basal clades of the subfamily Aroideae) corresponds to the value of a thermal model of heat conduction in a cylinder with an internal heat source, suggesting that strong physical constraints apply on this character. However, biological constraints cannot be ruled out as they are of great importance in the thermoregulated phase of Symplocarpus (Seymour, 2004), particularly variations in metabolic heat rates among species or over time. To date, all the available models and simulations are based on fixed parameters and/or a reduced part of the thermogenic process, and do not take into account evaporative heat loss. Further studies are thus necessary in order to understand and simulate the dynamics of the thermogenic process and its evolution.

APPENDIX 1

List of aroid specimens and measured data used in this study.

Species	Spadix temperature (°C)	Air temperature (°C)	Male zone length (cm)	Diameter (cm)	Volume (cm3)	Site*	Source†
Philodendron solimoesense	39·7	24·6	17	2	53·38	FG	2
P. solimoesense	37·7	23·6	15·5	1·9	43·92	FG	1
P. acutatum	39	25	13·8	1·7	31·31	FG	2
P. acutatum	36·9	23·5	13	1·7	29·49	FG	2
P. melinonii	36·9	23·4	11	1·6	22·11	FG	3
P. pedatum	34·6	22·8	9·2	1·4	14·16	FG	2
Montrichardia aborescens	35·5	24·2	8	1·7	18·15	FG	5
Homanolema rubescens	31·8	21·3	6·1	1·3	8·09	MBG	6
P. melinonii	34·7	24·6	11·4	1·6	22·91	MBG	3
M. aborescens	35·4	25·8	9	1·5	15·90	FG	5
P. pterotum	31·4	22·4	13	1·2	14·69	MBG	6
P. distantilobum	30·2	23	9·3	1·2	10·51	MBG	This study
Dieffenbachia maculata	27·9	21·6	10·2	1·1	9·69	MBG	6
P. cannifolium	26·4	20·4	6·7	1	5·26	MBG	This study
Anubias afzelii	27·8	22·2	2·7	1	2·12	MBG	6
D. maculata	25·4	20·5	9·5	1	7·46	MBG	6
Anubias sp	26·4	21·7	2·9	1	2·27	MBG	This study
P. squamiferum	24·4	20·5	6	0·9	3·81	MBG	6
P. squamiferum	26·9	23·7	5·8	0·9	3·69	MBG	4
P. squamiferum	26·9	23·8	5·3	1	4·16	FG	4
Culcasia saxatilis	22·7	20·2	5	0·6	1·41	MBG	This study
Cercestis stigmaticus	30·1	27·6	4·2	0·6	1·19	MBG	This study
Aglaonema crispum	27·8	25·4	3·6	0·6	1·02	MBG	This study
Cercestis stigmaticus	30·8	28·9	4·1	0·5	0·80	MBG	6
Culcasia sp	25·2	23·6	4·3	0·6	1·21	MBG	This study
Culcasia sp	23·2	21·8	4·2	0·5	0·82	MBG	This study
Anubias barteri	25·3	23·9	1·8	0·8	0·90	MBG	6
Anubias barteri	22·7	21·5	2·2	0·6	0·62	MBG	This study

^*Site: FG, French Guiana; MBG, Montreal Botanical Garden.

^†Sources: 1, Gibernau et al. (1999); 2, Gibernau and Barabé (2000); 3, Gibernau et al. (2000); 4, Gibernau and Barabé (2002); 5, Gibernau et al. (2003); 6, Barabé and Gibernau (2000).

Abbreviations used in the text.

ATP	Adenosine tri-phosphate
D	Inflorescence diameter (m)
g	Acceleration due to gravity (ms−2)
L	Length of male zone inflorescence (m)
h CV	Convective heat exchange coefficient (Wm−2 K−1)
h r	Linearized heat exchange coefficient (Wm−2 K−1)
N̅u̅ h	Mean Nusselt's number
Pr	Prandtl's number
p v	Volume-specific heat production rate of the flower (Wm−3)
Rah	Rayleigh's number
Rs or r	Inflorescence radius (m)
S	Lateral surface of the inflorescence (m2)
T S	Surface temperature of the inflorescence (°C)
T i	ith numerically calculated temperature (°C)
T m	Mean temperature (°C)
T C	Constant value at the centre of the flower (°C)
T ∞	Ambient air temperature (°C)
V	Male zone volume (m3)
Y i	ith experimentally measured temperature (°C)
ΔTV	Temperature difference, ΔTV = T(r = Rs) – T∞ (K)
β	Volumic expansion coefficient of air (K−1)
ε	Emissivity coefficient
σ	Boltzmann's constant (Wm−2 K−4)
λ	Conductivity coefficient of the inflorescence (Wm−1 K−1)
λa	Conductivity coefficient of stagnant air (Wm−1 K−1)
δ	Thickness of the conductive boundary layer (m)
ΦV	Dry heat flux leaving the male zone inflorescence (W)
υ	Kinematics viscosity of air (m2 s−1)