Maximum Likelihood Inference and Bootstrap Methods for Plant Organ Growth via Multi-phase Kinetic Models and their Application to Maize

Abstract

• Background and Aims Fitting the parameters of models of plant organ growth is a means to investigate how environmental conditions affect plant architecture. The aim of this article is to evaluate some non-linear methods for fitting the parameters of multi-phase models of the kinetics of extension of plant organs such as laminae, sheaths and internodes.

• Methods A set of computational procedures was developed allowing parameter-fitting of multi-phase models, using the maximum likelihood criterion, in which phases are identified with reference to ontogenic processes. Two bootstrap methods were compared to assess the precision of the estimates of fitted parameters, and of functions of these parameters such as the final leaf length, and the duration and rate of the rapid extension phase. Methods were applied to an experimental dataset, representing the kinetics of laminae, sheaths and internodes along the maize shoot, for two contrasting densities.

• Key Results A set of multi-phase models was proposed to describe the extension of laminae, sheaths and internodes along the shoot. The distinguishable phases differed between laminae, sheaths and internodes. For sheaths and laminae, but not for internodes, the same model could be fitted to all phytomers along the shoot. The variation of parameters along the shoot and between density treatments, as well as derived functions such as the durations of the phases of extension, are presented for laminae. It was the duration of the fast extension period, rather than its rate, which determined the difference in final length between treatments.

• Conclusions Such methods permit a large degree of objectivity and facilitate the analysis of such rather complicated but co-ordinated datasets. The work also illustrates some natural limitations of maximum likelihood methods, and viable ways of overcoming them by including a priori knowledge in the model fitting method are discussed.

INTRODUCTION

Plasticity of architecture is a major way in which plants adapt to the environment. In order to capture these regulations with sufficient detail in simulation models, there is ongoing work in developing plant models that simulate the development of the architecture at the level of individual organs (Fournier and Andrieu, 1998; Gautier et al., 2000). Such an approach requires the ability to quantify experimentally how contrasting growth conditions or differences in behaviour between genotypes impact on the kinetics of extension of individual organs.

A general framework for such a question is to use experimental data to fit parameters of dynamic models. Such models, once fitted, allow faithful reproduction of what has occurred and can be used to calculate variables that have not been measured but may help in interpreting the experiment: Andrieu et al. (2004) present an example where fitting a 3D model was used to investigate the relationship between leaf width and the light environment perceived by the leaf during its extension. In addition, if models are appropriately parameterized, the parameters may have an intrinsic value, which can be used to express the results of an experiment in a compact way, e.g. analysing the effect of a factor on the architecture amounts to analysing the effect of this factor on model parameters (Tardieu, 2003; Reymond et al., 2004).

In this paper we consider the problem of fitting non-linear growth kinetics models to organ length measurements obtained at different dates during the growing season. This problem is related to that of the analysis of longitudinal data (Diggle et al., 2002). The fitting of model parameters from experimental data raises complex issues that are closely linked to the balance between the amount of information contained in the experimental dataset and the number of model parameters (e.g. Monteith, 1996). For a given dataset and model, most common methods for parameter-fitting amount to seeking the set of parameters that minimize some distance measure between observations and predictions. Of course, the choice of the model in itself is an important issue (e.g. Burnham and Anderson, 2002). Some subjectivity exists in the choice between models having few parameters, which favour the accuracy of their estimation, and more complex formalisms that are generally required to express ideas on biological processes.

Global functions such as the Richards equation (Richards, 1959), improved by Zwietering et al. (1990) have been used successfully to fit experimental data representing growth functions, including extension of plant organs (Thomas and Potter, 1985; Stewart and Dwyer, 1994; Gautier et al., 2001). However, besides their flexibility, there is no specific justification to the use of such functions. Alternatively, the development of organs can be seen as a succession of distinct phases: a meristematic phase, the development of an elongation zone, then the functioning of the established growing zone. This succession of phases of organ development can be captured using multi-phase models (e.g. Fournier and Andrieu, 2000; Dosio et al., 2003).

Multi-phase models generally require more parameters than global models, which makes it more difficult to estimate their parameter values. There have been very few examples where multi-phase models of organ extension have been fitted to an experimental dataset for the whole sequence of phytomers along a shoot (Fournier and Andrieu, 2000; Lafarge and Tardieu, 2001; Dosio et al., 2003), and few details have been given on statistical aspects—which are important to appreciate the accuracy of the estimates. When a choice must be made, there exist a number of objective criteria to determine the best of a range of proposed models, such as the MSEP (mean square error of prediction; Wallach and Goffinet, 1987), and the LRT (likelihood ratio test; Seber and Wild, 2003). In our case, such criteria are difficult to apply since we have preferred a strategy by which model selection is made with respect to a set of plant organs rather than on a case-by-case basis (as detailed later), and this has meant a greater degree of subjectivity in the model selection. Moreover it is not our objective to explore this issue in detail nor to select those models that are the best predictors of organ growth but, rather, to focus on the methodological aspects of fitting multi-phase models, and on the accuracy of the estimation of their parameters. This is illustrated in a case study where parameters for multi-phase models of extension for laminae, sheaths and internodes of the whole sequence of maize shoot phytomers were fitted to field measurements.

MODELS

Extension kinetics models

A multi-phase framework, with phases corresponding to distinct biological growth phases, was chosen for extension of laminae, sheaths and internodes as a function of thermal time. In monocots, for laminae and internodes, early growth tends to be exponential (corresponding to the development of the extension zone), whereas later on it is likely to be linear (corresponding to a more or less stationary behaviour of the elongation zone) (Sachs, 1965; Martin, 1988; Morrison et al., 1994; Tardieu et al., 1999; Lafarge and Tardieu, 2001; Muller et al., 2001; Ljutovac, 2002). The period of increasing elongation rate may actually be subdivided into two separate exponential phases of possibly different relative elongation rate (RER), the first one corresponding to meristematic extension, and the second corresponding to the development of the elongation zone (e.g. Williams, 1961; Fournier and Andrieu, 2000; Muller et al., 2001; Dosio et al., 2003). The biological perspective thus suggests a general model of four growth phases:

1. A meristematic phase during which organ extension is exponential.

2. A phase of establishment of the elongation zone, during which growth is exponential, but the RER generally differs from that in the meristematic phase.

3. A phase of rapid, linear extension corresponding to stationary behavior of the elongation zone.

4. A brief phase during which the rate of extension drops to zero.

However, the first two phases may or may not be distinguishable, depending on whether the RERs are sufficiently different and depending also on the duration of each phase. For example, two exponential phases have been consistently identified in the extension of laminae in wheat (Malvoisin, 1984; Ljutovac, 2002; Fournier et al., 2005) and in the extension of internodes for maize and wheat (Fournier and Andrieu, 2000; Ljutovac, 2002). On the other hand, only one exponential phase was identified for sorghum laminae (Lafarge and Tardieu, 2001).

Indeed in numerous cases, especially for sheaths and laminae, our data did not allow the identification of four phases. This was apparent either through visual inspection of the data, which did not reveal, for example, two exponential phases, or else became apparent because it was impossible to fit a model using the methods described later. Moreover, it soon became clear that we could not identify a phase of decay of growth rate from our data, and hence we merely approximated that the rapid, linear phase stops abruptly at the end of organ extension.

Thus even accepting the four-phase framework presented above, the number of phases that can actually be identified is an open question. It depends on the biological behaviour (if the phases are sufficiently long and contrasted) and on the experimental protocol (sampling interval, accuracy of measurement). Moreover, the objective of the work, to compare the effect of treatments on the extension of the series of phytomers, imposes that the choice of models is consistent between phytomers and treatments.

In order to address this question, we defined a hierarchy of models and a strategy for model choice. These models have between one and three growth phases and are defined in detail below. We then adopted the following strategy for model choice. For a given organ type, and for all phytomers, data was displayed visually on normal and log scales to attempt to distinguish phases. A choice of a single model for all organs of this type was then made based on which model appeared to be the most generally suitable across all phytomers. An attempt would then be made to fit the chosen model to all organs of this type. In those cases where this general model could not be fitted with the algorithms described in the next section, the data was inspected again, and a different model was attempted. Because the methods used generally fail if there are too many parameters in the model in relation to the data (as discussed later), this alternative model generally had fewer parameters than the first one attempted.

The standard model (containing two growth phases) supposes that Phases 1 and 2 are indistinguishable, having a single exponential phase for the meristematic growth and the establishment of the elongation zone, eqn (1), followed by a linear extension phase for stationary extension, eqn (2), and a plateau, eqn (3) when extension is complete. The model is as follows:

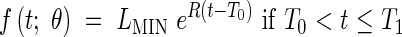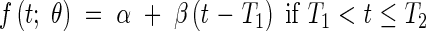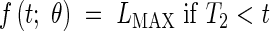with constraints

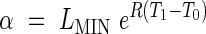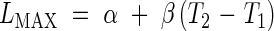to ensure continuity of the function at the phase transitions. The model defined by eqns (1)–(5) is referred to as Model 2. We may or may not wish to ensure the continuity of the 1st derivative at the transition between the exponential and linear phases, which would give the additional constraint

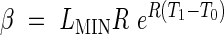The model defined by eqns (1)–(6) is referred to as Model 2-C. L_MIN may be fixed arbitrarily to be the length at which the modelling begins, which means that there are five parameters in Model 2 (R, T₀, T₁, T₂, b) and four parameters in Model 2-C (R, T₀, T₁, T₂).

In certain cases, it is possible to distinguish the two early exponential phases. This allows a model with three dynamic phases; meristematic growth [eqn (7)], establishment of the elongation zone [eqn (8)], and stationary elongation [eqn (9)]. It has analogous constraints to Model 2-C, and is given thus:

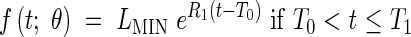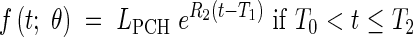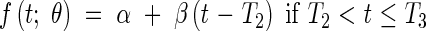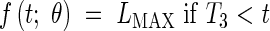where L_PCH is the length at the first change of phase. In this case the continuity constraints take the form

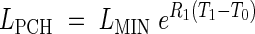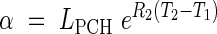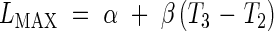and the constraint on the continuity of the derivative.

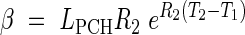This model is further referred to as Model 3-C. Given that L_MIN may be arbitrarily assigned as in the other models, it includes six parameters to be estimated: R₁, R₂, T₀, T₁, T₂ and T₃.

In other cases, the data only suggested an exponential extension followed by a plateau. In these cases we have proposed the model (henceforth called Model 1) given as follows:

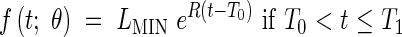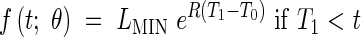In this case there are only three parameters to estimate: R₁, T₀ and T₁.

The RER in the early phases of organ extension is an informative measure of the conditions of establishment of the growing zone. This is given by R₁ and possibly R₂ in our models. However there is also particular interest in the final organ lengths, and the rate and duration of the fast (linear) phase of growth, since the greater part of the organ extension generally occurs in the linear extension phase. Although these quantities are not given explicitly as model parameters, they may be calculated as functions of these. The final lengths [eqns (5), (13), (16)] and the slopes of the linear phase [eqns (6), (14)] are obtained directly from the model definitions, whereas the duration of the linear phase is T₃ − T₂ in Model 3-C, T₂ − T₁ in Models 2 and 2-C, and T₁ − T₀ in Model 1. The use of bootstrap techniques (presented later) has allowed an estimation of the precision of the estimates of these quantities, and thus permitted a comparison between treatments. A summary of model names and characteristics is given in Table 1.

Table 1.

Summary of model names and characteristics

Name	Phases	Continuity of slope between exponential and linear phases	Equations	Number of parameters
Model 1	Exponential—Plateau	N/A	(15), (16)	3
Model 2-C	Exponential—Linear—Plateau	Yes	(1)–(6)	4
Model 2	Exponential—Linear—Plateau	No	(1)–(5)	5
Model 3-C	Exponential—Exponential—Linear—Plateau	Yes	(7)–(15)	6

Maximum likelihood estimation of model parameters

Suppose we have the following model for organ elongation,

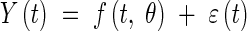where Y(t) is the measured value of the organ length, f(t, θ) is one of the models defined in earlier with θ the vector of model parameters, and ε(t) is the residual term—assumed to be normally distributed: ε(t) ≈ N(0, σ_t²) where σ_t² is the variance of ε(t).

For any value of the vector θ, the probability P[Y(t_i)|θ,σ_ti) of observing a measured data pair [t_i, Y(t_i)], for a given σ_t is given by:

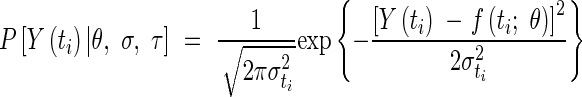The likelihood Λ of observing a set of data points [t₁, Y(t₁)],…,[t_n, Y(t_n)] is the product of the probabilities of observing the individual data pairs:

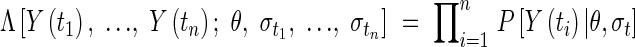Maximum likelihood techniques seek the values of θ that maximize the probability of observing the given experimental data. This differs from minimizing the RMSE (root mean squared error) in that the likelihood depends not only on the difference between observed and measured data but also on σ_t: in the case were σ_t is not constant, maximum likelihood techniques aim to appropriately weight data pairs according to σ_t. Numerical methods (a modified Gauss–Newton method is used here, see for example Seber and Wild, 2003; see also Press et al., 1987 for a general introduction to non-linear optimization methods) allow location of a local maximum of this likelihood function if an initial solution is proposed, via the iterative solution of linearized regression problems.

The computation of the likelihood then requires the specification of 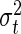for all dates of measurements. It is generally the case that for growth data of this type the variance is non-constant, increasing with organ size; however, it is not possible to estimate directly from replicates here, since this requires empirical calculation of the variance of the residuals at each date, and in our case there are often dates at which we have only one data point. Consequently, we defined a statistical model that relates to the organ length as follows:

for which both σ and τ are two unknown parameters. Parameterization of the model now additionally requires parameterization of the variance model for the residuals, necessitating the estimation of two additional parameters. The function gnls in ‘R’ (R, http://www.r-project.org; see, for example, Ellner, 2001 or Ripley, 2001), for example, is an optimization procedure that allows the incorporation of such a variance model and will estimate, using the maximum likelihood criterion, the values of σ and τ at the same time as θ. The incorporation of a realistic variance model should improve the realism of the likelihood function and yield more accurate estimations. This claim is explored later.

Assessing the accuracy of parameter estimates

The maximum likelihood method described above can be used to estimate the model parameter values. If we performed another experiment under the same conditions, the observed values Y(t₁),…,Y(t_n) would be different and, consequently, the estimated parameter values would also be different. The quantity var(), where is the maximum likelihood estimate of the model parameters, expresses the accuracy of the parameter estimates and hence the confidence in the parameter estimates. Its estimation is incorporated in most standard solvers.

In our example, we are not only interested in the model parameters θ but also in composite functions of the model parameters—for example, the duration of the linear phase, d_LIN, and the final length, L_MAX of the organ. Although there exist approximate formulae for var(), and formulae for d_LIN and L_MAX as functions of θ, it is not generally possible to obtain a parametric estimate of their standard errors.

The non-parametric bootstrap is a resampling method offering a solution to this problem. It is possible, working with the available data only, and using re-sampling techniques, to simulate alternative datasets that might have been obtained from the same field trial, and to use these simulated datasets to obtain a distribution of values for the model parameter estimates. Once this is done, quantities such as the standard error of the parameter estimates, and composites, may be calculated from the series of the estimated values obtained with the different samples. Under certain assumptions, as the number of re-samples becomes large, the standard error derived from the bootstrap method converges on the real standard error (e.g. Efron and Gong, 1983).

In general, if the dataset contains n data points, then the standard re-sampling method is to simply select n data points randomly, with repetition, from this dataset. Since there is repetition, this means that some datapoints may be selected more than once and some not at all. In our case, where each data point is in fact a (time, organ length) pair, there are possible problems associated with this method, since it is likely that the resampled distribution does not reproduce the original sampling regime, i.e. it does not respect the number of samples at a given point in time. Aside from the fact that this is contrary to the stated aim of bootstrap resampling above (to simulate alternative datasets that might be obtained with the same sampling regime on the same data), there is also the possibility that any given simulated data set actually contains fewer dates than the original, which may prohibit a numerical solver from converging. We thus also present an alternative, which focuses on resampling the residuals as opposed to the data pairs.

In this alternative method, which is outlined in Efron and Tibshirani, 1993, we first fit the model, and obtain the distribution of the errors by subtracting the estimated length from the observed value for all data points. Then, supposing the errors are normally distributed at any given point in time, we may use the variance model with the estimated 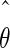to obtain a new set of errors E₁,…,E_k,…,E_M (where E_k is the set of ε_k,i, i = 1,…,n, with n the number of data points, sampled randomly from the normal distribution 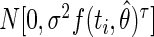), and then add these to the model in order to simulate new datasets, D₁,…,D_k,…,D_M, (with ). Assuming that the variance model is appropriate for the original data, this yields simulated datasets with, on average, the same properties as the original with respect to the residuals.

Henceforth we shall call the first of these two methods the non-parametric bootstrap, and the second the semi-parametric bootstrap.

The non-parametric bootstrap method performs a raw resampling of data pairs with repetition, and does not respect the original sampling regime. However, the ability of the semi-parametric method to generate appropriate simulated datasets depends on the accuracy of the kinetics model employed, and on whether the variance model is appropriate. There are thus potential problems with both methods. Since we have limited confidence in the applicability of our kinetics and variance models (it being partly the purpose of this work to determine these), we have chosen the non-parametric method as the standard one, and have applied it to all cases for which we successfully fitted a model. However, for the laminae of the ND treatment (introduced in the following section), we also used the semi-parametric method, in order to make a comparison with the non-parametric one. This is examined later.

EXPERIMENTS

Agronomic treatments

The experiments were performed to investigate how population density impacted on the development of successive leaves in maize (Zea mays L.) in field conditions. The hybrid ‘Déa’ was sown on 15 May 2000, at two contrasting densities: 9·5 and 30·5plantsm⁻². They will be referred to below as normal density (ND) and high density (HD), respectively. The experiments were carried out on the INRA campus of Thiverval-Grignon, France (48°51′N, 1°58′E) on a silty loam soil fertilized with 140 kg ha⁻¹ N, 100 kg ha⁻¹ P₂O₅, 100 kg ha⁻¹K₂O before sowing. A complementary application of 30 kg ha⁻¹ N was applied as a spray on 23 June, 2000 (corresponding to leaf stage 10·6). Plots were irrigated regularly and weeds were carefully controlled both manually and through herbicide treatment.

Monitoring plant development

Our sampling strategy was characterized by (1) the use of reference plants (rather than random sampling to select the plant to be dissected), and (2) the use of the median as the target criterion. This strategy was chosen because random sampling would have required rather large samples to obtain accurate parameter estimates, and the dissection of such large samples of plants would have been too time-consuming. This strategy is in agreement with the objective of the considered models, which aim to represent the growth of a median plant, without the expectation that the model will hold for all plants. (For example, in the HD treatment, a small percentage of plants showed a decrease in the rate of development and eventually died, as was the case for two out of the 15 reference plants. The use of the median of tagged plants as a target criterion allowed for robustness against such atypic behaviour.) Although we could have chosen the mode rather than the median, both were very close and the median is easier to establish in the field.

Estimating the kinetics of organ extension by destructive measurements requires that successively sampled plants will have developed synchronously. To ensure that this requirement was fullfilled, the sampling protocol included non-destructive monitoring of the development of a set of representative plants that served solely as a reference for choosing the plants to be dissected. The following was performed in each of the treatments to achieve this. At stage V3, 60 plants were randomly chosen and the median values for final length of Lamina 1 and for the emerged length of Lamina 3 were calculated. Then fifteen plants were tagged, being chosen so that their development was close to the median (within 2 cm for emerged length of Lamina 3 and 1 cm for final length of Lamina 1). Two or three times per week the number of visible and ligulated leaves, the length of the exposed part of the two youngest visible leaves, and the length of the youngest ligulated leaf were measured for each of the tagged plants. The median values for leaf stage and for length of the youngest ligulated leaf, calculated on tagged plants, served as references to select from between two and four (usually three) plants, which were dissected for measurements of the lengths of all internodes, sheaths and laminae. Destructive measurements were performed on the same days as the non-destructive measurements from stage V3 until the end of stem extension. Destructive measurements were performed under a binocular microscope (maximum magnification 50×) for early stages of development and with a ruler when dimensions exceeded 1 cm. It was found to be difficult to establish the boundaries of sheaths and internodes accurately in their early stages of development, and hence only measurements of larger than 3 mm were taken into account when fitting the models. This limit was not imposed for laminae.

At dissection, the plants were controlled again for homogeneity of the size of mature leaves and of final leaf number. Before ligulation of leaf 10, plants for which the length of the last ligulated leaf differed by more than 10% from the average length for that leaf number were disregarded. After ligulation of leaf 10, the selection was done based on the length of leaf 10. After floral transition the final number of leaves could be established, varying from 14 to 16, and being 15 in approximately 70% of the cases. Thus, after floral transition, only data from plants having exactly 15 leaves were considered for analysis.

Meteorological measurements and calculation of thermal time

For each treatment, the temperature of the soil at a depth of 3·5 cm, within a row and close to a plant (within 1–2 cm), was monitored in four places using thermocouples. Once the apices reached the level of the soil, the temperature of the growing zone was estimated using two thermocouples per treatment inserted behind a sheath, and repositioned regularly to maintain them at the height of the apex (as determined by dissection of similar plants). The thermocouples were inserted on the north-facing part of the stem to avoid direct sunlight on the sheath enclosing the thermocouple. The temperature measured in this way is representative of that of the growing zone (Birch et al., 2002; Fortineau et al., 2002). Data from equivalent thermocouples were consistent and were averaged. Finally, growing zone temperature was calculated from soil temperature when the apex was below the soil level, then from temperature monitored within the sheaths. Thermal time was calculated on an hourly basis, considering T_base to be 9·7°C.

RESULTS

We first present some results of the model-fitting on the data for laminae, sheaths and internodes, and compare the results for the two density treatments. We then exploit the laminae data for a comparison of the two bootstrap methods mentioned earlier, and to assess the importance of using an appropriate (in this case non-constant) model for the residuals.

Model choice and parameter fitting

Laminae

Visual observation of the log scale representation of the lamina data did not reveal any break points, such as might have resulted from the existence of two exponential phases or from a discontinuity in the extension rate at the onset of the linear phase. This suggests Model 2-C, but Model 2 was also tested and the two were compared. Comparison of the extension rates calculated with Model 2 before and after the exponential–linear transition suggests that there probably is a break, but with some non-systematic variation with phytomer number. On the other hand, the RER, the LER during the linear phase, and duration of all phases were very similar in both models. It was finally concluded that Model 2-C was the most appropriate since it has one free parameter less. Consequently results are presented for this model only.

In a first step, T₀ was estimated independently for each phytomer, but this resulted in large standard errors in T₀ and R₁ for some leaves for which too few data were available in the early stages of growth. To overcome this, we estimated T₀ (taken as the moment at which primordia measured 250 µm) independently of the model. Independently of treatment, we verified that there was a constant ratio between lengths of successive primordia in the early stages of growth [with L_n = 2·03L_n+1, R² = 0·85]. The plastochron index, PI (Erickson and Michelini, 1957), was calculated for a decimal count of the number of initiated leaves. T₀ was then estimated for all leaves from a linear regression of PI against thermal time (R² = 0·97).

This reduced the number of parameters to be estimated to three (R₁, T₁ and T₂). The model was successfully fitted on all phytomers (four to 15) with R² between 0·96 and 0·99 in most cases. Figure 1A illustrates the example of Phytomer 9. There appeared to be no period of leaf development for which the model departed systematically from the measurements, and thus a two-phase model seems to represent our measurements very faithfully. Most errors came from the between-plant variability of the plateaux at final length.

Fig. 1.

(A) Length of Lamina 9 in ND as a function of thermal time after emergence. Fitted with Model 2-C. Dotted verical lines represent, from left to right, T₀, T₁ and T₂. Left: proportional scale; right: log scale. (B) Length of Sheath 9 in ND as a function of thermal time after emergence. Fitted with Model 2. Dotted vertical lines represent, from left to right, T₀, T₁ and T₂. Left: proportional scale; right: log scale. (C) Length of Internode 9 in ND as a function of thermal time after emergence. Fitted with Model 3-C. Dotted vertical lines represent, from left to right, T₀, T₁, T₂ and T₃. Left: proportional scale; right: log scale. (D) Length of Internode 14 in ND as a function of thermal time after emergence. Fitted with Model 1. Dotted vertical lines represent, from left to right, T₀ and T₁. Left: proportional scale; right: log scale.

Internodes

Visual inspection of the log representation of the data for internodes revealed the presence of a break point for the central phytomers, thus suggesting a model with two exponential phases (Fig. 1C). Model 3-C was successfully fitted for Internodes 8 to 13 for ND and Internodes 9 to 12 in HD. For lower (6 and 7) and upper (14 and 15 in ND, and 13–15 in HD) phytomers, visual observation suggested that a single exponential represented the data well (Fig. 1D). Indeed, in these cases Model 3-C could not be fitted but Model 1 could. Internode 8 in HD appeared have an intermediate behaviour between that of lower (6, 7) and medium (8–13) phytomers and was fitted with Model 2-C. Finally, the hierarchy of models could be used to fit to all phytomers and, as with lamina, there was no range of phytomer development where the models showed a bias compared to the measurements, suggesting the number of phases considered reflected the actual behaviour quite accurately. The R² ranged between 0·96 and 0·99, except for one lower value for Internode 6, for which there was quite high between-plant variability. This variability may have resulted in the failure to discern two exponential phases, however this is not likely for Phytomer 7 and certainly not the case for the upper internodes, which appear to have a qualitatively different behaviour from the median ones.

Sheaths

Visual observation of sheath data show a period of exponential extension, separated by a discontinuity in RER from a period of decreasing RER (Fig. 1B). There was no strong evidence that the period of decreasing RER corresponded to a linear phase as, for some phytomers at least, it appeared to comprise a period of increasing LER and a period of decreasing LER. However, attempts to fit a model with more than two phases were unsuccessful as the solver did not converge, which might be explained by the lack of sufficiently detailed data. Only Model 2 could be fitted on a consistent range of phytomers, i.e. 6 to 15 with R² in the range 0·97 to 0·99. It is, however, important to state that the ‘linear’ rate of extension calculated for sheaths may reflect some average between a period of increasing and decreasing growth rate, rather than expressing a stationary state of the growing zone.

Table 2 recapitulates the model fitted for each organ. It demonstrates that a consistent choice of model could be fitted, allowing comparison of parameters between treatments and, with a few exceptions, between phytomers.

Table 2.

The model fitted to lamina, sheath and internodes for each of the phytomers in ND and HD treatments

	Lamina											Sheath											Internode
	ND					HD					ND					HD					ND					HD
Phytomer	Model	R2	RMSE	Model	R2	RMSE	Model	R2	RMSE	Model	R2	RMSE	Model	R2	RMSE	Model	R2	RMSE
4	2-C	0·96	1·79	2-C	0·96	2·09
5	2-C	0·97	2·21	2-C	0·97	2·91
6	2-C	0·98	2·72	2-C	0·98	3·30	2	0·97	0·93	2	0·98	0·93	1	0·83	1·01	1	0·90	1·17
7	2-C	0·99	2·43	2-C	0·99	3·52	2	0·98	0·87	2	0·98	1·01	1	0·94	1·20	1	0·96	1·21
8	2-C	0·99	2·81	2-C	0·99	3·71	2	0·99	0·74	2	0·97	1·08	3-C	0·97	1·16	2-C	0·98	1·02
9	2-C	0·99	2·75	2-C	0·99	3·81	2	0·99	0·61	2	0·99	0·72	3-C	0·98	1·14	3-C	0·97	1·44
10	2-C	0·99	2·77	2-C	0·99	3·24	2	0·99	0·75	2	0·99	0·70	3-C	0·99	1·07	3-C	0·99	1·04
11	2-C	0·99	2·74	2-C	0·99	2·97	2	0·99	0·67	2	0·99	0·66	3-C	0·98	1·24	3-C	0·98	1·41
12	2-C	0·99	2·72	2-C	0·98	3·01	2	0·99	0·7	2	0·99	0·67	3-C	0·98	1·52	2	0·98	1·14
13	2-C	0·99	2·96	2-C	0·98	3·01	2	0·99	0·55	2	0·99	0·61	3-C	0·99	0·95	3-C	0·97	1·14
14	2-C	0·99	2·29	2-C	0·97	2·93	2	0·99	0·57	2	0·99	0·64	1	0·98	1·26	1	0·99	0·69
15	2-C	0·96	3·45	2-C	0·92	2·52	2	0·99	0·66	2	0·97	0·77	1	0·98	1·10	1	0·99	0·54

In general, the quality of the fit of the models was good, with R² between 0·92 and 0·99 for laminae, 0·97 and 0·99 for sheaths, and 0·90 and 0·99 for internodes, except for one low value of 0·83 for Internode 6 of ND. As examples, we show in Fig. 1 the fitted models for the three components of Phytomer 9 for ND.

Comparison of the 2 density treatments

In Fig. 2 we compare the RER of the exponential phase and the slope of the linear phase of Model 2-C estimated for the laminae in both treatments. We also compare the modelled final lengths, and modelled durations of the linear phase. In all cases, the standard errors have been calculated via the non-parametric bootstrap method, using 500 repetitions.

Fig. 2.

Estimated values for (A) final length, (B) RER (R₁), (C) slope in the linear phase, and (D) duration of the linear phase for the laminae in ND and HD. Error bars represent ± 2 s.e., as calculated from the bootstrap.

Figure 2A shows the differential effect of density treatment on the final length of the laminae. Mature laminae from lower phytomers (1–8) are longer for HD in comparison with ND, whereas the opposite occurs for the laminae of Phytomer 9 and higher. This behaviour is similar to that observed in previous studies (e.g. Sonohat and Bonhomme, 1998). Figure 2(B–D) permits an analysis of how these changes occurred:

1. In both treatments, R₁ decreased with phytomer number, with a plateau for Phytomers 11 to 14. R₁ did not differ between treatments for lower phytomers, whereas for Phytomers 8 to 11 the decrease in R₁ was much stronger for HD than ND. Thus R₁ at the plateau was lower in HD (0·032 °C⁻¹ d⁻¹) than in ND (0·041 °C⁻¹ d⁻¹).

2. The rate of extension during the linear phase was either similar in the two treatments, or slightly higher in HD, for those leaves that had a lower RER. Thus, the variation in the duration of exponential phase over-compensated most of the variations in RER.

3. Most of the differences in final length were due to changes in the duration of the linear phase. Although both duration and rate of elongation positively influence final length, it is evident from Fig. 2 that the differences in rate and final length for higher phytomers are opposite in sign, whereas duration and final length are of the same sign and positively correlated (R² = 0·91, regression not shown). Thus in HD the increased duration of the linear phase for the lower phytomers (4–8) was responsible for most or all of the larger final length, and had the opposite effect for Phytomers 10–15, in which the reduced duration of the linear phase more than compensated for the higher rate of extension, and thus yielded a shorter final length.

What finally emerges from this analysis is that the differences in the final lengths are to a large extent attributable to the differences in the durations of the linear phase. Thus bottom leaves in the HD treatment were longer because they extended with the same RER and LER as in ND, but for a longer time. Upper leaves were shorter, despite a higher LER, because the duration of extension was reduced. The fact that changes in duration determines most of the changes in final length is contrary to the approximation made in most crop models that the thermal time schedule is fixed, and to the idea that the reduced availability in assimilate would determine a reduced final length through a slower functioning of the growing zone. It shows that understanding how the duration of the growth phase is regulated is important in understanding the regulation of architecture. This in turn militates for the development of models that explicitly treat the timing of phases of extension, and in procedures that allow estimation of these parameters.

The bootstrap methods

As stated earlier, the non-parametric bootstrap method applied to estimate the standard errors of the quantities analysed above may lead to non-convergence of the numerical minimization method used. However, the semi-parametric bootstrap method has the disadvantage that the resamples generated depend on the models chosen. Both methods have been tested against each other using the laminae data for ND, and against the solver gnls for those parameters that are estimated by gnls: comparisons have been made of the standard errors of the parameters R₁, T₁ and T₂ calculated from the bootstraps, with those obtained parametrically from gnls.

From Fig. 3 we observe, firstly, that the points follow reasonably closely the line of slope 1 passing through the origin, implying that the results returned from both bootstrap methods are in good agreement with the results from gnls. The RMSEs for T₁, T₂ and R_1, averaged over all phytomers are, respectively, 0·13 °Cd, 0·30 °Cd and 0·000020 for the non-parametric bootstrap, and 0·23 °Cd, 0·35 °Cd and 0·000039 for the semi-parametric bootstrap. This suggests that, since there is good agreement on those values that gnls returns, then for the standard errors of those composites of parameters which gnls is unable to return (i.e. the slopes and durations of the linear phase, the final organ length, etc.), we may trust those values obtained from the bootstraps.

Fig. 3.

Comparison of the standard errors for (A) T₁, (B) T₂ and (C) R₁ of Model 2-C, obtained using gnls (abscissa), the non-parametric bootstrap (open circles) and the semi-parametric bootstrap (solid squares). There is one data point of each type for Laminae 4–15.

Use of a non-constant model for the variance of the residuals

The method used to estimate the models' parameters assumes that the variance of the residuals increases as a function of organ size (eqn 19).

Although the data clearly suggested this functional form, one may question the practical value of imposing it during the minimization. As an exploration of this point, simulations have been carried out to test for the expected improvement in the estimation obtained by using of the appropriate variance model.

Fitted parameter values from the laminae of ND were used, together with the fitted σ and τ for the variance model to simulate, in each case, 100 new data sets in an identical way to the semi-parametric bootstrap method. We then performed non-linear regressions using gnls, using both a constant variance model and the power form model of eqn (18) in the calculation of the likelihood function.

It is known that both methods produce unbiased estimators (Huet et al., 2003). We confirmed that we had sufficient repetition in the tests by testing for bias and found it to be very small in general. The mean of the parameter values estimated in the repetitions was, in both cases, always within 0·1 % of that used to generate the data.

The variances in the estimated parameter values are shown in Fig. 4. In general, these variances were smaller when assuming a non-constant variance model than when assuming constant variance (although there are three phytomers for T₂ for which this is not true). In particular, there is a notable reduction in the variance of R₁ and T₁. This is likely to be because assuming a constant variance results in a low sensitivity of the optimization procedure to the behaviour of the model in the early growth phase, when the size is only a few millimetres.

Fig. 4.

The variance in the estimations of parameters (A) T₁, (B) T₂ and (C) R₁ for the laminae from ND assuming constant variance of the model residuals, ε(t), (open bars) and non-constant variance (solid bars).

DISCUSSION

The procedures developed here were intended to automate the estimation of multi-phase models describing the extension of plant organs. In summary, they impose a reasonable functional form for the model of the residuals and attempt to estimate, via the maximum likelihood criterion, all parameter values for a given organ. Except for a few cases, it was possible to propose a coherent set of models for laminae, sheath and internodes of different phytomers. This is important for comparison of model parameters between phytomers or treatments. We have illustrated, using data for leaf extension in maize, how this allowed quantitative comparison of the behaviour across two density treatments and showed that differences in mature length of the laminae resulted from differences in the duration of the phases of extension, rather than differences in the rate of extension.

Both proposed bootstrap methods appear, at least on the data studied, to yield reasonable estimates of the standard errors of the estimated parameters, and thus may be trusted to estimate the accuracy of composite functions of these parameters. Although it is true that the standard errors were relatively small in this case, and thus that it does not constitute a thorough test, from the behaviour in the case of laminae we may reasonably suppose that a large uncertainty would at least be represented using these methods.

The protocol for selecting plants to be measured allowed the assumption that individuals were nearly synchronous in their development and thus in the phase changes of their organs. There is, however, some variation and this is mainly due to differences in emergence date between plants. It is likely that a large part of what is taken to be variation of the dependent variable here is in fact error in the independent variable. In future, such variations could be reduced by using more severe criteria for selecting the plants to be dissected.

In this work, particularly during the choice of model for extension, we were confronted with problems that may arise when the complexity of the model is too great compared to the amount of information in the data set. Decreasing the complexity of the model generally improves the accuracy of parameter estimates, but may reduce the ability to interpret parameter values if distinct processes are expressed in a single parameter. This trade-off imposes on us the need to find a compromise.

When the objective of the parameter-fitting is to improve the prediction of the model, then there exist objective criteria, such as the MSEP, that determine when one choice of model is superior to another for a given data set. In our case the objective was not prediction—rather, it was to make a quantitative comparison of the behaviour of several phytomers and to establish the effect of density treatment on this behaviour. We thus considered model parameters to have an intrinsic value, and this led us to retain a model of sufficient complexity that the parameters can be interpreted from a biological point of view. The cost of this strategy is a reduced accuracy of the parameter estimates. It is probably not possible in such a case to define a unique criterion by which to compare different parameterizations (since the degree of ‘interpretability’ of parameters can not be quantified), and, as a consequence, there will always be some subjectivity in the model choice. However the variance of the parameter estimates allows us to define the confidence with which the results obtained from this choice can be interpreted, and this variance, of course, increases when the number of parameters is high compared to the number of observations.

Other than the choice of the model, two ways to improve the accuracy of the parameter estimates are:

1. To obtain a higher quality data set (redesigning the experiment plan).

2. To incorporate information external to the data set.

For the first of these there exist methods to determine the optimal design of an experiment in terms of estimating the parameters of a given model (e.g. Monod et al., 2002).

For the second, there is the possibility of using either Bayesian methods, or a ‘whole-plant’ model in order to incorporate a priori knowledge into the model-fitting. Bayesian methods allow the use of both the likelihood and an a priori distribution of θ (perhaps parameterized from other sources) to obtain the a posteriori estimates of θ. The downside of such an approach is that the result of the calculation depends on the a priori distribution, and thus there is a risk of loss of objectivity in the method, particularly when it is difficult to define the a priori distribution. In our case, this is further complicated by the fact that candidate a priori information is not so much based on the distribution of the value of parameters considered independently, but rather in the relations that should exist between parameters, due to the lamina–sheath–internode sequence of phytomer development, the acropetal pattern of shoot development, and the co-ordination between successive phytomers along the shoot (Sharman, 1942; Malvoisin, 1984; Skinner and Nelson, 1995; Fournier and Andrieu, 2000).

Incorporating a priori knowledge on developmental co-ordinations could be achieved using a more sophisticated ‘whole-plant model’, and preserving coherence at the plant level by fitting several organs simultaneously with respect to each other. For example, if a simplified analytical function may be used to describe the evolution of a parameter with phytomer number (such as the bell-shaped curve, Dwyer et al., 1992), then the number of parameters at the whole-plant level may be reduced. When such a global function cannot be derived, but information is sooner expressed as constraints coupling parameter values (e.g. for expressing developmental co-ordinations), an alternative might be to incorporate a cost function (Seber and Wild, 2003) so that the problem is no longer simply to maximize the likelihood, but also to penalize parameterizations that appear unrealistic in relation to other organs. In both of these cases, where several organs are to be parameterized simultaneously the number of parameters to be estimated at one time may be rather large (from a few tens to a few hundreds), and the problem thus becomes computationally expensive. However, general maximizers designed for large parameter sets do exist—for example, the routine M1QN3 in the MODULOPT library of INRIA (INRIA, 2002; Gilbert and Lemarechal, 1989)—and it might be interesting to apply them to this case.

A description of the computational procedures developed is contained in Hillier and Andrieu (2003), and may be obtained together with the procedures by contacting the corresponding author.