Modelling Below- and Above-ground Biomass for Non-woody and Woody Plants

Abstract

• Background and Aims Intraspecific relationships between below- and above-ground biomass (M_B and M_A, respectively) have been studied extensively to evaluate environmental effects on growth and development at the level of the individual plant. However, no current theoretical model for this relationship exists for broad interspecific trends. The aims of this paper are to provide a model and to test its predictions using a recently assembled, large database (1406 data entries for 257 species).

• Methods An allometric model was derived to predict the relationship between M_B and M_A for non-woody and woody plants based on previously developed scaling relationships for leaf, stem and root standing biomass and annual growth rates. The predictions of this model were tested by comparing the numerical values of predicted scaling exponents (the slopes of log-log regression curves) with those observed for the database.

• Key Results and Conclusions For non-woody plants and the juveniles of woody species, the model predicts an isometric scaling relationship (i.e. M_B ∝ M_A). For woody plants, a complex scaling function is predicted. But, for a particular set of biologically reasonable conditions, the model predicts M_B ∝ M_A across woody plants. These predictions accord reasonably well with observed statistical trends when non-woody and woody plants are studied separately (n = 1061 and 345 data entries, respectively). Although the reliability of regression formulas to estimate M_B based on M_A measurements increased with increasing plant size, estimates of M_B can be as much as two orders of magnitude off, even when using regression formulas with r² ≫ 0·90 and F ≫ 53 000.

INTRODUCTION

The relationship between above- and below-ground biomass (M_A and M_B, respectively) is frequently used to assess growth responses to ambient ecological conditions, or to evaluate the responses of individual plants to experimental manipulation (e.g. Crist and Stout, 1929; Bray, 1963; Monk, 1966; Ledig and Perry, 1965; Hunt and Burnett, 1973; Hunt and Lloyd, 1987). The literature treating this relationship indicates that growth-limiting conditions typically evoke increased allocations of biomass to those organs or body compartments that are initially most negatively affected (see Hunt and Lloyd, 1987, and references therein). However, despite recent reviews of the root-property dynamics of broad-scale ecological associations or taxonomic groups (Canadell et al., 1996; Jackson et al., 1996; Schulze et al., 1996; Levang-Brilz and Biondini, 2002), there is no current model for predicting M_B based on measurements of M_A across diverse species.

Here, such a model is presented and tested by comparing predicted scaling exponents (slopes of log-log regression curves) against those observed using a large database, which spans nine orders of magnitude in M_A and ten orders of magnitude in M_B. This database is also explored to determine whether M_B can be reliably estimated using interspecific M_B vs. M_A log-log regression curves.

The model emerges directly from prior allometric models, which predict that annual leaf, stem and root growth rates will remain isometric with respect to one another (i.e. scale as one-to-one proportionalities), and that standing leaf biomass will scale as the 3/4 power of stem (or root) biomass for woody plants (Niklas and Enquist, 2002a, b; Enquist and Niklas, 2002). The model that emerges from these scaling relationships predicts that below-ground biomass will scale isometrically with respect to above-ground biomass across non-woody plants (i.e. M_B ∝ M_A) and a nearly isometric relationship across woody plants (i.e. M_B ∝ M_A^∼1). To test these predictions, data were gathered for M_A and M_B (or for standing leaf, stem and root dry weight per plant to compute M_A and M_B). Data were also gathered for annual leaf, stem and root growth rates, because some authors suggest that the potential for organ growth influences the M_A and M_B relationship in addition to the absolute and relative amounts of above- and below-ground environmental stress (e.g. Hunt and Nicholls, 1986; Hunt et al., 1987). Data on growth rates were also important because they provide a method of determining whether shifts in M_A and M_B quotients result from changes in growth rates or the accumulation of secondary tissues in the stems and roots of woody plants (Grime and Hunt, 1975; Charles-Edwards et al., 1986; Hunt et al., 1987).

MATERIALS AND METHODS

The allometric model

Across vascular plants with woody stems and roots, prior allometric models predict that standing leaf biomass M_L should scale as the 3/4 power of standing stem biomass M_S, that M_L should scale as the 3/4 power of standing root biomass M_R, and that M_R will scale in direct proportion with respect to M_S. Therefore, across woody plants, 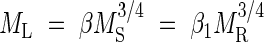and M_S = (β₁/β)^4/3M_R, where β denotes an allometric constant (the y-intercept of the log-log regression curve) whose subscript distinguishes its numerical value from that of other constants (Niklas and Enquist, 2002a, b).

Across non-woody plants and woody plant juveniles that lack secondary tissues (or have had insufficient time to accumulate them), standing M_L, M_S and M_R are equivalent to the annual leaf, stem and root growth rates, denoted by G_L, G_S and G_R, respectively. Therefore, across these plants, G_L = β₂G_S = β₃G_R and M_L = β₂M_S = β₃M_R (Niklas and Enquist, 2001).

Assuming that roots are the only underground organs such that M_R = M_B, it follows from these relationships that, for non-woody plants,

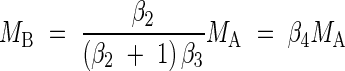whereas for woody plants, the relationship between M_B and M_A should comply with the formula

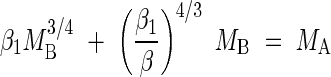Although eqn (1) predicts that the M_B and M_A of non-woody plants should invariably scale isometrically, eqn (2) stipulates a more complex scaling relationship for woody plants, i.e. the scaling exponent for M_A vs. M_B can range theoretically between 0·75 and 1·00 depending on the numerical values of β and β₁. However, if (β₁/β)^4/3 ≫ β₁, the exponent for M_B vs. M_A is expected to approach unity, i.e. .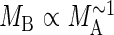

Data gathering and structure

As noted, the model predicts different scaling relationships for M_B vs. M_A depending on the numerical values of the allometric constants and depending on whether secondary tissues accumulate in stems or roots. Therefore, data were gathered with particular attention to whether each particular species is capable of producing woody stems or roots. The capacity for secondary growth was assessed on the basis of species-specific anatomy, or on the basis of the age reported for each particular plant, i.e. plants of woody species that were 1 year old or less were assumed to lack significant quantities of wood.

For woody plants, the large compendium for standing tree body part biomass and annual organ growth rates compiled by Cannell (1982) was used. This compendium redacts approx. 600 published reports on monospecific or mixed communities. It provides data on the number of plants per 1·0 ha (plant density), average plant height, total basal stem cross-sectional area, the total community standing dry weight of leaves, stems or roots and total community annual leaf stem or root biomass production (annual organ growth rates). Because some authors failed to report all of this information, useful data were extracted from a total of 169 communities compiled in the compendium. These data reflect a total of 695 observations because, for particular communities, authors studied sites over the course of many years and thus provide data for different plant densities, water or light conditions, fertilization or thinning regimes, etc. Among the 169 communities, 465 are monotypic and predominantly even-aged stands. The vast majority of the data was from tree-sized (or more rarely, juvenile) dicot and conifer species with self-supporting stems. A few data are from tree-sized monocot (palms and bamboo) species with self-supporting stems. The taxonomic composition of the Cannell compendium is biased in favour of conifer species and monotypic communities. The compendium contains 130 species that are not represented in the data set for non-woody species.

The standing biomass of leaves, stems and roots per ‘average’ plant in each community (and for each observation per community) was computed using the quotient of total community standing organ biomass and plant density; annual leaf, stem and root growth rates were computed by taking the quotient of annual body part biomass production and plant density. The portion of the Cannell (1982) compendium that provided useful data spans eight orders of magnitude in root weight and nine orders of magnitude in above-ground weight.

Although the Cannell compendium provides very limited useful data for the juveniles of woody species (i.e. n = 15), the vast majority of the data for non-woody plants used in this study was collected from the primary literature published between 1987 and 2003. Journals were selected on the basis of the likelihood that dry weight per organ-type would be reported. The volumes of each journal were examined in reverse chronological order to assist in tracking down the older primary literature. Data on annual organ growth rates were also collected (or computed based on reported values of germination and harvest times and standing biomass at the time of harvest). When necessary, all published units were converted into kilogram dry weight per plant (for standing biomass), or into kilogram dry weight per plant per year (for annual growth rates). The new data set represents 125 species not reported in the Cannell (1982) compendium, and spans eight orders of magnitude of above- and below-ground biomass. It should be noted that growth rates for plant less than 1 year old were computed on the basis of the actual age (typically reported in weeks or months). Likewise, the standing biomass for these plants is not necessarily indicative of ‘adult’ size, because many authors harvested plants before the end of the growing season.

Data analyses

Ordinary least squares (OLS) and reduced major axis (RMA) regression and correlation analyses were applied to the raw and the log₁₀-transformed data. OLS analyses were used to establish regression models with root biomass as the ‘predicted’ variable plotted on the ordinate; RMA analyses were used to establish functional allometric (scaling) models for above- and below-ground relationships and to evaluate the predictions of the allometric model, i.e. paired variables were considered as biologically interdependent.

Analyses of regression curve residuals indicated that all of the above- and below-ground relationships reported here were log-log linear. Therefore, the regression curve describing a relationship had the form log Y₂ = log β + αlog Y₁, where Y₂ and Y₁ are the variables plotted on the ordinate and abscissa, respectively, log β is the y-intercept of the regression curve (the allometric constant in RMA analyses) and α is the slope of the regression curve (the allometric or scaling exponent in RMA analyses). The α of the RMA curve was calculated using the formula α_RMA = α_OLS/r, where α_OLS and r are the OLS regression curve slope and the correlation coefficient, respectively; log β of the RMA regression curve was calculated using the formula 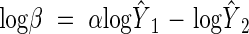, where 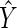denotes the mean value of the variable Y. The 95 % confidence intervals of log β and α were used to evaluate whether these regression curve parameters differed between the new and Cannell (1982) data sets.

The reliability of using M_B vs. M_A OLS regression formulas to predict below-ground biomass based on above-ground measurements was assessed numerically by calculating percentage prediction errors for the regression formula for each of the two data sets, i.e. % Pred. Error = [(Obs. M_B − Pred. M_B)/Pred. M_B] × 100 % (see Smith, 1980). Size-dependent trends in these errors were evaluated visually by plotting errors against above-ground biomass (see Fig. 2A). For these purposes, OLS regression statistics were used, because the objective was to predict M_B based on M_A measurements.

Fig. 2.

Bivariant plots of regression curve percentage prediction error and above- and below-ground quotients (M_A/M_B). (A) Percentage prediction error of the two ordinary least squares regression curves for below- versus above-ground biomass for the Cannell (1982) and new data sets plotted against log-transformed data for above-ground biomass. (B) Log of above- and below-ground biomass quotients plotted against log of total body mass (M_T = M_A + M_B). Data for plants developing from seeds with either large or small material investments (endosperm or cotyledons) are indicated for a limited number of reports.

RESULTS

The model predicts an isometric relationship for M_B vs. M_A across non-woody plants (see eqn 1). Even though it stipulates that the scaling exponent for this relationship can theoretically range between 0·75 and 1·00 for woody plants, the model predicts a near isometric scaling exponent when (β₁/β)^4/3 ≫ β (see eqn 2).

These predictions agreed reasonably well with the trends observed across the entire data set (despite significant differences in the allometric constants for the non-woody and woody plant data sets) and within each of the two data sets (Table 1 and Fig. 1). Across all species, M_B scaled as the 0·941 power of M_A (n = 1406, r² = 0·974, F = 53 071), and the upper 95 % confidence interval for this exponent approached unity (e.g. 0·946; see Table 1). With two exceptions (that can be rationalized), the exponents for all other scaling relationships were consistent with the expectations of the model as well as prior theory and empirical statistical trends (see Niklas and Enquist, 2001, 2002a, b; Enquist and Niklas, 2002).

Table 1.

Summary statistics of reduced major axis regression analyses of log₁₀-transformed data for above- and below-ground standing biomass (M_A and M_B; original units = kg d. wt plant⁻¹) and annual growth rate relationships (G_A and G_B; original units = kg d. wt plant⁻¹ year⁻¹)

	αPred.	αRMA ± s.e	95 % CI	Log βRMA ± s.e	95 % CI	n	r2	F
Across entire database (0·0000003 ≤ MA ≤ 2723 kg d. wt; 0·0000003 kg d. wt ≤ MR ≤ 462·5 kg d. wt)
MB vs. MA	3/4–1	0·941 ± 0·01	0·930–0·946	−0·517 ± 0·01	−0·548 to −0·499	1406	0·974	53071
MB vs. MS	1·0	0·924 ± 0·01	0·900–0·921	−0·386 ± 0·01	−0·391 to −0·361	878	0·975	34784
MB vs. ML	4/3	1·172 ± 0·01	1·154–1·184	0·438 ± 0·02	0·410 to 0·484	847	0·963	21796
GB vs. GA	1·0	0·946 ± 0·01	0·930–0·962	−0·678 ± 0·02	−0·709 to −0·647	406	0·970	12927
GB vs. GS	1·0	0·853 ± 0·01	0·835–0·869	−0·464 ± 0·02	−0·501 to −0·427	406	0·961	10012
GB vs. GL	1·0	0·956 ± 0·01	0·937–0·974	−0·303 ± 0·02	−0·341 to −0·264	426	0·960	10210
Across new data set (0·0000003 ≤ MA ≤ 6·70 kg d. wt; 0·0000003 kg d. wt ≤ MR ≤ 27·3 kg d. wt)
MB vs. MA	1·0	0·955 ± 0·01	0·934–0·974	−0·614 ± 0·03	−0·675 to −0·355	1061	0·883	8025
MB vs. MS	1·0	1·016 ± 0·02	0·976–1·056	−0·332 ± 0·06	−0·447 to −0·216	532	0·839	2765
MB vs. ML	1·0	1·058 ± 0·01	1·027–1·090	−0·054 ± 0·05	−0·144 to 0·037	504	0·891	4083
GB vs. GA	1·0	0·965 ± 0·02	0·920–1·010	−0·569 ± 0·06	−0·684 to −0·454	201	0·901	1812
GB vs. GS	1·0	0·906 ± 0·03	0·848–0·954	−0·398 ± 0·08	−0·558 to −0·238	201	0·841	1052
GB vs. GL	1·0	0·982 ± 0·02	0·935–1·022	−0·326 ± 0·06	−0·443 to −0·209	201	0·901	1999
Across Cannell (1982) data set (0·00126 ≤ MA ≤ 2723 kg d. wt; 0·00043 kg d. wt ≤ MR ≤ 462·5 kg d. wt)
MB vs. MA	3/4–1	0·924 ± 0·01	0·900–0·947	−0·429 ± 0·02	−0·475 to −0·383	345	0·944	5786
MB vs. MS	1·0	0·893 ± 0·01	0·871–0·917	−0·338 ± 0·02	−0·381 to −0·294	346	0·944	5806
MB vs. ML	4/3	1·195 ± 0·02	1·116–1·274	0·598 ± 0·03	0·539 to 0·657	343	0·724	876
GB vs. GA	1·0	1·019 ± 0·02	0·965–1·066	−0·747 ± 0·02	−0·794 to −0·700	205	0·884	1549
GB vs. GS	1·0	0·972 ± 0·02	0·936–1·009	−0·535 ± 0·02	−0·564 to −0·505	205	0·932	2771
GB vs. GL	1·0	0·926 ± 0·03	0·926–1·078	−0·278 ± 0·02	−0·325 to −0·230	205	0·768	671

In each case, P < 0·0001.

α_Pred. = predicted scaling exponent.

Fig. 1.

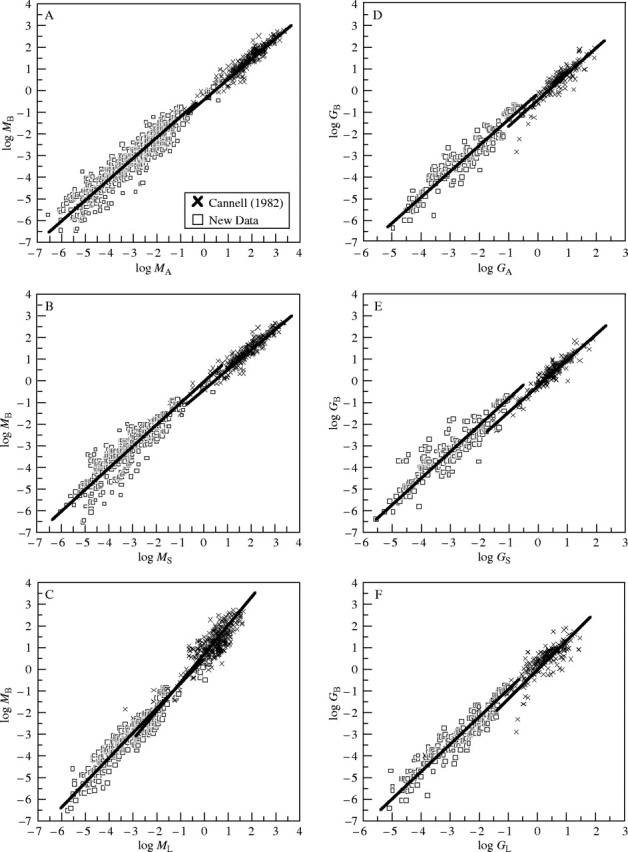
Bivariate plots of log-transformed data for below- and above-ground biomass (M_B and M_A, respectively), stem and leaf biomass (M_S and M_L, respectively), annual below- and above-ground growth rates (G_B and G_A, respectively), and stem and leaf annual growth rates (G_S and G_L, respectively). Solid lines denote ordinary least squares regression curves for the Cannell (1982) and new data sets (for symbols, see insert in A). Summary of statistical trends and parameters is provided in Table 1. (A) Bivariant plot of log M_B vs. log M_A. (B) Bivariant plot of log M_B vs. log M_S. (C) Bivariant plot of log M_B vs. log M_L. (D) Bivariant plot of log G_B vs. log G_A. (E) Bivariant plot of log G_B vs. log G_S. (F) Bivariant plot of log G_B vs. log G_L.

When the data sets for non-woody and woody species were examined separately, the relationship observed for M_B vs. M_A was even more consistent with that predicted by the model. Specifically, the model for non-woody plants predicts M_B ∝ M_A; the allometric constant for this relationship should equal β₄ = β₂/[(β₂ + 1)β₃] (see eqn 1). Analysis of the non-woody plant data set indicated that M_B scales as the 0·955 power of M_B (n = 1061, r² = 0·883, F = 8025). The upper 95 % confidence interval of this exponent is 0·974. Likewise, the empirical numerical value for the allometric constant for this relationship (i.e. β₄, see eqn 1) is 0·243, and its lower and upper 95 % confidence intervals are 0·211 and 0·442, respectively (Table 1). These values include the numerical value predicted by the model, i.e. analyses indicate that β₂ = 0·750 and β₃ = 1·13 such that β₄ = β₂/[(β₂ + 1)β₃] = 0·750/[(0·750 + 1·00)1·13] = 0·379. And, with one exception, the 95 % confidence intervals of all other non-woody scaling exponents include unity, as predicted by the model (Table 1). Likewise, reduced major axis regression of M_B vs. M_A yields log β_RMA = −0·614 such that the empirical numerical value for the allometric constant (i.e. β₄, see eqn 1) is 0·243. The lower and upper 95 % confidence intervals for log β_RMA = −0·614 are −0·675 and −0·355 (Table 1) such that the 95 % confidence intervals for β₄ are 0·211 and 0·442. These values include the numerical value predicted by the model, i.e. regression analyses indicate that β₂ = 0·750 and β₃ = 1·13 such that β₄ = β₂/[(β₂ + 1)β₃] = 0·750/[(0·750 + 1·00)1·13] = 0·379.

For woody plants, the model predicts a scaling exponent between 0·75 and 1·0 depending on the numerical values of β and β₁ (see eqn 2). However, when (β₁/β)^4/3 ≫ β₁ holds true, a near isometric scaling relationship is predicted. Regression analyses of the Cannell (1982) data set indicates that β = 0·232 and β₁ = 0·517. Noting that (β₁/β)^4/3 = 2·91 ≫ β₁ = 0·517, M_B is predicted to scale nearly isometrically with respect to M_B and the allometric constant for M_B vs. M_A is expected to approximately equal (β₁/β)^−4/3 = (0·517/0·232)^−4/3 = 0·344. Empirically, M_B scales as the 0·924 power of M_A (n = 345, r² = 0·944, F = 5786) and the upper 95 % confidence interval of this exponent approaches unity (Table 1). Likewise, reduced major axis regression of M_B vs. M_A for woody species gives log β_RMA = −0·429 (with 95 % confidence intervals of −0·475 and −0·383; see Table 1) and the antilogs of these intervals (i.e. 0·335 and 0·414) include the predicted value (β₁/β)^−4/3 = 0·344.

Finally, in terms of the reliability of using OLS regression curves to predict below-ground biomass based on above-ground measurements, the percentage prediction error across the entire data set ranged between −97·1 and 1994 and had a mean (±standard error) of 38·6 (±4·0) (Fig. 2A). The highest percentage over- and under-estimates were observed for the non-woody plant data set, which had a mean (±s.e.) percentage prediction error of 46·5 (±5·1) that contrasts with woody plants, which had a mean percentage prediction error of 11·9 (±3·4). The reliability of OLS regression formulas for estimating M_B based on M_A measurements therefore increased with increasing above-ground biomass. This tendency was consistent with the difference in M_B/M_A quotients observed for the two data sets (Fig. 2B).

DISCUSSION

A variety of factors may account for the slightly lower than predicted scaling exponent observed for M_B vs. M_A across the entire data set and within each of the data sets. An increased reliance on mycorrhiza for water and nutrient absorption with increasing body size might permit tree species of increasing size to invest a larger portion of their total annual growth into the construction of above-ground organs (leaves and stems). This possibility resonates with the allometric constant for the scaling of annual root growth rate with respect to annual stem growth (Table 1). Although the exponent for this relationship indicates that the annual investments in the construction of new root and stem tissues are nearly proportionally equivalent, the allometric constant for the relationship indicates that the absolute growth rate of roots is nearly one-third that of stems (Table 1). Noting that the stems and roots of woody species continue to accumulate wood as they age, the difference in the absolute annual growth rates of roots and stems would result in a progressive increase in above-ground biomass with respect to below-ground biomass. Curiously, this may contribute to why larger trees become more prone to wind-fall, because the size of their underground anchorage system fails to keep pace with the size-dependent wind drag generated by aerial portions of the plant body (see Niklas et al., 2002; Niklas and Spatz, 2000).

Alternatively, the difference between the observed and predicted scaling exponent for below- versus above-ground biomass for woody plants may be a statistical artefact resulting from a systematic underestimate of root biomass with increasing plant size. This bias would ‘deflate’ the scaling exponent when root biomass is plotted against shoot biomass. In this regard, progressively larger root systems, which are increasingly more difficult to excavate fully, are reported to have disproportionately larger small- and fine-root biomass fractions (Powell and Day, 1991; Makkonen and Helmissar, 2001; Niklas et al., 2002). The annual turnover of these roots may be faster for progressively larger root systems. Studies also suggest that fine root growth and turnover may vary on monthly scales (Baker et al., 2001) and that nonstructural carbon sources (e.g. starch) stored in roots can be mobilized and distributed into above-ground body compartments rapidly (Retslaff et al., 2001). Collectively, these phenomena may explain the slight numerical discrepancy between the observed and predicted scaling exponent for above- versus below-ground biomass (see Table 1) and the discrepancy between the observed and predicted scaling exponent for standing root biomass versus standing stem biomass (Table 1).

An important caveat is that the model presented here is incapable of predicting the numerical values of the allometric constants that dictate the absolute quantities invested for the construction of different body compartments. That these ‘constants’ numerically differ among species is evident from the four orders of magnitude occupied by observed quotients M_A/M_B (Fig. 2A). Inspection of the literature from which these data were gathered indicates that developmental features other than the capacity to form secondary tissues may account for this scatter.

For example, material investment during seed formation appears to contribute to biomass partitioning patterns during the early phase of growth, because seeds with large endosperm or cotyledons are reported to develop, on average, into seedlings with lower M_A/M_B quotients than those from plants developing from seeds with small amounts of endosperm or small cotyledons (see Fig. 2B). This trend is consistent with those reported by Ledig and Perry (1965), Hunt and Burnett (1973) and by Grime and Hunt (1975).

Developmental differences among species undoubtedly contribute to the huge range of M_A/M_B quotients, because the organographic composition of ‘below’- and ‘above’-ground body parts can vary dramatically among taxa and because different workers have used different criteria to establish whether the body compartments of different species are leaves, stems or roots (e.g. Cusset, 1994). For example, the model presented here assumes that below-ground biomass is entirely the result of root growth, and the prior models upon which it rests assume that the sole (or principal) photosynthetic organs are leaves. Yet, many species represented in the data sets for non-woody and woody plants have below-ground stems (rhizomes, corms, etc.), whereas some lack photosynthetically active leaves (Equisetum spp.). In this regard, it is particularly interesting that, regardless of the organographic composition of above- and below-ground body compartments, few if any of these atypical plants deviates from the isometric scaling rule adduced here.

Ecological factors also clearly play an important role. Numerous studies show that growth-limiting conditions or resources typically evoke increased allocations of biomass to the body compartments that are initially most negatively affected by these conditions or limiting resources (see Hunt and Lloyd, 1987, and references therein). In accord with this, plants that are water stressed tend to have lower above- and below-ground quotients compared with those that have access to water; plants grown in high density or shaded conditions tend to have higher above- and below-ground quotients compared with those grown in open conditions (e.g. Crist and Stout, 1929; Milthrope, 1961; Bray, 1963; Monk, 1966).

These and other ontogenetic, phylogenetic and ecological features undoubtedly contributed to the variation observed for M_A/M_B quotients (see Fig. 2B). Likewise, they significantly reduce the reliability of using regression formulas to estimate M_B based on M_A measurements, even in light of the remarkably high correlation coefficients (see Fig. 2A). Indeed, a widely unappreciated aspect of the relationship between the correlation coefficient and the magnitudes of residuals of bivariate regression curves is the fact that correlations must be exceedingly high before any substantial decrease in residual variance is observed (Smith, 1980). For example, the ratio of the standard deviation of residuals to the standard deviation of the original values of the variable plotted on the ordinate axis is 0·44 when r = 0·90 and remains high at 0·14 when r = 0·99. Nevertheless, it is worth noting that the average percentage error for the regression curve pertaining to the Cannell (1982) compendium, which is dominated by data from woody, tree-sized plants is 11·9. Arguably therefore, this regression curve may provide a reasonably good method to estimate (within acceptable limits) below-ground biomass based on above-ground measurements across a broad spectrum of tree species differing in size.