Root System Architecture of Quercus pubescens Trees Growing on Different Sloping Conditions

Abstract

• Background and Aims Plant roots' growth direction has important implications for plant development and survival; moreover it plays an effective and vital role in stabilizing weathered soil on a steep slope. The aim of this work was to assess the influence of slope on the architecture of woody root systems.

• Methods Five mature, single-stemmed Quercus pubescens trees growing on a steep slope and five on a shallow slope were excavated to a root diameter of 1 cm. A very precise numeric representation of the geometry and topology of structural root architecture was gained using a low-magnetic-field digitizing device (Fastrak, Polhemus). Several characteristics of root architecture were extracted by macros, including root volume, diameter, length, number, spatial position and branching order.

• Key Results The diameter at breast height (dbh) was the best predictor of the root volume but had no correlation with length and number of roots. The slope affected the root volume for each branching order, and the basal cross-sectional area (CSA), number and length of the first-order roots. Number and length of the second- and third-order laterals were closely related in both conditions, although this relationship was closer in the shallow trees, suggesting the influence of a genetic control. Sloping trees showed a clustering tendency of the first- and second-order lateral roots in the up-slope direction, suggesting that the laterals rather than the taproots provide much of the anchorage. In a steep-slope condition, the taproot tapering was positively correlated with the asymmetry magnitude of first-order roots, indicating compensation between taproot and main lateral roots' clustering tendency.

• Conclusions These results suggest that on a slope, on clayey soils, root asymmetry appears to be a consequence of several environmental factors such as inclination, shallow-slides and soil compactness. In addition, this adaptive growth seems to counteract the turning moment induced by the self-loading forces acting in slope conditions, and as a consequence improves the tree stability.

INTRODUCTION

It is widely believed that plants respond to mechanical stimulation (Jaffe, 1973; Gartner, 1994). However, until recently (Gartner, 1994; Stokes et al., 1995), little information has been available on the effects of such stimulation on root growth, despite the vital role of root systems in anchoring plants and preventing them from falling over. Moreover, and not less important, plant roots help stabilize forested slopes by providing root strength and by modifying the soil water regime (Burroughs and Thomas, 1977; O'Loughlin and Watson, 1979; Abe and Ziemer, 1991a, b; Watson et al., 1995). In the field, plants are subjected daily to mechanical forces caused by their static loading, wind and slope. The slope is a complex environmental condition that subjects plants to several mechanical stresses, such as the turning moment induced by the combination of the inclination and the weights of the stem and the soil. Hence, the plant undergoes a natural condition of instability where the growth of the shoot itself constantly alters the self-loading condition and induces a mechanical stress in the root system, which must strengthen the anchorage in order to avoid uprooting (Chiatante et al., 2001, 2003a, b). Acknowledging that anchorage is one of the two main functions of the root system (Coutts, 1983, 1987; Coutts et al., 1999), it was suggested that information on the root morphology and architecture of as many species as possible might provide further insight into the way in which form is related to function in root systems (Mickovski and Ennos, 2003). Although there is a voluminous literature on the effects of the soil environment on root architecture (see Coutts, 1987; Canadell et al., 1996), root networks are usually described as a system of laterals and sinkers, which decline in density with depth below the soil surface and with distance out from the trunk. The ongoing development of root patterns (diversity and plasticity) is driven by the interaction between genetically controlled root growth and the influence of exogenous factors, both localized and broad-scaled (Fitter, 1994; Lynch, 1995; Sultan, 1995). Thus, it is very difficult to determine what will be the final architecture of a given root system.

The optimal architecture for an anchorage system is the one that provides a given anchorage force for a minimum investment in structural material (Ennos, 1993). Allocation of assimilates to those parts of the tree under the greatest mechanical stress optimizes the use of available resources to stabilize the tree and counteract the ever-present turning moment induced by the shoot. Development of stem shape and buttresses at the base of the tree are believed to maintain uniform stress over the surface during wind loading (Mattheck and Breloer, 1994).

Adaptive growth below ground may be even more important as a compensatory mechanism to wind- and self-loading, but there is only limited information on biomass allocation between root and shoot (Canadell and Rodà, 1991; Nicoll and Ray, 1996) and within the structural root system of large forest trees (Coutts et al., 1999). For example, although the taproot is the most vigorous root of the young plant, its growth slows down as that of the lateral root increases (Coutts and Nicoll, 1991). Its size eventually becomes insignificant compared with that of the upper lateral roots in both broadleaved (Lyford, 1980) and conifer (Preisig et al., 1979) tree species. The upper lateral roots frequently show an uneven distribution around the trunk base in direct response to several differences in the rooting environment, such as mechanical impedance (Wilson, 1967; Quine et al., 1991) and nutrition, or indirectly to unidirectional dynamic loading such as wind (Stokes et al., 1995, 1997). The assessment of root system symmetry can reveal clearly the presence of a preferred direction of biomass allocation. However, this measurement has never been done on root systems growing in slope conditions. Root system symmetry has previously been measured in terms of centre of mass of all the main lateral coarse roots (Coutts et al, 1990). Root mass can be represented by root diameter (Quine et al., 1991) or root cross-sectional area (CSA; Nicoll and Ray, 1996). Although the same authors recently maintained it was not the ideal way of expressing symmetry (Coutts et al., 1999), the addition of 3D information makes the method better related to biomechanical and environmental factors. A 3D representation has previously been gained with a 3D-digitizer that provides topological and geometrical measurements together with detailed representations of the root system (Sinoquet and Rivet, 1997; Danjon et al., 1999). This device allows the researcher to determine the exact geometric position of any structural root in 3D space.

The aim of this study was to reveal the adaptations at root system level of undisturbed trees (seed origin, single stemmed) of Quercus pubescens to slope conditions. An improvement of the knowledge on root development and form is needed in order to understand the effects of forest practice, such as cultivation treatments, on the growth and, later, on the wind- or slope-stability of the crop (Coutts et al., 1990). Trees grown from bare-rooted plants have been found to be more liable to juvenile instability and basal bow than trees resulting from natural regeneration or grown in special containers that prevent root coiling (Burdett, 1979).

Biomass allocation within the structural root system and symmetry in the first- and second-order laterals were examined. Biomechanical considerations were also included. Seed-origin trees were chosen as it is well-known that coppicing alters root decay (O'Loughlin and Watson, 1979; Watson et al., 1999) and growth (Paukkonen and Kauppi, 1998). In general, these alterations might hide the species-specific responses to mechanical stress. Some aspects of root system biomechanics have been studied for a monocot (Allium porrum; Ennos, 1990), conifer trees of Pinus and Picea genus (Stokes et al., 1995, 1997; Nicoll and Ray, 1996), but information is poor for broadleaved dicot trees. In particular, the root volume was used instead of the root diameter or cross-sectional area (CSA) for the assessment of the centre of mass. Analyses based on cross-sectional area and root volume were compared; the latter parameter was more suitable than a single cross-section to analyse morphological information (bending, strong taper) relative to each single root axis.

MATERIALS AND METHODS

Site details

The study site is located in the Trigno river basin near Trivento (Molise, Italy), on the east side of the central Italian Apennine. The site itself is located on a north-facing slope (580–620 m altitude, latitude 41°43′N, longitude 14°33′E, mean slope of 19°) and is part of a complex of landslides with a varying degree of activity. The climate is montane Mediterranean with dry summers and cool, wet winters. The average yearly rainfall at this site is 656 mm, falling mostly as rain. The mean summer and winter temperatures are estimated to be 22·5 °C and 7·1 °C, respectively.

The formation date of the complex of landslides or its history are unknown, but recent activity is evident at the base of the complex where it is undercut by a stream. This active part encompasses two small secondary landslides that form the main units of the site. One of these landslides is a small slip under open, deciduous woodland and was selected for the sloping experiment site (steep-slope; 14–34°). Adjacent to the sloping area, an almost-flat condition breaking the slope was selected for the control (shallow-slope; 4–5°). Although soil chemical analyses were not done, valid comparisons were nevertheless possible because the control area was contiguous to the sloping area and there was no observable difference in site characteristics.

Mixed Quercus pubescens Willd. (downy or pubescent oak) and Quercus cerris L. (Turkey oak) forests cover most of the area. The forest has been intensively coppiced, and multi-stemmed trees make up a large fraction of the present tree population. The last thinning took place more than 25 years ago, and single-stemmed downy oaks (seed origin) are commonly present, although in low numbers.

Selection and extraction of trees

Ten seed-origin trees (single stemmed), five for each field condition respectively, with an age range between 25–30 years (with the only exception being the 50-year-old tree ‘OS23’) were chosen for the architectural analysis (Table 1). Only trees that had no neighbours in a radius of about 2 m were excavated. Before excavation, the reference to the horizontal plane was determined using two levels perpendicularly positioned on a large calliper and marked around the trunk base with a permanent pen. For all the trees studied, a nail was hammered in at the centre of the trunk-base surface facing magnetic north in order to record the orientation (hereafter referred to as the north point). The slope direction was also recorded. Each tree was then felled at 0·5 m above the root collar and total tree height, diameter at breast height (dbh, 1·30 m) and leader length were recorded. Tree characteristics along with site condition are summarized in Table 1.

Table 1.

Tree size, estimated age and site characteristics of the single-stemmed Quercus pubescens trees growing under the two field conditions

	Shallow-slope									Steep-slope
	OP01	OP02	OP03	OP05	OP07	OS05	OS07	OS23	OS31	OS32
dbh (cm)	13	13	15	10	8	10	10	18	9	7
Height (m)	10·4	9·35	6·1	7·2	6	6·3	6·6	11·5	9·15	5·65
Estimated age (years)	33	25	28	28	30	25	25	50	28	25
Slope angle (degree)	5	5	4	5	5	14	17	18	15	34
Direction from north (degree)	45°W	45°W	45°W	45°W	45°W	0°	34°E	20°E	2°W	21°W

Hydraulic or air-jet excavation was not possible in these areas because the clayey soil is strongly compacted during the summer season, and the use of a logging crane was not suitable for the root system integrity. Ten root systems, five trees for each growth condition, were carefully dug out by hand to an extent of 1·5–2 m in radial distance, 1 m depth and to a root diameter of 1 cm. They were then manhandled clear of the soil and were transported to the laboratory for digitizing. No larger sampling was possible as the excavation by hand was extremely time-consuming in these field conditions; the excavation and digitization of each root system required over 50 h of labour.

Root system architecture measurements

The X, Y, Z position coordinates of roots together with the diameter and the branching structure (i.e. branching and location of the root ends) were measured with a 3D digitiser (3 SPACE Fastrak, Polhemus, VT, USA; Polhemus, 1993) using low frequency electromagnetic field sensing (for details see Danjon et al., 1999). The root system was positioned on three or four woody supports with adjustable height so that the exact horizontalness of the marked line around the stem base could be restored with the north point in the positive X direction. Co-ordinates were determined every 10–20 cm when roots were straight and every 2 cm when roots were highly bent or tapered. All roots with a proximal diameter larger than 2 mm were measured. The original position of the woody oak roots were preserved after excavation, due to the high rigidity of Quercus root wood.

Root system architecture analysis

Calculations. Roots were assumed to be either circular in cross-section or elliptical with the larger diameter usually vertical. In any case, the perimeter of the root cross-section corresponding with each digitized point was manually determined by measuring the length of a thin rope adequately adjusted to the root surface. Root area was calculated by using the diameter of a circle with equal circumference. The output data file was analysed using the AMAPmod software (Godin et al., 1997), which handles topological structure at several scales and also providies 3D graphical reconstruction for data checking. Extracted data were exported to other software to perform specialized processing. The distance between two corresponding measurement points was used as the segment length. The segment volume was calculated as a truncated cone from its length and proximal and distal diameters. The root length or volume was the sum of length or volume of all its segments. The distance to the stump centre was termed ‘radial distance’.

Root symmetry and branching. The symmetry of root systems was evaluated in terms of centre of mass of all the first-order lateral roots using a method similar to that described by Quine et al. (1991) and Nicoll and Ray (1996). Each structural root, defined as a root with diameter larger than 1 cm at a distance of 5 cm from the taproot, was investigated. In this study, root volume replaces root diameter or cross-sectional area (CSA), and three-dimensional analysis is used in place of the limited two-dimensional analysis. In the previous methods, root diameter or CSA were measured only at certain points located at a discrete distance from the stump centre, with consequent loss of information of the root traits between the circles (bending, strong taper). Consequently, the vectorial sum calculated using the diameter or the CSA at a defined radial distance of two roots with equal values for these parameters but different lengths—due to the presence of a bending in one of them—did not indicate any difference between them.

With the method used in this work, the root system was spatially subdivided into concentric hemispheres of different radius at which all first-order root volume was determined. The centre of volume (COV) for an individual tree measured at a defined radial distance has 3D co-ordinates:

where X_i, Y_i and Z_i represent the unweighted cartesian co-ordinates of the interception point of the ith root (i = 1, 2, 3, … n) with a given hemisphere weighted by relative root volume V_i, where:

and v_i is the sum of volume of all the segments of the ith root to the considered radial distance.

Analysis of branching was conducted using the same criteria of the centre of volume, with the number of branching points of the ith root up to a defined radial distance in place of the root volume. In this way, the relative root volume V_i was substituted with B_i, where:

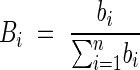and b_i is the sum of all the branching points of the ith root up to the considered radial distance. This method gave a measure of the uniformity of the branching density, named the centre of branching (COB).

These computations were made with Microsoft Visual Basic 6.0. When the origin of the first-order lateral roots is located far from the tree stump centre and roots develop toward the centre, as in the case of a strongly inclined taproot, it becomes difficult to attribute the biomass to a direction of allocation. However, no such cases were detected in this study.

The asymmetry magnitude of a root system in terms of root volume (COV) and root branching (COB) of the first-order laterals was measured as the horizontal distance expressed as a percentage of the reference hemisphere radius. It is given by:

where r is the radius of the reference hemisphere and its orientation is θ = tan⁻¹(X/Y).

Large values of the COV or COB magnitudes indicate that roots tend to cluster or to branch in a preferred direction, respectively, whereas small values imply uniformity around the tree trunk. Within each growth condition, the clustering tendency of the COV of the first- and second-order laterals and the COB of the first-order was evaluated using circular statistical methods, Rao's Spacing test in particular (Mardia and Jupp, 2000); calculations were performed using Oriana software v. 2.01 (Kovach Computing Services; Kovach, 1994). This test takes as its null hypothesis that the data are uniformly distributed. This is tested by seeing if spacing between adjacent points is equal around the circle. Such spacing should be roughly 360°/N (N being the number of observations). If the actual spacings deviate too much from this value, then the likelihood that the data are uniformly distributed is reduced. Differences between the two growth conditions were determined using Watson's U² test. This test is a two-sample test; instead of comparing a set of data to a theoretical distribution, two sets of data are compared using the mean-square deviations. The null hypothesis is that the two samples have the same distribution and a significant P-value (usually 0·05) leads to the rejection of this hypothesis.

Between-growth conditions differences in the various components of below-ground biomass were tested by analysis of covariance, with the dbh as covariate (SPSS Inc., V. 10.0, 2002). When interaction was not significant (P > 0·05), the model was recalculated without it (adjusted ANCOVA).

Soil measurements

Soil resistance to penetration was measured at field capacity with a Pen-ST-308 penetrometer (Effegi, Milan, Italy). It consisted of a manual spring dynamometer with a calibrated scale on the top of the stem. A cylinder with a diameter of 6·4 mm (cross-sectional area 0·322 cm²) was mounted on the measuring end of the penetrometer. Force was applied until the cylinder penetrated 6 mm into the soil, marked on the penetrometer longitudinal surface. Ten measurements were made every 10 cm in depth. The resistance of the soil was then calculated by dividing the penetrometer reading by the cross-sectional area of the cylinder. Soil bulk density measurement was performed using a metal sampling can with a volume of 100 cm³. Three samples along the soil profile, each one 10 cm in depth, were taken for each tree after excavation. Samples were weighed before and after oven drying at 75 °C for 4 d.

The idea behind taking measurements at field capacity was that this is the best-case scenario for roots. Penetration resistance will increase when the soil dries out, and root growth can then be expected to be limited. However, when the moisture content of the soil increases again, penetration resistance will decrease, and root growth will resume.

RESULTS

Root system characteristics

All downy oak had a taproot plus shallow horizontal roots. The major portion of the below-ground biomass in the sampled trees was located immediately below the trunk base, in the root crown. Most of the roots, in fact, were found at a depth less than 0·6 m. The horizontal extension of the whole root system, i.e. including roots thinner than 1 cm, is unknown. Root grafts were occasionally observed between roots of the same tree, but never between roots of different trees. Taproots and all horizontally orientated roots tapered quite rapidly. Only a small number of sinker roots with a small diameter reached the rooting depth of 1 m. The deepest root CSA measured was 6–10 % of the trunk-root base, thus we feel that only a minor part of the root system was left out by restricting the excavation to 1 m depth.

The dbh showed a significant effect on the root volume (ANCOVA, P < 0·001). Total root volume, at a given dbh, was significantly higher in the steep-slope condition (F_1,7 = 7·49, P = 0·03). First-order laterals' volume was similar in steep and shallow slopes. The volume again became significantly higher in the steep-slope for the second- (F_1,7 = 8·79, P = 0·02) and third-order laterals (F_1,7 = 5·66, P = 0·049) (Fig. 1).

Fig. 1.

Regressions of root volume components versus diameter at breast height (dbh) for five Quercus pubescens trees grown in shallow-slope (•) and five in steep-slope conditions (○), calculated within a radial distance of 1 m from the stump centre. Regression equations are as follows, where trv = total root volume; v1–v3 = volume of first-, second- and third-order roots. Shallow slope: (A) trv = 17810·80 + 2560·36dbh; (B) v1 = −14252·30 + 2084·68dbh; (C) v2 = −2743·30 + 391·47dbh; (D) v3 = −763·86 + 80·38dbh. Steep slope: (A) trv = −10912·58 + 2380·12dbh; (B) v1 = −6549·63 + 1644·68dbh; (C) v2 = −3707·82 + 634·39dbh; (D) v3 = −655·12 + 101·04dbh.

No dbh effect was apparent for the root length and the number of laterals for each branching order examined. The number of first-order laterals was significantly higher in the shallow-slope (P < 0·01). There were no differences for the second-order, whereas a reverse pattern emerged for the third-order laterals, with the mean values significantly higher in the steep-slope condition (P < 0·05) (Fig. 2).

Fig. 2.

Number of roots per branching order for Q. pubescens trees growing on a shallow-slope and a steep-slope. Bars are means of five replicates + s.e. Means significantly different at ^*P < 0·05 and ^**P < 0·01 (Student's t-test).

The total length of first-order laterals was significantly higher in shallow-slope conditions (F_1,7 = 14·07, P = 0·007). No differences emerged between the two growth conditions for the higher orders. There was a close relationship between number of roots and total length for all the root orders considered and in both the field conditions, although it was stronger for the shallow-slope trees (Table 2).

Table 2.

Regression equations for the relationship between root length for each branching order (y) and number of roots (x)

	Shallow-slope					Steep-slope
	Regression equation	R2	P	Regression equation	R2	P
1st order	y = 74·52x + 483·91	0·78	<0·001	y = 71·69x + 365·6	0·64	<0·001
2nd order	y = 54·19x − 116·25	0·98	<0·001	y = 37·63x + 496·26	0·56	<0·001
3rd order	y = 42·29x − 16·83	0·95	<0·001	y = 35·57x + 7·95	0·72	<0·001

As the total volume of the first-order roots showed no differences between the shallow and the steep slope conditions although the number was lower in the latter, a different size of these roots was expected depending on the growth conditions. Although in both conditions a greater portion of volume was concentrated in at least one or two roots with the proximal basal CSA markedly higher (weighted values), whatever the dbh considered (Fig. 3), in the steep-slope the weight of these roots was always higher than in the shallow-slope, with the only exception being tree ‘OS07’.

Fig. 3.

Basal cross-sectional area (CSA) of the first-order roots for each Q. pubescens tree grown in shallow (•) and steep (○) slope conditions. Values are weighted for the total CSA for each tree. Symbol size is proportional to the dbh (scale indicated on figure). Total first-order number is reported for each tree. The dotted line is a reference line indicating the maximum value shown by the shallow slope trees.

Root system symmetry, depth and branching

The relationship between the CSA-weighted vector and the volume-weighted vector for a given root was quite close (R² = 0·77, P < 0·001 in steep-slope; R² = 0·61, P < 0·001 in shallow-slope). On the other hand, at a given CSA value there were frequently more volume values, more or less different between them, independently from the tree and slope condition considered (no tree random effect, F_4,213 = 0·102, P = 0·987). In fact, the best-fit line through these data, V = 0·88CSA + 0·01 in steep slope, V = 0·69CSA + 0·01 in shallow slope (where V is volume), had a slope significantly different from 1·0 at the 0·05 level (95 % confidence interval: 0·77–0·97 and 0·6–0·79 respectively).

The COV of the first-order laterals is number- and/or diameter-dependent. For all the steep-slope trees, it was located near the largest roots on the up-slope side of the tree (Fig. 4; Table 3). For the shallow-slope trees, the weights of the first-order roots were quite similar, and thus the resulting vectorial sum was dependent on both parameters. However, even though there was only a slight inclination, the largest laterals were orientated towards the up-slope side of the tree (Fig. 4; Table 3). In steep-slope trees, the COVs for first-order roots showed a clustering tendency (Rao's spacing test, P < 0·01) toward the up-slope side of the tree at all radii considered, ranging from 2·6° to 19·63° (Rao's spacing test, P < 0·01; Table 3, Fig. 4). In shallow-slope trees, the centres of root COV were randomly distributed (Rao's spacing test, P > 0·05), although the mean direction changed from perpendicular to the slope direction when calculated at the 20 cm reference hemisphere (mean vector 69·51° from up-slope), toward up-slope with increasing distance from the stump centre. At the 80 cm reference hemisphere, it became significantly orientated toward the up-slope side of the tree even though the inclination was slight (mean vector 8·46° from up-slope) (Rao's spacing test, P < 0·01). There was no significant difference between the two mean vector directions of the two growth conditions at the 80 cm reference hemisphere (Watson's U² test, P > 0·5).

Fig. 4.

Orientation (circular direction) and weight (radial direction) of all the first-order lateral roots together with the orientation of the centres of volume (COV) for the first- (cross) and second-order (triangle) roots in trees of Q. pubescens. Weight values are expressed as a percentage of the total volume per each tree calculated at the 60 cm reference hemisphere. The slope direction is indicated on the figure.

Table 3.

Parameters of the vectorial circular analysis of the centre of volume (COV) of the first- and second-order laterals and the centre of branching (COB) of the first-order at increasing radial distance (20–80 cm) from the root-stump centre. Rao's test was used to test the uniformity of the distribution. N, number of data; μ, mean vector; r, length of μ; U, Rao parameter with the significance level P. COV and COB are significantly clustered at P < 0·05

Centres	Radii reference hemisphere (cm)	Slope inclination	Number	Mean vector (μ)	Length of mean vector (r)	Circular standard deviation	Rao's spacing test (U)	Rao's spacing test (P)
COV 1st order	20	Steep	5	177·403°	0·914	24·344°	225·118	<0·01
		Shallow	5	249·51°	0·368	81·014°	89·889	>0·50
	40	Steep	5	178·949°	0·951	18·167°	240·768	<0·01
		Shallow	5	195·563°	0·612	56·783°	124·363	>0·10
	60	Steep	5	162·622°	0·932	21·506°	233·195	<0·01
		Shallow	5	176·007°	0·801	38·182°	168·881	>0·05
	80	Steep	5	160·376°	0·921	23·223°	224·468	<0·01
		Shallow	5	171·539°	0·948	18·68°	233·388	<0·01
COB 1st order	40	Steep	5	154·683°	0·56	61·736°	143·777	>0·10
		Shallow	5	311·98°	0·419	75·589°	158·268	>0·10
	60	Steep	5	163·562°	0·974	13·117°	252·3	<0·01
		Shallow	5	250·554°	0·387	78·924°	104·199	>0·50
	80	Steep	5	159·3°	0·91	24·922°	221·53	<0·01
		Shallow	5	207·692°	0·274	92·246°	69·022	>0·90
COV 2nd order	40	Steep	5	230·134°	0·545	63·084°	144·005	>0·50
		Shallow	5	219·772°	0·113	119·589°	55·239	>0·50
	60	Steep	5	226·502°	0·489	68·51°	125·584	>0·50
		Shallow	5	255·001°	0·223	99·234°	60·478	>0·50
	80	Steep	5	212·558°	0·467	70·687°	119·848	>0·50
		Shallow	5	254·283°	0·098	123·516°	88·087	>0·50

The asymmetry magnitude increased with increasing distance from the stump centre in both the growth conditions (Fig. 5). For steep-slope trees, it did not change between 20 and 40 cm, but increased with larger distance, achieving at the 80 cm reference hemisphere a mean value significantly larger than those at 20 and 40 cm. In contrast, in shallow-slope trees, the COV magnitude did not significantly increase with the radial distance. For steep-slope trees, it was always higher than that of shallow-slope trees and this difference became significant only at 80 cm (P < 0·05). This result was relevant as the COV was constrained by the radii selected, but not directly by tree size.

Fig. 5.

Asymmetry magnitude expressed as the ratio between the horizontal distance and the hemisphere ray of the centre of volume (COV) for the first-order lateral roots at different radial distances from the stump centre. Values are means of five replicates analysed by one-way ANOVA. The bars indicate the LSD (P < 0·05) used for all pairwise comparisons.

In steep-slope conditions, the angle of deviation from the vertical (hereafter named ‘vertical deviation angle’) of the COV was significantly wider, i.e. closer to the horizontal plane, than that in shallow-slope at the 60 cm reference hemisphere (Table 4). No such difference was found when the angle of deviation was referred to the normal to the soil surface, i.e. referred to the soil depth. Differences became less if the magnitude in 3D was also taken into account (Table 4).

Table 4.

3D parameters of the centre of volume (COV) calculated at the 60 cm reference hemisphere for trees grown in shallow and steep slope conditions. Values are means of five replicates (±1 s.e.). P-value refers to pairwise t-test at a significance level of α = 0·05

	Shallow-Slope	Steep-slope	P
Vertical deviation angle	22·53 (4·29)	42·53 (7·44)	0·047
Soil–normal deviation angle	18·31 (4·73)	22·93 (7·41)	>0·05
Magnitude 3D	0·483 (0·055)	0·468 (0·042)	>0·05

With respect to the branching density, both steep-slope and shallow-slope trees showed no branching points on the first-order laterals within the radius of 20 cm. Within each growth condition, trees showed a high variability of the COB magnitude, although the direction showed a significant clustering tendency only in steep-slope conditions (Rao's spacing test, P < 0·01) toward 16·15° and 20·7° from up-slope at the 60 cm and 80 cm reference hemispheres, respectively (Table 3). These mean values coincided with those of the centres of volume (Watson's U² test, P > 0·5). The direction of the second-order centres of root COV showed no significant clustering tendency in both growth conditions, whatever the radial distance considered (Rao's test, P > 0·5; Table 3). However, in the steep-slope, the centres of major branching (COB) of the first-order roots and the COV of the second-order roots, calculated at the 60 and 80 cm reference hemisphere, coincided for three of five studied trees (‘OS23’, ‘OS31’ and ‘OS32’) and both were orientated on the up-slope side of the tree, along the self-loading action axis. No such coincidence was found in shallow-slope conditions (data not shown).

Taproot characteristics

The taproot of the largest trees showed a basal enlargement; this was a mass of woody tissue resulting from the more-or-less complete anastomosis of the basal part of the main roots. Moreover, in the largest trees, it was not always clear if it was the primary root or a first-order lateral that formed the observed main axis. Visual observation suggested the presence of a strong taper in most of the studied taproots. Furthermore, the morphology of the main axis seemed to be linked with such tapering. This link was investigated using regressions relating the asymmetry magnitude of the COV and the taproot taper, calculated as the difference between the diameter of the stump base and the diameter of the taproot at the leader length of 50 cm. The regression line indicated that for the steep-slope trees the asymmetry magnitude increased, calculated at the 60 cm reference hemisphere, with the taproot tapering, although this was not quite significant (R² = 0·697, P = 0·078 in steep-slope, R² = 0·106, P = 0·6 in shallow-slope).

Soil characteristics

In order to evaluate whether the soil bulk density and strength affected these results, penetrometer analysis was conducted on soil samples at different depths for both conditions. At the major depth of 25 cm, the bulk density (1·55 ± 0·121 g cm⁻³) was significantly higher than that at 5 cm (1·33 ± 0·102 g cm⁻³) (P < 0·01). There were no significant differences in maximum penetration resistance at the field capacity between the two soil layers (0·443 ± 0·061 MPa and 0·458 ± 0·059 MPa, respectively).

DISCUSSION

First-order laterals were fewer and larger when the slope was steeper. In the shallow slope, the higher number of first-order laterals (with a consequently higher total root length per soil volume) might be explained by the lower turning moment acting on the shoot. In a homogenous soil volume in plane conditions, a taproot system might develop symmetrically with all the uppermost first-order laterals having the same length. Consequently, an increase of the total root length might only be due to an increase of root number. The close relationship found in the present work between the number of root branches and the root length, also for the higher-branching order, is consistent with this hypothesis and the one reported for Norway spruce by Drexhage and Gruber (1998), supporting the theory of an inherent regular branching process, which is evidence of strong genetic control. In contrast, within a soil volume of 1 m³, the pool of coarse roots (>1 cm) up to the third branching order reached the same root length regardless of the growth condition and the tree size.

In both broadleaved (Lyford, 1980) and conifer (Preisig et al., 1979; Gruber, 1994) tree species, the architecture of the root system, depending on soil conditions, can be modified from taproot-type to sinker and superficial root systems. However, in a taproot system, the laterals that grow from the upper part of the taproot (frequently termed surface roots) are—under genetic control—programmed to a plagiogravitropic growth direction (at different angles from the vertical; Coutts and Nicoll, 1991). These laterals are gravi-responsive and in slope condition there is evidence of negative gravitropic growth in those growing up-slope (Marler and Discekici, 1997). On the downhill side of a steep slope, there is evidence to suggest that these roots could grow out from the soil; to avoid death by desiccation, they are obliged to change the growth direction (Coutts and Nicoll, 1991), bending their apex back into the deeper soil layers or beneath the soil surface. A similar behaviour has frequently been observed in partly exposed surface roots of mature Q. pubescens trees growing on steep slopes, which curve right back to the deeper soil layers (A. Di Iorio, pers. obs.). As a consequence of this adaptive growth, the down-slope biomass becomes lower than the up-slope one. From a biomechanical point of view, the up-slope roots' resistance to pull-out and shear stress might become the main component of tree anchorage in this growth condition. Root system architecture, in fact, can be considered as the network of directions followed by ‘self-loading’ forces during their transfer to the ground (Ennos, 1994). For fallen trees, Abe and Ziemer (1991a, b) reported that most of the roots broke near their tips, where the diameter is less than 1–2 cm. This suggests that most roots were pulled out leaving the finest distal portions still embedded in the soil. In general, it was assumed that roots crossing a shear zone generate tensile strength, are elongated in tension, and break at the tips, not in the shear zone. Thus, the mode of root failure is similar to that occurring during a pull-out test (O'Loughlin and Watson, 1979; Abe and Ziemer, 1991a, b). The pull-out resistance increases with the number, radius and length of the roots (Abe and Ziemer, 1991a, b; Ennos, 1993). Consequently, on a steep slope, the optimal architecture might consist of an increase of the total root cross-section and a displacement of the centre of mass (asymmetry indicator) toward the up-slope side of the tree. The results of this study for the steep-slope trees support this hypothesis. In these trees, roots facing down-slope at their emergence from the taproot bent towards up-slope in the younger portion. Even though measurements of nutrients in this work are absent, there was no evidence of uneven nutrition around trees on this site, which could have affected the growth direction of these laterals, as the study trees were all unrelated individuals grown from seed. In this soil type, similar bending could also be due to deformations induced by the tensile or bending stresses following slides, or the response of the plant to ameliorate the tree stability. The numerous crown-shaped cracks observed in the waterlogged soil around the trees after prolonged rainfall led us to favour the slides hypothesis.

Roots share the total cross-section with different weights depending on their size. The centre of mass in terms of volume (COV) takes into account such differences, as it is number- and/or volume-dependent. The results found here for the steep-slope trees showed a volume dependence because the COV is located near the largest roots clustered on the up-slope side of the tree. Roots with smaller volume are arranged approximately evenly around the stem. Even though the displacement of the COV also pointed toward the up-slope side of the tree in shallow conditions, the relative magnitude was significantly higher in the steep-slope. When the COV was referred to the normal to the soil surface, i.e. soil depth, it was located near this axis independently from the slope inclination. These findings are not surprising if the inclination of the taproot or the main axis is considered.

As expected, the root volume growth was closely related to the dbh both in shallow and steep slope conditions. Surprisingly, at a given dbh, the total root volume and the total volume of the second- and third-order laterals assumed values significantly higher in the steep slope, whereas there was no difference for the first-order laterals. In spite of the similar total volume, the number of first-order roots was significantly lower in steep-slope trees. In contrast, these trees had 1–2 of these roots with the basal CSA larger, without any relationship with the dbh. Moreover, even if not quantified, these roots presented an evident eccentricity at their bases, independently from the growth direction (Fig. 6). The cross-sectional shape was similar to the I-beam shape described by Nicoll and Ray (1996) for the conifer Sitka spruce, although the authors located it at greater distance from the taproot. Clearly, such changes have an adaptive value, because the basal diameter tends to increase in those roots laying along the axis of a unidirectional force such as wind (Stokes et al., 1995, 1997); their cross-sections also show oval or girder shapes that can optimize the bending resistance for a given amount of material in the structure (Stokes et al., 1997), reaching a flexural stiffness significantly larger than an equivalent sized circular root (Nicoll, 2000). Moreover, the roots growing in the up-slope direction have a higher stiffness than those extending downhill in several tree species (Schiechtl, 1980). According to these findings, Chiatante et al. (2003b) reported that the lateral roots developing in the down-slope direction show a higher degree of deformation than the laterals developing in the up-slope direction, and the micro-deformations measured in all the first-order roots of plants growing on a steep slope are always higher than those of plants growing on more gentle or shallow slopes. Since, at the field site, the maximum wind speed ranges between 10·5–11·5 ms⁻¹ and its persistence does not exceed 20 h during the year (data from the experimental station located in Trivento, according to the Guide to meteorological instruments and methods of observation, World Meteorological Organization, 1997), the larger basal CSA can only be due to the greater mechanical stress generated by the forces acting on the junction with the taproot of the tree roots facing up-slope. It is not possible to assume that all the present roots are the same ones present during the first years of growth, but in Fraxinus ornus and Quercus cerris a reduction in new primordia emergence during the first years of growth enables biomass accumulation in a reduced number of laterals, which may therefore improve their strength in anchorage (Chiatante et al., 2001).

Fig. 6.

Cross-section of an up-slope lateral root sample of Q. pubescens. The section shown was cut at a distance of 20 cm from the root base. The circle indicates the portion of wood characterized by a visible circular symmetry. The arrows indicate the directions in which wood has been added, probably in response to the mechanical stimulus.

In the trees growing on the steep slope, the results of this study revealed the role played in root anchorage by the second-order laterals. There were no differences in the total number of branching and branches between the two growth conditions examined, but branching points were not evenly distributed. Previous works have reported a branching increase along the wind-action or flexing axes (Stokes et al. 1995; Goodman and Ennos, 1998), or the slope direction in a young shrub (Chiatante et al., 2003a). Our findings showed many similarities with those to wind action, but add several important details. In three of five steep-slope trees, the centre of major branching of first-order coincided with the centre of mass (volume) of second-order roots. Furthermore, both centres were orientated on the up-slope side of the tree, along the self-loading action axis. In the shallow slope, the two centres did not coincide, and their orientation differed from tree to tree. Undoubtedly these results highlight the contribution of second-order laterals to the overall up-slope cross-sectional area increase.

Goodman and Ennos (1999) found that the taproot of sunflower tapered more rapidly in strong soil than in weak soil. Moreover, the basal diameter of the first-order lateral roots was generally thicker in the former than in the latter. In this study, the bulk density measured at 25 cm in depth (1·55 ± 0·121 g cm⁻³) was very high. It is well known that roots require oxygen, moisture and nutrients so they will not, in most instances, grow in soil that is poorly aerated, highly compacted or very dry (Helliwell, 1995). The results of this study are comparable to those of Goodman and Ennos (1999), but also revealed a close positive correlation between the tapering of the taproot and the asymmetry magnitude of the first-order laterals for the steep slope trees. Furthermore, branching points appeared over the 25–30 cm distance from the stump centre, in contrast with what was found for Norway spruce by Stokes and Mattheck (1996) who found a higher branching rate nearer the stem base. These differences are probably related to the genus or, on a broader scale, to the family that these species belong to. Their results showed that slightly tapered lateral roots in plate root systems were relatively stronger further away from the stem than the highly tapered laterals in heart and taproot systems. The high rate of branching near the stem, or large, rigid main taproot, found in heart and taproot systems, respectively, allows a faster dissipation of forces nearer the stem; therefore a high investment in strength further along the root is not necessary (Stokes and Mattheck, 1996). However, the stronger the taper, the shorter the lever arm will be (see references in Coutts et al., 1999). In the present study, most of the root biomass was concentrated in several large roots asymmetrically clustered, and the branching points were located further away from the stump. In consequence, the lever arm increased its length and the tree's resistance to the turning moment induced by slope, implying that the response to slope condition is the main effect involved.

The results of this study fit well to the Ennos model (1993), which expects a shorter taproot with an increased number of fibrous roots at its bottom. In the present work, larger surface roots took the place of those at the bottom; biomechanically, it is clear that having stronger laterals will further reduce the optimum length of the taproot.

In conclusion, mature Q. pubescens trees growing on clayey soils showed a root system architecture with intermediate behaviour between a taproot and superficial root system. The methods developed and used in this study worked well in revealing the root system architecture in the mature Q. pubescens trees in response to the slope condition. The results of this investigation suggest that, at least to an extent, in steep slope conditions root asymmetry appears to be a consequence of several environmental factors, such as inclination, shallow-slides and soil-compactness. Thus, the adaptive growth of structural roots of the shallowly rooted trees studied counteracts the self-loading forces acting in slope conditions and as a consequence improves tree stability. It must be acknowledged, however, that the results of such experiments remain strongly contingent upon the soil type considered and further investigations in different soil conditions are necessary.